图论习题一精编版
电子科技大学-图论第一次作业-

课本习题一:
4. 证明下面两图同构。
v1
u1
v2
v6
v10 v5
v7
v8 v9
v3
v4 (a)
u6 u5
u2
u8
u10
u3
u7
u9
u4
(b)
证明:作映射 f : vi ↔ ui (i=1,2….10)
容易证明,对vi v j E ((a)),有 f (v i vj,),,ui,uj,,E,((b))
中不
3.设 G 是阶大于 2 的连通图,证明下列命题等价:
(1)
G 是块
(2)
G 无环且任意一个点和任意一条边都位于同一
个圈上;
(3)
G 无环且任意三个不同点都位于同一条路上。
: 是块,任取 的一点 ,一边 ,在 边插入一点 ,使得 成为两条边,由此 得到新图 ,显然 的是阶数大于 的块,由定理 4, 中的 u,v 位于同一个 圈上,于是 中 u 与边 都位于同一个圈上。
件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图
有 11 个。
11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)
不是图序列。
证明:由于 7 个顶点的简单图的最大度不会超过 6,因此序列(7,6,5,4,3,3,2)不
是图序列;
(6,6,5,4,3,3,1)是图序列
(G1) 2 最小边割{(6,5),(8,5)} {(6,7),(8,7)}{(6,9),(8,9)}
1j 10 ) 由图的同构定义知,图(a)与(b)是同构的。
5.证明:四个顶点的非同构简单图有 11 个。
证明:设四个顶点中边的个数为 m,则有:
图论课后习题答案

图论课后习题答案图论是数学中的一个分支,主要研究图的结构和性质。
图论的课后习题通常包括证明题、计算题和应用题。
下面给出一些典型的图论课后习题答案:1. 证明题:证明一个图是连通的当且仅当它的任意两个顶点都存在一条路径相连。
答案:首先定义连通图的概念:一个图是连通的,如果对于任意两个顶点,都存在一条路径将它们连接起来。
接下来,我们证明两个方向:- 如果一个图是连通的,那么对于任意两个顶点\( u \)和\( v \),根据定义,必然存在一条路径\( P \)将它们连接起来。
- 反之,如果对于任意两个顶点\( u \)和\( v \),都存在一条路径将它们连接起来,那么我们可以构造一个从任意顶点\( u \)出发,访问图中所有顶点的路径,这表明图是连通的。
2. 计算题:给定一个有\( n \)个顶点的完全图,计算它的边数。
答案:在完全图中,每个顶点都与其他所有顶点相连。
因此,对于一个顶点,它将与\( n-1 \)个其他顶点相连。
但是,每条边被计算了两次(因为它连接了两个顶点),所以边数应该是\( \frac{n(n-1)}{2} \)。
3. 应用题:在一个社交网络中,每个用户可以与其他人建立联系。
如果一个用户与至少一半的用户建立了联系,那么这个社交网络是连通的吗?答案:是的,这个社交网络是连通的。
假设社交网络中有\( n \)个用户,如果一个用户与至少\( \lceil \frac{n}{2} \rceil \)个用户建立了联系,那么我们可以构造一条从任意用户\( u \)到这个中心用户的路径。
由于中心用户与至少一半的用户建立了联系,我们可以继续通过这些联系到达其他用户,从而证明社交网络是连通的。
4. 证明题:证明在任何图中,边数至少是顶点数减一。
答案:考虑一个图的生成树,它是一个最小的连通子图,包含图中的所有顶点,并且没有环。
在生成树中,边数等于顶点数减一。
由于任何图都至少包含一个生成树,因此原图的边数至少与生成树的边数相同,即至少是顶点数减一。
图论习题课
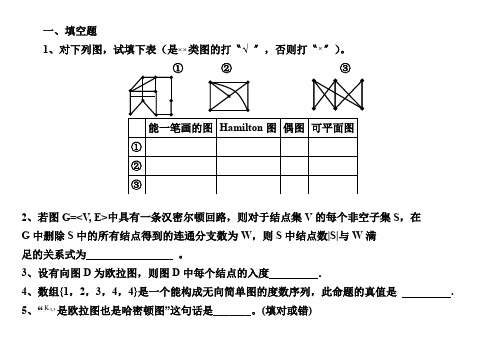
一、填空题1、对下列图,试填下表(是⨯⨯类图的打〝√ 〞,否则打〝⨯〞)。
① ② ③2、若图G=<V , E>中具有一条汉密尔顿回路,则对于结点集V 的每个非空子集S ,在 G 中删除S 中的所有结点得到的连通分支数为W ,则S 中结点数|S|与W 满 足的关系式为 。
3、设有向图D 为欧拉图,则图D 中每个结点的入度 .4、数组{1,2,3,4,4}是一个能构成无向简单图的度数序列,此命题的真值是 .5、“3,3K 是欧拉图也是哈密顿图”这句话是_______。
(填对或错)6、极大可平面图的每一个面的次数都是_________.7、5阶完全图的边连通度是.8、图G是2-色的当且仅当G是.二、选择题1、下列无向图可能不是偶图的是( )(A) 非平凡的树(B)无奇圈的非平凡图(C) n(1)n 方体图(D) 平面图2、关于平面图,下列说法错误的是( )(A) 简单连通平面图中至少有一个度数不超过5的顶点;(B)极大外平面图的内部面是三角形,外部面也是三角形;(C) 存在一种方法,总可以把平面图的任意一个内部面转化为外部面;(D) 平面图的对偶图也是平面图。
3、已知图G的邻接矩阵为,则G有().A.5点,8边B.6点,7边C.6点,8边D.5点,7边4、设图G=<V, E>,则下列结论成立的是( ).A.deg(V)=2∣E∣B.deg(V)=∣E∣C.EvVv2)deg(=∑∈D.EvVv=∑∈)deg(5、设完全图K n有n个结点(n≥2),m条边,当()时,K n中存在欧拉回路.A.m为奇数B.n为偶数C.n为奇数D.m为偶数6、设G是连通平面图,有v个结点,e条边,r个面,则r= ( ).A.e-v+2 B.v+e-2 C.e-v-2 D.e+v+27、下列定义正确的是( ).A含平行边或环的图称为多重B不含平行边或环的图称为简单图C含平行边和环的图称为多重D不含平行边和环的图称为简单图8、以下结论正确是( ).A仅有一个孤立结点构成的图是零图B无向完全图Kn每个结点的度数是nC有n(n>1)个孤立结点构成的图是平凡图D图中的基本回路都是简单回路9、下列数组能构成简单图的是( ).(A) (0,1,2,3) (B) (2,3,3,3) (C) (3,3,3,3) (D) (4,2,3,3)10、n阶无向完全图Kn中的边数为().(A) 2)1(+nn(B) 2)1(-nn(C) n (D)n(n+1)11、以下命题正确的是( ).(A) n(n≥1)阶完全图Kn都是欧拉图(B) n(n≥1)阶完全图Kn都是哈密顿图(C) 连通且满足m=n-1的图<V,E>(∣V∣=n,∣E∣=m)是树(D) n(n≥5)阶完全图Kn都是平面图12、下列结论不正确是( ).(A) 无向连通图G是欧拉图的充分必要条件是G不含奇数度结点(B) 无向连通图G有欧拉路的充分必要条件是G最多有两个奇数度结点(C) 有向连通图D是欧拉图的充分必要条件是D的每个结点的入度等于出度(D) 有向连通图D有有向欧拉路的充分必要条件是除两个结点外,每个结点的入度等于出度13、无向完全图K4是().(A)欧拉图(B)哈密顿图(C)树(D)平面图14、在如下各图中()欧拉图。
《图论》练习题201410

《图论》练习题(2014)1、利用Dijkstra 算法求下图中顶点0v 到其它各顶点的距离,并写出到顶点8v 的最短路。
2、1、列出色数3为的三个图: 。
2、p 阶完全图的色数为: 。
3、p 阶树的邻接多项式为: 。
4、p 阶完全图的邻接多项式为: 。
5、如下图所示的图的邻接矩阵为 ,关联矩阵为 。
6、度序列为(2,2,2,2,2,2)的简单图是 。
7、是否存在度序列为(2,2,3,4,5,6),(1,2,3,4,4,5)的简单图?若存在,给出一个图;若不存在,请说明理由。
8、画出如下图的所有生成子图。
9、设图G 如下图所示,求该图的生成树个数)(G 。
v 2v 6v 4v 610、已知图G (V 、E ),画出G -V 5,G -v 3v 4,G[{v 2,v 3,v 5}],G[{v 3v 4,v 4,v 6,v 7v 8}]G :11、已知图G 的邻接矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2111102112011111A ,画出G ,并求出度序列。
12、证明:偶图G 的任意子图H 仍为偶图。
13、证明:设图G (V 、E )的度序列为(p d d d ,,,21 ),边数为q ,则q i d pi 21==∑14、证明:在任何图中,奇顶点个数为偶数。
15、证明:整数序列(6,6,5,4,3,3,1)不可能为一个简单图的图序列。
16、证明顶点度数均为2的简单连通图是圈。
17、证明非平凡树T 的边连通度为'()1T κ=。
18、n 阶完全图n K 的连通度为()1T n κ=-。
19、设G 是一个p 阶图,且()()21,-≥∈∀p v d G V v ,则G 连通图。
20、若图G 是 不连通的,则其补图G C 是连通的。
21、证明:设G 是由1G 和2G 两个连通分支组成的图,则);();();(21x G P x G P x G P =。
v 1v 2v 3v 4v 5v 6v 8v 722、证明:设G 是由1G 和2G 两个连通分支组成的图,则)}(),(max{)(21G G G χχχ=。
图论习题课
三、简答题(每小题5分,共20分)
2. 给出集合X={1,2,3,4,5,6}上的一个等价关系 R (3分)
并给出他们的等价类
(2分)
22
三、简答题(每小题5分,共20分)
3.集合A={3, 4, 12, 24, 36}, A在整除关系“|” 下构成一个偏序集(A, |),
请画出偏序集(A, |)的哈斯图。(5分)
3
习题
6(P209).在一个有n个人的宴会上,每个人至少有m 个朋友(2m n)。试证:有不少于m+1个人,使 得他们按某种方法坐在一张圆桌旁,每人的左右均是他 的朋友。
证明: 把n个人作为n个顶点,是朋友的顶点间连边构成图 图GG的每个顶点的度数都大于等于m 原题的意思是每个顶点的度数都不小于m的图必有长 度至少为m+1的圈。
是 m=
10(P228n).证明具有奇数个顶点的偶图不是哈密顿 图?
9
习题
1(P216).若图G不是连通图,则GC是连通图, 证明:
由于G不连通,假设G有两个分支,V1和V2,分别有m 和n个顶点。
在GC V1和V2任意两点间都有边; 对于任意顶点u和v,假如u和v在G中位于两个分支中, u和v在GC中必有边相连; 否则假设都位于V1中,设w是V2中顶点, u和v在GC 中都与w邻接,因次u与v之间有路。
......
31
17
考试题型
一、选择题 20分 二、判断题 10分 三、简答题 40分 四、证明题 15分 五、计算题 15分
18
一、填空题(每小题2分,共20分)
1. 集合的 表述方法能够引起悖论。
2. 自反关系在关系图中的特ห้องสมุดไป่ตู้是 。
图论习题答案

图论习题答案
《图论习题答案》
图论作为数学中的一个重要分支,研究的是图的性质和图之间的关系。
在学习
图论的过程中,我们常常会遇到各种各样的习题,通过解答这些习题可以帮助
我们更好地理解图论的知识。
下面就让我们来看一些图论习题的答案吧。
1. 问:一个图中有多少条边?
答:一个图中的边数可以通过计算每个顶点的度数之和再除以2来得到。
2. 问:一个图中有多少个连通分量?
答:一个图中的连通分量可以通过使用深度优先搜索或广度优先搜索来求得。
3. 问:一个图中是否存在欧拉回路?
答:一个图中存在欧拉回路的充分必要条件是每个顶点的度数都是偶数。
4. 问:一个图中是否存在哈密顿回路?
答:一个图中存在哈密顿回路的判定是一个NP难题,目前还没有有效的多项式时间算法。
5. 问:一个图中的最小生成树有多少条边?
答:一个图中的最小生成树的边数恰好等于顶点数减一。
通过解答这些图论习题,我们可以更好地掌握图论的基本概念和算法。
图论不
仅在数学领域有着重要的应用,而且在计算机科学、电信网络等领域也有着广
泛的应用。
因此,熟练掌握图论知识对我们的学习和工作都有着重要的意义。
希望通过本文的分享,能够帮助大家更好地理解图论知识,提高解决问题的能力。
同时也希望大家在学习图论的过程中能够多多练习,勇于挑战各种各样的
图论习题,不断提升自己的图论水平。
祝大家在图论的学习道路上取得更大的
进步!。
图论1-3藏习题解答

学号:0441 姓名:张倩 习题14.证明图1-28中的两图是同构的证明:将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )?u i (1? i ? 10)容易证明,对?v i v j ?E((a)),有f(v i v j )?u i u j ?E((b)) (1? i ? 10, 1?j? 10 ) 由图的同构定义知,图1-27的两个图是同构的。
5.证明:四个顶点的非同构简单图有11个。
证明:设四个顶点中边的个数为m ,则有: m=0:m=1 :(a)v 2 v 3u 4u (b)m=2:m=3:m=4:m=5:m=6:因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。
11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。
证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列;(6,6,5,4,3,3,1)是图序列()11123121,1,,1,,,=d d n d d d d d π++---L L 是图序列(5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。
12.证明:若δ≥2,则G 包含圈。
证明 只就连通图证明即可。
设V(G)={v1,v2,…,vn},对于G 中的路v1v2…vk,若vk 与v1邻接,则构成一个圈。
若vi1vi2…vin 是一条路,由于?? 2,因此,对vin ,存在点vik 与之邻接,则vik?vinvik 构成一个圈 。
17.证明:若G 不连通,则G 连通。
证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支,显然u 与v 在_G 中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,则u 与w ,v 与w 分别在_G 中连通,因此,u 与v 在_G 中连通。
离散数学——图论部分习题课

之和为24,而图G中其余点的度数小于3,即图G中其余点的
度数只可能是2或1(由于图G是连通图,所以无零度点). 由此可知,图G中至少有11个顶点: 3个4度点,4个3度点和 4个2度点; 至多有15个顶点: 3个4度点,4个3度点和8个1
度点.
7. 设G1,G2,G3,G4均是4阶3条边的无向简单图,
n ( n 1) 2
即m=n(n-1)/4, 而m为正整数,所以要么n=4k或n=4k+1, 所以不存在3个顶点和6个顶点的自补图.
9. 设有向简单D的度数列为2,2,3,3,入度列为 0,0,2,3,试求D的出度列。 解:设有向简单图D的度数列为2,2,3,3, 对应的顶点分别为v1,v2,v3,v4,
(1)1,1,2,3,5 (3)1,3,1,3,2 答案(2) (2)1,2,3,4,5 (4)1,2,3,4,6
Байду номын сангаас
)
则它们之间至少有几个是同构的? 解: 4阶3条边非同构的无向简单图共有3个,因此 G1,G2,G3,G4中至少有2个是同构的。
8. 是否存在3个顶点和6个顶点的自补图? 解: 由于顶点为n的无向完全图的边数为
n ( n 1) 2
.
设G的自补图为G’,则G与G’的边数相等. 设它们的边数各为m,于是有m+m=
本章重点
一、掌握有关图的基本概念:
邻接 关联 有向图
平行边 多重图
无向图
n阶图
底图
连通图
自回路(环) 简单图
二、掌握图中顶点的度数,握手定理及其推论 定理:设图G是具有n个顶点、m条边的无向图, 其中点集V={v1, v2,… vn }, 则
deg(
i 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
……………………………………………………………最新资料推荐………………………………………………… 1 离散数学图论部分综合练习辅导 图论作为离散数学的一部分,主要介绍图论的基本概念、理论与方法。教学内容主要有图的基本概念与结论、图的连通性与连通度、图的矩阵表示、最短路问题、欧拉图与汉密尔顿图、平面图、对偶图与着色、树与生成树、根树及其应用等。 本次综合练习主要是复习这一部分的主要概念与计算方法,与集合论一样,
也安排了五种类型,有单项选择题、填空题,判断说明题、计算题、证明题。这样的安排也是为了让同学们熟悉期末考试的题型,能够较好地完成这一部分主要内容的学习。下面分别讲解。 一、单项选择题 1.设图G的邻接矩阵为
0101010010000011100000100
则G的边数为( ). A.5 B.6 C.3 D.4 正确答案:D 上学期的作业中,有的同学选择答案B。主要是对邻接矩阵的概念理解不到位。我们复习定义: 定义3.3.1 设G=是一个简单图,其中V={v1,v2,…, vn},则 n阶方阵A(G)=(aij)称为G的邻接矩阵.其中各元素
jivvvvajijiij不相邻或与相邻与01
而当给定的简单图是无向图时,邻接矩阵为对称的.即当结点vi与vj相邻时,结点vj与vi也相邻,所以连接结点vi与vj的一条边在邻接矩阵的第i行第j列处和第j行第i列处各有一个1,题中给出的邻接矩阵中共有8个1,故有82=4条边。 2.设图G=,则下列结论成立的是 ( ).
A.deg(V)=2E B.deg(V)=E C.EvVv2)deg( D.EvVv)deg(
正确答案:C 该题主要是检查大家对握手定理掌握的情况。复习握手定理: 定理3.1.1 设G是一个图,其结点集合为V,边集合为E,则 VvEv||2)deg(
3.图G如右图所示,以下说法正确的是 ( ) .
a b
d f ……………………………………………………………最新资料推荐………………………………………………… 2 A.{(a, d)}是割边 B.{(a, d)}是边割集 C.{(d, e)}是边割集 D.{(a, d) ,(a, c)}是边割集 正确答案:C 上学期许多同学选择答案A。主要是对割边、边 割集的概念理解不到位。复习割边、边割集的定义: 定义3.2.9 设无向图G=为连通图,若有边集E1E,使图G删除了E1的所有边后,所得的子图是不连通图,而删除了E1的任何真子集后,所得的子图是连通图,则称E1是G的一个边割集.若某个边构成一个边割集,则称该边为割边(或桥) 如果答案A正确,即删除边(a, d)后,得到的图是不连通图,但事实上它还是连通的。因此答案A是错误的。 4.设G是连通平面图,有v个结点,e条边,r个面,则r= ( ). A.e-v+2 B.v+e-2 C.e-v-2 D.e+v+2 正确答案:A 该题主要是检查大家对平面图的欧拉定理的理解情况。 定理4.3.2(欧拉定理) 设连通平面图G的结点数为v,边数为e,面数为r,则下列欧拉公式成立. v-e+r =2 5.无向图G存在欧拉通路,当且仅当( ).
A.G中所有结点的度数全为偶数 B.G中至多有两个奇数度结点 C.G连通且所有结点的度数全为偶数 D.G连通且至多有两个奇数度结点 正确答案:D 上学期许多同学选择答案C。主要是将题中的“欧拉通路”误认为“欧拉回路”了。其实应该运用定理4.1.1进行选择,才是正确的。复习定义和定理: 定义4.1.1 给定无孤立结点图G,若存在一条路经过图G的每条边一次且仅一次,则该路称为欧拉路; 若存在一条回路经过图G的每条边一次且仅一次,在该回路称为欧拉回路; ……
定理4.1.1 无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或2个奇数度数的结点. 推论 一个无向图具有一条欧拉回路,当且仅当该图是连通的,并且它的结点度数都是偶数. 所以,正确答案应该是D. ……………………………………………………………最新资料推荐………………………………………………… 3 6.设G是有n个结点,m条边的连通图,必须删去G的( )条边,才能确定G的一棵生成树. A.1mn B.mn C.1mn D.1nm 正确答案:A 上学期许多同学选择答案D。主要是把定理5.1.1给出的图T为树的等价定义之一是图T连通且e=v-1中的公式用错了.大家只要把m代入公式e=v-1中的e,把n代入公式e=v-1中的v,可以知道答案A是正确。 定理5.1.1 给定图T,则以下关于图T为树的定义等价. (1)无回路的连通图. (2)无回路且e=v-1,其中e是边数,v是顶点数. (3)连通且e=v-1. (4)无回路,但增加任一新边,得到且仅得到一个回路. (5)连通,但删去任一边后图便不连通.(v≥2) (6)每一对顶点之间有且仅有一条路.(v≥2) 定理5.1.1的六个等价定义,大家应该熟记的.最主要的是:无向简单图G是棵树,当且仅当G连通且边数比结点数少1. 二、填空题
1.已知图G中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G的边数是 . 应该填写:15 主要检查大家对握手定理掌握的情况。 定理3.1.1(握手定理) 设G是一个图,其结点集合为V,边集合为E,则
VvEv||2)deg(
因为图G中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,即Vvv3044332211)deg(,所以边数有152/30E。
问:若无向树T中有8个结点,4度,3度,2度的分 支点各一个,那么T的树叶数为多少? 2.设给定图G(如右图所示),则图G的点割集是 . 应该填写:{f},{c,e} 上学期许多同学填错答案主要对点割集的概念理解 不正确。 定义3.2.7 设无向图G=为连通图,若有点集V1V,使图G删除了V1
的所有结点后,所得的子图是不连通图,而删除了V1的任何真子集后,所得的子
图是连通图,则称V1是G的一个点割集.若某个结点构成一个点割集,则称该结点为割点.
c a b
e d f ……………………………………………………………最新资料推荐…………………………………………………
4 上学期许多同学填写的{f,c},主要是没有完全理解定义3.2.7,因为{f}是{f,c}的真子集,而删除{f}后,图是不连通的。 3.设无向图G=是汉密尔顿图,则V的任意非空子集V1,都有 V1. 应该填写:W(G- V1) 因为具有汉密尔顿回路的图称为汉密尔顿图.而由 定理4.2.1 若图G=中具有一条汉密尔顿回路,则对于结点集V的每个非空子集S均有W(G-S) |S|成立,其中W(G-S)是(G-S)中连通分支数. 因此应该填写:W(G- V1).
4.设有向图D为欧拉图,则图D中每个结点的入度 . 应该填写:等于出度 如果大家记住“具有欧拉回路的图称为欧拉图”和定理4.1.2:一个有向图具有单向欧拉回路,当且仅当它是连通的,且每个结点的入度等于出度.大家一定能填写出正确答案的。 5.设完全图Kn有n个结点(n2),m条边,当 时,Kn中存在欧拉回路. 应该填写:n为奇数 上学期许多同学填错答案主要对完全图的概念理解不正确。 定义3.1.6 简单图G=中,若每一对结点间都有边相连,则称该图为完全图.有n个结点的无向完全图记为Kn. 由定义可知,完全图Kn中的任一结点v到其它结点都有一条边,共有n-1
条边,即每个结点的度数是n-1,当n为奇数时,n-1为偶数。 由定理4.1.1的推论可知,应该填写:n为奇数。 6.给定一个序列集合{1,01,10,11,001,000},若去掉其中的元素 ,
则该序列集合构成前缀码. 应该填写:1 因为在二进制中1是10和11的前缀。而前缀码的定义是(定义5.2.10):给定一个序列集合,若没有一个序列是另一个序列的前缀,该序列集合称为前缀码. 填写该题答案时大家一定要对前缀码的定义理解非常清楚。
问:若把序列集合中的1换成0,应该去掉哪个元素? 三、判断说明题 1.给定两个图G1,G2(如下图所示): (1)试判断它们是否为欧拉图、汉密尔顿图?并说明理由. (2)若是欧拉图,请写出一条欧拉回路.
v1 ……………………………………………………………最新资料推荐………………………………………………… 5 分析:先复习欧拉图的判别定理和汉密尔顿图的定义: 定理4.1.1的推论:一个无向图具有一条欧拉回路,当且仅当该图是连通的,并且它的结点度数都是偶数. 定义4.2.1:若存在一条回路经过图G的每个结点一次且仅一次,则该回路称为汉密尔顿回路;具有汉密尔顿回路的图称为汉密尔顿图. 解:(1)图G1是欧拉图. 因为图G1中每个结点的度数都是偶数. 图G2是汉密尔顿图. 因为图G2存在一条汉密尔顿回路(不惟一): a(a, b)b(b, e) e(e, f) f (f, g) g(g, d) d(d, c) c(c, a)a 问题:请大家想一想,为什么图G1不是汉密尔顿图,图G2不是欧拉图。 (2)图G1的欧拉回路为:(不惟一): v1(v1, v2) v2 (v2, v3) v3 (v3, v4) v4 (v4, v5)v5 (v5, v2) v2 (v2, v6)v6 (v6, v4) v4 (v4, v1)v1 (上学期的学生在书写欧拉回路时不规范,大家要按照正确的方法写法。) 2.判别图G(如右图所示)是不是平面图, 并说明理由. 分析:平面图的定义是 定义4.3.1 设G=是一个无向图, 如果能把G的所有结点与边画在平面上,并且 使得任何两条边除端点外没有其他的交点,则 称G是一个平面图(也称可平面图). 显然平面图的边与边只在结点处相交.
解:图G是平面图. 因为只要把结点v2与v6的连线(v2, v6)拽 到结点v1的外面,把把结点v3与v6的连线 (v3, v6)拽到结点v4, v5的外面,就得到一个平 面图. 注意:定理4.3.3 设G是一个有v个结点e条边 的连通简单平面图,若v≥3,则e≤3v-6. 会用于判断不是平面图。
四、计算题 1.设图GV,E,其中Va1, a2, a3, a4, a5,
v2
v3 v
4
v5
v6
v5
v1 v
2
v4
v6
v
3
v5
v1
v
2
v4
v6
v
3
