2015年秋新人教版八年级数学上册名师课堂练习13.2.1画轴对称图形.doc
八年级数学上册第13章轴对称13.2画轴对称图形第1课时画轴对称图形课件新版新人教版

直平分 .
画轴对称图形 几何图形都可以看成是由点组成.对于某些图形,只要画出图形中的 一些
特殊点(如线段端点)的对称点
轴对称图形.
,连接这些对称点,就可以得到原图形的
自我诊断 作已知点关于某直线的对称点的第一步是( C ) A.过已知点作一条直线与已知直线相交 B.过已知点作一条直线与已知直线平行 C.过已知点作一条直线与已知直线垂直 D.不确定
解:如图.
6.作出△ABC 关于直线 l1 的轴对称图形△A1B1C1,然后再作出△A1B1C1 关于 l2 的轴对称图形△A2B2C2.
解:略.
1.分别以直线 l 为对称轴,所作轴对称图形错误的是C′关于直线 MN 对称,其中 A、A′是一组对称点, B 与 B′、C 与 C′是对称点,则 AA′ ⊥ MN,线段 AA′、BB′、CC′都被 MN 垂直平分 .
3.在图中,画出△A′B′C′,使△A′B′C′与△ABC 关于 l 成轴对称 图形.
数学 八年级 上册•R
2018秋季
第十三章 轴对称
13.2 画轴对称图形
第1课时 画轴对称图形
轴对称图形的性质 由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图 形的 形状 、 大小 完全相同;新图形上的 每一点 都是原图形上的某一 点关于直线 l 的 对称点 ;连接任意一对 对应点 的 线段 被 对称轴垂
解:
4.如图,△AOD 关于直线 l 进行轴对称变换后得到△BOC,则以下结论中 不正确的是( D ) A.∠1=∠2 B.∠3=∠4 C.l 垂直平分 AB,且 l 垂直平分 CD D.AC 与 BD 互相平分
5.如图 7×6 的网格,点 A、B、C 在格点(小正方形的顶点)上.在图中确 定格点 D,并画出一个以 ABCD 为顶点的四边形,使其为轴对称图形.
初中数学人教版八年级上册第十三章《轴对称》练习册(含答案)13.2 画轴对称图形
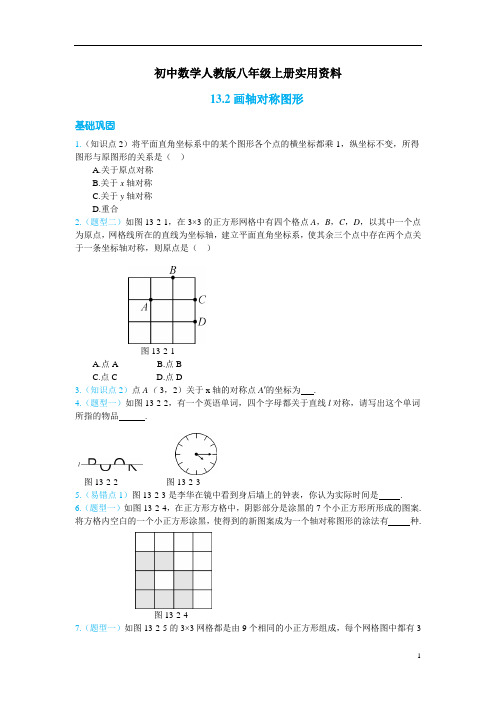
初中数学人教版八年级上册实用资料13.2画轴对称图形基础巩固1.(知识点2)将平面直角坐标系中的某个图形各个点的横坐标都乘-1,纵坐标不变,所得图形与原图形的关系是()A.关于原点对称B.关于x轴对称C.关于y轴对称D.重合2.(题型二)如图13-2-1,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在的直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是()图13-2-1A.点AB.点BC.点CD.点D3.(知识点2)点A(-3,2)关于x轴的对称点A′的坐标为.4.(题型一)如图13-2-2,有一个英语单词,四个字母都关于直线l对称,请写出这个单词所指的物品.图13-2-2 图13-2-35.(易错点1)图13-2-3是李华在镜中看到身后墙上的钟表,你认为实际时间是.6.(题型一)如图13-2-4,在正方形方格中,阴影部分是涂黑的7个小正方形所形成的图案.将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有种.图13-2-47.(题型一)如图13-2-5的3×3网格都是由9个相同的小正方形组成,每个网格图中都有3个小正方形已涂上阴影,请在剩下的6个空白小正方形中,按下列要求涂上阴影:选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形(给出三种方法)(1)(2)(3)图13-2-58.(题型一)如图13-2-6,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).(1)请画出△ABC关于直线l对称的△A1B1C1;(2)将线段AC向左平移3个单位长度,再向下平移5个单位长度,画出平移后得到的线段A2C2,并以它为一条边作一个格点三角形A2B2C2,使A2B2=C2B2.图13-2-69.(题型二)如图13-2-7,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,-3),E(0,-4).写出点D,C,B关于y轴的对称点F,G,H的坐标,并在图13-2-7中作出点F,G,H.顺次而平滑地连接A,B,C,D,E,F,G,H,A各点.观察你画出的图形,说明它具有怎样的性质,像我们熟知的什么图形.图13-2-710.(题型二)图13-2-8中的“鱼”是将坐标分别为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接而成的.(1)利用轴对称变换,画出原图案关于x轴的对称图形,形成美丽的“双鱼座”;(2)求两个图案的公共部分的面积(直接写结果).图13-2-8能力提升11.(题型四)如图13-2-9,将长方形纸片首先沿虚线AB按箭头方向对折,接着将对折后的纸片沿虚线CD按箭头方向对折,然后剪下一个小三角形,最后将纸片打开,则打开后的图形是()图13-2-912.(题型三)如图13-2-10,在平面直角坐标系中,线段OA与线段OA′关于直线l:y=x对称.已知点A的坐标为(2,1),则点A′的坐标为.图13-2-1013.(题型一)如图13-2-11,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,请在下面所给的格纸中一一画出(所给的六个格纸未必全用).图13-2-1114.(题型三)如图13-2-12,在平面直角坐标系中,△ABO的顶点坐标分别为O(0,0),A (2a,0),B(0,-a),线段EF两端点的坐标分别为E(-m,a+1),F(-m,1)(2a>m>a).直线l∥y轴,交x轴于点P(a,0),且线段EF与CD关于y轴对称,线段CD与MN关于直线l对称.(1)求点M,N的坐标(用含m,a的代数式表示).(2)△ABO与△MFE通过平移能重合吗?能与不能都要说明理由,若能,请你说出一种平移方案(平移的长度用m,a表示).图13-2-12答案基础巩固1. C 解析:将各个点的横坐标都乘-1,纵坐标不变,即各个点的横坐标变成它的相反数,纵坐标不变,所以所得图形与原图形关于y轴对称.故选C.2. B 解析:如图D13-2-1,以B为原点建立平面直角坐标系,此时存在两个点A,C关于y轴对称.故选B.图D13-2-13.(-3,-2)4. 书解析:如图D13-2-2,这个单词所指的物品是书.图D13-2-25. 7:45 解析:由镜面对称性可知,实际时间应该是7:45.6. 3 解析:在1,2或3处(如图D13-2-3)涂黑都可得到一个轴对称图形,故涂法有3种.图D13-2-37. 解:如图D13-2-4.图D13-2-48. 解:(1)如图D13-2-5,△A1B1C1即为所求.图D13-2-5(2)如图D13-2-5,△A2B2C2即为所求.(答案不唯一)9. 解:由题意,得F(-2,-3),G(-4,0),H(-2,4).如图D13-2-6,这个图形关于y轴对称,是我们熟知的轴对称图形.图D13-2-610. 解:(1)如图D13-2-7.(2)两个图案的公共部分的面积为1/2×3×2×2+1/2×2×2=6+2=8.图D13-2-7能力提升11. D 解析:∵第三个图形中剪去的是三角形,∴将第三个图形展开,可得A项不符合题意.再展开可知三角形的短边正对着,且在内侧,∴B,C项不符合题意.故选D.12.(1,2)解析:图D13-2-8如图D13-2-8,过点A作AC⊥x轴于点C,过点A′作A′C′⊥y轴于点C′,连接AA′,交直线l于点D.∵线段OA与线段OA′关于直线l:y=x对称,∴△ODA′≌△ODA,∠C′OD=∠COD,∴∠A′OD=∠AOD,A′O=AO.∴∠A′OC′=∠AOC.在△AC O和△A′C′O中,∠AOC=∠A′OC′,∠ACO=∠A′C′O=90°,AO=A′O,∴△ACO≌△A′C′O(AAS),∴AC=A′C′,CO=C′O.∵点A 的坐标为(2,1),∴点A′的坐标为(1,2).13解:与△ABC成轴对称且以格点为顶点的三角形如图D13-2-9.图D13-2-9`14. 解:(1)∵线段EF与CD关于y轴对称,线段EF两端点的坐标分别为E(-m,a+1),F(-m,1),∴C(m,a+1),D(m,1).设CD与直线l之间的距离为x.∵CD与MN关于直线l对称,l与y轴之间的距离为a,∴MN与y轴之间的距离为a-x.又∵x=m-a,∴点M的横坐标为a-(m-a)=2a-m.∴M(2a-m,a+1),N(2a-m,1).(2)能重合.理由如下:由(1)知EM=2a-m-(-m)=2a=OA,EF=a+1-1=a=OB.∵EF∥y轴,EM∥x轴,∴∠MEF=∠AOB=90°,∴△ABO≌△MFE(SAS),∴△ABO与△MFE通过平移能重合.平移方案:先将△ABO向上平移(a+1)个单位长度,再向左平移m 个单位长度,即可重合.。
八年级数学上册第13章轴对称13.2画轴对称图形第1课时画轴对称图形课件新版新人教版

6.作出△ABC 关于直线 l1 的轴对称图形△A1B1C1,然后再作出△A1B1C1 关于 l2 的轴对称图形△A2B2C2.
解:略.
编后语
听课不仅要动脑,还要动口。这样,上课就能够主动接受和吸收知识,把被动的听课变成了一种积极、互动的活动。这对提高我们的学习积极性和口 头表达能力,以及考试时回答主观题很有帮助的。实践证明,凡积极举手发言的学生,学习进步特别快。上课的动口,主要有以下几个方式:
1.分别以直线 l 为对称轴,所作轴对称图形错误的是( C )
2.如图,△ABC 和△A′B′C′关于直线 MN 对称,其中 A、A′是一组对称点, B 与 B′、C 与 C′是对称点,则 AA′ ⊥ MN,线段 AA′、BB′、CC′都被 MN 垂直平分 .
3.在图中,画出△A′B′C′,使△A′B′C′与△ABC 关于 l 成轴对称 图形.
解:
4.如图,△AOD 关于直线 l 进行轴对称变换后得到△BOC,则以下结论中 不正确的是( D ) A.∠1=∠2 B.∠3=∠4 C.l 垂直平分 AB,且 l 垂直平分 CD D.AC 与 BD 互相平分
5.如图 7×6 的网格,点D,并画出一个以 ABCD 为顶点的四边形,使其为轴对称图形.
2018秋季
数学 八年级 上册•R
第十三章 轴对称
13.2 画轴对称图形 第1课时 画轴对称图形
轴对称图形的性质
由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图 形的 形状 、 大小 完全相同;新图形上的 每一点 都是原图形上的某一 点关于直线 l 的 对称点 ;连接任意一对 对应点 的线段 被 对称轴垂 直平分 .
第一,复述。
课本上和老师讲的内容,有些往往非常专业和生硬,不好理解和记忆,我们听课时要试着用自己的话把这些知识说一说。有时用自己的话可能要啰 嗦一些,那不要紧,只要明白即可。
最新人教版八年级数学上册13.2 第1课时 画轴对称图形习题课件

2.(4分)如图,小红把一张含30°角的直角三角形纸片ABC沿较短边
的垂直平分线翻折,则∠BOC=
60° .
3.(4分)如图所示,指出图中△ABC至少经过 △DEF.
两 次轴对称变换后得到
4.(4分)下列说法:①角的两边关于角平分线对称 ;②两点关于连接
它们的线段的垂直平分线对称;③成轴对称的两个三角形的对应点或
(1)略 (2)10
15.(10分)如图,将矩形纸片ABCD沿对角线BD折叠,使点C落在点 C′处,BC′交AD于点E. (1) 若∠ DBC = 22.5° , 则在不添加任何辅助线的情况下 , 图中 45° 的角(虚线也视为角的边)有多少个? (2) 你认为图中有全等三角形吗?如果有 , 请写出图中一对全等的三 角形,并说明理由;如果没有,也请说明理由. (1)5个 (2)有,△BCD≌△DAB≌△BC′D, △ABE≌△C′DE,理由略
状,然后再画.
一、选择题(每小题5分,共15分)
Hale Waihona Puke 9.中国国旗上的一个五角星的对称轴的条数是( C )
A.1条 B.2条 C.5条 D.10条
10.如图,△AOD关于直线l进行轴对称变换后得到△BOC,则以下
结论中不正确的是( D )
A.∠1=∠2
B.∠3=∠4
C.l垂直平分AB,且l垂直平分CD
第十三章 轴对称
13.2 画轴对称图形
第1课时 画轴对称图形
作某些图形关于某直线对称的图形 , 只要作出图形中的一些特殊点 的 对称点 ,再连接这些 对称点 ,就可以得到原图形关于某直线对称 的图形.
1.(4分)如图,△ABC关于直线m进行轴对称变换后得到△DEF,则
m是线段AD的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.2 画轴对称图形
第1课时 画轴对称图形
要点感知1 画轴对称图形的依据:由一个平面图形可以得到它关于一条直线成轴对称的图
形,这个图形与原图形的______完全一样;新图形上的每一点都是原图形上某一点关于对称
轴的____;连接任意一对对应点的线段被对称轴____.
预习练习1-1 如图,△ABC和△A′B′C′关于直线MN对称,其中A,A′是一组对称点.若
AA′=6 cm,则AA′____MN,且A′D=____cm.
要点感知2 几何图形都可以看作由点组成.某些图形,只要作出图形中的一些特殊点(如线段
端点)的对称点,连接这些对称点,就可以得到原图形的____.
预习练习2-1 如图所示,在网格纸上,分别画出所给图形关于直线l对称的图形.
知识点1 补全轴对称图形
1.如图,一轴对称图形画出了它的一半,请你以中间直线为对称轴画出它的另一半.
知识点2 补全成轴对称的其中一个图形
2.如图,画出△ABC关于直线l对称的图形.
3.如图所示是轴对称图形的一部分,请以l为对称轴,画出它的另一部分.
4.(郴州中考)在下面的方格纸中.
(1)作出如△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
挑战自我
5.(乐山中考)如图,在10×10的正方形的网格中,每个小正方形的边长都为1,网格中有一
个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1,
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
参考答案
课前预习
要点感知1 形状、大小 对称点 垂直平分
预习练习1-1 ⊥ 3
要点感知2 轴对称图形
预习练习2-1 图略.
当堂训练
1.图略. 2. 图略.
课后作业
3.图略 .4.(1)图略.(2)由B1,B2在图上的位置可知,B1先向右平移6格;再向下平移2格,
因此△A2B2C2是由△A1B1C1先向右平移6格;再向下平移2格得到的.
5.(1)图略.(2)S四边形BB1C1C=12.
