高二数列单元复习
高二数学数列复习小结

课 题:数列复习小结(一)教学目得:1.系统掌握数列得有关概念与公式2.了解数列得通项公式n a 与前n 项与公式n S 得关系.3.能通过前n 项与公式n S 求出数列得通项公式n a .授课类型:复习课课时安排:1课时教 具:多媒体、实物投影仪教学过程:一、等比数列等差数列表示方法图像与函数的关系前n 项和通项定义数列正整数集上函数及性质数列知识结构二、知识纲要(1)数列得概念,通项公式,数列得分类,从函数得观点瞧数列.(2)等差、等比数列得定义.(3)等差、等比数列得通项公式.(4)等差中项、等比中项.(5)等差、等比数列得前n 项与公式及其推导方法.三、方法总结1.数列就是特殊得函数,有些题目可结合函数知识去解决,体现了函数思想、数形结合得思想.2.等差、等比数列中,a 1、n a 、n 、d (q )、n S “知三求二”,体现了方程(组)得思想、整体思想,有时用到换元法.3.求等比数列得前n 项与时要考虑公比就是否等于1,公比就是字母时要进行讨论,体现了分类讨论得思想.4.数列求与得基本方法有:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等.四、等差数列 1相关公式:(1) 定义:),1(1为常数d n d a a n n ≥=-+(2)通项公式:d n a a n )1(1-+=(3)前n 项与公式:d n n na a a n S n n 2)1(2)(11-+=+=(4)通项公式推广:d m n a a m n )(-+=2、等差数列}{n a 得一些性质(1)对于任意正整数n,都有21a a a a n n -=-+(2)}{n a 得通项公式2()(2112a a n a a a n -+-=(3)对于任意得整数s r q p ,,,,如果s r q p +=+,那么r q p a a a a +=+(4)对于任意得正整数r q p ,,,如果q r p 2=+,则q r p a a a 2=+(5)对于任意得正整数n>1,有12-++=n n n a a a (6)对于任意得非零实数b,数列}{n ba 就是等差数列,则}{n a 就是等差数列(7)已知}{n b 就是等差数列,则}{n n b a ±也就是等差数列 (8)}{},{},{},{},{23133122---n n n n n a a a a a 等都就是等差数列(9)n S 就是等差数列{}n a 得前n 项与,则k k k k k S S S S S 232,,-- 仍成等差数列,即(323m m m S S S -=(10)若)(n m S S n m ≠=,则=+n n S(11)若p S q S q p ==,,则(q p S q p +-=+ (12)bn an S n +=2,反之也成立五、等比数列1相关公式:(1)定义:)0,1(1≠≥=+q n q a a n n (2)通项公式:1-=n n q a a(3)前n 项与公式:⎪⎩⎪⎨⎧≠--==q 1)1(1q 11q q a na S n n (4)通项公式推广:n m n q a a -=2、等比数列}{n a 得一些性质(1)对于任意得正整数n,均有121a a a n n =+ (2)对于任意得正整数s r q p ,,,,如果s r q p +=+,则r q p a a a a =(3)对于任意得正整数r q p ,,,如果r p q +=2,则2q r p a a a =(4)对于任意得正整数n>1,有12+-=n n n a a a (5)对于任意得非零实数b,}{n ba 也就是等比数列(6)已知}{n b 就是等比数列,则}{n n b a 也就是等比数列(7)如果0>n a ,则}{log n a a 就是等差数列 (8)数列}{log n a a 就是等差数列,则}{n a 就是等比数列(9)}{},{},{},{},{23133122---n n n n n a a a a a 等都就是等比数列(10)n S 就是等比数列{}n a 得前n 项与,①当q =-1且k 为偶数时,k k k k k S S S S S 232,,--不就是等比数列、 ②当q ≠-1或k 为奇数时,k k k k k S S S S S 232,,-- 仍成等比数列六、数列前n 项与(1)重要公式:2)1(321+=+++n n n ; 6)12)(1(3212222++=+++n n n n ; 33322112(123)[(1)]2n n n n ++=+++=+ (2)等差数列中,mnd S S S n m n m ++=+(3)等比数列中,n m m m n n n m S q S S q S S +=+=+(4)裂项求与:111)1(1+-=+n n n n ;(!)!1(!n n n n -+=⋅) 七、例题讲解例1 一等差数列共有9项,第1项等于1,各项之与等于369,一等比数列也有9项,并且它得第1项与最末一项与已知得等差数列得对应项相等,求等比数列得第7项.选题意图:本题主要考查等差、等比数列得通项公式及前n 项与公式. 解:设等差数列为{a n },公差为d ,等比数列为{b n },公比为q 、由已知得:a 1=b 1=1,813692)(99919=⇒=+=a a a S 又b 9=a9,∴q8=81,∴q2=3,∴b 7=b1q6=27,即等比数列得第7项为27.说明:本题涉及得量较多,解答要理清关系,以免出错.例2 已知数列}{n a 得前n 项与1+n S =4n a +2(n ∈N +),a 1=1、(1)设n b =1+n a -2n a ,求证:数列}{n b 为等比数列,(2)设C n =n n a 2,求证:}{n C 就是等差数列. 选题意图:本题考查等差、等比数列得定义及逻辑推理能力.证明:(1) 1+n S =4n a +2, 2+n S =41+n a +2,相减得2+n a =41+n a -4n a ,),2(22112n n n n a a a a -=-∴+++,21n n n a a b -=+又.21n n b b =∴+,1,2411212=+=+=a a a a S 又,32,51212=-==∴a a b a∴}{n b 就是以3为首项,2为公比得等比数列,∴n b =3×21-n 、 (2) ∵,2n n n a C = n n n n n n a a C C 22111-=-∴+++1122++-=n n n a a 12+=n n b 4322311=⨯=+-n n 21211==a C ∴}{n C 就是以21为首项,43为公差得等差数列. 说明:一个表达式中既含有n a 又含有Sn,一般要利用 n a =n S -1-n S (n≥2),消去n S 或n a ,这里就是消去了n S .八、课后作业:1、 已知数列{n a }得前n 项与n S ,满足:log 2(n S +1)=n+1.求此数列得通项公式n a .解:由log 2(n S +1)=n+1,得n S =21+n -1 当n=1时,a 1=S 1=22-1=3;当n ≥2时,n a =n S -1-n S =21+n -1-(2n -1)=2n.2、 在数列{n a }中,a 1=0,1+n a +n S =n 2+2n(n ∈N+).求数列{n a }得通项公式.解:由于1+n a +n S =n 2+2n ,1+n a =1+n S -n S , 则1+n a +n S =1+n S -n S +n S =1+n S ,即1+n S = n 2+2n.九、板书设计(略)十、课后记:。
人教版高中数学高二-数列基础知识复习要点

数列基础知识复习要点数列是高中代数的重要内容,是中学数学联系实际的主渠道之一,同时又是学习高等数学的基础,故在高考数学中占有重要的地位.【基本内容概述】数列主要内容有三个方面:第一方面是数列的基本概念,如等差数列的定义、等比数列的定义、通项公式、等差中项、等比中项等;第二方面是数列的运算,即运用通项公式、前n项和公式以及数列的有关性质求数列的一些基本量(a1、a n 、n、d(q)、Sn)的问题;第三方面是解题思想方法与解题规律,利用公式列方程(组),例如等差、等比数列中的“知三求二”问题,利用函数图象、单调性、最值解题,待定系数法、分类讨论思想、方程思想等思想方法的应用.【高考热点透视】1.高考对数列基本知识的考查侧重以下几个方面:⑴等差、等比数列的定义、通项公式以及等差、等比数列的性质一直是考查的重点,这方面的考题多以选择题、填空题的形式出现,一般是中、低档难度题,但解题方法灵活多样,技巧性较强;⑵数列的运算,即用有关公式和性质求解一些基本量问题,特别是an 与Sn的关系问题(考生易漏掉n = 1时的情况)历来是考查的热点;⑶综合题型在数列中考查比较多,这类考题多是数列与函数、数列与不等式、数列与解析几何等知识的交汇点,此类问题往往难度大,综合性强,需运用的数学思想方法较多;⑷近几年来,探索性题型在数列中考查比较多.解决探索性问题应具备较高的数学思维能力,即观察、分析、归纳、猜想问题的能力,这正是“以能力立意”的命题原则的生动体现.可以设想,在今后的命题趋势中探索性题型仍将是热点和重点之一.⑸应用题型在数列中近几年明显增加.从近几年与数列有密切联系的应用题看,以关注热点、贴近生活,抓住考生身边的重要事件作素材,比如,当前大家都关注的:下岗职工再就业问题,住房改革与医疗改革问题,个人储蓄与养老保险问题,分期付款购买家具、电器、汽车、住房问题,环境保护问题,国土资源与人口发展问题等等,借助数列知识将实际问题抽象为数学问题.2.高考对数列基本思想方法的考查侧重以下几个方面:.⑴分类讨论思想:如等比数列的求和分公比等于1和不等于1两种情形;已知数列前n项和Sn 求通项an分n = 1和n≥2两种情形;求数列极限时对两个参数进行大小比较的讨论等;⑵函数思想:将数列视为定义域为正整数集或其子集的函数;⑶数形结合思想:如等差数列的通项公式an 和前n项和公式Sn分别视为直线和抛物线方程;⑷转化思想:如将非等差数列、等比数列转化为等差数列、等比数列.【知识要点精析】1.数列的表示方法应注意的两个问题⑴{ an }与an是不同的,前者表示数列a1,a2,…,an,…,而后者仅表示这个数列的第n项.⑵数列a1,a2,…,an,…,与集合{ a1,a2,…,an,…,}不同,差别有两点:数列是一列有序排布的数,而集合是一个有确定范围的整体;数列的项有明确的顺序性,而集合的元素间没有顺序性.2.数列通项公式的三个要点⑴一个数列如果有通项公式,那么它是一个函数式,这个函数的定义域是正整数集+N .⑵并非所有的数列都有通项公式,如数列0.1,0.10,0.101,0.1010,…,就没有通项公式.⑶有的数列的通项公式在形式上并不唯一,如数列11,102,1003,10004,…的通项公式可以写成:a n =10n + n 或 a n =10n + n + (n -1)(n -2)(n -3)(n -4).3.一个数列是等差(等比)数列的必要非充分条件等差(等比)数列的定义中有两个要点:一是“从第2项起”,二是“每一项与它前一项的差等于同一个常数”.这里的“从第2项起”是为了使每一项与它前面一项都确实存在,而“同一个常数”则是保证至少含有3项.所以,一个数列是等差(等比)数列的必要非充分条件是这个数列至少含有3项.4.判断或证明所给数列是否为等差数列的常用方法证明数列{ a n }为等差数列,应该用等差数列的定义,一般采用的形式为: ① 当n ≥2时,有a n -a 1-n = d (d 为常数); ②当n +∈N 时,有a 1+n -a n = d (d 为常数); ③当n ≥2时,有a 1+n -a n = a n -a 1-n 成立; ④a 2+n -2a 1+n +a n = 0; ⑤S n = an 2+ bn .若判断数列{ a n }不是等差数列,只需有a 3-a 2≠a 2-a 1即可. 5.等差数列的基本性质⑴公差为d 的等差数列,各项同加一数所得数列仍是等差数列,其公差仍为d .⑵公差为d 的等差数列,各项同乘以常数k 所得数列仍是等差数列,其公差为kd .⑶若{ a n }、{ b n }为等差数列,则{ a n ±b n }与{ka n +b}(k 、b 为非零常数)也是等差数列.⑷对任何m 、n +∈N ,在等差数列{ a n }中有:a n = a m + (n -m)d ,特别地,当m = 1时,便得等差数列的通项公式,此式较等差数列的通项公式更具有一般性.⑸、一般地,如果l ,k ,p ,…,m ,n ,r ,…皆为自然数,且l + k + p + … = m + n + r + … (两边的自然数个数相等),那么当{a n }为等差数列时,有:a l + a k + a p + … = a m + a n + a p + … .⑹公差为d 的等差数列,从中取出等距离的项,构成一个新数列,此数列仍是等差数列,其公差为kd( k 为取出项数之差).⑺如果{ a n }是等差数列,公差为d ,那么,a n ,a 1-n ,…,a 2、a 1也是等差数列,其公差为-d ;在等差数列{ a n }中,a l m +-a l = a k m +-a k = md .(其中m 、k 、l ∈+N )⑻在等差数列中,从第一项起,每一项(有穷数列末项除外)都是它前后两项的等差中项.⑼当公差d >0时,等差数列中的数随项数的增大而增大;当d <0时,等差数列中的数随项数的减少而减小;d =0时,等差数列中的数等于一个常数.6.等差数列前n 项和公式S n 的基本性质⑴数列{ a n }为等差数列的充要条件是:数列{ a n }的前n 项和S n 可以写成S n = an 2+ bn 的形式(其中a 、b 为常数).⑵在等差数列{ a n }中,当项数为2n (n ∈N *)时,S 偶-S 奇= nd ,偶奇S S =1+n na a ;当项数为(2n -1) (n +∈N )时,S 偶-S 奇= a n ,偶奇S S =1-n n. ⑶若数列{ a n }为等差数列,则S n ,S n 2-S n ,S n 3-S n 2,…仍然成等差数列.7.正确理解等比数列的含义理解等比数列的定义,要注意下列三点:⑴q 是指从第2项起每一项与前一项的比,顺序不要错,即q =nn a a 1+ (n +∈N )或q =1-n na a (n ≥2). ⑵由定义可知,等比数列的任意一项都不为0,因而公比q 也不为0. ⑶要证明一个数列是等比数列,必须对任意n +∈N ,nn a a 1+= q ;或1-n na a = q (n ≥2)都成立.8.判断或证明所给数列是否为等比数列的常用方法 ⑴a 1+n = a n q (a n ≠0)⇔{ a n }为等比数列.⑵21+n a = a n a 1+n ( a n a 1+n ≠0)⇔{ a n }为等比数列.9.等比中项与等差中项的主要区别如果G 是a 与b 的等比中项,那么a G =Gb,即G 2= ab ,G =±ab .所以,只要两个同号..的数才有等比中项,而且等比中项有两个,它们互为相反数;如果A 是a 与b 的等差中项,那么等差中项A 唯一地表示为A=2ba +,其中,a 与b 没有同号..的限制.在这里,等差中项与等比中项既有数量上的差异,又有限制条件的不同.10.等比数列的基本性质⑴公比为q 的等比数列,从中取出等距离的项,构成一个新数列,此数列仍是等比数列,其公比为q m ( m 为等距离的项数之差).⑵对任何m 、n +∈N ,在等比数列{ a n }中有:a n = a m · q m n -,特别地,当m = 1时,便得等比数列的通项公式,此式较等比数列的通项公式更具有普遍性.⑶一般地,如果t ,k ,p ,…,m ,n ,r ,…皆为自然数,且t + k ,p ,…,m + … = m + n + r + … (两边的自然数个数相等),那么当{a n }为等比数列时,有:a t .a k .a p .… = a m .a n .a p .… ..⑷若{ a n }是公比为q 的等比数列,则{| a n |}、{a 2n }、{ka n }、{na 1}也是等比数列,其公比分别为| q |}、{q 2}、{q}、{q1}. ⑸如果{ a n }是等比数列,公比为q ,那么,a 1,a 3,a 5,…,a 12-n ,…是以q 2为公比的等比数列.⑹如果{ a n }是等比数列,那么对任意在n +∈N ,都有a n ·a 2+n = a 2n ·q 2>0. ⑺两个等比数列各对应项的积组成的数列仍是等比数列,且公比等于这两个数列的公比的积.⑻当q >1且a 1>0或0<q <1且a 1<0时,等比数列为递增数列;当a 1>0且0<q <1或a 1<0且q >1时,等比数列为递减数列;当q = 1时,等比数列为常数列;当q <0时,等比数列为摆动数列.11.等比数列前n项和公式Sn的基本性质⑴如果数列{an}是公比为q 的等比数列,那么,它的前n项和公式是Sn =⎪⎩⎪⎨⎧≠--=.1,1)1(,1,11时当时当qqqaqnan也就是说,公比为q的等比数列的前n项和公式是q的分段函数的一系列函数值,分段的界限是在q = 1处.因此,使用等比数列的前n项和公式,必须要弄清公比q是可能等于1还是必不等于1,如果q可能等于1,则需分q = 1和q ≠1进行讨论.⑵当已知a1,q,n时,用公式Sn=qqa n--1)1(1;当已知a1,q,a n时,用公式Sn =qqaan--11.⑶若Sn 是以q为公比的等比数列,则有Smn+= S m+qS n.⑵⑷若数列{ an }为等比数列,则Sn,Sn2-Sn,Sn3-Sn2,…仍然成等比数列.⑸若项数为3n的等比数列(q≠-1)前n项和与前n项积分别为S1与T1,次n项和与次n项积分别为S2与T2,最后n项和与n项积分别为S3与T3,则S1,S2,S3成等比数列,T1,T2,T3亦成等比数列.12.求数列{ an}的前n项和常用方法⑴拆项分别求和,例如:an= n+(21)1-n,求数列{ a n}的前n项和S n,将其拆成一个等差数列和一个等比数列,然后分别求和即可.⑵倒序相加求和,将一个数列倒过来排列(倒序),当它与原数列相加时,若有公因式可提,并且剩余的项的和易于求得,则这样的数列可用倒序相加法求和.如等差数列的求和公式的推导就是用的这种方法.⑶错位相减法,这是在推导等比数的前n项和公式时所用的方法,这种方法主要用于求数列{ an · bn}的前n项和,其中{ an}、{ bn}分别是等差数列和等比数列.【特别提示】1.在运用公式an = Sn-S1-n时,一定要注意它的前提条件是“n≥2”,因为当n = 1时,S1-n没有意义.2.一个数列为等比数列的必要条件是该数列各项均不为0,因此,在研究等比数列时,要注意an ≠0,因为当an= 0时,虽有a2n= a1-n· a1+n成立,但{an}不是等比数列,即“b2= a · c”是a、b、c成等比数列的必要非充分条件;对比等差数列{an},“2b = a + c”是a、b、c成等差数列的充要条件,这一点同学们要分清.3.⑴如果三个数成等差数列,一般可设为a-d,a,a+d;⑵如果四个数成等差数列,一般可设为a-3d,a-d,a+d,a+3d。
高二数学 数列的全章复习与巩固 知识讲解
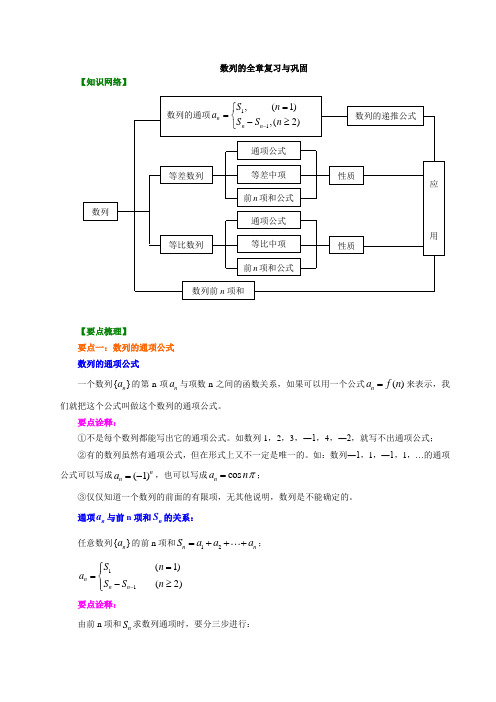
数列的全章复习与巩固【知识网络】【要点梳理】要点一:数列的通项公式 数列的通项公式一个数列{}n a 的第n 项n a 与项数n 之间的函数关系,如果可以用一个公式()n a f n =来表示,我们就把这个公式叫做这个数列的通项公式。
要点诠释:①不是每个数列都能写出它的通项公式。
如数列1,2,3,―1,4,―2,就写不出通项公式; ②有的数列虽然有通项公式,但在形式上又不一定是唯一的。
如:数列―1,1,―1,1,…的通项公式可以写成(1)n n a =-,也可以写成cos n a n π=;③仅仅知道一个数列的前面的有限项,无其他说明,数列是不能确定的。
通项n a 与前n 项和n S 的关系: 任意数列{}n a 的前n 项和12n n S a a a =+++;11(1)(2)n n n S n a S S n -=⎧⎪=⎨-≥⎪⎩要点诠释:由前n 项和n S 求数列通项时,要分三步进行:(1)求11a S =,(2)求出当n≥2时的n a ,(3)如果令n≥2时得出的n a 中的n=1时有11a S =成立,则最后的通项公式可以统一写成一个形式,否则就只能写成分段的形式。
数列的递推式:如果已知数列的第一项或前若干项,且任一项n a 与它的前一项1n a -或前若干项间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式,简称递推式。
要点诠释:利用递推关系表示数列时,需要有相应个数的初始值,可用凑配法、换元法等. 要点二:等差数列判定一个数列为等差数列的常用方法①定义法:1n n a a d +-=(常数)⇔{}n a 是等差数列; ②中项公式法:122(*){}n n n n a a a n N a ++=+∈⇔是等差数列; ③通项公式法:n a pn q =+(p ,q 为常数)⇔{}n a 是等差数列; ④前n 项和公式法:2n S An Bn =+(A ,B 为常数)⇔{}n a 是等差数列。
高二数学复习考点知识精讲与练习4 等比数列的前n项和公式

高二数学复习考点知识精讲与练习专题4 等比数列的前n项和公式【考点梳理】考点一等比数列的前n项和公式考点二等比数列前n项和的性质1.数列{a n}为公比不为-1的等比数列(或公比为-1,且n不是偶数),S n为其前n项和,则S n,S2n-S n,S3n-S2n仍构成等比数列.2.若{a n}是公比为q的等比数列,则S n+m=S n+q n S m(n,m∈N*).3.若{a n}是公比为q的等比数列,S偶,S奇分别是数列的偶数项和与奇数项和,则:①在其前2n项中,S偶S奇=q;②在其前2n+1项中,S奇-S偶=a1-a2+a3-a4+…-a2n+a2n+1=a1+a2n+1q1-(-q)=a1+a2n+21+q(q≠-1).考点三:等比数列前n项和的实际应用1.解应用问题的核心是建立数学模型.2.一般步骤:审题、抓住数量关系、建立数学模型.3.注意问题是求什么(n ,a n ,S n ). 注意:(1)解答数列应用题要注意步骤的规范性:设数列,判断数列,解题完毕要作答. (2)在归纳或求通项公式时,一定要将项数n 计算准确. (3)在数列类型不易分辨时,要注意归纳递推关系.(4)在近似计算时,要注意应用对数方法,且要看清题中对近似程度的要求.【题型归纳】题型一:等比数列前n 项和公式的基本运算1.(2022·江苏南通·高二期末)已知等比数列{}n a 的前6项和为1894,公比为12,则6a =( ) A .738B .34C .38D .242.(2022·河南商丘·高二期中(理))已知正项等比数列{}n a 中,22a =,48a =,数列{}2n n a a ++的前n 项和为n S ,则62SS =( )A .32B .21C .16D .83.(2022·全国·高二课时练习)设正项等比数列{}n a 的前n 项和为n S ,若23S =,3412a a +=,则公比q 等于( ).A .1B .2C .3D .4题型二:等比数列的判断和性质的应用4.(2022·全国·高二课时练习)设等比数列{}n a 前n 项和为S n ,若S 3=8,S 6=24,则a 10+a 11+a 12=( ) A .32B .64 C .72D .2165.(2022·广西·田东中学高二期末(理))已知数列{}n a 是等比数列,n S 为其前n 项和,若1234a a a ++=,4568a a a ++=,则12S =( ) A .40B .60C .32D .506.(2020·四川·双流中学高二期中(理))设n S 是等比数列{}n a 的前n 项和,若423S S =,则64S S =( ) A .2B .73C .310D .12或题型三:等比数列奇偶项和的性质7.(2020·河南·高二月考(理))已知等比数列{}n a 共有32项,其公比3q =,且奇数项之和比偶数项之和少60,则数列{}n a 的所有项之和是( ) A .30B .60C .90D .1208.(2022·全国·高二课时练习)已知等比数列{}n a 中,11a =,132185k a a a ++++=,24242k a a a +++=,则k =( )A .2B .3C .4D .59.(2022·全国·高二课时练习)已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的公比和项数分别为( ) A .8,2B .2,4C .4,10D .2,8题型四:等比数列中an 与Sn 的关系10.(2022·全国·高二课时练习)记数列{}n a 的前n 项和为n S ,21n n S a =-,则2020S =( )A .202021-B .202121-C .2020122⎛⎫- ⎪⎝⎭D .2021122⎛⎫- ⎪⎝⎭11.(2022·宁夏·六盘山高级中学高二月考(理))已知数列{}n a 的前n 项和112nn S ⎛⎫=- ⎪⎝⎭,那么数列{}n a ( ) A .是等差数列但不是等比数列 B .或者是等差数列,或者是等比数列 C .是等比数列但不是等差数列D .既不可能是等差数列,也不可能是等比数列12.(2020·江苏·高二专题练习)设数列{}n a 的前n 项和为n S ,若11a =,121n n S S +=+,则6S =( )A .63B .127C .128D .256题型五:等比数列的简单应用13.(2022·甘肃·西北师大附中高二期中(理))中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.那么请问此人前两天所走的里程为( ) A .189里B .216里C .288里D .192里14.(2022·全国·高二课时练习)为全力抗战疫情,响应政府“停课不停学”的号召,某市中小学按照教学计划,开展在线课程教学和答疑.某高一学生家长于3月5日在某购物平台采用分期付款的形式购买了一台价值m 元的平板电脑给学生进行网上学习使用,该平台规定:分12个月还清,从下个月5日即4月5日开始偿还,每月5日还款,且每个月还款钱数都相等.若购物平台的月利率为p ,则该家长每月的偿还金额是( )A .12m 元B .()()1212111mp p p ++-元C .()12112m p +元D .()()1313111mp p p ++-元 15.(2022·北京朝阳·高二期末)光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F 值表示,光圈的F 值系列如下:F 1,F 1.4,F 2,F 2.8,F 4,F 5.6,F 8,…,F 64.光圈的F 值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F 8调整到F 5.6,进光量是原来的2倍.若光圈从F 4调整到F 1.4,则单位时间内的进光量为原来的( ) A .2倍B .4倍C .8倍D .16倍【双基达标】一、单选题16.(2022·河南·高二期中(文))n S 为等比数列{}n a 的前n 项和,且33a =,26S =,则5a 的值为( )A .34B .3或12C .3或34D .12或3417.(2022·河南商丘·高二期中(理))在正项等比数列{}n a 中,512a =,673a a +=,{}n a 的前n 项和为n S ,前n 项积为n T ,则满足1n n S a T +>的最大正整数n 的值为( ) A .11B .12 C .13D .1418.(2022·江西·九江市第三中学高二期中(理))若{}n a 是等比数列,已知对任意*n N ∈,2121n n a a a ++=-,则2222123n a a a a ++++=( )A .2(21)n -B .121(2)3n -C .41n -D .1(41)3n -19.(2022·全国·高二课时练习)等比数列{a n }中,a 1a 2a 3=1,a 4=4,则a 2+a 4+a 6+…+a 2n =( )A .2n-1B .413n -C .()143--nD .()123n--20.(2022·江西·景德镇一中高二期中(文))已知数列{}n a 满足11a =,若1114()n n nn N a a ++-=∈,则数列{}n a 的通项n a =( ) A .341n -B .431n -C .413n -D .314n -21.(2022·河南洛阳·高二期中(文))已知等比数列{}n a 的前n 项和为21nn S a b =⋅+-,则44a b +的最小值为( ) A .2B..4D .522.(2022·全国·高二课时练习)在等比数列{}n a 中,已知42S =,86S =,17181920a a a a +++=( )A .32B .16C .35D .16223.(2022·全国·高二课时练习)已知n S 是等比数列{}n a 的前n 项和,若存在*m ∈N ,满足29m mS S =,2511m m a m a m +=-,则m 的值为( )A .-2B .2C .-3D .324.(2022·全国·高二课时练习)某人于2020年6月1日去银行存款a 元,存的是一年定期储蓄,2022年6月1日将到期存款的本息一起取出再加a 元之后还存一年定期储蓄,此后每年的6月1日他都按照同样的方法在银行取款和存款.设银行定期储蓄的年利率r 不变,则到2025年6月1日他将所有的本息全部取出时,取出的钱共有( )A .()41a r +元B .()51a r +元C .()61a r +元D .()()611a r r r⎡⎤+-+⎣⎦元 25.(2022·江苏·高二单元测试)设{}n a 是公差为d 的等差数列,{}n b 是公比为q 的等比数列.已知数列{}n n a b +的前n 项和()2*51N n n S n n =+-∈,则d q -=( )A .3-B .1-C .2D .4【高分突破】一:单选题26.(2022·江苏省苏州第十中学校高二月考)已知等比数列{a n }的首项为1,公比为2,则a 12+a 22+⋯+a n 2=( ) A .(2n ﹣1)2B .()1213n -C .4n ﹣1D .()1413n - 27.(2022·全国·高二学业考试)已知一个项数为偶数的等比数列{}n a ,所有项之和为所有偶数项之和的4倍,前3项之积为64,则1a =( ) A .1B .4 C .12D .3628.(2022·全国·高二单元测试)设n S 为数列{}n a 的前n 项和,()112322n n n a a n ---=⋅≥,且1232a a =.记n T 为数列1nn a S ⎧⎫⎨⎬+⎩⎭的前n 项和,若对任意*n ∈N ,n T m <,则m 的最小值为( ) A .3B .13C .2D .1229.(2022·全国·高二单元测试)在正项数列{}n a 中,首项12a =,且()()22*12,,2n n a a n n -∈≥N 是直线80x y -=上的点,则数列{}n a 的前n 项和n S =( ) A .()122n--B .122n +-C .12n +D .122n-30.(2022·江苏·苏州市苏州高新区第一中学高二月考)公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟领先他10米,当阿基里斯跑完下一个10米时,乌龟先他1米.所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为0.001米时,乌龟爬行的总距离为( )A .61019000-米B .410190-米C .510990-米D .5101900-米31.(2022·全国·高二课时练习)等比数列{a n }的前n 项和为S n ,已知a 2a 3=2a 1,且a 4与2a 7的等差中项为54,则S 5=( ) A .29B .31C .33D .3632.(2022·全国·高二课时练习)若正项等比数列{}n a 满足13116a a =,4322a a a +=,则()1121111n n nS a a a +=-++-=( )A .()2123n ⎡⎤+-⎣⎦B .()2123n -C .()2123n +D .()2123n⎡⎤--⎣⎦33.(2022·广西·崇左高中高二月考)已知{}n a 是公比不为1的等比数列,n S 为其前n 项和,满足2021201920192020a a a a -=-,则下列等式成立的是( )A .2202020212019S S S =B .2020202120192S S S +=C .2201920212020S S S =D .2019202120202S S S +=34.(2022·全国·高二课时练习)如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )A . 3. 213. 853D . 3413二、多选题35.(2022·江苏苏州·高二期中)已知等比数列{}n a 的各项均为正数,其前n 项和为n S ,若5432a a a +=,且存在两项m a ,n a ,使得14m n a a a =,则( ) A .12n n a a +=B .12n n S a a =-C .5mn =D .6m n +=36.(2022·全国·高二课时练习)n S 是数列{}n a 的前n 项的和,且满足11a =,12n n a S +=,则下列说法正确的是( ) A .{}n a 是等比数列 B .1123n n a -+=⨯C .{}n a 中能找到三项p a ,q a ,r a 使得p q r a a a =D .1n a ⎧⎫⎨⎬⎩⎭的前n 项的和74n T <37.(2022·江苏·高二单元测试)已知等比数列{}n a 的公比为q ,前n 项和0n S >,设2132n n n b a a ++=-,记{}n b 的前n 项和为n T ,则下列判断正确的是( )A .若2q ,则n n T S =B .若2q >,则n n T S >C .若14q =-,则n n T S >D .若34q =-,则n n T S <38.(2022·全国·高二单元测试)已知等比数列{}n a 的前n 项和为n S ,且214S a =,2a 是11a +与312a 的等差中项,数列{}n b 满足1n n n n a b S S+=⋅,数列{}n b 的前n 项和为n T ,则下列命题正确的是( )A .数列{}n a 的通项公式为13-=n n aB .31n n S =-C .数列{}n b 的通项公式为()()1233131nn nn b +⨯=--D .n T 的取值范围是11,86⎡⎫⎪⎢⎣⎭39.(2022·全国·高二课时练习)记数列{}n a 的前n 项和为n S ,若存在实数H ,使得对任意的*n ∈N ,都有n S H <,则称数列{}n a 为“和有界数列”.下列说法正确的是( ) A .若数列{}n a 是等差数列,且公差0d =,则数列{}n a 是“和有界数列” B .若数列{}n a 是等差数列,且数列{}n a 是“和有界数列”,则公差0d = C .若数列{}n a 是等比数列,且公比q 满足1q <,则数列{}n a 是“和有界数列” D .若数列{}n a 是等比数列,且数列{}n a 是“和有界数列”,则公比q 满足1q <40.(2022·全国·高二单元测试)已知数列{}n a 满足11a =,()*1N 23n n naa n a +=∈+,则下列结论正确的是( )A .13n a ⎧⎫+⎨⎬⎩⎭为等比数列B .{}n a 的通项公式为1123n n a -=- C .{}n a 为递增数列D .1n a ⎧⎫⎨⎬⎩⎭的前n 项和2234n n T n +=--三、填空题41.(2022·全国·高二课时练习)数列a 1,a 2-a 1,a 3-a 2,…,a n -a n -1,…是首项为1,公比为2的等比数列,那么a n =________.42.(2022·全国·高二课时练习)设正项等比数列{a n }的首项a 1=12,前n 项和为S n ,且210S 30-(210+1)S 20+S 10=0,则公比q =________.43.(2022·全国·高二课时练习)已知等比数列{a n }的公比为12-,则135246a a a a a a ++++的值是________.44.(2022·江西·景德镇一中高二期中)在数列{}n a 及{}n b中,1n n n a a b +=+1n n n b a b +=+11a =,11b =.设11n n nc a b =+,则数列{}n c 的前2022项和为__________.45.(2022·全国·高二课时练习)等比数列{a n }的各项均为实数,其前n 项的和为S n ,已知S 3=74,S 6=634,则a 8=______.四、解答题46.(2022·河南商丘·高二期中(文))已知正项数列{}n a 满足19a =,()12n n n a a a +=+,设()lg 1n n b a =+.(1)求数列{}n b 的通项公式;(2)设1n n c a =+,数列{}n c 的前n 项积为n S ,若lg n n S b λ<恒成立,求实数λ的取值范围.47.(2022·河南商丘·高二期中(文))设公差不为0的等差数列{}n a 的前n 项和为n S ,已知636S =,且2a 是1a ,5a 的等比中项. (1)求{}n a 的通项公式;(2)设2nn n b a =⨯,求数列{}n b 的前n 项和n T .48.(2022·陕西·延安市宝塔区第四中学高二月考)已知数列{}n a 的前n 项和S n =2n +1+A ,若{}n a 为等比数列.(1)求实数A 及{}n a 的通项公式;(2)设b n =log 2a n ,求数列{a n b n }的前n 项和T n .49.(2022·河南洛阳·高二期中(理))已知正项数列{}n a 的前n 项和为n S ,且11a =,211n n n S S a +++=,数列{}n b 满足12b =,2112na n nb b ++⋅=. (1)求证{}n a 为等差数列;(2)求证:12122n na a ab bb ++⋅⋅⋅+<.50.(2022·甘肃省民乐县第一中学高二期中(文))已知数列{}n a 的前n 项和为n S ,111,1(*)n n a a S n N +==+∈,数列{}n b 满足11b =,12n n n b a b +=+.(1)求数列{}n a 、{}n b 的通项公式;(2)若数列{}n c 满足1nn n n ac b b +=,求证:1212n c c c +++<.【答案详解】1.B解:根据题意,等比数列{}n a 的前6项和为1894,公比为12,则有616(1)18914a q S q -==-,解可得124a =,则56134a a q ==; 故选:B . 2.B 【详解】设正项等比数列{}n a 的公比为q,则2q ==, 所以,()()()()()()()66111263486421234112412635121221151212a a a a a a a a SS a a a a a --++++++++⨯--====+++--. 故选:B. 3.B解:由题意,正项等比数列{}n a 中, 因为23S =,3412a a +=,所以()121221234331212a a a a q a a a a +=+=⎧⎧⇒⎨⎨+=+=⎩⎩,解得24q =. 因为0q >,所以2q .故选:B 4.B【详解】由于S 3、S 6-S 3、S 9-S 6,S 12-S 9成等比数列,S 3=8,S 6-S 3=16,故其比为2, 所以S 9-S 6=32,a 10+a 11+a 12=S 12-S 9=64. 故选:B . 5.B 【详解】由等比数列的性质可知,数列36396129,,,S S S S S S S ---是等比数列,即数列4,8,96129,S S S S --是等比数列,因此9661291216,12,32,32161260S S S S S S -==-==++=.故选:B. 6.B 【详解】设24,3S k S k ==,由数列{}n a 为等比数列(易知数列{}n a 的公比1q ≠-),得24264,,S S S S S --为等比数列又242,2S k S S k =-=644S S k ∴-= 67,S k ∴=647733S k S k ∴== 故选:B . 7.D 【详解】设等比数列{}n a 的奇数项之和为1S ,偶数项之和为2,S则311531a a S a a =++++,()2463213531123a a a a q a a a a S S ++++=++++==又1260S S +=,则11603S S +=,解得1230,90S S ==, 故数列{}n a 的所有项之和是3090120+=. 故选:D 8.B 【详解】设等比数列{}n a 的公比为q , 则132112285k k a a a a a a q q +++++++==,即()2285184k q a a ++=-=,因为24242k a a a +++=,所以2q,则()21123221112854212712k k k a a a a a ++⨯-+++++=+==-,即211282k +=,解得3k =, 故选:B. 9.D解:设等比数列项数为2n 项,所有奇数项之和为S 奇,所有偶数项之和为S 偶, 根据题意得:S 奇=85,S 偶=170, ∴q S S ==偶奇2,又a 1=1,∴S 奇()21211na q q -==-85,整理得:1﹣4n =﹣3×85,即4n =256,解得:n =4,则这个等比数列的项数为8.故选D . 10.A 【详解】依题意21n n S a =-,当n=1时,a 1=2a 1-1,解得a 1=1; 当2n ≥时,由21n n S a =-得1121n n S a --=-,两式相减,得1122n n n n S S a a ---=-,即12n n a a -=,所以12nn a a -=()2n ≥, 所以数列{}n a 是首项为1,公比为2的等比数列, 所以12n na ,202020202020122112S -==--. 故选:A . 11.C解:数列{}n a 的前n 项和112nn S ⎛⎫=- ⎪⎝⎭,∴当2n 时,1111112212nn nn n n a S S -- ⎡⎤=-=--=-⎢⎥⎢⎭⎛⎫⎛⎫⎛⎫- ⎪⎪⎪⎝⎝⎭⎝⎣⎭⎥⎦,当1n =时,1111122a S ==-=-,上式也成立.∴12nn a ⎛⎫=- ⎪⎝⎭可得112n n a a -=,∴数列{}n a 是首项为12-,公比为12的等比数列,但不是等差数列. 故选:C .12.A在121n n S S +=+中,令1n =,得23S =,所以22a =. 由121n n S S +=+得2121n n S S ++=+,两式相减得212n n a a ++=,即212n n a a ++=,又11a =,212a a =,所以数列{}n a 是以1为首项,2为公比的等比数列,所以66126312S -==-. 故选:A . 13.C 【详解】由题意,记每天走的路程为{}n a 是公比为12的等比数列,又由6161[1()]2378112-==-a S ,解得1192a =, 所以11192()2-=⨯n n a ,则21192()962a =⨯= 故前两天所走的路程为:192+96=288 故选:C 14.B 【详解】设每月的偿还金额都是a 元, 则()()()()122111111m p a a p a p a p +=+++++++,即()()()121211111a p m p p ⎡⎤-+⎣⎦+=-+,解得()()1212111mp p a p +=+-.故选:B 15.C 【详解】由题可得单位时间内的进光量形成公比为12的等比数列{}n a ,则F 4对应单位时间内的进光量为5a ,F 1.4对应单位时间内的进光量为2a ,从F 4调整到F 1.4,则单位时间内的进光量为原来的258a a =倍.故选:C. 16.C 【详解】设公比为q ,则211136a q a a q ⎧=⎨+=⎩解得12q =-或1q =,故25334a a q ==或53a =.故选:C. 17.B 【详解】设正项等比数列{}n a 的公比为q ,则()25267556a q q a a q qa a ++==+=,即260q q +-=,0q >,则2q,514132a a q ∴==, 所以,()11221321232n n nS --==-,()()211112122121122232nn n n n n n n n T a a a a --+++-⎛⎫=⋅⋅⋅=⋅=⋅= ⎪⎝⎭,因为1n n S a T +>,即211221123232n nn--+>,即2115222n n n -->,即213100n n -+<,n <,因为1112<,则25122<<, 因此,满足条件的正整数n 的最大值为12. 故选:B. 18.D 【详解】因为对任意*n N ∈,2121n n a a a ++=-①,当1n =时,11a =, 当2n ≥时,211121n n a a a --++=-②,①-②得11222n n n n a ---==,满足11a =,则()221124n n n a --==,即{}2n a 是首项为1,公比为4的等比数列,所以()22221231141(41)143n n n a a a a ⨯-++++==--. 故选:D. 19.B 【详解】由a 1a 2a 3=1得321,a =∴a 2=1,又a 4=4,故q 2=4,所以a 2+a 4+a 6+…+a 2n =1414n--=413n -. 故选:B20.A 【详解】根据题意,由1114n n n aa +-=, 得12121321111111444n nn a a a a a a --⎛⎫⎛⎫⎛⎫-+-++-=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,化简得()114141144143n n n a a -⨯---==-,因11a =,所以1413n n a -=,即341n n a =-.故选:A. 21.C 【详解】当1n =时,1121a S a b ==+-,当2n ≥时,11121221n n n n n n a S S a b a a b ---==⋅+--⋅⋅--+=从而22a a =,34a a = 因为{}n a 是等比数列所以公比322a q a ==,且212a a a ==,即21ab a +-=,即1a b += 所以444a b ≥==+,当且仅当44a b =,即12a b ==时,等号成立所以44a b +的最小值为4 故选:C 22.A 【详解】解:由等比数列前n 项和的性质知,当数列依次每k 项和不为0时,则依次每k 项和仍成等比数列,所以4S ,84S S -,128S S -,1612S S -,2016S S -成等比数列,且公比为4q .又441232S a a a a =+++=,484567844S S a a a a S q -=+++==,所以42q =,所以16201617181920432S S a a a a S q -=+++==.故选:A 23.D 【详解】设等比数列{}n a 的公比为q . 当1q =时,21122m m S ma S ma ==与29m m S S =矛盾,不合乎题意;当1q ≠时,()()2122111119111m m m m m m m a q S q q q S qa q q---===+=---,则8mq =, 又2511m mma m q a m +==-,即5181m m +=-,解得3m =. 故选:D. 24.D设此人2020年6月1日存入银行的钱为1a 元,2022年6月1日存入银行的钱为2a 元,以此类推,则2025年6月1日存入银行的钱为6a 元,那么此人2025年6月1日从银行取出的钱有()6a a -元.由题意,得1a a =,()21a a r a =++,()()2311a a r a r a =++++,……,()()()()()5432611111a a r a r a r a r a r a =++++++++++,所以()()()256111a a a r r r ⎡⎤-=++++++⎣⎦()()()()()561111111r r a r r r a r ⎡⎤+-+⎣⎦⎡⎤=+-++⋅⎣-=⎦. 故选:D . 25.A 【详解】设数列{}n a 和{}n b 的前n 项和分别为,n n A B ,则()()1211111,222111n n n n b q n n db d d q A a n a n n B q q q --⎛⎫=+=-+==-⎪---⎝⎭(1q ≠), 若1q =,则1n B nb =,则2211()5122n n n n dd S A n B a n n nb =+==+++--,显然没有出现5n ,所以1q ≠,所以21121221511n n b n b q d d a n n q q ⎛⎫-++-+= ⎪--⎝-⎭, 由两边的对应项相等可得110,1,5,1221bd d a q q -====--,解得111,2,5,4a d q b ====, 所以3d q -=-. 故选:A 26.D 【详解】由等比数列的定义,11122n n n a --=⋅=故222124n n n n b a --===由于112144,104n n n n b b b ---===≠ 故{}n b 是以1为首项,4为公比的等比数列a 12+a 22+⋯+a n 2=1(14)41143nn ⋅--=-故选:D 27.C 【详解】由题意可得所有项之和S S +奇偶是所有偶数项之和S 偶的4倍,所以,4S S S +=奇偶偶,故13S S =奇偶设等比数列{}n a 的公比为q ,设该等比数列共有()2k k N *∈项,则()242132113k k S a a a q a a a qS S -=+++=+++==奇奇偶,所以,13q =,因为3212364a a a a ==,可得24a =,因此,2112aa q ==.故选:C. 28.B解:由()112322n n n a a n ---=⋅≥,得()111322424n n n n a a n --=⋅+≥,∴()111112242n n n n a a n --⎛⎫-=-≥ ⎪⎝⎭. 又由()112322n n n a a n ---=⋅≥,得2126a a -=,又1232a a =,∴13a =.所以111122a -=, ∴数列12n n a ⎧⎫-⎨⎬⎩⎭是以12为首项,14为公比的等比数列,则12111112242n n n n a --⎛⎫⎛⎫-=⋅= ⎪ ⎪⎝⎭⎝⎭,∴()12122122n n n nn a --=+=+,∴()()231111212112122222221221212nn nn n n n S --⎛⎫- ⎪-⎛⎫⎝⎭=++⋅⋅⋅+++++⋅⋅⋅+=+=⋅- ⎪-⎝⎭-,∴111112222232n n n n n n na S --==+++⋅-⋅.∴+12111111111122113222332312n n n n T ⎛⎫- ⎪⎛⎫⎛⎫⎝⎭=++⋅⋅⋅+=⨯=-< ⎪ ⎪⎝⎭⎝⎭-. ∵对任意*n ∈N ,n T m <,∴m 的最小值为13. 故选:B. 29.B 【详解】在正项数列{}n a 中,12a =,且()2212,n n a a -是直线80x y -=上的点,可得22128n n a a -=,所以12n n a a -=,可得数列{}n a 是首项为2,公比为2的等比数列, 则{}n a 的前n 项和()12122212n n n S +-==--.故选:B 30.A由题意,乌龟每次爬行的距离构成等比数列{}n a , 其中11100,10a q ==,且30.00110n a -==, 所以乌龟爬行的总距离为3611110010(1)101101119000110nn n a a qa q S q q---⨯---====---. 故选:A. 31.B 【详解】由题意,231136112522a q a a q a q ⎧=⎪⎨+=⎪⎩,则3161214a q a q ⎧=⎪⎨=⎪⎩,可得q 3=18, ∴q =12,a 1=16,∴S 5=551116[1()](1)231112a q q--==-. 故选:B 32.D 【详解】由题意,2132116a a a ==,得214a =.令{}n a 的公比为0q >,由4322a a a +=,得2210q q +-=,得12q =,∴112a =,∴12n na =,令()111n n n b a +=-,则()2nn b =--,∴()()()12212212123nn n n S b b b ⎡⎤--⎣⎦⎡⎤=++⋅⋅⋅+==--⎣⎦--, 故选:D. 33.B 【详解】设等比数列{}n a 的公比为q (q ≠1),又2021201920192020a a a a -=-,即201920129290120a a q a q -=+,而20190a ≠,则220q q +-=,解得2q =-,则201911201923a a S +⋅=,2019112020223a a S -⋅=,2019112021423a a S +⋅=,10a ≠,20192019201922111111202020212019(22)(42)(2)99a a a a a a S S S -⋅⋅+⋅+⋅=≠=,A 不正确;20192020202120192019201911111122422223323a a a a S a S a S -⋅+⋅+⋅=+==+,B 正确;20192019201922111111201920212020(2)(42)(22)99a a a a a a S S S +⋅⋅+⋅-⋅=≠=,C 不正确;2019201920191111201920212020112422523323a a a a a a S S S +⋅+⋅+⋅=+=+≠,D 不正确.故选:B 34.D 【详解】根据三角形中位线的性质可知:这五个正三角形的边长形成等比数列{}n a :前5项分别为:2,1,12,14,18, 所以这五个正三角形的面积之和为22222222461111112121248222⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫++++=++++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦51414114⎛⎫⨯- ⎪⎝⎭==-,故选:D . 35.BD 【详解】解:设等比数列{}n a 的公比为q ,且0q >因为5432a a a +=,即4321112a q a q a q +=化简得:221q q +=解得:12q =或1q =-(舍去)对A ,因为12q =,所以112n n a a +=,故A 错误;对B ,1111112211112nn n n n a a a a q a a q S a a q q ---====----,故B 正确; 对C,因为1a,即1a =,化简得:2214m n q+-=,又12q =解得6m n +=,当2m =,4n =时,8mn =,故C 错误; 对D ,由C 知,6m n +=,故D 正确. 故选:BD. 36.BD 【详解】当1n =时,211222a S a ===;当2n ≥时,由12n n a S +=可得12n n a S -=, 两式相减得12n n n a a a +=-,所以13n n a a +=,且2123aa =≠, 则数列{}n a 从第二项开始成以3为公比的等比数列,则222323n n n a a --=⋅=⨯,所以21,1,23,2,n n n a n -=⎧=⎨⨯≥⎩则1123n n a -+=⨯,所以A 选项错误,B 选项正确. 由题意可知,数列{}n a 为单调递增数列,设p q <,若在数列{}n a 中能找到三项p a ,q a ,r a ,使得p q r a a a =, 则r q p >>且p ,q ,*r ∈N ,若1p =,则p r a a =,这与数列{}n a 单调递增矛盾, 若2p ≥,则224323292p q p q p q a a --+-=⨯⨯⨯=⨯,232r r a -=⨯,由p q r a a a =,可得42322p q r +--⨯=,由于432b q +-⨯能被3整除,22r -不能被3整除,故C 选项错误;因为21,1,11,2,23n n n a n -=⎧⎪=⎨≥⎪⨯⎩所以11T =;当2n ≥时,122111111113137231111112232323434413n n n n T ---⎛⎫- ⎪⎛⎫⎝⎭=++++⋅⋅⋅+=+=+-<+= ⎪⨯⨯⨯⎝⎭-,故选项D 正确. 故选:BD 37.AB 【详解】由于{}n a 是等比数列,0n S >,所以110a S =>,0q ≠, 当1q =时,10n S na =>,符合题意; 当1q ≠时,()1101n n a q S q-=>-,即101nq q->-, 等价于1010n q q ⎧->⎨->⎩或1010n q q ⎧-<⎨-<⎩,对于1010n q q ⎧->⎨->⎩,由于n 可能是奇数,也可能是偶数,所以(1,0)(0,1)q ∈-⋃,对于1010n q q ⎧-<⎨-<⎩可得:1q >.综上所述,q 的取值范围是(1,0)(0,)-+∞;因为2213322n n n n b a a a q q ++⎛⎫=-=- ⎪⎝⎭,所以232n n T q q S ⎛⎫=- ⎪⎝⎭,所以2311(2)22n n n n T S S q q S q q ⎛⎫⎛⎫-=⋅--=⋅+⋅- ⎪ ⎪⎝⎭⎝⎭,因为0n S >,且(1,0)(0,)q ∈-⋃+∞,所以,当12q =-或2q 时,0n n T S -=,即n n T S =,故A选项正确.当112q -<<-或2q >时,0n n T S ->,即n n T S >,故B 选项正确,D 选项错误. 当12(0)2q q -<<≠时,0n n T S -<,即n n T S <,故C 选项错误; 故选:AB. 38.BD 【详解】A :由214S a =可得213a a =,所以等比数列{}n a 的公比3q =,所以113n n a a -=⨯. 由2a 是11a +与312a 的等差中项,可得2131212a a a =++,即()2111123132a a a ⨯=++⨯,解得12a =,所以123n n a -=⨯,所以A 不正确; B :()()1121331113nnnn a q S q-⨯-===---,所以B 正确;C :()()111123111331313131n n n n n n n n n a b S S -+++⨯⎛⎫===- ⎪⋅----⎝⎭,所以C 不正确;D :12n n T b b b =++⋅⋅⋅+1223111111111111113333231313131313131n n n ++⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+-=- ⎪ ⎪ ⎪ ⎪-------⎝⎭⎝⎭⎝⎭⎝⎭所以数列{}n T 是递增数列,得11110326n T T ⎛⎫≤<⨯-= ⎪⎝⎭,所以1186n T ≤<,所以D 正确.故选:BD. 39.BC【详解】若数列{}n a 是公差为d 的等差数列,则211(1)()222n n n d d dS na n a n -=+=+-, 当0d =时,若10a ≠,则1n S a n =⋅,n S 是n 的一次函数,不存在符合题意的H ,A 错误; 数列{}n a 是“和有界数列”,当0d ≠时,n S 是n 的二次函数,不存在符合题意的H ,当0d =,10a =时,存在符合题意的H ,B 正确;若数列{}n a 是公比为(1)≠q q 的等比数列,则1(1)1-=-n n a q S q,因q 满足1q <,则||1n q <,即|1|2nq -<,11|||||1|2||11n n a a S q qq=⋅-<--,则存在符合题意的实数H ,即数列{}n a 是“和有界数列”,C 正确;若等比数列{}n a 是“和有界数列”,当1q =-时,若n 为偶数,则0n S =,若n 为奇数,则1n S a =,即1=n S a ,从而存在符合题意的实数H ,D 错误. 故选:BC 40.AD 【详解】因为123nn n a a a +=+,所以112323n nn n a a a a ++==+, 所以111323n n a a +⎛⎫+=+ ⎪⎝⎭,且11340a +=≠, 所以13n a ⎧⎫+⎨⎬⎩⎭是以4为首项,2为公比的等比数列,即11342n na -+=⨯,所以1231n na +=-,可得1123n n a +=-,故选项A 正确,选项B 不正确;因为1231n na +=-单调递增,所以1123n n a +=-单调递减,即{}n a 为递减数列,故选项C 不正确;1n a ⎧⎫⎨⎬⎩⎭的前n 项和()()()()2312132323232223n n n T n ++=-+-+⋅⋅⋅+-=++⋅⋅⋅+- 22122323412nn n n +-=⨯-=---.故选项D 正确;故选:AD . 41.2n -1(n ∈N *) 【详解】a n -a n -1=a 1q n -1=2n -1,即21232112,2,2n n n a a a a a a ---=⎧⎪-=⎪⎨⎪⎪-=⎩ 各式相加得a n -a 1=2+22+…+2n -1=2n -2, 故a n =a 1+2n -2=2n -1(n ∈N *). 又1n =时,11a =符合a n =2n -1 故答案为:2n -1(n ∈N *). 42.12 【详解】由210S 30-(210+1)S 20+S 10=0, 得210(S 30-S 20)=S 20-S 10.∴302010201012S S S S -=-,∵数列{a n }是等比数列∴10302021222330201011121320S S a a a a q S S a a a a -++++==-++++ 故101012q =,解得:12q =± 因为等比数列{a n }为正项数列,所以0q >,故12q = 故答案为:12 43.2- 【分析】由等比数列的通项公式与性质求解即可 【详解】∵等比数列{a n }的公比为12-,则()1351352461352a a a a aa a a a q a a a ++++==-++++.故答案为:2-44.4042. 【详解】由1n n n a a b +=+1n n n b a b +=+ 两式相加可得:()112n n n n a b a b +++=+,故数列{}n n a b +是以2为首项,2为公比的等比数列, 所以2nn n a b +=;两式相乘可得:()()222112n n n n n n n n a b a b a b a b ++⋅=+-+=⋅,故数列{}n n a b ⋅是以1为首项,2为公比的等比数列, 所以12n n n a b -⋅=, 故112n nn nn n n a b c a b a b ⎛⎫+=+==⎪⋅⎝⎭, 故数列{}n c 的前2022项和为2021202124042S =⨯=, 故答案为:4042 45.32 【详解】当q =1时,显然不符合题意;当q ≠1时,3161(1)714(1)6314a q q a q q ⎧-=⎪-⎪⎨-⎪=⎪-⎩,解得1142a q ⎧=⎪⎨⎪=⎩,∴a 8=14×27=32. 故答案为:32 46.(1)12n n b -=(2)[)2,+∞ (1)由已知可得()2111++=+n n a a ,所以()()1lg 12lg 1++=+n n a a ,即12n n b b +=, 又()()11lg 1lg 191b a =+=+=,所以{}n b 是首项为1,公比为2的等比数列,所以12n n b -=.(2)由(1)可知()1lg 12n n n a b -=+=,所以12101n n a -=-,12110n n n c a -=+=.所以021112222122212122101011010100n nn n n S c c c --+++⋅⋅⋅+-⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅==⋅=⋅.lg n n S b λ<即1212n n λ--<,即1122n λ->-, 因为1122n --关于n 单调递增,而11222n --<且无限接近于2, 所以实数λ的取值范围是[)2,+∞. 47.(1)21n a n =-(2)()12326n n T n +=-⨯+(1)设{}n a 的公差为d (0d ≠).由题可知()()1211165636,24,a d a d a a d ⨯⎧+=⎪⎨⎪+=+⎩解得11,2,a d =⎧⎨=⎩所以{}n a 的通项公式为()12121n a n n =+-=-. (2)由(1)可知()212nn b n =-⨯,所以()()231123252232212n nn T n n -=⨯+⨯+⨯+⋅⋅⋅+-⨯+-⨯…①()()23412123252232212n n n T n n +=⨯+⨯+⨯+⋅⋅⋅+-⨯+-⨯…②①-②得()()23122222212n n n T n +-=+⨯++⋅⋅⋅+--⨯()()()211121222212322612n n n n n -++⨯-=+⨯--⨯=-⨯--,所以()12326n n T n +=-⨯+.48.(1)A =-2,2nn a =.(2)()1122n n T n ++=-(1)根据题意,数列{}n a 的前n 项和S n =2n +1+A , 则a 1=S 1=22+A =4+A ,a 2=S 2-S 1=(23+A )-(22+A )=4, a 3=S 3-S 2=(24+A )-(23+A )=8,又由{}n a 为等比数列,则a 1×a 3=(a 2)2,即(4+A )×8=42=16, 解可得A =-2,则a 1=4-2=2,即数列{}n a 是首项为2,公比为2的等比数列, 则2nn a =, (2)设2n n b log a =,则设222nn n b log a log n ===, 则2nn n a b n ⨯=,故231222322nn T n ⨯⨯⨯⋯⋯⨯=++++,①则有()23121222122n n n T n n ⨯+⨯+⋯⋯+⨯⨯+=-+,② ①-②可得:()231122222122n n n n T n n +++++⋯⋯+⨯-=-=--,变形可得:()1122n n T n ++=-,故()1122n n T n ++=-.49. (1)证明:由题意有22111,(2)n n n n n n S S a S S a n ++-+=+=≥,两式相减得2211n n n n a a a a +++=-,即()22110n n n n a a a a ++--+=,所以()()1110n n n n a a a a ++--+=,因为数列{}n a 为正项数列,所以10n n a a ++>, 所以11(2)n n a a n +-=≥,又因为2212S S a +=,即22122a a a +=,解得22a =,且11a =, 所以211a a -=也满足上式,所以*11()n n a a n N +-=∈,所以数列{}n a 为以1为首项1为公差的等差数列; (2)证明:由(1)有()111n a n n =+-⨯=,又2112na n nb b ++⋅=,所以2112n n n b b ++⋅=,()21122n n n b b n --⋅=≥,两式相除有()2112112422n n n n b n b ++--==≥,又12b =,24b =, 所以135721,,,,,n b b b b b -是以12b =为首项,公比为4的等比数列,24682,,,,,n b b b b b 是以24b =为首项,公比为4的等比数列,所以数列{}n b 是以12b =为首项,公比为2的等比数列,所以2nn b =,所以2n n na nb =,令1212n n na a a Tb b b =++⋅⋅⋅+, 则()2111111212222n n nT n n -=⨯+⨯+⋅⋅⋅+-⨯+⨯, ()2311111112122222n n n T n n +=⨯+⨯+⋅⋅⋅+-⨯+⨯, 两式相减可得231111111111111222112222222212nn n n n n n T n n +++⎛⎫- ⎪+⎝⎭=++++-⨯=-⨯=--,所以222n nn T +=-, 因为n N ∈,所以2222n nn T +=-<,从而得证原不等式成立. 50. (1)解:由11n n a S +=+,得11(2)n n a S n -=+≥, 所以11(2)2(2)n n n n n a a a n a a n ++-=≥=≥,即 又由11a =,得22a =,满足12n n a a +=,所以12n n a ,而122n n n n b b a +-==,所以1211222n n n b b ---=++⋯+,所以()1211212221=2121n n n nn b --⨯-=++++=--…;(2) 证明:因为11+12111()2(21)(21)2121n nn n n n c -+==-----, 所以121223111111111111()=(1)22221212121212121n n n n c c c ++++=-+-+--<-------.。
高二数学复习考点知识精讲与练习1 数列的概念

高二数学复习考点知识精讲与练习专题1 数列的概念【考点梳理】考点一数列及其有关概念1.一般地,我们把按照确定的顺序排列的一列数称为数列,数列中的每一个数叫做这个数列的项.数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示,第二个位置上的数叫做这个数列的第2项,用a2表示……,第n个位置上的数叫做这个数列的第n项,用a n表示.其中第1项也叫做首项.2. 数列的一般形式可以写成a1,a2,a3,…,a n,…,简记为{a n}.考点二数列的分类考点三函数与数列的关系数列{a n}是从正整数集N*(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项a n,记为a n=f(n).考点四数列的单调性考点五 1.如果数列{a n }的第n 项a n 与它的序号n 之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.2.通项公式就是数列的函数解析式,以前我们学过的函数的自变量通常是连续变化的,而数列是自变量为离散的数的函数. 考点六 数列的递推公式如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.考点七 数列的前n 项和S n 与a n 的关系 重难点大规律归纳1.把数列{a n }从第1项起到第n 项止的各项之和,称为数列{a n }的前n 项和,记作S n ,即S n =a 1+a 2+…+a n .2.a n =⎩⎨⎧S 1,n =1,S n -S n -1,n ≥2.(1)由于数列是特殊的函数,所以可以用研究函数的思想方法来研究数列的相关性质,如单调性、最大值、最小值等,此时要注意数列的定义域为正整数集或其有限子集{1,2,…,n }这一条件.(2)可以利用不等式组⎩⎨⎧ a n -1≤a n ,a n ≥a n +1,找到数列的最大项;利用不等式组⎩⎨⎧a n -1≥a n ,a n ≤a n +1,找到数列的最小项.【题型归纳】题型一:数列的有关概念和分类1.(2022·全国·高二课时练习)下面四个结论:①数列可以看作是一个定义在正整数集(或它的有限子集{}1,2,3,,n )上的函数; ②数列若用图像表示,从图像上看都是一群孤立的点; ③数列的项数是无限的; ④数列通项的表达式是唯一的. 其中正确的是( ).A .①②B .①②③C .②③D .①②③④2.(2022·全国·高二课时练习)下列叙述正确的是( ) A .数列1,3,5,7与7,5,3,1是相同的数列 B .数列0,1,2,3,…可以表示为{n } C .数列0,1,0,1,…是常数列 D .数列1n n ⎧⎫⎨⎬+⎩⎭是递增数列 3.(2022·全国·高二专题练习)下列有关数列的说法正确的是( ) ①数列1,2,3与数列3,2,1是同一数列; ②数列{a n }与{a 2n -1}表达同一数列;③数列-1,1,-1,1,…的通项公式不唯一;④数列-1,1,3,5,8,…的通项公式为a n =2n -3,n ∈N *.A .①④B .②③C .③D .①②题型二:判断或者写出数列的项4.(2022·河北·衡水市第十四中学高二月考)已知数列-1,14,-19,…,21(1)n n -⋅,…,则它的第6项的值为( ) A .16B .16-C .136-D .1365.(2022·江西·新余四中高二月考(理))以下通项公式中,不可能是数列3,5,9,…的通项公式的是( ) A .21n n a =+B .23n a n n =-+ C .322255733n a n n n =-+-+D .21n a n =+ 6.(2022·全国·高二课时练习)已知数列{a n }的通项公式a n =1nn +,则a n ·a n +1·a n +2等于( ) A . 2n n +B . 3n n +C . 12n n ++D . 13n n ++题型三:根据数列的单调性求数列的最大(小)项数7.(2022·江苏省阜宁中学高二月考)在数列{}n a 中,22293n a n n =-++,则此数列最大项的值是( )A .107B .9658C .9178D .1088.(2022·全国·高二课时练习)数列{}n a 中, n a =100项中的最大项与最小项分别是( ) A .150,a a B .144,a a C .4544,a a D .4550,a a9.(2022·全国·高二课时练习)已知数列{a n }的通项公式为a n =-2n 2+21n ,则该数列中的数值最大的项是( ) A .第5项B .第6项C .第4项或第5项D .第5项或第6项题型四:由递推公式求数列的指定项10.(2022·河南洛阳·高二期中(文))数列{}n a 满足121a a ==,且12n n n a a a --=+,(3)n ≥,则5a =( ) A .1B .2C .5D .811.(2022·江西九江·高二期中(理))若数列{}n a 满足1222a a ==,且21n n na a a ++=-,则{}n a 的前100项和为( ) A .67B .68C .134D .16712.(2022·全国·高二课时练习)已知数列{}n a 中,11a =,22a =,21n n n a a a ++=-,则4a =( )A .-2B .-1C .1D .2题型五:由递推公式求通项公式13.(2022·广西师范大学附属外国语学校高二月考)数列1,3,6,10,15,…的递推公式是( ) A .*1,n n a a n n N +=+∈ B . *1,2n n a a n n N n -=+∈≥, C .()*11,,2n n a a n n N n +=++∈≥ D .*11,2()n n a a n n N n -=+-∈≥,14.(2022·天津市南仓中学高二期末)已知数列{}n a ,满足111n na a +=-,若112a =,则10a =( )A .12B .2C .1D .1-15.(2020·全国·高二课时练习)已知数列{}n a 满足11a =,()*11n n na a n n +=∈+N ,则n a =( ) A .1n +B .n C .11n +D .1n题型六:利用S n 与a n 的关系求通项公式16.(2022·河南·高二月考)已知数列{}n a 的前n 项和为n S ,且满足2n S n =,110n n na b a +=-,则n b 的最小值为( ) A .16-B .15-C .13-D .11-17.(2022·江苏·常熟中学高二月考)数列{}n a 的前n 项和为n S ,若11a =,13(1)n n a S n +=≥,则n a 等于( )A .34n⨯B .341n⨯+C .21,134,2n n n -=⎧⎨⨯≥⎩D .21,1341,2n n n -=⎧⎨⨯+≥⎩ 18.(2022·宁夏·六盘山高级中学高二月考(文))数列{}n a 满足211232223n n na a a a -++++=,则n a =( ) A .13n B .3n n C .1123n -⋅D .1132n -⋅【双基达标】一、单选题19.(2022·全国·高二课时练习)数列2,4,6,8,10,…的递推公式是( ) A .a n =a n -1+2(n ≥2) B .a n =2a n -1(n ≥2)C .a 1=2,a n =a n -1+2(n ≥2)D .a 1=2,a n =2a n -1(n ≥2)20.(2022·全国·高二课时练习)若数列{a n }满足a n =3n ,则数列{a n }是( ) A .递增数列B .递减数列 C .常数列D .摆动数列21.(2022·全国·高二课时练习)给出以下通项公式:①()11nn a ⎤=--⎦;②n a③()()21N 0,2Nn n k k a n k k **=-∈==∈⎪⎩,,0,0,…的通项公式的是( )A .①②B .②③C .①③D .①②③22.(2022·河南洛阳·高二期中(理))数列{}n a 满足11a =,21a =,且12n n n a a a --=-,()3n ≥,记数列{}n a 的前n 项和为n S ,则20S =( ) A .0B .1C .2D .1423.(2022·福建省龙岩第一中学高二月考)数列{}n a 满足12a =,111nn na a a ++=-,其前n 项积为n T ,则10T 等于( ) A .16B .16-C .6D .6-24.(2022·河南·高二月考)已知在数列{}n a 中,11a =,22a =,且2121n n n a a a ++=++,则5a =( )A .3B .15C .37D .6325.(2022·江苏·高二单元测试)在数列{}n a 中,25n a n n=+,则12232425a a a a a a -+-++-=( )A .25B .32C .62D .7226.(2022·全国·高二单元测试)已知数列{}n a 满足13a =,()111n n a a n n +=++,则n a =( ) A .14n+B .14n-C .12n+D .12n-27.(2022·河南·高二月考(文))猜想数列282680,,,,3579--⋅⋅⋅的一个通项公式为n a =( ) A .()31121nn n --+B .()12121n n n +-+ C .()121121n n n +--+D .()31121n n n --+【高分突破】一:单选题28.(2022·全国·高二课时练习)已知函数f (x )=7(13)10(6)(6),x a x x a x --+≤⎧⎨>⎩若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递减数列,则实数a 的取值范围是( ) A .1(,1)3B .11(,)32C .15(,)36D .5(,1)629.(2022·宁夏·六盘山高级中学高二月考(理))对于正项数列{}n a ,定义12323nn a a a na G n++++=为数列{}n a 的“匀称值”.已知数列{}n a 的“匀称值”为2n G n =+,则该数列中的9a 等于( ) A .83B .125C .2110D .19930.(2022·全国·高二专题练习)已知下列命题:①已知数列{a n },()12n a n n =+ (n ∈N *),那么1120是这个数列的第10项,且最大项为第1项;②…,的一个通项公式是a n =(-1)n + ③已知数列{a n },a n =kn -5,且a 8=11,则a 17=29; ④已知a n +1=a n +3,则数列{a n }为递增数列.其中命题正确的个数为( ) A .4B .3C .2D .1二、多选题31.(2022·江苏·高二课时练习)下列四个选项中,不正确的是( ) A .数列2345,,,3456,⋯的一个通项公式是1n n a n =+ B .数列的图象是一群孤立的点C .数列1,1-,1,1-,⋯与数列1-,1,1-,1,⋯是同一数列D .数列11,24,⋯,12n是递增数列 32.(2022·全国·高二课时练习)意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”,记n S 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68a =B .733S =C .1351920a a a a a +++⋅⋅⋅+=D .2462019a a a a S +++⋅⋅⋅+=33.(2022·全国·高二专题练习)若数列{}n a 满足()12121,1,3,n n n a a a a a n n N --+===+≥∈,则称数列{}n a 为斐波那契数列,又称黄金分割数列.在现代物理、准晶体结构,化学等领域,斐波那契数列都有直接的应用.则下列结论成立的是( ) A .713a =B .135********a a a a a ++++=C .()2233n n n a a a n -+=+≥D .62420202021a a a a a ++++=34.(2022·江苏·高二课时练习)已知数列{}n a 满足()*,01n n a n k n N k =⋅∈<<,下列命题正确的有( )A .当12k =时,数列{}n a 为递减数列 B .当45k =时,数列{}n a 一定有最大项 C .当102k <<时,数列{}n a 为递减数列D .当1kk-为正整数时,数列{}n a 必有两项相等的最大项三、填空题35.(2022·安徽·六安一中高二期中)已知在数列{}n a 中,12a =,111n na a +=-,*n N ∈,则2021a =________.36.(2022·广西·崇左高中高二月考)已知数列{}n a 的前n 项和为n S ,且223n S n =+,则4a =__________.37.(2022·全国·高二课时练习)已知数列{}n a 满足112,0,2121,1,2n n n n n a a a a a ⎧≤<⎪⎪⎨⎪-≤<⎪⎩+=若167a =,则2017a =________.38.(2022·全国·高二)如图,根据下列图形及相应图形中顶点的个数,找出其中的一种规律,写出第n 个图形中共有___________个顶点.四、解答题39.(2022·全国·高二课时练习)在数列{}n a 中,()()10111nn a n n *⎛⎫=+∈ ⎪⎝⎭N .(1)求证:数列{}n a 先递增后递减; (2)求数列{}n a 的最大项.40.(2022·全国·高二课时练习)根据下列条件,写出数列的前4项,并归纳猜想它的通项公式.(1)()*110,21n n a a a n n +==+-∈N ;(2)*11()11n nn a a a a n n +==+∈+N ,; (3)*111()(11)n n a a a n n n +=-=+∈+N ,.41.(2022·全国·高二单元测试)在数列{}n a 中,12a =,点()1,n n a a +在函数()21xf x x=+的图象上.(1)求2a ,3a ,4a 的值;(2)猜想数列{}n a 的一个通项公式.42.(2022·全国·高二单元测试)已知数列{}n a 的通项公式为2299291n n n a n -+=-. (1)求这个数列的第10项; (2)98101是不是该数列中的项?为什么? (3)在区间12,33⎛⎫⎪⎝⎭内是否有数列中的项?若有,求出有几项;若没有,请说明理由.【答案详解】1.A 【详解】数列的项数可以是有限的,也可以是无限的.数列作为一个函数,它的定义域是正整数集或正整数集的有限子集,数列通项的表达式可以不唯一,例如,数列1,0,-1,0,1,0,-1,0,…的通项可以是πsin 2n n a =,也可以是()3πcos 2n n a +=.故①②正确,③④错误. 故选:A . 2.D 【详解】A 由数列的概念可知数列1,3,5,7与7,5,3,1是不同的数列,故A 错误;B 因为首项是0,所以不能表示为{n },故B 错误;C 根据常数列的概念可知数列0,1,0,1,…不是常数列,故C 错误;D 由数列的通项a n =1n n +知, a n +1-a n =12n n ++-1nn +=1(2)(1)n n ++>0, 即数列{1nn +}是递增数列,故D 正确; 故选:D . 3.C 【详解】①是错误的,数列各项顺序不同,即表示不同的数列; ②是错误的,数列{a n }表达数列a 1,a 2,a 3,a 4,…,a n ,…,而数列{a 2n -1}表达数列a 1,a 3,a 5,…,a 2n -1,…,不是同一数列;③是正确的,数列-1,1,-1,1,…的通项公式可以是a n =(-1)n ,a n =cosnπ等; ④是错误的,显然当n =5时,a 5=7,不是数列中的项. 故选:C. 4.D 【详解】由题设,数列的通项公式为21(1)n n -⋅, ∴当n =6时,该项为6211(1)636-⨯=. 故选:D. 5.D解:对A. 1233,5,9a a a ===,可能是数列3,5,9,…的通项公式; 对B. 1233,5,9a a a ===,可能是数列3,5,9,…的通项公式; 对C. 1233,5,9a a a ===,可能是数列3,5,9,…的通项公式; 对D. 1233,5,7a a a ===,不可能是数列3,5,9,…的通项公式; 故选:D. 6.B 【详解】12121233n n n n n n n a a a n n n n ++++⋅⋅=⋅⋅=++++. 故选:B. 7.D解:22298172293248n a n n n ⎛⎫=-++=--+ ⎪⎝⎭,因为n ∈+N ,且78108,107a a ==, 所以此数列最大项为7108a =. 故选:D. 8.C 【详解】 由201120122011120122012n n a n n --==+--,所以当[]1,44n ∈且n N +∈时,{}n a 单调递减; 当[45,)n ∈+∞且n N +∈时,{}n a 单调递减, 结合函数()201220112012f x x -=-的图象,如图所示可得当45n =时,n a 取得最大值,即()45max n a a =, 当44n =时,n a 取得最大值,即()44min n a a =. 故选:C.9.A解:2221441221248n a n n n ⎛⎫=-+=--+ ⎪⎝⎭,因为*21,564n N ∈<<,且5655,54a a ==, 所以数值最大的项为第5项. 故选:A . 10.C解:因为121a a ==,且12n n n a a a --=+,(3)n ≥,所以3212a a a =+=,432213a a a =+=+=,543325a a a =+=+=故选:C 11.B 【详解】 因为1222a a ==, 所以122,1a a ==, 因为21n n na a a ++=-,所以数列的项依次为2,1,1,0,1,1,0,…, 所以从第2项起,3项一个循环,所以{}n a 的前100项的和为233(110)68+⨯++=, 故选:B . 12.B 【详解】因为数列{}n a 中,11a =,22a =,21n n n a a a ++=-,所以3211a a a =-=,所以432121a a a =-=-=-. 故选:B 13.B 【详解】设数列1,3,6,10,15,…为{}n a ,所以2132432,3,4a a a a a a -=-=-=, *5415,2n n a a a a n n N n --=⋯-=∈≥,,,, 所以*1,2n n a a n n N n -=+∈≥,.故选:B. 14.A 【详解】 由111n n a a +=-,且112a = 则211121112a a ===--,32111112a a ===---,()431111112a a ===--- 所以()3*n n a a n N +=∈,即数列{}n a 是以3为周期的周期数列 所以10112a a == 故选:A 15.D 【详解】由题意,数列{}n a 满足()*11n n n a a n n +=∈+N ,所以11n n a n a n +=+, 所以13211221122111132n n n n n aaaan n a a a a a a n n n -----=⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯=-.故选:D . 16.C 【详解】 ∵21,1n S n a =∴=,当2n ≥时,221(1)21n n n a S S n n n -=-=--=-,此时11a =,综上,数列{}n a 的通项公式为21n a n =-.∴110n n nab a +=-21121112112n n n +==---, 记()121112f x x=--,则()f x 在(),5.5∞-与()5.5,∞+上都是增函数, ∴数列{}n b 的最小项是第6项,值为13-. 故选:C 17.C 【详解】1n =时,211333a S a ===,2n ≥时,13n n a S -=,所以()111343n n n n n n n a a S S a a a +-+⇒=-==-,而12134a a a ≠=,所以数列{}n a 从第二项起是以3为首项,4为公比的等比数列,所以21,134,2n n n a n -=⎧=⎨⨯≥⎩. 故选:C. 18.D 【详解】当1n =时,则有113a =; 当2n ≥时,由221123122223n n n n na a a a a ---+++++=,① 可得22123112223n n n n a a a a ---++++=,② ①-②可得1123n n a -=,所以,1132n n a -=⋅,113a =满足1132n n a -=⋅. 故对任意的n *∈N ,1132n n a -=⋅. 故选:D. 19.C解:A ,B 中没有告诉某一项的值,无法递推;D 中a 1=2,a 2=4,a 3=6,不合题意.只有选项C 符合题意. 故选:C 20.A 【详解】a n +1-a n =3n +1-3n =2×3n >0,∴a n +1>a n ,即{a n }是递增数列. 故选:A. 21.D对于①:当1,2,3,4,5,6n =000,故①正确; 对于②:当1,2,3,4,5,6n =000,故②正确;对于③:当1,2,3,4,5,6n =000,故③正确; 所以①②③的通项公式都符合题意, 故选:D.22.C 【详解】因为11a =,21a =,且12n n n a a a --=-,()3n ≥,所以321110a a a -=-==;432011a a a ==--=-;543101a a a =-=--=-;654110a a a =---==;()765011a a a =--=-=;876101a a a -=-==;同理递推可得:90a =;101a =-;111a =-;120a =;131a =;141a =;150a =;161a =-;171a =-;180a =;191a =;201a =.所以()()()()()()2011001111001111001111S =++++-+-+++++-+-+++++-+-++=2. 故选:C 23.D 【详解】 当1n =时,121131a a a +==--;当2n =时,2321112a a a +==--;当3n =时,3431113a a a +==-;当4n =时,454121a a a+==-;…,∴数列{}n a 是以4为周期的周期数列,()()1231123123n n n n a a a a n N *+++⎛⎫∴=⨯-⨯-⨯=∈ ⎪⎝⎭,()10891012236T T a a a a ∴=⋅==⨯-=-.故选:D. 24.C 【详解】因为2121n n n a a a ++=++且121,2a a ==,则321432543216,2115,2137a a a a a a a a a =++==++==++=.25.B解:令函数25,0y x x x=+>, 由对勾函数的性质得函数25y x x=+在()0,5上单调递减,在()5,+∞上单调递增, 所以当5n ≤时,{}n a 是单调递减数列,当5n ≥时,{}n a 是单调递增数列, 所以34567451222a a a a a a a a a >>><<<<<>所以12232425a a a a a a -+-++-()()()()()()()1223423455672456a a a a a a a a a a a a a a =-+-+---++--++25152262621032a a a +-=+-⨯==故选:B 26.B 【详解】由题意可得()111111n n a a n n n n +-==-++,所以21112a a -=-,321123a a -=-,…,1111n n a a n n--=--, 上式累加可得()()()121321--=-+-++-n n n a a a a a a a a111111112231=-+-++-=--n n n, 又13a =,所以14=-n a n. 故选:B . 27.D根据数列可得,分母3,5,7,9,…满足21n , 分子2,8,26,80,…满足31n -,又数列的奇数项为负,偶数项为正,所以可得()31121n nn a n -=-+. 故选:D. 28.C 【详解】由题意得()()1300176a a f f ⎧-<⎪<<⎨⎪<⎩即()1301161310a a a ⎧>⎪⎪<<⎨⎪<-+⎪⎩解得1536a <<故选:C 29.D 【详解】 解:12323nn a a a na G n+++⋯+=,数列{}n a 的“匀称值”为2n G n =+,12323(2)n a a a na n n ∴+++⋯+=+,①2n ∴时,123123(1)(1)(1)n a a a n a n n -+++⋯+-=-+,②①-②,得21n na n =+,21n n a n+∴=,2n , 当1n =时,113a G ==满足上式,21n n a n+∴=,∴9199a =. 故选:D 30.A 【详解】 ①a n =1(2)n n +=1120⇒n =10,易知最大项为第1项,故①正确;对于②,…,则a n =(-1)n +1②正确; 对于③,a n =kn -5,且a 8=11⇒k =2⇒a n =2n -5⇒a 17=29,故③正确; 对于④,由a n +1-a n =3>0,易知④正确. 故选:A 31.ACD 【详解】对于A ,当通项公式为1n n a n =+时,11223a =≠,不符合题意,故选项A 错误; 对于B ,由数列的通项公式以及*n N ∈可知,数列的图象是一群孤立的点,故选项B 正确;对于C ,由于两个数列中的数排列的次序不同,因此不是同一数列,故选项C 错误; 对于D ,数列11,24,⋯,12n是递减数列,故选项D 错误. 故选:ACD . 32.ABCD 【详解】对于A :写出数列的前6项为1,1,2,3,5,8,故A 正确.对于B :71123581333S =++++++=,故B 正确.对于C :由12a a =,342a a a =-,564a a a =-,…,192018a a a =-,可得1351920a a a a a +++⋅⋅⋅+=,故C 正确.对于D :斐波那契数列总有21n n n a a a ++=+,则24620223418191234181919a a a a a a a a a a a a a a a a S +++⋅⋅⋅+=++++⋅⋅⋅++=++++⋅⋅⋅++=,故D 正确.故选:ABCD 33.ABC 【详解】由题意345672,3,5,8,13a a a a a =====,A 正确;20202019201820192017201620192017322019201731a a a a a a a a a a a a a a =+=++==++++=++++,B 正确;21112n n n n n n n n a a a a a a a a ++--=+=++=+,又12n n n a a a --+=,所以221123n n n n n n n a a a a a a a +---+=++-=,C 正确;2021202020192020201820172020201843a a a a a a a a a a =+=++==++++20202018421a a a a a =+++++,D错.故选:ABC . 【点睛】关键点点睛:本题考查数列的递推公式,解题关键是利用递推公式求数列的项,对数列的项进行变形.如BD 在变形以最后一项时要注意是哪一项. 34.BCD 【详解】当12k =时,1212a a ==,知A 错误;当45k =时,1415n n a n a n ++=⋅,当4n <,11n na a +>,4n >,11n n a a +<, 所以可判断{}n a 一定有最大项,B 正确; 当102k <<时,11112n na n n k an n +++=<≤,所以数列{}n a 为递减数列,C 正确;当1k k -为正整数时,112k >≥,当12k =时,1234a a a a =>>>,当112k >>时,令*1km N k=∈-, 解得1mk m =+,则()()111n n m n a a m m ++=+,当n m =时,1n n a a +=, 结合B ,数列{}n a 必有两项相等的最大项,故D 正确; 故选:BCD. 35.12 【详解】由题意12a =,211122a =-=,311112a =-=-,41121a =-=-,所以数列{}n a 是周期数列,周期为3,所以202136732212a a a ⨯+===. 故答案为:12. 36.14 【详解】223n S n =+()()22443=243233=14a S S ∴=-⨯+-⨯+故答案为:14 37.67【详解】因为112,0,2121,1,2n n n n n a a a a a ⎧≤<⎪⎪⎨⎪-≤<⎪⎩+= 所以215217a a =-=,323217a a =-=,43627a a ==,535271a a -==… 故数列{}n a 是以3为周期的周期数列, 又知201736721=⨯+,所以2017167a a ==. 故答案为:67. 38.256n n ++ 【详解】可以先计算1,2,3,n =⋅⋅⋅时顶点的个数,可发现顶点计算的一般规律. 当1n =时,顶点个数为12333=+⨯; 当2n =时,顶点个数为20444=+⨯; 当3n =时,顶点个数为30555=+⨯;…其规律为:第n 个图形应由正2n +边形“扩展”而来,原有顶点个数为2n +,每条边向外扩展正2n +边形,多出2n +个顶点,因此第n 个图形有()()()()222256n n n n n ++++=++个顶点.故答案为:256n n ++. 39. (1)证明:令()112n n a n a -≥≥,即()11011111011nn n n -⎛⎫+ ⎪⎝⎭≥⎛⎫⎪⎝⎭,整理得11110n n +≥,解得10n ≤. 令11n n a a +≥,即()()110111110211nn n n +⎛⎫+ ⎪⎝⎭≥⎛⎫+ ⎪⎝⎭,整理得110211n n +≥+,解得9n ≥. 所以数列{}n a 从第1项到第9项递增,从第10项起递减. (2)解:由(1)知1091091011a a ==最大.40.(1)22113430,211=1,221=4,231=9a a a a a a a =∴=+⨯-=+⨯-=+⨯-, 归纳猜想()()2*1,n a n n -=∈N ;(2)312213231435,2,112213211a a a a a a a a a a ===+=∴=+++=+=+,, 归纳猜想()*1,2n n a n +=∈N ; (3)22134311111,,122111342334a a a a a a a =-∴=+=-=+=+=-⨯=-⨯⨯,, 归纳猜想()*1,n a n n=-∈N41. 【详解】(1)因为点()1,n n a a +在函数()21xf x x=+的图象上, 所以121+=+nn na a a ,又12a =,所以1212413a a a ==+,2324228341713a a a ⨯===++, 343822167811517a a a ⨯===++. (2)由(1)中数列{}n a 的前4项的规律,可归纳出数列{}n a 的一个通项公式为221nn n a =-.42. 【详解】()()()()2231329923291313131n n n n n n a n n n n ---+-===--++.(1)令10n =,得第10项102831a =. (2)令329831101n n -=+,得9300n =. 此方程无正整数解,∴98101不是该数列中的项. (3)令13223313n n -<<+,则31969662n n n n +<-⎧⎨-<+⎩, 解得7863n <<.又n *∈N ,∴2n =.∴区间12,33⎛⎫⎪⎝⎭内有数列中的项,且只有一项.。
高二数列知识点归纳总结

高二数列知识点归纳总结数列作为数学中的重要概念,是高中数学中常见的一种数学对象。
在高二的数学学习中,数列也是重要的考点之一。
为了帮助同学们更好地理解和掌握高二数列知识,在本文中,将对高二数列的知识点进行归纳总结,以便同学们能够系统地学习和应用数列相关的知识。
一、等差数列等差数列是最基本的数列之一,其特点是每个相邻的数之间的差值相等。
它的通项公式为:an = a1 + (n-1)d其中,an表示第n项,a1表示首项,d表示公差。
在等差数列中,我们常常用到的两个重要公式是:1. 等差数列的前n项和Sn的公式:Sn = (a1 + an) * n / 22. 等差数列的前n项和Sn与公差d的关系:Sn = (2a1 + (n-1)d) * n / 2二、等比数列等比数列也是高中数学常见的一类数列,其特点是每个相邻的数之间的比值相等。
它的通项公式为:an = a1 * r^(n-1)其中,an表示第n项,a1表示首项,r表示公比。
在等比数列中,我们常常用到的两个重要公式是:1. 等比数列的前n项和Sn的公式(当r ≠ 1时):Sn = a1 * (1 - r^n) / (1 - r)2. 等比数列的前n项和Sn与公比r的关系(当r ≠ 1时):Sn = a1 * (r^n - 1) / (r - 1)三、数列求和公式的应用在实际问题中,我们经常会遇到需要计算数列前n项和的情况。
除了等差数列和等比数列的求和公式,还有一些常见的数列求和公式可以帮助我们快速求解问题,例如:1. 跳台阶问题:一共有n级台阶,每次可以跳1级或2级,求共有多少种跳法。
这个问题可以转化为求解斐波那契数列的第n+2项,所以答案是f(n+2)。
2. 简单利息问题:某人存钱,第一年存入x元,以后每年比上一年多存入x元,存满n年,求存钱的总数。
这个问题可以转化为求解等差数列的前n项和,所以答案是Sn = n * (a1 + an) / 2。
高二数列整理知识点归纳总结
高二数列整理知识点归纳总结数列是数学中的重要概念,广泛应用于各种数学问题的解决和模型的建立中。
在高二阶段的数学学习中,数列是一个重点和难点内容,需要我们对其进行深入的了解和掌握。
本文将对高二数列相关的知识点进行整理、归纳和总结,旨在帮助同学们更好地掌握数列的概念、性质、求和公式等内容。
一、数列的概念和基本性质1. 数列的定义:数列是按照一定顺序排列的一组数,用{}表示,如{a₁, a₂, a₃, ...}。
2. 数列的项:数列中的每个数叫做数列的项,用a₁, a₂, a₃, ...表示。
3. 数列的通项公式:数列的通项公式又称为递推公式,是用来表示数列中第n项与前面项之间的关系的公式,通常用an表示第n项。
4. 数列的表示方式:数列可以用直接表示法、递推表示法和递归表示法来表示。
5. 数列的有界性:数列可以是有界的(有上界和下界),也可以是无界的。
6. 等差数列:等差数列是指数列中任意两个相邻的项之差都等于同一个常数d,称为等差数列的公差。
7. 等比数列:等比数列是指数列中任意两个相邻的项之比都等于同一个常数q,称为等比数列的公比。
二、数列的求和公式1. 等差数列的求和公式:对于首项为a₁,公差为d的等差数列,前n项的和Sn可以用如下公式表示:Sn = n/2 * [2a₁ + (n-1)d]2. 等比数列的求和公式:对于首项为a₁,公比为q的等比数列,当|q| < 1时,前n项的和Sn可以用如下公式表示:Sn = a₁ * (1 - qⁿ) / (1 - q)三、常见数列的性质和特点1. 等差数列的性质:- 任意一项为an的等差数列,其项与项之间的差值都相等,即aₙ₊₁ - an = d。
- 等差数列的通项公式an = a₁ + (n - 1)d。
- 等差数列的前n项和公式Sn = n/2 * [2a₁ + (n-1)d]。
- 等差数列的性质包括公差、通项、首项、末项、项数和和等。
2. 等比数列的性质:- 任意一项为an的等比数列,其相邻两项的比值都相等,即an₊₁/an = q。
高二数学等差数列和等比数列的复习
等差数列和等比数列的复习一、知识要点1.等差数列和等比数列是两种最基本,最常见的数列.应熟练掌握等差、等比数列的定义、通项公式、前n项和公式,通过通项公式与前n项和公式联系着五个基本量a1,d(或q),n, a n, S n,“已知其三必可求其余二”,将等差、等比数列问题,转化为关于这五个基本量的运算问题,是常见的解题方法.2.等差、等比数列具有很多特殊性质,在运算时,除转化为基本量,运用方程思想解决之外,还常通过灵活运用性质,从而简化运算,常用性质如下:①考察数列的项的下标之间的联系:等差等比m,n属于N,则a n=a m+(n-m)d m,n属于N,则a n=a m·q n-mm,n,p,q属于N,m+n=p+q,则a m+a n=a p+a q m,n,p,q属于N,m+n=p+q,则 a m·a n=a p·a q ②数列的运算:若{a n}, {b n}为等差数列,则{a n±b n}为等差数列若{a n}, {b n}为等比数列,则{a n,b n}, {}(b n≠0)为等比数列若{a n}为正项等比数列,则{lga n}为等差数列若{a n}为等差数列,则{}(C为正常数)为等比数列等.还可以运用等差,等比数列的定义,证明通过其他运算所产生的新数列具有等差或等比的特征,我们应对此加以关注,从而了解新数列的特殊性,运用等差,等比性质解题.③等差或等比的子数列所具有的性质:等差等比若m,n,p成等差,则a m,a n,a p成等差若m,n,p成等差,则a m,a n,a p成等比,公比为q n-m.S m, S2m-S m, S3m-S2m成等差,公差为m2d S m, S2m-S m, S3m-S2m成等比,公比为q m如等差数列{a n}的前m项和为30, 前2m项和为100,求它的前3m项的和.可设前m项之和为V1,m+1到2m项之和为V2,2m+1到3m项之和为V3,利用V1,V2,V3成等差数列,于是:V1=30, V2=100-30=70, d=70-30=40,所以 V3=V2+d=70+40=110.所以前3m项之和S3m=S m+(S2m-S m)+(S3m-S2m)=V1+V2+V3=210.再如,{a n}是由正数组成的等比数列,公比q=2, 且a1·a2·a3……a30=230, 求a3·a6·a9……a30的值.若利用等比数列的性质,将数列{a n}的前30项分成三组,于是设a1a4a7……a28=xa2a5a8……a29=x·210a3a6a9……a30=x·220于是有230=x(x·210)·(x·220)=x3·230,所以 x=1又 x属于R, 所以x=1,所以 a3a6a9……a30=220,由以上两个例可以看出,灵活运用等差、等比数列的有关性质,可以提高解题技能,减少运算量.3.注意运用函数的观点和方法揭示等差数列和等比数列的特征,在分析和解决数列综合题时要注意运用数学思想方法以及和函数,不等式知识的联系.二、典型问题:例1.已知数列{a n}的前n项和S n=10n-n2,数列{b n}的每一项都有b n=|a n|,求数列{b n}的前n项和T n.分析与解答:①判断{a n}是等差数列:a1=S1=9当n≥2时,a n=S n-S n-1=(10n-n2)-[10(n-1)-(n-1)2]=11-2n.又当n=1, 11-2n=9=a1,所以数列{a n}的通项公式为 a n=11-2n.所以数列{a n}是以9为首项,以-2为公差的等差数列.②判断{b n}的特征并转化为等差数列求和,因为b n=|a n|,而{a n}中,当n≤5时,a n>0,当n>5时,a n<0,所以 {|a n|}的前5项与{a n}对应项相同,从第6项起,{|a n|}各项与{a n}对应项符号相反,绝对值相同,所以当n≤5时,T n=S n=10n-n2.当n≥6时,T n=a1+a2+……+a5-a6-a7-……-a n=-(a1+a2+……+a n)+2(a1+a2+……+a5)=-S n+2S5=n2-10n+50.综上所述,可得数列{b n}的前n项和T n为T n=点评:运用函数观点去认识数列问题,{b n}虽不是等差数列,但可寻找它与等差数列的联系,通过分类讨论,可将{b n}转化,利用等差求和.所以,结果需用分段函数加以表述.例2.已知数列{a n}中,S n是它的前n项和,并且S n+1=4a n+2(n=1,2,……), a1=1,(1)设b n=a n+1-2a n(n=1,2,……),求证数列{b n}是等比数列.(2)设C n=(n=1,2,……),求证数列{C n}是等差数列.(3)求数列{a n}的通项公式及前n项和的公式分析与解答:(1)因为S n+1=4a n+2 所以 S n+2=4a n+1+2以上两式等号两边分别相减,得 S n+2-S n+1=4a n+1-4a n(n=1,2,……)即 a n+2=4a n+1-4a n变形,得 a n+2-2a n+1=2(a n+1-2a n) 因为 b n=a n+1-2a n(n=1,2,……)所以 b n+1=2b n.由此可知,数列{b n}是公比为2的等比数列.由S2=a1+a2=4a1+2, a1=1, 所以 a2=5, 所以 b1=a2-2a1=3,所以 b n=3·2n-1(2) C n=(n=1,2,……)所以 C n+1-C n=将 b n=3·2n-1,代入得,C n+1-C n=(n=1,2,……)由此可知,数列{C n}是公差为的等差数列,它的首项C1=,故C n=(n-1)=n-.(3)C n=n-=(3n-1) 所以 a n=2n·C n=(3n-1)·2n-2(n=1,2,……)当n≥2时,S n=4a n-1+2=(3n-4)2n-1+2由于S1=a1=1也适合此公式,故所求{a n}的前n项和公式是S n=(3n-4)2n-1+2.点评:该题是着眼于数列间的相互关系的问题,解题时,要注意利用题设的已知条件,通过合理转换,将非等差,等比数列转化为等差,等比数列,求得问题的解决利用等差(比)数列的概念,将已知关系式进行变形,变形成能做出判断的等差或等比数列,这是数列问题中的常见策略.例3.已知a>0, a≠1,数列{a n}的首项是a,公比也是a的等比数列,令b n=a n·lga n(n属于N).(1)求数列{b n}的前n项和S n;(2)当数列{b n}中的每一项总小于它后面的项时,求a的取值范围. 分析与解答:(1) 由题意得, a n=a n, b n=n·a n lga,S n=b1+b2+b3+……+b n =(1·a+2·a2+3·a3+……+n·a n)lgaaS n=(1·a2+2·a3+3·a4+……+n·a n+1)lga以上两式相减得:(1-a)S n=(a+a2+a3+……+a n-n·a n+1)lga =[-n·a n+1]·lga=[1-(1+n-na)a n]因为a≠1,所以S n=[1-(1+n-na)a n].(2)由b k+1-b k=(k+1)a k+1lga-k·a k lga=a k lga[k(a-1)+a]由题意知,b k+1-b k>0,而a k>0, 所以 lga[k(a-1)+a]>0...........①若a>1, 则lga>0, k(a-1)+a>0, 所以不等式①显然成立,若0<a<1,则 lga<0,故不等式①成立k(a-1)+a<00<a<恒成立.因为 k属于N, 所以 ()min=,所以 0<a<恒成立0<a<,综上,a的取值范围是a属于(0,)u(1,+∞).点评:①对于数列的求和问题,要注意运用教材中推导等比数列前n项和公式的基本方法.②在解决第二问时,要注意将数列与不等式,函数有机结合,揭示知识间的内在联系,确定a 的取值范围.三、课后练习:(1)已知a1,a2,……a8为各项都大于零的等比数列,公比q≠1,则().A、a1+a8>a4+a5B、a1+a8<a4+a5C、a1+a8=a4+a5D、a1+a8和a4+a5的大小关系不能由已知条件确定(2)已知a,b,c的倒数或等差数列,且a,b,c互不相等,则为().A、 B、 C、 D、(3)一个等差数列共 2n+1项,其中奇数项之和为305,偶数项之和为244,则第n+1项为().A、63B、62C、61D、60(4)设A、B、C分别是等比数列 {a n}的前n项和,数列{b n}是等差数列,公差d=,若log x a n-b n=log x a1-b1,求x.(5)设A、B、C分别是等比数列{a n}的前n项和,前2n项和,前3n项和,试比较A2+B2与A(B+C)的大小.(6) 某企业在“减员增效”中,对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的领取工资.该企业根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,没有利润,第二年每人可获b元收入,从第三年起,每人每年的收入可在上一年基础上递增50%,如果某人分流前工资收入每年a元,分流后第n年的总收入为a n元.①试写出a n与n(n≥2)的函数关系;②当b=a时,这个人哪一年收入最少,最少收入是多少?③当b≥a时,是否一定可以保证这个人分流一年后的年收入永远超过分流前的年收入.参考答案:(1) A (2)C (3)C (4)x=8 (5) A2+B2=A(B+C)(5)①a n=a()n-1+b()n-2 (n≥2)②n=3③当n≥2时,a n=a()n-1+b()n-2≥a()n-1+a()n-2≥2=2=a.上述等号成立,须b=a,且a()n-1=a()n-1,即 ()2n-2=()2, 所以 n=1+, 因为 1+>1+=2 所以 1+不是自然数.因此等号不能取到,即当n>2时,有a n>a,但当n=2时,a2=a+a=a>a.综上,当b≥a时,一定可以保证这个人分流一年后的年收入永远想过分流前的年收入.。
高二数列六大方法知识点
高二数列六大方法知识点数列是高中数学中的重要概念,也是很多数学问题的基础。
在高二数学中,数列的学习是相当重要的一部分。
在本文中,我们将介绍高二数列中的六大方法知识点,帮助同学们更好地掌握和应用数列的知识。
一、等差数列等差数列是指数列中的相邻两项之间的差恒定的数列。
等差数列常用的表示方法是:an = a1 + (n-1)d,其中an是数列的第n项,a1是数列的首项,d是等差。
等差数列的求和公式为:Sn = (a1 + an) × n ÷ 2。
二、等比数列等比数列是指数列中的相邻两项之间的比恒定的数列。
等比数列常用的表示方法是:an = a1 ×r^(n-1),其中an是数列的第n项,a1是数列的首项,r是公比。
等比数列的求和公式为:Sn = a1 × (1 - r^n) ÷ (1 - r)。
三、递推数列递推数列是指数列中的每一项都通过前面的项进行计算得出的数列。
递推数列的表示方法较为灵活,常用的有递推式和初值两种形式。
递推数列的计算可以通过不断递推或者构建递推关系式来完成。
四、求通项公式通项公式是求数列中的第n项的公式,它可以通过观察数列的特点让我们找到规律,从而便于计算数列中任意一项的值。
常见的数列如等差数列和等比数列都有通项公式,利用这些通项公式可以简化数列计算的过程。
五、数列的性质和应用数列除了一些基本的概念和计算方法外,还有一些性质和应用,这些内容通常也是高二数列的重点和难点。
比如数列的单调性、极限、递归和数列在实际问题中的应用等等,这些内容需要同学们深入理解和掌握。
六、综合练习与解题技巧数列的应用十分广泛,相应地解题技巧也是多种多样的。
在学习数列的过程中,同学们需要通过大量的练习来提高对数列特点的把握和运用能力。
可以通过课后习题、模拟试卷等方式进行综合练习,并结合老师的指导进行解题技巧的学习和掌握。
综上所述,高二数列的六大方法知识点对于同学们掌握数列的概念和运用都非常重要。
数列期末复习专题(一)学案-2023-2024学年高二下学期数学人教A版(2019)选择性必修第二册
期末复习——数列专题(一)* 学习目标:1.复习并掌握数列,等差数列以及等比数列的概念与性质.2.复习并掌握等差数列前n 项和与等比数列前n 项和的公式以及性质. 一、知识梳理等差数列等比数列概 念一般地,如果一个数列从第2项起, 每一项与它的前一项的差等于同一个常数,那么这个数列叫做等差数列. 即:a n +1-a n =d (d 为常数) 一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数(不为0),那么这个数列叫做等比数列.即:a n +1a n =q (q 为非零常数)通 项 公 式a n =a 1+(n -1)d拓展公式:a n =a m +(n -m )d a n =a 1∙q n -1拓展公式:a n =a m ∙q n -m 数 列 判 定①定义法:a n +1-a n =d①中项法:a n -1+a n +1=2a n ①函数法:a n =kn +b①前n 项和公式法:S n =An 2+Bn①定义法:a n +1a n=q①中项法:a n -1∙a n +1=a 2n ①函数法:a n =k ∙q n①前n 项和公式法:S n =k ∙q n -k数 列 性 质(1)单调性: ①d >0 ① 递增数列; ①d <0 ① 递减数列; ①d =0 ① 常数列. (2)对偶性:若m +n =p +q ,则a m +a n =a p +a q(3)等差中项:若a ,b ,c 成等差数列,则b 叫做a 与c 的等差中项,满足关系a +c =2b .(1)单调性:①⎩⎪⎨⎪⎧a 1>0q >1或⎩⎪⎨⎪⎧a 1<00<q <1 ① 递增数列;①⎩⎪⎨⎪⎧a 1<0q >1或⎩⎪⎨⎪⎧a 1>00<q <1 ① 递减数列;① q =1 ① 常数列. (2)对偶性: 若m +n =p +q ,则a m ·a n =a p ·a q (3)等比中项: 若a ,b ,c 成等比数列,则b 叫做 a 与c 的等比中项,满足关系a ∙c =b 2 前n 项 和公式 S n =n (a 1+a n )2=na 1+n (n -1)2dS n =⎩⎪⎨⎪⎧na 1 (q =1)a 1(1-q n )1-q =a 1-a n q 1-q (q ≠1) 等距连 续性质 S m ,S 2m -S m ,S 3m -S 2m ,…成等差数列,公差为m 2d当S k ≠0,k ①N *时,有S k ,S 2k -S k ,S 3k -S 2k ,…也成等比数列,公比为q k 等距间 隔性质“a k ,a k +m ,a k +2m ,…”成等差数列, 公差为md (k ,m ①N *)“a n ,a n +k ,a n +2k ,…”成等比数列, 公比为q k等差数列常用性质补充:1.两个等差数列{a n },{b n }的前n 项和S n ,T n 之间的关系为S 2n -1T 2n -1=a nb n .2.已知数列{a n }是等差数列,S n 是其前n 项和. (1)若{b n }是等差数列,则{pa n +qb n }也是等差数列. (2)数列}{nS n成等差数列;(3)若等差数列的项数为2n ,则S 2n =n (a n +a n +1),S 偶-S 奇=nd ,S 偶S 奇=a n +1a n(S 奇≠0).(4)若等差数列的项数为2n +1,则S 2n +1=(2n +1)a n +1(a n +1是数列的中间项),S 偶-S 奇=-a n +1,S 偶S 奇=nn +1(S奇≠0).(5)在等差数列中,若S n =m ,S m =n ,则S m +n =-(m +n ). 等比数列常用性质补充:1.若{a n },{b n }(项数相同)是等比数列,则{λa n }(λ≠0),}1{n a ,{a 2n },{a n ·b n },}{nn b a 仍是等比数列. 2. m nm n m n n m S S q S S q S +=+=+; 3.当等比数列项数为偶数时,S q S =偶奇;—————————————————————————————————————————————————二、典例分析 题型一 等差数列的通项公式及其应用 例1 在数列{a n }中,已知a 1=3,当n ≥2时, 1a n -1a n -1=15,则a 16=______________例2 已知单调递增的等差数列{a n }的前三项之和为21,前三项之积为231,求数列{a n }的通项公式.题型二 等差数列与函数的关系例3 已知数列{}a n 是等差数列,且a n =an 2+n ()n ∈N *,则实数a =________. 题型三 等差数列的判定例4 已知a 1=2,若a n +1=2a n +2n +1,证明}2{n na 为等差数列,并求{a n }的通项公式.例5 已知数列{a n }满足a n +1=6a n -4a n +2,且a 1=3(n ∈N *).(1)证明:数列}21{-n a 是等差数列;(2)求数列{a n }的通项公式.题型四 等差数列的性质例6 在等差数列{a n }中,已知a 2=5,a 8=17,求数列的公差及通项公式.例7 已知等差数列{a n }中,a 3+a 6=8,则5a 4+a 7=_____例8 若关于x 的方程x 2-2x +m =0和x 2-2x +n =0(m ≠n )的四个根可组成首项为14的等差数列,则|m -n |的值是________.题型五 由等差数列生成的新等差数列例9 已知两个等差数列{a n }:5,8,11,…,与{b n }:3,7,11,…,它们的公共项组成数列{c n },则数列{c n }的通项公式c n =________;若数列{a n }和{b n }的项数均为100,则{c n }的项数是________.题型六 等差数列前n 项和公式,性质与最值 例10 在等差数列{a n }中:(1)已知a 5+a 10=58,a 4+a 9=50,求S 10 =_______. (2)设S n 是等差数列{a n }的前n 项和.若a 1=-2 021,S 6-2S 3=18,则S 2 023=________.例11 (1)已知等差数列{a n }和{b n }的前n 项和分别为S n 和S n ′,如果S n S n ′=7n +14n +27(n ∈N *),则a 11b 11的值是__________.(2)等差数列{a n }的前m 项和为30,前2m 项和为100,求数列{a n }的前3m 项的和S 3m .例12 已知等差数列{a n }中,S n 为数列{a n }的前n 项和,若S 2=16,S 4=24,求数列{|a n |}的前n 项和T n .例13 设{a n }为等差数列,S n 为数列{a n }的前n 项和,已知a 2+a 5=1,S 15=75,T n 为数列⎩⎨⎧⎭⎬⎫S n n 的前n 项和.(1)求S n ; (2)求T n 的最小值.题型七 等比数列的一些基本概念例14 (1)以下数列中,能判定数列是等比数列的有____ ①数列{}a n 中,已知a 2a 1=2,a 3a 2=2;②常数列a ,a ,…,a ,…;③数列{}a n 中,a n +1a n =q (q ≠0),其中n ∈N *.(2)若1,a ,3成等差数列,1,b ,4成等比数列,则ab 的值为________.(3)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.题型八等比数列的判定及性质例15 (1)已知数列{}a n是等比数列,且公比大于0,则“q>1”是“数列{}a n是递增数列”的()A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件(2)已知数列{}a n,且a1=2,a n+1=4a n-3n+1(n∈N*),①证明:数列{a n-n}是等比数列;②求出{a n}的通项公式.例16 已知{a n}为正项等比数列.(1)若a2a4+2a3a5+a4a6=25,求a3+a5;(2)若a5a6=9,求log3a1+log3a2+…+log3a10的值.题型九等比数列前n项和公式,性质例17 (1) a1+a3=10,a4+a6=54,求S5;(2)已知数列{a n}是首项为a1,公比为q的等比数列,其前n项和为S n,且有5S2=4S4,求公比q的值.例18 (1)等比数列{a n}的前n项和为S n,S2=7,S6=91,则S4为__________.(2)正项等比数列{a n}的前n项和为S n,其中S n=2,S3n =14则S4n为__________.(3)等比数列{a n}的前n项和为S n,公比q=2,S99=56,则a3+a6+a9+…+a99 =__________.例19 一个等比数列的首项是1,项数是偶数,其奇数项的和为85,偶数项的和为170,求此数列的公比和项数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
第一章 数列 (一)
题型1 已知数列的前几项,求通项公式na.
1、求下列数列的一个通项公式:
(1),,33,17,9,5,3 (2),,9910,638,356,154,32 (3)
,,21,15,10,6,3,1
题型2 已知数列的前n项和,求通项公式
2、已知下列数列na的前n项和nS,分别求它们的通项公式
n
a
.
⑴nnSn322; ⑵
13nnS
.
题型3 已知数列的递推式,求通项公式
3、数列na中,)2(22,1111naaaannn,求5432,,,aaaa,并归纳出
n
a
.
4、数列na中,12,111nnaaa,求
通项公式
n
a
.
题型4 已知数列通项公式,判断数列单调性并求项数及最大(最小)项
5、数列na中,
452nna
n
.
⑴18是数列中的第几项?
⑵n为何值时,na有最小值?并求最小值
.
6、数列na中,122nnan.求数列na的最小项;
题型5 已知通项公式na与前n项和nS的关系式,求通项公式na
7、已知数列na的首项112a,其前n项和21nnSnan.求数列na 的通项公式.(先用
n-1替换n,再用迭乘法)
8、nS为数列na的前n项和, )2,(23nNnaSnn,求数列na的通项公式.
2
题型6知等差数列的某些项,求某项
9、na为等差数列,20,86015aa,则75a
题型7知前n项和nS及其某项,求项数.
10、若一个等差数列的前4项和为36,后4项和为124,且所有项的和为780,求这个数列的项数n.
题型8已知等差数列前n项和,求含绝对值问题
【解题思路】利用nS求出na,把绝对值符号去
掉转化为等差数列的求和问题. 含绝对值符号的数列求和问题,要注意分类讨论.
11、已知nS为等差数列na的前n项和,212nnSn.
⑴求321aaa;
⑵求10321aaaa;
⑶求naaaa321.
等差数列的性质
12、⑴已知nS为等差数列na的前n项和,1006a,则11S ;
⑵已知nS为等差数列na的前n项和,)(,mnnSmSmn,则nmS .
⑵令BnAnSn2,则
nmmnBmnAnBmAmmBnAn)()(
22
2
2
.
mn,
1)(BmnA
,
)()()(2nmnmBnmASnm
;
13、含12n个项的等差数列其奇数项的和与偶数项的和之比为 .
14、设nS、nT分别是等差数列na、na的前n项和,327nnTSnn,则55ba .
15、设数列na中,112,1nnaaan,则通项na .(利用累加法)
3
判断或证明数列是等差数列的方法有:
⑴定义法:daann1(Nn,d是常数)na是等差数列;
⑵中项法:212nnnaaa(Nn)na是等差数列;
⑶通项公式法:bknan(bk,是常数)na是等差数列;
⑷前n项和公式法:BnAnSn2(BA,是常数,0A)na是等差数列.
题型9知等比数列的某些项,求某项
16、已知na为等比数列,162,262aa,则10a
题型10已知前n项和nS及其某项,求项数.
17、已知nS为等比数列na前n项和,93nS,48na,公比2q,则项数n
.
题型11已知nS为等比数列na前n项和,nnna3)12(,求nS. (
错位相减法求和.)
等比数列的判定方法:
⑴定义法:qaann1(Nn,0q是常数)na是等比数列;
⑵中项法:221nnnaaa(Nn)且0nana是等比数列.
18、已知nS为等比数列na前n项和,54nS,602nS,则nS3 .
19、已知数列na中,nnnaaa32,111,求数列na的通项公式
.
20、已知nm,且naaam,,,,321和nbbbbm,,,,,4321都是等差数列,则2313bbaa
21、已知函数.424)(xxxf则 ①)32()31(ff ;
②)20092008()20092()20091(fff .
4
题型12 公式法、性质法求和
22、⑴等比数列,222132,,,中的第5项到第10项的和为:
⑵等差数列na的前n项和为18,前n2项为和28,则前n3项和为
题型13 裂项相消法求和,数列的常见拆项有
:111)1(1nnnn;
nnnn1
1
1
;)2)(1(1)1(121)2)(1(1nnnnnnn
23、求和:
)1(1431321211nn
.
求和:
)13)(23(11071741411nn
;
求和:
nn1134123112
1
.
题型14 倒序相加法求和
24、
设221)(xxxf,求:⑴)4()3()2()()()(213141ffffff;
⑵).2010()2009()2()()()()(21312009120101fffffff
题型15 等差、等比数列的综合应用
25、已知等差数列na与等比数列nb中,633221,,1ababab,求nb的通项.
26、设nS是数列na的前n项和,11a,)2(212nSaSnnn.
⑴求na的通项; ⑵设12nSbnn,求数列nb的前n项和nT.
