中值定理命题证明中的辅助函数构造
【最新精选】辅助函数法的构造及应用

浅析辅助函数的构造及应用陈小亘(湛江师范学院信息科学与技术学院 广东 湛江524048)摘要:本文阐述了辅助函数的基本特征与构造辅助函数的原则,并介绍几种较为典型的构造辅助函数的方法应用.关键词:辅助函数;原函数法;参数变易法;常数k 值法中图分类号:O13;O17;O172;O174;O174.4 文献标识码: A1 引言辅助函数法是数学证明中经常使用的一种非常有用的方法,是数学解题中构造的辅助问题的一种.它是依据数学问题所提供的信息而构造的函数,再利用这个函数的特性进行求解.构造辅助函数是将原来的数学间题转化为容易解决的辅助函数问题.这就要求我们在所掌握的数学知识基础上,全面把握数学问题所提供的信息即问题本身的特点、背景以及与其它问题之间的关系,运用基本的数学思想,经过认真的观察,深入的思考,才能构造出所需要的辅助函数.这个构造过程是一个从特殊到一般的过程,而运用辅助函数返回去解决原数学问题又是一个从一般到特殊的过程.这是一种创造性的思维过程,具有较大的灵活性,需要技巧.如何才能找到合适的辅助函数?这是教学过程中的难点之一,教师难教,学生难学.许多教科书和教学参考书中常常是直接给出辅助函数,使学生感到突然,遇到难题无从下手.2 辅助函数的基本特点及构造原则所谓构造法,就是按一定方式,经有限步骤能够实现的方法,在解题时常表现的是不对问题本身求解,而是构造一个与问题有关的辅助函数问题进行求解.它具有两个显著的特征:直观性和可行性.正是这两个特性,在数学解题中经常运用它,但是如何构造辅助函数,始终是一个难点,因此应重视这种思想方法的引导和渗透,多做归纳总结.辅助函数有许多基本特点.首先,辅助函数题设中没有,结论中也没有,仅是解题中间过程中构造出来的,类似于平面几何中的辅助线,起辅助解题的作用.其次,同一个命题可构造多个辅助函数用于解题.再次,构造辅助函数的思想较宽广. 然而,不同的辅助函数直接关系到解题的难易,因此构造最恰当的辅助函数是关键.如何构造辅助函数?事实上,我们在构造辅助函数时,必须遵循一定的原则.这是因为辅助函数的构造是有一定规律的,当某些数学问题使用通常办法按定势思维去考虑很难奏效时,可根据题设条件和结论的特征、性质展开联想,进而构造出解决问题的特殊模式.构造辅助函数的第一原则是:将未知化为已知.在一元微积分学中许多定理的证明都是在分析所给命题的条件、结论的基础上构造一个函数,将要证的问题转化为可利用的已知结论来完成. 其次,将复杂化为简单.一些命题较为复杂,直接构造辅助函数往往较困难,可通过恒等变形,由复杂转化为简单,从中探索辅助函数的构造,以达到解决问题的目的.再次,利用几何特征.在许多教科书中,微分中值定理的证明是利用对几何图形的分析,探索辅助函数的构造,然后加以证明.本文给出几种常用构造辅助函数的方法应用. 3 几种构造辅助函数的方法应用3.1 原函数法 (亦称积分法或逆推法)原函数法是指从所要证明的结论出发,如欲证0)(='ξF ,则可通过倒推,分析了原函数)(x F 的形式,从而构造出辅助函数的方法.这一方法适用于“证明至少存在一点ξ,使得 关于ξ及其函数的代数式成立”这类命题的证明.构造辅助函数的步骤:第一步:将命题中的ξ换成x ;第二步:通过恒等变形将结论化为易消除导数符号的形式;第三步:用观察法或积分法求出原函数,为方便积分常数常常取为零;第四步:移项使等式一边为零,则另一边即是所求辅助函数)(x F .例3.1 设函数)(),(x g x f 在],[b a 上二阶可导,且0)()()()(====b g a g b f a f ,0)(≠x g ,0)(≠''x g ,证明:至少存在一点),(b a ∈ξ,使得)()()()(ξξξξg f g f ''''=. 分析:令x =ξ,则)()()()(ξξξξg f g f ''''=⇒)()()()(x g x f x g x f ''''= ⇒)()()()(x f x g x g x f ''=''⇒dt t g t f dt t g t f xx o ⎰⎰''=''0)()()()(⇒dt t g t f x g x f dt t g t f x g x f xx o ⎰⎰''-'=''-'0)()()()()()()()( ⇒)()()()(x g x f x g x f '='⇒0)()()()(='-'x g x f x g x f .证明:令x =ξ,=)(x F )()()()(x g x f x g x f '-',依条件,)(x F 在],[b a 上连续,在),(b a 内可导,且0)()(==b F a F ,由罗尔中值定理可知,至少存在一点),(b a ∈ξ,使得0)(='ξF ,即 0)()()()(='-'ξξξξg f g f . 由于0)(≠ξg ,0)(≠''ξg ,故)()()()(ξξξξg f g f ''''=. 如下的命题也可以用这一方法来证明: 如果函数)(),(x g x f 在],[b a 上可导,且0)(≠'x g ,则至少存在一点),(b a ∈ξ,使得)()()()()()(ξξξξg f b g g f a f ''=--.3.2 参数变易法参数变易法是指把命题中的某个参数“变易”为变量x ,从而构造出相应的辅助函数的方法. 命题的证明思路:第一步:将命题中的某一参数(a 或b )换成x ;第二步:移项使等式一边为零,则另一边即是所求辅助函数)(x F ;第三步:根据有关定理完成命题的证明.例3.2 设)(),(t g t f 是在],[b a 上连续增加函数,0,>b a ,证明:⎰⎰⎰-≤b ab a ba dt t g t f ab dt t g dt t f )()()()()( 证明:把上式中的b 换成x ,移项,然后作辅助函数 ⎰⎰⎰--=x ax a xa dt t g t f a x dt t g dt t f x F )()()()()()(. 由于)()()()()()()()()()(x g x f a x dt t g t f dt t f x g dt t g x f x F x a x a x a ---+='⎰⎰⎰ ))()()()()()()()(⎰⎰⎰⎰--+=xa x a x ax a dt x g x f dt t g t f dt t f x g dt t g x f ⎰---=xa dt t g x g t f x f )]()()][()([. 又)(),(t g t f 均为连续增加函数,因此,0)(<'x F ,)(x F 为减少函数.0)()(=≤a Fb F . 即0)()()()()(≤--⎰⎰⎰ba b a ba dt t g t f ab dt t g dt t f . 所以⎰⎰⎰-≤b ab a ba dt t g t f ab dt t g dt t f )()()()()(. 如下的命题也可以用这一方法来证明: 如果)(x f 是在],[b a 上连续函数,且0)(>x f ,则2)()(1)(a b dx x f dx x f b a b a -≥⎰⎰. 3.3 泰勒公式法泰勒公式法是指利用泰勒公式来构造辅助函数的方法. 这一方法适用于“含有被积函数)(x f 有二阶或二阶以上连续导数”这类命题的证明.命题的证明思路:第一步:令辅助函数⎰=xa dt t f x F )()(;第二步:将)(x F 在所需点处进行泰勒展开;第三步:对泰勒余项作适当处理(可考虑用介值定理).例 3.3设函数)(x f 在],[b a 上具有连续的二阶导数,证明在),(b a 内存在一点ξ,使得⎰ba dx x f )(=)2()(b a f a b +-+()(2413f a b ''-ξ) 证明:令⎰=xa dt t f x F )()(,则有0)(=a F ,)()(x f x F =',)()(x f x F '='',)()(x f x F ''=''',)(x F 在0x 2b a +=处的二阶泰勒公式为 2)2)(2(!21)2)(2()2()(b a x b a F b a x b a F b a F x F +-+''++-+'++=+3)2)((!31b a x F +-'''ξ F =)2(b a ++f )2(b a +-x (2b a +)f '+!21)2(b a +-x (2b a +2)+)(!31ξf ''-x (2b a +3) 其中ξ在x 与2b a +之间. 分别将b x =,a x =代入上式,并相减,则得 2)()()(241)2()()()(213ξξf f a b b a f a b a F b F +''-++-=-, 其中1ξ,2ξ分别在2b a +与b ,a 与2b a +之间. 不妨设)()(21ξξf f ''≤'',则2)()()(211ξξξf f f ''+''≤'')(2ξf ''≤,考虑到)(x f ''的连续性及介值定理,可知在1ξ,2ξ之间至少存在一个),(b a ∈ξ使2)()()(21ξξξf f f ''+''=''. 故 )()()(a F b F dx x f ba -=⎰=)2()(b a f a b +-+()(2413f a b ''-ξ). 3.4常数k 值法在要证明的命题中,把常数分离,然后用以下步骤求辅助函数:第一步:将常数部分记作k ;第二步:恒等变形,使等式一端为a 的代数式,另一端为b 的代数式;第三步:分析关于端点的表达式是否为对称式,若果是,只要把端点a 改成x ,则换变量后的端点表达式就是所求的辅助函数.这样的方法就是常数k 值法.例3.4 设)(x f ''在],[b a 上存在,b c a <<,证明:至少存在一点),(b a ∈ξ,使得)(21))(()())(()())(()(ξf b c a c c f c b a b b f c a b a a f ''=--+--+--. 分析:令k b c a c c f c b a b b f c a b a a f =--+--+--))(()())(()())(()(. ⇒))()(()()()()()()(c b c a b a k c f b a b f a c a f c b ---=-+-+-,这是关于端点c b a ,,的轮换对称式,令x b =(可以令x a =或x c =),于是))()(()()()()()()()(c x c a x a k c f x a x f a c a f c x x F -----+-+-=.证明:令))()(()()()()()()()(c x c a x a k c f x a x f a c a f c x x F -----+-+-=,则)(x F 在],[],,[b c c a 上满足罗尔定理,于是分别存在),(),,(21b c c a ∈∈ξξ使得0)()(21='='ξξF F ,又))(())(()()()()()(c a x a k c x c a k x f a c c f a f x F -----+'-+-='.)(2)()()(c a k x f a c x F -+''-=''. 由罗尔中值定理,至少存在),(),(21b a ⊂∈ξξξ,使得0)(=''ξF ,即0)(2)()(=-+''-c a k f a c ξ. 从而)(21ξf k ''=. 命题得证. 3.5 微分方程法微分方程法是指通过求一个常微分方程的通解而构造辅助函数的方法.构造出辅助函数的步骤:第一步:将命题中的ξ换成x ;第二步:移项使等式一边为零,得一个常微分方程;第三步:求得常微分方程的通解,在通解中的常数令为零可得辅助函数.例3.5 设函数)(x f 在]1,0[上可导,且满足关系 )1()(2210f dx x xf ⎰=. 证明:至少存在一点)1,0(∈ξ,使得 0)()(=+'ξξξf f .分析:令x =ξ,0)()(=+'ξξξf f ⇒0)()(=+'x x f x f ⇒xx f x f 1)()(-=',积分得c x x f ln ln )(ln +-=⇒xc x f =)(⇒c x xf =)(. (令0=c ). 令)()(x xf x F =. 证明:由条件知)()(x xf x F =在]1,0[上连续,在)1,0(可导. 于是由积分中值定理,至少存在一点),0(21∈η,使得 )()(2)(2)1(210210ηηηηf dx f dx x xf f ⎰⎰===.可见)()()1()1(ηηηf F f F ===. 对)()(x xf x F =,由罗尔中值定理,至少存在一点)1,(ηξ∈,使得0)(=ξF ,即0)()(='+ξξξf f . 也就是0)()(=+'ξξξf f .总之,构造辅助函数有许多方法(见[1],[2],[3],[4],[5],[6]). 对于不同的命题,我们必须根据实际情况灵活地选择不同的构造辅助函数的方法. 有时,对于一个命题,可以同时利用不同的方法来完成命题的证明.这就要求我们在教与学的过程中不断去探索新的方法.参考文献:[1 ] 同济大学. 高等数学(第五版) [M ]. 北京: 高等教育出版社, 2002.[2 ] 刘玉琏,付沛仁. 数学分析讲义[M]. 北京: 高等教育出版社, 1997.[3 ] 龚冬保. 高等数学典型题解法、技巧、注释[M ]. 西安:西安交通大学出版社, 2000.[4 ] 陈文灯. 考研数复习指南[M] . 北京: 世界图书出版公司,2009.[5 ] 李君士. 两个微分中值定理证明中辅助函数的多种作法[ J ]. 数学的实践与认识, 2004, 34 (10) : 165 - 169.[6 ] 郭乔. 如何作辅助函数解题[J ]. 高等数学研究, 2002, 3 (5) , 48- 49.A Brief of the Construct Method and Its Application for Auxiliary FunctionChen Xiaogen(School of Information Science and Technology , Zhanjiang Normal College Zhanjiang Guangdong 524048) Abstract: This paper elaborate the basic characteristic of the auxiliary function and the principle of coustructing the auxiliary function, meanwhile, introduce the several typical applications of methods for coustructing the auxiliary function.Key words: Auxiliary function; Primary function mothod; the method of variation of parameters; Constant -k- value methnod附加公文一篇,不需要的朋友可以下载后编辑删除,谢谢(关于进一步加快精准扶贫工作意)为认真贯彻落实省委、市委扶贫工作文件精神,根据《关于扎实推进扶贫攻坚工作的实施意见》和《关于进一步加快精准扶贫工作的意见》文件精神,结合我乡实际情况,经乡党委、政府研究确定,特提出如下意见:一、工作目标总体目标:“立下愚公志,打好攻坚战”,从今年起决战三年,实现全乡基本消除农村绝对贫困现象,实现有劳动能力的扶贫对象全面脱贫、无劳动能力的扶贫对象全面保障,不让一个贫困群众在全面建成小康社会进程中掉队。
罗尔定理构造辅助函数万能公式

罗尔定理构造辅助函数万能公式郭元春陈思源马晓燕1.西安思源学院基础部陕西西安 710038;2.西安思源学院高等教育营销研究中心陕西西安 710038微分中值定理在微积分学中占有十分重要的地位,是用函数局部性质推断整体性质的有力工具。
罗尔定理是微分中值定理中最为基础的一个,定理内容:若函数f(x)满足在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则存在某个中值ξ∈(a,b),使得等式f′(ξ)=0。
利用罗尔定理证明中值等式问题的难点就是辅助函数的构造。
刘文武、张军、肖俊等人[1-3]采用逆向思维法对该类问题做了相应的研究。
逆向思维法是从结果出发分析中值等式的特点,选择适当的方法构造辅助函数。
微分中值等式问题常见的形式是:已知函数f(x)满足在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(x)满足某些附加条件,求证存在某个中值ξ∈(a,b),使得等式F(ξ,f(ξ),f′(ξ))=0。
该等式左边看作是某个函数g(x)在点ξ处的导数,即g′(ξ)=0。
由拉格朗日中值定理可知,g(x)=C 是满足该等式的最简单的函数。
显然这个隐函数是原微分方程的通解,因此,在微分中值问题中,一般把通解中的积分常数令为辅助函数。
本文采用逆向思维法,对微分中值问题中构造辅助函数的常见题型作归纳和总结。
一、利用分离变量法构造辅助函数(一)证明的等式是关于ξ,f(ξ),f′(ξ)的微分方程例1[4]:设函数f(x)在闭区间[0,π]上连续,在开区间(0,π)内可导,证明:在开区间(0,π)内至少存在一点ξ,使得f′(ξ)sinξ=-f(ξ)cosξ。
证明:令F(x)=f(x)sinx,显然,F(x)在闭区间[0,π]上连续,在开区间(0,π)内可导,且F(0)=F(π),故由罗尔定理知,在开区间(0,π)内至少存在一点ξ,使得F′(ξ)=0,而F′(ξ)=f′(ξ)sinξ+f(ξ)cosξ,也就是说,在开区间(0,π)内至少存在一点ξ,使得f′(ξ)sinξ=-f(ξ)cosξ。
lagrange中值定理的证明
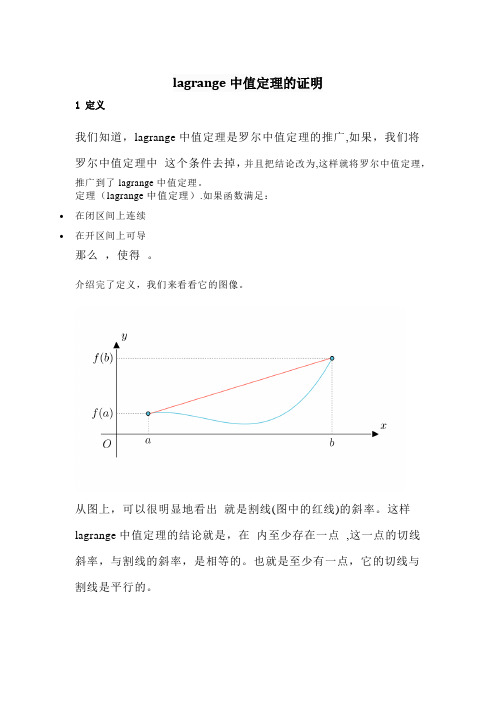
lagrange中值定理的证明1 定义我们知道,lagrange中值定理是罗尔中值定理的推广,如果,我们将罗尔中值定理中这个条件去掉,并且把结论改为,这样就将罗尔中值定理,推广到了lagrange中值定理。
定理(lagrange中值定理).如果函数满足:•在闭区间上连续•在开区间上可导那么,使得。
介绍完了定义,我们来看看它的图像。
从图上,可以很明显地看出就是割线(图中的红线)的斜率。
这样lagrange中值定理的结论就是,在内至少存在一点 ,这一点的切线斜率,与割线的斜率,是相等的。
也就是至少有一点,它的切线与割线是平行的。
2 联系前面我们说过,lagrange中值定理是罗尔中值定理的推广,这在几何上就有所体现。
具体地,罗尔中值定理,可以看做lagrange中值定理旋转到特定角度后的结果。
在上面这组图中,可以看出罗尔中值定理lagrange中值定理左边的图右边的图这说明,lagrange中值定理确实是罗尔中值定理的推广。
3 证明定理(lagrange中值定理).如果函数满足:•在闭区间上连续•在开区间上可导那么,使得。
证明.引进辅助函数:容易知道,满足:•在闭区间上连续•在开区间上可导•所以根据罗尔中值定理可知,使得,即:由此可得。
看懂上面这个证明并没有难度,但要自己写出来却不容易,其中的难点,就是构造出辅助函数。
那为什么在上面那个证明中,要构造出这个辅助函数呢,下面我们就来分析一下。
3.1 辅助函数构造首先对lagrange中值定理的结论进行变形结合罗尔定理,我们很自然联想(1)式左边是某个函数的导数就好了这样,可以假设很容易验证则满足罗尔中值定理,存在使得即(1)式成立,由此lagrange中值定理就证明出来了。
关于柯西中值定理的几种证明方法

关于柯西中值定理的几种证明方法微分中值定理是微分学中的重要定理,其应用广泛,涉及到的应用有研究函数或导数所对应的方程的根的个数及根的范围;根据函数的性质研究导函数的性质,或者是根据导函数的性质研究函数的性质;再有证明一些不等式及求极限等。
为解决上述问题,对微分中值定理的深入理解是很必要的。
现介绍柯西中值定理的几种新的证明方法,以使其更好地被认知和应用。
柯西中值定理的叙述如下:若f(x)与g(x) 在[a,b]上连续,在(a,b)可导,且x(a,b),g“(x)≠0则在(a,b)内至少存在一点使=二、柯西中值定理的证明柯西中值定理证明方法的探讨与研究历来是一个引人注目的问题。
一般常见的证明方法是构造辅助函数再根据罗尔定理加以证明。
下面将给出关于这一定理的几种新的证明方法。
1. 利用复合函数证明柯西中值定理在柯西中值定理中,考虑将g(x)看成自变量t,x看成自变量t 的函数,则将f(x)看成中间变量为x,自变量t的复合函数。
从而由题设,任意的x(a,b),g“(x)存在且g"(x)≠0。
由达布定理知,g"(x)在(a,b)内保号,令t=g(x),则t是[a,b]上的单调连续函数。
于是,存在单调且连续的反函数x=g-1(t),t[g(a),g(b)]。
由f(x)在[a,b]上连续知,在[g(a),g(b)]上存在连续的复合函数y=f[g-1(t)]=h(t)。
根据参数方程求导公式有==,x(a,b),故在x(a,b)即t[g(a),g(b)]内存在。
从而y=h(t)在[g(a),g(b)]上满足拉格朗日中值定理条件,故至少存在一点使t=g()(g(a),g(b))使==,得=,(a,b)。
2. 利用同增量性证明柯西中值定理引理1在同一闭区间上连续且在其内部可导的两个函数,若在这一区间上有相同的增量,则在这区间内至少存在一点,使这两个函数在该点的导数值相等。
证明:由题设f(x),g(x) 在[a,b]上连续,在(a,b)内可导,且f(a)-f(b)=g(a)-g(b)。
谈谈拉格朗日中值定理的证明(考研中的证明题)

谈谈拉格朗日中值定理的证明引言众所周至拉格朗日中值定理是几个中值定理中最重要的一个,是微分学应用的桥梁,在高等数学的一些理论推导中起着很重要的作用. 研究拉格朗日中值定理的证明方法,力求正确地理解和掌握它,是十分必要的. 拉格朗日中值定理证明的关键在于引入适当的辅助函数. 实际上,能用来证明拉格朗日中值定理的辅助函数有无数个,因此如果以引入辅助函数的个数来计算,证明拉格朗日中值定理的方法可以说有无数个. 但事实上若从思想方法上分,我们仅发现五种引入辅助函数的方法. 首先对罗尔中值定理拉格朗日中值定理及其几何意义作一概述.1罗尔()Rolle中值定理如果函数()xf满足条件:()1在闭区间[]b a,上连续;()2在开区间()b a,内可导;(3)()()b faf=,则在()b a,内至少存在一点ζ ,使得()0'=ζf罗尔中值定理的几何意义:如果连续光滑曲线()xfy=在点BA,处的纵坐标相等,那么,在弧 ⋂AB 上至少有一点()(),C f ζζ ,曲线在C 点的切线平行于x 轴,如图1,注意 定理中三个条件缺少其中任何一个,定理的结论将不一定成立;但不能认为定理条件不全具备,就一定不存在属于()b a ,的ζ,使得()0'=ζf . 这就是说定理的条件是充分的,但非必要的. 2拉格朗日()lagrange 中值定理若函数()x f 满足如下条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;则在()b a ,内至少存在一点ζ,使()()()ab a f b f f --=ζ'拉格朗日中值定理的几何意义:函数()x f y =在区间[]b a ,上的图形是连续光滑曲线弧 ⋂AB 上至少有一点C ,曲线在C 点的切线平行于弦AB . 如图2,从拉格朗日中值定理的条件与结论可见,若()x f 在闭区间[]b a ,两端点的函数值相等,即()()b f a f =,则拉格朗日中值定理就是罗尔中值定理. 换句话说,罗尔中值定理是拉格朗日中值定理的一个特殊情形.正因为如此,我们只须对函数()x f 作适当变形,便可借助罗尔中值定理导出拉格朗日中值定理. 3 证明拉格朗日中值定理教材证法证明 作辅助函数 ()()()()f b f a F x f x x b a-=--显然,函数()x F 满足在闭区间[]b a ,上连续,在开区间()b a ,内可导,而且()()F a F b =.于是由罗尔中值定理知道,至少存在一点ζ()b a <<ζ,使()()()()0''=---=a b a f b f f F ζζ.即()()()ab a f b f f --=ζ'. 用作差法引入辅助函数法证明 作辅助函数 ()()()()()()⎥⎦⎤⎢⎣⎡---+-=a x a b a f b f a f x f x ϕ 显然,函数()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,内可导,()()0==b a ϕϕ,因此,由罗尔中值定理得,至少存在一点()b a ,∈ζ,使得()()()()0''=---=a b a f b f f ζζϕ,即 ()()()ab a f b f f --=ζ'推广1 如图3过原点O 作OT ∥AB ,由()x f 与直线OT 对应的函数之差构成辅助函数()x ϕ,因为直线OT 的斜率与直线AB 的斜率相同,即有:()()a b a f b f K K AB OT --==,OT 的直线方程为:()()x ab a f b f y --=,于是引入的辅助函数为:()()()()x ab a f b f x f x ---=ϕ. (证明略) 推广2 如图4过点()O a ,作直线''B A ∥AB ,直线''B A 的方程为:()()()a x ab a f b f y ---=,由()x f 与直线函''B A 数之差构成辅助函数()x ϕ,于是有:()()()()()a x a b a f b f x f x ----=ϕ. (证明略) 推广3 如图5过点作()O b ,直线''B A ∥AB ,直''B A 线的方程为()()()b x ab a f b f y ---=,由()x f 与直线A B ''函数之差构成辅助函数()x ϕ,于是有:()()()()()b x ab a f b f x f x ----=ϕ. 事实上,可过y 轴上任已知点()m O ,作//B A ∥AB 得直线为()()m x ab a f b f y +--=,从而利用()x f 与直线的''B A 函数之差构成满足罗尔中值定理的辅助函数()x ϕ都可以用来证明拉格朗日中值定理. 因m 是任意实数,显然,这样的辅助函数有无多个.用对称法引入辅助函数法在第二种方法中引入的无数个辅助函数中关于x 轴的对称函数也有无数个,显然这些函数也都可以用来证明拉格朗日中值定理.从几何意义上看,上面的辅助函数是用曲线函数()x f 减去直线函数,反过来,用直线函数减曲线函数()x f ,即可得与之对称的辅助函数如下: ⑴ ()()()()()()x f a x a b a f b f a f x -⎥⎦⎤⎢⎣⎡---+=ϕ ⑵ ()()()()x f x a b a f b f x ---=ϕ⑶ ()()()()()x f a x a b a f b f x ----=ϕ ⑷ ()()()()()x f b x ab a f b f x ----=ϕ 等等.这类能用来证明拉格朗日中值定理的辅助函数显然也有无数个. 这里仅以⑵为例给出拉格朗日中值定理的证明.证明 显然,函数()x ϕ满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;()3()()()()ab a bf b af b a --==ϕϕ.由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()()()0''=---=ζζϕf ab a f b f ,从而有()()()ab a f b f f --=ζ',显然可用其它辅助函数作类似的证明. 转轴法由拉格朗日中值定理的几何图形可以看出,若把坐标系xoy 逆时针旋转适当的角度α,得新直角坐标系XOY ,若OX 平行于弦AB ,则在新的坐标系下()x f 满足罗尔中值定理,由此得拉格朗日中值定理的证明.证明 作转轴变换ααsin cos Y X x -=,ααcos sin Y X y +=,为求出α,解出Y X ,得()()x X x f x y x X =+=+=ααααsin cos sin cos ① ()()x Y x f x y x Y =+-=+-=ααααcos sin cos sin ② 由()()b Y a Y =得 ()()ααααcos sin cos sin b f b a f a +-=+-,从而()()ab a f b f --=αtan ,取α满足上式即可.由()x f 在闭区间[]b a ,上连续,在开区间()b a ,内可导,知()x Y 在闭区间[]b a ,上连续,在开区间()b a ,内可导,且()()b Y a Y =,因此,由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()()0cos sin '=+-=αζαζf Y ,即()()()ab a f b f f --==αζtan ' 用迭加法引入辅助函数法让()x f 迭加一个含待顶系数的一次函数m kx y +=,例如令()()()m kx x f x +-=ϕ或()()m kx x f x ++-=ϕ,通过使()()b a ϕϕ=,确定出m k ,,即可得到所需的辅助函数.例如由 ()()()m kx x f x +-=ϕ,令()()b a ϕϕ=得()()()()m kb b f m ka a f +-=+-,从而()()ab a f b f k --=,而m 可取任意实数,这样我们就得到了辅助函数()()()m x ab a f b f x ---=ϕ,由m 的任意性易知迭加法可构造出无数个辅助函数,这些函数都可用于证明拉格朗日中值定理.用行列式引入辅助函数法证明 构造一个含()x f 且满足罗尔中值定理的函数()x ϕ,关键是满足()()b a ϕϕ=.我们从行列式的性质想到行列式()()()111x f x af a bf b 的值在,x a x b ==时恰恰均为0,因此可设易证()()()()111xf x x af a bf b ϕ=,展开得 ()()()()()()()x f b x bf a af x af b f a x bf x ϕ=++---.因为()x f 在闭区间[]b a ,上连续,在开区间()b a ,内可导,所以()x ϕ在闭区间[]b a ,上连续,在开区间()b a ,内可导,且()()0a b ϕϕ==,所以由罗尔中值定理知,至少存在一点()b a ,∈ζ,使得()0'=ζϕ. 因为()()()()()0''=---=ζζϕf b a b f a f即: ()()()ab a f b f f --=ζ' 数形相结合法引理 在平面直角坐标系中,已知ABC ∆三个顶点的坐标分别为()(),A a f a ,()(),B b f b ,()(),C c f c ,则ABC ∆面积为()()()1112ABC af a S b f b a cf c ∆=, 这一引理的证明在这里我们不做介绍,下面我们利用这一引理对拉格朗日中值定理作出一种新的证明. 这种方法是将数形相结合,考虑实际背景刻意构造函数使之满足罗尔中值定理的条件.如图, 设()(),c f c 是直线AB 与()y f x =从A 点开始的第一个交点,则构造()()()()211141af a x c f c x f x ϕ=, 易验证()x ϕ满足罗尔中值定理的条件:在闭区间[],a c 上连续,在开区间(),a c 内可导,而且()()b a ϕϕ=,则至少存在一点()b a ,∈ζ,使()/0ϕζ=,即:()()()()()()01111111'=ζζζf c f c a f a f c f c a f a 但是()()()1101af a cf c f ζζ≠,这是因为,如果 ()()()1101a f a c f c f ζζ=, 则()()()()f f c f c f a c c aζζ--=--,这样使得()(),f ζζ成为直线AB 与()y f x =从A 点的第一个交点,与已知矛盾).故()()()0111=ζζf c f ca f a,即()()()()()ac a f c f a b a f b f f --=--=ζ'. 若只从满足罗尔中值定理的要求出发,我们可以摈弃许多限制条件,完全可以构造()()()()111af a x bf b xf x ϕ=来解决问题,从而使形式更简洁,而且启发我们做进一步的推广:可构造()()()()()()()111g a f a x g b f b g x f x ϕ=来证明柯西中值定理.区间套定理证法证明 将区间[],I a b =二等分,设分点为1ζ,作直线1x ζ=,它与曲线()y f x = 相交于1M ,过1M 作直线11L M ∥弦b a M M . 此时,有如下两种可能:⑴ 若直线11M L 与曲线()y f x =仅有一个交点1M ,则曲线必在直线11M L 的一侧.否则,直线11M L 不平行于直线a b M M . 由于曲线()y f x =在点1M 处有切线,根据曲线上一点切线的定义,直线11M L 就是曲线()y f x =在点1M 处的切线,从而()()()ab a f b f f --=1ζ.由作法知,1ζ在区间(),a b 内部,取ζζ=1于是有 ()()()ab a f b f f --=ζ⑵ 若直线11M L 与曲线()y f x =还有除1M 外的其他交点,设()111,N x y 为另外一个交点,这时选取以11,x ξ为端点的区间,记作[]111,I a b =,有1,112b a l I b a -⊇-<,()()()()1111f b f a f b f a b a b a--=--,把1I 作为新的“选用区间”,将1I 二等分,并进行与上面同样的讨论,则要么得到所要求的点ζ,要么又得到一个新“选用区间”2I .如此下去,有且只有如下两种情形中的一种发生:(a) 在逐次等分“选用区间”的过程中,遇到某一个分点k ζ,作直线k x ζ=它与曲线()y f x =交于k M ,过点k M 作直线k k L M ∥弦b MM , 它与曲线()y f x =只有一个交点k M ,此时取ζζ=k 即为所求.(b) 在逐次等分“选用区间”的过程中,遇不到上述那种点,则得一闭区间序列{n I },满足:① 12I I I ⊇⊇⊇ []n n n b a I ,=② ()02n n n b ab a n --<→→∞ ③()()()()n n n n f b f a f b f a b a b a--=-- 由①②知,{n I }构成区间套,根据区间套定理,存在唯一的一点() 3,2,1=∈n I n ζ,此点ζ即为所求. 事实上ζ==∞→∞→n n n n b a lim lim ,()f ξ存在()()()ζf a b a f b f n n n n n =--∞→lim ,由③lim n →∞()()()()n n n n f b f a f b f a b a b a --=--,所以()()()ab a f b f f --=ζ,从“选用区间”的取法可知,ζ确在(),a b 的内部. 旋转变换法证明 引入坐标旋转变换A : cos sin x X Y αα=- ⑴ ααcos sin Y X y += ⑵因为 22cos sin cos sin 10sin cos αααααα-∆==+=≠所以A 有逆变换/A :()()cos sin cos sin X x y x f x X x αααα=+=+= ⑶()()sin cos sin cos Y x y x f x Y x αααα=-+=-+= ⑷ 由于()x f 满足条件: ()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导,因此⑷式中函数()Y x 在闭区间[]b a ,上连续,在开区间()b a ,内可导.为使()Y x 满足罗尔中值定理的第三个条件,只要适当选取旋转角α,使()()Y a Y b =, 即()()sin cos sin cos a f a b f b αααα-+=-+,也即()()tan f b f a b a α-=-. 这样,函数()Y x 就满足了罗尔中值定理的全部条件,从而至少存在一点()b a <<ζζ,使()()0cos sin =+=αζαζf Y 即()αζtan =f . 由于所选取旋转角α满足()()a b a f b f --=αtan ,所以()()()ab a f b f f --=ζ.结论本论文仅是对拉格朗日中值定理的证明方法进行了一些归纳总结其中还有很多方法是我没有想到的,而且里面还有很多不足之处需要进一步的修改与补充. 通过这篇论文我只是想让人们明白数学并不是纯粹的数字游戏,里面包含了很多深奥的内容. 而且更重要的是我们应该学会去思考,学会凡是多问几个为什么,不要让自己仅仅局限于课本上的内容,要开动脑筋学会举一反三,不要单纯为了学习而学习,让自己做知识的主人!总之,数学的发展并非是无可置疑的,也并非是反驳的复杂过程,全面的思考问题有助于我们思维能力的提高,也有助于创新意识的培养.参考文献[1] 华东师范大学数学系. 数学分析(上册)(第二版)[M].北京:高等教育出版社.1991:153-161[2] 吉林大学数学系. 数学分析(上册)[M].北京:人民教育出版社.1979:194-196[3] 同济大学应用数学系. 高等数学(第一册)[M].北京:高等教育出版社(第五版).2004:143-153[4] 周性伟,刘立民. 数学分析[M].天津:南开大学出版社.1986:113-124[5] 林源渠,方企勤. 数学分析解题指南[M].北京:北京大学出版社.2003:58-67[6] 孙清华等. 数学分析内容、方法与技巧(上)[M].武汉:华中科技大学出版社.2003:98-106[7] 洪毅. 数学分析(上册)[M].广州:华南理工大学出版社.2001:111-113[8] 党宇飞. 促使思维教学进入数学课堂的几点作法[J].上海:数学通报.2001,1:15-18[9] 王爱云. 高等数学课程建设和教学改革研究与实践[J].西安:数学通报.2002,2:84-88[10] 谢惠民等. 数学分析习题课讲义[M].北京:高等教育出版社.2003:126-135[11] 刘玉莲,杨奎元等. 数学分析讲义学习指导书(上册)[M].北京:高等教出版社.1994:98-112[12] 北京大学数学力学系. 高等代数. 北京:人民教育出版社. 1978:124-135[13] 裴礼文. 数学分析中的典型问题与方法[M].北京:高等教育出版社.1993:102-110[14] 郑琉信.数学方法论[M].南京:广西教育出版社.1996:112-123[15] 陈传璋等. 数学分析(上册)[M].北京:人民教育出版社.1983:87-92[16] 李成章,黄玉民. 数学分析(上)[M].北京:科学出版社.1995:77-86附 录柯西中值定理若 ⑴ 函数()f x 与()g x 都在闭区间[]b a ,上连续;⑵ ()x f '与()x g '在开区间()b a ,内可导;⑶ ()x f ' 与()x g '在()b a ,内不同时为零;⑷ ()()g a g b ≠,则在()b a ,内至少存在一点ζ,使得()()()()a b a f b f g f --=ζζ''. 区间套定理若[]{},n n a b 是一个区间套,则存在唯一一点ζ,使得[],n n a b ζ∈,1,2,n = 或 n n a b ζ≤≤,1,2,n =。
如何构造辅助函数证明中值等式
e(, ) g (
) ( )
) 0 =
) ( =0 + )
, a g( ) f ( g a 一 = ( ) 一 ) ( ) 0 , g( ) , ( g ) 0 ( + ) ( = ) ) ( ) f” g ) 0 一 ( ( = )
维普资讯
第2 9卷
第 2期
四 川 兵 工 学 报
20 0 8年 4月
【 理论与探索】
如 何 构 造 辅 助 函数 证 明 中值 等 式
张 跃, 董 俊
60 1) 102
( 西南交通大学 峨眉校 区, 四川 峨眉山
摘要 : 当利用 中值定理证 明等式成立 时 , 辅助 函数 的构造往往 是证 明等式成立 的难 点和关键 , 通过构 造一个或 多 个辅助函数来说明构造辅助 函数证明 中值等式 的方法 . 介绍 了 3 常用构造辅 助函数的方法 . 种 关键词 : 辅助 函数 ; 凑导法 ; 常数 k 值法 ; 乘积因子法
表 1 常 用 凑 导 法 来 构 造 辅 助 函数 的题 型
中值 等式 G ) ( =0
凑成导函数等式 ( =0 ) ) 0
( + )
一
[g , ] 0 e( () =
[ [ ) ] =0 ) =0 ]
f 一 = )句 ) ( 0
( + ) 一 1
[ 卜0 [ ]0 = ( 12 +)
1 1 涉及 罗尔定理证 明中值 等式的命题 . .
题 型 1 证明存在 ∈( ,)使 , ( ) g ( )( = , 的辅助 函数 为 ( )=g , . n 6 , , ) 0构造 = ‘ ( e )
维普资讯
16 0
彳 厂 ( =2 ^ . 争 ) 9( ) 分析
浅谈定积分不等式证明中辅助函数的构造方法
浅谈定积分不等式证明中辅助函数的构造方法构造辅助函数法是高等数学中解决问题的一种重要方法,在解决实际问题中有着广泛的应用,通过研究微积分学中辅助函数的构造法,构造与问题相关的辅助函数,从而得出欲证明的结论。
尤其关于定积分不等式的证明在近几年的研究生数学考试中又频繁出现。
借助适当的辅助函数来证明定积分不等式是一种非常重要且行之有效的方法。
本文对某些定积分不等式中辅助函数的构造方法简单探讨。
标签:定积分不等式;构造;辅助函数;变限法当某些数学问题使用通常办法去考虑而很难奏效时,可根据题设条件和结论特征、性质展开联想,进而构造出解决问题的特殊模式——构造辅助函数。
辅助函数构造法是高等数学中一个重要的思想方法,在高等数学中广泛应用。
构造辅助函数是把复杂问题转化为已知的容易解决问题的一种方法,在解题时,常表现为不对问题本身求解,而是构造一个与问题有关的辅助问题进行求解。
微积分学中辅助函数的构造是在一定条件下利用微积分中值定理求解数学问题的方法。
可以解决高等数学中众多难题,尤其是在微积分证明题中应用颇广,可达到事半功倍的效果。
特别是定积分不等式的证明,往往需要借助恰当的辅助函数才能顺利完成,然而,对基础一般的学生来说,构造恰当的辅助函数是相当有难度的。
笔者在教学中进行探索,找到一些可行的方法,在此与广大读者进行交流。
一、构造辅助函数的原则辅助函数的构造是有一定规律的。
当某些数学问题使用通常的方法按定势思维去考虑很难奏效时,可根据题设条件和结论的特征、性质展开联想,进而构造出解决问题的特殊模式,这就是构造辅助函数解题的一般思路。
二、构造辅助函数方法探讨1.仅告知被积函数连续的命题的证法一般来说,这类命题的证明要做辅助函数(或者说用辅助函数法更简便)。
在定积分不等式中,辅助函数φ(x)的构造方法是将定积分不等式中,积分上限(或下限)及相同字母换成x,移项使不等式一端为0,则另一端即为所设的辅助函数φ(x)。
这类命题的证明思路:(1)做辅助函数φ(x);(2)求φ(x)的导数φ’(x),并判别φ(x)的单调性;(3)求φ(x)在积分区间[a,b]的端点值φ(a),φ(b),其中必有一个值为“0”,由第2条思路可推出φ(b)>φ(a)(或φ(b)<φ(a)),从而得出命题的证明。
关于拉格朗日中值定理的证明
引证文献(4条) 1.宋振云.陈少元.涂琼霞 微分中值定理证明中辅助函数的构造[期刊论文]-高师理科学刊 2009(2) 2.徐娟 拉格朗日定理证明中辅助函数的构造[期刊论文]-内江科技 2008(8) 3.赵芳玲 Lagrange中值定理的证明[期刊论文]-西安航空技术高等专科学校学报 2007(1) 4.张娅莉.汪斌 拉格朗日中值定理的证明和应用[期刊论文]-信阳农业高等专科学校学报 2005(4)
!
! !
拉格朗日中值定理是高等数学中重要定理之
一, 它的证明通常以罗尔中值定理作为预备定理, 关 键在于构造一个辅助函数, 而辅助函数应满足罗尔 中值定理的全部条件, 证明的过程就是对辅助函数 应用罗尔中值定理推出拉格朗日中值定理的结论" 由于构造辅助函数的思路不同, 因此, 拉格朗日中值 定理有多种证法" 本文就异于教科书上的证明方法, 给出如下两种不同的证明方法" ! ! 证明拉格朗日中值定理的一般方法 ( 也是教科 ! ! ! ! % 书上的证明方法)是通过曲线弧与弦的坐标差构造 辅助函数: ( & *)’ ( & () ( $ ’ () ! ! ! # ( $) % ( & $)’ ( & ()) * ’( 由# ( $)满足罗尔定理的条件, 利用罗尔定理得出 结论" 所以有逆变换 记! ! ! 因为 9’4 ! 4/* ! ’ 4/* ! % > ($ ! 9’4 !
对区间套定理给出一个推论,然后建立了四个引理.在此基础上通过构造区间套依次证明了罗尔中值定理、拉格朗日中值定理和柯西中值定理.
5.期刊论文 卢玉峰 微分中值定理历史与发展 -高等数学研究2008,11(5)
构造辅助函数的两种方法
维普资讯
6 4
由题 设 有 :
1 F( 在 [ ,]上 连续 ; ) z) 口 6
而左 端 恰 好 是 /( ) g( )在 处 的导 数 值 , 可作 z/ z 故 辅 助 函数 F( z)= /( l z 由题 设 条 件显 然 有 : z)g( ), 2 在 ( ,)内 可导 ; ) 口6
1 )内可导 , 厂( ) 0 厂( ) 0 证 明存 在 ∈ ( , 且 O= , 1一 , O 1 使得 : ),
从 而 有 f ( g ) ( )一 厂 ) ( g ( )= 0 ,
故
f () g( )= /( ) . g ()
类 似 可得 例 2的结 论 .
湖 北 工 学 院 学
报 Leabharlann 20 0 2年 第 3 期
f )一 一 ( ) ) ( 厂( / .
在微 分 学 中 , 用微 分 中值 定理 解 决 问题 时 , 利 通
常需 要 构 造 一 个 辅 助 函数 , 个 函 数 必 须 满 足 某 个 这
例 2 设 0< 口< b 厂( , z)在 [ ,]上 连 续 , 口6 在
( ,) 口 6 内可 导 , a b 一 b ( )一 0 证 明 : ( 6 且 f( ) fa , 在 口,)
维普资讯
第 1 7卷 第 3期
Vo .1 O.3 1 7N
湖 北 工 学 院 学 报
J u n lo b iP l t c n c Un v r iy o r a f Hu e o y e h i i e s t
拉格朗日中值定理辅助函数构造法的证明
其 中 g x 是方程 ( )的解 , () 3 具有形式 ( )gc 4 ;,使得式( ) 5 成立 。
于是 因为 F )= ) q )+c ( ) ( [H ( ]+q ( ) ( ) I x g x - l F口 ( )=, 口 [日 ( )+c ( ) ( ) g 口 口 ]+q 口 H( ) F 6 6 [日 ( )+c 6 ]+g ( ) ( )= ) g 6 月 () 日 6
F( ) = )一 ( 一口 口 )一 )
这里 p( ) 函数 )与 g x =一kx一口 f 口 x 是 () ( )- ( )之 和 : x p( )=
)+g x 。 ( )
本文要讨论的是辅助 函数 p x ( )的更一般的形式 。 借助罗尔定理证明拉格朗 日定理所作 的辅助函
利用 上一 节选 取 g x ( )的思 路 , 时 g x 这 ( )是 微分 方 程
x g( ) )+砖 ( g )+q ( )=0 ( ( ) =H ) hx hx ( ) 的解 。 () 3
微分 方程 理论 指 出 g x ( )有 如下形 式 :
g )=q ( ( H。 )+c r ) 月2 ( () 4
厂( g )+ ) ( 由于 g )满 足方 程 ( ) 所 以 ( 3,
( )+ ) )+g ( =0 g( ^ ) 厂( )=I 口 < <6 。 i } ( ) 又 () 6
由 ( )得 F 口 =F( )故 有 F ( 5 () 6, ):0 口 < < b , ( ) 即 ) )+g ( =0 g( ^ ) ,
数 p( ) x 要满 足三 个条 件 :) x 在 区间 [ ,] 连续 , 开 区间 ( ,)内可导 ;) ( )=F( )3 1 r( ) 口b 上 在 口b 2F 口 b ;)由 F( )=0能导 出 厂( )= k 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
computingApplic毗i咖,H岫柚unlve雌时ofArts蛆d science.cha。唱dc,H皿蚰415000,chim)
coⅡ昨u№000,04,10,蛐d缸ds^ntr0 htrIll.2000.04.10
【2】常明.陈球垄基于sGML,)(ML的文件结构化研究与实现【J】 计算机研究与发展,2002.39f2)
f3】s Fu,J.Y chu“g,w.Di州ch,ct a1.A pr扯tic矗I appr0∽h fo‘ web—based Inkmet EDIf刀19tll IEEE Jn地瑚血m蚰con船舶驿
Research and Implementation of Lesson-arrangement Based on XML
●
^
M|EI
x{∞誓on窖.ⅪAo
2
zhen}hong
Dcp叭咖t (1
of computer sci∞cc,H皿叫unive体时of Ans孤d science.ch卸gde,HllII肌415000,chma;2 R鹪咖曲I地htLIte of
图3是运行是系统生成的排课数据所见即所得 的界面,界面上 部可以按照班 级、教师和教室 选择的控件,下 部是具体数据信 息浏览效果.
3 结论
图3输出运行结果
xML以其合理的数据组织结构和可扩展特性, 结合目前的net和Java技术,使得开发的过程更加便 捷.但由于xML推出时问较短,特别是大多数行业
证明 在区间(口,c)内存在一点f,使
『,(口)g(d)矗(d)I
一2j南l,(6)g(6)6(6’l 、 l,”(善)91(掌)厅。(孝)1
憾薰笼卜叫删.若 分析 l厂(6) g(6)^(6)l~2(6一d)4=o.若 l,”(毒) g”(考) A”(善)l
令}=j ,且m卜永憾薰剖一
函数构造:将}换成x,得一个一阶微分方程. 解此方程,得到含有常数c的通解,移项,使c在等 式一边,则另一边即为所需构造的函数.
中d(或6)换成x,令等式一边为—Fb)即可,但此时
导数,且g。(功≠O.,(∞=.厂(6)=g(口)=g(6)=0.
凡T)中的高需用常数表达式表示.
证明 在(口,6)内至少存在一点},使得
例6设,(z)在h圳上连续,在扣,6)内可导,
笪掣=,(亭)+∥喈). 证明 存在一点 {e0,∞, 使得
分析 此题型中常数已分离,可令
l,(口)g(口)矗(口)l Il d ol
2(6一n)4)出=I.厂(6)g(6)^(6)卜卅l 6 oI(数值转
s需证撇鬻=篇脚
l,(#)g增)即咧lo o 2J
成行列式),此时F(口),F(6)符号不易判断,因此需 令G’(z)=F(J),并结合已知条件的形式设
l,(口)g【口)矗(口)I |1 n n2l G(j)=l/(6)g(6)^(d)卜爿11 6 62I,命题可证
例7 设函数,(』)在【口,卅上可导,且 ,2(x)≠z2,,(口)=,(6)=0,证明至少存在一点
{e(n,a),使得,’(f)=。ij}{!;;{;i.
有,=—箬≮,解此微分方程的去=c.即 分析将所需证结论中{换成x,令y=,(x),
蔬=cx‘一y‘x‘+y‘ , 于是可得辅助函数
F(∞=燕.依罗尔定理,命题可证.
【l】毛纲源高等数学方法导论【M】武汉:武汉测绘科技大学出 版社.1992 78
【2】陈文灯数学最后冲刺:理工类【M】.北京:国家行政学院出 版杜,19卿.
【3]宋向荣,陈梦华谈几类中值定理辅助函数的构造方法【盯榆 林高等专科学校学报.200l,ll(2):2l一23 (下转第5l页)
万方数据
第12巷
函数构造:取辅助函数只∞,使FI∞中含有,0)
因式,积分或解方程求出F∞的一个原函数(c=0). 并且H口>叫6)或,(c)=H力(p,砷c缸6)),利用罗尔
定理求解
例l设肛),go。在开区间(廿'6)内可导,且
,(』1)=,(J2)=0,置J2∈(口,6),试证在Jl与也之间
,(x)坝x培U)至少存在一个零点.
还未形成公开的、标准的DTD和schema,所以其潜 力还没有得到充分的挖掘.随着xML的不断发展和 完善,它将在更多的领域广泛应用.是基于xML技 术设计的排课程序,它克服了单机环境的缺点,象 常德师范学院教务排课,其管理跨3个校区.共272 个班级,大大提高了教务管理水平和工作效率.
参考文献
[IJE D11mbiII,xML,standards皿d you【EB,OU h却:,/www,xml
l,(x)g(x)矗(x)l 11 z x2I
6.需证结论:所证等式中常数易分离,且变形 后等式两边关于端点的表达式具有对称性或是轮换
函数构造:将}换成x,利用分部积分法,求不
定积分,即f,枷’(∞g‘卜2’(x)出=k“’o),‘卜2’(x)dx,
于
是
有
,‘”(J)g‘扣”(x)一l。g‘”。’(J),n。’(x)
例3若,(J),g(x)在[d,6]上可导,且g(x)≠0,
则存在一俅(删,使筹器=舞.12J
分析 』!尘二』!盟:£!曼业岜,』!尘=』!生:
g(掌)一g(6) g’(毒)
g(J)一暑(6)
.』j芸——tIL+,(口)g’(x)+g(6),7(J)=(g(z),(J”.:;兰一
,(x)g(z)=_厂(口)g(x)+g(6),(x).令只x卜I,(x)gO)
分析因所证结论中函数由含导数的两部分和
组成,但又不完全满足“,v+“v’=似v)’,因此对上式
变形为e7(“’+“vr)=(“e”)7,故考虑构造
FI曲=【,r(J)+,(J)g协)],‘”,利用罗尔定理可证.
2.需证结论:/∽>gO).
函数构造:将所证不等式通过变形后,一端可
写成!鱼上盟型,将而(或。:)换成;得F(x), 而一也
证明时验证拉格朗日定理条件,对F’({)进行适当放
大或缩小,再代入F’({)与J的关系式即可证得
结论.
例2证明÷<ln(1“)q,‘庐o).【11
I十J
分析 ÷<ln(1十砷q j÷<ln(1竹)一
l+J
I+X
ln(1+o心一oj.士c些型二警塑c1.瞰沪
l十J
j—U
可得倦)=些坐等学, 1n(1+0,f∈[o,加.此时,(f)在[o,x】上满足拉格朗日
定理条件,
似)。南-因为o‘#旬·所以,击‘壶‘ 1j÷<击龟,命题可证.
I+x I十g
3需证结论:至少存在一点{∈(口,6),使得
/”’(孝)=七(七≠o).
函数构造:将结论中f换觑,通过恒等变形、
积分或解常微分方程,得出原函数.移项,使等式
右边为0,令等式左边为唯).证明时判断:(1)若
F(。)=,(6),利用罗尔定理证明;(2)若只旬尺6)<O 时,利用费马定理证明.
第1 2卷第3期 2003年9月
湖南城建高等专科学校学报
JoURNAL OF HUNAN URBAN CONSTRUCTION COLLEGE
Voll 2 No 3
“中值定理"命题证明中的辅助函数构造
游学民
(襄樊学院数学系,湖北襄樊441053)
摘要:高等数学中有关“中值定理”的命题的题型复杂事变,技巧性强,学生在解决这类问题时,往
!!!!兰篁!塑
成“泰勒”公式 例5设函数,(x),g(』),^(x)在区问【口,卅上连
F(』)=_;j粤杀.依罗尔定理,命题可证.
续.且存在~、二阶导数;又设6∈(口,c),√满足
7.需证结论:,’({)=兀伊(f)】 ‘3】
l,(a) g(口) 矗(。)l ll 口 口2l
方程l_厂(6)g(6)^(6)|_All 6 6 2l=o. J/(f) g(f) ^(c)J Jl c c2
将6(或口)取为J,则取_厂(口)=,(占)=0.证明至少存
F∽=,∽F∞一g“),『(z).依罗尔定理,命题可得.
在一点fe(q6),使得,增)2ij{!箩%.
参考文献:
有,=罢.解此微分方程的去=c,即 分析将所需证结论中{换成x,令y=,(J),
揣=cx’一y‘x‘+y‘ , 于是可
fg”。1’(z),似一2’(J)dx+c = ,‘“’(x)g‘”-11(x)一
g‘”’(J),”-1’(z)=c, 于是有辅助函数
对称性.
F(x);_厂‘”’(x)g‘“。’(x)一g‘1’(曲_厂‘卜1’(z)
函数构造:l令常数为K;2恒等变形,将等式
例8设函数,(x)和g(x)在【吼卅上存在二阶
后,有F(d)≠F(6). 函数构造:令G-(x)=F(J),积分得G(x),汪明
时使用两次中值定理或在某些情况下将G(J)展开
收麓日期:2003_03一17 作者简介:游学民(1967.).男,湖北安陆人.讲师.主要从事高等数学教学与研究
万方数据
里———————————望堕壁壅壹董童翌兰壁兰堡
分析 x。,(而)=I:,(曲出—竺£!÷矿(J);
£,扛)血_+矿(J)一f,(z)血=o.若有F(x);可(x)一
f1,(x)出,不易证得,(o)=F(1),故令
G,(z)=矿(砷一f,(z)出,从而G(J)=r,(,)d,,G(x)
满足罗尔定理.命题可证. 5.需证结论:形式同3,但通过3构造函数F(j)
女:笪堑;二型盟,6,(6)一拍:妒(。)一妇(对称式),
丛盟:£盟
g(喜) g。(孝)
将fjx.整理得,(x)g。(J)=g(z),’(J),两边
同时求不定积分得,(x)g’(曲一f,’(x)g’(z)“= g(z) ,7“)一Ⅳ’o)g’(f)出+c , 从而有
,(x)g’【x)一g(x),’(x)=c,于是有辅助函数
