道路养护与管理专业《项目二任务二路线平面线形组成分析(缓和曲线)》
缓和曲线在公路平曲线设计中的应用

TRANSPOWORLD 2010 No.22 (Nov)116前言公路的平面线形,由于其位置受社会经济、自然地理和技术条件等因素的制约,公路从起点到终点在平面上不可能是一条直线,而是许多直线段和曲线段(包括圆曲线和缓和曲线)组合而成。
对平面线形而言,一般可分解为直线、圆曲线及缓和曲线,三要素的合理组合,才能构成合理的、行车舒适的平面线形。
而缓和曲线是组成平曲线的重要线形要素,现行规定,三级标准以上公路,当圆曲线半径达不到不设超高的最小半径时,应在直线与圆曲线连接处设置缓和曲线。
但缓和曲线设置应考虑众多条件,亦即缓和曲线长度取用应当合理。
本人结合设计实践以及对路线设计规范缓和曲线在公路平曲线设计中的应用文 / 刘凤娟的理解,着重叙述山区公路缓和曲线在应用时应综合考虑的条件及注意事项,以求得平曲线设计的连续和均衡。
缓和曲线的作用便于驾驶员操作方向盘。
满足乘客乘车的舒适与稳定,减少离心力变化。
满足超过、加宽缓和段的过渡,利于平稳行车。
与圆曲线配合得当,增加线性美观。
缓和曲线应用条件由于山区公路受到复杂地形和经济因素的制约,缓和曲线不能像平原区那样设置较长,在设计时一不注意就造成缓和曲线长度不够,满足了这一条件却忽视了另一条件。
基本条件缓和曲线常采用回旋线,基本公式为:A 2=lr式中:A ——回旋线参数;l ——回旋线上某点的曲线长r ——回旋线上某点的曲线半径回旋线与圆曲线连接处,其曲线半径为圆曲线半径R ,这时回旋线的长度就是通常所取的缓和曲线长度,公式为:A 2=LR在选定缓和曲线长度时,应注意回旋线参数A 与圆曲线半径R 的关系:1/3R ≤A ≤R ,一般情况下这是比较容易满足的。
表1 各级公路缓和曲线最小长度公路等级高速公路一 二 三 四计算行车速度(km/h ) 120 100 80 60 100 60 80 40 60 30 40 20最短缓和曲线长度(m ) 100 85 70 50 85 50 70 35 50 25 35 20TRAFFIC ENGINEERING交通工程1172010年第22期 《交通世界》(11月下)最小缓和曲线长规范规定的最小缓和曲线长是按照汽车行驶理论,由缓和段过渡到圆曲线的最小长度,是按设计时速的0.83倍计算而得,等级越高,其长度越长,规范中按公路等级列表示出(见表1),应该注意的是,达到了最小缓和曲线长,设计不一定就是合理的。
《道路平面线形 》课件

道路平面线形与 环境保护的协调: 道路平面线形设 计应考虑环境保 护因素,如采用 生态设计、绿色 交通等,以实现 道路与环境的和 谐共生。
道路平面线形与 环境保护的案例: 介绍一些成功的 道路平面线形与 环境保护的案例, 如绿色交通、生 态设计等。
道路平面线形与景观协调
道路平面线形与景观的关系:道路平面线形应与周围景观相协调,以保持 景观的完整性和美观性。
山区公路平面线形实例
地形特点:山区地形复杂,坡度大,弯道多 设计原则:安全、舒适、经济、环保 线形设计:采用S形、U形、C形等线形,以适应地形变化 弯道处理:设置弯道加宽、减速带等设施,确保行车安全 坡度控制:合理控制坡度,避免坡度过大导致行车困难 环保措施:采用生态防护、绿化等措施,保护生态环境
美观性:注重道路线形的美观性, 提升城市形象和居民生活质量
THANK YOU
汇报人:
汇报时间:20XX/XX/XX
YOUR LOGO
绘制道路平面线形图,并进行优化和调整
完成道路平面线形设计,并进行评审和验 收
设计优化
优化道路平面线形,提高 道路通行效率
考虑道路周边环境,减少 对环境的影响
优化道路平面线形,提高 道路安全性
优化道路平面线形,降低 道路建设成本
道路平面线形与其他因素的关系
道路平面线形与交通安全
道路平面线形对交通安全 的影响
绿色生态设计理念
生态环保:采用环保材料,减少环境污染 节能减排:优化交通流量,降低能源消耗 生态景观:融入自然景观,提升道路美观度 生态交通:提倡绿色出行,减少交通拥堵
多元化能
性
现代设计风 格:注重创 新和个性化
生态设计风 格:注重环 保和可持续
发展
第二章平面曲线

2.纸上定线
以直线为主定交点:主要用于平原、微丘区,是根据地形、地物条件,选设定作为路 线基本轴线的直线,再根据两两直线相交得交点,继而设置圆曲线和缓和曲线,该方法称以 直线为主定交点法,也是传统的方法。
以曲线为主定交点:常用于互通立交匝道布线、定线或山岭、重丘区高速公路、一级 公路选线、定线,是根据地形及环境条件和路线技术要求设置圆曲线(或圆曲线与缓和曲线
一定建筑物等措施。 长直线或长下坡尽头的平曲线,应对路面超高、停
车视距等进行检验,必要时须采用设置标志、增加 路面抗滑能力等安全措施。
2.直线的最小长度
相邻两曲线之间应有一定长度的直线,这个直线是指前一曲线的终点(HZ或YZ)到 后一曲线的起点(ZH或ZY)之间的长度。
(1)同向曲线间的直线最小长度 同向曲线:是指两个转向相同的相邻曲线之间连以直线而形成的平面线形。 断背曲线:同向曲线间连以短的直线。
断背曲线的错觉 ①当直线较短时,在视觉上容易形成直线与两端曲线构成反弯的错觉; ②当直线过短甚至把两个曲线看成是一个曲线。
危害: 破坏了线形的连续性,造成驾驶操作失误,应尽量避免。
解决办法: 因为是视觉上的判断错觉,最好的办法是在两同向曲线间插入长的直线段,让驾驶
员在前一个曲线上看不到下一个曲线。
在直线纵坡路段,易错误估计车间距离、行车 速度及上坡坡度。
易对长直线估计得过短或产生急躁情绪,超速 行驶。
二、直线的运用
采用直线线形时必须注意线形与地形的关系,在运用直 线线形并决定其长度时,必须慎重考虑,一般不宜采用长直线。 路线完全不受地形、地物限制的平坦地区或山间的宽阔河谷
地带; 城镇及其近郊道路,或以直线为主体进行规划的地区; 长大桥梁、隧道等构造物路段; 路线交叉点及其附近; 双车道公路提供超车的路段。
第二章 道路平面线形设计

直线、曲线及转角表
交 点 号 JD 交 点 桩 号 转角值 α 左转 角 αz 右转 角 αy 曲线要素值(m) 半径 R 缓和 曲线 参数 A 缓 和 曲 线 长 度 l 7 切 线 长 度 T 曲线位置 第一缓和 曲 外 校 第一缓和 线 距 正 曲线或超高 曲线终点或 长 E 值 缓和长度加 圆曲线起点 J 宽缓和长度 HY(ZY) 度 L 起点ZH
在弯道上,当车辆行驶在双向横坡的车道外侧时,车重 的水平分力将增大横向侧滑力,所以当采用的圆曲线半径 小于不设超高的最小半径时,为抵消车辆在曲线路段上行 驶时所产生的离心力,将曲线段的外侧路面横坡做成与内 侧横坡同方向的单向横坡称为超高。其作用是为了使汽车 在圆曲线上行驶时能获得一个指向内侧的横向分力,用以 克服离心力,减小横向力,从而保证汽车行驶的稳定性及 乘客的舒适性。
曲率半径ρ与汽车的转角成反比例变化,汽车的转角从道路直线段上 的零逐渐增加到圆曲线上的固定值(图1-4-3)。
设汽车在缓和曲线上的行驶速度为v(m/s),行驶t秒后,方向盘转 ,前轮的转动角φ,则两者关系为: 动角度为 K (K<=1)
(二)缓和曲线长度的计算 `
按司机操作反应时间计算:ຫໍສະໝຸດ 各级公路的圆曲线最小半径 表
设计速度(km/h) 极限值(m) 一般值(m) 不设 超高 最小 半径 路拱 ≤2.0 % 路拱 >2.0% 120 650 1000 5500 100 400 700 4000 80 250 400 2500 60 125 200 1500 40 60 100 600 30 30 65 350 20 15 30 150
第二节 行车视距
行车视距包括停车视距、会车视距和超车视距。
汽车行驶时,司机看到前方障碍物后,紧急、制动至 到达障碍物前安全停止所须的最短行车距离称为停车视距。 此时司机视线高度取1.2m,障碍物高出路面0.1m。 在双向混合的公路上,往往两辆对向行驶的车辆可能 会相互碰撞,从双向采取措施进行制动直至停止时两辆汽 车同时所行驶的距离为会车视距。根据计算,会车视距约 为两倍的停车视距。 在双向行驶的道路上,若公路上的车辆相对比较密集 时,后车会超越前车,从开始驶离原车道至可见逆行车并 能超车后安全驶回原车道所需的安全距离,即为超车视距。
道路平面线型组合类型

道路平面线型组合类型
在进行道路平面线形设计时,一般会遵循下列原则:1、平面线形应直捷、连接、顺适,并与地形地物相适应,与周围环境相协调;2、必须满足行驶力学要求,视觉和心理上的要求对高速路应尽量满足;3、保持平面线形的均衡与连贯;4、应避免连续急弯的线形;5、平曲线应有足够的长度。
一般来说道路线型分为以下六类:
1、基本型
直线+缓和曲线+圆曲线+缓和曲线+直线,这种线型和地铁平曲线里的大部分线型是一样的。
2、S型
缓和曲线1+圆曲线1+缓和曲线1+(反向)+缓和曲线2+圆曲线2+缓和曲线2
S型曲线几点注意:
(1)相邻两个回旋参数A1和A2宜相等,当采用不同参数时,A1/A2<2.0,有条件时应<1.5;
(2)两反向曲线之间不设直线,不得已插入直线时,必须尽量短,其直线长度或重合段的长度应满足L≤(A1+A2)/40。
(3)S型两圆曲线半径之比不宜过大,宜为:R2/R1=11/3。
3、卵型
缓和曲线1+圆曲线1+缓和曲线(过渡)+圆曲线2+缓和曲线2
卵型曲线的几点注意:
(1)卵型上的回旋参数A不应小于该级公路关于回旋线最小参数的规定,同时宜在下列界限内:R2/2≤ A≤ R2(R2为小圆半径);
(2)两圆曲线半径之比宜在下列界限之内:0.2≤R2/R1≤ 0.8(R1为大圆半径);
(3)两圆曲线的间距,宜在下列界限之内:0.003≤D/R2≤ 0.03(D为两圆曲线最小间距)。
4、凸型
直线+缓和曲线1+(同向)缓和曲线2+直线
5、复合型
直线+缓和曲线1+(同向)缓和曲线2+圆曲线+……
6、C型
圆曲线1+缓和曲线1+(同向)缓和曲线2+圆曲线2。
道路工程测量(圆曲线缓和曲线计算公式)

顶岗实习报告道路工程测量(圆曲线缓和曲线计算公式) 实习时间:2013年7月至2013年9月17日 工程项目名称:乌鲁木齐绕城高速公路(东线)WRDX-3实习报告内容:经过实习的一段时间发现道路测量与建筑测量之间有很大的差别,道路测量主要就是曲线上放样,而建筑测量中为直线直角放样。
因此道路测量人员必须掌握曲线放样的内容。
而曲线放样的内容主要就是圆曲线和缓和曲线,一般采用的方法就是交点放样法和偏角法下面就是我在这一段时间内学习到的关于曲线放样的基本内容。
重点:圆曲线、缓和曲线的要素计算和主点测设方法;切线支距法和偏角法的计算公式和测设方法;路线纵断面的基平、中平测量和横断面测量方法 难点:缓和曲线的要素计算和主点测设方法;缓和曲线的切线支距法和偏角法的计算公式和测设方法。
交点转点转角及里程桩的测设一、 道路工程测量概述分为:路线勘测设计测量 (route reconnaissance and design survey) 和道路施工测量 (road construction survey) 。
(一) 勘测设计测量 (route reconnaissance and design survey) 分为:初测 (preliminary survey) 和定测 (location survey) 1、 初测内容:控制测量 (control survey) 、测带状地形图 (topographical map of a zone)和纵断面图 (profile) 、收集沿线地质水文资料、作纸上定线或现场定线,编制比较方案,为初步设计提供依据。
2、 2、定测内容:在选定设计方案的路线上进行路线中线测量 (center line survey) 、测纵断面图 (profile) 、横断面图 (cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查,为施工图设计提供资料。
道路平面设计线形要素与配置

道路平面设计线形要素与配置摘要:根据汽车行驶的力学性质和行驶轨迹要求,合理地确定道路各线形要素和几何参数,保持线形的连续性和均衡性,避免长直线,并注意使线形与地形、地物、环境和景观等协调。
对于车速较高的道路,线形设计还应考虑行驶美学、驾驶员的视觉及心理上的要求,因此本次着重讨论圆曲线的半径、缓和曲线长度以及直线、曲线的合理配置等。
关键词:道路;线形要素;长直线;圆曲线;半径;缓和曲线;长度;合理配置1 道路线形要素基本概述1.1路线平面的基本线形道路是一条三维空间的实体,是一个带状构造物。
它是由路基、路面、桥梁、涵洞、隧道和沿线设施所组成的线形构造物。
1.2直线a.直线的特点:直线距离短,直捷,通视条件好。
汽车在直线上行驶受力简单,方向明确,驾驶操作简易。
便于测设。
直线线形大多难于与地形相协调,若长度运用不当,不仅破坏了线形的连续性,也不便达到线形设计自身的协调。
过长的直线易使驾驶人感到单调、疲倦,难以目测车间距离。
b. 宜采用直线线形的路段:(1)不受地形、地物限制的平坦地区或山间的开阔谷地;(2)市镇及其近郊,或规划方正的农耕区等以直线条为主的地区;(3)长的桥梁、隧道等构造物路段;(4)路线交叉点及其前后;(5)双车道公路提供超车的路段。
1.3圆曲线是平面线形中常用的基本线形,在道路遇到障碍或地形需要改变时设置。
1.4缓和曲线设置在曲线与圆曲线或不同半径的两圆曲线之间,用以缓和人体感到的离心加速度的急骤变化,从而达到驾驶员操作流畅,视觉平顺,线形连续。
缓和曲线目前有:回旋曲线、三次抛物线、双纽曲线等。
汽车行驶轨迹与道路平面线形,行驶中汽车重心轨迹的几何特征:(1)轨迹连续。
这个轨迹是连续的和圆滑的。
(2)曲率连续,即轨迹上任一点不出现两个曲率的值。
(3)曲率变化连续:其曲率的变化率是连续的,即轨迹上任一点不出现两个曲率变化率的值。
2 圆曲线2.1概述它是路线平面设计中的主要组成部分,它具有易与地形相协调、可循性好、线形美观、容易测设等优点,使用十分普遍。
公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析
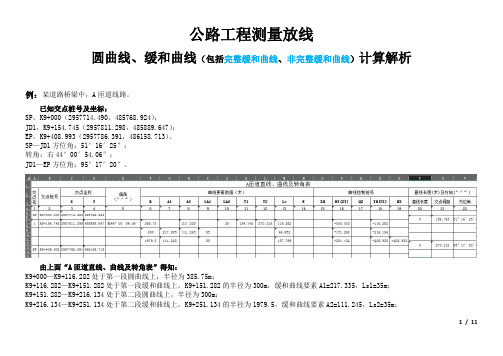
公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线)计算解析例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
由上面“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;1 / 11K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
2 / 113 / 11y 轴。
过圆曲线上任意点P 的切线与ZY —JD 相交,夹角(切线角)为β,ZY —P 与ZY —JD 的夹角(弦切角)为α,ZY —P 的弧长为L ,ZY —P 的直线距离为d ,圆曲线的半径为R 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、 缓和曲线 1.设置缓和曲线的条件 当圆曲线半径小于不设超高的最小半径,公路等级在三级及以上时,应在直线和圆曲线间设置缓和曲线以满足曲率半径逐渐过渡的要求。 2.缓和曲线的作用与性质 1〕缓和曲线的作用 〔1〕有利于驾驶员操纵方向盘 汽车从直线进入圆曲线,或从大半径圆曲线驶入小半径圆曲线时,插入缓和曲线,可使汽车前轮转向角逐渐从0°至°转向,从而有利于驾驶员操纵方向盘,保证平安行驶。 〔2〕消除离心力的突变,提高乘客的舒适性 在直线段中,离心力为零。在圆曲线上,离心力最大。当插入缓和曲线时,因为缓和曲线的曲率是逐渐变化的,可以消除离心力的突变,从而保证乘客舒适与稳定。 〔3〕满足超高和加宽的过渡 当圆曲线上有超高与加宽时,由直线段上无超高及加宽过渡到圆曲线的全超高及全加宽时,必须有一个缓和段,设置了缓和曲线就可以在缓和曲线完成超高及加宽的逐渐过渡。 〔4〕与圆曲线配合得当,线形美观 圆曲线与直线径向连接,在连接处曲率突变,在视觉上有不平顺的感觉,设置缓和曲线后,使线形连续圆滑,增加线形的美观,同时有良好的视觉效果和心理效果。 2〕缓和曲线的性质 〔1〕汽车行驶轨迹方程 当汽车逐渐由直线驶入圆曲线,假定汽车作匀速行驶,假定驾驶员操作方向盘作匀角速转动,当方向盘转动角度为时,前轮相应转动角度为,如图2-5所示。通过理论推导得出弧长和曲率半径的关系为:
图2-5 汽车行驶轨迹图 cs 〔2-8〕
式中:s——汽车从直线终点进入曲线经t时间后行驶的弧长,m; c——常数; ——曲线上所求点处的曲率半径,m。 由式〔2-8〕汽车转弯时的理论轨迹方程可知,汽车从直线进入圆曲线其行驶轨迹的弧长与曲线的曲率半径的乘积为常数,即弧长和半径成反比。 〔2〕缓和曲线形式——盘旋线 从盘旋线的数学定义可知,其曲率半径随曲线上某一点至该曲线起点之距离s成反比〔盘旋线是曲率半径随曲线长度增长而减小的曲线〕。即:
sc 〔2-9〕
式〔2-9〕与式〔2-6〕中汽车转弯时的理论行驶轨迹完全吻合,即用盘旋线作为缓和曲线,有充分的理论依据。我国?标准?规定缓和曲线采用盘旋线。 令〔2-9〕中 2
AC
那么
2A
s 〔2-10〕
式中:s——汽车从直线终点进入曲线经t时间后行驶的弧长,m; A——盘旋线参数; ——曲线上某点曲率半径,m。 令 hls
R 那么由式〔2-10〕得:
RAlh2 〔2-11〕
盘旋线参数A确实定: 2
AlRh
hlRA
式中:R—圆曲线半径,m;
hl—缓和曲线长度,m。 只要设计选定圆曲线半径和缓和曲线长度,盘旋线参数也就确定了。 3.缓和曲线最小长度 缓和曲线的最小长度应能满足直线与圆曲线平顺过渡,限制离心力突变,并保证有必要的时间顺适驾驶员操纵方向盘。 〔1〕从旅客感觉舒适度考虑,离心加速度增长率应控制。 〔2〕从行驶时间恰当角度考虑。一般认为,汽车在缓和曲线上行驶时间最少3s。 〔3〕从超高渐变率适虑 超高渐变率是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。由于在缓和曲线上要完成超高过渡,设置超高缓和段,如果缓和曲线太短使超高渐变太快,不但对行车和路容不利,还影响到舒适性;如果缓和曲线太长,使超高渐变率太小,对排水不利。?标准?规定了适中的超高渐变率,由此可导出计算缓和曲线最小长度的计算公式。 超高缓和段长度计算公式知:
piblc'
pibllch' 〔2-12〕
式中:cl
——超高缓和段长度,m;
hl——缓和曲线最小长度,m; b——旋转轴至行车道〔设路缘带时为路缘带〕外侧边缘的宽度,m; i——超高旋转轴外侧的最大超高坡度与原路拱坡度代数差,%; p——超高渐变率,参考表2-9。 〔4〕从视觉上应有平顺感来考虑 根据视觉要求,缓和曲线的起点和终点的切线角最好在3°~29°之间,这样可获得良好的视觉效果。由如图2-6所示。
图2-6 按视觉要求的盘旋线长度 Rlh2 而 hl
A
R2
那么 2
2
2Al
h
〔2-
13〕 将3及29代入上式那么得 RAR
3 〔2-14〕
或 21slsh
〔2-15〕 按上述四点要求,计算缓和曲线长度的公式与设计速度关系最大,与半径的关系那么有差异。为此,?标准?规定按设计速度来确定缓和曲线最小长度,同时考虑了行车时间和附加纵坡的要求,因此在相同设计速度的公路上,不管曲线半径大小如何,都可取同一个缓和曲线长度。 〔5〕缓和曲线长度取值 各级公路最小缓和曲线长度见表2-5。选用缓和曲线长度时取5m的整倍数。缓和曲线长度应随圆曲线半径的增大而增大。圆曲线按规定需设置超高时,缓和曲线长度应不小于超高缓和段长度。 表2-5 缓和曲线最小长度
设计速度〔m/h〕 12021 00 80 60 40 30 2021 和曲线最小长度〔m〕 100 85 70 50 35 25 2021 :四级公路为超高、加宽缓和段长度。
4.缓和曲线的计算 1〕切线角 〔1〕缓和曲线上任意点的切线角x
缓和曲线的切线角,是指缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。在图2-7所示,以缓和曲线起点〔ZH或HZ〕为坐标原点,以该点切线为轴,法线为y轴,缓和曲线上任意一点p的切线与起点〔ZH或HZ〕切线相交所组成的角为
x
角,设p点处曲率半径为,曲线长度为l,p点处坐标为、y。 图2-7 缓和曲线的直角坐标 dldx
dld
xx
将lA2
代入并积分得:
o222218022hxRllAlAldl
〔2-16〕
式中:l—从缓和曲线起点ZH〔HZ〕点至缓和曲线上任意一点之弧长,m;
hl—缓和曲线全长,m; R—缓和曲线终点HY〔YH〕处的半径,即圆曲线半径,m;
x—缓和曲线任意一点的切线角。 〔2〕缓和曲线总的切线角
在hl终点处Rllh,
代入式〔2-16〕,那么得:
o180
2Rl
h 〔2-
17〕 式中:—缓和曲线终点YH〔HY〕处的切线角。 2〕缓和曲线直角坐标 在图2-7中,任意一点p处有一微分弧段dl,其所对应的中心角为xd
,那么:
xxdldydldxsincos
将xsin
及xcos用函数幂级数展开可得:
)!7!5!3()!6!4!21(753642xxxxxxxdldydldx
积分后略去高次项并化简得: 33
73
22
5
336640hhhlRlRllylRllx
〔2-18〕
当hll
时,那么缓和曲线终点的坐标为:
34223
336640RlRlyRllxhhhhhh
〔2-19〕
式中: —缓和曲线上任意一点的横坐标; y—缓和曲线上任意一点的纵坐标;
hx—缓和曲线终点处的横坐标;
hy—缓和曲线终点处的纵坐标。 其余符号意义同前。 3〕缓和曲线常数 为了能在直线与圆曲线之间插入缓和曲线,必须将原有圆曲线向内移动一定的距离p,才能使缓和曲线的起点切于直线上。圆曲线需内移,内移有两种方法:—种是圆心不变,使圆曲线半径减小,从而使圆曲线向内移动;另一种是半径不变,而圆心沿内角的分角线向内移动,使圆曲线向内移动半径减小。由于后者是不平行移动,圆曲线上的各点的内移值不相等,测设工作麻烦,因此采用第一种方法。 采用圆心不动的平行移动方法,可以看成是平曲线在未设置缓和曲线时的圆曲线半径为pR,而该平曲线要插入缓和曲线,向内移动距离p后,圆曲线半径正好减小一个p值,即为R,如图2-8所示。 内移值p和外延值q: 〔1〕设有缓和曲线后圆曲线内移距离为p,内移后的圆曲线半径为R。
342R268824hhlRl
P
〔2-2021〔2〕设有缓和曲线后切线增长值为q:
232402Rll
qhh 〔2-
21〕
