【全国百强校word】河北省武邑中学2018届高三下学期期中考试历史试题
河北省武邑中学2018届高三下学期期中考试文综地理试题有答案
河北省武邑中学2018届高三下学期期中考试文综地理试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4. 考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
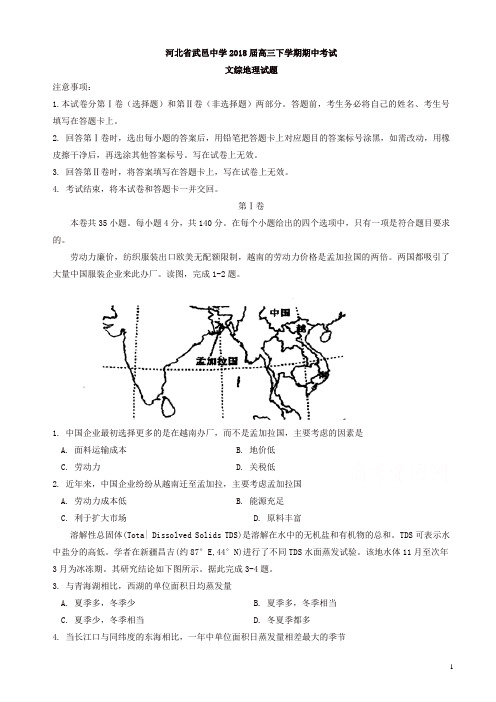
劳动力廉价,纺织服装出口欧美无配额限制,越南的劳动力价格是孟加拉国的两倍。
两国都吸引了大量中国服装企业来此办厂。
读图,完成1-2题。
1. 中国企业最初选择更多的是在越南办厂,而不是孟加拉国,主要考虑的因素是A. 面料运输成本B. 地价低C. 劳动力D. 关税低2. 近年来,中国企业纷纷从越南迁至孟加拉,主要考虑孟加拉国A. 劳动力成本低B. 能源充足C. 利于扩大市场D. 原料丰富溶解性总固体(Tota| Dissolved Solids TDS)是溶解在水中的无机盐和有机物的总和。
TDS可表示水中盐分的高低。
学者在新疆昌吉(约87°E,44°N)进行了不同TDS水面蒸发试验。
该地水体11月至次年3月为冰冻期。
其研究结论如下图所示。
据此完成3-4题。
3. 与青海湖相比,西湖的单位面积日均蒸发量A. 夏季多,冬季少B. 夏季多,冬季相当C. 夏季少,冬季相当D. 冬夏季都多4. 当长江口与同纬度的东海相比,一年中单位面积日蒸发量相差最大的季节A. 华北地区的空气湿度小B. 黄河三角洲的面积增速减缓C. 太湖的自净能力增强D. 新疆博斯腾湖水体更新速度慢的的喀喀湖(图中a湖)是南美洲地势最高的湖泊。
该湖位于安第斯山脉的普纳高原北部,湖面海拔达3821米,湖水面积大约为8300平方千米,平均水深140-180米,最深处达280米。
【全国百强校】河北省衡水市武邑中学2018届高三下学期第六次模拟考试数学(理)试题(解析版)

河北武邑中学2018届高三下学期第六次模拟考试数学试题(理)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填涂在答题卡上.1. 已知,,则( )A. B. C. D.【答案】C【解析】由题意得:,,∴故选:A2. 若复数(,且),且,则的实部为( )A. B. C. D.【答案】A【解析】【分析】利用复数模的公式列方程求出,利用复数乘法的运算法则化简复数,从而可得结果.【详解】因为复数(,且),所以,解得,可得,所以,的实部为,故选A.【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.3. 已知函数,则的图象大致为( )A. B. C. D. 学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...学§科§网...【答案】A【解析】【分析】可以排除法,利用奇偶性可排除选项;利用,可排除选项,从而可得结果.【详解】因为,所以函数是奇函数,其图象关于原点对称,可排除选项;又因为,可排除选项.故选A.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象4. 已知双曲线的一条渐近线与直线垂直,则双曲线的离心率等于( )A. B. C. D.【答案】B【解析】【分析】由题意判断出直线与渐近线垂直,利用相互垂直的直线的斜率之间的关系和离心率公式即可得结果.【详解】双曲线的渐近线方程为,又直线可化为,可得斜率为3,双曲线的一条渐近线与直线垂直,,双曲线的离心率,故选B.【点睛】本题主要考查双曲线的渐近线及离心率,属于中档题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出,从而求出;②构造的齐次式,求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解..5. 《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”,其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”.现若向此三角形内随机投一粒豆子(视为点),则豆子落在其内切圆外的概率是( )A. B. C. D.【答案】B【解析】由题意可知:直角三角向斜边长为17,由等面积,可得内切圆的半径为:落在内切圆内的概率为,故落在圆外的概率为6. 已知函数的部分图象如图所示,则函数图象的一个对称中心可能为( )A. B. C. D.【答案】C【解析】由题意得,即,把点代入方程可得,所以,可得函数的一个对称中心为,故选C.7. 下图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的值分别为8,10,0,则输出和的值分别为( )A. 2,4B. 2,5C. 0,4D. 0,5【答案】B【解析】【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的、的值.【详解】模拟执行程序框图,可得,,不满足,不满足;满足;满足;满足;不满足,满足,输出的值为2,的值为,故选B.【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.8. 已知,,则的值为( )A. B. C. D.【答案】B【解析】【分析】由,可得,由平方关系可得,从而得,进而可得结果.【详解】因为,所以,可得,因为,所以,,,所以的值为,故选B.【点睛】三角函数求值有三类,(1)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.(2)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.(3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,确定角.9. 若关于的混合组有解,则的取值范围为( )A. B. C. D.【答案】C【解析】【分析】问题等价于函数的图象与条件表示的可行域有交点,作出可行域,由图可知必有且图象在过两点的图象之间,从而可得结果.【详解】关于的混合组有解,等价于函数的图象与条件表示的可行域有交点,画出可行域如图所示,求得,由图可知,欲满足条件必有且图象在过两点的图象之间,当图象过点时,,当图象过点时,,故的取值范围是,故选C.【点睛】本题主要考查可行域、含参数目标函数最优解和均值不等式求最值,属于难题.含参变量的线性规划问题是近年来高考命题的热点,由于参数的引入,提高了思维的技巧、增加了解题的难度,此类问题的存在增加了探索问题的动态性和开放性,此类问题一般从目标函数的结论入手,对目标函数变化过程进行详细分析,对变化过程中的相关量的准确定位,是求最优解的关键.10. 已知直线与函数的图象相切,则切点的横坐标为( )A. B. C. 2 D.【答案】A【解析】【分析】设切点坐标为,根据导数的几何意义、点在直线上且在曲线上,列出方程组求出切点坐标. 【详解】由可得,设切点坐标为,则,解得,故选A.【点睛】本题主要考查利用导数求切线斜率,属于难题. 应用导数的几何意义求切点处切线的斜率,主要体现在以下几个方面:(1) 已知切点求斜率,即求该点处的导数;(2) 己知斜率求切点即解方程;(3) 巳知切线过某点(不是切点) 求切点, 设出切点利用求解.11. 已知为抛物线的焦点,为抛物线上三点,当时,称为“和谐三角形”,则“和谐三角形”有( )A. 0个B. 1个C. 3个D. 无数个【答案】D【解析】【分析】当时,为的重心,连接并延长至,使,当在抛物线内部时,设,利用“点差法”可证明总存在以为中点的弦,从而可得结果.【详解】抛物线方程为为曲线上三点,当时,为的重心,用如下办法构造,连接并延长至,使,当在抛物线内部时,设,若存在以为中点的弦,设,则则,两式相减化为,,所以总存在以为中点的弦,所以这样的三角形有无数个,故选D.【点睛】本题主要考查平面向量的基本运算以及“点差法”的应用,属于难题.对于有弦关中点问题常用“点差法”,其解题步骤为:①设点(即设出弦的两端点坐标);②代入(即代入圆锥曲线方程);③作差(即两式相减,再用平方差公式分解因式);④整理(即转化为斜率与中点坐标的关系式),然后求解. 12. 祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理: “幂势既同,则积不容异”.意思是:夹在两个乎行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现将曲线绕轴旋转一周得到的几何体叫做椭球体,记为,几何体的三视图如图所示.根据祖暅原理通过考察可以得到的体积,则的体积为( )A. B. C. D.【答案】D【解析】【分析】由三视图可得几何体是一个底面半径为,高为的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点,上底面为底面的圆锥,由祖暅原理可得结果.【详解】由三视图可得几何体是一个底面半径为,高为的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点,上底面为底面的圆锥,则圆柱的体积为,圆锥的体积,利用祖暅原理可计半椭球的体积为,所以的体积为,故选D.【点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力以及几何体的体积,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.二.填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卡上相应位.13. 设平面向量与向量互相垂直,且,若,则_____________.【答案】5【解析】由平面向量与向量互相垂直可得所以,又,故答案为.【方法点睛】本题主要考查向量的模及平面向量数量积公式,属于中档题.平面向量数量积公式有两种形式,一是,二是,主要应用以下几个方面:(1)求向量的夹角,(此时往往用坐标形式求解);(2)求投影,在上的投影是;(3)向量垂直则;(4)求向量的模(平方后需求).14. 展开式中,的系数为_____________.【答案】【解析】【分析】根据展开式的通项公式,分两种情况可得展开式的系数.【详解】展开式的通项公式为,故分别令,可得展开式与的系数分别为故展开式的系数为,故答案为.【点睛】本题主要考查二项展开式定理的通项与系数,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.15. 现有个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球赢.如果甲先抓,那么下列推断正确的是_____________.(填写序号)①若,则甲有必赢的策略;②若,则乙有必赢的策略;③若,则甲有必赢的策略;④若,则乙有必赢的策略.【答案】③【解析】【分析】如果甲先抓,若甲有必贏的策略,必贏的策略为:甲先抓1球,当乙抓1球时,再抓3球;当乙抓2球时,甲再抓2球;当乙抓3球时,甲再抓1球;这时还有4个小球,轮到乙抓,按规则,乙最少抓1个球,最多抓3个球,无论如何抓,都会至少剩一个球,至多剩3个球;甲再抓走所有剩下的球,从而甲胜. 【详解】现有个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球贏,,如果甲先抓,则甲有必赢的策略,必赢的策略为:(1)甲先抓1球,(2)当乙抓1球时,甲再抓3球;当乙抓2球时,甲再抓2球;当乙抓3球时,甲再抓1球;(3)这时还有4个小球,轮到乙抓,按规则,乙最少抓1个球,最多抓3个球,无论如何抓,都会至少剩一个球,至多剩3个球;(4)甲再抓走所有剩下的球,从而甲胜,故答案为③.【点睛】本题主要考查推理案例,属于难题.推理案例的题型是高考命题的热点,由于条件较多,做题时往往感到不知从哪里找到突破点,解答这类问题,一定要仔细阅读题文,逐条分析所给条件,并将其引伸,找到各条件的融汇之处和矛盾之处,多次应用假设、排除、验证,清理出有用“线索”,找准突破点,从而使问题得以解决.16. 中,角的对边分别为,,面积为,当最大时,_____________.【答案】【解析】,当且仅当,取等号,∴∠C的最大值为75°,此时sinC=,,∴.故答案为:三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17. 已知数列的前项和.(1)求;(2)求.【答案】(1);(2)【解析】【分析】(1)由可得当时,,两式相减,检验当时是否适合,从而可得结果;(2)利用错位相减法,结合等比数列的求和公式即可得结果.【详解】(1)当时,.当时,,故.(2) ①,②,②-①得,.【点睛】本题主要考查数列的通项公式与前项和公式之间的关系以及错误相减法求和,属于中档题. 已知数列前项和与第项关系,求数列通项公式,常用公式,将所给条件化为关于前项和的递推关系或是关于第项的递推关系,若满足等比数列或等差数列定义,用等比数列或等差数列通项公式求出数列的通项公式,否则适当变形构造等比或等数列求通项公式. 在利用与通项的关系求的过程中,一定要注意的情况.18. 2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区,消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:请根据上表提供的数据,用最小二乘法求出变量关于变量的线性回归方程(保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求的分布列及数学期望.参考公式及数据:,,,.【答案】(1)2000;(2)见解析【解析】试题分析:(1)依据公式计算回归方程,在根据求出的结果得到相应的预测值.(2)是离散型随机变量,它服从超几何分布,故根据公式计算出相应的概率,得到分布列后再利用公式计算期望即可.解析:(1)由已知有,,故变量关于变量的线性回归方程为,所以当时,.(2)由题意可知的可能取值有1,2,3,4.,.所以的分布列为19. 如图,已知平面平面,为线段的中点,,四边形为边长为1的正方形,平面平面,,,为棱的中点.(1)若为线上的点,且直线平面,试确定点的位置;(2)求平面与平面所成的锐二面角的余弦值.【答案】(1)见解析;(2)【解析】【分析】(1)连接,由直线平面,,又为的中点,从而得为的中位线,为的中点;(2)先证明平面,可得两两相垂直,以为坐标原点,分别以所在直线为轴,轴,轴建立空间直角坐标系,平面的一个法向量,利用向量垂直数量积为零列方程求出平面的一个法向量,由空间向量夹角余弦公式可得结果.【详解】(1)连接,直线平面,平面,平面平面,又为的中点,为的中位线,为的中点.(2) 则,又为的中点,.又平面平面,平面平面四边形为平行四边形.又,四边形为菱形.又,,,,平面平面平面,两两相垂直以为坐标原点,分别以所在直线为轴,轴,轴建立空间直角坐标系依题意,得,,.设平面的一个法向量则由且得:且令,得.又平面的一个法向量所求锐二面角的余弦值约:.【点睛】本题主要考查线面平行的判定定理以及利用空间向量求二面角,属于中档题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.20. 已知抛物线和圆的公共弦过抛物线的焦点,且弦长为4.(1)求抛物线和圆的方程;(2)过点的直线与抛物线相交于两点抛物线在点处的切线与轴的交点为,求面积的最小值. 【答案】(1);(2)【解析】试题分析:(1)由题意可知,求得的值,得到抛物线的方程,进而求得圆的方程.(2)设直线的方程为:,联立方程组,求的及,利用导数求得切线方程,得到,利用点到直线的距离公式,求的距离,表示出面积的表达式,利用导数,研究函数的单调性和最值,即可得到结论.试题解析:(1)由题意可知,,所以,故抛物线的方程为.又,所以,所以圆的方程为.(2)设直线的方程为:,并设,联立,消可得,.所以;.,所以过点的切线的斜率为,切线为,令,可得,,所以点到直线的距离,故,分又,代入上式并整理可得:,令,可得为偶函数,当时,,,令,可得,当,,当,,所以时,取得最小值,故的最小值为.点睛:本题主要考查抛物线的方程与性质、直线与圆锥曲线的位置关系,解答此类题目,利用题设条件确定圆锥曲线方程是基础,通过联立直线方程与椭圆(圆锥曲线)方程的方程组,应用一元二次方程根与系数的关系,得到“目标函数”的解析式,利用函数的性质进行求解,此类问题易错点是复杂式子的变形能力不足,导致错漏百出,本题能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等.21. 已知函数.(1)若函数在区间上为增函数,求的取值范围;(2)当且时,不等式在上恒成立,求的最大值.【答案】(1);(2)3【解析】试题分析:(1)依题意可得,函数在区间上为增函数等价于在上恒成立,即在上恒成立,从而可得的取值范围;(2)不等式在上恒成立等价于对任意恒成立,令,利用导数研究函数的单调性,从而可得的最小值,即可求得的最大值.试题解析:(1)依题意可得.∵函数在区间上为增函数∴在上恒成立,即在上恒成立,即在上恒成立,而.∴,即的取值范围为.(2)当时,.∵∴原不等式可化为,即对任意恒成立.令,则.令,则.∴在上单调递增.∵,∴ 存在使,即,即当时,,即;当时,,即.∴在上单调递减,在上单调递增.由,得,∴∵∴.点睛:本题主要考查利用导数研究函数的单调性以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数恒成立(即可)或恒成立(即可);② 数形结合(图象在上方即可);③ 讨论最值或恒成立;④ 讨论参数.22. 在平面直角坐标系中,将曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,的极坐标方程为.(1)求曲线的参数方程;(2)过原点且关于轴对称的两条直线与分别交曲线于和,且点在第一象限,当四边形周长最大时,求直线的普通方程.【答案】(1),(为参数);(2)【解析】试题分析:(Ⅰ)首先求得的普通方程,由此可求得的参数方程;(Ⅱ)设四边形的周长为,点,然后得到与的关系式,从而利用辅助角公式求得点的直角坐标点,从而求得的普通方程.试题解析:(Ⅰ),(为参数).(Ⅱ)设四边形的周长为,设点,,且,,所以,当()时,取最大值,此时,所以,,,此时,,的普通方程为.点睛:将曲线的参数方程化为普通方程的关键是消去其中的参数,此时要注意其中的(它们都是参数的函数)的取值范围,即在消去参数的过程中一定要注意普通方程与参数方程的等价性.23. 已知函数.(1)解不等式;(2)若,不等式对恒成立,求的取值范围.【答案】(1)或;(2)或【解析】【分析】(1) 对分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果;(2),恒成立等价于.因为,,所以由原不等式恒成立,得,从而可得结果. 【详解】(1) ,原不等式等价于:或或,解得: ,或,或,综上所述,不等式解集是: 或;(2) ,恒成立等价于.因为,所以的最大值为;时,;时,;时,,所以,所以由原不等式恒成立,得:,解得:或.【点睛】绝对值不等式的常见解法:①利用绝对值不等式的几何意义求解,体现了数形结合的思想;②利用“零点分段法”求解,体现了分类讨论的思想;③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.。
(推荐)河北省武邑中学2018届高三下学期期中考试数学(理)试卷(含答案)

河北省武邑中学2018届高三下学期期中考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合},06|{2N x x x x A ∈>++-=,}2,1,0,1{-=B ,则=B A ( ) A .}2,1{ B .}2,1,0{ C .}1,0{ D .}2,1,0,1{- 2.已知实数n m ,满足53)24)((+=-+i i ni m ,则=+n m ( ) A .59 B .511 C .49 D .4113.给出下列命题:①已知R b a ∈,,“1>a 且1>b ”是“1>ab ”的充分条件;②已知平面向量,,“1||,1||>>”是“1||>+”的必要不充分条件; ③已知R b a ∈,,“122≥+b a ”是“1||||≥+b a ”的充分不必要条件; ④命题p :“R x ∈∃0,使100+≥x ex 且1ln 00-≤x x ”的否定为p ⌝:“R x ∈∀,都有1+<x e x 且1ln ->x ”.其中正确命题的个数是( ) A .0 B .1 C .2 D .34.若定义在R 上的偶函数)(x f 满足)()2(x f x f =+,且当]1,0[∈x 时,x x f =)(,则函数||log )(3x x f y -=的零点个数是( )A .6个B .4个C .3个D .2个 5.设函数)3cos()(ϕ+=x x f ,其中常数ϕ满足0<<-ϕπ.若函数)(')()(x f x f x g +=(其中)('x f 是函数)(x f 的导数)是偶函数,则ϕ等于( ) A .3π-B .65π-C .6π-D .32π- 6.执行如图的程序框图,如果输入的k b a ,,分别为3,2,1,输出的815=M ,那么判断框中应填入的条件为( )A .k n <B .k n ≥C .1+<k nD .1+≥k n 7.总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体编号为A .08B .07C .02D .018.已知R k ∈,点),(b a P 是直线k y x 2=+与圆32222+-=+k k y x 的公共点,则ab 的最大值为( ) A.15B.9C.1D. 35-9.若不等式组⎪⎩⎪⎨⎧≤-+≤+-≥+-08010502y x y x y x 所表示的平面区域存在点),(00y x ,使0200≤++ay x 成立,则实数a 的取值范围是( )A .1-≤aB .1-<aC .1>aD .1≥a10.北京某大学为第十八届四中全会招募了30名志愿者(编号分别是1,2,…,30号),现从中任意选取6人按编号大小分成两组分配到江西厅、广电厅工作,其中三个编号较小的人在一组,三个编号较大的在另一组,那么确保6号、15号与24号同时入选并被分配到同一厅的选取种数是( ) A .25 B .32 C .60 D .10011.已知在ABC Rt ∆中,两直角边1=AB ,2=AC ,D 是ABC ∆内一点,且060=∠DAB ,设),(R ∈+=μλμλ,则=μλ( ) A .332 B .33C .3D .32 12.已知函数)(x f 的定义域为D ,若对于)(),(),(,,c f b f a f D b a ∈∀分别为某个三角形的边长,则称)(x f 为“三角形函数”.给出下列四个函数:①)(ln )(32e x e x xf ≤≤=;②x x f cos 4)(-=;③)41()(21<<=x x x f ;④1)(+=x xe e xf .其中为“三角形函数”的个数是( )A .1B .2C .3D .4二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥+≥32320y x y x x ,则y x z -=的最小值是 .14.若5)1(-ax 的展开式中3x 的系数是80,则实数a 的值是 . 15.已知几何体的三视图如图所示,其中俯视图为一正方形,则该几何体的表面积为 .16.若函数)(x f 的图象上存在不同的两点),(11y x A ,),(22y x B ,其中2211,,,y x y x 使得222221212121||y x y x y y x x +⋅+-+的最大值为0,则称函数)(x f 是“柯西函数”. 给出下列函数:①)30(ln )(<<=x x x f ;②)0(1)(>+=x xx x f ;③82)(2+=x x f ;④82)(2-=x x f .其中是“柯西函数”的为 .三、解答题 (本大题共6题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列}{n a 的前n 项和为n S ,且满足*),1(34N n a S n n ∈-=. (1)求数列}{n a 的通项公式; (2)令n n a b 2log =,记数列})1)(1(1{+-n n b b 的前n 项和为n T ,证明:2131<≤n T . 18.高二某班共有20名男生,在一次体检中这20名男生被平均分成两个小组,第一组和第二组男生的身高(单位:cm )的茎叶图如下:(1)根据茎叶图,分别写出两组学生身高的中位数;(2)从该班身高超过180cm 的7名男生中随机选出2名男生参加篮球队集训,求这2名男生至少有1人来自第二组的概率;(3)在两组身高位于)180,170[(单位:cm )的男生中各随机选出2人,设这4人中身高位于)180,175[(单位:cm )的人数为X ,求随机变量X 的分布列和数学期望.19.菱形ABCD 的对角线AC 与BD 交于点O ,6,2==AC AB ,点F E ,分别在CD AD ,上,45==CF AE ,EF 交BD 于点H ,将D E F ∆沿EF 折到EFD '∆位置,10'=OD .(1)证明:⊥H D '平面ABCD ; (2)求二面角C A D B --'的正弦值.20.设抛物线)0(42>=m mx y 的准线与x 轴交于1F ,抛物线的焦点2F ,以21,F F 为焦点,离心率21=e 的椭圆与抛物线的一个交点为)362,32(E ;自1F 引直线交抛物线于Q P ,两个不同的点,设F F 11λ=. (1)求抛物线的方程椭圆的方程; (2)若)1,21[∈λ,求||PQ 的取值范围. 21.已知函数21)ln(21)(2+--=ax a x x a x f . (1)设xx f x g 1)()(+=,求函数)(x g 的单调区间; (2)若0>a ,设))(,()),(,(2211x f x B x f x A 为函数)(x f 图象上不同的两点,且满足1)()(21=+x f x f ,设线段AB 中点的横坐标为0x ,证明:10>ax . 请考生在22、23二题中任选一题作答,如果都做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程已知直线l 的参数方程为⎩⎨⎧=+=ααsin cos t y t m x (t 为参数,πα<≤0),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 4=,射线)44(πϕπϕθ<<-=,4πϕθ+=,4πϕθ-=分别与曲线C交于C B A ,,三点(不包括极点O ). (1)求证:||2||||OA OC OB =+;(2)当12πϕ=时,若C B ,两点在直线l 上,求m 与α的值.23.选修4-5:不等式选讲已知函数|12|||)(-++=x m x x f . (1)当1=m ,解不等式3)(≥x f ; (2)若41<m ,且当]2,[m m x ∈时,不等式|1|)(21+≤x x f 恒成立,求实数m 的取值范围.数 学(理科)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在答题卡中对应题号后的横线上.13.3- 14.2 15.23224++ 16.①④三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤. 17.解:(1)当1=n 时,有)1(34111-==a S a ,解得41=a , 当2≥n 时,有)1(3411-=--n n a S ,则 )1(34)1(3411---=-=--n n n n n a a S S a 整理得41=-n na a ∴数列}{n a 是以4=q 为公比,以41=a 为首项的等比数列∴)(444*1N n a n n n ∈=⨯=-. (2)由(1)有n a b nn n 24log log 22===,则)12(1121(21)12)(12(1)1)(1(1+--=-+=-+n n n n b b n n∴)12)(12(1531311+-++⨯+⨯=n n T n )121121()5131()311[(21+--++-+-=n n)1211(21+-=n 易知数列}{n T 为递增数列, ∴211<≤n T T ,即2131<≤n T .18.(1) 第一组学生身高的中位数为1742176172=+, 第二组学生身高的中位数为5.1742175174=+; (2)记“这2名男生至少有1人来自第二组”为事件A ,761)(2723=-=C C A P ,∴这2名男生至少有1人来自第二组的概率为76; (3)X 的所有可能取值是0,1,2,3101)0(23252223===C C C C X P ,52)1(23251223221213=+==C C C C C C C X P ,3013)2(23251213122222=+==C C C C C C C X P ,151)3(23251222===C C C C X P X 的分布列为15153302521)(=⨯+⨯+⨯=X E . 19.解:(1)∵45==CF AE , ∴CDCFAD AE =,∴AC EF //,∵四边形ABCD 为菱形, ∴BD AC ⊥,∴BD EF ⊥,∴DH EF ⊥,∴H D EF '⊥ ∵6=AC , ∴3=AO ;又5=AB ,OB AO ⊥,∴4=OB ,∴1=⋅=OD AOAEOH ,∴3'==H D DH , ∴222|'||||'|H D OH OD +=,∴H D OH '⊥,又∵H EF OH = , ∴⊥H D '平面ABCD .(Ⅱ)建立如图所示的空间直角坐标系:)0,3,1(),3,0,0('),0,3,1(),0,0,5(-A D C B ,)0,6,0(),3,3,1(),0,3,4(=-==,设平面'ABD 的一个法向量为),,(1z y x n =,由⎪⎩⎪⎨⎧=⋅=⋅0'011AD n n 得⎩⎨⎧=++-=+033034z y x y x ,取⎪⎩⎪⎨⎧=-==543z y x , ∴)5,4,3(1-=n ,同理可得平面C AD '的法向量为)1,0,3(2=n ,∴25571025|59||||||cos |2121=⨯+==n n θ,∴25952sin =θ.20.解:(1)设椭圆的标准方程为)0(12222>>=+b a by ax ,由题意得⎪⎪⎩⎪⎪⎨⎧=-==+211924942222a b a a c b a ,解得⎪⎩⎪⎨⎧==3422b a∴椭圆的方程为13422=+y x ∴点2F 的坐标为)0,1(,∴1=m ,∴抛物线的方程是x y 42=(2)由题意得直线PQ 的斜率存在,设其方程为)0)(1(≠+=k x k y , 由⎩⎨⎧=+=xy x k y 4)1(2消去x 整理得0442=+-k y ky ()∵直线PQ 与抛物线交于两点, ∴016162>-∆k ,设),(),,(2211y x Q y x P ,则421=y y ①,ky y 421=+②, ∵F F 11λ=,)0,1(1-F ∴),1(),1(2211y x y x +=+λ ∴21y y λ=,③由①②③消去21,y y 得22)1(4+=λλk .∴||PQ 22221221222121616)11(4))[(11())(11(k k ky y y y ky y k-+=-++=-+=441616k k -=,即=2||PQ 441616k k -,将22)1(4+=λλk 代入上式得, =2||PQ 16)21(16)12(16)4(222224-++=-++=-+λλλλλλλ,∵λλλ1)(+=f 在)1,21[∈λ上单调递减,∴)21()()1(f f f ≤<λ,即2512≤+<λλ, ∴<041716)21(2≤-++λλ, ∴217||0≤<PQ ,即||PQ 的取值范围为]217,0(. 21.解:(1) 21)ln(2)(2+-=ax a x a x g ,xax a x a a x g )2(2)('2-=-= ①0>a 时, )(x g 定义域为),0(+∞当)2,0(a x ∈时,0)('<x g ,故)(x g 在)2,0(a上单调递减; 当),2(+∞∈a x 时,0)('>x g ,故)(x g 在),2(+∞a上单调递增; ②0<a 时,)(x g 定义域为)0,(-∞当)2,(a x -∞∈时,0)('>x g ,故)(x g 在)2,(a-∞上单调递增; 当)0,2(a x ∈时,0)('<x g ,故)(x g 在)0,2(a上单调递减.(2)10>ax 2121212x ax a x x ->⇔>+⇔0)1(21)('222≥-=-+=a xx ax a x f ,故)(x f 在定义域),0(+∞上单调递增, 只需证:1)()1(2=+x f x f ,21)1(=af ,不妨设2110x ax <<< axa x x a ax x ax a a x f x a f x F ln 21)2ln(221)2(1)()2()(22--+-----=-+-=则0)2()1(4222)2(1)('2232222≤---=-+---=ax x ax ax a x a ax a x x F ax 1≥∀, 从而)(x F 在),1[+∞a 上单调递减,故0)1()(2=<aF x F ,即()式. 22.解:(1)证明:依题意,ϕcos 4||=OA ,)4cos(4||πϕ+=OB ,)4cos(4||πϕ-=OC ,则=+||||OC OB ++)4cos(4πϕ||2cos 24)4cos(4OA ==-ϕπϕ(2)当12πϕ=时,C B ,两点的极坐标分别为)6,32(),3,2(ππ-,化为直角坐标)3,1(B ,)3,3(-C , 经过点C B ,的直线方程为)2(3--=x y , 又直线l 经过点)0,(m ,倾斜角为α,故2=m ,32πα=. 23.解:(1) 当1=m 时,|12||1|)(-++=x x x f ,则⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤---<-=)21(3)211(2)1(3)(x x x x x x x f由3)(≥x f 解得1-≤x 或1≥x ,即原不等式的解集为),1[]1,(+∞--∞ . (2)|1|)(21+≤x x f ,即|1||12|21||21+≤-++x x m x ,又]2,[m m x ∈且41<m 所以410<<m ,且0>x 所以|12|21|1|221--+≤+x x m x 即|12|2--+≤x x m 令|12|2)(--+=x x x t ,则⎪⎪⎩⎪⎪⎨⎧≥-<<+=)21(3)210(13)(x x x x x t ,所以]2,[m m x ∈时, 13)()(min +==m m t x t , 所以13+≤m m ,解得21-≥m , 所以实数m 的取值范围是)41,0(.欢迎访问“高中试卷网”——。
河北省武邑中学2018届高三下学期期中考试数学(文)试卷(含答案)-精品

河北省武邑中学2018届高三下学期期中考试数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合},32|{Z x x x A ∈≤≤-=,}3|{2-==x y y B ,则B A 的子集个数共有( )A .1个B .2个C .3个D .4个 2.若复数z 满足5)43(=+z i ,则下列说法不正确的是( ) A .复数z 的虚部为i 54-B .复数z z -为纯虚数C .复数z 在复平面内对应的点位于第四象限D .复数z 的模为1 3.已知命题p :命题“若0>a ,则R x ∈∀,都有1)(>x f ”的否定是“若R x ∈∀,都有1)(>x f ,则0≤a ”;命题q :在ABC ∆中,角C B A ,,的对边分别为c b a ,,,则“B A >”是“b a >”的充要条件,则下列命题为真命题的是( )A .q p ∧⌝)(0B .)(q p ⌝∨C .q p ∧D .)()(q p ⌝∧⌝4.在ABC ∆中,1||,3,==⊥AB AD ,则=⋅( ) A .1 B .2 C .3 D .45.我国南宋数学家秦九韶给出了求n 次多项式0111a x a x a x a n n n n ++++-- 当0x x =时的值的一种简捷算法,该算法被后人命名为“秦九韶算法”.例如,可将3次多项式改写成:012233a x a x a x a +++ 0123))((a x a x a x a +++=,然后进行求值.运行如图所示的程序框图,是求哪个多项式的值( )A .432234++++x x x xB .5432234++++x x x xC .3223+++x x xD .43223+++x x x 6.一个四棱柱的三视图如图所示,该四棱柱的体积为( )A .12B .24C .36D .48 7.已知函数)sin()(ϕω+=x A x f ,且)6()6(),3()3(x f x f x f x f -=+--=+ππππ,则实数ω的值可能是( )A .2B .3C .4D .58.如图,网格纸上小正方形的边长为1,粗线画出的是某集合体的三视图,则该三视图的体积是( )A.9B.227C.18D. 27 9.已知n m ,为异面直线,⊥m 平面α,⊥n 平面β,直线l 满足βα⊄⊄⊥⊥l l n l m l ,,,,则( )A .βα//且α//lB .βα⊥且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l 10.记函数22)(x x x f -+=的定义域为A ,在区间]6,3[-上随机取一个数x ,则A x ∈的概率是( ) A .32 B .31 C .92 D .91 11.已知双曲线12222=-by a x (b a ,均为正数)的两条渐近线与抛物线x y 42=的准线围成的三角形的面积为3,则双曲线的离心率为( ) A .2 B .3 C .6 D .3212.已知偶函数)(x f (0≠x )的导函数为)('x f ,且满足0)1(=f .当0>x 时,)(2)('x f x xf <,则使得0)(>x f 成立的x 的取值范围是( )A .)1,0()1,( --∞B .),1()1,(+∞--∞C .)1,0()0,1( -D .),1()0,1(+∞-二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若31)4cos(=+πα,则α2sin 的值为 .14.曲线xxe x f =)(在点))1(,1(f 处的切线在y 轴上的截距是 .15.在平面直角坐标系xOy 中,若动圆C 上的点都不在不等式组⎪⎩⎪⎨⎧≥++≥+-≤0330333y x y x x 表示的平面区域内,则面积最大的圆C 的标准方程为 .16.设函数⎪⎩⎪⎨⎧≤-->-=0,230,21)(3x mx x x e x f x (其中e 为自然对数的底数)有3个不同的零点,则实数m 的取值范围是 .三、解答题 (本大题共6题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知等差数列}{n a 的前n 项和为n S ,且满足100,11106==S a . (1)求数列}{n a 的通项公式; (2)设1)1(+⋅-=n n nn a a nb ,求数列}{n b 的前n 项和为n T .18.某商场举行有奖促销活动,顾客购买一定金额的商品即可抽奖一次.抽奖方法是:从装有标号为1,2,3,4的4个红球和标号为1,2的2个白球的箱中,随机摸出2个球,若摸出的两球号码相同,可获一等奖;若两球颜色不同且号码相邻,可或二等奖,其余情况获三等奖.已知某顾客参与抽奖一次. (1)求该顾客获一等奖的概率; (2)求该顾客获三等奖的概率.19.如图,在四棱锥ABCD P -中,⊥PD 平面ABCD ,底面ABCD 为梯形,CD AB //,060=∠BAD ,2===AB AD PD ,4=CD ,E 为PC 的中点.(1)证明://BE 平面PAD ; (2)求三棱锥PBD E -的体积.20.如图,已知椭圆C :)0(12222>>=+b a by a x ,其左右焦点为)0,1(1-F 及)0,1(2F ,过点1F 的直线交椭圆C 于B A ,两点,线段AB 的中点为G ,AB 的中垂线与y 轴分别交于E D ,两点,且||1AF 、||21F F 、||2AF 构成等差数列. (1)求椭圆C 的方程;(2)记D GF 1∆的面积为1S ,OED ∆(O 为原点)的面积为2S ,试问:是否存在直线AB ,使得2112S S =?说明理由.21.已知函数x a x x f ln 2)(2+=.(1)若函数)(x f 的图象在))2(,2(f 处的切线斜率为1,求实数a 的值; (2)若函数)(2)(x f xx g +=在]2,1[上是减函数,求实数a 的取值范围. 请考生在22、23二题中任选一题作答,如果都做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 的参数方程为⎩⎨⎧=+=ty tx sin 2cos 22(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为θρsin 2=,曲线3C C 的极坐标方程为)0(6>=ρπθ.(1)求曲线1C 的普通方程和3C 的直角坐标方程; (2)设3C 分别交21,C C 于点Q P ,,求PQ C 1∆的面积. 23.选修4-5:不等式选讲已知函数|12|||)(-++=x m x x f . (1)当1=m ,解不等式3)(≥x f 的解集; (2)若41<m ,且当]2,[m m x ∈时,不等式|1|)(21+≤x x f 恒成立,求实数m 的取值范围.数 学(文科)参考答一、选择题:二、填空题: 13.97 14.e - 15.4)1(22=+-y x 16.),1(+∞三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤.17.解:(1)12-=n a n . (2))121121(41)1()1(1++-⋅⋅-=⋅-=+n n a a n b n n n nn .18.标号为1,2,3,4的4个红球记为4321,,,A A A A ,标号为1.2的2个白球记为21,B B .从中随机摸出2个球的所有结果有:},{21A A ,},{31A A ,},{41A A ,},{11B A ,},{21B A ,},{32A A ,},{42A A ,},{12B A ,},{22B A ,},{43A A ,},{13B A ,},{23B A ,},{14B A ,},{24B A ,},{2B B 共15个,这些事件的出现是等可能的(1)摸出的两球号码相同的的结果有:},{11B A ,},{22B A 共2个 所以,“该顾客获一等奖”的概率152=P . (2)摸出的两球颜色不同且号码相邻的结果有:},{21B A ,},{12B A ,},{23B A 共3个则“该顾客获二等奖”的概率51153==P 所以“该顾客获三等奖”的概率32511521=--=P . 19.解:(1)设F 为PD 的中点,连接FA EF ,, 因为EF 为PDC ∆的中位线,所以CD EF //,且221==CD EF 又CD AB //,2=AB ,所以EF AB =,EF AB //, 故四边形ABEF 为平行四边形,所以AF BE //又⊂AF 平面PAD ,⊄BE 平面PAD ,所以//BE 平面PAD (2)因为E 为PC 的中点,所以三棱锥BCD P BCD E PBD E V V V ---==21又AB AD =,060=∠BAD ,所以ABD ∆为等边三角形因此2==AB BD ,又4=CD ,060=∠=∠BAD BDC ,所以BC BD ⊥因为⊥PD 平面ABCD ,所以三棱锥BCD P -的体积3343222123131=⨯⨯⨯⨯=⋅=∆-BCD BCD P S PD V 所以三棱锥PBD E -的体积332=-PBD E V . 20.解:(1)因为1AF 、12F F 、2AF 构成等差数列, 所以1212224a AF AF F F =+==,所以2a =, 又因为1c =, 所以23b =,所以椭圆C 的方程为22143x y +=.(2)假设存在直线AB ,使得1212S S =,显然直线AB 不能与x , y 轴垂直. 设AB 方程为()1y k x =+ ()0k ≠,由()221{ 143y k x x y =++=消去y 整理得()22224384120k x k x k +++-=, 显然()()()()22222844*********k k k k ∆=-+-=+>.设()11,A x y , ()22,B x y ,则2122843k x x k -+=+, 故点G 的横坐标为21224243x x k k +-=+, 所以22243,4343k k G k k ⎛⎫- ⎪++⎝⎭.设(),0D D X ,因为DG AB ⊥,所以2223431443Dkk k kx k +⨯=---+,解得2243D k x k -=+,即22,043k D k ⎛⎫- ⎪+⎝⎭. ∵1Rt GDF ∆和Rt ODE ∆相似,且1212S S =, 则GD OD =,=, 整理得2390k -+=,解得23k =,所以k =,所以存在直线AB 满足条件,且直线AB 的方程为)1y x =+.21.解:(1) xax x a x x f 2222)('2+=+= 由已知1)2('=f ,解得3-=a 由x a x xx g ln 22)(2++=,得x ax x x g 222)('2++-=, 由已知函数)(x g 在]2,1[上是减函数, 则0)('≤x g 在]2,1[上恒成立 令21x xa -≤在]2,1[上恒成立 令21)(x x x h -=,在]2,1[上0)21(21)('22<+---=x xx x x h , 所以)(x h 在]2,1[上是减函数,27)2()(min -==h x h ,所以27-≤a .22.解:(1)曲线1C 的普通方程4)2(22=+-y x ,即0422=-+x y x 所以1C 的极坐标方程为0cos 42=-θρρ,即θρcos 4=.曲线3C 的直角坐标方程:)0(33>=x x y(2)依题意,设点Q P ,的坐标分别为)6,(1πρ,)6,(2πρ, 将6πθ=代入θρcos 4=,得321=ρ 将6πθ=代入θρsin 2=,得12=ρ所以132||||21-=-=ρρPQ ,依题意得,点1C 到曲线6πθ=的距离为16sin||1==πOC d所以213)132(21||211-=-=⋅=∆d PQ S PQ C . 23.解:(1) 当1=m 时,|12||1|)(-++=x x x f ,则⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤---<-=)21(3)211(2)1(3)(x x x x x x x f由3)(≥x f 解得1-≤x 或1≥x ,即原不等式的解集为),1[]1,(+∞--∞ . (2)|1|)(21+≤x x f ,即|1||12|21||21+≤-++x x m x ,又]2,[m m x ∈且41<m 所以410<<m ,且0>x 所以|12|21|1|221--+≤+x x m x 即|12|2--+≤x x m 令|12|2)(--+=x x x t ,则⎪⎪⎩⎪⎪⎨⎧≥-<<+=)21(3)210(13)(x x x x x t ,所以]2,[m m x ∈时, 13)()(min +==m m t x t ,11 所以13+≤m m ,解得21-≥m , 所以实数m 的取值范围是)41,0(.欢迎访问“高中试卷网”——。
2018年全国卷Ⅲ文综历史高考试题(word版含答案)

2018年全国卷Ⅲ文综历史高考试题(word版含答案)DA.学术文化水平迅速提升B.士人的地位显著提高C.经世致用思想影响广泛D.崇尚文化的氛围浓厚28.英国科学家赫胥黎的《进化论与伦理学及其他》认为不能将自然的进化论与人类社会的伦理学混为一谈。
但严复将该书翻译成《天演论》时,“煞费苦心”地将二者联系起来,提出自然界进化规律同样适用于人类社会。
严复意在A.纠正生物进化论的错误B.为反清革命提供理论依据C.传播“中体西用”思想D.促进国人救亡意识的觉醒29.1920年,一些人撰文批评工读互助等社会改良活动,认为“零零碎碎的救济”“无补大局”,主张对社会进行“根本改造”,走进工厂,深入工人群众。
这表明当时A.民主与科学观念广泛传播B.实业救国运动如火如荼C.马克思主义影响日益增强D.批判传统礼教成为共识30.1956年,刘少奇在中共八大政治报告中指出:“我们目前在国家工作中的迫切任务之一,是着手系统地制定比较完备的法律,健全我们国家的法制。
”这反映了当时A.法制建设开始迈向制度化B.法制工作围绕组建新政权展开C.法制建设与国内主要矛盾的变化密切相关D.政治体制改革推动了依法治国的全面实行31.表2 中国乡镇企业行业分布表(单位:万个)表2中的数据变化说明,这一时期我国A.农村剩余劳动力大量转移B.城乡一体化逐步实现C.社会主义市场经济体制已建立D.工业结构趋于合理32.公元前5世纪,雅典公民获得更多表达自己想法的机会,公民的成功“依赖于在大型公共集会上谈话、论辩与说服的能力”。
据此可知,在当时雅典A.公民必须能言善辩B.参政议政十分活跃C.民主政治出现危机D.内乱引发思想纷争33.18世纪前半期的法国,先前往来于凡尔赛宫的思想家、文学家、戏剧家们,开始热衷于参加沙龙聚会,讨论的话题广泛,不再局限于传统的信仰和礼仪,思想极为活跃,上流社会不少人也乐于资助他们。
这表明A.启蒙思想逐渐流行B.宫廷文化普及到民间C.专制王权已经衰落D.贵族与平民趋于平等34.表3 1929~1931年美国部分行业工人周工资变化表(单位:%)据表3可知,当时美国A.最低工资标准失效B.产业结构迅速调整C.经济危机不断加深D.政府财政支出锐减35.1959年,苏共二十一大讨论通过了七年经济计划,规定7年内工业生产总值提高80%,其中发电量、钢铁产量都要求成倍增长。
【全国百强校】河北省衡水市武邑中学2018届高三下学期第六次模拟考试数学(理)试题(原卷版)

河北武邑中学2018届高三下学期第六次模拟考试数学试题(理)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填涂在答题卡上.1. 已知,,则( )A. B. C. D.2. 若复数(,且),且,则的实部为( )A. B. C. D.3. 已知函数,则的图象大致为( )A. B. C. D. ......4. 已知双曲线的一条渐近线与直线垂直,则双曲线的离心率等于( )A. B. C. D.5. 《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”,其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”.现若向此三角形内随机投一粒豆子(视为点),则豆子落在其内切圆外的概率是( )A. B. C. D.6. 已知函数的部分图象如图所示,则函数图象的一个对称中心可能为( )A. B. C. D.7. 下图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的值分别为8,10,0,则输出和的值分别为( )A. 2,4B. 2,5C. 0,4D. 0,58. 已知,,则的值为( )A. B. C. D.9. 若关于的混合组有解,则的取值范围为( )A. B. C. D.10. 已知直线与函数的图象相切,则切点的横坐标为( )A. B. C. 2 D.11. 已知为抛物线的焦点,为抛物线上三点,当时,称为“和谐三角形”,则“和谐三角形”有( )A. 0个B. 1个C. 3个D. 无数个12. 祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理: “幂势既同,则积不容异”.意思是:夹在两个乎行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现将曲线绕轴旋转一周得到的几何体叫做椭球体,记为,几何体的三视图如图所示.根据祖暅原理通过考察可以得到的体积,则的体积为( )A. B. C. D.二.填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卡上相应位.13. 设平面向量与向量互相垂直,且,若,则_____________.14. 展开式中,的系数为_____________.15. 现有个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球赢.如果甲先抓,那么下列推断正确的是_____________.(填写序号)①若,则甲有必赢的策略;②若,则乙有必赢的策略;③若,则甲有必赢的策略;④若,则乙有必赢的策略.16. 中,角的对边分别为,,面积为,当最大时,_____________.三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17. 已知数列的前项和.(1)求;(2)求.18. 2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区,消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:请根据上表提供的数据,用最小二乘法求出变量关于变量的线性回归方程(保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求的分布列及数学期望.参考公式及数据:,,,.19. 如图,已知平面平面,为线段的中点,,四边形为边长为1的正方形,平面平面,,,为棱的中点.(1)若为线上的点,且直线平面,试确定点的位置;(2)求平面与平面所成的锐二面角的余弦值.20. 已知抛物线和圆的公共弦过抛物线的焦点,且弦长为4.(1)求抛物线和圆的方程;(2)过点的直线与抛物线相交于两点抛物线在点处的切线与轴的交点为,求面积的最小值.21. 已知函数.(1)若函数在区间上为增函数,求的取值范围;(2)当且时,不等式在上恒成立,求的最大值.22. 在平面直角坐标系中,将曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,的极坐标方程为.(1)求曲线的参数方程;(2)过原点且关于轴对称的两条直线与分别交曲线于和,且点在第一象限,当四边形周长最大时,求直线的普通方程.23. 已知函数.(1)解不等式;(2)若,不等式对恒成立,求的取值范围.。
【全国百强校】河北省衡水市武邑中学2018届高三下学期第六次模拟考试数学(理)试题(原卷版)
河北武邑中学2018届高三下学期第六次模拟考试数学试题(理)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填涂在答题卡上.1. 已知,,则( )A. B. C. D.2. 若复数(,且),且,则的实部为( )A. B. C. D.3. 已知函数,则的图象大致为( )A. B. C. D. ......4. 已知双曲线的一条渐近线与直线垂直,则双曲线的离心率等于( )A. B. C. D.5. 《九章算术》中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”,其大意:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”.现若向此三角形内随机投一粒豆子(视为点),则豆子落在其内切圆外的概率是( )A. B. C. D.6. 已知函数的部分图象如图所示,则函数图象的一个对称中心可能为( )A. B. C. D.7. 下图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的值分别为8,10,0,则输出和的值分别为( )A. 2,4B. 2,5C. 0,4D. 0,58. 已知,,则的值为( )A. B. C. D.9. 若关于的混合组有解,则的取值范围为( )A. B. C. D.10. 已知直线与函数的图象相切,则切点的横坐标为( )A. B. C. 2 D.11. 已知为抛物线的焦点,为抛物线上三点,当时,称为“和谐三角形”,则“和谐三角形”有( )A. 0个B. 1个C. 3个D. 无数个12. 祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理: “幂势既同,则积不容异”.意思是:夹在两个乎行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现将曲线绕轴旋转一周得到的几何体叫做椭球体,记为,几何体的三视图如图所示.根据祖暅原理通过考察可以得到的体积,则的体积为( )A. B. C. D.二.填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卡上相应位.13. 设平面向量与向量互相垂直,且,若,则_____________.14. 展开式中,的系数为_____________.15. 现有个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球赢.如果甲先抓,那么下列推断正确的是_____________.(填写序号)①若,则甲有必赢的策略;②若,则乙有必赢的策略;③若,则甲有必赢的策略;④若,则乙有必赢的策略.16. 中,角的对边分别为,,面积为,当最大时,_____________.三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17. 已知数列的前项和.(1)求;(2)求.18. 2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区,消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:请根据上表提供的数据,用最小二乘法求出变量关于变量的线性回归方程(保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求的分布列及数学期望.参考公式及数据:,,,.19. 如图,已知平面平面,为线段的中点,,四边形为边长为1的正方形,平面平面,,,为棱的中点.(1)若为线上的点,且直线平面,试确定点的位置;(2)求平面与平面所成的锐二面角的余弦值.20. 已知抛物线和圆的公共弦过抛物线的焦点,且弦长为4.(1)求抛物线和圆的方程;(2)过点的直线与抛物线相交于两点抛物线在点处的切线与轴的交点为,求面积的最小值.21. 已知函数.(1)若函数在区间上为增函数,求的取值范围;(2)当且时,不等式在上恒成立,求的最大值.22. 在平面直角坐标系中,将曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,的极坐标方程为.(1)求曲线的参数方程;(2)过原点且关于轴对称的两条直线与分别交曲线于和,且点在第一象限,当四边形周长最大时,求直线的普通方程.23. 已知函数.(1)解不等式;(2)若,不等式对恒成立,求的取值范围.。
河北省武邑中学2018届高三下学期期中考试政治试题Word版含答案
河北省武邑中学2018届高三下学期期中考试政治试题
一、选择题(在下列符合题意的四个选项中,有一项是符合题目要求的。
共35题,每小题4分,满分140分)
12. 2016 年人民币对美元汇率走势图(下图)如下。
根据走势图,不考虑其他因素,汇率
变动对中国经济的积极影响是
◎ Z " " ■■■? 1—- "*•-* ■ F ・ . 停・" 1 1 ■—-叩匸―二:” _ - : ”
M 3M 4»6A 7fl 個9A 1QH 11H 12R
①中国公民赴美留学费用增加
②提升中国外汇储备国际购买力
③中国企业海外投资成本增加
④中国商品出口美国更具价格优势
A.①③ B .①④ C .②③ D .②④
13. 2017年1月1日起,全国范围内实施“国五”车用汽油标准。
90、93、97三个标号汽油调整为89、92、95、98四个标号。
新标号汽油有害物质减少,油品质量升级,但同时油价上涨
0.5 —0.6元。
这一汽油标准的实施
①旨在保护环境,引导绿色消费
②能增加油企利润,提高生产效率
③能发挥价格杠杆的作用,增加汽车销量
④促进新能源的开发与利用,增强可持续发展能力
A.①④ B .②③ C .③④ D .①②
14. 2016年5月6日,人社部、财政部下发通知,2016年各级财政对居民医保的补助标准
提高到每人每年420元。
其中,中央财政对120无基数部分按原有比例补助,对增加的300元按照西部地区80%中部地区60%勺比例补助,对东部地区各省份分别按一定比例补助。
这一举措表明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.《春秋》载,公元前651年,因周王力不能及,齐桓公乃召集诸侯盟誓: 不得修筑有码邻国的水利,不在天灾时阻碍谷米流通;《孟子》提到治水的有11次,其中有一段直接指责当时人以洪水冲刷邻国的不道行为。这些史实反映了 A王权衰微分封制被破坏 B.农业稳定发展的重要性 C.建立统一国家的必要性 D.儒家学者高度关注民生 25.汉初史官司马谈在《论六家委旨》中这样概括儒家:“儒者博而寡要,劳而少功,是以其事难尽从;然其序君臣父子之礼,列夫妇长幼之别,不可易也。”据此,下列说法最准确的是 A.理论体系庞杂使儒学难有实际功用 B.儒家学说有利于加强中央集权统治 C.强化伦理道德规范是儒学主要功能 D.政治形势影响司马谈对儒学的认识 26.王阳明在《传习录》中提到:“夫学贵得之心,求之于心而非也,虽其言之出于孔子,不敢以为是也……求之于心而是也,虽其言之出于庸常,不敢以为非也。”该思想意在 A.宣扬“知行合一” B.否定孔子思想 C.反对“格物致知” D.强调主体意识 27.有学者认为:“科举制的废除,斩断了2000多年来经过许多步骤而加强起来的社会整合制度的根基,好像舵手在获得一个新的罗盘以前就抛弃了旧的,遂使社会进入一个盲目漂流的时代。”该观点旨在说明 A.科举制的废除冲击清朝的根基 B.戊成变法加剧社会秩序的混乱 C.政治制度的变革应当循序渐进 D.传统入仕渠道受阻引发了革命 28.据统计,1904-1908年,政府登记在册的近代中国公司有227家,到1912年,运作的中国公司已有20749家。其中绝大部分是小型或中型企业,只有750家公司雇工超过100人。材料主要表明 A.民族企业在前行中仍有不足 B.外国资本制约民族工业发展 C.新政成为民族工业发展主因 D.近代工业先天不足后天畸形 29.学者张鸣在《再说戊成变法》中说:“从某种意义上讲,康党(即维新派) 是中国社会急于事功(改变中国命运)的普遍心理造就出来的一批特别热衷于急功近利的思想家和政治家”。其意在强调维新派能登上历史舞台是因为 A.急于改变中国命运的社会心理 B.民族危机的日益加深 C.社会各阶层普遍接受变革思想 D.民族资本主义的发展 30.1930年11月12日的《民国日报》有这样一则报道:“上海闸北区永安县丝厂职员金吉城,月收入约50余元。然而,1930年9月9日,全沪丝厂100余家停业,永安亦在停办之列,金因此失业……。”对该材料解读最准确的是 A.当时中国存在极其严重的工人失业问题 B.官僚资本的压迫导致民族工业步履维艰 C.列强加紧资本输出使民族工业生存艰难 D.世界经济危机影响中国民族工业的发展 31.1950年,美国国会通过“中国地区援助法案”够正案,允许中国留学生就学期间和毕业以后在美国工作。1953年8月,美国总绕签署“难民解救法案”,允许至少一部分留在美国的中国留学生从学生身份转为永久居民。这些法案的出台表明 A.科技革命促使美国招揽中国人才 B.美国对新中国进行科技封锁 C.祖国强大提升了留美学生的地位 D.美国向新中国释放外交善意 32.查士丁尼《法学法典》规定:“各省总督应注意各自治市之强制性公务,应依惯例合理分派,并依年龄和地位轮换。务使重担不经常压在同一批人身上而造成自治市人力和资源之枯竭。”这反映了 A.帝国内的管理实行轮换制 B.帝国对自治市的管理制度化法律化 C.帝国放松对自治市的控制 D.帝国内的地方“自治”权力有名无实 33.20世纪60年代,美国著名学者杜兰特夫妇在其著作《历史的教训》中认为:“现在俄国的社会主义,正在恢复个人主义的激励机制,以使得这个体制拥有更大的生产动力。……对资本主义的恐惧,迫使社会主义不断扩大自由。”与材料中“正在恢复个人主义的激励机制”相关的是俄国 A.加强了工业部门的管理体制 B.可以租借、租让工业企业 C.扩大了国营农场的自主权 D.用市场调节方式管理经济 34.备受世人推崇的美国《1787年宪法》虽然解决了邦联的弊病,但在宪法正文中根本没有出现“slave”这个词,更没有涉及解决黑人奴隶制存废问题的内容。以下对此理解最准确的是 A.美国宪法违背了民主的精神 B.当时黑人对民权的要求不强烈 C.美国宪法并未实践人民主权 D.美国宪法体现了原则与妥协的宪政精神 35.下图是创作于1957年的时政漫画《祝君晚安》。漫画上,三位“病人”躺在病床上,他们盖的被子上有“北大西洋集团”的字样,床头的小牌上写着“美国导弹基地”的字样,他们的头上高悬着写有“US”字样的美国巨型导弹。下列对漫画信息解读正确的是 A.美国成立北大西洋集团对苏联进行核威慑 B.北约集团内部对美国的冷战政策有所不满 C.以美苏为首的两大阵营在欧洲冷战对峙加剧 D.美国大力发展核力量以扶植和控制西欧盟友 40.阅读材料,完成下列要求。(25分) 材料一 为了维护家庭的稳定与和谐,古代思想家们提出了父慈子孝、夫义妻顺、兄友弟悌等家庭伦理道德规范。中国传统家庭伦理以父慈子孝作为调节父子关系的基本行为规范,从根本上服从于“父为子纲”。它片面强调“子孝”,否定子女的独立人格,维护了传统家庭中的不平等的尊卑制度。夫权逐渐强化,男尊女卑、夫主妻从等伦理也随之被强化。人一出生受被包围在层层的家庭关系中,个人是血缘链条上的一个环节,上以继宗庙,下以续万世.传统的政治以伦理为本位,伦理以血缘为原型,最终的原理是家庭血缘的情理上升为国家政治的法则。 ——摘编自王苏《试析传统家庭伦理的内容及其特征》 材料二 近代以来历次思想解放运动都提出了“婚烟革命”的口号。20世纪初,有人用西洋音乐简谱写了一首《自由结婚纪念歌》:“世事新,男女平等,文明国,自由结婚乐”。随着西学的传入,人们的婚姻观念发生了一些变化。清末民初的婚姻变化体现了这一点,浙江遂安“近日妇女解放声起,离婚別嫁也日益见多”。太平天国运动、戊戌变法运动、辛亥革命、新文化运动都不同程度批判了传统男尊女卑观念,把妇女问题作为改造社会的基本问题。1920年陈独秀在《新青年》发表《男系制与遗产制》一文,文章建议男女平等地拥有财产继承权。女子也能继承遗产,一战后,欧洲各国离婚增加,中国一些留学生受其影响,亦热衷于离婚。 ——摘编自李桂海《略论近代中国家庭的嬗变及其启示》 (1)根据材料一并结合所学知识。概括中国古代家庭伦理的主要特征。并说明其成因。(12分) (2) 根据材料一、二并结合所学知识,指出近代家庭伦理的新变化,并予以评析。(13分) 41.阅读材料,完成下列要求。(12分) 材料 英国批评家斯图尔特·霍尔曾经在四个层面上对“现代性”的内涵进行了界定: 政治层面——世俗政体与现代民族国家的建立; 经济层面——市场经济以及私有制基础上的资本积累; 社会层面——劳动与性别分工体系的形成; 文化层面——宗教的衰落以及世俗物质文化的兴起,尤其是个人主义与工具理性的文化取向。 ——摘编自(英)布洛克《西方人文主义传统》 结合材料与所学世界史的相关知识,围绕“现代性”自行拟定一个具体的论题,并就所拟论题进行简要阐述。(要求明确写出所拟论题,阐述须有史实依据,逻辑严密。) 44.【历史-选修1: 历史上重大改革眸】(15分) 材料 北宋末年,在与西夏接壤的陕西四路和河东路西部地区,编组少数民族的部族兵,称为“番兵”。北宋初期。酆延路金明县(夸陕西安塞北)李士彬家族世代任北宋的番兵首领,抗御西夏,康定元年(1040年)为西夏所袭杀。次年,王尧臣提出重组番兵后,番兵成为宋军的主要兵种之一。陕西四路的番兵,分为番兵与强人,番兵使用官马;而强人使用自备马,称为壮马。治平二年(1065年)时,番兵集中在酆延路,计1.4万多人; 四路强人计91万多人,两者合计10万多人。各路番兵都以部族为基础编排。按部族大小,大首领为都军主。作为各级备兵长官。立功后另授刺史、诸卫将军。及诸司使、副使和承制至殿侍(大小使臣}衔。 ——摘编自《宋代军事制度》 (1)根据材料,说明宋朝西北番兵的特点。(7分) (2)根据材料并结合所学知识,分析农朝丙北兵制改革的原因利影响。(8分) 45.【历史 选修2: 20 世纪的战争与和平】(15分) 材料 俄国爆发社会主义革命后,一直遭到主要西方国家的排斥,没有真正进入国际社会,这不仅有损于苏联的国家利益,而且会严重阻碍世界局势的正常发展。30年代国际形势的变化,給苏联提供了重返国际社会的机遇。苏联首先向一直未与之建交的美国传送建交的意愿。罗斯福就任总统不久,即向苏联政府提议正式举行建交谈判。不久,两国正式建立了外交关系。苏联还趁此机会,同西班牙、匈牙利等一系列国家建立外交关系。 30年代随着国际形势的变化,苏联对国际联盟的态度也发生转变,从支持德国打破凡尔赛体系转为支持国际联盟维护世界和平。1933年11月,法国外长巴尔都向苏联大使提出苏联参加国际联盟的建议,希望争取苏联进入国际联盟,以国联的力量来抑制德国。在得到苏联同意后,他又做了大量工作。1934年9月苏联正式加入国际联盟。 ——摘编自王斯德《世界通史(第三编)》 (1)根据材斜,概括苏联重返国际社会的表现。(6分) (2)根据材料和所学知识,评价20世纪30年代苏联重返国际社会。(3分) 46.【历史——选修3: 中外历史人物评说】(15分) 材料 民国初期,梅兰芳投身于京剧改良运动,结识了一批接受新思想的文化人,创排了多部新戏。他的戏不再局限于才子佳人、忠孝节义。他扮演的角色也突破了受苦的小姑娘、受难的小媳妇的框框,而将具有历史文化内容的人物如嫦娥、西施、虞姬、杨玉环作为戏的主人公。他在展示人物的外象时,更注意划画人物的内心;作展示戏的本身时,更注意将戏和历史结合起来。据说,当时来华访问的外国人到北京必看梅剧。 1930年初,梅兰芳率团赴美演出,获得巨大成功。美国观众对梅兰芳的表演惊叹不已,梅兰芳并非单纯地模仿女人的一姿态态,而是艺术地传达出中国女性的端庄、温柔、秀丽和高雅,透过梅兰芳饰演的各种中国妇女形象,大大改变了美国人对中国如女的认识。“梅兰芳热”在美国迅速兴起。 ——摘编白李伶伶《梅兰芳评传》 (1)根据材料并结合所学知识,概拓梅剧的特点。(7分) (2)根据材料并结合所学知识,简析梅兰芳赴美演出的历史作用。(8分)
