圆的弧长和扇形面积公式及变形
弧长与扇形面积计算公式

弧长与扇形面积计算公式
一、弧长
①半径为R的圆,周长是2兀R
②圆的周长可以看作是360度的角所对的孤
③1度的圆心角所对的弧长是
360/2兀1=180/兀R
l=孤长
一度的圆心角所对的弧长是180/兀R
那么由上所得弧长公式就是
l=180/n兀R
二、扇形的面积
由组成圆心角的两个半径和圆心角所对的弧所围成的图形叫作扇形
①半径为R的圆,面积是兀R方
②圆面可以看作是360度圆心角所对的扇形
③1度圆心角所对的扇形面积是
S扇形=360/n兀R方
=360/兀R方
由上所得扇形面积公式
S扇形=360/n兀R方
已有扇形
那么用这个扇形弧长的2/1
再乘以半径就是这个扇形的面积。
弧长扇形面积与弦长的计算

弧长扇形面积与弦长的计算弧长(arc length)与扇形面积(sector area)是圆形几何中的重要概念。
弧长指的是圆的一部分弧的长度,而扇形面积是由这一弧和与之相交的两条半径所围成的图形的面积。
在数学中,我们可以通过一些公式和方法来计算弧长、扇形面积以及它们与弦长(chord length)之间的关系。
一、弧长的计算在计算弧长时,我们需要知道圆的半径和所对应的圆心角(central angle)。
根据圆的性质,我们可以得出以下公式来计算弧长。
1. 当圆心角使用弧度制时:弧长 = 半径 ×圆心角弧长的单位与半径的单位相同,例如,如果半径使用米(m)作为单位,则弧长也使用米(m)作为单位。
2. 当圆心角使用度数制时:弧长 = (半径 ×圆心角× π) / 180这里的π是一个常数,近似取3.14159。
例如,假设圆的半径为5m,对应的圆心角为60度,则根据上述公式计算得到弧长为(5 × 60 × 3.14159) / 180 ≈ 5.24m。
二、扇形面积的计算扇形面积是由圆心、弧和两条半径所围成的区域。
计算扇形面积时,我们需要知道圆的半径和所对应的圆心角。
扇形面积的计算公式如下:扇形面积 = (半径的平方 ×圆心角) / 2其中,半径的平方表示半径的平方值。
与弧长计算中的圆心角一样,如果圆心角使用度数制,则计算扇形面积时需要将圆心角转换为弧度制。
例如,假设圆的半径为4cm,对应的圆心角为45度,则根据上述公式计算得到扇形面积为(4^2 × 45 × 3.14159) / (2 × 180) ≈ 5.65cm²。
三、弦长与弧长、扇形面积的关系弦是圆内连接两个任意点的线段,它与圆的弧和扇形面积有一定的关系。
1. 弧长与弦长的关系当弧长和弦长的夹角(内切角)相同时,弦长越长,对应的弧长也越长。
2. 扇形面积与弦的关系当扇形面积和弦的夹角(内切角)相同时,弦越长,对应的扇形面积也越大。
弧长和扇形面积公式

弧长和扇形面积公式在几何学中,弧长和扇形面积是与圆形和圆的扇形相关的重要概念和计算方法。
这些公式可以用于解决许多几何问题,例如计算圆的周长、计算弧长和扇形的面积等。
本文将详细介绍关于弧长和扇形面积的公式及其推导过程。
首先,我们先来介绍一下什么是圆和圆的扇形。
圆是一个平面上所有点到一个固定点的距离都相等的图形。
而圆的扇形则是由半径为r的圆上的一段弧和两条半径所围成的图形。
1.弧长公式:弧长是圆上一段弧的长度,由于圆在数学上具有无限个点,所以我们可以定义一个角度来度量弧长。
我们知道圆的一周是360度,因此弧长的度量可以用度数或弧度来表示。
当我们用度数来度量弧长时,弧长和弧度的关系可以由以下公式得到:弧长=弧度×半径该公式是通过比较整个圆的周长与360度的比例得到的。
当我们用弧度来度量弧长时,弧度的定义是:圆的半径等于半径所对应的弧长的度数。
因此,当我们用弧度来度量弧长时,直接使用半径和弧度的乘积即可表示弧长。
2.扇形面积公式:扇形是由圆心、圆上一段弧和两条半径所围成的图形。
扇形的面积就是扇形所覆盖的圆的面积。
扇形面积可以由以下公式得到:扇形面积=(弧度÷2π)×πr²该公式是通过将圆的面积与圆的周长的比例乘以扇形所对应的弧长所得到的。
推导过程如下:假设圆的半径为r,圆心角为θ度,则该圆心角所对应的弧长为:弧长=(θ÷360)×2πr由于扇形是由半径为r的圆上一段弧和两条半径所围成的,所以扇形的面积可以表示为:扇形面积=(θ÷360)×πr²化简得到:扇形面积=(θ÷2π)×πr²将弧度用θ表示,得到最终的扇形面积公式:扇形面积=(弧度÷2π)×πr²需要注意的是,使用上述公式计算扇形面积时,角度必须使用弧度表示。
如果给出的是度数,则需将角度转换为弧度后再进行计算。
弧长面积公式变形

弧长面积公式变形首先,我们来回顾弧长面积公式的表达式。
设一个圆的半径为r,弧度为θ的弧长为s,该弧所对应的扇形的面积为A。
那么,弧长面积公式可以表示为:s=rθ(1)A=1/2*r^2*θ(2)现在,我们将展示一系列公式变形,以便更好地理解和应用弧长面积公式。
1.弧度与角度之间的转换弧度是衡量角度的一种单位。
我们可以通过以下公式将角度转换为弧度:θ(弧度)=θ(角度)*π/180同样地,我们可以将弧度转换为角度:θ(角度)=θ(弧度)*180/π这样,我们可以在计算过程中根据需要选择使用弧度或角度。
2.求弧长已知圆的半径r和角度θ,我们可以通过弧长面积公式中的第一式进行计算。
s=rθ3.求扇形面积已知圆的半径r和角度θ,我们可以通过弧长面积公式中的第二式进行计算:A=1/2*r^2*θ4.求半径已知弧长s和角度θ,我们可以通过公式(1)解出r:r=s/θ5.求角度已知弧长s和半径r,我们可以通过公式(1)解出θ:θ=s/r6.求弦长弦是圆上连接两个点的线段,它的长度可以通过半径和角度来计算。
设弧长为s和半径为r,弦长为c,我们可以利用正弦定理推导出以下公式:c = 2r*sin(θ/2)7.求扇形的弦长已知扇形的半径r和角度θ,我们可以通过弦长公式求解:c = 2r*sin(θ/2)8.求扇形的高扇形的高是指从圆心到弧上一点的线段长度。
已知半径r和角度θ时,可以通过余弦函数求解:h = r - r*cos(θ/2)9.求扇形的面积已知半径r和扇形的高h时,可以通过以下公式求解:A=r*h10.求扇形的周长扇形的周长可以通过弧长和半径来计算。
已知半径r和角度θ时,可以通过以下公式求解:P = s + 2r*sin(θ/2)通过以上的公式变形,我们可以根据已知的数据求解需要的参数,或者根据已知的参数计算出其他参数。
这些变形公式在几何学和物理学中有着广泛的应用,如求解圆锥体的体积、计算悬链线形状等。
因此,了解和灵活运用弧长面积公式的变形公式是很重要的。
第28课 圆的弧长和图形面积的计算

探究提高
扇形面积公式和弧长公式容易混淆.
n 1 2 S 扇形= πR = lR. 360 2
知能迁移2 (1)如图,半圆的直径AB=10,P为AB上一点,
点C、D为半圆的三等分点,则阴影部分的面积等于 __________.(结果用π表示)
解析 连接 CD、OC、OD、BC.
∵ AC = CD = DB =60° , ∴∠ABC=∠BCD=30° . ∴CD∥AB. ∴S△PCD=S△OCD. 60 25 ∴S 阴影=S△PCD+S 弓形=S△OCD+S 弓形=S 扇形 COD= π×52= π. 360 6 25 答案 π 6
②设 BC 的中点为 O,由(1)可知 O 即为圆心,连接 OA、OD, 过 O 作 OE⊥AD 于 E.在 Rt△AOE 中,∠AOE=30° . ∴OE=OA· 30° cos = 1 3 S△AOD= ×3× 2 2 3 2 9 4 3 , 3,源自答案B解析
如图,可知外圆的半径为 9,
内圆的半径为 7,S 圆环=S 外圆-S 内圆 =π×92-π×72=81π-49π=32π.
3.(2011· 宁波)如图,Rt△ABC 中,∠ACB=90° ,AC=BC=2 2, 若把 Rt△ABC 绕边 AB 所在直线旋转一周,则所得几何体的表 面积为( A.4π ) B.4 2π C.8π D.8 2π
解析
答案 6π
90 π(3+4+5)=6π. 180
(2) (2011· 广州)如图,AB 切⊙O 于点 B,OA=2 弦 BC∥OA,则劣弧 BC 的弧长为( A. 3 π 3 B. 3 π 2 C.π ) D. 3 π 2
3,AB=3,
解析
连接 OB、OC,则 OB⊥AB,
弧长和扇形面积公式

A
D
B
C
这节课你有什么收获?
一、弧长的计算公式
n R l 180
二、扇形面积计算公式
n 1 2 s R 或 s lR 360 2
布置作业
P114 第1、5题
解:
n r 50 l = 3 cm 180
50 cm 答:此圆弧的长度为 3
n R l 180
1、弧长与哪些因素有关?
2、在3个量l、R、n中,只要已知其中两
个量就可以求第三个量,那么请将公式变
形求出R和n。
180 l R n
180 l n R
巩固深化(一)
1.已知弧所对的圆心角为900,半径是4,则弧 长为 2π 。 2. 已知一条弧的半径为9,弧长为8π,那么这 条弧所对的圆心角为 1600 。 3、已知一条弧的弧长为4π ,那么这条弧所对 的圆周角为450 ,这条弧所在的半径 8 。 4. 钟表的轴心到分针针端的长为5cm,那么经过 40分钟,分针针端转过的弧长是( B )
4 3、已知半径为2cm的扇形,其弧长为 3 4 3 则这个扇形的面积,S扇形=——.
,
再
探
例1 如图,圆心角为60°的扇形的半径为 10厘米,求这个扇形的面积和周 长.(π ≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为 nr 2 60 3.14 10 2 S ≈52.33(平方厘米); 360 360 扇形的周长为 nr 60 3.14 10 l 2r 20 180 180 ≈ 30.47(厘米)。
S 扇形
nR 360
2
若设⊙O半径为R, n°的 圆心角所对的扇形面积为S, A 则 2
S 扇形
知识点全面梳理--04圆和扇形--师
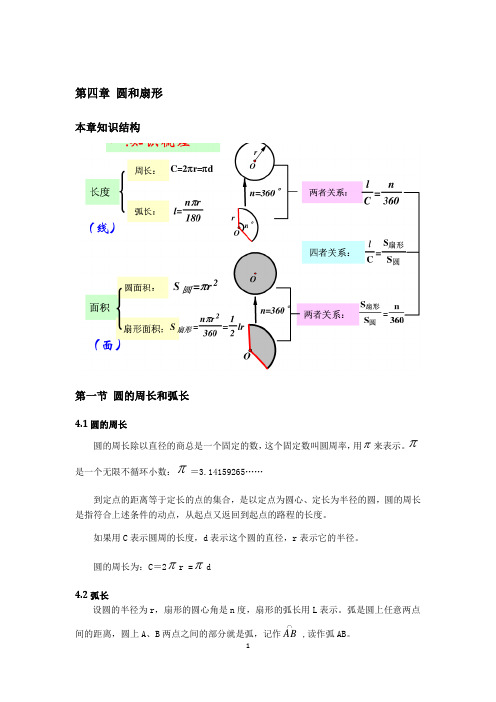
第四章圆和扇形本章知识结构第一节圆的周长和弧长4.1圆的周长圆的周长除以直径的商总是一个固定的数,这个固定数叫圆周率,用π来表示。
π是一个无限不循环小数:π=3.14159265……到定点的距离等于定长的点的集合,是以定点为圆心、定长为半径的圆,圆的周长是指符合上述条件的动点,从起点又返回到起点的路程的长度。
如果用C表示圆周的长度,d表示这个圆的直径,r表示它的半径。
圆的周长为:C=2πr =πd4.2弧长设圆的半径为r,扇形的圆心角是n度,扇形的弧长用L表示。
弧是圆上任意两点间的距离,圆上A、B两点之间的部分就是弧,记作⋂AB ,读作弧AB。
1802360110r r ππ=⨯=圆心角所对的弧长; 18023600rn r n L n ππ=⨯=圆心角所对的弧长。
第二节 圆和扇形的面积4.3圆的面积2r S π=圆的面积4.4扇形的面积由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
设组成扇形的半径为r ,圆心角为0n ,弧长为l ,扇形的面积:S =360n ×πr 2=21Lr本章最重点内容本章是圆与扇形,掌握圆的周长的计算公式和弧长的概念,会计算圆的面积及扇形的面积,是我们学习的重点。
1.圆的周长公式:r d C ⋅=⋅=ππ2. 2.弧长公式:180360rdl ⋅=⋅=ππ.3.圆的面积公式:2r S ⋅=π 4.扇形面积公式:lr r n S 213602=⋅=π扇. 5.特别地:360n C l =,360n S S =扇,即:SSC l 扇=. 本章错题集【结合个人平时作业具体情况总结、整理、添加】1.如图,一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动。
当小圆盘的中心围绕大圆盘中心转动90度后,小圆盘运动过程中扫过的面积是多少平方厘米?(3π=)【答案】:小圆盘运动过程中扫过的面积由两部分组成,即两半圆加四分之一环形。
2221(64)418S πππ=⨯+⨯-⨯÷=平方厘米。
弧形、扇形公式解说和运用

弧形、扇形公式解说和运⽤弧形、扇形公式解说和运⽤知识点1、弧长公式因为360°的圆⼼⾓所对的弧长就是圆周长C=2R,所以1°的圆⼼⾓所对的弧长是,于是可得半径为R的圆中,n°的圆⼼⾓所对的弧长l的计算公式:,说明:(1)在弧长公式中,n表⽰1°的圆⼼⾓的倍数,n 和180都不带单位“度”,例如,圆的半径R=10,计算20°的圆⼼⾓所对的弧长l时,不要错写成。
(2)在弧长公式中,已知l,n,R中的任意两个量,都可以求出第三个量。
知识点2、扇形的⾯积如图所⽰,阴影部分的⾯积就是半径为R,圆⼼⾓为n°的扇形⾯积,显然扇形的⾯积是它所在圆的⾯积的⼀部分,因为圆⼼⾓是360°的扇形⾯积等于圆⾯积,所以圆⼼⾓为1°的扇形⾯积是,由此得圆⼼⾓为n°的扇形⾯积的计算公式是。
⼜因为扇形的弧长,扇形⾯积,所以⼜得到扇形⾯积的另⼀个计算公式:。
知识点3、⼸形的⾯积(1)⼸形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做⼸形。
(2)⼸形的周长=弦长+弧长(3)⼸形的⾯积如图所⽰,每个圆中的阴影部分的⾯积都是⼀个⼸形的⾯积,从图中可以看出,只要把扇形OAmB的⾯积和△AOB的⾯积计算出来,就可以得到⼸形AmB的⾯积。
当⼸形所含的弧是劣弧时,如图1所⽰,当⼸形所含的弧是优弧时,如图2所⽰,当⼸形所含的弧是半圆时,如图3所⽰,例:如图所⽰,⊙O的半径为2,∠ABC=45°,则图中阴影部分的⾯积是()(结果⽤表⽰)分析:由图可知由圆周⾓定理可知∠ABC=∠AOC,所以∠AOC=2∠ABC=90°,所以△OAC是直⾓三⾓形,所以,所以圆周长弧长圆⾯积扇形⾯积公式(2)扇形与⼸形的联系与区别(2)扇形与⼸形的联系与区别图⽰⾯积知识点4、圆锥的侧⾯积圆锥的侧⾯展开图是⼀个扇形,如图所⽰,设圆锥的母线长为l,底⾯圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2,圆锥的侧⾯积,圆锥的全⾯积说明:(1)圆锥的侧⾯积与底⾯积之和称为圆锥的全⾯积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的弧长和扇形面积公式及变形
圆的弧长公式:圆的弧长等于半径与弧所对的圆心角的夹角度数的乘积,公式为L=θr(其中L表示弧长,r表示半径,θ表示圆心角的夹角度数)。
圆的扇形面积公式:圆的扇形面积等于半径的平方乘以圆心角的夹角度数除以360度,公式为S=1/2r²θ(其中S表示扇形面积,r 表示半径,θ表示圆心角的夹角度数)。
圆的弧长和扇形面积的变形公式:当圆的弧长和扇形面积不同于标准形式时,可以通过变形公式求解。
如圆的弧长为L,圆心角的夹角度数为θ,则弧长对应的圆的半径为r=L/θ;若扇形的面积为S,圆心角的夹角度数为θ,则扇形对应圆的半径为r=√(2S/θ)。
