33光程 杨氏双缝干涉实验 劳埃德镜
杨氏双缝

当 d 、d ' 一定时,条纹间隔 x 随波长 的变化情况
4 )光源不在双缝轴线上 若光源向轴线下方移动,则中央明条纹偏离原来位置,
同级明条纹向上移动。
5 )用薄玻璃片盖住一条缝,使该缝光程增加了 2.5 λ 。 在屏幕上原中央明条纹处,将出现第三级暗条纹。
* 思考问题:
这是一种什么现象? 为什么会产生这样的现象 ? 明纹分布有什么规律 ?
( 三 ) 定性分析
1 s 1 、 s 2 是同一波面上的两点,发出的光是相干光。 2 两相干光在屏幕相遇,产生干涉现象。 3 干涉的结果是光能量重新分布,产生明暗条纹。
(四 ) 定量分析
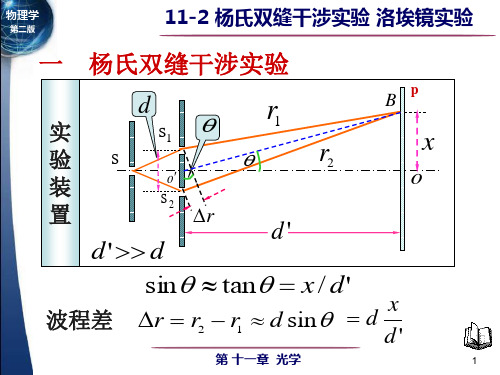
1 光程差 设 s 1 、 s 2 发出的光传播到 P 点,光程分别为 r 1 、
r 2 ,光程差为 ,
= r2 - r1 = x d/d’
s1
d
r1
r2
B
x
o
s2
d'
= r2 - r1 = x d/d’
2 明条纹 1 )明条纹的条件
= ±( 2 k )λ/2
k = 1、2、3 …
2 )明条纹中心坐标
x = ± k d’λ /d
k = 0 、1、2 …
式子表明:点的坐标满足上述条件,出现明纹。
第一级暗条纹中心; 第二级暗条纹中心; 第三级暗条纹中心. . .
4 ) 暗条纹间距
x =xn+1 - xn= d’λ /d
式子表明 : 杨氏双缝实验中 , 暗条纹等间距分布, 与干涉级数无关。
4 介于明暗条纹之间的点
若点的坐标既不满足明条纹条件,也不满足暗条纹条 件,则亮度介于明暗之间。
杨氏双缝干涉与洛埃镜干涉

Δx D 1000 610 4 3(mm)
d
0.2
【例12-2】把一个很薄的云母片(n=1.58)插入到杨氏双 缝实验装置的一个缝上后,观测到屏幕中心移过7级明纹。如果 入射光波长λ=550nm,试求此云母片的厚度e。
【解】在一个缝上插入云母片后,仅一个缝发出光的光程发 生了变化,其改变量等于插云母片前后两相干光的光程差改变量 Δδ,即
r22
D2
x
d 2
2
r22 r12 (r2 r1)(r2 r1) 2dx
通常D
d,故r2+r1≈2
x
根据式(12–4)可知,两束光干涉相长出现明纹时,光程
差为:
d x k(k=0,1,2…)
D
则明纹中心的位置为:
x k D(k=0,1,2…)
d 在O点,δ=0,对应k=0,因此,O点为明纹中心,这个明
物理学
杨氏双缝干涉与洛埃镜干涉
1.1 杨氏双缝干涉
如下图所示,由单色光源发出的光照射在单缝S上,形成线 光源。在单缝S前的遮光屏上开有两个与S平行的狭缝S1和S2。S1 和S2相距很近,且它们与S之间的距离相等。因S1和S2是由同一 光源S形成的,满足频率相同、振动方向相同、相位差恒定的相 干条件,故为相干光源。S1和S2发出的光在空间相遇时,将产生 干涉现象,在屏幕上出现明暗相间的条纹,称为干涉条纹。
11-2杨氏双缝干涉实验_洛埃镜
第 十一章 光学
9
物理学
第二版
1111-2 杨氏双缝干涉实验 洛埃镜实验
已知 d = 0.2 mm d'=1 m 求 (1) ∆x14 = 7.5 nm λ = ? ) (2) λ = 600 nm ∆ x ' = ? ) d′ 解 (1) xk = ± kλ , k = 0 , 1, 2,⋯ ) d d′ ∆x14 = x4 − x1 = (k 4 − k1 )λ d d ∆x14 λ= = 500 nm d ' (k 4 − k1 ) 1 d′ (2) ∆x' = ) λ = 1.5 mm 2d
m处有一电磁波接收 例2 如图 离湖面 h=0.5 m处有一电磁波接收 当一射电星从地平面渐渐升起时, 器位于 C ,当一射电星从地平面渐渐升起时, 接收器断续地检测到一系列极大值 . 已知射 电星所发射的电磁波的波长为20.0 cm,求第一 次测到极大值时, 次测到极大值时,射电星的方位与湖面所成 2 的角度.
d 'λ 条纹间距 ∆ x = d
( ∆k = 1)
第 十一章 光学
4
物理学
第二版
1111-2 杨氏双缝干涉实验 洛埃镜实验 (1) ) 变化, 将怎样变化? d 、 ' 一定时,若 λ 变化, 则 ∆x 将怎样变化? d 一定时,
第 十一章 光学
5
物理学
第二版
1111-2 杨氏双缝干涉实验 洛埃镜实验
第 十一章 光学
8
物理学
第二版
1111-2 杨氏双缝干涉实验 洛埃镜实验
以单色光照射到相距为0.2 例2 以单色光照射到相距为 mm的双缝 的双缝 双缝与屏幕的垂直距离为1 上,双缝与屏幕的垂直距离为 m. (1)从第一级明纹到同侧的第四级明纹间的 ) 距离为7.5 距离为 mm,求单色光的波长; ,求单色光的波长; (2)若入射光的波长为 )若入射光的波长为600 nm,中央明纹中 , 心距离最邻近的暗纹中心的距离是多少? 心距离最邻近的暗纹中心的距离是多少?
12-2杨氏双缝干涉劳埃德镜

12-2杨氏双缝干涉劳埃德镜
11-2杨氏双缝干涉劳埃德镜chapter11光学opticsHOH
AIUNIVERSITY
z
**************.cn托马斯·杨ThomasYoung杨ThomasYoung(1773-1829
)英国物理学家。
1799年完成双缝干涉实验,是光的波动说逐步确立地位过程中第一个重要实验。
明条纹位置明条纹位置
明条纹位置实验现象实验装置J2515型双缝干涉实验仪p实验装置一杨氏双缝干涉实验波程差减弱加强
暗纹明纹p讨论条纹间距明暗条纹的位置白光照射时,出现彩色条纹暗纹明纹1)条纹间距与的关系;
若变化,则将怎样变化?一定时,一定时,若变化,则
将怎样变化?1)白光将形成紫、蓝、青、绿、黄、橙、红有序排列的彩色条纹,成为彩色光谱。
中央明纹仍
为白色条纹,其余各级条纹,特别是较高级次条纹会出现色彩重叠。
当用白光作为光源时2)
条纹间距与的关系如何?一定时,二双缝干涉光强分布合光强干涉项若其中则光强分布图紫光光强分布图波长不同条纹间距不同红光光强分布图P四双面镜。
14-02杨氏双缝干涉 光程 劳埃镜
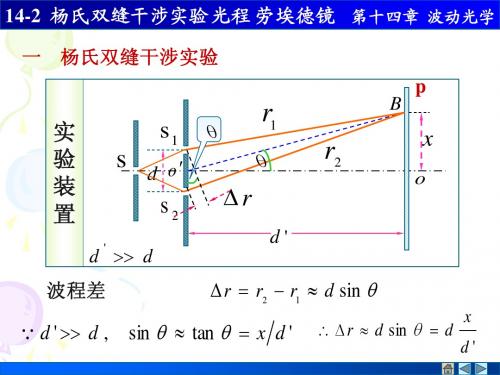
实 验 装 置
'
s
s1
d o
r1
B
p
r2
d'
x
o
s2
d d
r
r r2 r1 d sin
波程差
d ' d , sin tan x d '
x r d sin d d'
r1
nr2 r1
相位差
2π
nr2 r1
)
14-2 杨氏双缝干涉实验 光程 劳埃德镜 第十四章 波动光学
相位差 2π 光程差 nr2 r1 干涉加强 2kπ , k 0,1 2π (2k 1)π , k 0,1 干涉减弱
1 光程
D
n0
2π 2π
D (nD )
n
光程=几何路程
折射率
(真空中,n=1,即为D)
光在媒质中的几何路程D相当于在真空中的几何路程nD (相位变化 相同) 计算光程的意义:计算与媒质中几何路程相当的真
空中的路程,即把牵涉到不同介质的复杂情况,都变成
真空中的情形,这并不改变相干光在相遇点的相位差。
求(1)条纹如何移动(2)云母片厚度 t = ? 解(1) (r t ) n0 1
(n 1)t (r1 r2 ) O 点 (n 1)t
O’点 0 , 则 r 1
tn r2n0 r1 t nt r2 S1
S2
r1 r2
o'
高三物理课件-双缝干涉[整理] 精品
![高三物理课件-双缝干涉[整理] 精品](https://img.taocdn.com/s3/m/37bfca33453610661ed9f4be.png)
n3 n2 n1
r 2dn2
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
增透膜和增反膜
利用薄膜干涉可以提高光学器件的透光率 . 例1 为了增加透射率 , 求 氟化镁膜的最小厚度. 已知 空气 n1 1.00 ,氟化镁 n2 1.38 , 550nm
23 解
Δr 2dn2 (2k 1)
1
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
2d 2 32 n2 1 sin r 2n2 d cos r cos r 2 2 2 2 2 反射光的光程差 r 2d n2 n1 sin i
2
P
加强 k (k 1,2,)
n2 n1
k 1
2n
13
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
2)厚度线性增长条纹等间距,厚度非线性增长 条纹不等间距 3)条纹的动态变化分析(
n, ,
变化时)
14
§3杨氏双缝干涉实验 薄膜干涉 17-2 双镜 劳埃德镜
一、等倾干涉
n2 n1
CDAD
M1 M2
1
2
L 3
P
n1
n2
i
A
D
sin i n2 sin n1
B 4
C
e
n1
5
E
32 n2 ( AB BC) n1 AD
AB BC e cos
2
AD AC sin i 2e tg sin i
7
n
L
5.89 10 m n 1.53 5 3 2 8 10 2.4 10 m
第十一章-1相干光-2杨氏双缝干涉-劳埃德镜-教案
§11-1 相干光件及获得方法2. 能分析杨氏双缝干涉条件、条纹分布规律和位置;理解劳埃德镜光干涉规律三、教学过程:引言:什么是光的干涉现象?与机械波类似,光的干涉现象表现为在两束光的相遇区域形成稳定的、有强有弱的光强分布。
即在某些地方光振动始终加强(明条纹),在某些地方光振动始终减弱(暗条纹),从而出现明暗相间的干涉条纹图样。
光的干涉现象是波动过程的特征之一。
光的干涉:两束光的相遇区域形成稳定的、有强有弱的光强分布。
实际是满足一定条件的两列相干光波相遇叠加,在叠加区域某些点的光振动始终加强,某些点的光振动始终减弱,即在干涉区域内振动强度有稳定的空间分布。
干涉条纹:所形成的均匀分布的图样。
§11-1相干光一、相干光:两束满足相干条件的光称为相干光1、相干条件(Coherent Condition):这两束光在相遇区域:①振动方向相同;②振动频率相同;③相相位同或相位差保持恒定那么在两束光相遇的区域内就会产生干涉现象。
2、相干光的获得(1)普通光源的发光机理当原子中大量的原子(分子)受外来激励而处于激发状态。
处于激发状态的原子是不稳定的,它要自发地向低能级状态跃迁,并同时向外辐射电磁波。
当这种电磁波的波长在可见光范围内时,即为可见光。
原子的每一次跃迁时间很短(10-8 s )。
由于一次发光的持续时间极短,所以每个原子每一次发光只能发出频率一定、振动方向一定而长度有限的一个波列。
由于原子发光的无规则性,同一个原子先后发出的波列之间,以及不同原子发出的波列之间都没有固定的相位关系,且振动方向与频率也不尽相同,这就决定了两个独立的普通光源发出的光不是相干光,因而不能产生干涉现象。
(2)获得相干光源的两种方法a.原理:将同一光源上同一点或极小区域(可视为点光源)发出的一束光分成两束,让它们经过不同的传播路径后,再使它们相遇,这时,这一对由同一光束分出来的光的频率和振动方向相同,在相遇点的相位差也是恒定的,因而是相干光。
14-2 杨氏双缝干涉 劳埃德镜 光程 (2)
n水 -1)r (
s1 *
r
r
空气
P
s 2*
[(r2 e)n ne] nr1
(r2 r1 e)n ne
水
s1 *
s2 *
n
r1
n'
e
r2
P
第十四章 波动光学
14 – 2 杨氏双缝干涉实验 劳埃德镜 光程
物理学教程 (第二版)
例2 如图,将一折射率为 n 1.58 的云母片盖 住双缝的上缝以后,中央明纹移到第7级明纹,求云 母片的厚度。(已知入射波长为550nm)。 解:设厚度为x 未放云母片时,O处的光程差为0 放入云母片后,O处的光程差为: 放入云母片前后, 光程差的变化量
d
红
d' x1 d
紫
(k 1)
中央亮纹
紫
x=0
d' x '1 d
(k 0) (k 1)
红
第十四章 波动光学
14 – 2 杨氏双缝干涉实验 劳埃德镜 光程
物理学教程 (第二版)
(5) 条纹变化 若光源S向上移动,条纹将如何变化?
S’ S
提示:对于中央亮纹,两束光波程相等。 结论:条纹向下移动。
物理学教程 (第二版)
杨氏双缝干涉实验
s
s1
d o
r1
B
p
r2
d'
x
o
s2
d ' d
干涉条件:
d r x d'
第十四章 波动光学
r
k
(2k 1)
加强
2
k 0,1, 2,
杨氏双缝干涉实验
x k D 明纹中心
2a
k0,1,2,
x0 0 中央明纹
x1
D
2a
一级明纹
D
x2 a
二级明纹┄┄
2a
x D
(2k
1)
2
干涉减弱
x(2k1)D
4a
暗纹中心 k0 ,1 ,2 ,
x1
D
4a
一级暗纹
x2
3D
4aa
二级暗纹 ┄┄
2a x k 干涉加强
a
12
例4、
a
13
例5、
a
14
二、分波阵面干涉的其他实验
1.菲涅耳双面镜
M1
s1
d
s2
sL
o
M2
D
a
P
15
2.劳埃德镜
P'
P
s1
d
s2
ML
D
当P移动到P/时屏与反射镜M接触,由于半波损失,接触处为暗纹。
d x k 加强
D2
明纹x公 ( k式 -1) D
2d
a
16
总结杨氏双缝干涉
k = -2 k = -1 k =0
k =1
k =2
a
9
暗纹公式
d
x D
(2k 1)
2
x(2k1)D
2d
第五级暗纹 k 4
x 9D
2d
注意:当缝间距为d时
暗纹公式 x(2k1)D k =1,2,3…
2d
明纹公式 x k D
d
k =0,1,2,3…
条纹间距
a
x
D
d
10
a
11
17-02杨氏双缝干涉 双镜 劳埃镜
n1 < n2
n2
反射波 折射波
n1
n1 > n2
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
第十七章 波动光学
以单色光照射到相距为0.2mm的双缝上 双缝与 的双缝上,双缝与 例1 以单色光照射到相距为 的双缝上 屏幕的垂直距离为1m. 屏幕的垂直距离为 (1) 从第一级明 纹 到同侧 的第四级明 纹的距离为 7.5mm,求单色光的波长 求单色光的波长; 求单色光的波长 (2) 若入射光的波长为 若入射光的波长为600nm,求相邻两明纹间的距离 求相邻两明纹间的距离. 求相邻两明纹间的距离
4I 0 , δ = ±k λ
干涉项
则
2 δ I = 4I0 cos (π ) = λ
0, δ = ±(2k + 1) λ 2
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
则
δ I = 4I0 cos (π ) = λ
2
第十七章 波动光学 4I 0 , δ = ±k λ
0, δ = ±(2k + 1) λ 2
明纹中心 暗纹中心
k = 0 ,1, 2 , L
17-2 杨氏双缝干涉实验 双镜 劳埃德镜 明暗条纹的位置 明暗条纹的位置
第十七章 波动光学
x=
d' λ ± ( 2 k + 1) d 2
d' ±k λ d
明纹 暗纹
k = 0 ,1 , 2 , L
(1)屏幕中央(x=0)为明条纹,两侧分布明暗相间的条纹; )屏幕中央( )为明条纹,两侧分布明暗相间的条纹; (2)条纹宽度 ∆ x = ) ∝λ, (3) ∆x∝λ,可见对于白光,零级明纹仍为白色,但是 ) ∝λ 可见对于白光,零级明纹仍为白色,但是x≠0时明 时明 条纹有色散,内侧紫,外侧红; 条纹有色散,内侧紫,外侧红; 实验结果 (1)屏幕中央为明纹,两侧分布明暗相间的条纹; )屏幕中央为明纹,两侧分布明暗相间的条纹; ∝λ。 (2)单色光条纹间距 ∆x∝λ。 ) ∝λ (3)对于白光,明条纹有色散,内侧紫,外侧红; )对于白光,明条纹有色散,内侧紫,外侧红;
