上海市卢湾区2007学年第一学期高三数学期末考试试卷

合集下载

上海卢湾区高三第一学期期末试卷

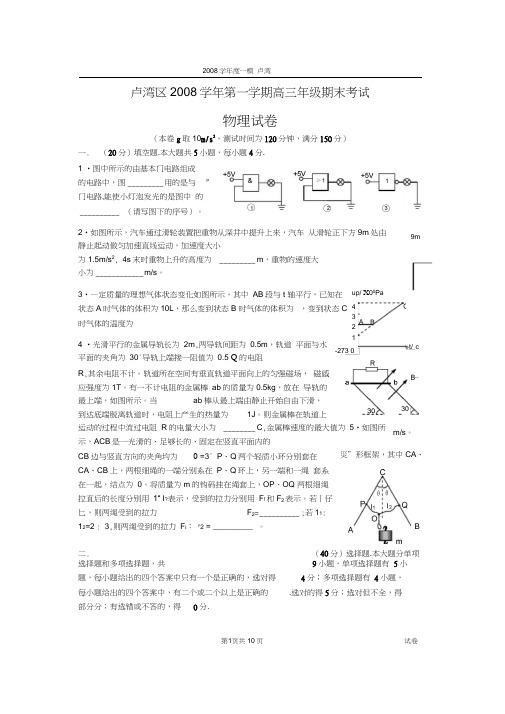
第1页共10页试卷卢湾区2008学年第一学期高三年级期末考试物理试卷（本卷g 取10m/s 2，测试时间为120分钟，满分150分）一. （20分）填空题.本大题共5小题，每小题4分. 1 •图中所示的由基本门电路组成的电路中，图 _________ 用的是与门电路,能使小灯泡发光的是图中的 __________ （请写图下的序号）。

2•如图所示，汽车通过滑轮装置把重物从深井中提升上来，汽车从滑轮正下方9m 处由静止起动做匀加速直线运动，加速度大小为1.5m/s 2, 4s 末时重物上升的高度为 _________ m ，重物的速度大小为 ____________ m /s 。

3•—定质量的理想气体状态变化如图所示，其中 AB 段与t 轴平行，已知在状态A 时气体的体积为10L ，那么变到状态B 时气体的体积为，变到状态C 时气体的温度为4 •光滑平行的金属导轨长为 2m ,两导轨间距为 0.5m ，轨道平面与水平面的夹角为 30°导轨上端接一阻值为 0.5 Q 的电阻R ,其余电阻不计。

轨道所在空间有垂直轨道平面向上的匀强磁场，磁感应强度为1T 。

有一不计电阻的金属棒 ab 的质量为0.5kg ，放在导轨的最上端，如图所示。

当ab 棒从最上端由静止开始自由下滑，到达底端脱离轨道时，电阻上产生的热量为1J 。

则金属棒在轨道上运动的过程中流过电阻 R 的电量大小为 ________ C ,金属棒速度的最大值为 5•如图所示，ACB 是一光滑的、足够长的、固定在竖直平面内的 CB 边与竖直方向的夹角均为0 =3° P 、Q 两个轻质小环分别套在CA 、CB 上，两根细绳的一端分别系在 P 、Q 环上，另一端和一绳套系在一起，结点为 0。

将质量为m 的钩码挂在绳套上，OP 、OQ 两根细绳拉直后的长度分别用 1“ I ?表示，受到的拉力分别用 F ! 和F 2表示。

上海市卢湾区2008学年高三年级第一次质量调研数学试卷2009.1

上海市卢湾区2008学年高三年级第一次质量调研数学试卷2009.1一．填空题（本大题满分55分）本大题共有11题，只要求直接填写结果，请将结果直接填在答题纸规定的横线上，每题填对得5分，否则一律得零分． 1．函数123(1)x y x -+=->的反函数为____________．2．函数2,[2,0)(0,2]y x x x=+∈-U 的单调递减区间为_____________ ． 3．若圆锥的侧面积为20π，且母线与底面所成的角为4arccos5，则该圆锥的体积为___________． 4．在长方体1111ABCD A B C D -中，若12,1,3AB BC AA ===，则1BC 与平面11BB D D 所成的角θ可用反三角函数值表示为θ=____________．5．若取地球的半径为6371米，球面上两点A 位于东经O12127'，北纬O 318'，B 位于东经O 12127'，北纬O 255'，则A B 、两点的球面距离为_____________千米(结果精确到1千米)．6．在二项式9的展开式中，第四项为_____________．7．若集合2{|(3)50,},A x x k x k x R A R +=+-++=∈≠ΦI ，则实数k 的取值范围为___________．8.若()y f x =为定义在D 上的函数，则“存在0x D ∈，使得2200[()][()]f x f x -≠”是“函数()y f x =为非奇非偶函数”的__________________条件.9．已知函数()y f x =既为偶函数，又是以6为周期的周期函数，若当[0,3]x ∈时，2()24,f x x x =-++则当[3,6]x ∈时，()f x =____________．10．若集合*{|100,3,}A a a a k k N =≤=∈，集合*{|100,2,}B b b b k k N =≤=∈，在A B U 中随机地选取一个元素，则所选取的元素恰好在A B I 中的概率为____________． 11.记123n a a a a L 为一个n 位正整数，其中12,,,n a a a L 都是正整数，119,09(2,3,,)i a a i n ≤≤≤≤=L .若对任意的正整数(1)j j n ≤≤，至少存在另一个正整数(1)k k n ≤≤，使得j k a a =，则称这个数为“n 位重复数”.根据上述定义，“五位重复数”的个数为.____________.二．选择题（本大题满分20分）本大题共有4题，每题都给出四个结论，其中有且只有一个结论是正确的．必须在答题纸上按正确填涂的方法用2B 铅笔将正确结论的字母代号框涂黑，每题涂对得 5分，否则一律得零分．12．函数2sin 2y x =是一个（）A.周期为π的奇函数B.周期为π的偶函数C.周期为2π的奇函数 D.周期为2π的偶函数13．若α为第二象限角，则cot cos sin = ( )A ．22sin αB ．22cos α-C ．0D ．214．24222222k nn n n n C C C C +++++L L 的值为（）A.2nB.212n -C.21n -D.2121n --15.已知函数()y f x =的定义域为D ，若对于任意的1212,()x x D x x ∈≠，都有1212()()()22x x f x f x f ++<，则称()y f x =为D 上的凹函数.由此可得下列函数中的凹函数为 ( )A.2log y x =B.y =2y x = D.3y x =三．解答题（满分75分）本大题共有5题，解答下列各题必须写出必要的步骤． 16．（本题满分10分）解不等式：221122log (325)log (45)x x x x --≤+-.17．（本题满分15分）第1小题满分4分，第2小题满分11分设函数2()|2|(,f x x x a x R a =+-∈为实数).(1)若()f x 为偶函数，求实数a 的值； (2)设2a >，求函数()f x 的最小值.18．（本题满分16分）第1小题满分6分，第2小题满分10分.已知四边形OABC 为直角梯形，O 90AOC OAB PO ∠=∠=⊥，平面AC ，且3,6,2, 3.OA AB OC PO ====(理)若13PD PB =u u u r u u u r，求：(1)点D 的坐标；(2)异面直线PC AD 与所成的角θ(用反三角函数值表示).(文)(1)求证：AB PA ⊥；(2)求异面直线PB 与OA 所成的角θ(用反三角函数值表示).19．（本题满分16分）第1小题满分10分，第2小题满分6分.(理)袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不返回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量ξ为此时已摸球的次数，求：.(1)随机变量ξ的概率分布律；(2)随机变量ξ的数学期望与方差.(文)袋中有同样的球9个，其中6个红色，3个黄色，现从中随机地摸6球，求：(1)红色球与黄色球恰好相等的概率(用分数表示结果) (2)红色球多于黄色球的不同摸法的和数.ABCOP20．（本题满分18分）第1小题满分8分，第2小题满分10分.在△ABC 中，已知OO45,75,A B ∠=∠=点D 在AB 上，且10CD =. (1)若点D 与点A 重合，试求线段AB 的长；(2)在下列各题中，任选一题，并写出计算过程，求出结果.①(解答本题，最多可得6分)若CD AB ⊥，求线段AB 的长；②(解答本题，最多可得8分)若CD 平分ACB ∠，求线段AB 的长；③(解答本题，最多可得10分)若点D 为线段AB 的中点，求线段AB 的长.参考答案一、1.21log (3)(32)y x x =-+-<<2.[U3.16π4.arcsin55.6736.-7.(,1]-∞- 8.充分且非必要条件 9.21020x x -+- 10.166711.62784 二、12.D 13.B 14.D 15.C三、16.解：原不等式的解集为5{|3}4x x -≤<-17.解：(1)由已知()(),|2||2|,0f x f x x a x a a -=-=+=即解得；(2)2212,2()12,2x x a x a f x x x a x a ⎧+-≥⎪⎪=⎨⎪-+<⎪⎩，当12x a ≥时，22()2(1)(1)f x x x a x a =+-=+-+，由12,,2a x a >≥得1x >，从而1x >-，故()f x 在12x a ≥时单调递增，()f x 的最小值为2()24a a f =；当12x a <时，22()2(1)(1)f x x x a x a =-+=-+-，故当12ax <<时，()f x 单调递增，当1x <时，()f x 单调递减，则()f x 的最小值为(1)1f a =-；由22(2)(1)044a a a ---=>，知()f x 的最小值为1a -.18. (理)解：(1)(1,2,2)D ；(2)θ=. (文)解：(1)略；(2)θ=。

[高考数学] 2007年上海高考数学真题(理科)试卷(原卷版)

绝密★启用前 2007年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分． 1．函数y =lg ( 4−x )x−3的定义域是．2．若直线1210l x my ++=：　与直线231l y x =-：平行，则m = ．3．函数f(x)=xx−1的反函数f −1(x)= ．4．方程 96370x x-•-=的解是．5．已知x y ∈+R ，，且x +4y =1，则x y •的最大值是．6．函数y =sin ( x +π3 )sin ( x +π2 )的最小正周期T = ．7．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）．8．以双曲线x 24−y 25=1的中心为焦点，且以该双曲线的左焦点为顶点的抛物线方程是．9．对于非零实数a b ，，以下四个命题都成立：① a +1a ≠0； ② (a +b)2=a 2+2ab +b 2； ③ 若|a| = |b|，则a =±b ； ④ 若a 2=ab ，则a =b ．那么，对于非零复数a b ，，仍然成立的命题的所有序号是．10．在平面上，两条直线的位置关系有相交、平行、重合三种．已知αβ，是两个相交平面，空间两条直线12l l ，在α上的射影是直线x y ∈+R ，，12l l ，在β上的射影是直线12t t ，．用s 1与s 2，t 1与t 2的位置关系，写出一个总能确定l 1与l 2是异面直线的充分条件：．11．已知P 为圆x 2+( y −1 )2=1上任意一点（原点O 除外），直线OP 的倾斜角为θ弧度，记d = |OP |．在右侧的坐标系中，画出以()d θ，为坐标的点的轨迹的大致图形为二．选择题（本大题满分16分）本大题共有4 题，每题都给出代号为A ，B ，C ，D的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分． 12．已知a b ∈R ，，且2+a i,b +i （i 是虚数单位）是实系数一元二次方程 x 2+px +q =0的两个根，那么p q ，的值分别是（）Ａ．45p q =-=，Ｂ．43p q =-=，Ｃ．45p q ==，Ｄ．43p q ==，13．设a b ，是非零实数，若a <b ，则下列不等式成立的是（）Ａ．a 2<b 2 Ｂ．ab 2<a 2b Ｃ．1ab2<1a 2bＤ．b a<ab14．直角坐标系xOy 中，i j ，分别是与x y ，轴正方向同向的单位向量．在直角三角形ABC 中，若AB ⃗⃗⃗⃗⃗⃗ =2 i +j ,AC ⃗⃗⃗⃗⃗⃗ =3 i +k j ，则k 的可能值个数是（）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．415．设f(x)是定义在正整数集上的函数，且f(x)满足：“当2()f k k ≥成立时，总可推出(1)f k ≥(k +1)2成立”．那么，下列命题总成立的是（）Ａ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｂ．若(5)25f ≥成立，则当5k ≤时，均有2()f k k ≥成立Ｃ．若f( 7 )<49成立，则当8k ≥时，均有f( k )<k 2成立Ｄ．若f( 4 )=25成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤． 16．（本题满分12分）如图，在体积为1的直三棱柱ABC −A 1B 1C 1中，∠ACB =90∘, AC =BC =1．求直线A 1B 与平面BB 1C 1C 所成角的大小（结果用反三角函数值表示）．CB1B 1A A1C17．（本题满分14分）在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若a =2,C =π4，cos B2=2√55，求ABC △的面积S ．18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2% （如，2003年的年生产量的增长率为36%）．（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数f(x)=x 2+ax ( x ≠0，常数)a R ．（1）讨论函数f(x)的奇偶性，并说明理由；（2）若函数f(x)在[2)x ∈+∞，上为增函数，求a 的取值范围．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123n a a a a ，，，，（n 为正整数）满足条件a 1=a n ，a 2=a n−1，…，a n =a 1，即a i =a n−i+1（12i n =，，，），我们称其为“对称数列”．例如，由组合数组成的数列01mm m mC C C ，，，就是“对称数列”．（1）设{ b n }是项数为7的“对称数列”，其中1234b b b b ，，，是等差数列，且b 1=2， b 4=11．依次写出{ b n }的每一项；（2）设{ c n }是项数为2k −1(正整数k >1)的“对称数列”，其中121k k k c c c +-，，，是首项为50，公差为−4的等差数列．记{ c n }各项的和为S 2k−1．当k 为何值时，S 2k−1取得最大值？并求出S 2k−1的最大值；（3）对于确定的正整数m >1，写出所有项数不超过2m 的“对称数列”，使得211222m -，，，，依次是该数列中连续的项；当m 1500时，求其中一个“对称数列”前2008项的和S 2008．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．我们把由半椭圆x 2a 2+y 2b 2=1 (0)x ≥与半椭圆y 2b2+x 2c2=1 (0)x ≤合成的曲线称作“果圆”，其中a 2=b 2+c 2，a >0，b >c >0．如图，点F 0，F 1，F 2是相应椭圆的焦点，A 1，A 2和B 1，B 2分别是“果圆” 与x ，y 轴的交点．（1）若012F F F △是边长为1的等边三角形，求“果圆”的方程；（2）当|A 1A 2||B 1B 2|时，求b a 的取值范围；（3）连接“果圆”上任意两点的线段称为“果圆”的弦．试研究：是否存在实数k ，使斜率为k 的“果圆” 平行弦的中点轨迹总是落在某个椭圆上？若存在，求出所有可能的k 值；若不存在，说明理由．y 1B O 1A2B2A..1F0F 2F x .祝福语祝你考试成功!。

2007年高考.上海卷.文科数学试题及解答

已知函数 f (x) x 2 a ( x 0 ，常数 a R) ． x
（1）当 a 2 时，解不等式 f (x) f (x 1) 2x 1；
（2）讨论函数 f (x) 的奇偶性，并说明理由．
20．（本题满分 18 分）本题共有 3 个小题，第 1 小题满分 3 分，第 2 小题满分 6 分，第 3 小题满分 9
兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在 42%，到 2010 年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的 95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到 0.1%）？
19．（本题满分 14 分）本题共有 2 个小题，第 1 小题满分 7 分，第 2 小题满分 7 分．
生产量的增长率为 34%．以后四年中，年生产量的增长率逐年递增 2%（如，2003 年的年生产量的增长率为 36%）．
（1）求 2006 年全球太阳电池的年生产量（结果精确到 0.1 兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006 年的实际安装量为 1420
第 2页（共 6页）
求正四棱锥 P ABCD 的体积V ．
P
D
C
17．（本题满分 14 分）
A
在 △ABC 中， a，b，c 分别是三个内角 A，B，C 的对边．若 a 2,
求 △ABC 的面积 S ．
B
C π ， cos B 2 5 ，
4
25
18．（本题满分 14 分）本题共有 2 个小题，第 1 小题满分 6 分，第 2 小题满分 8 分．近年来，太阳能技术运用的步伐日益加快．2002 年全球太阳电池的年生产量达到 670 兆瓦，年
分．

2007年高考试题及答案-文科数学-上海卷

1CCB1B1AA2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)考生注意：1．答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚．2．本试卷共有21道试题，满分150分．考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分． 1．方程9131=-x 的解是．2．函数11)(-=x x f 的反函数=-)(1x f．3．直线014=-+y x 的倾斜角=θ ． 4．函数πsec cos 2y x x ⎛⎫=∙+⎪⎝⎭的最小正周期=T ．5．以双曲线15422=-yx的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是．6．若向量a b ，的夹角为60，1==b a ，则()a a b-= ． 7．如图，在直三棱柱111C B A A B C -中，90=∠ACB ， 21=AA ，1==BC AC ，则异面直线B A 1与AC 所成角的大小是（结果用反三角函数值表示）．8．某工程由A B C D ，，，四道工序组成，完成它们需用时间依次为254x ，，，天．四道工序的先后顺序及相互关系是：A B ，可以同时开工；A 完成后，C 可以开工；B C ，完成后，D 可以开工．若该工程总时数为9天，则完成工序C 需要的天数x 最大是． 9．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）． 10．对于非零实数a b ，，以下四个命题都成立：ABlC① 01≠+aa ； ②2222)(b ab a b a ++=+； ③ 若||||b a =，则b a ±=； ④ 若ab a =2，则b a =．那么，对于非零复数a b ，，仍然成立的命题的所有序号是． 11．如图，A B ，是直线l 上的两点，且2=AB ．两个半径相等的动圆分别与l 相切于A B，点，C 是这两个圆的公共点，则圆弧AC ，CB 与线段AB 围成图形面积S 的取值范围是．二．选择题（本大题满分16分）本大题共有4 题，每题都给出代号为A ，B ，C ，D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分．12．已知a b ∈R ，，且i 3,i 2++b a （i 是虚数单位）是一个实系数一元二次方程的两个根，那么a b ，的值分别是（）Ａ．32a b =-=，Ｂ．32a b ==-，Ｃ．32a b =-=-，Ｄ．32a b ==，13．圆01222=--+x y x 关于直线032=+-y x 对称的圆的方程是（）Ａ．21)2()3(22=-++y x Ｂ．21)2()3(22=++-y xＣ．2)2()3(22=-++y xＤ．2)2()3(22=++-y x14．数列{}n a 中，22211100010012n n na n n n n ⎧⎪⎪=⎨⎪⎪-⎩，≤≤，，≥，则数列{}n a 的极限值（）Ａ．等于0 Ｂ．等于1 Ｃ．等于0或1 Ｄ．不存在15．设)(x f 是定义在正整数集上的函数，且)(x f 满足：“当2()f k k ≥成立时，总可推出(1)f k +≥2)1(+k 成立”．那么，下列命题总成立的是（）Ａ．若1)1(<f 成立，则100)10(<f 成立Ｂ．若4)2(<f 成立，则(1)1f ≥成立Ｃ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｄ．若(4)25f ≥成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．16．（本题满分12分）在正四棱锥ABCD P -中，2=PA ，直线PA 与平面ABCD 所成的角为 60，求正四棱锥ABCD P -的体积V ．17．（本题满分14分）在ABC △中，a bc ，，分别是三个内角A B C ，，的对边．若4π,2==C a ，5522cos=B ，求ABC △的面积S ．18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2%（如，2003年的年生产量的增长率为36%）．PBCAD（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数0()(2≠+=x xa x x f ，常数)a ∈R ．（1）当2=a 时，解不等式12)1()(->--x x f x f ；（2）讨论函数)(x f 的奇偶性，并说明理由．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123ma a a a ，，，，（m 为正整数）满足条件m a a =1，12-=m a a ，…，1a a m =，即1+-=i m i a a （12i m = ，，，），我们称其为“对称数列”．yO 1A2B2A1B. . .M 1F 0F 2Fx. 例如，数列12521，，，，与数列842248，，，，，都是“对称数列”．（1）设{}n b 是7项的“对称数列”，其中1234b b b b ，，，是等差数列，且21=b ，114=b ．依次写出{}n b 的每一项；（2）设{}n c 是49项的“对称数列”，其中252649c c c ，，，是首项为1，公比为2的等比数列，求{}n c 各项的和S ；（3）设{}n d 是100项的“对称数列”，其中5152100d d d ，，，是首项为2，公差为3的等差数列．求{}n d 前n 项的和n S (12100)n = ，，，．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分9分．我们把由半椭圆12222=+by ax (0)x ≥与半椭圆12222=+cx by (0)x ≤合成的曲线称作“果圆”，其中222c b a +=，0>a ，0>>c b ．如图，设点0F ，1F ，2F 是相应椭圆的焦点，1A ，2A 和1B ，2B 是“果圆” 与x ，y轴的交点，M 是线段21A A 的中点．（1）若012F F F △是边长为1的等边三角形，求该 “果圆”的方程；（2）设P 是“果圆”的半椭圆12222=+cx by(0)x ≤上任意一点．求证：当PM 取得最小值时，P 在点12B B ，或1A 处；（3）若P 是“果圆”上任意一点，求PM 取得最小值时点P 的横坐标．PBCADO2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)答案要点一、填空题（第1题至第11题） 1． 1-=x 2． )0(11≠+x x3． 4arctan π- 4． π 5． x y 122= 6．21 7． 66arccos8． 39． 3.010． ② ④11． π022⎛⎤- ⎥⎝⎦，二、选择题（第12题至第15题）题号 1213 1415答案ACB D三、解答题（第16题至第21题）16．解：作⊥PO 平面ABCD ，垂足为O ．连接AO ，O 是正方形ABCD 的中心，PAO ∠是直线PA 与平面 A B C D 所成的角．PAO ∠＝ 60，2=PA ．∴ 3=PO ．1=AO ，2=AB ，112332333ABC D V PO S ∴==⨯⨯=．17．解：由题意，得3cos 5B B =，为锐角，54sin =B ，10274π3sin )πsin(sin =⎪⎭⎫⎝⎛-=--=B C B A ，由正弦定理得 710=c ，∴ 111048sin 222757S ac B ==⨯⨯⨯= ．18．解：（1）由已知得2003，2004，2005，2006年太阳电池的年生产量的增长率依次为%36，%38，%40，%42．则2006年全球太阳电池的年生产量为8.249942.140.138.136.1670≈⨯⨯⨯⨯(兆瓦)．（2）设太阳电池的年安装量的平均增长率为x ，则441420(1)95%2499.8(142%)x ++≥．解得0.615x ≥．因此，这四年中太阳电池的年安装量的平均增长率至少应达到%5.61． 19．解：（1）1212)1(222->----+x x x x x ，0122>--x x ，0)1(<-x x ． ∴ 原不等式的解为10<<x ．（2）当0=a 时，2)(x x f =，对任意(0)(0)x ∈-∞+∞ ，，，)()()(22x f x x x f ==-=-，)(x f ∴为偶函数．当0≠a 时，2()(00)a f x x a x x=+≠≠，，取1±=x ，得 (1)(1)20(1)(1)20f f f f a -+=≠--=-≠，， (1)(1)(1)f f ff ∴-≠--≠，，∴ 函数)(x f 既不是奇函数，也不是偶函数．20．解：（1）设数列{}n b 的公差为d ，则1132314=+=+=d d b b ，解得 3=d ， ∴数列{}n b 为25811852，，，，，，．（2）4921c c c S +++= 25492625)(2c c c c -+++= ()122212242-++++= ()3211222625-=--==67108861．（3）51100223(501)149d d ==+⨯-=，．由题意得 1250d d d ，，，是首项为149，公差为3-的等差数列．当50n ≤时，n n d d d S +++= 21 n n n n n 230123)3(2)1(1492+-=--+=．当51100n ≤≤时，n n d d d S +++= 21()n d d d S ++++= 525150 (50)(51)37752(50)32n n n --=+-+⨯75002299232+-=n n ．综上所述，22330115022329975005110022n n n n S n n n ⎧-+⎪⎪=⎨⎪-+⎪⎩，≤≤，，≤≤．21．解：（1） ()()2222012(0)00F c F b c F b c ---，，，，，，()222220212121F F bccb F F bc ∴=-+===-=，，于是22223744c a b c ==+=，，所求“果圆”方程为2241(0)7x y x +=≥，2241(0)3y x x +=≤．（2）设()P x y ，，则2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222()1()04b a c x a c x b c x c ⎛⎫-=---++- ⎪⎝⎭，≤≤，0122<-cb ，∴ 2||PM 的最小值只能在0=x 或c x -=处取到．即当PM 取得最小值时，P 在点12B B ，或1A 处．（3）||||21MA M A = ，且1B 和2B 同时位于“果圆”的半椭圆22221(0)x y x ab+=≥和半椭圆22221(0)y x x bc+=≤上，所以，由（2）知，只需研究P 位于“果圆”的半椭圆22221(0)x y x ab+=≥上的情形即可．2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222222224)(4)(2)(c c a a c a b c c a a x ac ---++⎥⎦⎤⎢⎣⎡--=．当22()2a a c x a c-=≤，即2a c ≤时，2||PM 的最小值在222)(cc a a x -=时取到，此时P 的横坐标是222)(cc a a -．当a cc a a x >-=222)(，即c a 2>时，由于2||PM 在a x <时是递减的，2||PM 的最小值在a x =时取到，此时P 的横坐标是a ．综上所述，若2a c ≤，当||PM 取得最小值时，点P 的横坐标是222)(cc a a -；若c a 2>，当||PM 取得最小值时，点P 的横坐标是a 或c -．。

2007年上海高考数学试卷与答案(理科)

2007年全国普通高等学校招生统一考试（上海卷）一．填空题（本大题满分44分）1．函数3)4lg(--=x x y 的定义域是．2．若直线1210l x my ++=：　与直线231l y x =-：平行，则=m ．3．函数1)(-=x xx f 的反函数=-)(1x f ．4．方程 96370x x -∙-=的解是．5．若x y ∈+R ，，且14=+y x ，则x y ∙的最大值是． 6．函数⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+=2πsin 3πsin x x y 的最小正周期=T ． 7．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）．8．以双曲线15422=-y x 的中心为焦点，且以该双曲线的左焦点为顶点的抛物线方程是． 9．对于非零实数a b ，，以下四个命题都成立： ① 01≠+aa ； ② 2222)(b ab a b a ++=+； ③ 若||||b a =，则b a ±=； ④ 若ab a =2，则b a =．那么，对于非零复数a b ，，仍然成立的命题的所有序号是． 10．在平面上，两条直线的位置关系有相交、平行、重合三种．已知αβ，是两个相交平面，空间两条直线12l l ，在α上的射影是直线12s s ，，12l l ，在β上的射影是直线12t t ，．用1s 与2s ，1t 与2t 的位置关系，写出一个总能确定1l 与2l 是异面直线的充分条件： .11．已知P 为圆1)1(22=-+y x 上任意一点（原点O 除外），直线OP 的倾斜角为θ弧度，记||OP d =．在右侧的坐标致图形为系中，画出以()d θ，为坐标的点的轨迹的大二．选择题（本大题满分16分） 12．已知a b ∈R ，，且i ,i 2++b a （i 是虚数单位）是实系数一元二次方程02=++q px x 的两个根，那么p q ，的值分别是（）Ａ．45p q =-=，Ｂ．43p q =-=，Ｃ．45p q ==，Ｄ．43p q ==，13．设a b ，是非零实数，若b a <，则下列不等式成立的是（）Ａ．22b a < Ｂ．b a ab 22< Ｃ．ba ab 2211< Ｄ．b aa b <14．直角坐标系xOy 中，i j ，分别是与x y ，轴正方向同向的单位向量．在直角三角形ABC 中，若j k i j i+=+=3,2，则k 的可能值个数是（）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．415．设)(x f 是定义在正整数集上的函数，且)(x f 满足：“当2()f k k ≥成立时，总可推出(1)f k +≥2)1(+k 成立”．那么，下列命题总成立的是（）Ａ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｂ．若(5)25f ≥成立，则当5k ≤时，均有2()f k k ≥成立Ｃ．若49)7(<f 成立，则当8k ≥时，均有2)(k k f <成立Ｄ．若25)4(=f 成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分） 16．（本题满分12分）如图，在体积为1的直三棱柱111C B A ABC -中，1,90===∠BC AC ACB．求直线B A 1与平面C C BB 11所成角的大小（结果用反三角函数值表示）．17．（本题满分14分）4π,2==C a ，在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若5522cos=B ，求ABC △的面积S ． 18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2%（如，2003年的年生产量的增长率为36%）．（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数0()(2≠+=x xax x f ，常数)a ∈R ．（1）讨论函数)(x f 的奇偶性，并说明理由；（2）若函数)(x f 在[2)x ∈+∞，上为增函数，求a 的取值范围．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123n a a a a ，，，，（n 为正整数）满足条件n a a =1，12-=n a a ，…，1a a n =，即1+-=i n i a a （12i n =，，，），我们称其为“对称数列”．例如，由组合数组成的数列01mm m m C C C ，，，就是“对称数列”．（1）设{}n b 是项数为7的“对称数列”，其中1234b b b b ，，，是等差数列，且21=b ，114=b ．依次写出{}n b 的每一项；（2）设{}n c 是项数为12-k (正整数1>k )的“对称数列”，其中121k k k c c c +-，，，是首项为50，公差为4-的等差数列．记{}n c 各项的和为12-k S ．当k 为何值时，12-k S 取得最大值？并求出12-k S 的最大值；（3）对于确定的正整数1>m ，写出所有项数不超过m 2的“对称数列”，使得211222m -，，，，依次是该数列中连续的项；当m 1500>时，求其中一个“对称数列”前2008项的和2008S ．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．我们把由半椭圆12222=+b y a x (0)x ≥与半椭圆12222=+cx b y (0)x ≤合成的曲线称作“果圆”，其中222c b a +=，0>a ，0>>c b ．如图，点0F ，1F ，2F 是相应椭圆的焦点，1A ，2A 和1B ，2B 分别是“果圆”与x ，y 轴的交点．（1）若012F F F △是边长为1的等边三角形，求 “果圆”的方程；（2）当21A A >21B B 时，求ab的取值范围；（3）连接“果圆”上任意两点的线段称为“果圆”的弦．试研究：是否存在实数k ，使斜率为k答案要点一、填空题（第1题至第11题）1． {}34≠<x x x 且 2． 32- 3．）（11≠-x x x 4．7log 3 5． 161 6． π 7． 3.0 8． )3(122+=x y9．②④10． 21//s s ，并且1t 与2t 相交（//1t 2t ，并且1s 与2s 相交）11．二、选择题（第12题至第15题）三、解答题（第16题至第21题）16．解法一：由题意，可得体积11111122ABC V CC S CC AC BC CC ====△， ∴ 211==CC AA ．连接1BC ．1111111AC B C AC CC ⊥⊥，，⊥∴11C A 平面C C BB 11，11BC A ∠∴是直线B A 1与平面C C BB 11所成的角． 52211=+=BC CC BC ，51tan 11111==∠∴BC C A BC A ，则 11BC A ∠＝55arctan ．即直线B A 1与平面C C BB 11所成角的大小为55arctan．解法二：由题意，可得体积11111122ABC V CC S CC AC BC CC ∆====， 21=∴CC ，如图，建立空间直角坐标系．得点(010)B ，，， 1(002)C ，，，1(102)A ，，．则1(112)A B =--，，，平面C C BB 11的法向量为(100)n =，，．设直线B A 1与平面C C BB 11所成的角为θ，A 1与的夹角为ϕ，则116cos 6A B n A Bn ϕ==-， 66arcsin ,66|cos |sin ===∴θϕθ，即直线B A 1与平面C C BB 11所成角的大小为66arcsin． 17．解：由题意，得3cos 5B B =，为锐角，54sin =B ，10274π3sin )πsin(sin =⎪⎭⎫ ⎝⎛-=--=B C B A ，由正弦定理得 710=c ， ∴ 111048sin 222757S ac B ==⨯⨯⨯=．18．解：（1）由已知得2003，2004，2005，2006年太阳电池的年生产量的增长率依次为 %36，%38，%40，%42．则2006年全球太阳电池的年生产量为8.249942.140.138.136.1670≈⨯⨯⨯⨯(兆瓦)．（2）设太阳电池的年安装量的平均增长率为x ，则441420(1)95%2499.8(142%)x ++≥．解得0.615x ≥．因此，这四年中太阳电池的年安装量的平均增长率至少应达到%5.61． 19．解：（1）当0=a 时，2)(x x f =，对任意(0)(0)x ∈-∞+∞，，，)()()(22x f x x x f ==-=-， )(x f ∴为偶函数．当0≠a 时，2()(00)af x x a x x=+≠≠，，取1±=x ，得 (1)(1)20(1)(1)20f f f f a -+=≠--=-≠，， (1)(1)(1)(1)f f f f ∴-≠--≠，，∴ 函数)(x f 既不是奇函数，也不是偶函数．（2）解法一：设122x x <≤， 22212121)()(x a x x a x x f x f --+=-[]a x x x x x x x x -+-=)()(21212121，要使函数)(x f 在[2)x ∈+∞，上为增函数，必须0)()(21<-x f x f 恒成立．121204x x x x -<>，，即)(2121x x x x a +<恒成立．又421>+x x ，16)(2121>+∴x x x x ． a ∴的取值范围是(16]-∞，．解法二：当0=a 时，2)(x x f =，显然在[2)+∞，为增函数．当0<a 时，反比例函数xa在[2)+∞，为增函数，xax x f +=∴2)(在[2)+∞，为增函数．当0>a 时，同解法一．20．解：（1）设{}n b 的公差为d ，则1132314=+=+=d d b b ，解得 3=d ， ∴数列{}n b 为25811852，，，，，，．（2）12112112-+--+++++++=k k k k k c c c c c c S k k k k c c c c -+++=-+)(2121 ，50134)13(42212-⨯+--=-k S k ，∴当13=k 时，12-k S 取得最大值．12-k S 的最大值为626．（3）所有可能的“对称数列”是： ① 22122122222221m m m ---，，，，，，，，，，； ② 2211221222222221m m m m ----，，，，，，，，，，，； ③ 122221222212222m m m m ----，，，，，，，，，，； ④ 1222212222112222m m m m ----，，，，，，，，，，，．对于①，当2008m ≥时，1222212008200722008-=++++= S ．当15002007m <≤时，200922122008222221----+++++++=m m m m S 2009212212---+-=m m m 1222200921--+=--m m m ．对于②，当2008m ≥时，1220082008-=S ．当15002007m <≤时，2008S 122200821--=-+m m ．对于③，当2008m ≥时，2008200822--=m m S ．当15002007m <≤时，2008S 3222009-+=-mm ．对于④，当2008m ≥时，2008200822--=m m S ．当15002007m <≤时，2008S 2222008-+=-mm ．21．解：（1） ()()012(0)00F c F F ，，，，，021211F F b F F ∴==，，于是22223744c a b c ==+=，，所求“果圆”方程为2241(0)7x y x +=≥，2241(0)3y x x +=≤．（2）由题意，得 b c a 2>+，即a b b a ->-222． 2222)2(a c b b =+> ，222)2(a b b a ->-∴，得54<a b ．又21,222222>∴-=>a b b a c b ． 45b a ⎫∴∈⎪⎪⎝⎭，．（3）设“果圆”C 的方程为22221(0)x y x a b +=≥，22221(0)y x x b c+=≤．记平行弦的斜率为k ．当0=k 时，直线()y t b t b =-≤≤与半椭圆22221(0)x y x a b +=≥的交点是P t ⎛⎫ ⎪ ⎪⎝⎭，与半椭圆22221(0)y x x b c +=≤的交点是Q t ⎛⎫- ⎪ ⎪⎝⎭． ∴ P Q ，的中点M ()x y ，满足 221,2a ct x b y t ⎧-⎪=-⎨⎪=⎩，得122222=+⎪⎭⎫ ⎝⎛-b y c a x ． b a 2<，∴ 22220222a c a c b a c b b ----+⎛⎫-=≠ ⎪⎝⎭．综上所述，当0=k 时，“果圆”平行弦的中点轨迹总是落在某个椭圆上．当0>k 时，以k 为斜率过1B 的直线l 与半椭圆22221(0)x y x a b +=≥的交点是22232222222ka b k a b b k a b k a b ⎛⎫- ⎪++⎝⎭，．由此，在直线l 右侧，以k 为斜率的平行弦的中点轨迹在直线x kab y 22-=上，即不在某一椭圆上．当0<k 时，可类似讨论得到平行弦中点轨迹不都在某一椭圆上．。

上海市卢湾区2020学年第一学期高三数学期末考试试卷

上海市卢湾区2020学年第一学期高三年级期末考试数学试卷2020.01（完卷时间：120分钟满分：150分）一、填空题（每小题4分，共44分） 1．函数2()1f x x =-（0x <）的反函数为1()f x -=___________．2．函数1()tan 23f x x π⎛⎫=+⎪⎝⎭的最小正周期为___________．3．抛物线22y x =的焦点坐标为___________．4．过直线3270x y +-=与直线420x y --=的交点，且与直线230x y -+=垂直的直线的方程为___________．5．若将函数()3sin 24cos 2f x x x =-化为()cos()f x A x ωϕ=+（0A >，0ω>， 02ϕπ<≤）的形式，则ϕ可用反正切函数值表示为ϕ=___________． 6．已知全集{200,}I n n n =∈+Z ≤，若集合{3,,}A n n k k n I ==∈∈+Z ，B ={5,n n k =,}k n I ∈∈+Z ，则集合A B U 的补集所含有的元素个数为________． 7．在△ABC 中，若60A ∠=︒，8AB =，7BC =，则AC =___________． 8．若数列{}n a 是一个首项为3-，公差为2的等差数列，且4731n n T a a a +=+++L ，则10T =___________．9．若已知点(4,2)A ，(1,3)B --，(1,5)P ，点Q 为线段AB 上的动点，则直线PQ 的斜率k 的取值范围为___________． 10．若过点(1,0)A ，且与y 轴的夹角为6π的直线与抛物线24y x =交于P 、Q 两点，则PQ =___________．11．现行银行三年期定期储蓄存款年利率为5.40%，某人用10万元连存两期此类储蓄，若假定利率保持不变，则六年到期时此人所得的本利和最多为___________元（精确到１分）．二、选择题（每小题4分，共16分） 12．有下列命题：（1）函数tan y x =为递增函数；（2）函数sin y x =在第一象限内为递增函数；（3）函数cos y x =的递增区间为[2,2]()22k k k ππππ-+∈Z ；其中真命题的个数为……………………………………………………………（）（A ）0；（B ）1；（C ）2；（D ）3． 13．若有数列{}n a 、{}n b ，则lim n n a →∞和lim n n b →∞分别存在是limnn na b →∞存在的………（）（A ）充分非必要条件；（B ）必要非充分条件；（C ）充分且必要条件；（D ）非充分且非必要条件． 14．已知x 、y 为不相等的实数，若记1122x y l --=+，m =22x yn +=，则l ，m ，n三数的大小关系为………………………………………………（）（A ）l n m <<；（B ）n l m <<；（C ）n m l <<；（D ）不能确定． 15．若曲线C 的方程不是(,)0F x y =，则曲线C 上……………………………（）（A ）任意一点的坐标都不满足方程(,)0F x y =；（B ）存在无数个点，它们的坐标都不满足方程(,)0F x y =；（C ）至少存在一点，其坐标不满足方程(,)0F x y =；（D ）任意一点的坐标有可能都满足方程(,)0F x y =．三、解答题（第16、17题每题12分，第18题14分，第19题16分，第20、21题每题18分，共90分）16．求下列不等式组的解集：2220.50.5670log (56)log (3611)x x x x x x ⎧--⎪⎨++>-+⎪⎩≤，．17．（1）求证：sin tan21cos ααα=+；（2）已知4cos 5α=，求tan 2α．18．试讨论函数(0)a y x a x=+>在[1,)+∞上的单调性，并在你所得的结论中选择一个单调递减（或递增）区间予以证明．19．（1）已知椭圆C ：)0(12222>>=+b a by a x ，)0,(1c F 为C 的一个焦点，),(y x P 为C 上的任意一点，1PF l =，试写出l 关于点P 的横坐标x 的函数解析式)(x f l =，并求证当l 取最大值和最小值时，点),(y x P 分别位于椭圆长轴的两个端点；（2）2020年11月5日中国“嫦娥”一号卫星成功实现第一次近月制动，卫星进入距月球表面近月点高度约210公里，远月点高度约8600公里，且以月球的球心为一个焦点的椭圆形轨道．已知月球半径约3475公里，试利用（1）的结论求卫星航行轨道的轨迹方程．20．已知函数()y f x =满足(4)(4)f x f x +=-，且当4x ≤时，1()24xf x =⋅．（1）求当4x >时，函数()y f x =的解析式；（2）若数列{}n a 的通项公式为()n a f n =，求n a 的表达式，并求lim n n a →∞的值；（3）若数列{}n a 的前n 项和为n S ，求n S 的表达式，并求lim n n S →∞的值．21．已知曲线C 的方程为422(1)y x =-．（1）试指出方程所表示的是怎样的曲线，并在所给的平面直角坐标系中作出该曲线的大致图像；（2）试就实数k 的不同取值，讨论直线l ：2y kx =-与曲线C 的交点的个数．。

[高考数学] 2007年上海高考数学真题(理科)试卷(word解析版)

绝密★启用前 2007年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分． 1．函数y =lg ( 4−x )x−3的定义域是．2．若直线1210l x my ++=：　与直线231l y x =-：平行，则m = ．3．函数f(x)=xx−1的反函数f −1(x)= ．4．方程 96370x x-•-=的解是．5．已知x y ∈+R ，，且x +4y =1，则x y •的最大值是．6．函数y =sin ( x +π3 )sin ( x +π2 )的最小正周期T = ．7．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）．8．以双曲线x 24−y 25=1的中心为焦点，且以该双曲线的左焦点为顶点的抛物线方程是．9．对于非零实数a b ，，以下四个命题都成立：① a +1a ≠0； ② (a +b)2=a 2+2ab +b 2； ③ 若|a| = |b|，则a =±b ； ④ 若a 2=ab ，则a =b ．那么，对于非零复数a b ，，仍然成立的命题的所有序号是．10．在平面上，两条直线的位置关系有相交、平行、重合三种．已知αβ，是两个相交平面，空间两条直线12l l ，在α上的射影是直线12s s ，，12l l ，在β上的射影是直线12t t ，．用s 1与s 2，t 1与t 2的位置关系，写出一个总能确定l 1与l 2是异面直线的充分条件：．11．已知P 为圆x 2+( y −1 )2=1上任意一点（原点O 除外），直线OP 的倾斜角为θ弧度，记d = |OP |．在右侧的坐标系中，画出以()d θ，为坐标的点的轨迹的大致图形为二．选择题（本大题满分16分）本大题共有4 题，每题都给出代号为A ，B ，C ，D的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分． 12．已知a b ∈R ，，且2+a i,b +i （i 是虚数单位）是实系数一元二次方程 x 2+px +q =0的两个根，那么p q ，的值分别是（）Ａ．45p q =-=，Ｂ．43p q =-=，Ｃ．45p q ==，Ｄ．43p q ==，13．设a b ，是非零实数，若a <b ，则下列不等式成立的是（）Ａ．a 2<b 2 Ｂ．ab 2<a 2b Ｃ．1ab2<1a 2bＤ．b a<ab14．直角坐标系xOy 中，i j ，分别是与x y ，轴正方向同向的单位向量．在直角三角形ABC 中，若AB ⃗⃗⃗⃗⃗⃗ =2 i +j ,AC ⃗⃗⃗⃗⃗⃗ =3 i +k j ，则k 的可能值个数是（）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．415．设f(x)是定义在正整数集上的函数，且f(x)满足：“当2()f k k ≥成立时，总可推出(1)f k ≥(k +1)2成立”．那么，下列命题总成立的是（）Ａ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｂ．若(5)25f ≥成立，则当5k ≤时，均有2()f k k ≥成立Ｃ．若f( 7 )<49成立，则当8k ≥时，均有f( k )<k 2成立Ｄ．若f( 4 )=25成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤． 16．（本题满分12分）如图，在体积为1的直三棱柱ABC −A 1B 1C 1中，∠ACB =90∘, AC =BC =1．求直线A 1B 与平面BB 1C 1C 所成角的大小（结果用反三角函数值表示）．CB1B 1A A1C17．（本题满分14分）在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若a =2,C =π4，cos B2=2√55，求ABC △的面积S ．18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2% （如，2003年的年生产量的增长率为36%）．（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数f(x)=x 2+ax ( x ≠0，常数)a R ．（1）讨论函数f(x)的奇偶性，并说明理由；（2）若函数f(x)在[2)x ∈+∞，上为增函数，求a 的取值范围．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123n a a a a ，，，，（n 为正整数）满足条件a 1=a n ，a 2=a n−1，…，a n =a 1，即a i =a n−i+1（12i n =，，，），我们称其为“对称数列”．例如，由组合数组成的数列01mm m mC C C ，，，就是“对称数列”．（1）设{ b n }是项数为7的“对称数列”，其中1234b b b b ，，，是等差数列，且b 1=2， b 4=11．依次写出{ b n }的每一项；（2）设{ c n }是项数为2k −1(正整数k >1)的“对称数列”，其中121k k k c c c +-，，，是首项为50，公差为−4的等差数列．记{ c n }各项的和为S 2k−1．当k 为何值时，S 2k−1取得最大值？并求出S 2k−1的最大值；（3）对于确定的正整数m >1，写出所有项数不超过2m 的“对称数列”，使得211222m -，，，，依次是该数列中连续的项；当m 1500时，求其中一个“对称数列”前2008项的和S 2008．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．我们把由半椭圆x 2a 2+y 2b 2=1 (0)x ≥与半椭圆y 2b2+x 2c2=1 (0)x ≤合成的曲线称作“果圆”，其中a 2=b 2+c 2，a >0，b >c >0．如图，点F 0，F 1，F 2是相应椭圆的焦点，A 1，A 2和B 1，B 2分别是“果圆” 与x ，y 轴的交点．（1）若012F F F △是边长为1的等边三角形，求“果圆”的方程；（2）当|A 1A 2||B 1B 2|时，求b a 的取值范围；（3）连接“果圆”上任意两点的线段称为“果圆”的弦．试研究：是否存在实数k ，使斜率为k 的“果圆” 平行弦的中点轨迹总是落在某个椭圆上？若存在，求出所有可能的k 值；若不存在，说明理由．y 1B O 1A2B2A..1F0F 2F x .绝密★启用前 2007年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分． 1．函数y =lg ( 4−x )x−3的定义域是．【答案】 { x| x <4 且 x ≠3 }【解析】 4030x x ->⎧⎨-≠⎩⇒ { x| x <4 且 x ≠3 } 2．若直线1210l x my ++=：　与直线231l y x =-：平行，则m = ．【答案】−23【解析】 2123113m m =≠⇒=--- 3．函数f(x)=xx−1的反函数f −1(x)= ．【答案】xx−1 （ x ≠1 ）【解析】由(1)11x yy x y x y =⇒=≠⇒--()111x f x x x -=≠-（）4．方程 96370x x-•-=的解是．【答案】3log 7x =【解析】 2(3)63703731x x x x-⋅-=⇒==-或（舍去），3log 7x ∴=。

2007年高考.上海卷.文科数学试题及解答

1CC B1B1AA 2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)考生注意：1．答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚．2．本试卷共有21道试题，满分150分．考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．1．方程9131=-x 的解是． 2．函数11)(-=x x f 的反函数=-)(1x f ．3．直线014=-+y x 的倾斜角=θ ．4．函数πsec cos 2y x x ⎛⎫=∙+⎪⎝⎭的最小正周期=T ． 5．以双曲线15422=-y x 的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是．6．若向量a b ，的夹角为60，1==，则()a ab -= ．7．如图，在直三棱柱111C B A ABC -中，90=∠ACB ，21=AA ，1==BC AC ，则异面直线B A 1与AC 所成角的大小是（结果用反三角函数值表示）．8．某工程由A B C D ，，，四道工序组成，完成它们需用时间依次为254x ，，，天．四道工序的先后顺序及相互关系是：A B ，可以同时开工；A 完成后，C 可以开工；B C ，完成后，D 可以开工．若该工程总时数为9天，则完成工序C 需要的天数x 最大是．9．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）．10．对于非零实数a b ，，以下四个命题都成立：① 01≠+aa ； ② 2222)(b ab a b a ++=+； ③ 若||||b a =，则b a ±=； ④ 若ab a =2，则b a =．那么，对于非零复数a b ，，仍然成立的命题的所有序号是．11．如图，A B ，是直线l 上的两点，且2=AB ．两个半径相等的动圆分别与相切于A B ，点，C 是这两个圆的公共点，则圆弧AC ，CB 线段AB 围成图形面积S 的取值范围是．二．选择题（本大题满分16分）本大题共有4 题，每题都给出代号为A ，B ，C ，D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分．12．已知a b ∈R ，，且i 3,i 2++b a （i 是虚数单位）是一个实系数一元二次方程的两个根，那么a b ，的值分别是（）Ａ．32a b =-=，Ｂ．32a b ==-，Ｃ．32a b =-=-，Ｄ．32a b ==，13．圆01222=--+x y x 关于直线032=+-y x 对称的圆的方程是（）Ａ．21)2()3(22=-++y x Ｂ．21)2()3(22=++-y x Ｃ．2)2()3(22=-++y xＤ．2)2()3(22=++-y x14．数列{}n a 中，22211100010012n n n a n n n n ⎧⎪⎪=⎨⎪⎪-⎩，≤≤，，≥，则数列{}n a 的极限值（）Ａ．等于0 Ｂ．等于1 Ｃ．等于0或1 Ｄ．不存在15．设)(x f 是定义在正整数集上的函数，且)(x f 满足：“当2()f k k ≥成立时，总可推出(1)f k +≥2)1(+k 成立”．那么，下列命题总成立的是（）Ａ．若1)1(<f 成立，则100)10(<f 成立Ｂ．若4)2(<f 成立，则(1)1f ≥成立Ｃ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｄ．若(4)25f ≥成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．16．（本题满分12分）在正四棱锥ABCD P -中，2=PA ，直线PA 与平面ABCD 所成的角为60，求正四棱锥ABCD P -的体积V ．17．（本题满分14分）在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若4π,2==C a ，5522cos =B ，求ABC △的面积S ．18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2%（如，2003年的年生产量的增长率为36%）．（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420P B C A D1兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数0()(2≠+=x xax x f ，常数)a ∈R ．（1）当2=a 时，解不等式12)1()(->--x x f x f ；（2）讨论函数)(x f 的奇偶性，并说明理由．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123m a a a a ，，，，（m 为正整数）满足条件m a a =1，12-=m a a ，…，1a a m =，即1+-=i m i a a （12i m =，，，），我们称其为“对称数列”．例如，数列12521，，，，与数列842248，，，，，都是“对称数列”．（1）设{}n b 是7项的“对称数列”，其中1234b b b b ，，，是等差数列，且21=b ，114=b ．依次写出{}n b 的每一项；（2）设{}n c 是49项的“对称数列”，其中252649c c c ，，，是首项为1，公比为2的等比数列，求{}n c 各项的和S ；（3）设{}n d 是100项的“对称数列”，其中5152100d d d ，，，是首项为2，公差为3的等差数列．求{}n d 前n 项的和n S (12100)n =，，，．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分9分．我们把由半椭圆12222=+b y a x (0)x ≥与半椭圆12222=+cx b y (0)x ≤合成的曲线称作“果圆”，其中222c b a +=，0>a ，0>>c b ．如图，设点0F ，1F ，2F 是相应椭圆的焦点，1A ，2A 和1B M 是线段21A A 的中点．（1）若012F F F △是边长为1的等边三角形，求该 “果圆”的方程；（2）设P 是“果圆”的半椭圆12222=+cx b y(0)x ≤上任意一点．求证：当PM 取得最小值时，P 在点12B B ，或1A 处；（3）若P 是“果圆”上任意一点，求PM 取得最小值时点PPBCADO2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)答案要点一、填空题（第1题至第11题） 1． 1-=x 2． )0(11≠+x x3． 4arctan π- 4． π 5． x y 122= 6．217． 66arccos8． 39． 3.010． ② ④11． π022⎛⎤- ⎥⎝⎦，二、选择题（第12题至第15题）三、解答题（第16题至第21题）16．解：作⊥PO 平面ABCD ，垂足为O ．连接AO ，O 是正方形ABCD 的中心，PAO ∠是直线PA 与平面 A B C D 所成的角．PAO ∠＝ 60，2=PA ．∴ 3=PO ． 1=AO ，2=AB ，11233ABCD V PO S ∴==17．解：由题意，得3cos 5B B =，为锐角，54sin =B ，10274π3sin )πsin(sin =⎪⎭⎫ ⎝⎛-=--=B C B A ，由正弦定理得 710=c ， ∴ 111048sin 222757S ac B ==⨯⨯⨯=．18．解：（1）由已知得2003，2004，2005，2006年太阳电池的年生产量的增长率依次为 %36，%38，%40，%42．则2006年全球太阳电池的年生产量为8.249942.140.138.136.1670≈⨯⨯⨯⨯(兆瓦)．（2）设太阳电池的年安装量的平均增长率为x ，则441420(1)95%2499.8(142%)x ++≥．解得0.615x ≥．因此，这四年中太阳电池的年安装量的平均增长率至少应达到%5.61．19．解：（1）1212)1(222->----+x x x x x ， 0122>--x x ， 0)1(<-x x ． ∴ 原不等式的解为10<<x ．（2）当0=a 时，2)(x x f =，对任意(0)(0)x ∈-∞+∞，，，)()()(22x f x x x f ==-=-，)(x f ∴为偶函数．当0≠a 时，2()(00)af x x a x x=+≠≠，，取1±=x ，得 (1)(1)20(1)(1)20f f f f a -+=≠--=-≠，， (1)(1)(1)f f f f ∴-≠--≠，， ∴ 函数)(x f 既不是奇函数，也不是偶函数． 20．解：（1）设数列{}n b 的公差为d ，则1132314=+=+=d d b b ，解得 3=d ，∴数列{}n b 为25811852，，，，，，．（2）4921c c c S +++= 25492625)(2c c c c -+++=()122212242-++++= ()3211222625-=--==67108861．（3）51100223(501)149d d ==+⨯-=，．由题意得 1250d d d ，，，是首项为149，公差为3-的等差数列．当50n ≤时，n n d d d S +++= 21n n n n n 230123)3(2)1(1492+-=--+=．当51100n ≤≤时，n n d d d S +++= 21()n d d d S ++++= 525150(50)(51)37752(50)32n n n --=+-+⨯75002299232+-=n n ．综上所述，22330115022329975005110022n n n n S n n n ⎧-+⎪⎪=⎨⎪-+⎪⎩，≤≤，，≤≤．21．解：（1）((012(0)00F c F F ，，，，，021211F F b F F ∴=====，，于是22223744c a b c ==+=，，所求“果圆”方程为2241(0)7x y x +=≥，2241(0)3y x x +=≤．（2）设()P x y ，，则2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222()1()04b a c x a c x b c x c ⎛⎫-=---++- ⎪⎝⎭，≤≤， 0122<-cb ，∴ 2||PM 的最小值只能在0=x 或c x -=处取到．即当PM 取得最小值时，P 在点12B B ，或1A 处．（3）||||21MA M A = ，且1B 和2B 同时位于“果圆”的半椭圆22221(0)x y x a b+=≥和半椭圆22221(0)y x x b c +=≤上，所以，由（2）知，只需研究P 位于“果圆”的半椭圆22221(0)x y x a b +=≥上的情形即可．2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222222224)(4)(2)(c c a a c a b c c a a x a c ---++⎥⎦⎤⎢⎣⎡--=．当22()2a a c x a c -=≤，即2a c ≤时，2||PM 的最小值在222)(c c a a x -=时取到，此时P 的横坐标是222)(cc a a -．当a cc a a x >-=222)(，即c a 2>时，由于2||PM 在a x <时是递减的，2||PM 的最小值在a x =时取到，此时P 的横坐标是a ．综上所述，若2a c ≤，当||PM 取得最小值时，点P 的横坐标是222)(cc a a -；若c a 2>，当||PM 取得最小值时，点P 的横坐标是a 或c -．。

2007普通高等学校招生全国统一考试文科数学试题及答案-上海卷

1CCB1B1AA2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)考生注意：1．答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚．2．本试卷共有21道试题，满分150分．考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．一．填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．1．方程9131=-x 的解是． 2．函数11)(-=x x f 的反函数=-)(1x f ．3．直线014=-+y x 的倾斜角=θ ．4．函数πsec cos 2y x x ⎛⎫=∙+ ⎪⎝⎭的最小正周期=T ．5．以双曲线15422=-y x 的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是．6．若向量a b ，的夹角为60，1==b a ，则()a ab -= ． 7．如图，在直三棱柱111C B A ABC -中，90=∠ACB ， 21=AA ，1==BC AC ，则异面直线B A 1与AC 所成角的大小是（结果用反三角函数值表示）．8．某工程由A B C D ，，，四道工序组成，完成它们需用时间依次为254x ，，，天．四道工序的先后顺序及相互关系是：A B ，可以同时开工；A 完成后，C 可以开工；B C ，完成后，D 可以开工．若该工程总时数为9天，则完成工序C 需要的天数x 最大是． 9．在五个数字12345，，，，中，若随机取出三个数字，则剩下两个数字都是奇数的概率是（结果用数值表示）． 10．对于非零实数a b ，，以下四个命题都成立：① 01≠+aa ； ② 2222)(b ab a b a ++=+； ③ 若||||b a =，则b a ±=； ④ 若ab a =2，则b a =．那么，对于非零复数a b ，，仍然成立的命题的所有序号是． 11．如图，A B ，是直线l 上的两点，且2=AB A B ，点，C 是这两个圆的公共点，则圆弧AC ，CB 线段AB 围成图形面积S 的取值范围是．二．选择题（本大题满分16分）本大题共有4 题，每题都给出代号为A ，B ，C ，D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分．12．已知a b ∈R ，，且i 3,i 2++b a （i 是虚数单位）是一个实系数一元二次方程的两个根，那么a b ，的值分别是（）Ａ．32a b =-=，Ｂ．32a b ==-，Ｃ．32a b =-=-，Ｄ．32a b ==，13．圆01222=--+x y x 关于直线032=+-y x 对称的圆的方程是（）Ａ．21)2()3(22=-++y x Ｂ．21)2()3(22=++-y x Ｃ．2)2()3(22=-++y xＤ．2)2()3(22=++-y x14．数列{}n a 中，22211100010012n n n a n n n n ⎧⎪⎪=⎨⎪⎪-⎩≤≤，，≥，则数列{}n a 的极限值（）Ａ．等于0 Ｂ．等于1Ｃ．等于0或1Ｄ．不存在15．设)(x f 是定义在正整数集上的函数，且)(x f 满足：“当2()f k k ≥成立时，总可推出(1)f k +≥2)1(+k 成立”．那么，下列命题总成立的是（）Ａ．若1)1(<f 成立，则100)10(<f 成立Ｂ．若4)2(<f 成立，则(1)1f ≥成立Ｃ．若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立Ｄ．若(4)25f ≥成立，则当4k ≥时，均有2()f k k ≥成立三．解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．16．（本题满分12分）在正四棱锥ABCD P -中，2=PA ，直线PA 与平面ABCD 所成的角为60，求正四棱锥ABCD P -的体积V ．17．（本题满分14分）在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若4π,2==C a ，5522cos=B ，求ABC △的面积S ． 18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．近年来，太阳能技术运用的步伐日益加快．2002年全球太阳电池的年生产量达到670兆瓦，年生产量的增长率为34%．以后四年中，年生产量的增长率逐年递增2%（如，2003年的年生产量的增长率为36%）．PBCA D（1）求2006年全球太阳电池的年生产量（结果精确到0.1兆瓦）；（2）目前太阳电池产业存在的主要问题是市场安装量远小于生产量，2006年的实际安装量为1420兆瓦．假设以后若干年内太阳电池的年生产量的增长率保持在42%，到2010年，要使年安装量与年生产量基本持平（即年安装量不少于年生产量的95%），这四年中太阳电池的年安装量的平均增长率至少应达到多少（结果精确到0.1%）？19．（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．已知函数0()(2≠+=x xax x f ，常数)a ∈R ．（1）当2=a 时，解不等式12)1()(->--x x f x f ；（2）讨论函数)(x f 的奇偶性，并说明理由．20．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分．如果有穷数列123m a a a a ，，，，（m 为正整数）满足条件m a a =1，12-=m a a ，…，1a a m =，即1+-=i m i a a （12i m =，，，），我们称其为“对称数列”．1例如，数列12521，，，，与数列842248，，，，，都是“对称数列”．（1）设{}n b 是7项的“对称数列”，其中1234b b b b ，，，是等差数列，且21=b ，114=b ．依次写出{}n b 的每一项；（2）设{}n c 是49项的“对称数列”，其中252649c c c ，，，是首项为1，公比为2的等比数列，求{}n c 各项的和S ；（3）设{}n d 是100项的“对称数列”，其中5152100d d d ，，，是首项为2，公差为3的等差数列．求{}n d 前n 项的和n S (12100)n =，，，．21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分9分．我们把由半椭圆12222=+b y a x (0)x ≥与半椭圆12222=+cx b y (0)x ≤合成的曲线称作“果圆”，其中222c b a +=，0>a ，0>>c b ．如图，设点0F ，1F ，2F 是相应椭圆的焦点，1A ，2A 和1B ，2B 是“果圆” 与x ，y轴的交点，M 是线段21A A 的中点．（1）若012F F F △是边长为1的等边三角形，求该 “果圆”的方程；（2）设P 是“果圆”的半椭圆12222=+cx b y(0)x ≤上任意一点．求证：当PM 取得最小值时，P 在点12B B ，或1A 处；（3）若P 是“果圆”上任意一点，求PM 取得最小值时点P 的横坐标．PBCADO2007年全国普通高等学校招生统一考试（上海卷）数学试卷(文史类)答案要点一、填空题（第1题至第11题） 1． 1-=x 2． )0(11≠+x x3． 4arctan π- 4． π 5． x y 122= 6．217． 66arccos8． 39． 3.010． ② ④11． π022⎛⎤- ⎥⎝⎦，二、选择题（第12题至第15题）三、解答题（第16题至第21题）16．解：作⊥PO 平面ABCD ，垂足为O ．连接AO ，O 是正方形ABCD的中心，PAO ∠是直线PA 与平面 A B C D 所成的角．PAO ∠＝ 60，2=PA ．∴ 3=PO ．1=AO ，2=AB ，11233ABCD V PO S ∴==⨯=17．解：由题意，得3cos 5B B =，为锐角，54sin =B ，10274π3sin )πsin(sin =⎪⎭⎫ ⎝⎛-=--=B C B A ，由正弦定理得 710=c ， ∴ 111048sin 222757S ac B ==⨯⨯⨯=．18．解：（1）由已知得2003，2004，2005，2006年太阳电池的年生产量的增长率依次为%36，%38，%40，%42．则2006年全球太阳电池的年生产量为8.249942.140.138.136.1670≈⨯⨯⨯⨯(兆瓦)．（2）设太阳电池的年安装量的平均增长率为x ，则441420(1)95%2499.8(142%)x ++≥．解得0.615x ≥．因此，这四年中太阳电池的年安装量的平均增长率至少应达到%5.61．19．解：（1）1212)1(222->----+x x x x x ， 0122>--x x ， 0)1(<-x x ． ∴ 原不等式的解为10<<x ．（2）当0=a 时，2)(x x f =，对任意(0)(0)x ∈-∞+∞，，，)()()(22x f x x x f ==-=-，)(x f ∴为偶函数．当0≠a 时，2()(00)af x x a x x=+≠≠，，取1±=x ，得 (1)(1)20(1)(1)20f f f f a -+=≠--=-≠，， (1)(1)(1)f f f f ∴-≠--≠，，∴ 函数)(x f 既不是奇函数，也不是偶函数．20．解：（1）设数列{}n b 的公差为d ，则1132314=+=+=d d b b ，解得 3=d ， ∴数列{}n b 为25811852，，，，，，．（2）4921c c c S +++= 25492625)(2c c c c -+++= ()122212242-++++= ()3211222625-=--==67108861．（3）51100223(501)149d d ==+⨯-=，．由题意得 1250d d d ，，，是首项为149，公差为3-的等差数列．当50n ≤时，n n d d d S +++= 21 n n n n n 230123)3(2)1(1492+-=--+=．当51100n ≤≤时，n n d d d S +++= 21()n d d d S ++++= 525150 (50)(51)37752(50)32n n n --=+-+⨯75002299232+-=n n ．综上所述，22330115022329975005110022n n n n S n n n ⎧-+⎪⎪=⎨⎪-+⎪⎩，≤≤，，≤≤．21．解：（1）((012(0)00F c F F ，，，，，021211F F b F F ∴====，，于是22223744c a b c ==+=，，所求“果圆”方程为2241(0)7x y x +=≥，2241(0)3y x x +=≤．（2）设()P x y ，，则 2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222()1()04b a c x a c x b c x c ⎛⎫-=---++- ⎪⎝⎭，≤≤， 0122<-cb ，∴ 2||PM 的最小值只能在0=x 或c x -=处取到．即当PM 取得最小值时，P 在点12B B ，或1A 处．（3）||||21MA M A = ，且1B 和2B 同时位于“果圆”的半椭圆22221(0)x y x a b +=≥和半椭圆22221(0)y x x b c +=≤上，所以，由（2）知，只需研究P 位于“果圆”的半椭圆22221(0)x y x a b+=≥上的情形即可． 2222||y c a x PM +⎪⎭⎫ ⎝⎛--=22222222224)(4)(2)(c c a a c a b c c a a x a c ---++⎥⎦⎤⎢⎣⎡--=．当22()2a a c x a c -=≤，即2a c ≤时，2||PM 的最小值在222)(cc a a x -=时取到，此时P 的横坐标是222)(cc a a -．当a cc a a x >-=222)(，即c a 2>时，由于2||PM 在a x <时是递减的，2||PM 的最小值在a x =时取到，此时P 的横坐标是a ．综上所述，若2a c ≤，当||PM 取得最小值时，点P 的横坐标是222)(cc a a -；若c a 2>，当||PM 取得最小值时，点P 的横坐标是a 或c -．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上海市卢湾区2007学年第一学期高三年级期末考试数学试卷
2008.01

（完卷时间：120分钟满分：150分）
题号一二三总分
1~11 12~15 16 17 18 19 20 21

得分

一、填空题（每小题4分，共44分）
1．函数2()1fxx（0x）的反函数为1()fx___________．

2．函数1()tan23fxx的最小正周期为___________．
3．抛物线22yx的焦点坐标为___________．
4．过直线3270xy与直线420xy的交点，且与直线230xy垂直
的直线的方程为___________．
5．若将函数()3sin24cos2fxxx化为()cos()fxAx（0A，0，
02≤
）的形式，则可用反正切函数值表示为___________．

6．已知全集{200,}Innn+Z≤，若集合{3,,}AnnkknI+Z，

B
{5,nnk
,}knI+Z

，则集合AB的补集所含有的元素个数为________．

7．在△ABC中，若60A，8AB，7BC，则AC___________．
8．若数列na是一个首项为3，公差为2的等差数列，且4731nnTaaa，
则10T=___________．
9．若已知点(4,2)A，(1,3)B，(1,5)P，点Q为线段AB上的动点，则直线PQ的
斜率k的取值范围为___________．
10．若过点(1,0)A，且与y轴的夹角为6的直线与抛物线24yx交于P、Q两点，
则PQ___________．
11．现行银行三年期定期储蓄存款年利率为5.40%，某人用10万元连存两期此类储蓄，若假定利
率保持不变，则六年到期时此人所得的本利和最多为___________元（精确到１分）．
二、选择题（每小题4分，共16分）
12．有下列命题：
（1）函数tanyx为递增函数；
（2）函数sinyx在第一象限内为递增函数；
（3）函数cosyx的递增区间为[2,2]()22kkkZ；
其中真命题的个数为„„„„„„„„„„„„„„„„„„„„„„„（）
（A）0；（B）1；（C）2；（D）3．
13．若有数列{}na、{}nb，则limnna和limnnb分别存在是limnnnab存在的„„„（）

（A）充分非必要条件；（B）必要非充分条件；
（C）充分且必要条件；（D）非充分且非必要条件．
14．已知x、y为不相等的实数，若记1122xyl，212122xym，22xyn，则l，m，
n
三数的大小关系为„„„„„„„„„„„„„„„„„„（）
（A）lnm；（B）nlm；（C）nml；（D）不能确定．
15．若曲线C的方程不是(,)0Fxy，则曲线C上„„„„„„„„„„„（）
（A）任意一点的坐标都不满足方程(,)0Fxy；
（B）存在无数个点，它们的坐标都不满足方程(,)0Fxy；
（C）至少存在一点，其坐标不满足方程(,)0Fxy；
（D）任意一点的坐标有可能都满足方程(,)0Fxy．
三、解答题（第16、17题每题12分，第18题14分，第19题16分，第20、21题每题18分，
共90分）

16．求下列不等式组的解集：2220.50.5670log(56)log(3611)xxxxxx≤，．

17．（1）求证：sintan21cos；
（2）已知4cos5，求tan2．
18．试讨论函数(0)ayxax在[1,)上的单调性，并在你所得的结论中选择一个单调
递减（或递增）区间予以证明．

19．（1）已知椭圆C：)0(12222babyax，)0,(1cF为C的一个焦点，),(yxP 为
C上的任意一点，1PFl，试写出l
关于点P的横坐标x的函数解析式)(xfl，并求证

当l取最大值和最小值时，点),(yxP分别位于椭圆长轴的两个端点；
（2）2007年11月5日中国“嫦娥”一号卫星成功实现第一次近月制动，卫星进入距月球表面近
月点高度约210公里，远月点高度约8600公里，且以月球的球心为一个焦点的椭圆形轨道．已
知月球半径约3475公里，试利用（1）的结论求卫星航行轨道的轨迹方程．
20．已知函数()yfx满足(4)(4)fxfx，且当4x≤时，1()24xfx．
（1）求当4x时，函数()yfx的解析式；
（2）若数列na的通项公式为()nafn，求na的表达式，并求limnna的值；

（3）若数列na的前n项和为nS，求nS的表达式，并求limnnS的值．

21．已知曲线C的方程为422(1)yx．
（1）试指出方程所表示的是怎样的曲线，并在所给的
平面直角坐标系中作出该曲线的大致图像；
（2）试就实数k的不同取值，讨论直线l：2ykx
与曲线C的交点的个数．

y
O
1