2009年考研数学三试卷点评
考研数学三(多元函数微积分学)-试卷4

考研数学三(多元函数微积分学)-试卷4(总分:68.00,做题时间:90分钟)一、选择题(总题数:9,分数:18.00)1.选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
(分数:2.00)__________________________________________________________________________________________ 解析:2.二元函数f(x,y)在点(0,0)处可微的一个充分条件是(分数:2.00)A.B.C. √D.解析:解析:按可微定义, f(x,y)在(0,0)C项即A=B=0的情形,因此可得出f(x,y)在(0,0)可微.故选C.3.设函数f(x,y)连续,则二次积分等于(分数:2.00)A.B. √C.D.解析:解析:本题更换二次积分的积分次序,先根据二次积分确定积分区域,然后写出新的二次积分.由sinx≤y≤1,则0≤y≤1,π—arcsiny≤x≤π,故应选B.(分数:2.00)A.B.C.D. √D.5.累次积分可以写成(分数:2.00)A.B.C.D. √解析:解析:由累次积分f(rcosθ,rsinθ)rdr可知,积分区域D为由r=cosθ为圆心在x轴上,直径为1的圆可作出D的图形如图4—3所示.该圆的直角坐标方程为故用直角坐标表示区域D可见A、B、C均不正确,故选D.6.设g(x)有连续的导数,g(0)=0,g’(0)=a≠0,f(a,y)在点(0,0)的某邻域内连续,则=((分数:2.00)A.B.C. √D.C.7.设f(x)为连续函数,F(t)=∫ 1t dy∫ y t f(x)dx,则F’(2)等于( )(分数:2.00)A.2f(2).B.f(2).√C.一f(2).D.0.解析:解析:交换累次积分的积分次序,得F(t)=∫ 1t dy∫ y t f(x)=∫ 1t dx∫ 1x f(x)dy =∫ 1t(x-1)f(x)dx 于是F’(t)=(t一1)f(t),从而F’(2)=f(2).故选B.8.设有平面闭区域,D={(x,y)|一a≤x≤a,x≤y≤a},D 1={(x,y)|0≤x≤a,x≤y≤a},则=( )(分数:2.00)A. √B.C.D.解析:解析:将闭区间D={(x,y)|一a≤x≤a,x≤y≤a}按照直线y=一x将其分成两部分D 1和D 2,如图4—4所示,其中D 1关于y轴对称,D 2关于x轴对称,xy关于x和y均为奇函数,因此在D 1和D 2上,均有=0.而cosxsiny是关于x的偶函数,关于y的奇函数,在D 1积分不为零,在D 2积分值为零.因此故选项A正确.9.累次积分∫ 01dx∫ x1 f(x,y)dt+∫ 12dy∫ 02-y f(x,y)dx可写成( )(分数:2.00)A.∫ 02dx∫ x2-x f(x,y)dy.B.∫ 01dy∫ 02-y f(x,y)dx.C.∫ 01dx∫ x2-x f(x,y)dy.√D.∫ 01dy∫ 12-x f(x,y)dx.解析:解析:原积分域为直线y=x,x+y=2,与y轴围成的三角形区域,故选C.二、填空题(总题数:12,分数:24.00)10.设函数f(u)可微,且z=f(4x 2一y 2 )在点(1,2)处的全微分dz| (1,2) = 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:4dx一2dy)11.二元函数f(x,y)=x 2 (2+y 2 )+ylny的极小值为 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:[*])解析:解析:由题干可知 f x "=2x(2+y 2 ),f y "=2x 2 y+lny+1.12.函数f(x,y)=x 2 y(4一x一y)在由直线x+y=6,x轴和y轴所围成的闭区域D上的最小值是 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:一64)解析:解析:根据题意可知,得区域D内驻点(2,1),则有 f xx "=8y一6xy一2y 2; f xy "=8x 一3x 2一4xy; f yy "=-2x 2.则A=一6,B=一4,C=一8,有AC—B 2 =32>0,且A<0.所以,点(2,1)是z=f(x,y)的极大值点,且f(2,1)=4.当y=0(0≤x≤6)时,z=0;当x=0(0≤y≤6)时,z=0;当x+y=6(0≤y≤6)时,z=2x 3一12x 2(0≤x≤6),且令.解得x=4.则y=2,f(4,2)=一64,且f(2,1)=4,f(0,0)=0.则z=f(x,y)在D上的最大值为f(2,1)=4,最小值为f(4,2)=一64.13.设D={(x,y)|x 2 +y 2≤1},则(分数:2.00)填空项1:__________________14.设z=(x+e y ) x,则(分数:2.00)填空项1:__________________ (正确答案:正确答案:2ln2+1)解析:解析:由z=(x+e y ) x,故z(x,0)=(x+1) x,代入x=1得,15.设某产品的需求函数为Q=Q(p),其对应价格P的弹性E p =0.2,则当需求量为10000件时,价格增加1元会使产品收益增加 1元.(分数:2.00)填空项1:__________________ (正确答案:正确答案:8000)解析:解析:本题考查弹性和微分的经济意义.根据已知收益函数为R=pQ(p);对收益函数做微分为当Q=10000,dp=1时,产品的收益会增加dR=8000.16.设函数dz| (1,1) = 1.(分数:2.00)填空项1:__________________ (正确答案:正确答案:(1+2ln2)dx+(一1一2ln2)dy)17.设连续函数z=f(x,y)满足dz| (0,1) = 1(分数:2.00)填空项1:__________________ (正确答案:正确答案:2dx一dy)解析:解析:根据以及函数z的连续性可知f(0,1)=1,从而已知的极限可以转化为的定义可知,f(x,y)在点(0,1)处是可微的,且有f x’(0,1)=2,f y’(0,1)=一1,所以dz| (0,1)=2dx 一dy.18.设函数z=z(x,y)由方程(z+y) x =xy确定(分数:2.00)填空项1:__________________ (正确答案:正确答案:2—2ln2)解析:解析:把点(1,2)代入(z+y) x=xy,得z(1,2)=0.在(z+y) x=xy两边同时对x求偏导数,有将x=1,y=2,z(1,2)=0代入得19.设函数z=z(x,y)由方程z=e 2x-3z +2y确定,则(分数:2.00)填空项1:__________________ (正确答案:正确答案:2)解析:解析:在z=e 2x-3z +2y的两边分别对x,y求偏导,z为x,y的函数.20.设函数y=y(x)由方程y=1一xe y确定,则(分数:2.00)填空项1:__________________ (正确答案:正确答案:一e)解析:解析:将x=0代入方程y=1一xe y,得y=1.方程两边对x求导,得y’=一e y一xe y y’.y’(1+xe y )=一e y,因此21.设f(u,v)(分数:2.00)填空项1:__________________三、解答题(总题数:13,分数:26.00)22.解答题解答应写出文字说明、证明过程或演算步骤。
考研数学三(微积分)历年真题试卷汇编9(题后含答案及解析)

考研数学三(微积分)历年真题试卷汇编9(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(03年)设可微函数f(χ0,y0)在点(χ,y)取得极小僵,则下列结论正确的是【】A.f(χ0,y)在y=y0处导数等于零.B.f(χ0,y)在y=y0处导数大于零.C.f(χ0,y)在y=y0处导数小于零.D.f(χ0,y)在y=y0处的导数不存在.正确答案:A解析:由于f(χ,y)在(χ0,y0)取得极小值,则f(χ0,y)在y=y0取得极小值.又f(χ,y)在(χ0,y0)点处可微,则f′y(χ0,y0)存在,从而有f′y(χ0,y0)=0,即f(χ0,y)在y=y0处的导数为零,故应选A.知识模块:微积分2.(05年)设I1=,I2=cos(χ2+y2)dσ,I3=cos(χ2+y2)2dσ,其中D ={(χ,y)|χ2+y2≤1},则【】A.I3>I2>I1B.I1>I2>I3C.I2>I1>I3D.I3>I1>I2正确答案:A解析:由于当0≤χ≤时,cosχ是减函数,而当0≤χ2+y2≤1时,≥χ2+y2≥(χ2+y2)2,则cos≤cos(χ2+y2)≤cos(χ2+y2)2 故即I1≤I2≤I3 知识模块:微积分3.(06年)设f(χ,y)与φ(χ,y)均为可微函数,且φ′y愤怒(χ0,y0)≠0,已知(χ0,y0)是f(χ,y)在约束条件φ(χ,y)=0下的一个极值点,下列选项正确的是【】A.若f′χ(χ0,y0)=0,则f′y(χ0,y0)=0.B.若f′χ(χ0,y0)=0,则f′y(χ0,y0)≠0.C.若f′χ(χ0,y0)≠0,则f′y(χ0,y0)=0.D.若f′χ(χ0,y0)≠0,则f′y(χ0,y0)≠0.正确答案:D解析:由拉格朗日乘数法知,若(χ,y)是f(χ,y)在条件φ(χ,y)=0下的极值点,则必有若f′χ(χ0,y0)≠0,由①式知λ≠0,由原题设知φ′y(χ0,y0)≠0,由②式可知f′y(χ0,y0)≠0,故应选D.知识模块:微积分4.(07年)设函数f(χ,y)连续,则二次积分f(χ,y)dy等于【】A.B.C.D.正确答案:B解析:二次积分对应的二重积分的积分域D如图所示.交换二次积分次序得故应选B.知识模块:微积分5.(08年)已知f(χ,y)=,则【】A.f′χ(0,0),f′y(0,0)都存在.B.f′χ(0,0)不存在,f′y(0,0)存在.C.f′χ(0,0)存在,f′y(0,0)不存在.D.f′χ(0,0),f′y(0,0)都不存在.正确答案:B解析:f(χ,0)=e|χ|,在χ=0处不可导,事实上而不存在,则f′χ(0,0)不存在又f(0,y)=在y=0处可导,则f′y(0)存在,故应选B.知识模块:微积分6.(08年)设函数f连续,若F(u,v)=,其中区域Duv为图中阴影部分,则=【】A.vf(u2).B.f(u2).C.vf(u).D.f(u).正确答案:A解析:故应选A.知识模块:微积分填空题7.(01年)设生产函数为Q=ALαKβ,其中Q是产出量,L是劳动投入量,K是资本投入量,而A,α,β均为大于零的参数,则当Q=1时K关于L的弹性为_______.正确答案:解析:当Q=1时,1=ALαKβ等式两边对L求导,得0=αAL α-1Kβ+βALαKβ-1 解得由弹性计算公式知,K关于L的弹性为知识模块:微积分8.(02年)交换积分次序=_______.正确答案:解析:由原累次积分可知积分域如图2.16因此:知识模块:微积分9.(03年)设a>0,f(χ)=g(χ)=,而D表示全面,则I=f(χ)g(y-χ)d χdy=_______.正确答案:a2解析:由题意知f(χ)g(y-χ)=令Ω={(χ,y)|0≤χ≤1且0≤y -χ≤1}.则I==a2 其中区域Ω的面积为1.知识模块:微积分10.(04年)函数,(u,v)由关系式f[χg(y),y]=χ+g(y)确定,其中函数g(y)可微,且g(y)≠0,则=_______.正确答案:解析:令χg(y)=u,y=v,则χ=,g(y)=g(v),则知识模块:微积分11.(05年)设二元函数z=χeχ+y+(χ+1)ln(1+y),则dz|(1,0)=_______.正确答案:2edχ+(e+2)dy.解析:知识模块:微积分12.(06年)设函数f(u)可微,且f′(0)=,则z=f(4χ2-y2)在点(1,2)处的全微分dz|(1,2)=_______正确答案:4dχ-2dy.解析:则dz|(1,2)4dχ-2dy 知识模块:微积分13.(07年)设f(u,v)是二元可微函数,z=,则=_______.正确答案:解析:知识模块:微积分14.(08年)设D={(χ2,y2)|χ+y≤1},则(χ2-y)dχdy=_______.正确答案:解析:知识模块:微积分15.(09年)设z=(z+ey)χ,则=_______.正确答案:2ln2+1解析:由z=(χ+eyy)χ知,z(χ,0)=(χ+1)χ.代入χ=1得,=2ln2+1.知识模块:微积分解答题解答应写出文字说明、证明过程或演算步骤。
青岛大学数学分析2009-2017年考研初试真题

五、(每题 5 分, 共 15 分)计算下列各积分:
(1)
e3x+ex e4x−e2x+1
dx
;
(2) 1 x+2dx ;
x x−2
(3)
1 0
xexdx
六、(20 分)求下列函数
fx =
π
− 4 , − π ≤ x 0h
0,
x = 0h
π
4, 0
的傅里叶展开式。
七、(20 分)证明函数项级数
∞ cos nx n=1 n
1
7. (本题满分 30 分) 证明:
(1) (1)n1 sin 1 收敛;
n3
n
(2)
(1)n1 sin
1 n
n3 (ln n)x
在[0, ) 一致收敛;
(3)
lim
x0
n3
(1)n1 sin (ln n)x
1 n
(1)n1 sin
1. (本题满分 30 分) 求下列极限:
(1) lim( n a n b )n , 其中 a 0,b 0, a 1,b 1 ;
n
2
(2) lim sin( n2 1) ; n
nn
(3)
lim
n
3n
n!
.
2.
(本题满分
20
分)证明数列
{xn}
收敛,其中
x1
3
,
xn1
在一点 [a,b], 使得
b f (x)g(x)dx f ( )
b
g(x)dx .
a
a
6. (本题满分15分) 证明:广义积分 cos x dx 收敛,而 | cos x | dx 发散.
2009新课标高考数学试卷分析

1
2B
4
无最大值.
2
x2y 2 3
C
7. 等比数列{an }的前n项和为Sn , 且4a1, 2a2 , a3成等差数列
若a1 1, 则S4 ( C )
A. 7
B. 8
C. 15
D.16
4a1, 2a2 , a3成等差数列, 4a1 a3 4a2 , 即4a1 a1q2 4a1q,q2 4q 4 0, q 2, S4 1 2 4 8 15
2
44
2
T5
将(2
,1)代入y
sin
4 5
x
,
得
sin
8 5
1,
8 2k , k Z ,
5
2
2k 11 , k Z
10
又 ,
所以 9
10
15. 7名志愿者中安排6人在周六、周日两天参加社区 公益活动。若每天安排3人,则不同的安排方案共 有________1_4_0______种(用数字作答)。
又S2m1 (2m 1)am 38, 得2m 1 19, m 10
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17. 为了测量两山顶M, N间的距离,飞机沿水平方向在A, B 两点进行测量. A, B, M, N在同一个铅垂平面内(如示意 图).飞机能够测量的数据有俯角和A, B间的距离.请设计 一个方案,包括:①指出需要测量的数据(用字母表示,并 在图中标出);②用文字和公式写出计算M, N间的距离的 步骤.
(1)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙 为B类工人;
(1)甲、乙被抽到的概率均为 1 , 10
且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立
考研数学三N维向量-试卷3_真题(含答案与解析)-交互

考研数学三(N维向量)-试卷3(总分54, 做题时间90分钟)1. 选择题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.下列向量组α1,α2,…,α3中,线性无关的是SSS_SINGLE_SELA (1,2,3,4),(4,3,2,1),(0,0,0,0).B (a,b,c),(b,c,d),(c,d,e),(d,e,f).C (a,l,b,0,0),(c,0,d,2,3),(e,4,f,5,6).D (a,1,2,3),(b,1,2,3),(c,4,2,3),(d,0,0,0).分值: 2答案:C解析:有零向量的向量组肯定线性相关,任意n+1个n维向量必线性相关.因此(A),(B)均线性相关.对于(D),若d=0,肯定线性相关;若d≠0,则 (a,1,2,3)-(b,1,2,3)= (d,0,0,0),即α1,α2,α4线性相关,而线性相关的向量组再增加向量肯定仍是线性相关,因此不论哪种情况,(D)是线性相关的.由排除法可知(C)入选.另一方面,若能观察出β1=(1,0,0),β2 =(0,2,3),β3=(4,5,6)所构成的行列式则可知β1,β2,β3线性无关,而α1,α2,α3是其延伸组,即不论如何扩充均线性无关,故选(C).2.已知向量组α1,α2,α3,α4线性无关,则命题正确的是SSS_SINGLE_SEL Aα1+α2,α2+α3,α3+α4,α4+α1线性无关.Bα1 -α2,α2-α3,α3-α4,α4-α1线性无关.Cα1+α2,α2+α3,α3-α4,α4-α1线性无关.Dα1+α2,α2-α3,α3-α4,α4-α1线性无关.分值: 2答案:D解析:由观察法可知(α1+α2)-(α2+α3)+(α3+α4)-(α4+α1 )=0,即(A)线性相关.对于(B),(α1-α2)+(α2-α3)+(α3-α4)+(α4-α1)=0,即(B)线性相关.而(C)中,(α1+α2)-(α2+α3)+(α3-α4)+(α4-α1)=0,即(C)线性相关.由排除法可知(D)正确.作为复习并掌握基本方法,请读者直接证明(D)线性无关.3.设α1,α2,…,αs是n维向量,则下列命题中正确的是SSS_SINGLE_SELA如αs 不能用α1,α2,…,αs-1线性表出,则α1,α2,…,αs线性无关.B如α1,α2,…,αs线性相关,αs不能由α1,α2,…,αs-1线性表出,则α1,α2,…,αs-1线性相关.C如α1,α2,…,αs中,任意s-1个向量都线性无关,则α1,α2,…,αs线性无关.D零向量0不能用α1,α2,…,αs线性表出.分值: 2答案:B解析:(A),(C),(D)均错,仅(B)正确. (A)中当αs 不能用α1,α2,…,αs-1线性表出时,并不保证每一个向量αi(i=1,2,…,s-1)都不能用其余的向量线性表出.例如,α1 =(1,0),α2=(2,0),α3=(0,3),虽α3不能用α1,α2线性表出,但2α1-α2+0α3=0,α1,α2,α3是线性相关的. (C)如α1,α2,…,αs线性无关,可知它的任何一个部分组均线性无关.但任一部分组线性无关并不能保证该向量组线性无关.例如 e1 =(1,0,0,…,0),e2=(0,1,0,…,0),…,en=(0,0,0,…,1),α=(1,1,1,…,1),其中任意n个都是线性无关的,但这n+1个向量是线性相关的. (D)在线性表出的定义中,对组合系数没有任何约束条件,因此,零向量可以用任何向量组线性表出,最多组合系数全取为0,即0=0α1+0α2,+ 0s.其实,零向量0用α1,α2,…,αs 表示时,如果组合系数可以不全为0,则表明α1,α2,…,αs是线性相关的,否则线性无关.关于(B),由于α1,α2,…,αs线性相关,故存在不全为0的ki (i=1,2,…,s),使 k1α1+k2α2+…+ksαs =0.显然,ka=0(否则αs可由α1,…,αs-1线性表出),因此α1,α2,…,αs-1线性相关.4.设向量组Ⅰ:α1,α2,…,αr可由向量组Ⅱ:β1,β2,…,βs线性表出,则下列命题正确的是SSS_SINGLE_SELA 若向量组Ⅰ线性无关,则ar≤s.B 若向量组Ⅰ线性相关,则r>s.C 若向量组Ⅱ线性无关,则r≤s.D 若向量组Ⅱ线性相关,则r>s.分值: 2答案:A解析:因为Ⅰ可由Ⅱ线性表出,故r(Ⅰ)≤r(Ⅱ).当向量组Ⅰ线性无关时,有r(Ⅰ)=r(α1,α2,…,αr)=r.由向量组秩的概念自然有r(Ⅱ)=r(β1,β2,…,βs)≤s.从而(A)正确.若α1= ,可见(B)、(D)均不正确.若α1= ,可知(C).不正确.2. 填空题1.已知向量组α1 =(1,2,-1,1) T,α2=(2,0,a,0) T,α3=(0,-4,5,1-a) T的秩为2,则a=______.SSS_FILL分值: 2答案:正确答案:3解析:根据三秩相等定理及经初等变换秩不变定理,对(α1,α2,α3)作初等变换,有所以a=3.2.若α1 =(1,0,5,2) T,α2=(3,-2,3,-4) T,α3=(-1,1,t,3) T线性相关,则t=______.SSS_FILL分值: 2答案:正确答案:1解析:α1,α2,α3线性相关的充要条件是齐次方程组x1α1+x2α2 +x3α3=0有非零解.对系数矩阵高斯消元,化为阶梯形,于是有因为齐次方程组有三个未知数,它若有非零解则阶梯形方程组中方程个数必不大于2,故知t=1.3.若α1 =(1,-1,2,4) T,α2=(0,3,1,2) T,α3=(3,0,7,a)T,α4=(1,-2,2,0) T线性无关,则a的取值范围为________.SSS_FILL分值: 2答案:正确答案:a≠14解析:n个n维向量α1,α2,…,αn线性无关|α1,α2,…,αn|≠0.因为所以a≠14.4.若β=(1,2,t) T可由α1 =(2,1,1) T,α2=(-1,2,7) T,α3=(1,-1,-4) T线性表出,则t=_______.SSS_FILL分值: 2答案:正确答案:5解析:β可以由向量组α1,α2,α3线性表出的充要条件是线性方程组x1α1+x2α2+x3α3=β有解.对增广矩阵高斯消元,化为阶梯形,即5.设α1 =(1,2,1) T,α2=(2,3,a) T,α3=(1,a+2,-2) T,若β1=(1,3,4) T可以由α1,α2,α3线性表出,β2=(0,1,2) T不能由α1,α2,α3线性表出,则a=_____.SSS_FILL分值: 2答案:正确答案:-1解析:依题意,方程组x1α1+x2α2+x3α3=β1有解,而方程组x1α1 +x2α2+x3α3=β2无解.因为两个方程组的系数矩阵相同,故可合并一次加减消元,即可见a=-1时,方程组x1α1+x2α2+x3α3=β1有解,而x1α1+x2α2+x3α3=β2无解,故a=-1.3. 解答题解答题解答应写出文字说明、证明过程或演算步骤。
2009年考研数学一真题评注
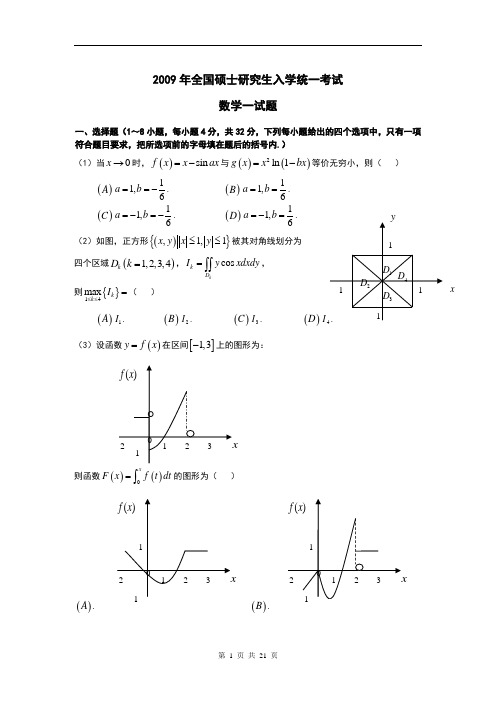
2009年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==.()C 11,6a b =-=-.()D 11,6a b =-=.(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为 四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14m ax k k I ≤≤=( )()A 1I .()B 2I .()C 3I .()DI (3)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0xF x f t dt =⎰的图形为( )()A .()B .x()C .()D .(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则( )()A 当1n n b ∞=∑收敛时,1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时,1n n n a b ∞=∑发散.()C 当1n n b ∞=∑收敛时,221nnn a b ∞=∑收敛.()D 当1n n b ∞=∑发散时,221n n n a b ∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为( ) ()A 101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫-⎪ ⎪ ⎪-⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪-⎪⎪ ⎪- ⎪⎝⎭.(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( ) ()A **32O B A O ⎛⎫⎪⎝⎭.()B **23O B A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =( ) ()A 0.()B 0.3.()C 0.7.()D 1.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为( )()A 0.()B 1. ()C 2.()D 3.二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.) (9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2z x y∂=∂∂ 。
考研数学三(概率论与数理统计)历年真题试卷汇编2(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编2(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(16年)设随机变量X与Y相互独立,且X~N(1,2),Y~N(1,4),则D(XY)=【】A.6.B.8.C.14.D.15.正确答案:C解析:由题意知:EX=1,DX=2,EY=1,DY=4,于是E(X2)=DX+(EX)2=2+12=3,E(Y2)=DY+(EY)2=4+12=5,注意到X2与Y2是独立的,于是D(XY)=E(XY)2-[E(XY)]2 =E(X2Y2)-[EX.EY]2 =E(X2).EY2-(EX)2(EY)2 =3×5-12×12=14 故选C.知识模块:概率论与数理统计2.(94年)设X1,X2,…,Xn是来自正态总体N(μ,σ2)的简单随机样本,是样本均值,记则服从自由度为n-1的t分布的随机变量是【】A.B.C.D.正确答案:B 涉及知识点:概率论与数理统计3.(02年)设随机变量X和Y都服从标准正态分布,则【】A.X+Y服从正态分布.B.X2+Y2服从Z2分布.C.X2和Y2都服从χ2分布.D.X2/Y2服从F分布.正确答案:C解析:∵X~N(0,1),Y~N(0,1)∴X2~χ2(1),Y2~χ2(1),故选C.知识模块:概率论与数理统计4.(11年)设总体X服从参数为λ(λ>0)的泊松分布,X1,X2,…,Xn(n ≥2)为来自该总体的简单随机样本.则对于统计量T1=和T2=,有【】A.ET1>ET2,DT1>DT2.B.ET1>ET2,DT1<DT2.C.ET1<ET2,DT1>DT2.D.ET1<ET2,DT1<DT2.正确答案:D解析:由题意知X1,X2,…,Xn独立同分布,EXi=DXi=λ,i=1,2,…,n.故:可见ET1<ET2,DT1<DT2,故选D.知识模块:概率论与数理统计5.(12年)设X1,X2,X3,X4为来自总体N(1,σ2)(σ>0)的简单随机样本,则统计量的分布为【】A.N(0,1)B.t(1)C.χ2(1)D.F(1,1)正确答案:B解析:由题意得:E(X1-X2)=EX1-EX2=1-1=0,D(X1-X2)=DX1+DX2=σ2+σ2=2σ2,∴X1-X2~N(0,2σ2) 同理,E(X3+E4)=EX3+EX4=1+1=2,D(X3+X4)=DX3+DX4=2σ2,∴X3+X4~N(2,2σ2) 又∵X1-X2与X3+X4独立,故知识模块:概率论与数理统计6.(14年)设X1,X2,X3为来自正态总体N(0,σ2)的简单随机样本,则统计量S=服从的分布为【】A.F(1,1)B.F(2,1)C.t(1)D.t(2)正确答案:C解析:由题意可知:X1-X2~N(0,2σ),∴~N(0,1) 又:~N(0,1),∴~χ2(1)且X3与X1-X2独立,故~t(1) 即S~t(1),故选C.知识模块:概率论与数理统计7.(15年)设总体X~B(m,θ),X1,X2,…,Xn为来自该总体的简单随机样本,一为样本均值,则【】A.(m-1)nθ(1-θ).B.m(n-1)θ(1-θ).C.(m-1)(n-1)θ(1-θ).D.mmθ(1-θ).正确答案:B 涉及知识点:概率论与数理统计8.(92年)设n个随机变量X1,X2,…,Xn独立同分布,DX1=σ2,,则【】A.S是σ的无偏估计量.B.S是σ的最大似然估计量.C.S是σ的相合估计量(即一致估计量).D.S与相互独立.正确答案:C 涉及知识点:概率论与数理统计9.(05年)设一批零件的长度服从正态分布N(μ,σ2),其中μ,σ2均未知.现从中随机抽取16个零件,测得样本均值=20(cm),样本标准差s=1(cm),则μ的置信度为0.90的置信区间是【】A.(20-t0.05(16),20+t0.05(16))B.(20-t0.1(16),20+t0.1(16))C.(20-t0.05(15),20+t0.05(15))D.(20-t0.1(15),20+t0.1(15))正确答案:C 涉及知识点:概率论与数理统计填空题10.(10年)设X1,X2,…,Xn是来自总体N(μ,σ2)(σ>0)的简单随机样本.记统计量T=,则ET=_______.正确答案:σ2+μ2解析:由题意知EXi=μ,DXi=σ2,∴EXi2=DXi十(EXi)2=σ2+μ2,i=1,2,…,n.故ET==σ2+μ2.知识模块:概率论与数理统计11.(14年)设总体X的概率密度为其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若=θ2,则c=_______.正确答案:解析:由题意得:故c=知识模块:概率论与数理统计12.(93年)设总体X的方差为1,根据来自X的容量为100的简单随机样本,测得样本均值为5.则X的数学期望的置信度近似等于0.95的置信区间为_______.正确答案:(4.804,5.196) 涉及知识点:概率论与数理统计13.(96年)设由来自正态总体X~N(μ,0.92)容量为9的简单随机样本,得样本均值=5.则未知参数μ的置信度为0.95的置信区间是_______.正确答案:(4.412,5.588)解析:由题意知X~N(μ,) ∴~N(0,1) 故0.95==P{-0.3×u0.975<μ<+0.3×u0.975 而u0.975=1.96,=5,故得μ的置信度为0.95的置信区间为(5-0.3×1.96,5+0.3×1.96)=(4.412,5.588) 知识模块:概率论与数理统计14.(02年)设总体X的概率密度为而X1,X2,…,Xn是来自总体X 的简单随机样本,则未知参数θ的矩估计量为_______.正确答案:解析:知识模块:概率论与数理统计15.(06年)设总体X的概率密度为f(χ)=(-∞<χ<+∞),X1,X2,…,Xn为总体X的简单随机样本,其样本方差为S2,则ES2=_______.正确答案:2 涉及知识点:概率论与数理统计16.(95年)设X1,…,Xn是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知.记则假设H0:μ=0的t检验使用的统计量t=_______.正确答案:涉及知识点:概率论与数理统计17.(89年)设X为随机变量且EX=μ,DX=σ2.则由切比雪夫不等式,有P{|X-μ|≥3σ}≤_______.正确答案:涉及知识点:概率论与数理统计解答题解答应写出文字说明、证明过程或演算步骤。
考研数学三(微积分)-试卷6

考研数学三(微积分)-试卷6(总分:64.00,做题时间:90分钟)一、选择题(总题数:13,分数:26.00)1.选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
(分数:2.00)__________________________________________________________________________________________ 解析:2.下列各式中正确的是((分数:2.00)A. √B.C.D.解析:解析:由重要极限结论=e,可立即排除B、D。
对于A、C选项,只要验算其中之一即可。
对于C选项,因=e —1,故C不正确,选A。
3.设对任意的x,总有φ(x)≤f(x)≤g(x),且[g(x)—φ(x)]=0(分数:2.00)A.存在且等于零B.存在但不一定为零C.一定不存在D.不一定存在√解析:解析:取φ(x)=f(x)=g(x)=x,显然有φ(x)≤f(x)≤g(x),且[g(x)—φ(x)]=0,但[g(x)一φ(x)]=0=1,可见C也不正确,敬选D。
4.设f(x)在[a,b]可导,f(a))(分数:2.00)A.f +"(0)=0B.f +"(a)≥0C.f +"(A)<0D.f +"(a)≤0√解析:解析:由题设条件f +"(a)D。
5.设f(x)在(1—δ,1+δ)内存在导数,f"(x)严格单调减少,且f(1)=f"(1)=1,则()(分数:2.00)A.在(1—δ,1)和(1,1+∞内均有f(x)<x √B.在(1—δ,1)和(1,1+∞内均有f(x)>xC.在(1—δ,1)有f(x)<x,在(1,1+δ)内均有f(x)>xD.在(1—δ,1)有f(x)>x,在(1,1+δ)内均有f(x)<x解析:解析:f"(x)在(1—δ,1+δ)上严格单调减少,则f(x)在(1—δ,1+δ)是凸的,因此在此区间上,y=f(x)在点(1,1)处的切线为y—l=f"(1)(x—1),即y=x在此曲线的上方(除切点外)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年考研数学三试卷点评
2009年全国硕士研究生统一入学考试初试已经结束,数学三和数学四合并后的新数学三首次与考生见面,部分考生和考研辅导教师认为比去年数学题难度有所下降。
一、考查内容
考研数学辅导专家说,新数学三试题突出了该科考试大纲较原数学四大纲新增加的内容。
如无穷级数部分考了一道基本题、数理统计部分考了一道填空题。
这两道客观题不是很难。
微分方程和解的结构定理,以及二阶微分方程及差分方程的相关内容,在2009年的试卷中没有反映。
二、难度分析
考研数学辅导教师认为,2009年数学试题整体难度有所降低,主要是线性代数和概率论与数理统计部分试题难度减小,高等数学部分与去年难度相当。
线性代数部分的试题难度降低原因主要有2个。
一是试题基本涉及线性代数考试大纲6个章节的重要知识点,每章都有考题,而且题目难度不高;二是试题计算量不大,如果考生将基本知识点掌握了,就可以用比较简洁的方法将题目解出来。
如:试卷第20题考核考生最常见的数字非齐次线性方程组求解,然后判断3个向量线性无关。
做此题时,考生用3个向量构成矩阵行列式不等于零就可以,这
些是线性代数中的基本要求。
第21题考核二次型,也是一个很规范的题目,只是第二小问略有难度,需要考生用到平时积累的结论。
第23题是有关点估计的题目,题型也常见。
2009年考研数学题的明显特点是考试内容涉及较广,且符合考试大纲要求,没出偏题、怪题,难度适中。
赵达夫说,今年数学试题更重视考查基本概念、公式、性质、定理和原理,提高了对考生综合知识的考核。
如数学三考了求幂级数的收敛半径,数学一考了求体积和微分方程等综合题。
今年数学试卷还延续了去年考试的特点,考查了考试大纲中所要求的重要定理的证明,数一、数二、数三都考了拉格朗日微分中值定理的证明,利用这个定理证明这道题的第二问。
【。
