极坐标(高中数学经典问题选编)(高中数学,选修4-4)
1.3.2 直线的极坐标方程 课件(人教A选修4-4)

[悟一法]
求直线极坐标方程的步骤: (1)设(ρ,θ)为直线上任一点的极坐标. (2)写出动点满足的几何条件. (3)把上述条件转化为ρ,θ的等式. (4)化简整理.
[通一类] 1.若将例题中的“平行”改为“垂直”,如何求解?
π 解:如图所示,在直线 l 上任意取点 M(ρ,θ),∵A(2,4), π ∴|OH|=2cos 4= 2. 在 Rt△OMH 中, |OH|=|OM|cos θ, ∴ 2=ρcos θ,即 ρcos θ= 2. π ∴过 A(2,4)且垂直于极轴的直线方程为 ρcos θ= 2.
[小问题· 大思维]
1.在直线的极坐标方程ຫໍສະໝຸດ ,ρ的取值范围是什么?提示:ρ的取值范围是全体实数,即ρ∈R. 2.在极坐标系中,点M(ρ,θ)与点P(-ρ,θ)之间有什么关 系? 提示:若ρ<0,则-ρ>0,因此点M(ρ,θ)与点P(-ρ,θ)关 于极点对称.
[研一题]
[例 1] π 求过点 A(2,4)且平行于极轴的直线的极坐标方程.
2
[答案]
3
点击进入 创新演练大冲关
标方程,然后在直角坐标系下研究所要求解的问题,最后再将 直角坐标方程转化为极坐标方程即可.
[通一类] 3.在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线 ρ(cos θ+sin θ)=1 与 ρ(sin θ-cos θ)=1 的交点的极坐标.
人教高中数学选修 4-4 极坐标与参数方程 知识点
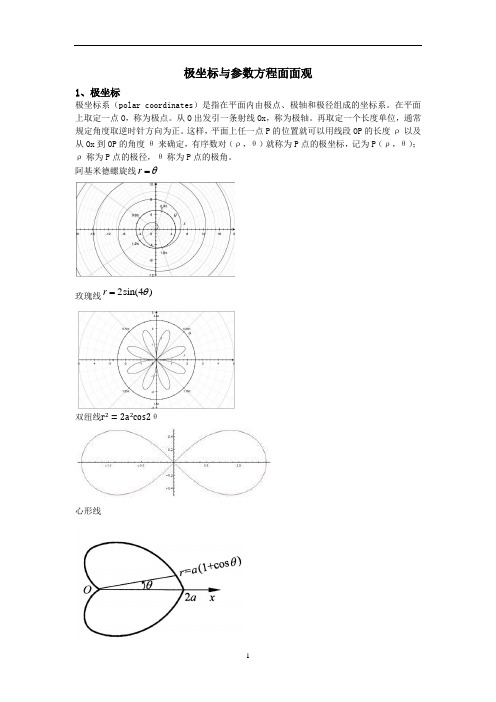
极坐标与参数方程面面观1、极坐标极坐标系(polar coordinates)是指在平面内由极点、极轴和极径组成的坐标系。
在平面上取定一点O,称为极点。
从O出发引一条射线Ox,称为极轴。
再取定一个长度单位,通常规定角度取逆时针方向为正。
这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。
阿基米德螺旋线rθ=玫瑰线2sin(4) rθ=双纽线r2=2a2cos2θ心形线极坐标中的直线一般方程a ρcos θ+b ρcos θ+c =0(θ为倾斜角)极坐标中的圆圆心在极点,半径为R :ρ=R (θ任意)半径为R 的圆过(R,0)点:ρ=2Rcos θ.圆心(a ,α)半径为r :r 2=ρ2+a 2−2a ρcos (α−θ)ρ^2-2R ρ(sin θ+cos θ)+R^2=0圆心在(a ,π2)处且过极点:ρ=2asin θ(θ∈[0,π]) 椭圆、双曲线、抛物线统一的极坐标方程为: θρcos 1e ep -=.(p 是定点F 到定直线的距离,p >0 ).当0<e <1时,方程表示椭圆;当e >1时,方程表示双曲线,若ρ>0,方程只表示双曲线右支,若允许ρ<0,方程就表示整个双曲线;当e=1时,方程表示开口向右的抛物线.2、参数方程 定义:一般的,在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数't’的函数{x=f(t),y=g(t)}并且对于't‘的每一个允许值,由上述方程组所确定的点M (x,y)都在这条曲线上,那么上述方程则为这条曲线的参数方程,联系x ,y 的变数't‘叫做变参数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
(注意:参数是联系变数x ,y 的桥梁,可以是一个有物理意义和几何意义的变数,也可以是没有实际意义的变数)圆的参数方程它的参数方程为:cos ()sin x a r y b r θθθ=+⎧⎨=+⎩为参数(θ∈ [0,2π) ) (a,b) 为圆心坐标,r 为圆半径。
数学:4.1.2《极坐标系(1))课件(新人教选修4-4)

三、小
结
[1]建立一个极坐标系需要哪些要素 极点;极轴;长度单位;角度单位和它的正方向. [2]极坐标系内一点的极坐标有多少种表达式? 无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ ) 四、课后作业 教材P14-15页5,8,9,10,11 思考: 极坐标系中, 点M的坐标为(-10, ), 则下列各 3 坐标中, 不是M点的坐标的是( ) (A) (10, 4) (B) (-10, - 5) (C) (10, - 2) (D)(10, 2) 3 3 3 3
5 3 (-, +)
(, 2k+)
[-, +(2k+1)]
都是同一点的 极坐标.
例3. 已知点Q(, ),分别按下列条件求出点P的坐标: (1) P是点Q关于极点O的对称点; (2) P是点Q关于直线 的对称点. 2 (3) P是点Q关于极轴的对称点。 注意点M的极坐标具有多值性.
引一条射线OX,叫做极轴。
再选定一个长度单位和角度单位及它 的正方向(通常取逆时针方向). O 这样就建立了一个极坐标系.
X
2、极坐标系内一点的极坐标的规定 对于平面上任意一点M,用表示线段OM的长度, 用表示以射线OX为始边,射线OM为终边所成的 角,叫做点M的极径, 叫做点M的极角,有序数对 (,)就叫做M的极坐标。
情境2:请问到深大附中怎么走? 从这向南走200米.
请分析上面这句话,他告诉了问路人什么?
从 这 向 南 走 2 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的 位置。这种用方向和距离表示平面上一点的位置的 思想,就是极坐标的基本思想。
高中数学选修4-4解答题

选修4-4一、解答题1.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin (θ+)=2.(1)写出C1的普通方程和C2的直角坐标方程;(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.2.在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.3.在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|•|OP|=16,求点P的轨迹C2的直角坐标方程;(2)设点A的极坐标为(2,),点B在曲线C2上,求△OAB面积的最大值.4.在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)-=0,M为l3与C的交点,求M的极径.5.已知曲线C:+=1,直线l:(t为参数)(Ⅰ)写出曲线C的参数方程,直线l的普通方程.(Ⅱ)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.6.已知直线l的参数方程为 (t为参数),曲线C的极坐标方程为ρ2cos2θ=1.(1)求曲线C的直角坐标方程.(2)求直线l被曲线C截得的弦长.7.将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.(Ⅰ)写出C的参数方程;(Ⅱ)设直线l:2x+y-2=0与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.8.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),直线l与抛物线y2=4x相交于A,B两点,求线段AB的长.9.在直角坐标系xOy中,曲线C1:(t为参数,t≠ 0),其中0 ≤ α < π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:,C3:。
高中数学选修4-4检测:极坐标系及其极直互化(附解析)

⎪⎭⎝4A.(2,2) B.(2,-2) C.(2,2) D.(-2,2)2.点M 的直角坐标为⎪⎭⎫⎝⎛20π,,则点M 的极坐标可以为( )A. ⎪⎭⎫ ⎝⎛0,2πB.⎪⎭⎫ ⎝⎛20π,C.⎪⎭⎫ ⎝⎛22ππ,D.⎪⎭⎫⎝⎛2-2ππ,3.下列各点与⎪⎭⎫⎝⎛32π,表示极坐标系中同一点的是( )A. ⎪⎭⎫ ⎝⎛322π,B.(2,π)C. ⎪⎭⎫⎝⎛372π, D.(2,2π)4.把点的直角坐标(3,-4)化为极坐标(ρ,θ)(限定ρ≥0,0≤θ<2π),则( )A .ρ=3,θ=4B .ρ=5,θ=4C .ρ=5,tan θ=43D .ρ=5,tan θ=-435.极坐标系中,直角坐标为(1,-3)的点的极角为________.6.在极坐标系中,已知点P 1⎪⎭⎫ ⎝⎛46π,、P 2⎪⎭⎫⎝⎛438π,,则|P 1P 2|等于( ) A.9 B.10 C.14 D.27.下列的点在极轴上方的是( )A.(3,0)B.⎪⎭⎫⎝⎛673π,C. ⎪⎭⎫ ⎝⎛474π, D .⎪⎭⎫ ⎝⎛4174π,8.点M ⎪⎭⎫⎝⎛656π,到极轴所在直线的距离为________.9.若A ,B 两点的极坐标为A (4,0),B ⎪⎭⎫ ⎝⎛24π,,则线段AB 的中点的极坐标为( )A. ⎪⎭⎫⎝⎛422π, B.⎪⎭⎫⎝⎛42π, C.⎪⎭⎫ ⎝⎛44π, D.⎪⎭⎫ ⎝⎛42π,10.在极坐标系中,若A ⎪⎭⎫ ⎝⎛33π,,B ⎪⎭⎫ ⎝⎛674π,,求△ABO 的面积(O 为极点)为( ) A .2 B .3 C .4D .6⎪⎭⎝4A.(2,2) B.(2,-2) C.(2,2) D.(-2,2) 解析 x =ρcos θ=2,y =ρsin θ=- 2. 答案 B2.点M 的直角坐标为⎪⎭⎫⎝⎛20π,,则点M 的极坐标可以为( )A. ⎪⎭⎫ ⎝⎛0,2πB.⎪⎭⎫ ⎝⎛20π,C.⎪⎭⎫ ⎝⎛22ππ,D.⎪⎭⎫⎝⎛2-2ππ,解析 ∵ρ=x 2+y 2=π2,且θ=π2,∴M 的极坐标为⎪⎭⎫⎝⎛22ππ,.答案 C 3.下列各点与⎪⎭⎫⎝⎛32π,表示极坐标系中同一点的是( )A. ⎪⎭⎫⎝⎛322π,B.(2,π)C. ⎪⎭⎫⎝⎛372π, D.(2,2π) 解析 与极坐标⎪⎭⎫ ⎝⎛32π,相同的点可以表示为⎪⎭⎫ ⎝⎛+ππk 232,(k ∈Z),只有⎪⎭⎫⎝⎛372π,适合.答案 C4.把点的直角坐标(3,-4)化为极坐标(ρ,θ)(限定ρ≥0,0≤θ<2π),则( )A .ρ=3,θ=4B .ρ=5,θ=4C .ρ=5,tan θ=43D .ρ=5,tan θ=-43解析:由公式得ρ=x 2+y 2=32+(-4)2=5,tan θ=y x =-43,θ∈[0,2π).答案:D5.极坐标系中,直角坐标为(1,-3)的点的极角为________.解析:直角坐标为(1,-3)的点在第四象限,tan θ=-3,所以θ=2k π-π3(k ∈Z).答案:2k π-π3(k ∈Z)6.在极坐标系中,已知点P 1⎪⎭⎫ ⎝⎛46π,、P 2⎪⎭⎫⎝⎛438π,,则|P 1P 2|等于( )A.9B.10C.14D.2解析 ∠P 1OP 2=3π4-π4=π2,∴△P 1OP 2为直角三角形,由勾股定理可得|P 1P 2|=10.答案 B7.下列的点在极轴上方的是( )A.(3,0)B.⎪⎭⎫ ⎝⎛673π,C. ⎪⎭⎫ ⎝⎛474π, D .⎪⎭⎫⎝⎛4174π,解析 建立极坐标系,由极坐标的定义可得点(3,0)在极轴上,点⎪⎭⎫ ⎝⎛673π,,⎪⎭⎫⎝⎛474π,在极轴下方,点⎪⎭⎫⎝⎛4174π,在极轴上方,故选D.8.点M ⎪⎭⎫⎝⎛656π,到极轴所在直线的距离为________.解析 依题意,点M ⎪⎭⎫⎝⎛656π,到极轴所在的直线的距离为d =6×sin 5π6=3.答案 3 9.若A ,B 两点的极坐标为A (4,0),B ⎪⎭⎫⎝⎛24π,,则线段AB 的中点的极坐标为( )A. ⎪⎭⎫⎝⎛422π, B.⎪⎭⎫⎝⎛42π, C.⎪⎭⎫ ⎝⎛44π, D.⎪⎭⎫ ⎝⎛42π,解析:由题易知点A ,B 的直角坐标分别为(4,0),(0,4),则线段AB 的中点的直角坐标为(2,2).由ρ2=x 2+y 2,得ρ=2 2. 因为tan θ=22=1,且点(2,2)在第一象限,所以θ=π4.故线段AB 的中点的极坐标为⎪⎭⎫⎝⎛422π,.答案:A10.在极坐标系中,若A ⎪⎭⎫ ⎝⎛33π,,B ⎪⎭⎫ ⎝⎛674π,,求△ABO 的面积(O 为极点)为( ) A .2 B .3 C .4D .6解析:由题意可知,在△ABO 中,OA =3,OB =4,∠AOB =7π6-π3=5π6,所以△ABO 的面积为S =12|OA |·|OB |·sin ∠AOB =12×3×4×sin 5π6=12×3×4×12=3.答案:B。
数学:4.1.2《极坐标系(1))课件(新人教选修4-4)

M
O X
(, ) (2) 平面内点的极坐标用_____表示.
(0, ), 可为任意值. 极点的极坐标为_________________
例1. 如图,写出各点的极坐标: 2 A(4,0) 4 5 B(3, ) 4 6 D C(2, 2 ) • C • • B 5 E A D(5, ) 。 • • 6 x O E(4.5, )
F
•
G
4 3
•
5 3
F(6, 4) 3 G(7, 5 ) 3
[变式训练1 ] 在课本P6的图上描下列点:
三、小
结
[1]建立一个极坐标系需要哪些要素 极点;极轴;长度单位;角度单位和它的正方向. [2]极坐标系内一点的极坐标有多少种表达式? 无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ ) 四、课后作业 教材P14-15页5,8,9,10,11 思考: 极坐标系中, 点M的坐标为(-10, ), 则下列各 3 坐标中, 不是M点的坐标的是( ) (A) (10, 4) (B) (-10, - 5) (C) (10, - 2) (D)(10, 2) 3 3 3 3
请说出点M的极坐标的其他表达式 思考:这些极坐标之间有何异同? 极径相同,不同的是极角 思考:这些极角有何关系? 这些极角的始边相同,终边也相同。也就是说它们 是终边相同的角。 π 2kπ+ 4, 本题点M的极坐标统一表达式: 4 O
4
Байду номын сангаас
1.3.2 直线的极坐标方程 课件(人教A选修4-4)

∴两条直线的交点的直角坐标为(0,1), π 化为极坐标为(1,2).
直线的极坐标方程与直角坐标方程的转化及直线与圆的位置 关系的判断是高考模拟的重点内容.2012 年陕西高考以填空题的 形式考查了直线和圆的极坐标方程以及直线与圆的位置关系.
标方程,然后在直角坐标系下研究所要求解的问题,最后再将 直角坐标方程转化为极坐标方程即可.
[通一类] 3.在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线 ρ(cos θ+sin θ)=1 与 ρ(sin θ-cos θ)=1 的交点的极坐标.
解:由 ρ(cos θ+sin θ)=1,得 x+y=1; 由 ρ(sin θ-cos θ)=1,得 y-x=1.
[悟一法]
求直线极坐标方程的步骤: (1)设(ρ,θ)为直线上任一点的极坐标. (2)写出动点满足的几何条件. (3)把上述条件转化为ρ,θ的等式. (4)化简整理.
[通一类] 1.若将例题中的“平行”改为“垂直”,如何求解?
π 解:如图所示,在直线 l 上任意取点 M(ρ,θ),∵A(2,4), π ∴|OH|=2cos 4= 2. 在 Rt△OMH 中, |OH|=|OM|cos θ, ∴ 2=ρcos θ,即 ρcos θ= 2. π ∴过 A(2,4)且垂直于极轴的直线方程为 ρcos θ= 2.
[精讲详析]
本题考查直线的极坐标方程的求法,解题的关
键是通过解直角三角形得到动点 M 的等式.然后转化为关于 ρ, θ 的等式. 如图所示,设 M(ρ,θ)为直线 l 上的任意一点.
过点 M 作 MH⊥x 轴, π ∵A(2,4), π ∴|MH|=2sin 4= 2. 在 Rt△OMH 中,|MH|=|OM|sin θ,即 ρsin θ= 2. π ∴过点 A(2,4)且平行于极轴的直线的极坐标方程为. ρsin θ= 2.
[整理版]高中数学选修4—4(坐标系与参数方程)知识点总结
![[整理版]高中数学选修4—4(坐标系与参数方程)知识点总结](https://img.taocdn.com/s3/m/73936effb9f67c1cfad6195f312b3169a451eac1.png)
坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy yλλϕμμ'=>⎧⎨'=>⎩ 的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数.特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角.4.常见曲线的极坐标方程注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极坐标(高中数学经典问题选编)(高中数学,选修4-4)
高中数学经典问题选编----极坐标
知识点:
1. 极坐标系:点的极坐标与直角坐标的互化。
2. 一般约定,极径是非负的。
3. 极点的极径为0,极角可取任意值。
4. 极直互化:双系的前提;(点/线)的极坐标与直角坐标的互化。
5. 直线和圆的极坐标方程:设点,解三角形。
有需要的同行和小朋友自行收藏。
以下为拓展内容:
5. 圆锥曲线的极坐标方程。
6. 笛卡尔的心形线----一个凄美的爱情故事(以下来自网络,有
删改)。
1650年,斯德哥尔摩的街头,笛卡尔邂逅了18岁的瑞典公主克
里斯汀,这一年,他52岁。
落魄的笛卡尔穿着破破烂烂的衣服,随身带着几本数学书籍,生
性清高的他默默地低头在纸上写写画画,潜心于他的数学世界。
一个宁静的午后,笛卡尔照例坐在街头,沐浴在阳光中研究数学
问题。突然,有人拍了拍他的肩膀,“你在干什么呢?”扭过头,笛
卡尔看到一张年轻秀丽的睑庞,一双清澈的眼睛如湛蓝的湖水,楚楚
动人,长长的睫毛一眨一眨的,期待着他的回应。
她,克里斯汀,瑞典小公主,国王最宠爱的女儿。她蹲下身,拿
过笛卡尔的数学书和草稿纸,和他交谈起来。他发现,这女孩思维敏
捷,对数学有着浓厚兴趣。
几天后,他意外地接到通知,国王聘请他做小公主的数学老师。
满心疑惑的笛卡尔来到皇宫。从远处传来的银铃般的笑声中,他转过
身来,看到了前儿天在街头偶遇的女孩子。
在他悉心指导下,公主的数学突飞猛进,他们之间也变得亲密起
来。笛卡尔向她介绍了他研究的新领域——直角坐标系。通过它,代
数与几何可以结合起来,这就是日后笛卡尔创立的解析几何学的雏形。
克里斯汀走进了奇妙的坐标世界,她对曲线着了迷。每天的形影
不离也使他们爱慕,一段纯粹、美好的爱情悄然萌发。
然而,好景不长,他们的恋情传到了国王的耳朵里。国王大怒将
他放逐回国,而公主被软禁在宫中。
当时,欧洲大陆正在流行黑死病。身体孱弱的笛卡尔回到法国后
染上重病。在生命进入倒计时的那段日子,他日夜思念的还是街头偶
遇的那张温暖的笑脸。他每天坚持写信,盼望着她的回音。然而,这
些信都被国王拦截下来,公主一直没有收到他的任何消息。
在笛卡尔给克里斯汀寄出第十三封信后,他永远地离开了这个世
界。此时,被软禁在宫中的小公主依然徘徊在皇宫的走廊里,思念着
远方的情人。
这最后一封信上没有写一句话,只有一个方程:r=a(1-sinθ)。
今年上高二的一个文科班和理科班,平时收集和提炼了一些资料,
想一个章节一个章节的整理下来,发到这里,以此见证曾经走过的路
和曾经所做的努力。也希望能给同行们提供一些方便,给小朋友们提
供一些参考,当然,更希望得到大家的回应,包括点赞和收藏,批评
和建议。
一路上有你,苦一点也愿意。
