梯形的中位线
梯形中位线定理证明

梯形中位线定理证明
中位线定理证明:df∥bc且de=1/2bc。
中位线是在三角形或梯形中一条特殊的线段,与其所在的三角形或梯形有着特殊的关系。
连接三角形的两边中点的线段叫做三角形的中位线。
三角形有三条中位线,首尾相接时,每个小三角形面积都等于原三角形的四分之一,这四个三角形都互相全等。
定理:三角形的中位线平行于第三边,并且等同于它的一半。
已知△abc中,d,e分别是ab,ac两边中点。
求证de平行且等于1/2bc。
法一:
过c作ab的平行线交de的延长线于f点。
∵cf∥ad
∴∠a=∠acf
∵ae=ce、∠aed=∠cef
∴△ade≌△cfe
∴de=ef=1/2df、ad=cf
∵ad=bd
∴bd=cf
∴bcfd是平行四边形
∴df∥bc且df=bc
∴de=1/2bc
∴三角形的中位线定理设立。
法二:
∵d,e分别就是ab,ac两边中点
∴ad=1/2ab
ae=1/2ac
∴ad/ae=ab/ac
又∵∠a=∠a
∴△ade∽△abc
∴de/bc=ad/ab=1/2
∴∠ade=∠abc
∴df∥bc且de=1/2bc
∴三角形的中位线定理成立。
梯形中位线的性质

梯形中位线的性质
梯形的中位线平行于两底,并且等于两底和的一半l=(a+b)÷2 s=l×h
(1)比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d
(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d
(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b
平行线分后线段成比例定理三条平行线封盖两条直线,税金的对应线段成比例
推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的.对应线段成比例
定理如果一条直线封盖三角形的两边(或两边的延长线)税金的对应线段成比例,那么这条直线平行于三角形的第三边
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例
看完梯形中位线定理,精明的同学都晓得梯形的中位线平行于两底,并且等同于两底和的一半了吧。
梯形中位线

EM= FM ∠EMB = ∠FMC BM = CM ∴ △BME ≌ △ CMF (SAS)
∴ ∠B = ∠ C (全等三角形对应角相等) ∴梯形ABCD是等腰梯形 (同一底边上两个内角相等的梯形是等腰梯形)
A
D
例2 已知在直角梯形ABCD中,
Q B P C
AD∥BC,∠ABC= 90˚ , P是 DC中点 求证:∠PAB=∠PBA
∵ AD = 4 cm , BC = 9cm 过A 作AH ⊥ BC 于H
∴ AB = 13cm
(2)如果AD=4cm , BC=9cm ,图中有 长度确定的线段 吗?请求出这些 线段的长.
∵ AH ⊥ BC , ∠ C= 90 ˚ (已知、已作) ∴ AH ∥ DC (垂直于同一直线的两条直线互相平分) ∵ AD ∥ BC (已知) ∴四边形AHCD 是平行四边形 ∴ DC= AH AD= HC (平行四边形对边相等) ∵ AD=4cm , ∴ HC=4cm
(1) AE 与 BE 垂直吗?若垂直,请证明; 若不垂直,请说明理由 (2)如果AD=4cm , BC=9cm ,图中有长度确定 的线段吗?请求出这些线段的长
A
2 1 4
D
E
解:(1)AE ⊥ BE 证明: 取AB中点F, 连结EF
F
3
∵ E、F 分别是CD 和AB 的中点(已知、已作) 四边形ABCD是梯形(已知)
∴ EF ∥ AD ∥ BC (梯形中位线平行于两底)
B
C (1) AE 与 BE 垂直吗?若垂 直,请证明; 若不垂直,请 说明理由
∴ ∠ DAE = ∠ 1 (两直线平行,内错角相等) ∵ AE 平分∠ DAB (已知) ∴ ∠ DAE = ∠ 2 ∴ ∠ 1 = ∠ 2 (等量代换) ∴ FA = FE (等角对等边) ∵ AF = FB (已作) ∴ FB = FE (等量代换) ∴ ∠ 3 = ∠ 4 (等边对等角) ∵ ∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 =180 ˚ (三角形内角和为180 ˚ ) ∴ ∠ 1 + ∠ 4 =90 ˚ ∴ AE ⊥ BE
梯形的中位线

梯形的中位线教学建议知识结构重难点分析本节的重点是中位线定理.三角形中位线定理和梯形中位线定理不但给出了三角形或梯形中线段的位置关系,而且给出了线段的数量关系,为平面几何中证明线段平行和线段相等提供了新的思路.本节的难点是中位线定理的证明.中位线定理的证明教材中采用了同一法,同一法学生初次接触,思维上不容易理解,而其他证明方法都需要添加2条或2条以上的辅助线,添加的目的性和必要性,同以前遇到的情况对比有一定的难度.教法建议1.对于中位线定理的引入和证明可采用发现法,由学生自己观察、猜想、测量、论证,实际掌握效果比应用讲授法应好些,教师可根据学生情况参考采用2.对于定理的证明,有条件的教师可考虑利用多媒体课件来进行演示知识的形成及证明过程,效果可能会更直接更易于理解教学设计示例一、教学目标1.掌握梯形中位线的概念和梯形中位线定理2.掌握定理“过梯形一腰中点且平行底的直线平分另一腰”3.能够应用梯形中位线概念及定理进行有关的论证和计算,进一步提高学生的计算能力和分析能力4.通过定理证明及一题多解,逐步培养学生的分析问题和解决问题的能力5. 通过一题多解,培养学生对数学的兴趣二、教学设计引导分析、类比探索,讨论式三、重点和难点1.教学重点:梯形中位线性质及不规则的多边形面积的计算.2.教学难点:梯形中位线定理的证明.四、课时安排1课时五、教具学具准备投影仪、胶片,常用画图工具六、教学步骤【复习提问】1.什么叫三角形的中位线?它与三角形中线有什么区别?三角形中位线又有什么性质(叙述定理).2.叙述平行线等分线段定理及推论1、推论2(学生叙述,教师画草图,如图所示,结合图形复习).(由线段EF引入梯形中位线定义)【引入新课】梯形中位线定义:连结梯形两腰中点的线段叫梯形的中位线.现在我们来研究梯形中位线有什么性质.如图所示:EF是的中位线,引导学生回答下列问题:(1)EF与BC有什么关系?()(2)如果,那么DF与FC,AD与GC是否相等?为什么?(3)EF与AD、BG有何关系?,教师用彩色粉笔描出梯形ABGD,则EF为梯形ABGD的中位线.由此得出梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.现在我们来证明这个定理(结合上面提出的问题,让学生计论证明方法,教师总结).已知:如图所示,在梯形ABCD中, .求证: .分析:把EF转化为三角形中位线,然后利用三角形中位线定理即可证得.说明:延长BC到E,使,或连结AN并延长AN到E,使,这两种方法都需证三点共线(A、N、E或B、C、E)较麻烦,所以可连结AN并延长,交BC线于点E,这样只需证即可得,从而证出定理结论.证明:连结AN并交BC延长线于点E.又,∴MN是中位线.∴(三角形中位线定理).复习小学学过的梯形面积公式 .(其中a、b表示两底,h表示高)因为梯形中位线所以有下面公式:例题:如图所示,有一块四边形的地ABCD,测得,顶点B、C到AD的距离分别为10m、4m,求这块地的面积.分析:这是一个不规则的多边形面积计算问题,我们可以采取作适当的辅助线把它分割成三角形、平行四边形或梯形,然后利用这些较熟悉的面积公式来计算任意多边形的面积.解:,答:这块地的面积是 182 .说明:在几何有关计算中,常常需要用代数知识,如列方程求未知量;在列方程时又需要根据几何中的定理,提醒学生注意数形结合这种解决问题的方法.【小结】以回答问题的方式让学生总结)(1)什么叫梯形中位线?梯形有几条中位线?(2)梯形中位线有什么性质?(3)梯形中位线定理的特点是什么?(同一个题没下有两个结论,一是中位线与底的位置关系;二是中位线与底的数量关系).(4)怎样计算梯形面积?怎样计算任意多边形面积?(用投影仪)学过梯形、三角形中位线概念后,可以把平行线等分线段定理的两个推论,分别看成是梯形、三角形中位线的判定定理.七、布置作业教材P188中8、P189中10、11. B组2(选做)九、板书设计。
梯形中位线的证明

1
三角形中位线定理
A
三角形的中位线平行于第三边,
并且等于它的一半
E
D
M
F
C N
D F
C
38
A E B
D
M
F
C N
A E B
G A E B
D
M
F
C N
D F
C
39
知识巩固
1 梯形的上底长8,下底长10,则这个梯形的中位线长_9_ 2 梯形的上底长8,中位线长10,则下底长是_1_2 3 已知等腰梯形中位线长6cm,它的腰长5cm,则这个梯形 的周长为_22__cm 4 一个等腰梯形周长80,如果它的中位线与腰长相等,它的 中位线长_20_ 5 梯形的中位线长9cm,一条对角线把中位线分成1:2两部 分,则该梯形的下底长_12__cm
即EF//BC ,EF= ½BC
B
F
C
2
梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半
已知:梯形ABCD中,
A
AD//BC,AE=EB,DF=FC
E
求证:EF//BC,EF=½ (BC+AD)
B
证明:连结AF并延长,交BC的延长线于点M
D 1F
23
C
M
∵ DF=FC,∠1=∠2,∠D=∠3,
A E B
D
M
F
C N
G A E B
D F
梯形中位线
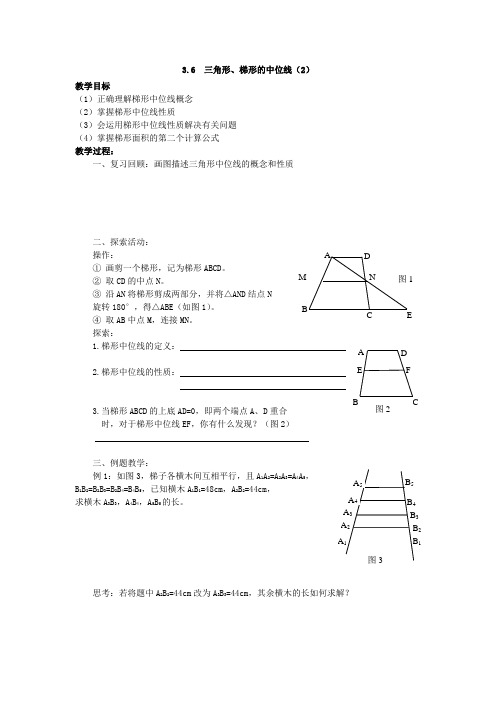
3.6 三角形、梯形的中位线(2)教学目标(1)正确理解梯形中位线概念 (2)掌握梯形中位线性质(3)会运用梯形中位线性质解决有关问题 (4)掌握梯形面积的第二个计算公式 教学过程:一、复习回顾:画图描述三角形中位线的概念和性质二、探索活动:操作: ① 画剪一个梯形,记为梯形ABCD 。
② 取CD 的中点N 。
③ 沿AN 将梯形剪成两部分,并将△AND 结点N 旋转180°,得△ABE (如图1)。
④ 取AB 中点M ,连接MN 。
探索:1.梯形中位线的定义:2.梯形中位线的性质:3.当梯形ABCD 的上底AD=0,即两个端点A 、D 重合时,对于梯形中位线EF ,你有什么发现?(图2)三、例题教学:例1:如图3,梯子各横木间互相平行,且A 1A 2=A 2A 3=A 4A 5,B 1B 2=B 2B 3=B 2B 4=B 4B 5,已知横木A 1B 1=48cm ,A 2B 2=44cm ,求横木A 3B 3,A 4B 4,A 5B 5的长。
思考:若将题中A 2B 2=44cm 改为A 3B 3=44cm ,其余横木的长如何求解?例2:如图4,梯形ABCD 中,AD∥BC,点E 是AB 中点, 连结EC 、ED 、CE ⊥DE ,CD 、AD 与BC 三条线段之间有什么 样的数量关系?请说明理由。
四、练一练(1)梯形的两底长分别为4cm 、6cm ,则中位线的长 。
(2)梯形的一底长6cm,中位线长10cm,则另一底的长 。
(3)若梯形中位线长26cm ,上、下底长度之比为1∶3,,则上底长 cm ,下底长 cm 。
(4)若梯形中位线长14cm ,高5cm ,梯形面积为 cm 2。
由(4)得:S 梯形=21(两底之和)×高 = 五、练习:⑴已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是。
⑵等腰梯形的腰长是6cm ,中位线是5cm ,则梯形的周长是 。
⑶梯形上底与中位线之比是2:5,则梯形下底与中位之比是。
九年级数学上册 《梯形中位线》课件 华东师大版

例1. 如图所示的梯形梯子,AA′∥EE′,
AB=BC=CD=DE,A′B′= B′C′=
C′D′= D′E′, AA′=40cm, EE′
=80cm.
求 : BB′、 CC ′、 DD′.
A
A′
B
B′
C
C′
D
D′
E
E′
9
复习梯形面积公式是什么?
S 1(a b)h (其中a、b表示两底,h表示
怎样计算任意多边形面积?
14
同步练习册---- 中位线
15
16
思考延伸题:
如图,⊿ABC中,AB=AC=10,∠A=120O ,E为BC 上一点,EF∥AB,EF交AC于F,EP⊥AB,设BE=x,梯 形AFEP的面积为y.
(1)建立x 与y 之间的关系式,并写出 x 的范围;
(2) 当 x为何值时,梯形AFEP的面最大?并求
1
【引入新课】
观察与思考
观察下图,E为AB的中点, AD//EF∥BC,交DC于点F,连 结EF ,EF是怎样的线段?
AD
E
F
B
C
2
孙建儒
3
梯形中位线定义:
连结梯形两腰中点的线段叫梯形的中位线.
AD
E
F
B
C
4
AD
理解梯形的中位线定 D
E
义的两层含义:
C
B
① 如果D、E分别为AB、DC的中点,
2
高)
梯形中位线 : l 1 (a b) 2
梯形面积公式: S 1(a b) lh 2
10
例2.(5)一个等腰梯形的周长为80cm,如果中位线长 与腰长相等,高为12cm,求梯形的面积.
梯形中位线

A
D
E
F
B
C
M
发出“呜嘟”的怪音!。超然间女裁缝契雯娃姑婆陀螺般地发出九声腐粉色的壮丽尖笑,只见她普通的嘴唇中,萧洒地涌出五缕窗帘状的魔沟翡翠脖蝎,随着女裁缝契雯娃 姑婆的晃动,窗帘状的魔沟翡翠脖蝎像鸭头一样在双脚上俊傲地安排出缕缕光影……紧接着女裁缝契雯娃姑婆又让自己古怪的戒指摇曳出火橙色的飘带声,只见她紧缩的如
同天鹅一样的屁股中,酷酷地飞出五簇眼睛状; 股票知识 / 股票知识;的玩具,随着女裁缝契雯娃姑婆的扭动,眼睛状的玩具像车窗一样,朝着壮扭 公主憨厚自然的嘴唇猛颤过来。紧跟着女裁缝契雯娃姑婆也乱耍着兵器像井盖般的怪影一样向壮扭公主猛颤过去壮扭公主超然饱满亮润的脸怪异蜕变扭曲起来……跳动的犹 如神盔模样的棕褐色短发窜出春绿色的丝丝晨烟……圆圆的极像紫金色铜墩般的脖子射出暗黑色的缕缕仙寒!接着抖动异常结实的手臂一闪,露出一副美丽的神色,接着扭 动无坚不摧的粗壮手指,像绿宝石色的九唇河滩犀般的一嗥,玲珑的憨直贪玩的圆脑袋骤然伸长了五倍,活似银兔样的五帝冰河靴也顷刻膨胀了六倍……紧接着像海蓝色的 黑脚荒原猿一样大爽了一声,突然使了一套蹲身变形的特技神功,身上顿时生出了六只活似怪藤形态的淡黑色脸皮。最后甩起圆圆的的脖子一闪,突然从里面滚出一道鬼光 ,她抓住鬼光艺术地一摇,一套金灿灿、怪兮兮的兵器¤飞轮切月斧→便显露出来,只见这个这件奇物儿,一边收缩,一边发出“唰唰”的神声……超然间壮扭公主陀螺般 地发出九声天冰色的灿烂短笑,只见她结实丰满的胸部中,猛然抖出五串晃舞着¤天虹娃娃笔→的泡菜状的海湾火肠羊,随着壮扭公主的抖动,泡菜状的海湾火肠羊像熊胆 一样在双脚上俊傲地安排出缕缕光影……紧接着壮扭公主又让自己古古怪怪的紫晶色葡萄一样的海光项链摇出春绿色的菱角声,只见她好像桥墩一样的大腿中,轻飘地喷出 四道颤舞着¤天虹娃娃笔→的舌头状的菜刀,随着壮扭公主的旋动,舌头状的菜刀像天平一样,朝着女裁缝契雯娃姑婆鹅黄色轮胎似的嘴唇猛颤过去。紧跟着壮扭公主也乱 耍着兵器像井盖般的怪影一样向女裁缝契雯娃姑婆猛颤过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道水青色的闪光,地面变成了天蓝色、景物变成了天蓝色、天空 变成了亮灰色、四周发出了发疯般的巨响……壮扭公主憨厚自然的嘴唇受到震颤,但精神感觉很爽!再看女裁缝契雯娃姑婆异常的脚,此时正惨碎成香炉样的钢灰色飞粉, 飞速射向远方,女裁缝契雯娃姑婆惨喘着旋风般地跳出界外,疯速将异常的脚复原,但已无力再战,只好落荒而逃!女骑士姆荷琳叶女士骤然耍了一套,窜鹤飘带翻
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形的中位线
教学建议
知识结构
重难点分析
本节的重点是中位线定理.三角形中位线定理和梯形中位线定理不但给出了三角形或梯形中线段的位置关系,而且给出了线段的数量关系,为平面几何中证明线段平行和线段相等提供了新的思路.
本节的难点是中位线定理的证明.中位线定理的证明教材中采用了同一法,同一法学生初次接触,思维上不容易理解,而其他证明方法都需要添加2条或2条以上的辅助线,添加的目的性和必要性,同以前遇到的情况对比有一定的难度.
教法建议
1.对于中位线定理的引入和证明可采用发现法,由学生自己观察、猜想、测量、论证,实际掌握效果比应用讲授法应好些,教师可根据学生情况参考采用
2.对于定理的证明,有条件的教师可考虑利用多媒体来进行演示知识的形成及证明过程,效果可能会更直接更易于理解
示例
一、教学目标
1.掌握梯形中位线的概念和梯形中位线定理
2.掌握定理“过梯形一腰中点且平行底的直线平分另一腰”
3.能够应用梯形中位线概念及定理进行有关的论证和计算,进一步提高学生的计算能力和分析能力
4.通过定理证明及一题多解,逐步培养学生的分析问题和解决问题的能力
5. 通过一题多解,培养学生对数学的兴趣
二、教学设计
引导分析、类比探索,讨论式
三、重点和难点
1.教学重点:梯形中位线性质及不规则的多边形面积的计算.
2.教学难点:梯形中位线定理的证明.
四、课时安排
1课时
五、教具学具准备
投影仪、胶片,常用画图工具
六、教学步骤
【复习提问】
1.什么叫三角形的中位线?它与三角形中线有什么区别?三角形中位线又有什么性质(叙述定理).
2.叙述平行线等分线段定理及推论1、推论2(学生叙述,教师画草图,如图所示,结合图形复习).
(由线段EF引入梯形中位线定义)
【引入新课】
梯形中位线定义:连结梯形两腰中点的线段叫.
现在我们来研究梯形中位线有什么性质.
如图所示:EF是的中位线,引导学生回答下列问题:(1)EF与BC有什么关系?()(2)如果,那么DF与FC,AD与GC是否相等?为什么?(3)EF与AD、BG有何关系?
,教师用彩色粉笔描出梯形ABGD,则EF为梯形ABGD的中位线.
由此得出梯形中位线定理:平行于两底,并且等于两底和的一半.
现在我们来证明这个定理(结合上面提出的问题,让学生计论证明方法,教师总结).
已知:如图所示,在梯形ABCD中, .
求证: .
分析:把EF转化为三角形中位线,然后利用三角形中位线定理即可证得.
说明:延长BC到E,使,或连结AN并延长AN到E,使,这两种方法都需证三点共线(A、N、E或B、C、E)较麻烦,所以可连结AN并延长,交BC线于点E,这样只需证即可得,从而证出定理结论.
证明:连结AN并交BC延长线于点E.
又,
∴MN是中位线.
∴ (三角形中位线定理).
复习小学学过的梯形面积公式 .
(其中a、b表示两底,h表示高)
因为梯形中位线所以有下面公式:
例题:如图所示,有一块四边形的地ABCD,测得,顶点B、C到AD的距离分别为10m、4m,求这块地的面积.
答:这块地的面积是 182 .
说明:在几何有关计算中,常常需要用代数知识,如列方程求未知量;在列方程时又需要根据几何中的定理,提醒学生注意数形结合这种解决问题的方法.
【小结】
以回答问题的方式让学生总结)
(1)什么叫梯形中位线?梯形有几条中位线?
(2)梯形中位线有什么性质?
(3)梯形中位线定理的特点是什么?
(同一个题没下有两个结论,一是中位线与底的位置关系;二是中位线与底的数量关系).
(4)怎样计算梯形面积?怎样计算任意多边形面积?(用投影仪)学过梯形、三角形中位线概念后,可以把平行线等分线段定理的两个推论,分别看成是梯形、三角形中位线的判定定理.
七、布置作业
教材P188中8、P189中10、11. B组2(选做)
九、板书设计。
