《信号与系统》试题及答案
信号与系统复习试题(含答案)

76.某二阶LTI系统的频率响应H (j)
A.y2y3y
B。y3y2yf2
D。y3y2yf
H(s)的共轭极点在虚轴上,则它的
2,-1,H ()1,则系统函数H(s)为(
C。(s1)(s2)
(t)的傅氏变换是(
B。j(
D。j(2
A.系统在(t)作用下的全响应
C.系统单位阶跃响应的导数
6。对于一个三阶常系数线性微分方程描述的连续时间系统进行系统的时域模拟时,所需积
分器数目最少是__3个_____个。
7。一线性时不变连续因果系统是稳定系统的充分且必要条件是系统函数的极点位于S平面
的___左半平面_______。
8.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为
其中x(0)是初始状态,
f(t)为激励,y(t)为全响应,试回答该系统是否是线性的?[答案:非线性]
2.y'(t)sinty(t)f(t)试判断该微分方程表示的系统是线性的还是非线性的,
是时变的还是非时变的?[答案:线性时变的]
3.已知有限频带信号f(t)的最高频率为100Hz,若对f(2t)*f(3t)进行时域取样,
B。f(t)f(t8)
12
C.f(t)f(t8)
D。f(t3)f(t1)
69.已知一连续系统在输入f(t)的作用下的零状态响应为yzs(t)f(4t),则该系统为()
70.已知f(t)是周期为T的函数,f(t)-f (t
T)的傅里叶级数中,只可能有(
71.一个线性时不变的连续时间系统,其在某激励信号作用下的自由响应为(e
h(t)=(1et)(t),则其系统函数
15.已知一信号f(t)的频谱F(j)的带宽为,则f(2t)的频谱的带宽为
信号与系统试题附答案
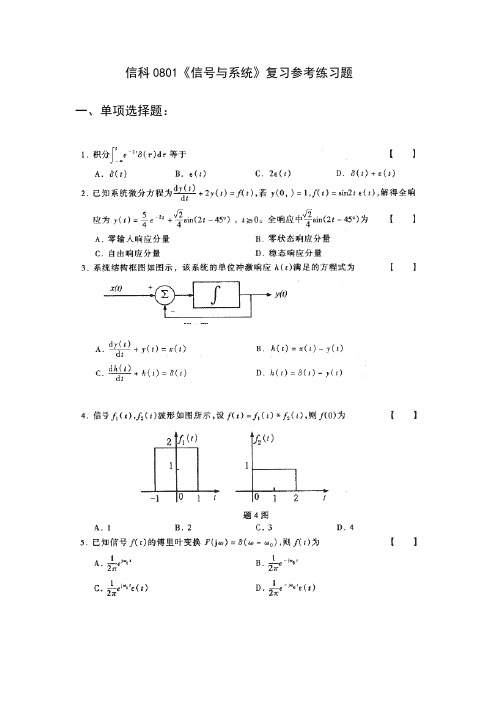
信科0801《信号与系统》复习参考练习题一、单项选择题:14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。
200 rad /s C 。
100 rad /s D 。
50 rad /sf如下图(a)所示,其反转右移的信号f1(t) 是()15、已知信号)(tf如下图所示,其表达式是()16、已知信号)(1tA、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是()A、f(-t+1)B、f(t+1)C、f(-2t+1)D、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是( )19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( )A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( )A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号 23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δD.)()0(t f δ 24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f 25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)-ε(t -2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+,则其2个特征根为( )A 。
信号与系统题库答案(完整版)

1 −2( s +1) 1 −2 s e (2) e s +1 s +1 e2 2cos 2 + s sin 2 − s (3) (4) ie s +1 s2 + 4 1 ⎛ 1 1⎞ ⎛ 1 2⎞ (5) 2 [1 − (1 + s )e − s ]e − s (6) ⎜ 2 + ⎟ e − s − ⎜ 2 + ⎟ e −2 s s s⎠ s⎠ ⎝s ⎝s (1)
[3]解 A 点: FA (ω ) =
1 [G1 (ω + ω0 ) + G1 (ω − ω0 )] 2 j B 点: FB (ω ) = [G1 (ω + ω0 ) − G2 (ω − ω0 )] 2 1 C 点: FC (ω ) = [ FA (ω ) + FB (ω )] ⋅ π [δ (ω + ω0 ) + δ (ω − ω0 )] 2π 1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2
1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2
信号与系统试题及答案

信号与系统试题及答案一、选择题1. 信号f(t)=cos(2πt+π/4)是()。
- A. 偶函数- B. 奇函数- C. 周期函数- D. 非周期函数答案:C2. 系统分析中,如果输入信号为x(t),输出信号为y(t),那么系统的冲激响应h(t)与输出信号y(t)的关系是()。
- A. y(t) = x(t) * h(t)- B. y(t) = ∫x(t)h(t)dt- C. y(t) = x(t) + h(t)- D. y(t) = x(t) - h(t)答案:B3. 一个线性时不变(LTI)系统,其频率响应H(ω)是输入信号X(ω)的傅里叶变换与系统冲激响应的乘积,那么该系统的逆傅里叶变换是()。
- A. X(ω) * H(ω)- B. X(ω) / H(ω)- C. 1 / (X(ω) * H(ω))- D. H(ω) / X(ω)答案:A二、简答题1. 解释什么是单位冲激函数,并说明它在信号与系统分析中的作用。
答案:单位冲激函数是一种理想化的信号,其在t=0时的值为1,其他时间的值为0。
数学上通常表示为δ(t)。
在信号与系统分析中,单位冲激函数是系统冲激响应分析的基础,它允许我们通过将输入信号分解为单位冲激函数的叠加来分析系统的响应。
单位冲激函数的傅里叶变换是常数1,这使得它在频域分析中也非常重要。
2. 描述连续时间信号的傅里叶变换及其物理意义。
答案:连续时间信号的傅里叶变换是一种数学变换,它将时域信号转换为频域信号。
对于一个连续时间信号x(t),其傅里叶变换X(ω)可以表示为:\[ X(ω) = \int_{-\infty}^{\infty} x(t) e^{-jωt} dt \] 其中,e^(-jωt)是指数形式的复指数函数。
物理意义上,傅里叶变换揭示了信号的频率成分,即信号由哪些频率的正弦波和余弦波组成。
通过分析X(ω),我们可以了解信号的频率特性,这对于信号处理和系统分析至关重要。
信号和系统试题及答案

信号和系统试题及答案一、选择题(每题4分,共20分)1. 信号的频谱分析中,傅里叶变换的物理意义是什么?A. 信号的时域表示B. 信号的频域表示C. 信号的相位信息D. 信号的幅度信息答案:B2. 在线性时不变系统中,系统的输出与输入的关系是什么?A. 线性关系B. 非线性关系C. 时变关系D. 随机关系答案:A3. 下列哪个函数不是周期函数?A. sin(t)B. cos(2t)C. e^(-t)D. cos(2πt)答案:C4. 系统稳定性的判定可以通过什么方法?A. 奈奎斯特准则B. 伯德图C. 相位裕度D. 所有以上答案:D5. 系统函数H(s)的零点和极点分别代表什么?A. 系统输入和输出B. 系统稳定性和不稳定性C. 系统增益和衰减D. 系统频率响应答案:B二、填空题(每题4分,共20分)1. 连续时间信号的傅里叶变换定义为:X(jω) = ____________。
答案:∫x(t)e^(-jωt)dt2. 如果一个系统的冲激响应h(t)是因果的,则系统的零状态响应y(t)与输入x(t)的关系为:y(t) = ____________。
答案:∫h(t-τ)x(τ)dτ3. 一个线性时不变系统的特性可以用其系统函数H(s)来描述,其中s 是复频域变量,代表的是 ____________。
答案:拉普拉斯变换4. 如果一个系统的频率响应H(jω)在ω=ω0处有极点,则在时域中对应的响应h(t)将具有 ____________。
答案:振荡特性5. 系统的因果性意味着系统的输出不会在输入之前出现,这可以用系统的冲激响应h(t)满足的条件来表示:h(t) = ____________。
答案:0,t < 0三、简答题(每题10分,共30分)1. 请简述傅里叶级数与傅里叶变换的区别。
答案:傅里叶级数适用于周期信号,是将周期信号分解为正弦和余弦函数的和,而傅里叶变换适用于非周期信号,是将信号分解为复指数函数的积分。
2022年《信号与系统》试卷

《信号与系统》卷子〔A 卷〕一、填空题〔每空1分,共18分〕1.假设)()(s F t f ↔,则↔)3(t F 。
2.ℒ()n t t ε⎡⎤=⎣⎦,其收敛域为 。
3.()(21)f t t ε=-的拉氏变换)(s F = ,其收敛域为 。
4.利用拉氏变换的初、终值定理,可以不经反变换计算,直接由)(s F 决定出()+o f 及)(∞f 来。
今已知)3)(2(3)(+++=s s s s s F ,[]Re 0s > 则)0(+f ,)(∞f = 。
5.已知ℒ[]022()(1)f t s ωω=++,Re[]1s >-,则()F j ω=ℱ[()]f t = 。
6.已知ℒ0220[()](1)f t s ωω=-+,Re[]1s >,则()F j ω=ℱ[()]f t = 。
7.已知()[3(1)](1)t f t e Sin t t ε-=--,试写出其拉氏变换()F s 的解析式。
即()F s = 。
8.对连续时间信号进行均匀冲激取样后,就得到 时间信号。
9.在LTI 离散系统分析中, 变换的作用类似于连续系统分析中的拉普拉斯变换。
10.Z 变换能把描述离散系统的 方程变换为代数方程。
11.ℒ 0(3)k t k δ∞=⎡⎤-=⎢⎥⎣⎦∑ 。
12.已知()()f t F s ↔,Re[]s α>,则↔--)1()1(t t f e t ε ,其收敛域为 。
13.已知22()(1)sse F s s ω-=++,Re[]1s >-,则=)(t f 。
14.单位样值函数)(k δ的z 变换是 。
二、单项选择题〔在每题的备选答案中,选出一个正确答案,并将正确答案的序号填在括号内。
每题1分,共8分〕 1.转移函数为327()56sH s s s s=++的系统,有〔 〕极点。
A .0个 B .1个 C .2个 D .3个 2.假设11)(1+↔s t f ,Re[]1s >-;)2)(1(1)(2++↔s s t f ,Re[]1s >-,则[]12()()()y t f t f t =-的拉氏变换()Y s 的收敛区是〔 〕。
(完整版)《信号与系统》期末试卷与答案

《信号与系统》期末试卷A 卷班级: 学号:__________ 姓名:________ _ 成绩:_____________一. 选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是 D 。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint),该系统是 C 。
A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t,该系统是 A 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是 D 。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω,,j X ,则x(t)为 B 。
A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为 A 。
A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n]奇部的傅立叶变换为C 。
A. )}(Re{ωj eX j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 D 。
A. 500 B. 1000 C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x e t g t=,其傅立叶变换)(ωj G 收敛,则x(t)是 C 。
信号与系统期末考试试卷(有详细答案).doc

格式《信号与系统》考试试卷(时间 120 分钟)院 / 系专业姓名学号题号一二三四五六七总分得分一、填空题(每小题 2 分,共 20 分)得分1.系统的激励是 e(t) ,响应为 r(t) ,若满足de(t)r ( t) ,则该系统为线性、时不变、因果。
dt(是否线性、时不变、因果?)2 的值为 5。
2.求积分 (t1)(t2)dt3.当信号是脉冲信号f(t)时,其低频分量主要影响脉冲的顶部,其高频分量主要影响脉冲的跳变沿。
4.若信号f(t)的最高频率是2kHz,则 f(2t)的乃奎斯特抽样频率为8kHz。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为一常数相频特性为 _一过原点的直线(群时延)。
6.系统阶跃响应的上升时间和系统的截止频率成反比。
.若信号的F(s)=3s j37。
,求该信号的 F ( j)(s+4)(s+2) (j+4)(j+2)8.为使LTI 连续系统是稳定的,其系统函数H(s ) 的极点必须在S 平面的左半平面。
1。
9.已知信号的频谱函数是0)()F(( ,则其时间信号f(t)为0j)sin(t)js110.若信号 f(t)的F ( s ) ,则其初始值f(0)1。
2(s1 )得分二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题 2 分,共 10 分)《信号与系统》试卷第1页共 7页专业资料整理格式1.单位冲激函数总是满足 ( t )( t ) (√)2.满足绝对可积条件 f ( t ) dt 的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
(×)3.非周期信号的脉冲宽度越小,其频带宽度越宽。
(√)4.连续 LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
(√)5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
(×)得分三、计算分析题(1、 3、 4、 5 题每题 10 分, 2 题 5 分,6 题15 分,共 60 分)t 10t11.信号f(t)2eu(t) ,1,信号 f ,试求 f 1 (t)*f 2 (t)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统》试题及答案2012 年度教学质量综合评估测验卷《信号与系统》试题 题组::1、开课学院:信息工程学院学院 题组2、:题纸上。
电子3、类适专用业班级:信息工程学院通信工程专业及 电子4、类在专答业写所要求填 卷面题型及分值:)题 答 不 内 线 封 密名姓研12组0 分钟,所有答案均写在答 发两张答题纸上认真填 。
总总分二 三 四 五 六 七 八 九 十100 20 20 60一、选择题(每小题 2 分,共 10小题。
每一小题仅有一个选项是正确的。
共计 20 分)列说法不正确的是( 一般周期信号为功率信号。
时限信号 (仅在有限时间区间不为零的非周期信号 )为能量信号。
ε(t)是功率信号; 1、 A 、 B 、 C 、)。
D 、 e t 为能量信号 列关于冲激函数性质的表达式不正确的是( 2、 A 、 C 、 3、 A 、 4、 f (t) (t) f (0) (t)H(s)B、(at))d (t)D 、 1ta(-t)(t)(s2s 1()s (s 2)2),属于其极点的是(B 、2C 、 )。
1 If f1(t) ←→ F1(j ω), f2(t) ←→ F2(j ω) A 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) *b F2(j ω) ] B 、[a f1(t) + b f2(t) ] ←→ [aF1(j ω) - b F2(j ω) ] C 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) + b F2(j ω) ] D 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) /b F2(j ω) ] 5、下列说法不正确的是( )。
A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当趋于 0。
Then[ D 、-2k →∞时,响应均B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。
C 、H(z) 在单位圆上的高阶极点或单位圆外的极点, 其所对应的响应序列都是递 增的。
即当 k →∞时,响应均趋于∞。
D 、 H(z)的零点在单位圆内所对应的响应序列为衰减的。
即当 k →∞时,响应均 趋于 0。
本试卷共 4 页,本页为第 1页6、函数 f(t) 的图像如图所示, f(t) 为()A 、偶函数 C 、奇谐函数 7、系统的幅频特性 |H(jω)|和相频特性 如图 (a)(b)所示,则下列信号通过 该系统时,不产生失真的是(A 、 f(t) = cos(2t) + cos(4t)B 、 f(t) = sin(2t) + sin(4t)C 、 f(t) = sin2(4t)D 、 f(t) = cos2(4t)+ sin(2t)8、已知某 LTI 连续系统当激励为 f (t)时,系统的冲击响应为 h(t) ,零状态响应为 y zs (t) ,零输入响应为 y zi (t ) ,全响应为y 1(t) 。
若初始状态不变时,而激励 为2f(t) 时,系统的全响应 y 3(t)为()。
A 、y zi (t) 2y zs (t)B 、y zi (t) 2f(t)C 、4y zs (t)D 、4y zi (t)、设有一个离散反馈系统,其系统函数为:H(z)zz 问若要使该系2(1 k) ,统稳定,常数应 k 该满足的条件是()。
、0.5 k 1.5 B 、 k 0.5C、 k 1.5D 、k0、已知信号 f 1(t) 2[ (t 2) (t)](t 2)[ (t) (t 2)]1B 、奇函数D 、都不是 (b)) -10 (a)10则f(t) f(1 2t)[ (t 2) (t 1)]的波形是()s 2 2有两个极点,则 x(t)是 双边信号)。
选填:左边信号、右边信号或者23z 22z 23z 2 (1 z 2 ,则 x( n)18、无失真传输系统 r(t) 2e(t 3 ,其冲激响应为 h(t)19、为使 LTI 连续系统是稳定的,其系统函数 H( s)的极点必须在 的信号 f 1(t) 2e t u(t),信号 f 2(t )1,1,11、信号 f (t) 、填空题(每小题 sin( 4πt) 12、求积分 2 分,共 10 小题,共 20 分) cos( πt) 3 的基本周期是 (t 2 1) (t 2)dt 的值为 本试卷共 4 页,本页为第 2页13、已知信号的频谱函数是 F ( j ) ( 0)为 ,则其时间信号 f(t) 14、 为 若 信 号 f(t) 的 最 高 频 率 是 2kHz , 则 f( 2t) 的 乃 奎 斯 特 抽 样 频 率 15、设 x(t)绝对可积,其拉普拉斯变换 X(s)为有理拉氏变换, X(s)在 s1 2,16、信号 f (t)(t 1)u(t) 的拉氏变换为0t 其他1,试求 f 1(t )* f 2(t )。
X(z)17、已知S 平面系 统的激 励是 e(t ),响应为 r(t ), 为 。
(是否线性、时不变、三、综合题( 60 分) 21、(本题 10 分)20、 因果?若满足r(t ) de d (t t),则该系统22、(本题10 分)若连续信号f(t ) 的波形和频谱如下图所示,抽样脉冲为冲激抽样T(t ) (t nT s )。
n(1)求抽样脉冲的频谱; (3 分)(2)求连续信号 f ( t )经过冲激抽样后f s(t )的频谱F s( );(5分)(3)画出F s( )的示意图,说明若从f s(t )无失真还原f(t),冲激抽样的T s应该满足什么条件?( 2 分)本试卷共 4 页,本页为第 3 页23、(本题10 分)电路如图所示,写出电压转移函数H(w) V2(w),为得到无失真传输,元件参V1(w)数R1,R2,C1,C2 应满足什么关系?24、(本题10 分)1已知RLC 电路 ( 图8-2 ) 中, ,R 3 ,L 1H,C 1F ,初始条件21,v c '(0 ) 2 ,v i (t )为输入,试求( 1)以v c (t)为响应的微分方程;(2) 25、(本题10 分) 若离散系统的差分方程为v c (0 )v i(t) e 3t u(t) 时,确定v c(t)13、某离散系统差分方程为 y(n 2) 3y(n 1) 2y(n) x(n 1) 2x(n), 系统初始条 件为 y(0) 1, y( 1) 1,输入激励 x(n) 为单位阶跃函数,试求系统的零输入响 应儿 y zi (n),零状态响应 y zs (n)和全响应 y(n) ,并画出该系统的模拟框图。
本试卷共 4 页,本页为第 4页评卷答案:题仅有一个选项是正确的。
共计 30 分)5、D 10、B填空题(每小题 2分,共 10小题,共 20分) 12、1sin( 0t) j14、8kHz 15、双边信号3 y(n) y(n 1)4(1)求系统函数和单位样值响应; (3)画出系统的零、极点分布图; 26、(本题 10 分)18 y(n(2) (4)12) x(n) 3x(n 1) 讨论此因果系统的收敛域和稳定性; 定性地画出幅频响应特性曲线;、选择题(每小题 3 分,共 10 小题。
每一小 1、 2、B 3、B4、6、 7、C8、A 9、 11、 24s116、s s21( 0) 17、(n) 5u(n) 7 2 n u( n 1) 18、2 (t 1)19、20、21、左半平面线性、时不变、因果综合题(60 分)本题10 分)解法一:当t 0 时,f1(t )* t f1(t)* f2(t) 2e (t当1 t 0时,f1(t)* f2(t)02e12e (t )df2(t )=0)d 2 2e t当t 1时,解法二:f1(t)* f2(t) 2e t(e 1)L[ f1(t)* f2(t)]2 s 2s22 (1 e s) s 2 s2 2 s( )e ss s 22s(s 2)2ess(s 2)f1(t)* f2(t) 2u(t) 2e t u(t) 2u(t 1) 1t2e1 t u(t 1)22、本题10 分)解:1)T(t) (t nT sF[ T (t)] 2 F n ( n ),所以抽样脉冲的频谱F n T1s 。
s2)因为f s (t) f (t) (t),由频域抽样定理得到:1F[ f s (t)] F[ f (t) T (t)] 23F( )*F s ( )1TsOmF s( )的频谱是 F( )的频谱以 s为周期重复, 重复过1程中被 Ts所加权,若从f s (t )无失真还原 f(t),冲激其幅率特性为 122 2wR21C21抽样的 Ts应该满足若23、(本题 10 分) 解:电压转移函数11 / R2 jwC 2 111 / R 1 jwC 1 1 / R2 jwC 21jwH (w) V V 12((w w )) C 1C 1 C2 jwR 1C 1 R 1 R 2 R 1 R 2 C 1 C 2s 2 m , T sm。
1/ R 1 jwC 11/ R 1 1/ R 2 jw(C 1 C 2)其相频特性( w ) arctan R 1C 1w arctanR 1R2 C 1 C 2wR 1 R 2若信号无失真传输,直线,现令 (w)=0, 相频特性必为过原点的一条则有 1F ( n s ) T s n3) F s ( )的示意图如下H ( w)1R 1C 1w R 1R 2 C 1 C 2R 1 R 2R 1C 1 R 2C 2 常数C 1H(w)=C 1 C 2=常数,此时可知满足无失真传输检验 条件。
24、(本题 10 分)解:(1)以 v c(t)为响应电压列回路电压方程Cdv c (t ) Cdt回路电流为L di(t) LC dv c (t) L dt LCdt 2RC dv c (t) vc (t) LC d v c 2(t ) vi(t) dt c dt2 ii(t)回路电压为d v c 2(t ) 3dv c (t) 2vc(t) 2vi (t)dt 2 dtc i (2)先求零输入响应 特征方程 所以a 2 3a v zi (t)2 0,特征根a 1 1C 1e t C 2e 2ta 2 2C 1 C 2C 1 2C 2 21解得 C 14,又 所以 v zi(t)(3)求零状态响应 零初始条件下对微分方程两端取拉氏变换 s 2V c(s) 3sV c(s) 2V c(s) 2V i(s)H (s) V c (s) 2V i (s) s 2 3s 2C 2 34e 3e2tu(t)所以V i (s)s32 1 2 1V czs (s) H (s)V i (s) (s 1)(s 2)(s 3)v czs (t) 1[V czs (s)] [e t 2e 2t e 3t ]u(t) v (t) (5e t 5e 2t e 3t )u(t )c25、(本题 10 分)解:(1)利用 Z 变换的性质可得系统函数为:位样值响应为h(n) [130 (12)n 73(41)n ]u(n)3 2 3 41(2)因果系统 z 变换存在的收敛域是 z2,由于 H (z)的两个极点都在 z 平面的单位圆内,所以该 系统是稳定的。
