需求区间型运输问题的模糊优化模型
城市物流配送方案优化模型_数学建模
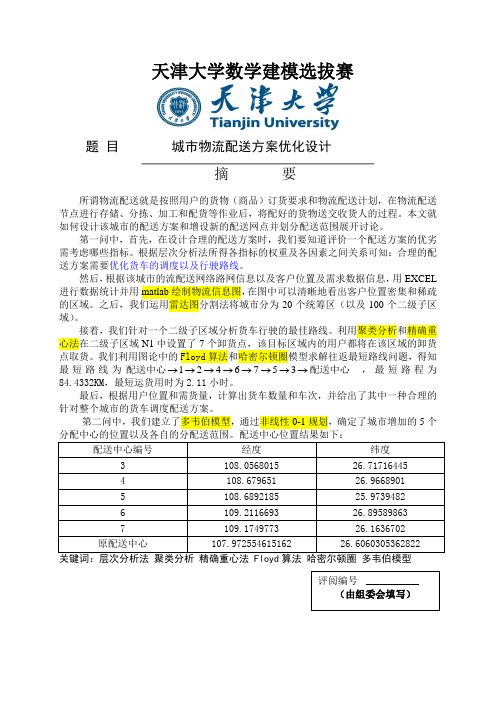
天津大学数学建模选拔赛题目城市物流配送方案优化设计摘要所谓物流配送就是按照用户的货物(商品)订货要求和物流配送计划,在物流配送节点进行存储、分拣、加工和配货等作业后,将配好的货物送交收货人的过程。
本文就如何设计该城市的配送方案和增设新的配送网点并划分配送范围展开讨论。
第一问中,首先,在设计合理的配送方案时,我们要知道评价一个配送方案的优劣需考虑哪些指标。
根据层次分析法所得各指标的权重及各因素之间关系可知:合理的配送方案需要优化货车的调度以及行驶路线。
然后,根据该城市的流配送网络路网信息以及客户位置及需求数据信息,用EXCEL 进行数据统计并用matlab绘制物流信息图,在图中可以清晰地看出客户位置密集和稀疏的区域。
之后,我们运用雷达图分割法将城市分为20个统筹区(以及100个二级子区域)。
接着,我们针对一个二级子区域分析货车行驶的最佳路线。
利用聚类分析和精确重心法在二级子区域N1中设置了7个卸货点,该目标区域内的用户都将在该区域的卸货点取货。
我们利用图论中的Floyd算法和哈密尔顿圈模型求解往返最短路线问题,得知最短路线为1246753配送中心配送中心,最短路程为→→→→→→→→84.4332KM,最短运货用时为2.11小时。
最后,根据用户位置和需货量,计算出货车数量和车次,并给出了其中一种合理的针对整个城市的货车调度配送方案。
第二问中,我们建立了多韦伯模型,通过非线性0-1规划,确定了城市增加的5个配送中心编号经度纬度3 108.0568015 26.717164454 108.679651 26.96689015 108.6892185 25.97394826 109.2116693 26.895898637 109.1749773 26.1636702原配送中心107.972554615162 26.6060305362822评阅编号(由组委会填写)一.问题重述配送是指在经济合理区域范围内,根据客户要求,对物品进行拣选、加工、包装、分割、组配等作业,并按时送达指定地点的物流活动,即按用户定货要求,在配送中心或其它物流结点进行货物配备,并以最合理方式送交用户。
基于模糊需求的灾后应急救援物资运输模型

基于模糊需求的灾后应急救援物资运输模型
邓先明;汪传旭
【期刊名称】《上海海事大学学报》
【年(卷),期】2009(030)002
【摘要】为研究地震发生后应急救援物资的运输问题,根据救援车辆从1个应急物资救援中心到多个受灾点的情况,运用模糊数学的可能性理论,建立基于模糊需求的带有单边硬时间窗的应急运输车辆路径优化模型.该模型以救援车辆的运输时间和在受灾点的救援时间最短为目的,利用节约算法对算例求解.具体算例表明,该模型具有一定的实用价值.
【总页数】6页(P72-77)
【作者】邓先明;汪传旭
【作者单位】上海海事大学经济管理学院,上海200135;上海海事大学经济管理学院,上海200135
【正文语种】中文
【中图分类】F252;F511.31;F512.3
【相关文献】
1.基于不确定需求的灾后应急救灾网络规划模型与算法 [J], 张玲;王晶;张敏
2.一类新的救援物资运输模型的求解 [J], 董丽;周强;张德扬
3.基于区间直觉模糊集和愿景效用函数的应急救援物资车辆运输路线优选 [J], 刘洲; 雍歧东; 胡道达; 李阳超; 郭湛
4.基于生存概率函数的救援物资运输模型 [J], 俞武扬
5.大规模应急救援物资运输模型的构建与求解 [J], 缪成;许维胜;吴启迪
因版权原因,仅展示原文概要,查看原文内容请购买。
一类需求不确定闭环物流系统的模糊规划模型与仿真

中国博 士后科学基金项 目( 目编号 :0 84 0 7 ) 项 20 0 4 10
作 者 简 介 : 家 旺 ( 96一) 男 , 西 九 江人 , 教 授 , 徐 16 , 江 副 主要 研 究 方 向 : 流 与 供 应链 管 理 , 物 E—ma : c87 2 @ yho tm.n i cb6 3 1 a o .o c 。 l
在 图 1所 示 的 闭环 物 流 系 统运 作 过 程 中 , 顾 客 的需求 是 不确 定 的 。 般情 况下 , 一 不确 定 性 可用
一
c) {
,iT T 2 C C ) < ≤ (
0, TC > TC
其 中 ,C i和 T 应 满 足 T T C C。 T ≤ ≤ C
T , C 它们 是 决 策者 根 据实 际情 况 给 出 的总成 本
个 区间来 表示 , 了分 析方 便 , 为 在此将 顾 客 的不
确定 性需 求 C 的波 动 范 围描 述 为 [ d , d d C C +
A d ] 其 中 , d 是 已知 的非 负常 数 , C 的 C 。 AC 为 d 伸缩 度 , 标志 顾客 需 求 的不 确 定 性 程 度 。 AC 令 d =p ×C ¨通过 改 变 P的值 来 表示 不 同的伸 缩 % d
的总 费用 。 为 了建 立 系 统运 作 的模 糊 规划 模 型 , 以上 将
的 目标模 糊化 后得 旧 标 的隶 属 函数 :
1, TC ≤ TC i
2… T r, T = ; ) 段f , , — )且∑ 。 1( 阶 顾客, - : 7 7 处
的 回收率 为 。
2 模 型
8 2
沈 阳 航 空 航 天 大 学 学 报
考虑模糊需求的多式联运路径优化

第42卷第3期2018年6月北京交通大学学报JO U R N A L O F B E IJIN G JIA O T O N G U N IV E R S rrYVol.4 2 No.3Jun. 2018文章编号:1673-0291 (2018)03-0023-07 D O I: 10.1 1860/j.issn.l 673-029 1.2018.03.004考虑模糊需求的多式联运路径优化于雪峤1a,郎茂祥1a1b,王伟哲1a,于潇2(1.北京交通大学a.交通运输学院城市交通复杂系统理论与技术教育部重点实验室,北京100044;2.中国铁道科学研究院集团有限公司通信信号研究所,北京100081)摘要:多式联运可有效降低物流成本,提高物流效率.本文构建了基于运量不确定的多式联运网 络规划,以节点作业时间窗和运输时限客户满意度为约束,建立了以总费用最低为目标的多式联运 路径优化模型,从运输路径和运输方式两个维度选择广义最短路径.应用Lingo 12.0实现模型的求 解,实验结果表明了多式联运相较单一运输方式在运输时间与费用上的优越性,并应用灵敏度分析 法,对比了仅考虑运输时限约束时客户满意度的变化,展示了运量的不确定性及运输弧与节点能力 对路径规划产生的影响,揭示了客户满意度、网络能力、运输路径与费用等因素的相互关系,验证了 所建模型的合理性.关键词:综合交通运输;路径规划;模糊需求;时间窗中图分类号:U116.2 文献标志码:AMultimodal transportation routing optimizationconsidering fuzzy demandsYU Xueqiao'a,L A N G M ao xia n g la'lb,W ANG Weizhela,YU Xiao2(1 a.School of Traffic an d T ran sp o rtatio n,lb. M OE Key Laboratory for U rban T'ransportation Com plex SystemTheory and T echnology,Beijing Jiaotong U niversity,Beijing 100044,C hina;2.Signal & Com m unication research institute Corporation L im ited,China Academy of Railway Sciences Corporation L im ited,Beijing 100081 »China) Abstract:The analysis of optimized multimodal transportation routing can contribute to effectively reduce the cost of transportation and enhance the efficiency of logistic management.This paper focuses on building an optimized multimodal transportation routing model with time windows?aiming to minimize the total expense and find the shortest route from the dimension of transportation route and mode.With the implementation of Lingo 12.0 tato the model analysis process,the results show the superiority of multimodal transportation compared with single transportation mode in transportation time and c ost.The sensitivity analysis method is applied to compare the change of customer satisfaction only when the transport time constraint is taken into account.Also 收稿日期=2017-01-20;修回日期:2018-01-02基金项目:国家重点研发计划(2016YFE0201700)国家自然科学基金(71390332-3)中国铁路总公司科技研究开发计划课题(2016X007-J) Foundation item s:National K e y R&D Program of China(2016YFE0201700);NationalNatural ScienceFoundationof China(71390332-3);Science andTechnologyResearch andDevelopment Program of ChinaRailw ay(20丄6X007-J)第一作者:于雪峤(990 —),男,黑龙江哈尔滨人,博士生.研究方向为运输组织优化.email: yuxueqiao@.通信作者:郎茂祥(9 69 —),男,山东聊城人,教授,博士,博士生导师.email: nixlang@.引用格式:于雪峤•郎茂祥.王伟哲•等.考虑模糊需求的多式联运路径优化方法北京交通大学学报.2018, 42(3):23-29.YU Xueqiao. LANG Maoxiang,WANG Weizhe.et ai.Muitimodai transportation routing optimization considering fuzzy dem an dsL J J. .Journal o f Beijing Jia o to n g U niversity,2018, 42 (. 3) : 23 — 29. (. in C'hinese)24北京交通大学学报第42卷it shows the influence of uncertainty of demand ? transportation arc and node capability on routing planning , which reveals the correlation between factors such as customer's satisfaction rating , transportation route and the expense spent , and the model has been proved feasible .Keyword s : multimodal transportation ; routing planning ; fuzzy demands ; time window作为控制产品成本的有效手段,多式联运路径 规划问题受到了运输供需双方的广泛关注,旨在从 路径规划的角度提出多式联运服务网络运营优化的 对策与措施,为提高多式联运服务网络的运营效率 和服务质量提供方法支撑[l ].国内外大多数对于集装箱多式联运路径规划问 题的研究以优化建模的方法展开,主要从优化对象 (单商品流规划与多商品流规划)、运输服务模式(单 服务模式与多服务模式)、求解策略(精确求解算法 与启发式求解算法)等方面探讨[2].文献[3]构建了 基于多式联运网络的模型,并设计了启发式算法对 模型求解,提供了可操作性的优化方法;文献[4]建 立了时间和费用最小的双目标的优化模型,在规划 多式联运路径时也考虑了客户对运输时效性的需 求,通过帕累托最优求得最优解,从多式联运经营人 角度出发,得到了满足客户需求下的广义费用最短 路径;文献[5 ]从实现总成本最小化的原则出发,从 定量角度分析了多式联运系统的合理组织;文献[6 ] 等将减少运输过程中的C 〇2排放量和污染性气体 排放量作为除费用最低之外的优化目标,并应用启 发式算法求解,强调多式联运服务网络运营在满足 客户需求的同时,应尽量减少对环境的影响.综上,本文作者在既有文献研究的基础上,考虑 了如下方面的内容:1)节点作业时间.既有文献[2-5]均将多式联运过程简化为连续的“运输—中转—运输”过程,而忽 略了不同运输方式运输组织模式的不同,例如在所 规划的方案中,货物到达某一节点的时刻不在该节 点的作业时间窗内或晚于班列的发车时刻,则无法 完成相应中转、运输任务,因此导致规划方案与实际 不符.2)模糊运量.既有大部分文献将运量设置为一定值进行优化建模,而忽略了客户运输需求的不确 定性且运输方案的设计具有一定的超前性,同时每 条运输路径及每个中转节点的能力又存在约束,更 进一步的考虑,即便到达某一节点的时间在其作业 时间窗内,如果能力不足就不能在规定的时间内完 成中转作业,同样会影响路径选择.3)运输时限客户满意度.既有文献在考虑运输 时限时,通常以运输时限最短作为优化目标,但实际中,企业会根据自己掌握的订货提前期订货,如果货 物过早到达,企业相应库存成本则会增加,如果过晚 到达,企业则会消耗安全库存甚至停产,因此,货物 在一个合理的时间段内到达才会达到较高的客户满意度.因此,本文作者综合考虑运输费用、节点作业时 间、运到时限、运输及中转能力等因素对运输方式及 路径选择的影响,从既有运输网络的有效利用角度 出发,针对具体客户需求,提高运输服务的质量,优 化物流资源配置.1问题描述与建模11带时间窗的多式联运路径优化问题1) 问题描述.公路、铁路组成的运输网络G (N ,A ,M ),其中:N 为运输网络中的节点个数,A 为两节点间的 运输弧,M 为运输方式集合.T ,代表货物运输过程 中可能经过的节点,s 代表有货运需求的节点.在运 输网络G 中,可以发生运输方式转换的节点具有作 业时间窗,要求货物必须在作业时间窗内到达换装 节点,且在客户满意时间到达终点.以运输过程费用 及换装费用最低为目标,找到O D 间的最短路径.2) 假设条件.假设集装箱在运输过程应符合以下条件:1)对 于同一种运输方式,相连节点间只有一条运输弧;2) 同一批货物在同一节点处最多换装一次;3 )同一批 货物在运输过程中,每个节点最多经过一次;4)同一 批货物在运输过程中必须整批运输,不可拆分.3) 符号说明.n :集装箱个数;办,:运输网络G 中的节点;:货物在运输网络中可能用到的运输方式;了 :与节点,相连的点的集合,/ G N ;M ,:与节点,相连的节点和节点,之间运输方 式的集合,M , G M ;M ,,:节点,到j 之间运输方式的集合,M ,, G M ,,^ N ,j ^ N ,(i ,j ) ^ A ;cj :在运输弧,上采用々运输方式的费用,TM G M ,;c f :在节点,由&运输方式换装到Z 运输方式第3期于雪峤等:考虑模糊需求的多式联运路径优化25的费用,^ G M,,Z G M,;:在运输弧G,j)上用々运输方式的距离;T?:货物在节点z由々运输方式换装到Z运输方式的时间;[7T,:TL]:节点z的作业时间窗;:货物到达节点z的时间;K T d:货物到达终点D时的客户满意度;〜:节点s的集装箱个数,可将其应用三角模糊数W e =(W eE,W e M,W e I,)表示,其中W e M表示节点S最可能出现的集装箱个数,〜E〜L分别表示货物的最小、最大运量;:运输弧(,人)上选用々运输方式的容量;wf:节点z由々运输方式换装到Z运输方式的能力;:第s个O D的货物在运输弧(,J)上选择f运输方式则为1,否则为0:第s个O D的货物在节点z由f运输方式换装到Z运输方式则为1 ,否则为01.2模型构建1.2.1模型描述综合考虑运输过程节点时间窗并保证货物在合理的时间段内到达终点,带时间窗的多式联运路径优化模型可表示如下目标函数min2:=2•ck j•ns +(t.j)eAkeM2 2•cj6T,-keM zeM约束条件2 2xh -he i ieM j22x j =<〇j e i m e M j z e dV z e t-z e o2xii <1,v (j ) e a m e M ij22y i<1,Vz e t-keMiieMi2y f= 2x h v z e t- v i e Mi keM i jei2^= 2y f,Vz e T-V k e Mi h e i i e M it[e[t f,t i] Vz e t-Ct+r2T l • yS + tj — tj) = 0k e M js(T d)>7(1)(2)(3)(4)(5)(6) ()(8)(9)n •x j <n j v z j)e A,Vk e M,(10)n •yS <n k,vz e T r,Vk l e Mz(11)k iys =0vz e{〇〇D}Vk e m i,v i e m i(12)式a)表示取运输总费用最小值,其中总费用包括运 输费用和中转换装费用;式(2)为每一个节点的流平 衡约束;式(3)表示货物在运输过程中不可拆分;式(4)表示每个节点最多换装一次;式(5)、式(6)表示 决策变量x y之间的关系:如果在一个节点发生中 转换装,那么一定有两条运输弧连接这个节点并且相邻的节点也在运输路径中;式(7)表示货物到达节 点(的时间需要在节点(的作业时间窗内;式(8)表 示货物到达节点j的时刻;式(9)表示到达终点的时 刻需要高于客户的最低满意度,Y为非负常数;式 (10)表示运输过程中运量不应超过所选运输弧的能 力;式(11)表示货运量不能超过所选节点换装的中转能力;式(12)表示在起点和终点货物不发生换装.1.2.2非线性约束线性化处理考虑模糊需求的多式联运路径规划模型为非线 性数学规划模型,若采用启发式算法求解,因其自身 寻优机制,难以确定所求得的可行解是否为全局最优解.在应用精确求解软件如Lingo等求解时,非线 性约束会导致计算结果陷人局部最优,且求解效率 大大降低,即失去了采用精确求解策略的意义,因此,将式(8)线性化处理.若在运输弧G j)上,选用了 l运输方式进行 货物运输,则xll= 1,推导结果需要保证t+2Tk •yS和t的平衡关系存在,即为k e M j0 <t +2T f •yS +t j —t < 〇(13)k e M j同理,若弧G j)上未用l运输方式进行货物运输,即x l =0,则式(8)可表示为—M<te+2T k l •y S+t j—t j <M(14)k e M j因此,非线性约束式(8)可以被线性化为如下两 个约束+2Tk •yk e M ijl i l —ie1t{j t j >M(x j—1) (15)+2Tkl •yk e M jl\l —S1t z t7<M(1 —x l)(16) 1.2.3客户满意度描述根据存货目的的不同,可将企业的库存分为周 转库存和安全库存两部分.其中,周转库存是为了满 足两次进货期间市场的平均需求或生产经营的需要 而存储的货物,这种库存随着每日的需要不断减少,当库存降低到某一水平,企业则要根据上游供应商26北京交通大学学报第42卷的制造周期及运输周期等因素,确定自己的订货提 前期,进行订货补充库存以维系正常生产.安全库存 则是指用于应对不确定性因素如大批量突发性订 货、交货期突然延长等而准备的库存.安全库存与市 场需求特性、订货周期的稳定性密切相关.市场需求 波动越小或需求越准确,则订货周期越稳定,所需的 安全库存越小.通常情况下,企业的安全库存仅在特 殊条件下启用,因此,若是因运输问题造成企业的周 转库存下降到一定值而没有适时补充,客户满意度 则会降低.另一方面,如果货物过早到达,则企业需 要支付更多的仓储成本,因而客户满意度会下降.仅 当货物到达的时间在一个合理的时间段内到达,才 会使得企业支付的库存费用较少,且不会担心因上 游原材料短缺而消耗安全库存,用T 。
物流配送中的优化模型及算法研究

物流配送中的优化模型及算法研究随着电商、零售等领域的不断发展,物流配送成为保障商品最终到达消费者手中的重要环节。
而物流配送过程中的时间、成本、效率等问题一直是企业关注的焦点。
如何利用信息技术和数学算法来优化物流配送模式,提升物流配送效率和实现成本控制,成为业内人士研究的重点。
物流配送中的问题在物流配送中,很多企业会面临这些问题:配送路线不合理、交通堵塞、配送距离过远、货物损坏等问题。
比如,一件商品的物流配送路线,往往需要考虑多个配送点、多条路线,同时需要考虑各个配送点的时间窗口、快递员的工作时间、保证货品不受损等问题。
这些问题有时会让企业的物流配送成本大幅增加,效率降低,无法满足客户的需求。
物流配送的优化模型针对物流配送中的问题,很多企业和研究机构尝试研究出不同的优化模型,来实现物流配送的优化和成本控制。
其中比较常见的优化模型有以下几种:1、TSP问题优化模型TSP问题是最经典的旅行商问题。
它的应用场景也很广泛,比如货车配送、网络节点的寻优等。
对于物流配送而言,利用TSP问题优化模型可以大幅缩短配送距离,提升配送效率。
这个模型的核心是建立不同的路径,然后依据时间、距离、成本等因素进行优化,从而找到一条最优化的路径。
2、VRP问题优化模型VRP问题是一种非常具有实际应用价值的优化模型。
这个模型可以将物流配送中多个配送点的问题转化为在有限时间内,最小化车辆行驶距离的问题。
在这个过程中,需要考虑到车辆容量限制、时间窗口限制、工作人员安排等问题,从而得到最优的物流配送路线。
3、GA算法实现模型GA算法(遗传算法)是一种计算学方法,可以模拟在进化过程中物种进行生物遗传机制的过程。
在物流配送的优化中,可以运用GA算法模拟进化过程,不断进行优化迭代,得出最优的物流配送方案。
物流配送优化算法除了常用的优化模型之外,物流配送优化还需要用到一些专门的数学算法,比如贪心算法、模拟退火算法、禁忌搜索算法等等。
1、贪心算法贪心算法是一种小而美的算法,可以利用贪心的思想,选择当前的最优解,快速得出整体的最优解。
第4章 运输及运输优化模型

13
1
2
3.准确 准确,就是在货物运输过程中,切实防止 各种差错事故,做到不错不乱,准确无误 地完成运输任务 4.安全 安全,就是货物在运输过程中,不发生霉 烂、残损、丢失、燃烧、爆炸等事故,保 证货物安全地运达目的地。
14
10/23
1
2
2.3 运输方式及其选择
铁路运输 水路运输 公路运输 航空运输 管道运输 联合运输
1
2
2.4 运输服务的提供者
(一)公路运输服务的提供者 1.公路承运人种类 (1)根据客户类型:分为普通承运人、合同
承运人 (2)根据业务形式:分为整车运输承运人、 零担运输承运人。 整车运输承运业务进入成本较低,而零担运 输承运业务进入成本高,因为零担货运业需 要一个广泛的场站网络来整合和分散货物配 10/23 30 送。
28
1
2
4.大陆桥运输
大陆桥运输是指使用铁路或公路系统作为桥
梁,把大陆两端的海洋运输连接起来的多式 联运方式。目前世界上主要的大陆桥有: (1)西伯利亚大陆桥; (2)远东至北美东岸和墨西哥湾大陆桥; (3)北美西海岸至欧洲大陆桥; (4)新亚欧大陆桥;以中国东部的连云港为起 点,以荷兰的鹿特丹港为终点的一条大陆桥。 10/23 它具有提前结汇、手续简便、节约费用、安 29
1
2
管道运输
优点 缺点
连续性强 损耗小 运输安全 建设投资省、占
管道运输是一个单向
地面积少等
10/23
的封闭输送系统,灵 活性很差 另外,为了进行连续 输送,需要在各中间 站建立储存库和加压 站,以促进管道运输 23 的畅通。
1
多目标多模式模糊运输问题的最优折衷解
多目标多模式模糊运输问题的最优折衷解
韩世莲;刘新旺
【期刊名称】《系统工程》
【年(卷),期】2007(25)9
【摘要】在不确定性运输问题研究现状的基础上,建立了目标函数费用系数、可供应量和需求量均为模糊数的多目标多模式运输问题(MOSTP)数学模型。
首先根据Zadeh的扩展原理将模糊数多目标多模式运输问题转化为不同截集水平α下的区间数多目标多模式运输问题。
然后根据区间数序关系,将区间数MOSTP转化为典型的MOSTP,并将模糊数约束转化为确定性的不等式约束。
通过运用模糊折衷规划方法求解,得到了模糊数MOSTP的最优折衷解。
文章最后采用具体算例论证了该方法的求解过程。
【总页数】7页(P26-32)
【关键词】模糊数;多模式运输问题;多目标规划;模糊折衷方法
【作者】韩世莲;刘新旺
【作者单位】南京财经大学营销与物流学院;东南大学经济管理学院
【正文语种】中文
【中图分类】U491
【相关文献】
1.多目标多模式运输问题的模糊规划方法解 [J], 韩世莲;李旭宏
2.模糊贴近度在多目标优化中的应用--从非劣解中寻求最优解 [J], 张鹏;肖芳淳
3.物流运输网络多目标最短路问题的模糊满意解 [J], 韩世莲;刘新旺
4.模糊线性多目标规划最优解的稳定性问题 [J], 奚文湘
5.解决模糊多目标线性规划问题的折衷模型研究 [J], 雷磊;王玺
因版权原因,仅展示原文概要,查看原文内容请购买。
铁路空车调配问题的区间线性规划模型及算法
铁路空车调配问题的区间线性规划模型及算法曲思源【摘要】铁路空车调配问题是合理解决空车需求与供应之间的不平衡问题。
在借鉴空车调配问题模型已有成果的基础上,围绕空车供应与需求量的不确定性、空车调配的时效性、路段通过能力的限制性3个方面,对区间数运用于空车调配问题加以适应性分析,以空车总走行公里最少和到达时间满足空车需求限定时间可信度加权和最大为目标,提出利用线性区间规划理论解决空车调配问题的模型和算法,并结合算例验证了区间规划的灵活性和简便性,使得空车调整模型符合运输生产实际并具有普遍意义,该模型的采用对路网上空车调整问题将起到很好的借鉴作用。
%Railway empty car distribution is a solution to the demand and supply imbalance of empty cars. On the ba⁃sis of the empty car distribution model, centering on three aspects including the supply and demand uncertainty of empty cars, the deployment timeliness and the limit of interval capability, this paper conducts adaptive analysis of the empty car distribution. To achieve minimum kilometers of the total empty mileage and the maximum weighted credibility of the empty demand for limited time in terms of arrival time, the paper proposes linear interval planning theory to obtain the model and algorithm of empty car distribution. Combined with examples to verify the flexibility and simplicity of the interval planning, it concludes the proposed empty distribution model can meet the practical transportation and production demands, providing reference and significance for the distribution of railway empty car.【期刊名称】《华东交通大学学报》【年(卷),期】2015(000)003【总页数】6页(P6-11)【关键词】铁路运输;区间规划;空车调配;模型【作者】曲思源【作者单位】上海铁路局运输处,上海 200071【正文语种】中文【中图分类】U292.45铁路空车调配问题是合理解决空车需求与供应之间的不平衡问题。
随机需求下港口内陆物流运输网络优化模型
tepo sd h r po e m od l or e f obt nig o i a s u i ai n ptm l ol ton. Re uls f xa pls ac a i i c t t a t m o l s s t o e m e c lulton ndia e h t he de i pr c ia1 a tc . ’
f n t n fu p ra d lwe n saen tc mp r be,o jcief n to n ev l etit nag rt m sa o td t u ci so p e n o ro e r o o aa l o be tv u c in itr a rs r i lo i co h i d p e o
随 机 需 求 下 港 口 内 陆 物 流 运 输 网 络 优 化 模 型
蒋 良奎 汪 传 旭 ,
( . 海海 事大 学 基础科 学 部 ,上海 2 0 3 ;2 上 海 海事 大学 经 济管理 学 院 , 海 2 0 3 ) 1上 015 . 上 0 1 5
摘 要 : 了对 随 机需 求 环 境 下 区 域 港 口 内陆 物 流 运 输 网 络 进 行 优 化 决 策 , 第 三 方 物 流 服 务 企 业 的 角 度 提 出该 为 从
物流配送优化模型及算法研究
物流配送优化模型及算法研究随着全球贸易的发展和电子商务的兴起,物流配送成为现代商业活动中至关重要的一环。
为了提高物流效率、降低成本、提升顾客满意度,物流配送优化成为了研究的焦点。
本文将对物流配送优化模型及算法进行研究,探讨如何通过算法优化物流配送过程,提高效率和降低成本。
一、物流配送优化模型物流配送的核心问题是如何在有限的资源下,为各个目的地选择最佳的路线和配送方案。
为了解决这一问题,研究者提出了一系列物流配送优化模型,包括TSP问题、VRP问题、CVRP问题等。
1. TSP问题(Traveling Salesman Problem)TSP问题是指一个旅行商需要依次访问多个城市,并返回起始城市,其中目标是找到最短的旅行路径。
在物流配送中,TSP问题可以应用于单一目的地的配送过程。
研究者通过构建数学模型和算法,以最小化旅行距离或时间为目标,从而优化配送路径。
2. VRP问题(Vehicle Routing Problem)VRP问题是指在有限数量的车辆下,为多个目的地选择最佳的路线和配送方案,以满足客户需求和优化配送成本。
研究者通过考虑车辆容量、路程、时间窗等因素,构建了各类VRP模型,如基本VRP、VRP with Time Windows (VRPTW)、VRP with Pickup and Delivery等。
3. CVRP问题(Capacitated Vehicle Routing Problem)CVRP问题是VRP问题的一种扩展,其中考虑了车辆的容量限制。
在物流配送中,车辆的容量限制会限制每次配送的货物数量,因此需要在满足客户需求的同时,最大程度地利用车辆容量,减少运输成本。
研究者通过构建数学模型和设计相应算法,解决了CVRP问题,提高了配送效率。
二、物流配送优化算法在物流配送优化模型的基础上,研究者设计了一系列算法,包括传统算法和启发式算法,用于解决上述问题。
1. 传统算法传统算法包括贪婪算法、分支定界法、动态规划法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刘梅 娇给 出 了上述 模 糊 优 化 问题 的一 种 求 解方 法 和解 的特点 本文 利用 三角模 糊数 的 m.
一
图 l 三角 模 糊 数 n的隶 属 函数
截集并结合文献 [0 中的方法将上述模 型转 1]
三角模 糊数 = (,,)的 一截集 是一个 2o r
3 实例
例1 … 设 有 3个 化肥 厂供 应 4个地 区 的农
化肥厂的总供应量为 10万吨 , 6 4个地区的最低 需求为 10万吨, 1 所以能够供应给地区Ⅳ的最大 量为 6 . 0 故可将地区Ⅳ的需求 区间缩减为 [0 1, 6 ], 的隶属度函数为 : O 相应
r
4
用 化肥 . 化 肥 厂 年 产 量 ( 位 : 吨 ) 各 地 区 各 单 万 、
≤∑ ≤ √= 一n 1 , 2 ;
i=t
来表示. 需求区间型运输问题在文 献[ ] 1 和文献 [ ] 已经提 到 , 般 通 过 添 加 虚 拟 的 产地 和销 2中 一 地, 变成产销平衡运输问题来求解. hns C aa_ 首次 3
研究 了具 有模 糊需 求 的运 输 问题 , 利用 参 数 规划
年需求量( 单位 : 万吨) 以及从各 化肥厂 到各地 区的单位运价( 单位 : 万 万吨) 如表 1 所示. 试
数学模 型 ; 旺 等建立 了一类 运输价格 、 刘新 可供 应量和需 求 量 均 为 区间 数 的运 输 问题 的数 学 模
定义 1 [ 设 是定义在实数 域 R上 的模糊 集合 , 称之为三角模 糊数 , 若 的隶属 函数为 :
1 f
.
,一 ≤ 0 0 f ≤ ;
糊优 化模 型 ; 据运 输 问题 的特 点 , 模糊 优化 模 型转 化 为 两 个等价 的运 输 问题 , 出模 糊 最 根 将 给 优判 决 A 的一个 定理 , 并给 出此 类运 输 问题 的一 种 简便 求 解 方 法 ; 最后 , 通过 实例验 证 方 法
的有 效性 .
[ 关键词] 模糊优化; 运输问题 ; 需求区间; 三角模糊数 [ 中图分类号] 19 [ O5 文献标志码] [ A 文章编号]63— 02 2 1)6 00 — 4 17 8 1 (0 10 — 05 0
时 ,
-
;
J= 1
∑ : i ,3 =1 ,; 2
。 3
≤ ∑ ≤ ,,4 ,=1 3 ; 2 ,
∑0一∑
I 1
≥ 0, i= 1 2, = 1 2, 4 , 3; , 3, .
代人数 据 , 求得 最优解 :
l 1=0,戈1 =5 1 2 0, 3=0, l =0, 2 4 1=0,
6
T T 有 唯一最 优解 , 其 最优 判决 P与 P 且
A 司 由定 理 1 出 . 解
立 如下 数学模 型 :
定理 1 对需 求 区间型运 输 问题 T 需求 区 P,
间 ,]且 ∑ ≤∑0≤∑ , 为[ _ , b J 则
(当 主 1 兰 )
≥ 0 i=12 … , j=12 … ,. , , , m; ,, n
其中, b ∑_ i ≤∑0≤∑ , 情 其他 况可以 容 较
易地转化为一般的运输问题. 当销售点的需求量
具 有弹 性时 , 易 用 表 上作 业 法 求 解 , 别 是 变 不 特 量 个数 较多 时更是 如此 . 我们 考 虑先 将 弹性 需求 模 糊化 , 将上 述 模 型 转 化 为模 糊 优 化 模 型 , 进 再
Sp : t 求解运输 问题 1 。得最优解 ; e3 ], P Se : 解运输 问题 T ,得 最优解 . tp4 求 P,
()={ x1, ≤3 ; () 【 /51 2一 5≤ 0 4
0. le es .
地 区 Ⅳ的需求 区间 为 [O +∞). 1, 由于 3个
+ A :
理. 当所有销地均以最低需求进货时 , 产地 的余
货 量为 ∑0一∑ , 地k 够 得的 大 则销 能 获 最
:1 J= 1
壹 √ 1, _, 2 …
≥ 0, : 1, … , i 2, m = 1, … , . 2, n
产品 + . 此, 量为 ∑口一∑ 因 销地k 需求 的
5
糊 数 . l=r=0时 , 即为普 通 实数 当
( T ).. F P St
∑ = i 1 , m = , …,; 2 J 1 = ∑ = √: 一r 1 , 2 t ;
≥ 0 i=12 … , j= 12 … ,. , , , m; ,, n
O
其中, =[j6 ], =12… , . b, , J ,, n
21 0 1年 1 2月
重庆文理学院学报 ( 自然科学版)
Jun l f hnqn nvri f r n c ne N trl c neE io ) ora o ogigU ie t o t adSi cs( a a Si c dt n C sy A s e u e i
De .。2 1 c 0 1
区 间
化为多 目标线性规划问题 ( T ) M P:
口 =[ 口一( 1一o f0+( L , ) 1一O)]. /r
1 2 弹性 需 求的模糊 化 .
mn1 iz =∑ ∑cq q i; j x
i 1 = =1
弹性 需 求 [ 6]是 一 个 区 间. 虑 到 销 地 6, 考 对 弹性 需求 区间 内各 点 的满 意 程度 是 不一 样 的 , 销售 点应避 免 进 货 过 多 或 过 少. 因此 , 文 采 用 本
‘ 1 J 1
区 可缩 问 减为[ 垒+ n一 ]利 . , ∑ ∑ . 用1 2
节方法可将其转化为三角模糊数.
当 丁b, 等ห้องสมุดไป่ตู้ 耋 > b iM 价: n+时T i P
a =∑ :1 i. rn i=1 ∑c t i j 舭 j J
∑ = i 1, m = ,…,; 2 ∑ : 一 m
J= 1
隶属度 可 解 释 为 销地 对 相 应 供 货 量 的满 意 度 , O一截集 可解 释为带 有一 定满 意度 的需 求 其 L 区 间. 时 , 此 运输 问题 不仅要 求 费用 最省 , 而且 要 求达 到更 高 的满 意度 .
1 3 需求 无上 限时 的处理 .
∑0 =∑ .
∑ ∑c . i J 1 =1 =
[ 收稿 日期] 0 1 0 0 2 1 — 9— 3
简记为 a=(,,) 称 a z r. a 为模糊数 的中心 , z 与 r 别称 为模糊 数 的左 右展 度 , 图 1 分 如 所示 . 特别地 , f 时 , 当 =r 称模糊集合 为正规三角模
J =1
∑ = i 1 , ,; = ,…m 2
+ A≤
以下方法将弹性需求区间 [ 转化为三角模 6, 糊数 5 其 隶属 函数形 式 如下 : ,
2x- b j
,
( T ). M P St .
r n
窆 _, , 1… ; 2n ,
i l =
≤ ~
糊数 , 建立相应的隶属度 函数. 地 区 I 模糊 需求 量 的隶属度 函数 :
r
O 一3, 0 ≤ ≤ 40; ・l 3
区 间型需求 运输 问题 的求 解步 骤 :
m- 您 Se : t 1 确定 I 韵弹 求因 司[ ] p 俞 孺 , ;
l
()={ — .x4 ≤5 ; () 【 01, 5 0≤ 0 3
.
型. 本文将弹性需求信息转化为三角模糊数 , 并利 用 模糊数学理论 建立运输 问题 的模糊优化模 型.
( = { )
f I
;
’ , ≤0 ● ¨、 n< ¨l + r
( 1 )
1 弹性 需求的模糊处理
本 文考 虑如 下形 式 的运 输 问题 ( P : T )
在实 际问题 中, 销量往 往具有 不确定 性. 导 这 致 销售点在 进货 时 不 能完 全 明确进 货 量 , 而是 根 据 以往 销售 情况来 进 货 , 即销 售 点 的需求 量 具有
一
∑ = i -m =1 - ; 2 ,
J =1
定 的弹性。 弹性 通 常 可 以用 区间 数或 模糊 数 这
行 求解 . 1 1 三角模糊 数 .
给出了此类问题的求解方法; 谢凡荣 将需求 区
间型运输 问题 转 化为 最小 费 用最 大 流 问题 , 出 给
了相应 的求解算法 ; 等 考虑 了供应量 、 曾霁 需求 量 以及运输 费用 皆为 区间数 的运 输 问题 的 区间规
划模型; 顾坤坤等 给出了具有模糊费用 系数和 随机需求的运输问题 的数学模 型; 罗霞等 利用 三角模糊数的大小关系建立了多 目标运输问题的
i=l
2 模糊优化模 型的建立与求解
、 三角模糊数表示弹性需求 区间后 , 用 可以得
到 区间需求 运输 问题 的模糊 优 化模型 ( T ) FP :
A 1 …, √: 2, 凡;
,
≥ 0, = 1, … , i 2, m = 1 2, , . , … n
mn =∑ ∑c iz i_ l . =一=1 — 1 J
第3 0卷
第 6期
V0 _ 0 No 6 l3 .
需 求 区 间型 运 输 问题 的模 糊 优 化 模 型
仇 海全 曹炳元 潘 , ,
(. 1 安徽科技学院理学院 , 安徽
花
广州 5 0 0 10 6)
凤阳 2 3 0 ; .广州大学数学与信息科学学院 , 3 10 2 广东
[ 摘 要] 为解决需求区间型运输 问题 , 弹性需求区间转化 为三角模糊数 , 将 建立该 问题 的模
