反比例函数与一次函数交点问题
反比例函数与一次函数交点线段相等

反比例函数与一次函数交点线段相等是一个重要的数学问题,它涉及到两种不同类型的函数之间的关系,对于理解两种函数的特性和性质有着重要的指导作用。
本文将从反比例函数和一次函数的定义、性质以及它们的交点线段等长度三个方面展开论述,以期为读者提供全面、深入的理论解释和具体实例分析,帮助读者更好地理解这一数学问题。
一、反比例函数和一次函数的定义和性质反比例函数是指函数的定义域为实数集,值域为非零实数集,并且函数的图像在直角坐标系中呈现出双曲线的函数。
一次函数是指形式为y=kx+b的函数,其中k和b为常数,且k不为零,其图像在直角坐标系中呈现出直线的函数。
从函数的定义和性质上来看,反比例函数和一次函数是两种截然不同的函数类型,反比例函数的图像是双曲线,而一次函数的图像是直线。
二、反比例函数和一次函数的交点反比例函数与一次函数的交点是指当两种函数的图像在直角坐标系中相交时的交点,这个交点的横纵坐标就是两种函数的自变量和因变量相等的值。
具体来说,当反比例函数y=k/x和一次函数y=kx+b相交时,就产生了交点。
三、反比例函数与一次函数交点线段相等反比例函数与一次函数交点线段相等,意味着从两种函数的交点开始,到两条函数的横坐标值相等时,所对应的纵坐标的长度是相等的。
这个性质是从函数的定义和性质以及它们的交点出发所得出的。
针对这一数学问题,可以通过具体的例子来进一步说明。
假设反比例函数为y=1/x,一次函数为y=2x+3,求它们的交点线段相等。
我们来求两种函数的交点。
当y=1/x和y=2x+3相交时,即1/x=2x+3,求解得到x=-1和x=1。
将x代入y=1/x和y=2x+3中,得到两个交点为(-1,-1)和(1,5)。
接下来,根据交点线段相等的定义,计算两条函数的横坐标值相等时,纵坐标的长度。
当x=1时,反比例函数的纵坐标为1,一次函数的纵坐标为5;当x=-1时,反比例函数的纵坐标为-1,一次函数的纵坐标为1。
可以看出,从两种函数的交点开始,到它们的横坐标值相等时,所对应的纵坐标的长度是相等的。
一次函数与反比例函数的交点问题

一次函数与反比例函数的交点问题一次函数与反比例函数的交点问题,是许多学习数学的人都会遇到的一个难题。
今天,我将从理论和实践两个方面来探讨这个问题,并希望能够给大家带来一些启示和帮助。
我们来看一下一次函数和反比例函数的基本概念。
一次函数是指形式为f(x)=ax+b的函数,其中a和b是常数,x是自变量。
反比例函数是指形式为g(x)=k/x的函数,其中k是常数,x是自变量。
这两种函数都有一个共同点,那就是它们的图像都是一条直线或曲线。
尽管一次函数和反比例函数在图像上看起来很相似,但它们在求交点的问题上却有着很大的不同。
对于一次函数来说,只要已知它的斜率和截距,就可以轻松地求出它与任意一条直线的交点;而对于反比例函数来说,即使知道了它的定义域和值域,也无法直接求出它与任意一条直线的交点。
这是因为反比例函数的图像是一个双曲线,而不是一条直线。
因此,要解决一次函数和反比例函数的交点问题,就需要采用一些特殊的方法。
其中一种比较常用的方法是“代入法”。
具体来说,就是先设出一条直线的方程,然后将这条直线代入到反比例函数中去,得到一个关于x的一元二次方程。
接下来再解这个一元二次方程,就可以得到这条直线与反比例函数的交点坐标了。
这种方法虽然比较繁琐,但在实际应用中却非常方便和有效。
除了“代入法”之外,还有一种比较简单且易于理解的方法叫做“待定系数法”。
具体来说,就是先设出一条直线的方程,然后根据这条直线与反比例函数的图像相交的条件,列出一组关于a、b、k的方程组。
最后再解这个方程组,就可以得到这条直线与反比例函数的交点坐标了。
这种方法不仅简单易懂,而且可以推广到其他类型的函数之间求交点的问题上。
一次函数和反比例函数的交点问题虽然看起来比较复杂,但只要掌握了一些基本的方法和技巧,就可以轻松地解决它。
希望大家在学习数学的过程中能够多多思考和探索,不断提高自己的能力和水平。
反比例函数与一次函数两个交点的关系

反比例函数与一次函数两个交点的关系你会发现自己在做数学题的时候,突然就被一个看似简单却又深奥的问题困住了。
比如那道题:反比例函数和一次函数的交点,究竟是什么关系?一开始看这题,肯定有人想:这不就是两个函数相交的地方嘛,简单不简单?但越想越觉得怪,怎么感觉有点复杂呢?反比例函数和一次函数的交点,真不是那么难理解。
说白了,就是我们要找这两条曲线在哪儿碰面。
反比例函数那是一个典型的“曲线”,它的形状像一个弯弯的U字型,越靠近坐标轴越陡。
它有个特点,x和y互相制约,你越大,它越小,反正就是“此消彼长”。
而一次函数嘛,那就是咱们常说的“直线”了,简单得不行,斜斜地从左下角伸到右上角,或者从右下角伸到左上角,取决于它的斜率。
但这两者相交的时候,可就有点意思了。
如果仔细想想,你会发现:反比例函数和一次函数的交点,完全是个“缘分”的问题!有时候它们相交一次,像偶遇的老友,聊个天就走;有时候它们根本就不理对方,擦肩而过;也它们可能在同一个地方久等不见,结果谁也没有找到谁。
听起来是不是有点神秘?这种“缘分”就和我们日常生活一样,不是所有的事都能控制得了。
反比例函数和一次函数相交的数量、位置、情况,其实是跟具体的方程式有关的。
比如,当你把反比例函数写成y = k/x,k又是一个常数,看看它和一次函数y = mx + b的交点,那就要解个方程了。
大家看着方程可能会觉得好像很复杂,但真正做起来也不过就是把两个式子“相等”而已。
假设咱们把这两个式子代进去,解出来的就是交点的x值。
然后再把这个x值代回去,计算出y值。
简单吧?如果解出来是两个不同的x值,那就说明它们有两个交点。
是不是很神奇?两个完全不同的数学对象,居然能在某个地方相遇,互相交错。
可是,你也可能碰到某些情况,解出来的方程没有实数解,结果就是两条线完全不相交。
这就像你和朋友约好在一个地方见面,可你提前到了,而他偏偏临时有事,根本没出现,俩人就“错过了”——这就没有交点。
26.1.2反比例函数与一次函数的交点问题

∟
y1>y2
o
x
③当X=-3 或X =1时, y1=y2
( N -3,-1)
例2::(2011台州)如图,反比例函数 (m≠0) 的图象与一次函数y2=x+2的图象交于点M,N,已 点M的坐标为M(1,3),点N的纵坐标为-1,回 答下列问题: (3)求△MON的面积。
y
y
M
A B
自学指导
例1::(2011台州)如图,反比例函数 (m≠0) 的图象与一次函数y2=x+2的图象交于点M,N,已 点M的坐标为M(1,3),点N的纵坐标为-1,回 答下列问题: X=-3 X=0X=1
(1)m= 3 ,
y
(-3,-1) 点N的坐标为 ;
( 2 )直接写出不等式 (2) ( 2 直接写出一次函数值大于 )直接写出不等式 m m 反比例函数时 x 的取值范围。 x+2x+2> >0的解集 的解集
例1. 如图,正比例函数 y=k x 与反比例函数 1 k y 2 的图象相交于A、B两点,其中点A的坐标 x 为(2,4) y (1)分别写出这两个函数的表达式; A (2)你能求出点B的坐标吗? o 你是怎样求的? x B 解后思考: 1.如果正比例函数与反比例函数图象有交点, 则交点坐标有什么特点? 2.正比例函数y=k1x与反比例函数y=k2/x有交 点,则k1和k2应满足什么条件?
k 变式:如图,已知,A,B是双曲线 y (k 0) x 上的两点,
(1)若A(2,3),求K的值 (2)在(1)的条件下,若点B的 D 横坐标为3,连OA,OB,AB,求 △OAB的面积。
o
y
A
E
B
C
x
反比例函数与一次函数的交点问题.doc

反比例函数与一次函交点问题1.如图,直线y=x﹣6分别交x轴,y轴于A,B,M是反比例函数y=(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,AC•BD=4,则k的值为()A.﹣3B.﹣4C.﹣5D.﹣62.如图,直线y=-x+m交双曲线y=于A、B两点,交x轴于点C,交y 轴于点D,过点A作AH⊥x轴于点H,连结BH,若OH:HC=1:5,S=1,则△ABHk的值为()A.1B.C.D.3.如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B(1,3),连接BO,下面三个结=1.5,;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1论:①S△AOB>x2,则y1<y2;③不等式x+2<的解集是0<x<1.其中正确的有()A.0个B.1个C.2个D.3个4.如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=﹣x+6上,若双曲线y=(x>0)与△ABC总有公共点,则k的取值范围是.5.直线y=kx(k>0)与双曲线y=交于A(x1,y1)和B(x2,y2)两点,则3x1y2﹣9x2y1的值为.6.如图,直线y=﹣x﹣与x,y轴分别交于点A,B,与反比例函数y=的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为.7.如图,过点O的直线AB与反比例函数y=的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=(x<0)的图象交于点C,连接AC,则△ABC 的面积为.8.如图,已知一次函数y=kx﹣3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=(x>0)交于C点,且AB=AC,则k的值为.9.如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=和y=在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是.10.如图,直线y=x与双曲线y=(k>0,x>0)相交于点A,将直线y=x 向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值是.11.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=,OB=4,OE=2.(1)求一次函数的解析式和反比例函数的解析式;(2)求△OCD的面积;(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.12.如图,直线y=2x+6与反比例函数y=(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?13.如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(x <0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.(1)求m的值;(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.14.如图,在平面直角坐标系xOy中,函数y=(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).(1)求m,k的值;(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=的图象于点N.①当a=4时,求MN的长;②若PM>PN,结合图象,直接写出a的取值范围.15.已知函数y=kx+b,y=,b、k为整数且|bk|=1.(1)讨论b,k的取值.(2)分别画出两种函数的所有图象.(不需列表)(3)求y=kx+b与y=的交点个数.16.如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=的图象经过点A(2,2).(1)分别求这两个函数的表达式;(2)将直线OA向上平移3个单位长度后与y轴交于B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;(3)反比例函数图象上是否存在点D,使DC⊥BC?若存在,请求出点D的坐标;若不存在,请说明理由.17.如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.(1)求抛物线的解析式;(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.。
反比例函数与一次函数交点问题
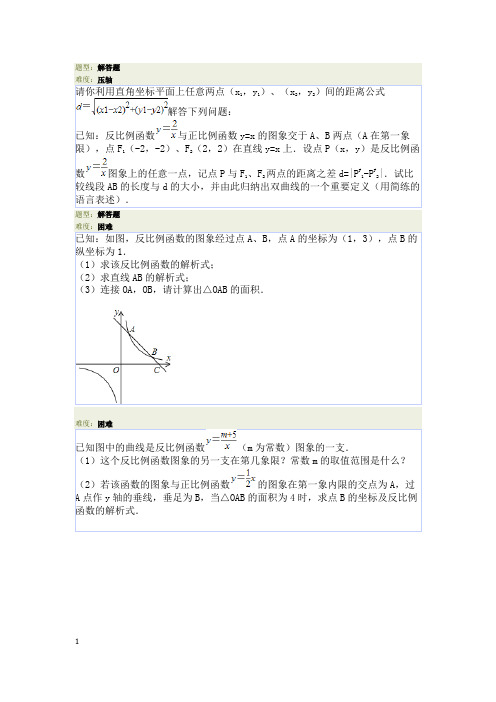
难度:压轴请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式解答下列问题:已知:反比例函数与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(-2,-2)、F2(2,2)在直线y=x上.设点P(x,y)是反比例函数图象上的任意一点,记点P与F1、F2两点的距离之差d=|P F1-P F2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).难度:困难已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1.(1)求该反比例函数的解析式;(2)求直线AB的解析式;(3)连接OA,OB,请计算出△OAB的面积.难度:困难已知图中的曲线是反比例函数(m为常数)图象的一支.(1)这个反比例函数图象的另一支在第几象限?常数m的取值范围是什么?(2)若该函数的图象与正比例函数的图象在第一象内限的交点为A,过A点作y轴的垂线,垂足为B,当△OAB的面积为4时,求点B的坐标及反比例函数的解析式.详细信息如图,正比例函数y=kx(k>0)与反比例函数y=的图象相交于A、B两点,过A作x轴的垂线交x轴于点C,连接BC,设△ABC的面积为S,则S= .详细信息直线y=2x与y轴交于A点,再将此直线向上平移一个单位,与曲线交于B、C两点,则△ABC的面积等于.详细信息已知反比例函数为常数,k≠2)(1)若在这个函数图象的每一支上,y随x增大而增大,求k的取值范围;(2)若P(-1,a)既在函数y=-2x+4的图象上,又在反比例函数图象上,求反比例函数的解析式.详细信息如图,已知反比例函数y=的图象与一次函数y=ax+b的图象交于M(3,2)和N(-2,m)两点.(1)求这两个函数的解析式;(2)求△MON的面积;(3)当x为何值时,一次函数值大于反比例函数值?难度:困难一次函数y=kx+b的图象与反比例函数y=的图象交于点A(2,1)、B(-1,n)两点.(1)求反比例函数的解析式;(2)求一次函数的解析式;(3)求△AOB的面积.难度:困难如图,已知A(-4,n),B(2,-6)是一次函数y1=k1x+b的图象和反比例函数的图象的两个交点,直线AB与x轴的交点为C (1)求反比例函数的解析式;(2)求△AOB的面积;(3)请根据函数图象,比较y1与y2的大小关系.题型:选择题难度:困难如图,已知函数y1=kx+b和的图象交于点P、Q,则根据图象可得一次函数的值大于反比例函数的值时x的解集是()A.x>-3 B.0>x>-3或x>1 C.x>1 D.x<-3题型:解答题难度:压轴如图,Rt△ABO的顶点A是双曲线与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且.(1)求这两个函数解析式;(2)若A(-1,3),C(3,-1),求△AOC的面积.(3)根据图象,写出一次函数大于反比例函数的x的取值范围.题型:解答题难度:困难如图,反比例函数的图象和一次函数的图象交于点A(-2,1)和点B(,m).(1)求反比例函数和一次函数的解析式.(2)O为坐标原点,求△AOB的面积.(3)当取何值时,y1>y2.。
反比例函数与一次函数交点问题-(2)课件
B.-1
C.1
D.2
变式1:若反比例函数y= k/x与一次函数y=x+2的
图象有两个交点,则k>__-_1_且__K_≠_0.
变式2:若反比例函数y= k/x与一次函数y=x+2的
图象只有一个交点,则k=__-_1_____.
变式3:若反比例函数y= k/x与一次函数y=x+2
的图象在第二象限内有交点,则k的取值范围为
(3)求△OAB的面积.
y=x+1
y=6/x
C
17
例2:如图,已知反比例函数y1=k/x(k≠0)的 图象与一次函数y2=-x + b相交于点P(1,4),
Q(4,m). (1)分别求出这两个k 函数的表达式;
(2)直接写出不等式-x +b ≥ 的解集;
x
(3)求△OPQ的面积.
18
(3)求△OPQ的面积。
N(-3, -1)
y1=y2
26
3.如图,反比例函数y1= k1/x的图象与正比
例函数y2=k2/x的图象交于点(2, 1),则使
y1>y2的x的取值范围是
.
27
4.如图,一次函数的图像与两坐标轴分别交于A、 B两点,与反比例函数交于C.D两点,点C.D分别在 第一、三象限,且OA=OB=2, C点坐标为(3,1). (1)试求一次函数和反比例函数的表达式; (2)根据图象直接回答,当x为何值时,反比例函数 值不小于一次函数值? (3)求△OCD的面积.
_-_1_≤_K__<__0.
15
自学指导3:(3分钟)
例:如图,反比例函数 (m≠0)的图象与一次
函数y2=x+2的图象交于点M、N,M(1, 3),求
中考数学总复习《反比例函数与一次函数交点问题》专项提升练习题(带有答案)
中考数学总复习《反比例函数与一次函数交点问题》专项提升练习题(带有答案)学校:___________班级:___________姓名:___________考号:___________1.如图1,一次函数()30y kx k =-≠的图象与y 轴交于点B ,与反比例函数()0m y x x=>的图象交于点()8,1A .(1)求出一次函数与反比例函数的解析式;(2)点C 是线段AB 上一点(不与A ,B 重合),过点C 作y 轴的平行线与该反比例函数的图象交于点D ,连接OC ,OD ,AD ,当tan 2ADC ∠=时,求点C 的坐标;(3)如图2,在(2)的前提下,将OCD 沿射线BA 方向平移一定的距离后,得到O C D ''',若点O 的对应点O '恰好落在该反比例函数图象上,求出点O '的坐标.2.如图所示,一次函数0y mx n m +≠=()的图象与反比例函数()0k y k x=≠的图象交于第二、四象限的点()2,A a -和点(),1B b -,过点A 作x 轴的垂线,垂足为点C ,OAC 的面积为4.(1)分别求出a 和b 的值;(2)结合图象直接写出k mx n x+<中x 的取值范围; (3)求AOB 的面积.3.如图,反比例函数()0k y k x=>的图象与过点()1,0-的直线AB 相交于A 、B 两点,已知点A 的坐标为()1,3.(1)求反比例函数和直线AB 的表达式;(2)点C 为x 轴上任意一点.如果9ABC S =,求点C 的坐标.4.如图,在平面直角坐标系xOy 中,一次函数2y x b =+的图象分别与x 轴、y 轴交于点A B 、,与反比例函数k y x=(0x >)的图象交于点C ,连接OC .已知点()0,4B ,BOC 的面积是2.(1)求b k 、的值;(2)求AOC 的面积;(3)观察图象,直接写出当2k x b x+≤(0x >)时,x 的取值范围.5.如图,直线1y kx b =+与双曲线2a y x =相交于A 、B 两点,直线AB 与x 轴相交于点C ,点B 的坐标是()3m m ,,OA=5,E 为x 轴正半轴上一点,且3os 5c AOE ∠=.(1)双曲线2y 的解析式是 ,直线1y 的解析式是 .(2)求证:3AOB COB S S =△△.(3)当12y y >时,x 的取值范围是 .6.如图,直线6y x =-+与反比例函数(0)k y x x=>的图象分别交于点()2,A m 和点B ,与坐标轴分别交于点C 和点D .(1)求k 和m 的值;(2)若在x 轴上找一点E ,使得以点E A D 、、为顶点的三角形与COD △相似,求满足要求的点E 的坐标.7.已知反比例函数1k y x=的图象与一次函数22y ax =+的图象交于点(1,4)A 和点B .(1)求这两个函数的表达式;(2)根据图象直接写出一次函数的值大于反比例函数的值的x 的取值范围.8.如图,一次函数1y k x b =+与反比例函数2k y x=的图象交于()2,A m ,(),2B n -两点,过点B 作BC x ⊥轴,垂足为C ,且5ABC S =.(1)求一次函数与反比例函数的解析式;(2)点P 在x 轴上,如果ACP △的面积为10,求点P 的坐标.(3)根据所给条件,请直接写出不等式21k k x b x+>的解集.9.如图,在平面直角坐标系中,一次函数12y x =+的图象与反比例函数()20k y k x=≠的图象相交于第一、三象限内的(),5A m ,B 两点.(1)求反比例函数的解析式和B 的坐标;(2)当12y y >时,请直接写出x 的取值范围.10.如图,一次函数y ax b =+的图像与反比例函数k y x =的图像交于A ,B 两点,与x 轴交于点C ,与y 轴交于点D .已知点()2,1A ,点()4B m -,.(1)求反比例函数与一次函数的解析式;(2)点M 是反比例函数图像上一点,当MAO △与AOD △的面积相等时,请直接写出点M 的横坐标;(3)将射线AC 绕点A 旋转α度后与双曲线交于另一点Q ,若1tan 3α=,请求出点Q 的坐标.11.如图,一次函数2y x =-+的图象与反比例函数2k y x =的图象交于()4,2A -、()2,B n -两点,与x 轴交于点()2,0C .(1)求2k ,n 的值;(2)请直接写出不等式22k x x-+<的解集;(3)将x 轴下方的图像沿x 轴翻折,点A 落在点A '处,连接A B '和A C ',求A BC '的面积.12.如图,一次函数()0y kx b k =+≠与反比例函数m y x=的图象交于点()()2,3,1A B n -,.(1)求一次函数和反比例函数的表达式;(2)设直线 AB 与y 轴相交于,M C 为线段BA 延长线上一点,作CD OM 与反比例函数m y x =交于点 D ,连接OD ,当四边形MCDO 为平行四边形时,求点C 的坐标.13.如图,平面直角坐标系中,直线1y kx b =+分别与x ,y 轴交于点A ,B ,与双曲线2m y x =分别交于点C ,D (点C 在第一象限,点D 在第三象限),作CE x ⊥轴于点E ,OA=4,OE=OB=2.(1)求反比例函数的解析式;(2)当12y y >时,求x 的取值范围;(3)在y 轴上是否存在一点P ,使ABP CEO SS =若存在,求出点P 的坐标;若不存在,请说明理由.14.如图,一次函数3y kx =-的图象与反比例函数m y x =(0x >)的图象交于点P ,PA x ⊥轴于点A ,PB y ⊥轴于点B ,一次函数的图象分别交x 轴、y 轴于点C 、点D ,且27DBP S =△和12OC CA =.(1)求点D 的坐标;(2)求一次函数与反比例函数的表达式;(3)根据图象写出当x 取何值时,一次函数的值大于反比例函数的值.15.如图所示,直线y ax b =+与双曲线k y x=交于A B 、两点,已知点A 坐标为()2,1-,点B 的纵坐标是3-,直线与y 轴交于点D .(1)求直线AB 的解析式和反比例函数解析式;(2)直接写出不等式k ax b x+≤的解集; (3)若点P 是反比例函数图象上的一点,OCP △的面积是ODB △的面积的2倍,求点P 的坐标.参考答案1.【答案】(1)132y x =- 8y x=;(2)()2,2C -;(3)()4,2. 2.【答案】(1)4,8a b (2)20x <<-或8x >(3)153.【答案】(1)3y x = 3322y x =+(2)点C 的坐标为()5,0-或()3,0 4.【答案】(1)4b = 6k =;(2)6;(3)01x <≤.5.【答案】(1)122,23y y x x ==+(3)60x -<<或3x > 6.【答案】(1)4m = 8k ;(2)满足条件的点E 坐标为()2,0或()20-,. 7.【答案】(1)反比例函数解析式为14y x=,一次函数解析式为222y x =+(2)20x -<<或1x > 8.【答案】(1)反比例函数解析式6y x =,一次函数的解析式为:1y x =+;(2)11,03⎛⎫ ⎪⎝⎭或29,03⎛⎫- ⎪⎝⎭;(3)2x >或30x -<<9.【答案】(1)反比例函数的解析式为15y x =,点B 的坐标为()5,3--(2)50x <<﹣或3x > 10.【答案】(1)反比例解析式为2y x =,一次函数的解析式为23y x =-(2)313x =313-±1,147⎛⎫-- ⎪⎝⎭或()12--, 11.【答案】(1)284k n =-=,(2)20x -<<或4x >(3)812.【答案】(1)122y x =+ 6y x =;(2)()2332,. 13.【答案】(1)26y x =(2)2x >或60x -<<(3)102⎛⎫ ⎪⎝⎭,或702⎛⎫ ⎪⎝⎭, 14.【答案】(1)()0,3-;(2)一次函数的表达式为332y x =-,反比例函数的表达式为36y x =;(3)6x >. 15.【答案】(1)双曲线的解析式为2y x =-,直线AB 的解析式为 322y x =--(2)20x -≤<或 23x ≥(3)()1,2P -或()1,2P -。
反比例函数与一次函数图像交点的坐标特征及其应用
反比例函数与一次函数图像交点的坐标特征及其应用
反比例函数与一次函数图像交点是一个非常重要的研究话题,其中包括了不少有价值的坐标特征及其应用,本文将就此作一简单的探讨。
反比例函数是一种函数形式,其定义为:函数f(x)是反比例函数当且仅当它满足f(x)的绝
对值与正值x相乘的结果等于c(c>0)的关系,即|f(x)|=cx(c>0),其中c是一个正常数,用以表示函数f(x)的反比例系数。
x轴和y轴坐标系上的反比例函数x(x)可以写成
y=c/x(c>0)或y=c/x+t(c>0,t为常数)
一次函数是一种形式比较简单的一元函数,其定义为式y=ax+b中的函数,其中a是一个
常数,b也是一个常数,且a≠0 。
因此它的图像是一条直线,这条直线的斜率是a,方程
的参数b表示直线的截距。
反比例函数与一次函数图像交点坐标特征是这样一种性质:反比例函数x(x)和一次函数函
数y=ax+b(a≠0)图像相交时,交点坐标(x,y)满足复原式:c/x=ax+b。
反比例函数与一次函数图像交点坐标特征及其应用广泛,其中,应用于物理、数学、社会
科学甚至商业领域等范围广泛。
诸如定义函数、计算对比比例、物体的平衡、产量的调节
和经济效率的提高等方面应用均需要掌握反比例函数与一次函数图像交点的位置特征来进
行计算分析,因此理解反比例函数与一次函数图像交点的坐标特征及其应用是十分重要的。
总结而言,反比例函数与一次函数图像交点的坐标特征及其应用可以为物理、数学、社会科学甚至商业领域等实际问题的解决提供有用的参考和指导。
一次函数与反比例函数交点与k关系
一次函数与反比例函数交点与k关系一次函数与反比例函数交点与k的关系是研究函数图像的重要内容之一。
在数学中,一次函数也称为线性函数,其函数表达式为y = kx + b,其中k和b为常数,k代表斜率,b代表y轴截距。
而反比例函数的函数表达式为y = k/x,其中k为常数。
要求出一次函数与反比例函数的交点,就是要找到满足两个函数表达式的相等的x和y的值。
即对于一次函数y = kx + b和反比例函数y = k/x,找到满足kx + b = k/x的x和y的值。
通过解由此方程组成的二元一次方程组,即可求出相应于某个特定值k的一次函数与反比例函数的交点。
为了更清楚地研究一次函数与反比例函数交点与k的关系,可以进行以下步骤:1. 假设一次函数的k取固定值,例如k = 2,代入到方程kx +b = k/x中,求解方程,找到关于b的值。
例如,当k = 2时,方程简化为2x + b = 2/x,将方程转化为2x² + bx - 2 = 0,通过求解二次方程,得到关于b的值。
2. 将得到的关于b的值代入到一次函数的表达式中,得到特定k值对应的一次函数。
3. 对于反比例函数y = k/x,假设x取不同的值(可以取正数或负数),计算出相应的y值。
4. 通过解方程kx + b = k/x,找到满足此方程的x和y的值。
5. 继续重复步骤1-4,对于不同的k值进行计算和求解,得到不同k值下的一次函数与反比例函数的交点。
通过以上步骤,可以逐步计算出一次函数与反比例函数的交点,并且得到一次函数与k的关系。
可以通过绘制函数图像、计算坐标点等方式来更具体地说明一次函数与反比例函数交点与k的关系。
同时,还可以考虑使用数学软件或计算工具来进行计算和可视化展示,例如使用Matlab、Python语言中的数学库等来进行数值计算和绘图分析,以更方便地研究一次函数与反比例函数交点与k的关系。
需要注意的是,以上只是一种可能的研究方法,具体的分析过程和结论还需要根据具体情况和问题来确定。
