数控加工中的切点坐标计算
第二章 编程坐标系与数值计算

上节回顾一、
1、遵循右手笛卡儿直角坐标系 2、永远假设工件是静止的,刀具相 对于工件运动。 3、刀具远离工件的方向为正方向。
第二章 数控车床加工工艺设计
上节回顾二、
1、先确定Z轴。 a、传递主要切削力的主轴为Z轴。 b、若没有主轴,则Z轴垂直于工件装夹面。 c、若有多个主轴,选择一个垂直于工件装夹面的主轴为Z轴。
第二章 数控车床加工工艺设计
【实例】 在CK6150型数控车床上加工一个轴类零件,零件图2-7所示, 其中ø80的外径不加工(可用于装夹)。
图2-7 轴类零件加工实例 (1)确定工件的装夹方式及加工工艺路线 由于这个工件是一个实心轴, 并且轴的长度不很长,所以采用工件的左端面和ø80外圆作为定位基准。 使用普通三爪自定心卡盘夹紧工件,取卡盘的端面中心为工件坐标系的 原点,如图2-7所示。 加工顺序为:①倒角粗车M36×4螺纹外圆、ø50外圆,R35圆弧面
3)编程原点要尽量与设计基准或工艺基准统一,以利于保 证加工精度。
第二章 数控车床加工工艺设计
2.3.1确定编程坐标系,选择编程原点 原点选择要尽量满足编程简单,尺寸换算少,引
起的加工误差小等条件。
一般情况下,以坐标式尺寸标注的零件,程序原 点应选在尺寸标注的基准点;对称零件或以同心圆 为主的零件,程序原点应选在对称中心线或圆心上。
2、再确定X轴。(X轴始终水平,且平行于工件装夹面) a、没有回转刀具和工件,X轴平行于主要切削方向。(牛头刨) b、有回转工件,X轴是径向的,且平行于横滑座。(车、磨) c、有刀具回转的机床,分以下三类: Z轴水平,由刀具主轴向工件看,X轴水平向右。 Z轴垂直,由刀具主轴向立柱看,X轴水平向右。 龙门机床,由刀具主轴向左侧立柱看,X轴水平向右。
30201数值计算(精)
上一页 下一页 返回 2 .节点坐标计算 数控系统一般只具备直线插补和圆弧插补功能。当零件的轮 廓有非圆曲线,而数控系统又不具备该曲线的插补功能时, 其数值计算就比较复杂。处理方法是:在满足允许的编程误 差条件下, 采用若干小直线段或圆弧段来逼近非圆曲线, 逼近线段间的交点称为节点, 如图2-8所示。 3 .刀位点轨迹计算 4 .辅助计算
上一页 下一页 返回
图2-8
零件轮廓的节点
返回
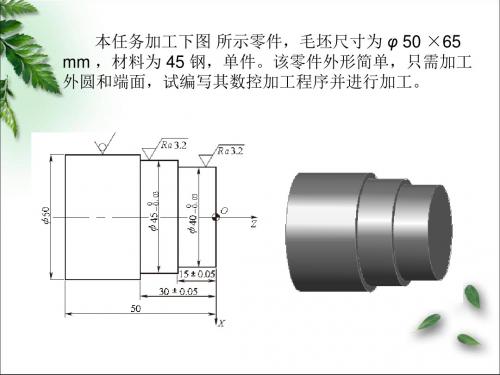
本任务加工下图 所示零件,毛坯尺寸为 φ 50 ×65 mm ,材料为 45 钢,单件。该零件外形简单,只需加工 外圆和端面,试编写其数控加工程序并进行加工。
数控编程数值计算
1 .基点坐标计算 基点就是构成零件轮廓的各相邻几何元素之间的交点或切点。 如两直线的交点、 直线与圆弧或圆弧与圆弧间的交点或切点、 圆弧与二次曲线的交点或切点等,均属基点。显然, 相邻基 点间只有一个几何元素。一般来说, 基点的坐标值利用一般 的解析几何或三角函数关系不难求得。
数控铣床第二章 手工编程中的数学处理

第二章 手工编程中的数学处理
一、作图计算法 作图计算法是以基准绘图为主,并辅以简单加减运算的一种处
理方法,也称作图法。因为这种方法完全依赖于手工及绘图仪的精 度,只适用于精度要求较低或加工轮廓比较简单的零件,因此比较 少用,在此不作介绍。
第二章 手工编程中的数学处理
二、代数、平面几何计算法 要求使用平面几何等数学知识来建立数学模型进行求解。 1)勾股定理:a2+b2=c2。 2)乘方公式:2=a2±2ab+b2。 3)一元二次方程:ax2+bx+c=0(a≠0)的求根公式为 4)圆的标准方程:2+2=R2。
种考级试题还是技能竞赛中都有出现,我们要重点掌握且要熟练运 用此方法。 1.直角三角形的边角关系
sinA=a/c,sinB=b/c,cosA=b/c,cosB=a/c 2.斜三角形的边角关系 1)由平面上任意两点间的距离公式得出余弦定理,即 =(2⁃4) 2)由三角形的面积公式可得出正弦定理,即 S=1/2bcsinA=1/2acsinB=1/2absinC(2⁃5)
图2-6 零件图一
第二章 手工编程中的数学处理
1.试说明基点与节点的区别,并说明利用CAD二维软件(AutoCAD、 CAXA)如何确定基点与节点坐标。 2.非圆曲线轮廓直线逼近的方法有哪些? 3.如图2-8所示,该轮廓形状由4条直线与3段圆弧组成,圆O1(0,4 0),R=25mm;圆O2(50,100),R=55mm;圆O3(60,20),R=15m m;F点坐标为(65,0),试求基点A、B、C、D、E在工件坐标系 中的坐标值。
第二章 手工编程中的数学处理
第二节 基点的计算 零件的轮廓是由许多不同的几何要素所组成的,如直线、圆弧、
数控车床常用计算公式
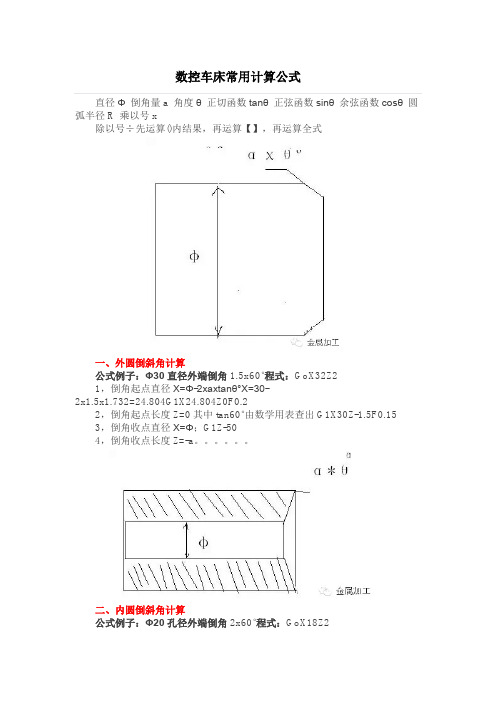
直径Φ 倒角量a 角度θ 正切函数tanθ 正弦函数sinθ 余弦函数cosθ 圆弧半径R 乘以号x除以号÷先运算()内结果,再运算【】,再运算全式一、外圆倒斜角计算公式例子:Φ30直径外端倒角1.5x60°程式:GoX32Z21,倒角起点直径X=Φ-2xaxtanθ°X=30-2x1.5x1.732=24.804G1X24.804Z0F0.22,倒角起点长度Z=0其中tan60°由数学用表查出G1X30Z-1.5F0.153,倒角收点直径X=Φ;G1Z-504,倒角收点长度Z=-a。
二、内圆倒斜角计算公式例子:Φ20孔径外端倒角2x60°程式:GoX18Z21,倒角起点直径X=Φ+2xaxtanθ°x=20+2x2x1.732=26.928G1x26.928Z0F0.2 2,倒角起点长度Z=0G1X20Z-2F0.153,倒角收点直径X=Φ;G1Z-304,倒角收点长度Z=-a。
三、外圆倒圆角计算公式例子:Φ35直径外端圆角R3程式:GoX36Z21,倒角起点直径X=Φ-2*RX=35-2x3=29G1X29Z0F0.22,倒角起点长度Z=0G3X35Z-3R3F0.153,倒角收点直径X=Φ;G1Z-304,倒角收点长度Z=-R。
四、内圆倒圆角计算公式例子;Φ20孔径外端圆角R2程式:G0X18Z21,倒角起点直径X=Φ+2*RX=20+2x2=24G1X24Z0F0.22,倒角起点长度Z=0G2X20Z-2R2F0.13,倒角收点直径X=Φ;G1Z-254,倒角收点长度Z=-R。
五、G90、G92数控指令R锥度值的计算:例子:大端Φ35小端Φ32锥体长20牙长16mm让刀3mm加工1、计算图上锥度比例值:(32-35)/20=-0.15程式;G0X37Z3(起始端直径-收点端直径)÷锥体长度G92X33.8Z-16R-1.425F22、计算G92实际R值(车牙时,起始端至收点端的半径差):-0.15X1/2X(16+3)=-1.425X33.1锥度比例值x1/2x(有效牙长度+让刀位置)X32.63、G92的收刀点直径:35+(-0.15X(20-16))-2X1=32.4X32.4锥体收点端直径+锥度比例值x(锥体长度—有效螺纹长度)—2x牙高。
课后习题答案

课后习题答案第一章1什么是数控系统?什么是数控机床?数控系统是实现数字控制相关功能的软、硬件模块的集成。
它能自动阅读输入载体上的程序,并将其译码,根据程序指令向伺服装置和其他功能部件发送信息,控制机床的各种运动。
数控机床是指应用数控技术对其运动和辅助动作进行自动控制的机床。
2简述数控加工的过程。
将被加工零件图上的几何信息和工艺信息用规定的代码和格式编制成加工程序,然后将该程序输入数控装置。
数控系统按照加工程序的要求,先进行相应的插补运算和编译处理,然后发出控制指令,使各坐标轴、主轴及辅助系统协调动作,实现刀具与工件的相对运动,自动完成零件的加工。
3判定数控机床坐标系的方法是什么?数控机床的坐标系采用笛卡儿右手直角坐标系。
基本坐标轴为X、丫、Z轴,它们与机床的主要导轨相平行,相对于每个坐标轴的旋转运动坐标分别为A、B、Co不论数控机床的具体结构是工件静止、刀具运动,还是刀具静止、工件运动,都假定工件不动,刀具相对于静止的工件运动。
机床坐标系X、丫、Z轴的判定顺序为:先Z轴,再X轴,最后按右手定则判定丫轴。
增大刀具与工件之间距离的方向为坐标轴运动的正方向。
4数控机床的坐标轴与运动方向是怎样规定的?(I)Z轴:平行于主轴轴线的坐标轴为Z轴,刀具远离工件的方向为Z轴的正方向。
(2) X轴:平行于工件装夹平面的坐标轴为X轴,它一般是水平的,以刀具远离工件的运动方向为X轴的正方向。
对于工件是旋转的机床,X轴为工件的径向。
对于刀具是旋转的立式机床,从主轴向立柱看,右侧方向为X轴的正方向。
对于刀具是旋转的卧式机床,从刀具(主轴)尾端向工件看,右侧方向为X轴的正方向。
(3) Y轴:丫轴垂直于X、Z轴,当X、Z轴确定之后,按笛卡儿直角坐标右手定则判断丫轴及其正方向。
(4)旋转运动A、B、C轴:旋转运动坐标轴A、B和C的轴线平行于X、Y和Z轴,其旋转运动的正方向按右手螺旋定则判定。
5工件原点的偏置方法有哪些?当工件在机床上固定以后,工件原点与机床原点也就有了确定的位置关系,即两坐标原点的偏差就已确定。
五轴联动数控加工中的刀具轨迹控制算法

五轴联动数控加工中的刀具轨迹控制算法五轴联动数控加工是一种高精度、高效率的加工方式,可以实现对复杂曲面的加工。
在五轴联动数控加工中,刀具轨迹控制算法起着至关重要的作用,决定了加工精度和效率。
本文将介绍几种常见的刀具轨迹控制算法,并对其原理和应用进行详细阐述。
1. 五轴联动数控加工概述五轴联动数控加工是指在数控加工机床上,通过同时控制五个坐标轴的运动,实现对工件的加工。
相比于传统的三轴加工,五轴联动可以更加灵活地加工复杂曲面,提高加工质量和效率。
2. 刀具轨迹控制算法的作用刀具轨迹控制算法是五轴联动数控加工中的关键技术之一。
它可以根据工件的三维模型和加工要求,计算出刀具在加工过程中的运动轨迹,从而实现精确的加工。
刀具轨迹控制算法的好坏直接影响加工精度和效率。
3. 刀具轨迹控制算法的分类刀具轨迹控制算法可以分为两类:离散点算法和曲线插补算法。
离散点算法是指将工件曲面离散化为一系列离散点,然后通过逐点加工来实现曲面加工。
常见的离散点算法有直线连接法、圆心法和切点法等。
这些算法简单直观,适用于加工简单曲面。
曲线插补算法是指根据工件的曲线方程和刀具半径,通过插补计算出刀具的运动轨迹。
常见的曲线插补算法有圆弧插补法、曲线插补法和样条插补法等。
这些算法可以实现对复杂曲面的高精度加工。
4. 圆弧插补算法圆弧插补算法是五轴联动数控加工中最常用的一种刀具轨迹控制算法。
它通过计算刀具半径和工件曲线的切向方向,确定刀具的圆弧插补路径。
圆弧插补算法具有计算简单、加工效率高的优点,适用于多数加工场景。
5. 曲线插补算法曲线插补算法是一种更加精细的刀具轨迹控制算法,可以实现对复杂曲面的高精度加工。
曲线插补算法通过计算刀具在曲线上的切向方向和曲率,确定刀具的插补路径。
与圆弧插补算法相比,曲线插补算法需要更复杂的计算和控制,但可以实现更高的加工精度。
6. 样条插补算法样条插补算法是一种基于数学样条曲线的刀具轨迹控制算法。
它通过计算曲面上的样条曲线,将刀具的运动路径进行插补。
数控编程之刀具点位坐标全套知识
数控编程之刀具点位坐标全套知识数控编程之刀具点位坐标全套知识1.刀位点刀位点是刀具上的一个基准点,刀位点相对运动的轨迹即加工路线,也称编程轨迹。
2.对刀和对刀点对刀是指操作员在启动数控程序之前,通过一定的测量手段,使刀位点与对刀点重合。
可以用对刀仪对刀,其操作比较简单,测量数据也比较准确。
还可以在数控机床上定位好夹具和安装好零件之后,使用量块、塞尺、千分表等,利用数控机床上的坐标对刀。
对于操作者来说,确定对刀点将是非常重要的,会直接影响零件的加工精度和程序控制的准确性。
在批生产过程中,更要考虑到对刀点的重复精度,操作者有必要加深对数控设备的了解,掌握更多的对刀技巧。
(1)对刀点的选择原则在机床上容易找正,在加工中便于检查,编程时便于计算,而且对刀误差小。
对刀点可以选择零件上的某个点(如零件的定位孔中心),也可以选择零件外的某一点(如夹具或机床上的某一点),但必须与零件的定位基准有一定的坐标关系。
提高对刀的准确性和精度,即便零件要求精度不高或者程序要求不严格,所选对刀部位的加工精度也应高于其他位臵的加工精度。
选择接触面大、容易监测、加工过程稳定的部位作为对刀点。
对刀点尽可能与设计基准或工艺基准统一,避免由于尺寸换算导致对刀精度甚至加工精度降低,增加数控程序或零件数控加工的难度。
为了提高零件的加工精度,对刀点应尽量选在零件的设计基准或工艺基准上。
例如以孔定位的零件,以孔的中心作为对刀点较为适宜。
对刀点的精度既取决于数控设备的精度,也取决于零件加工的要求,人工检查对刀精度以提高零件数控加工的质量。
尤其在批生产中要考虑到对刀点的重复精度,该精度可用对刀点相对机床原点的坐标值来进行校核。
(2)对刀点的选择方法对于数控车床或车铣加工中心类数控设备,由于中心位臵(X0,Y0,A0)已有数控设备确定,确定轴向位臵即可确定整个加工坐标系。
因此,只需要确定轴向(Z0或相对位臵)的某个端面作为对刀点即可。
对于三坐标数控铣床或三坐标加工中心,相对数控车床或车铣加工中心复杂很多,根据数控程序的要求,不仅需要确定坐标系的原点位臵(X0,Y0,Z0),而且要同加工坐标系G54、G55、G56、G57等的确定有关,有时也取决于操作者的习惯。
数控加工切削参数计算公式
数控加工切削参数计算公式
1.切削速度:切削速度是指工件表面上单位时间内被切削掉的长度。
切削速度的计算公式为:
切削速度(Vc)=π×刀具直径(D)×转速(n)
2.进给速度:进给速度是指切削刀具在单位时间内在工件上的移动距离。
进给速度的计算公式为:
进给速度(Vf)=切削速度(Vc)×进给量(f)
3.主轴转速:主轴转速是指主轴每分钟旋转的圈数,可以通过切削速度和刀具直径来计算,也可以根据机床性能和加工工艺选择合适的主轴转速。
4.加工时间:加工时间是指完成一次切削加工所需的时间,可以通过计算工件长度和进给速度来估算。
加工时间的计算公式为:
加工时间(T)=工件长度(L)/进给速度(Vf)
5.切削力:切削力是切削加工中刀具对工件产生的力,影响机床的刚性和切削质量。
切削力的计算公式包括切削力系数、切削力的方向和切削力的大小。
切削力的计算需要根据刀具的几何形状和材料的性质进行实验或理论推导。
6.切削功率:切削功率是指切削加工中刀具对工件消耗的功率,可以通过切削力和切削速度来计算。
切削功率的计算公式为:
切削功率(Pc)=切削力(Fc)×切削速度(Vc)。
数控加工中互成角度面的坐标系计算
数控加工中互成角度面的坐标系计算刘伟山推工程机械股份有限公司摘要在数控加工中,时有互成角度且非垂直的平面的加工。
为解决以往靠划线建立坐标系存在的误差较大的问题,本文介绍了一种新颖的坐标系计算方法。
关键词:数控;角度;坐标系Liu WeiSHANTUI CONSTRUCTION MACHINERY CO., LTD.AbstractIn CNC machining, there are angled and non-vertical planes sometimes. In order to resolve the problem of lineation error in establishing coordinate systems, this paper introduces a new way to calculate coordinate systems.Keywords: CNC; angled; coordinate systems1、问题描述在数控加工中,有时会遇到互成角度且非垂直的平面的加工。
以我厂加工过的某壳体类零件为例,先介绍一下以往采用的传统工艺方案。
工件外形如上图,需要加工的为正反两面、各孔、呈135°角的两平面及各螺纹孔。
该件为小批量生产,未投入工装。
大致的加工工艺为:划正反面线,粗铣正反面,划大孔十字线,车大孔及端面,精铣端面及打孔点,铣两侧面并钻攻侧面螺纹孔,钻攻两端面各孔。
铣两侧面工序在卧式加工中心上完成。
建立坐标系的过程大致如下:放平工件,按十字线拉直;用中心钻对出划线的X、Z坐标,计为十字线中心坐标;根据机床回转中心,利用CAD软件计算出两侧面旋转到垂直于主轴方向时的坐标,如下图所示:实际测量时,发现侧面到大孔中心的距离经常超出公差要求。
分析原因如下:1)十字线作为粗基准被重复使用了两次,形成了较大的基准不重合误差。
车削大孔后,大孔的圆心已与划线存在误差,铣面时再以划线为基准会累积此误差,约在1mm以内,2)用中心钻对线的方法,形成了较大的基准位移误差。
数控加工程序中的数值计算(小编整理)
数控加工程序中的数值计算(小编整理)第一篇:数控加工程序中的数值计算数控编程人员能否按照零件图的技术要求,编制出数控加工程序,其关键环节是编程尺寸的确定。
根据被加工零件图的要求,按照已经确定的加工工艺路线和允许的编程误差,计算机床数控系统所需要输入的数据,称为数值计算。
确定编程尺寸实际上是零件图件进行的数学处理,计算零件图进行的数学处理,计算零件图形和点在坐标系中的坐标值和运动轨迹。
数值计算一般包括以下内容。
1、基点和节点的坐标计算零件的轮廓是由直线、圆弧、二次曲线等几何要素组成的,各几何要素之间的连接点称为基点。
如两直线的交点,直线与圆弧、圆弧与圆弧的交点或切点,圆弧与其他二次曲线的交点或切点等。
基点的坐标是编程中必需的重要数据。
如果零件的轮廓是曲直线和圆弧以外的其他曲线构成的,而数控系统以不具备该曲线的插补功能时,就需要进行一定的数学外理。
数学处理的方法是:将构成零件的轮廓曲线,按数控系统插补功能的要求,在允许的编程误差的条件下,用若干直线段或圆弧去逼近零件轮廓非圆曲线,这些逼近线段与被加工曲线的交点或切点称为节点。
在编程时,一般按节划分程序段,节点多少是曲逼近线段的数目决定的。
逼的线段的近似区间越大,则节点数越少,程序段也会越少,但逼近误差应小于或等于编程允许误差。
考虑到工艺系统及计算误差的因素,一般取编程允许误差为零件公差的1/5——1/10。
2、刀位点轨迹的计算零件图上的数据是按零件轮廓尺寸给出的,加工时刀具是按刀位点轨迹运动的,零件的轮廓形状是由刀具切削刃进行切削形成的。
对于具有刀具半径补偿功能的数控机床面而言,只要在编写程序时,在程序的适当位置于写入建立刀具补偿的有关指令,就可以保证在加工过程中,使刀位点按一定的规则自动偏离编程轨迹,达到正确加工的目的。
这时可直接按零件轮廓的形状,计算各基点和节点坐标,并作为编程时的坐标数据。
对于没刀具半径补偿功能的数控机床,编程时,需按刀具的刀位点轨迹计算基点和节点坐标值,作为编程时的坐标数据,按零件轮廓的等距线编程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ISSN 1008—9446
7面
承德石油高等专科学校学报 第10卷第2期,2008年6月
Journal of Chengde Petroleum College Vo1.10,No.2,Jun.2008
数 控加工中的切点 坐标计算
倪红兵,邹克武
(承德石油高等专科学校机械工程系,河北承德067000)
摘要:在数控加工中,零件轮廓的数值计算是必须的,而两图素之间的圆弧过渡情况下求切点坐标是难点。
针对车间现场条件,总结出切点坐标的计算方法,给出计算式,为现场计算提供了极大方便。
关键词:切点计算;零件轮廓;数控加工
中图分类号:TG659 文献标识码:B 文章编号:1008—9446(2008)02-0034-02
Calculation of Points of Tangency in CNC Machining
NI Hong.bing.Z0U Ke.WLi
(Department of Mechanical Engineering,Chengde Petroleum College,Chengde 067000,Hebei,China)
Abstract:According to drawings,it is necessary and difficult to calculate the points of tangency.
The formulas of solving the problem are summarized.This is usable for technicians in CNC
machining.
Key words:calculation of the points of tangency;part contour;C NC machining
在数控加工中,当操作者得到图样,在编程前要进行数值计算。对于大多数的图素交点或特征点都
可以在图样中轻易获得,而当遇到两个图素之间是圆弧过渡时,其切点的计算就比较困难…。在没有计
算机,并且不能使用CAD软件的条件下,为赢得时间,提高效率,快速准确地计算出切点坐标,就很具有
实际意义。下面给出仅仅借助计算器就能算出切点坐标的计算方法。
1 计算方法
由于大多数的数控系统只有直线插补和圆弧插补两种 ,因此根据图样上的两个相邻图素之间为
圆弧过渡情况可分为三种,即直线与直线之间、直线与圆弧之间和圆弧与圆弧之间的过渡。在此,将两
个相邻图素称为轮廓图素,包括轮廓直线或轮廓圆弧,而过渡图素为过渡圆弧,轮廓图素与过渡图素之
间的切点坐标可通过切点与已知点坐标的增量关系来获得 。
1.1直线与直线之间的圆弧过渡
如图1所示,两条轮廓直线与过渡圆弧的切点 ( ,Ym)和Ⅳ( ,
Y ),已知:两直线夹角 , <180。,交点A( ,Y。);直线与 轴夹角分
别为卢和 ,卢≤90。, ≤90。;过渡圆弧半径R。
,n,、
设 Ⅳ : Ⅳd:,,那么z:R・ctgf号l。
、厶,
则切点 的坐标:X =X ±z・c0 ,Ym:YO±z・sin卢
公式中的“±”号要依据切点与交点A的坐标增量关系来选取,即
过点A作铅垂线和水平线,切点在铅垂线右侧, 计算式中取“+”,否
则取“一”;切点在水平线以上,y 计算式中取“+”,否则取“一”。
图l直线与直线之间的圆弧过渡
收稿日期:2008-03-22
作者简介:倪红兵(1967一),男,广西阳朔人,河北承德石油高等专科学校机械工程系工程师,学士,主要从事机械
设计和数控技术等方面的研究。
维普资讯 http://www.cqvip.com
倪红兵,等:数控加工中的切点坐标计算 ・35・
同理得切点Ⅳ的坐标: =X ±Z・COSg,,Yn=Y ±Z・sing,。式中“±”取法同上。
1.2直线与圆弧之间的圆弧过渡
如图2所示,轮廓直线和轮廓圆弧与过渡圆弧的切点分别为M(X ,Ym)和N(X ,y^),已知:过渡圆
弧半径R;轮廓直线与 轴夹角 , ≤90。;轮廓圆弧半径R ,圆心A( ,Y )。设过渡圆弧圆心P( ,
);轮廓圆弧与过渡圆弧中心线AP与X轴夹角JB,fl ̄<90。。图2直线与圆弧之间的圆弧过渡
由图样条件,分别写出轮廓圆弧的等距线方程(偏置距离为R)和轮
廓直线的等距线方程(偏置距离为R),两方程联立求解。可以解得两组
坐标,根据图样条件,排除不符合图样的一组坐标,最后得到过渡圆弧的
圆心P(Xp,y。)。
则切点 的坐标: :Xp±R・sins,rm=y口±R・COS O/
l y—y l
由t =l— l,可解得两圆弧的圆心连线与X轴夹角JB。 I
n
—
A.
p I
则切点Ⅳ的坐标:X =Xp±R・cos/3,Yn= ±R・sin JB
公式中的±号选择同样依据切点与已知点的坐标增量关系而判断。
1.3 圆弧与圆弧之间的圆弧过渡
如图3所示,两轮廓圆弧与过渡圆弧的切点分别为 ( ,Ym)
和Ⅳ( ,Yn),已知:过渡圆弧半径R;两轮廓圆弧半径R。和R ,圆心
分别为A( ,Ya)和 ( ,Y )。设三圆弧的中心线所成的△PAB的
两内角分别为Ot和JB,连线A 与 轴夹角 , ≤90。。
由余弦定理COSOt= 安;-_ ,可求得
,
同理也可求得JB。
则切点 的坐标:X
( ± )
图2直线与圆弧之间的圆弧过渡
=X
o
±Ro。c。s( ± ),ym= ±R。。sin 图3圆弧与圆弧之间的圆弧过渡
A
同理得Ⅳ的坐标: =X6±R6・cos(,e士 ),Yn=y6士R6・sin( ̄± )
以上两个切点的坐标计算式中都有两处“±”号需要判断,其中正弦和余弦中角度的“±”号选择要
依据两圆弧圆心A和 的高低来确定,而增量关系的符号判断要依据切点与圆弧圆心的关系来确定。
2 总结
以上所述计算方法具有通用性,是具有普遍意义的一般计算式,如果图样所示的已知条件特殊,例
如轮廓直线平行于某坐标轴,或者两个圆弧半径相等的情况,计算式可以更简化,而且更容易判断。
以上推导不是单纯的解数学题,而是解决工程实践中出现的问题,因此所列计算式对实际工作具有
很好的指导作用。而且在历届全国数控技能大赛中,都有类似的考题出现,考察选手在现场快速计算基
点和节点的能力 。虽然切点的计算方法并非唯一,但所列计算式简单实用,借助计算器能够很方便地
将问题解决在工作现场。
参考文献:
[1] 于春生.数控机床编程及应用[M].北京:高等教育出版社,2000.
[2]Thomas M.Crandel1.数控加工与编程[M].北京:化学工业出版社,2004.
[3] 沈建峰.数控铣床加工中心操作工(高级)[M].北京:机械工业出版社。2002
[4] 袁锋.全国数控大赛试题精选[M].北京:机械工业出版社,2005.
维普资讯 http://www.cqvip.com
