基于改进IGGⅢ和快速分解法的电力系统状态估计算法
基于动力学系统的状态估计算法

基于动力学系统的状态估计算法赵天骐;江晓东;李鹏;白浩;于力【摘要】状态估计的收敛性是电网在线实时监测和控制的关键问题,常用的高斯-牛顿最小二乘算法在系统出现严重的拓扑错误以及存在不可观状态变量时难以收敛.针对这一问题,本文提出基于动力学系统的状态估计算法,通过构造商梯度动力系统,使其退化的稳定平衡流形与状态估计的最小二乘解对应,然后追踪该动力学系统的轨迹从而得到原状态估计问题的解.本文从非线性动力学系统理论出发,证明了该商梯度动力学系统是渐近稳定的,从而保证了算法的收敛性.最后用IEEE 14节点和IEEE 118节点算例对算法进行测试,验证了该算法的有效性.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2018(030)008【总页数】6页(P81-86)【关键词】状态估计;动力学系统;加权最小二乘;不可观测性【作者】赵天骐;江晓东;李鹏;白浩;于力【作者单位】天津大学电气自动化与信息工程学院,天津 300072;天津大学电气自动化与信息工程学院,天津 300072;南方电网科学研究院有限责任公司,广州510080;南方电网科学研究院有限责任公司,广州 510080;南方电网科学研究院有限责任公司,广州 510080【正文语种】中文【中图分类】TM711电力系统状态估计是能量管理系统EMS(ener⁃gy management system)的主要功能之一,在监测和控制电力系统的可靠运行方面发挥着重要作用。
状态估计器通过电压、电流、线路功率、注入功率等测量来估计整个系统的状态,即每个母线的电压幅值和相角。
这些测量由数据采集与监视控制系统的远动终端提供。
状态估计结果为其他EMS功能,如安全分析、最优潮流、电压稳定性分析等提供基础。
因此状态估计的收敛性是电网在线实时监测和控制的关键。
基于高斯-牛顿迭代法的加权最小二乘WLS(weighted least squares)算法是最常用的状态估计算法。
面向高配电网的分布式状态估计及其优化算法

面向高配电网的分布式状态估计及其优化算法第一章前言随着电力行业的快速发展,电网规模不断扩大,电力系统复杂度不断提高。
对高配电网的需求越来越迫切。
高配电网需要面对更多的挑战,如更高的电压等级、更大的电流负载、更复杂的故障特性等。
在这种情况下,传统的电力系统管理方法已经远远不能满足需求。
分布式状态估计技术应运而生。
本文将详细介绍面向高配电网的分布式状态估计及其优化算法。
第二章分布式状态估计基础知识分布式状态估计是一种集成分布式计算和协作控制思想的新型电力系统状态估计技术。
它通过在分布式计算机上同时执行一系列状态估计算法,从而实现对电力系统各电气量进行实时估计。
分布式状态估计技术的优势在于能够提高状态估计的精度和实时性,同时也降低了状态估计的计算负担。
分布式状态估计技术的关键技术包括分布式数据采集、分布式数据通信、分布式协同算法、分布式状态估计算法等。
其中,分布式数据采集是实现分布式状态估计的重要前提,它能够采集到分布式计算机上的各种电气量数据。
分布式数据通信能够实现分布式计算机之间的数据传输和共享。
分布式协同算法是以分布式计算机为基础,实现电力系统状态估计的关键技术。
分布式状态估计算法是指在整个电力系统中所有节点上同时运行的状态估计算法。
第三章面向高配电网的分布式状态估计优化算法在面向高配电网的分布式状态估计中,存在一些问题,如状态估计精度低、状态估计速度慢、通讯延迟等。
基于这些问题,本文提出了一种基于加权贡献度的面向高配电网的分布式状态估计优化算法。
该算法主要从以下几个方面进行改进:1. 加权贡献度的概念引入。
对于状态估计算法中每个变量的参数,计算其在整个电力系统中的权重和贡献度。
然后根据每个变量的权重和贡献度进行加权处理,以此提高状态估计算法的精度。
2. 网络拓扑结构的优化设计。
将电力系统划分成多个区域,并使用分层策略来设计区域的网络拓扑结构。
通过优化网络拓扑结构,减少分布式计算机之间的通讯延迟,提高状态估计算法的速度。
3节电力系统状态估计(WLS算法)
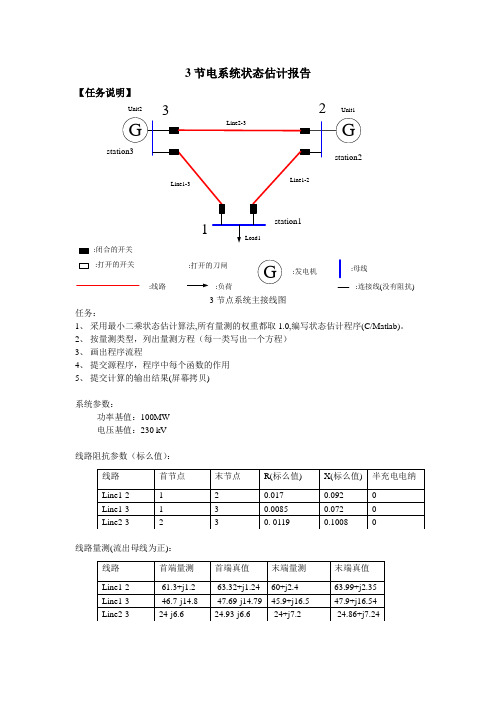
3节电系统状态估计报告【任务说明】:闭合的开关:打开的开关:打开的刀闸:线路:负荷G:发电机:母线:连接线(没有阻抗) Unit2Unit13节点系统主接线图任务:1、采用最小二乘状态估计算法,所有量测的权重都取1.0,编写状态估计程序(C/Matlab)。
2、按量测类型,列出量测方程(每一类写出一个方程)3、画出程序流程4、提交源程序,程序中每个函数的作用5、提交计算的输出结果(屏幕拷贝)系统参数:功率基值:100MW电压基值:230 kV线路阻抗参数(标么值):线路量测(流出母线为正):母线电压量测:负荷量测(流出母线为正):发电量测(流入母线为正):注:量测存在误差【数据预处理】首先根据基值将已知的量测值均转换为标幺值,并将功率值转换为流入量,得到如下数据:线路导纳参数(标么值):线路注入功率量测(标幺值):负荷点注入功率量测(标幺值):发电机节点注入量测(流入母线为正):发电机量测真值unit2 0.88-j0.0424 0.8892-j0.0424unit3 0.23+j0.24 0.2304+j0.2378母线电压量测(标幺值):母线电压量测真值(幅值/角度)1 1.0087 1.0130/02 1.0198 1.0242/3.233 1.0281 1.0281/1.82【量测方程】选择节点1的电压相角为参考,为0度,以vi表示误差值。
1)节点1电压量测方程:Vi=Vi+v1即1.0087=V1+v12)1-3支路1号节点处注入有功功率功率:P ij=V i2g ij-V i V j(g ij cos+b ij sin)+v20.613=V12g13-V1V3(g13cos+b13sin)+v2即0.613=-1.6171V12-V1V3(-1.6171cos +13.698sin)+v2 3)1号节点注入功率:P i=V i2G ii +G ij cos+B ij sin+v3P1=V12G11+G1j cos+B1j sin+v3即-1.11=3.5613V12+V1V2(-1.9442cos -10.5107sin)+V1V3(-1.6171 cos -13.698 sin)+v3【流程图】【计算结果】其中iterations 为迭代次数,可见本例的迭代次数为4,收敛较快,状态估计得到的节点1、2、3电压分别为:234.0144444444444444444444444444444444444444444444【程序说明】遥测数据给定V 0,,k=0计算H(V (k),)和h(V (k),)A=H T R -1H, b=H T R -1(Z-h)求解A X=b,得Xk=k+1X (k+1)=X (k)+XNmax|X|<Y结束1、计算h矩阵的函数cal_hfunction h=cal_h(V,th0,B,G) %其中,V为节点电压估计值,th0为节点电压相角估计%值,B为节点电导矩阵,G为节点电纳矩阵b=-B; %线路电导矩阵g=-G; %线路电纳矩阵P=zeros(3,1); %初始化,节点注入功率Q=zeros(3,1);PP=zeros(3,3); %线路注入功率QQ=PP;th=[0;th0]; %节点1的电压相角为0for i=1:3P_P=0;Q_Q=0;for j=1:3if(j~=i)P_P=P_P+V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));Q_Q=Q_Q+V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PP(i,j)=(V(i)^2)*g(i,j)-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQ(i,j)=-(V(i)^2)*b(i,j)-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));endendP(i)=(V(i)^2)*G(i,i)+P_P;Q(i)=-(V(i)^2)*B(i,i)+Q_Q;endVV=[V(1);V(2);V(3)];h=[P;Q;PP(1,2);PP(2,3);PP(3,1);QQ(1,2);QQ(2,3);QQ(3,1);PP(1,3);PP(2,1);P P(3,2);QQ(1,3);QQ(2,1);QQ(3,2);VV];2、计算H矩阵的函数cal_HHfunction H=cal_HH(V,th0,G,B,P,Q) %其中,P,Q为根据电压估计值计算得到的节点%注入电压b=-B;g=-G;PV=zeros(3,3); %节点注入功率对电压幅值的偏导数QV=zeros(3,3);Pth=zeros(3,3); %节点注入功率对电压相角的偏导数Qth=zeros(3,3);PPV=zeros(3,3); %P ij对V j的偏导数QQV=zeros(3,3); %Q ij对V j的偏导数PPth=zeros(3,3); %P ij对th j的偏导数QQth=zeros(3,3); %Q ij对th j的偏导数PPV1=zeros(3,3); %P ij对V i的偏导数QQV1=zeros(3,3); %Q ij对V i的偏导数PPth1=zeros(3,3); %P ij对th i的偏导数QQth1=zeros(3,3); %Q ij对th i的偏导数VV=eye(3);Vth=zeros(3,2);th=[0;th0];for i=1:3for j=1:3if (i~=j)PV(i,j)=V(i)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));QV(i,j)=V(i)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));PPV(i,j)=-V(i)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQV(i,j)=-V(i)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));PPV1(i,j)=2*V(i)*g(i,j)-V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));QQV1(i,j)=-2*V(i)*b(i,j)-V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));if (j~=1)Pth(i,j)=V(i)*V(j)*(G(i,j)*sin(th(i)-th(j))-B(i,j)*cos(th(i)-th(j)));Qth(i,j)=-V(i)*V(j)*(G(i,j)*cos(th(i)-th(j))+B(i,j)*sin(th(i)-th(j)));PPth(i,j)=-V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j)));QQth(i,j)=-V(i)*V(j)*(-g(i,j)*cos(th(i)-th(j))-b(i,j)*sin(th(i)-th(j)));endif(i~=1)PPth1(i,j)=V(i)*V(j)*(g(i,j)*sin(th(i)-th(j))-b(i,j)*cos(th(i)-th(j))); QQth1(i,j)=-V(i)*V(j)*(g(i,j)*cos(th(i)-th(j))+b(i,j)*sin(th(i)-th(j)));endelsePV(i,j)=(G(i,i)*(V(i)^2)+P(i))/V(i);QV(i,j)=(Q(i)-(V(i)^2)*B(i,i))/V(i);if (j~=1)Pth(i,j)=-B(i,i)*(V(i)^2)-Q(i);Qth(i,j)=P(i)-(V(i)^2)*G(i,i);endendendendH=[[PV,Pth(:,2:3)];[QV,Qth(:,2:3)];...[PPV1(1,2),PPV(1,2),0,PPth(1,2),0;...0,PPV1(2,3),PPV(2,3),PPth1(2,3),PPth(2,3);...PPV(3,1),0,PPV1(3,1),0,PPth1(3,1)];...[QQV1(1,2),QQV(1,2),0,QQth(1,2),0;...0,QQV1(2,3),QQV(2,3),QQth1(2,3),QQth(2,3);...QQV(3,1),0,QQV1(3,1),0,QQth1(3,1)];...[PPV1(1,3),0,PPV(1,3),0,PPth(1,3);...PPV(2,1),PPV1(2,1),0,PPth1(2,1),0;...0,PPV(3,2),PPV1(3,2),PPth(3,2),PPth1(3,2)];...[QQV1(1,3),0,QQV(1,3),0,QQth(1,3);...QQV(2,1),QQV1(2,1),0,QQth1(2,1),0;...0,QQV(3,2),QQV1(3,2),QQth(3,2),QQth1(3,2)];...[VV,Vth]];3、主程序calculate_all.m文件format longG=[3.5613,-1.9442,-1.6171;...-1.9442,3.0993,-1.1551;...-1.6171,-1.1551,2.7722]; %B为节点电导矩阵B=[-24.2087,10.5107,13.698;...10.5107,-20.295,9.7843;...13.698,9.7843,-23.4832]; %G为节点电纳矩阵P=[-1.11;0.88;0.23]; %节点注入功率量测值Q=[-0.135;-0.0424;0.24];PP=[0.613;-0.24;-0.459]; %线路1-2,2-3,3-1注入功率在首端的量测值QQ=[-0.012;0.066;-0.165];PP1=[0.467;-0.6;0.24]; %线路1-3,2-1,3-2注入功率在首端的量测值QQ1=[0.148;-0.024;-0.072];V=[1.0087;1.0198;1.0281]; %节点电压幅值量测值R=diag(ones(21,1)); %权重都取为1Z=[P;Q;PP;QQ;PP1;QQ1;V]; %量测值矩阵V0=[1;1;1]; %初值th0=[0;0];delta=100;iterations=0; %迭代次数while delta>0.000001iterations=iterations+1;h=cal_h(V0,th0,B,G); %计算h矩阵H=cal_HH(V0,th0,G,B,h(1:3,1),h(4:6,1)); %计算H矩阵A=H'*inv(R)*H;b=H'*inv(R)*(Z-h);d=A\b; %求解修正值delta=max(abs(d));V0=V0+d(1:3,1); %修正估计值th0=th0+d(4:5,1);enditerationsV0=V0*230; %转换为有名值th0=th0*180/pi; %转换为度for i=1:3j=num2str(i);v=num2str(V0(i));show1=strcat('The voltage magnitude of node ',j,' is', v,' kV');disp(show1);endfor i=1:2j=num2str(i+1);th=num2str(th0(i));show1=strcat('The phase angle of node ',j,' is ',th,' degrees');disp(show1);end。
基于等效功率变换的配电网状态估计算法

e
式中: I f s 表示计算得到的线路 lf s 上的电流幅值; V f 表示计算得到的节点 f 的电压幅值; P f s 和 Q f s 分别 表示计算得到的线路 lf s 首端有功和无功功率; W 和 e W 分别表示实际量测的权重和等效量测的权重。
5 添加零虚拟负荷量测提高数值可观性
李 建, 王心丰, 段 刚, 韩英铎
( 清华大学电机系, 北京市 100084)
摘要: 提出一种基于等效功率变换的配电网状态估计算法, 将配电网中的功率量测、 电压幅值量 测、 电流幅值量测统一变换为支路首端等效功率量测, 采用修正量测雅可比矩阵的迭代方法求解。 该方法能够利用配电网中的各种量测, 并且 P , Q 解耦迭代, 有较高的运算效率和数值稳定性, 对量 测配置也无特殊要求。 文中还提出一种通过添加零虚拟负荷量测提高数值可观性的方法, 使原本不 可估计的网络能够进行状态估计。 关键词: 状态估计; 量测变换; 配电系统; 等效功率变换 中图分类号: TM 744; TM 727. 2
节点电压幅值等效量测权重:
W
e
PV f
Pfs m = Vf Vf Qfs m Vf Vf
= =
Vf
( 17)
( 25)
Vf
Qfs =
me
W
QV f
e
3 等效量测函数
等效量测函数表示等效量测与状态变量之间的 关系, 因为将各种类型的量测都统一变换为支路首 端等效功率量测, 且取用支路首端功率作为状态量, 因此量测函数都可以线性表述。 支路首端功率等效量测函数: e hPf s = P f s ( 18) e hQ f s = Q f s 支路末端功率等效量测函数: e h P sf = - P f s
、电网考试重要知识点

电力系统无功负荷补偿应遵守的原则:最优网损微增率准则,无功电源最优分配原则:等网损微增率准则;有功负荷最优分配准则:耗量微增率原则。
故障分析静止元件(线路、变压器等),正负序阻抗相等,零序不等,;动态元件:正负零序都不等;三相三柱式:正负序相等,零序电抗较小;对于过电流保护,计算保护灵敏系数时,应用最小运行方式下的两相短路;电流互感器的二次绕线能反应各种类型的短路故障的是:三相星形接线;故障切除率为100% 两相不完全星形接线只能反应相间短路,不能反映接地短路,切除一条线路的概率是2/3;双侧电源电网中,母线两侧方向过电流保护的方向元件应安装在动作电流小,动作时限短的一侧;短路影响:三相短路>两相接地短路>两相短路>单相接地短路;三相短路短路电流最大—最大运行方式;两相短路短路电流最小—最小运行方式;短路最大危害:破坏电力系统并列运行的稳定性,引起系统震荡,甚至系统崩溃;采用方向阻抗继电器比采用全阻抗继电器灵敏系数提高了1/cos(Φs et-Φloa)架空地线使得零序电容变大,零序电抗变小;对于Y,d11接线的双绕组变压器,d形接线侧发生AB两相短路时,Y形接线的线电流都存在短路电流,其中B相是其他两相的两倍。
(滞后相电流最大,电压最小);电力系统只要三相电流不对称,一定存在负序分量;正常运行时只有正序分量;接地故障一定存在零序分量;发生不对称故障时,只有正序分量受两侧电动势相角差的影响;中性点不接地系统(小电流系统),单相接地时,接地点电压不变,非故障相电压升高为线电压(√3倍);零序电流的方向(容性无功功率方向)是由故障点流向母线,非故障相是由母线流向故障点;中性点接地系统(大电流系统),单相接地时,非故障相电压不变;两项短路,距离故障点越近,负序电压?非有效接地系统中,内部过电压是在线电压基础上发展起来的;有效接地系统中,内部过电压实在相电压基础上发展起来的。
潮流算法比较:计算潮流时,牛顿-拉夫逊法与高斯-赛德尔相比主要优点是收敛性好,计算速度快,占用内存小;缺点是对初值要求高,对于高斯-赛德尔不能求解的病态系统也能可靠收敛;电力系统稳定性:分析简单电力系统的暂态稳定性应用:等面积定则;提高电力系统静态稳定性的方法:1、采取自动调节励磁装置;2、减小元件电抗;3、改善电力系统结构4、采用中间补偿设备。
基于分块吉文斯旋转的电力系统状态估计

基于分块吉文斯旋转的电力系统状态估计
郭瑞鹏;邵学俭;韩祯祥
【期刊名称】《中国电机工程学报》
【年(卷),期】2006(26)12
【摘要】针对电力系统状态估计问题中状态量及量测雅可比矩阵的绝大多数非零元素均成对出现的实际状况,提出了一种基于分块吉文斯(Givens)旋转的快速状态估计算法。
该算法利用电力系统状态估计问题的上述特点对量测雅可比矩阵进行分块,对列编号进行优化,并采用变转轴逐列消元策略,既减少了所需的内存空间,又明显提高了执行效率。
试验系统的仿真结果表明,该方法具有较高的执行效率,能够更好地满足在线状态估计的要求。
【总页数】6页(P26-31)
【关键词】正交变换;Givens旋转;状态估计;量测雅可比矩阵;稀疏矩阵;分块矩阵【作者】郭瑞鹏;邵学俭;韩祯祥
【作者单位】浙江大学电气工程学院;杭州市电力局
【正文语种】中文
【中图分类】TM744
【相关文献】
1.一种基于PMU的分块解耦状态估计模型 [J], 刘凤袖
2.基于分块信息矩阵十字链表的快速状态估计方法 [J], 颜伟;项波;黄正波;卢建刚;李钦
3.基于分块雅可比矩阵的最小二乘状态估计算法 [J], 王珍意;周良松
4.基于动态分区和多估计准则的电力系统自适应鲁棒状态估计 [J], 俞文帅;黄蔓云;卫志农;孙国强;段方维;刘芮彤
5.基于分块QR分解的一种状态估计算法 [J], 杜正春;牛振勇;方万良
因版权原因,仅展示原文概要,查看原文内容请购买。
基于PMU分解协调的状态估计算法
基于PMU分解协调的状态估计算法
陈芳;韩学山;李华东
【期刊名称】《电力系统保护与控制》
【年(卷),期】2009(037)017
【摘要】PMU至少可实现系统局部可观,此性质必然产生系统的自动划分,即出现围绕PMU配置点集的若干可观测性子系统.基于这一思路,从状态估计快速性角度出发,提出电网分解协调的状态估计快速算法,分解是指依据PMU配置的可观测子系统的划分,协调是指各子系统如何达到无缝的衔接,在快速估计下达到与整体估计一样的效果.最后,以IEEE-39节点及IEEE-118节点系统对对算法进行了验证.【总页数】5页(P44-48)
【作者】陈芳;韩学山;李华东
【作者单位】山东大学电气工程学院,山东,济南,250061;山东大学电气工程学院,山东,济南,250061;哈尔滨工业大学电气工程及其自动化学院,黑龙江,哈尔滨,150001;山东省电力研究院,山东,济南,250012
【正文语种】中文
【中图分类】TM71
【相关文献】
1.基于PMU的电力系统状态估计算法研究 [J], 王筱芳;侯捷;任真
2.基于PMU的降阶二次状态估计算法研究 [J], 蒋建东;杜耀恒;燕跃豪;鲍薇
3.基于PMU测量数据的改进型戴维南等值参数递推估计算法 [J], 王木楠;刘宝柱;
黄俊
4.计及PMU的电力系统状态估计算法分析研究 [J], 吴雷;夏立
5.基于分解协调算法的互联电力系统状态估计 [J], 王永;郭志忠;彭茂君;肖勇因版权原因,仅展示原文概要,查看原文内容请购买。
基于改进最小二乘法的电力系统状态估计
)Pi′ xi−1
)
]
(9)
∑ Pi′
=
Pi−1 −
n j =1
µ P′ r r P′ T [i−1][ j−1] j j [i−1][ j−1]
′
1 + rjT P[′i−1][ j r −1] j µ′
(10)
µ µ P′[i−1][ j]
=
P[′i−1][
j −1]
−
P′ r r P′ T [i−1][ j−1] j j [i−1][ j−1] 1 + rjT P[′i−1][ r j−1] j ′
果表明在在动态情况下递推最小二乘法比最小二乘法有更好的控制效果以及鲁棒性。以上基
础研究表明递推最小二乘法在电力系统状态估计中的应用的可行性。
实际上测量到的数据总是有误差,包含测量噪声、模型误差等,因此必须对量测数据
进行修正,优化准则: JW (x) = (z − Hx)T W (z − Hx) + µ∆xT ∆x ,其中 µ 为阻尼因子,其
Pi−−11[ xi
−
xi −1 ]
(2)
其中, Pi−1 是状态变量 x 的第 i −1次估计值的方差阵,并以其逆矩阵作为权重。第 i 次测量
量 zi 与其相应的估计值 h(xi ) 的最小二乘目标函数为:
L2 (xi ) = [h(xi ) − zi ]T R−1[h(xi ) − zi ]
乘准则(WLS)假设量测严格服从正态分布,LMS 和 LTS 假设量测服从拉普拉斯分布,非
二次准则假设量测量服从 Huber 分布。
目前,在电力系统状态估计各种应用软、硬件设备中,应用最广泛的是基于最小二乘
准则的状估计器。这种估计器的优点是模型简单,计算量小,对理想正态分布的量测量估计
基于系统分割的保留非线性快速P-Q分解状态估计法
基于系统分割的保留非线性快速P-Q分解状态估计法
刘浩;戴居丰
【期刊名称】《电网技术》
【年(卷),期】2005(29)12
【摘要】提出了一种新的状态估计算法,既保留了量测方程非线性又利用了快速P-Q分解方法,因此数学模型精度高且保留了快速P-Q分解的优点,提高了状态估计的计算精度和速度。
采用系统分割方法将大系统分割为多个小系统,分别对每个小系统进行状态估计,然后对各小系统的状态估计结果进行协调,得到整个系统具有同一参考节点的状态估计结果,这样可大大提高状态估计的计算速度,有利于进行大电网的状态估计。
在18节点系统上进行的数字仿真实验验证了该方法的有效性。
【总页数】5页(P72-76)
【关键词】快速P-Q分解;非线性;状态估计法;状态估计算法;小系统;分解方法;量测方程;模型精度;计算精度;分割方法;计算速度;仿真实验;节点系统;大系统;大电网【作者】刘浩;戴居丰
【作者单位】山东建筑工程学院计算机科学与技术系;天津大学电信学院
【正文语种】中文
【中图分类】TM744;TP79
【相关文献】
1.保留非线性的快速P—Q分解状态估计程序设计 [J], 刘浩
2.保留非线性的快速P—Q分解状态估计法 [J], 刘浩;侯博渊
3.电力系统P-Q分解状态估计中的增益矩阵 [J], 罗清华
4.基于抗差理论的P-Q分解状态估计算法 [J], 卢志刚;张宗伟;杨斌
5.保留非线性的电力系统两级状态估计法 [J], 刘浩;魏明
因版权原因,仅展示原文概要,查看原文内容请购买。
基于深度学习的IGBT健康状态评估及剩余寿命预测
基于深度学习的IGBT健康状态评估及剩余寿命预测基于深度学习的IGBT健康状态评估及剩余寿命预测引言IGBT(Insulated Gate Bipolar Transistor)是一种重要的功率半导体器件,被广泛应用于电力电子系统中。
然而,由于IGBT的工作环境存在高温、高电压和高电流等恶劣条件,其寿命与可靠性成为电力电子设备中的瓶颈问题。
因此,准确评估IGBT的健康状态,并预测其剩余寿命至关重要,这不仅能够提高设备的可靠性,还能够降低维修成本。
一、IGBT健康状态评估方法1. 特征提取在IGBT健康状态评估过程中,特征提取是一个关键的步骤。
传统方法多采用基于统计学的特征提取方法,如均值、方差、峰值等。
然而,这种方法只能提取样本的整体统计信息,无法捕捉到样本内部的特征。
针对这个问题,基于深度学习的方法具有明显的优势。
例如,卷积神经网络(CNN)可以自动学习到IGBT故障模式中的特征信息,从而提高评估的准确性。
2. 健康状态评估模型构建在特征提取阶段之后,我们需要构建一个评估模型来准确地判断IGBT的健康状态。
传统的评估方法多采用支持向量机(SVM)或逻辑回归(LR)等机器学习算法,但其准确性有限。
近年来,深度学习中的循环神经网络(RNN)等算法被广泛应用于健康状态评估中,因其可以处理时间序列数据并具有很强的非线性建模能力。
3. 实验数据采集与准备为了验证所构建的评估模型的有效性,我们需要采集IGBT的工作数据并进行预处理。
实际中,可以在IGBT设备中潜入传感器,实时采集电流、电压、温度等参数,以及故障样本。
而后,通过对这些数据进行滤波、归一化等预处理操作,得到用于模型训练的数据集。
二、IGBT剩余寿命预测方法1. 特征提取IGBT的剩余寿命预测与健康状态评估类似,也需要进行特征提取。
但与健康状态评估不同的是,剩余寿命预测需要考虑时间因素。
因此,除了采用一些传统的统计特征外,还需要引入时间序列特征,如自相关系数、波峰波谷值等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WAN B n L ii WA G C u .ig, I T o, N G etn G ig, I -e, N h nyn LU a WA Jj Y. g e
(. rh at a lUnv ri , i n1 2 1 , i a 2 Jl lf l t o rSa o , i n 1 8 0 , i a 1 Note s Dini ie sy Jl 3 0 2 Chn ; . inOi i dHo we tt n Jl 3 0 0Chn ; t i i ・e P i i
n h i g l r h n me ao c e a dt esn u a p e o n f o f ce tma xwh c i in r i hma yma ete e t a o t pm a C U'S h e s lc o fI k h s m t n so i i y O C I Ot ee t no GGII o sa t , i I c n tn i i r v d i i a e . h s l f ac lt n e a l h w a i t o a to g r b sn s , g o v r e c p e s s mp o e t sp p r T er u t o c u a o x mp e s o t t h sme d h sr n o u t e s h h c n e g n e s e d a nh e s l i h t h s i
(. 1 东北 电力大学,吉林 吉林 1 2 1 ; 2 吉林油 田电厂 ,吉林 吉林 18 0 ; 02 3 . 00 3
3 齐 齐哈 尔 电业 局 , 黑龙 江 齐 齐哈 尔 1 1 0 ) . 600
摘要 : 快速分解算 法具有很好 的收敛特性 ,既能处理 支路上 的量测量 ,又能处理节 点注入型量测量 ,计算速度快 而又节省内
3 qh e l tcP w r ueu Q qhe 10 ,hn ) . iar e r o e ra , iiar 6 0 0C ia Qi E ci B 1
Ab t a t T e f s e o p e r h t a a t ac l t n s e d a d a e o o c mo y I C a d e t eme s r me t f sr c : h a t c u l d a i me i h s af s l u ai p e n c n mi a me r , t a h d t c c o l n n l a u e n so h
存, 是工程上一种公认的状态估计的优良实用算法, 但它无法处理实际运行的电网自动化系统中存在的少量粗差, 从而使状
态估计 的结果严重偏 离真值。通过分析比较几种典型的抗差估计方法,将基 于 IGI 法的抗差估计方法与快速分解算法相 G II 结合 ,用于抗拒 少量粗差对估计值的影响。 由于考虑到在粗差较大时,利用具有淘汰 区的 IGI 进行抗差估计可 能会 出现 G II 秩亏 ,信息矩阵 出 奇异现 象,系统 不可观 ,导致状 态估计不 能进行 ,故该文对 IG I 法 中的常数选取进行 改进 。算例结 现 G II 果表明 , 该改进算法具有 良 的抗粗 差能力和可 靠的收敛性 ,收敛速度快 ,并能够将抗粗差和状 态估计在计 算过程 中能同时 好 顺利完成 ,不需要进行多次状态估计计算。 关键词 :电力系统;状态估计; IG I 法 ;快速分解算 法 G II
r ss n et s m ai n W h n te g o s n0 s l o b g e di ec mmo t o f GGII su e s mae t er n . e e t e it c e t t . a O i o e r s lr a et i g r h e O n a t o f h n me d o h I I s d t e t t . k d fc i O i h a
Sa eetma o lo ih a e nt ei p o e t o fI t t s i i t n ag rt m b s do h m r v d me d o GGII h I
a d f s e o p e r t m e i n a t e u ld a h tc d i
wh c s o i e y te r b s e t t n me o f GGII d t e fs e o p e rt me ct e it e i f e c fl t u i r i h i c mb n d b o u t s ma o t d o h i i h I I t c u ld a i n a h a d h t O r ss l n e o t e o t e i h t n u i l l
e etnage t e it nfo h r au . c ri gt n l z e y ia rs i ra d va o r m tet ev le Ac o dn oa ay eafw tpc me o si o u t si t n ti p p ru e i u l h td nr b s etma o ,h s a e s sawa i y
维普资讯 http:/Hale Waihona Puke
第3 6卷 第 l 期 1
20 0 8年 6月 1日
继 电 器
RELA Y
Vb .6 No 1 13 . 1
J n , 0 8 u e1 2 0
基 于改进 I GI 和快速分解法 的 电力系统状 态估计 算法 G I I
王 冰 ,李积捷 ,王春 瑛 ,刘 涛 。 ,王野藤 。
h o ea r ha ten d n db a c n di 0 da dpa t a rtm ei f tt s ma o . tt o f ce tnh digg o ser rwhc n sag o n rc c l i i a h t o aee t t n Bu iS t e in i a l r s ro c s i i ’n i n n ihwi l l
