16.2 二次根式的乘除法(分母有理化)
合集下载
(完整word版)16.2 二次根式的乘除第2课时教案

(完整 word 版)16.2 二次根式的乘除第 2 课时教案
16。2 二次根式的乘除(第 2 课时)
【教学任务分析】
知识 1。会进行简单的二次根式的除法运算.
教 技能 2.使学生能利用二次根式的除法公式进行二次根式的化简与运算.
学
3。理解最简二次根式的概念,并运用它把不是最简二次根式的化成最简二次
难 熟练进行二次根式的除法运算.
点
【教学环节安排】
环节 教 学 问 题 设 计
教学活动设计
情 光明中学有一块直角三角形的空地, 已知直 教师出示问题,分析,点拨方法,
境 引
角边 AC= 5 m, BC=6m,你能求出斜边 AB 的长 适时设疑。
2
学生动手计算,体会结果
吗?
特点。
入
在上面的问题中,你会计算 169 的结果吗?
36
36
教师引导,分析 a,b 取值不同的原
合
规律: 9 16
9 ; 16 ______ 16 .
16 36
36
因。
作 2.结论 二次根式的除法法则:
交
a = a (a≥0,b〉0),
流
bb
反过来得到:
学生先自主探索,再小组讨论, 总结方法.进一步理解 a,b 的取值不 同的原因,
学生举例,验证两个公式的正确性
(2) 3 2 = 3 2 2 3 6 ; 27 3 3 3 3 3
成果 展示
补 充 提 高
(3) 8 = 2 2 2 a 2 a 。 2a 2 a a a a
这节课你有哪些收获?谈谈自己的想法. 师提问: (1)二次根式的除法公式与乘法公式 有什么区别和联系?它们各有何特点? (2)最简二次根式有什么特点?
16。2 二次根式的乘除(第 2 课时)
【教学任务分析】
知识 1。会进行简单的二次根式的除法运算.
教 技能 2.使学生能利用二次根式的除法公式进行二次根式的化简与运算.
学
3。理解最简二次根式的概念,并运用它把不是最简二次根式的化成最简二次
难 熟练进行二次根式的除法运算.
点
【教学环节安排】
环节 教 学 问 题 设 计
教学活动设计
情 光明中学有一块直角三角形的空地, 已知直 教师出示问题,分析,点拨方法,
境 引
角边 AC= 5 m, BC=6m,你能求出斜边 AB 的长 适时设疑。
2
学生动手计算,体会结果
吗?
特点。
入
在上面的问题中,你会计算 169 的结果吗?
36
36
教师引导,分析 a,b 取值不同的原
合
规律: 9 16
9 ; 16 ______ 16 .
16 36
36
因。
作 2.结论 二次根式的除法法则:
交
a = a (a≥0,b〉0),
流
bb
反过来得到:
学生先自主探索,再小组讨论, 总结方法.进一步理解 a,b 的取值不 同的原因,
学生举例,验证两个公式的正确性
(2) 3 2 = 3 2 2 3 6 ; 27 3 3 3 3 3
成果 展示
补 充 提 高
(3) 8 = 2 2 2 a 2 a 。 2a 2 a a a a
这节课你有哪些收获?谈谈自己的想法. 师提问: (1)二次根式的除法公式与乘法公式 有什么区别和联系?它们各有何特点? (2)最简二次根式有什么特点?
八年级下册数学16.2二次根式乘除

④最后要检验开出来的数及留在根号内的数都必须是非负数。
例题:
1. 2. 3. (m 4. (ab>0)
练习:
化简:
1. 2. 3. 4. (m >0)
2.若b < 0 ,则化简 的结果是()
A.-b B. b C题:
化简.
1. x x 2. -5 x x 3 3. x (a>0, b>0)
③运用二次根式乘法法则计算
练习:把下列根号外的因式移到根号内。
1. 2. (x > y > 0)3.ab (0< a<b)4.(a-2)
二.积的算术平方根。
1. = (a 0, b 0)
①每个因数(式)都必须是非负数
②被开方数一定是积的形式
③若积的因式不是非负数,则应将其化为非负数,运用性质进行化简。
1. = (a 0, b )
例题。
计算。
1. 2. 3. 4. (- ) (a>1, b>1)
练习。
1. 2. 3.- 4. (- ) (y> 0)
四.商的算术平方根。
1.作用---化简二次根式,将分母中的根号化去。(分母有理化)
2.方法:将分子和分母都乘分母的有理化因式。
(有理化因式---两个含有二次根式的代数式相乘,如果他们的积不含有二次根式,那么这两个代数式互为有理化因式)
4.常用的有理化因式: 与 , a + 与a - , + 与 , + 与 等。
例题:化简。
1. 2. 3. 4. (x>y>0)
5. 6. (a>0) 7. (x>0) 8. (x , y>1)
例题:分母有理化。
例题:
1. 2. 3. (m 4. (ab>0)
练习:
化简:
1. 2. 3. 4. (m >0)
2.若b < 0 ,则化简 的结果是()
A.-b B. b C题:
化简.
1. x x 2. -5 x x 3 3. x (a>0, b>0)
③运用二次根式乘法法则计算
练习:把下列根号外的因式移到根号内。
1. 2. (x > y > 0)3.ab (0< a<b)4.(a-2)
二.积的算术平方根。
1. = (a 0, b 0)
①每个因数(式)都必须是非负数
②被开方数一定是积的形式
③若积的因式不是非负数,则应将其化为非负数,运用性质进行化简。
1. = (a 0, b )
例题。
计算。
1. 2. 3. 4. (- ) (a>1, b>1)
练习。
1. 2. 3.- 4. (- ) (y> 0)
四.商的算术平方根。
1.作用---化简二次根式,将分母中的根号化去。(分母有理化)
2.方法:将分子和分母都乘分母的有理化因式。
(有理化因式---两个含有二次根式的代数式相乘,如果他们的积不含有二次根式,那么这两个代数式互为有理化因式)
4.常用的有理化因式: 与 , a + 与a - , + 与 , + 与 等。
例题:化简。
1. 2. 3. 4. (x>y>0)
5. 6. (a>0) 7. (x>0) 8. (x , y>1)
例题:分母有理化。
人教版八年级数学下册_16.2二次根式的乘除

特别提醒 进行二次根式的除法运算时,若两个被开方数可以
整除,就直接运用二次根式的除法法则进行计算;若两 个被开方数不能整除,可以对二次根式化简或变形后再 相除.
感悟新知
例 3 如果
a a-8
a a-8
成立,那么( D )
A.a ≥ 8
B.0 ≤ a ≤ 8
C.a ≥ 0
知3-练
D.a>8
解题秘方:紧扣“二次根式除法法则”成立的条
(式)移到根号外时,要注意应写在分母的位置上;
(3)“三化”,即化去被开方数中的分母.
感悟新知
知5-讲
特别提醒 判断一个二次根式是否是最简二次根式,要紧扣两个条件: 1. 被开方数不含分母; 2. 被开方数中每个因数(式)的指数都小于根指数2,即每个因
数(式)的指数都是1. 注意:分母中含有根式的式子不是最简二次根式.
感悟新知
知5-练
例8 下列各式中,哪些是最简二次根式?哪些不是最简二
次根式?不是最简二次根式的,请说明理由.
(1)
1 ;(2)
x2+y2 ;(3)
0.2;
3
(4)
24 x;(5)
2 .
3
解题秘方:紧扣“最简二次根式的定义”进行判断.
感悟新知
知5-练
解:(1)不是最简二次根式,因为被开方数中含有分母; (3) 不是最简二次根式,因为被开方数是小数(即含有分母); (4)不是最简二次根式,因为被开方数24x 中含有能开得尽 方的因数4,4=22; (2)(5)是最简二次根式.
感悟新知
知3-讲
(2)当二次根式根号外有因数(式)时,可类比单项式除以单 项式的法则进行运算,将根号外的因数(式)之商作为商 的根号外因数(式) ,被开方数(式)之商作为商的被开方 数(式) ,即a b÷c d = (a÷c ) b d ( b ≥ 0,d > 0,c ≠ 0 ).
16.2二次根式的乘除 课件 人教版数学八年级下册

2
= =
-a(a<0),
a(a≥0).
文字表述:一个数的平方的算术平方根等于这个数的
绝对值.
代数式:用基本运算符号(基本运算包括加、减、乘、
除、乘方和开方)把数或表示数的字母连接起来的式
子叫做代数式.
当 a, x 取怎样的实数时,下列各式在实数范围内有意义?
(1) + 5+ 1 − ;
=
22 × 32 × 32 × 2
= 2 × 3 × 3 × 2 = 18 2 .
(2)原式 = − 6 × 15= − 3 × 2 × 3 × 5
= − 32 × 2 × 5 = −3 10 .
2.化简 : 16 2 3
解:原式 = 16 ∙ ∙ 2 ∙ 3
=4 ∙ ∙ ∙ c
边,只要ab≥0即可.
计算:(1)
解:(1)方法一
方法二
3
5
3 6
(2)
.
27
;
3
5
3
=
3
=
5
3×5
=
5×5
3×5
15
15
;
=
52
5
15
=
=
=
.
5
5
5 × 5 ( 5)2
在方法二中,式子变形
3
5
15
=
中的根号(分母有理化).
3×5
是为了去掉分母
5× 5
计算: (1)
解:(2)
3
5;
3 6
27
=
(2)
简二次根式.
(1)被开方数不含分母;
即被开方数必须是整数(式)
= =
-a(a<0),
a(a≥0).
文字表述:一个数的平方的算术平方根等于这个数的
绝对值.
代数式:用基本运算符号(基本运算包括加、减、乘、
除、乘方和开方)把数或表示数的字母连接起来的式
子叫做代数式.
当 a, x 取怎样的实数时,下列各式在实数范围内有意义?
(1) + 5+ 1 − ;
=
22 × 32 × 32 × 2
= 2 × 3 × 3 × 2 = 18 2 .
(2)原式 = − 6 × 15= − 3 × 2 × 3 × 5
= − 32 × 2 × 5 = −3 10 .
2.化简 : 16 2 3
解:原式 = 16 ∙ ∙ 2 ∙ 3
=4 ∙ ∙ ∙ c
边,只要ab≥0即可.
计算:(1)
解:(1)方法一
方法二
3
5
3 6
(2)
.
27
;
3
5
3
=
3
=
5
3×5
=
5×5
3×5
15
15
;
=
52
5
15
=
=
=
.
5
5
5 × 5 ( 5)2
在方法二中,式子变形
3
5
15
=
中的根号(分母有理化).
3×5
是为了去掉分母
5× 5
计算: (1)
解:(2)
3
5;
3 6
27
=
(2)
简二次根式.
(1)被开方数不含分母;
即被开方数必须是整数(式)
八年级数学16.2二次根式的乘除---二次根式的除法

4 9
4 9
(2)
16 = 4
16 = 4
25 ___5____; 25 __5_____;
16 25
16 25
(3)
36 = 6
36 = 6
49 ___7____; 49 __7_____.
36 49
36 49
二次根式的除法法则:
规律: a a a 0,b 0
bb
6 2 ? 62 3
(2)原式= 2 1 1 1 = 2 3 6 = 6
5 26 52
5
(3) 2a = 2a a+b a+b a+b • a+b
注意: 如果根号 前有系数,就把 系数相除,仍旧 作为二次根号前 的系数。
=
2a a+b a+b
课堂小结
(1)通如过何本进节行课二的次学根习式,除法运算? (2)如何逆用二次根式除法法则化简二次根式? (3)我什收么获是了最…简二…次根式?
40 ;(3) 1.5
;(4)
4 3
.
解:(1) 32 16 2=4 2
(2) 40 410=2 10
(3)1.5 3= 3 2= 6 2 22 2
(4) 4= 4 3= 2 3 3 33 3
自我检测
1、辨别下列二次根式是否是最简二次根式。
× × × √ (1) 12
;(2)
课后作业
作业:教科书第10页习题16.2; 《351导学案》第7-8页。
1 3
; (3)
x2 y2
;(4)
x2 +y 2
2、计算:
(1) 2 3 40
121b5 (2) 16a2
(3) 2 5 27
二次根式的乘除第2课时教学设计
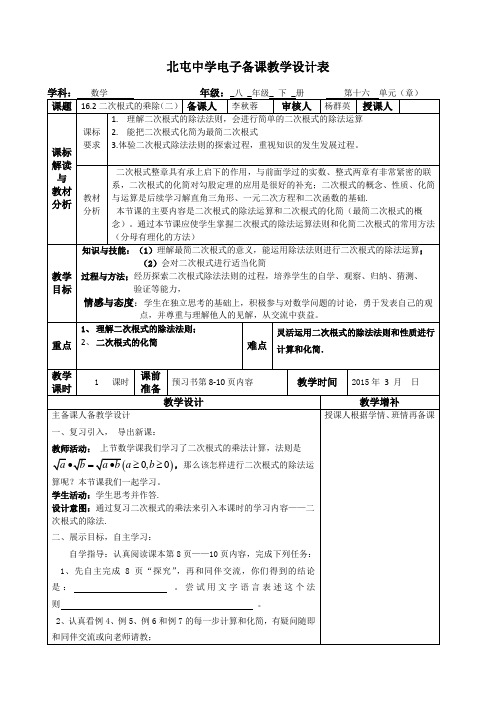
2.能把二次根式化简为最简二次根式
3.体验二次根式除法法则的探索过程,重视知识的发生发展过程。
教材分析
二次根式整章具有承上启下的作用,与前面学过的实数、整式两章有非常紧密的联系,二次根式的化简对勾股定理的应用是很好的补充;二次根式的概念、性质、化简与运算是后续学习解直角三角形、一元二次方程和二次函数的基础.
5、仿照例题格式 完成10页练习并和同伴互相找毛病。
教师活动:指导学生自学,并适时引导学生总结
学生活动:学生读题,思考后交流.(派学生代表发表观点)
设计意图:二次根式的化简,综合运用了二次根式的乘除法法则,这是本节课的重点和难点.教学中要让学生慢慢体会化简得最后结果.
三、检测反馈
1、师生共同解决“自学指导”中的问题。
验证等能力,
情感与态度:学生在独立思考的基础上,积极参与对数学问题的讨论,勇于发表自己的观点,并尊重与理解他人的见解,从交流中获益。
重点
1、理解二次根式的除法法则;
2、二次根式的化简
难点
灵活运用二次根式的除法法则和性质进行计算和化简.
教学课时
1课时
课前准备
预习书第8-10页内容
教学时间
2015年3月日
2、找同学演板10页练习1、2、3
学生活动:学生读题,思考后交流.(派学生代表发表观点)
教师活动:教师适时引导学生总结
设计意图:让学生通过练习,巩固所学知识,增强学好数学的自信心.
四、课堂小结:
本节课你有哪些收获?
(1)二次根式的除法法则是什么?请写在下面。
学生活动:学生读题,思考后交流.(派学生代表发表观点)
2.二次根式除法法则 例5
3.最简二次根式(1)被开方数不含分母例6
3.体验二次根式除法法则的探索过程,重视知识的发生发展过程。
教材分析
二次根式整章具有承上启下的作用,与前面学过的实数、整式两章有非常紧密的联系,二次根式的化简对勾股定理的应用是很好的补充;二次根式的概念、性质、化简与运算是后续学习解直角三角形、一元二次方程和二次函数的基础.
5、仿照例题格式 完成10页练习并和同伴互相找毛病。
教师活动:指导学生自学,并适时引导学生总结
学生活动:学生读题,思考后交流.(派学生代表发表观点)
设计意图:二次根式的化简,综合运用了二次根式的乘除法法则,这是本节课的重点和难点.教学中要让学生慢慢体会化简得最后结果.
三、检测反馈
1、师生共同解决“自学指导”中的问题。
验证等能力,
情感与态度:学生在独立思考的基础上,积极参与对数学问题的讨论,勇于发表自己的观点,并尊重与理解他人的见解,从交流中获益。
重点
1、理解二次根式的除法法则;
2、二次根式的化简
难点
灵活运用二次根式的除法法则和性质进行计算和化简.
教学课时
1课时
课前准备
预习书第8-10页内容
教学时间
2015年3月日
2、找同学演板10页练习1、2、3
学生活动:学生读题,思考后交流.(派学生代表发表观点)
教师活动:教师适时引导学生总结
设计意图:让学生通过练习,巩固所学知识,增强学好数学的自信心.
四、课堂小结:
本节课你有哪些收获?
(1)二次根式的除法法则是什么?请写在下面。
学生活动:学生读题,思考后交流.(派学生代表发表观点)
2.二次根式除法法则 例5
3.最简二次根式(1)被开方数不含分母例6
人教版八年级数学下册16.2二次根式的乘除法(教案)
-例子:计算√2 * √8,学生应得出√(2 * 8) = √16 = 4。
-掌握二次根式除法法则:√a / √b = √(a / b)。学生需理解除法法则的推导过程,并能应用于简化二次根式。
-举例:计算√27 / √3,学生应得出√(27 / 3) = √9 = 3。
-理解并运用二次根式的乘除法解决实际问题,如计算面积、体积等。
-例子:√20 / √5 = √(20 / 5) = √4 = 2,但√20 / √3需要将分母有理化,变为(√20 * √3) / (√3 * √3)= √60 / 3 = 2√5 / 3。
-难点三:理解二次根式乘除法则与整数的乘除法则的区别和联系,避免混淆。
-例如:学生应明白√2 * √3不等于2 * 3,而是等于√(2 * 3)。
-能够从实际例子中抽象出二次根式的乘除法则,培养数学抽象素养。
4.培养学生的数学应用意识:通过解决实际问题,让学生体会二次根式乘除法在实际生活中的应用,提高数学应用意识。
-能够将二次根式乘除法应用于解决实际问题,培养数学应用意识。
三、教学难点与重点
1.教学重点
-掌握二次根式乘法法则:√a * √b = √(a * b)。学生需理解乘法法则的推导过程,并能熟练应用于具体计算。
-能够运用二次根式乘除法法则进行正确运算,培养推理与论证能力。
2.培养学生的数学运算能力:通过实际操作,让学生熟练掌握二次根式的乘除运算,提高运算速度和准确性。
-能够迅速准确地完成二次根式的乘除运算,培养数学运算能力。
3.培养学生的数学抽象素养:使学生能够从具体实例中抽象出二次根式乘除法则,形成数学模型,提高数学抽象思维。
还有一点我觉得需要注意的是,在总结回顾环节,虽然大部分同学能够掌握今天所学的内容,但仍有少数同学对某些知识点存在疑问。为了确保每位同学都能跟上教学进度,我决定在课后设立一个答疑时间,专门解答同学们的疑问。
-掌握二次根式除法法则:√a / √b = √(a / b)。学生需理解除法法则的推导过程,并能应用于简化二次根式。
-举例:计算√27 / √3,学生应得出√(27 / 3) = √9 = 3。
-理解并运用二次根式的乘除法解决实际问题,如计算面积、体积等。
-例子:√20 / √5 = √(20 / 5) = √4 = 2,但√20 / √3需要将分母有理化,变为(√20 * √3) / (√3 * √3)= √60 / 3 = 2√5 / 3。
-难点三:理解二次根式乘除法则与整数的乘除法则的区别和联系,避免混淆。
-例如:学生应明白√2 * √3不等于2 * 3,而是等于√(2 * 3)。
-能够从实际例子中抽象出二次根式的乘除法则,培养数学抽象素养。
4.培养学生的数学应用意识:通过解决实际问题,让学生体会二次根式乘除法在实际生活中的应用,提高数学应用意识。
-能够将二次根式乘除法应用于解决实际问题,培养数学应用意识。
三、教学难点与重点
1.教学重点
-掌握二次根式乘法法则:√a * √b = √(a * b)。学生需理解乘法法则的推导过程,并能熟练应用于具体计算。
-能够运用二次根式乘除法法则进行正确运算,培养推理与论证能力。
2.培养学生的数学运算能力:通过实际操作,让学生熟练掌握二次根式的乘除运算,提高运算速度和准确性。
-能够迅速准确地完成二次根式的乘除运算,培养数学运算能力。
3.培养学生的数学抽象素养:使学生能够从具体实例中抽象出二次根式乘除法则,形成数学模型,提高数学抽象思维。
还有一点我觉得需要注意的是,在总结回顾环节,虽然大部分同学能够掌握今天所学的内容,但仍有少数同学对某些知识点存在疑问。为了确保每位同学都能跟上教学进度,我决定在课后设立一个答疑时间,专门解答同学们的疑问。
16.2.3 二次根式的乘除法混合运算
作 业
Homework
在下列各式中,哪些是最简二次根式? 哪些不是?对不是最简二次根式的进行化简.
(1) 45; (2) 1 ; 3 (3) 5 ; 2 (4) 0.5; 4 (5) 1 . 5
解:只有(3)是最简二次根式;
(1) 45 3 5;
1 1 1 3 3 (2) ; 3 3 3 3 3
(1 )
(3 )
=_____;(2)
=________;
=________.
=_________;(4)
新知2
二次根式的应用
例4 设长方形的面积为S,相邻两边长分别为a,b.
已知 S 2 3, b 10 ,求a的值. 解:∵ S ab,
S 2 3 2 3 10 30 . ∴a b 5 10 10 10
§16.2 二次根式的乘除法
§16 二次根式
复习 回顾
二次根式乘法法则:
一般地有 反之:
a
b = ab (a≥0,b≥0 ). b (a≥0,b≥0 ).
ab = a
二次根式除法法则:
a a (a 0, b 0). b b
m a m a (a 0, b 0, n 0). n b n b
a a (a 0, b 0). b b
新知1
最简二次根式
问题1 你还记得分数的基本性质吗?
f f ·h ( h 0 ). g g ·h
问题2 前面我们学习了二次根式的除法法则, 你会去掉
2 3
这样的式子分母的根号吗?
是不是可以用分数的 基本性质去掉分母的 根号呢?Βιβλιοθήκη 新知3最简二次根式
【例2】(1)已知长方体的体积V= 高h=
新人教版八年级数学下《16.2 二次根式的乘除 二次根式的除法》优质课教学设计_66
16.2.2 二次根式的除法
教学目标 知识与技能:掌握二次根式除法法则并熟练应用;能将二次根式化简为最简二次根式;熟练 掌握分母有理化的过程。 过程与方法:通过实践,观察,类比总结出二次根式的除法法则,发展学生小组合作、自主 归纳问题的水平;化简为最简二次根式的过程,让学生回顾旧知应用新知;通过学生自主探 究分母有理化的过程,使他们利用新知识解决相关问题,提升分析问题、解决问题水平。 情感态度与价值观:在实践中激发学生的学习兴趣,体验小组合作的乐趣,从而增强学生 学数学、用数学解决问题的意识。 教学重点和难点 教学重点:二次根式除法法则的探究及应用。 教学难点:二次根式除法的应用过程及分母有理化。 教学方式和教学手段 (一)教学方式:自主探究,启发引导、讲练结合。 (二)教学手段:多媒体辅助教学。 教学过程 问题与情境 一、知识回顾 (学生活动)请同学们完成下列各 题: 1、二次根式的定义. 2、二次根式的乘法公式 二、创设情景,引入新知 学生利用旧知填空, 教师板书课题。 学生观察四组计算 通过动手计算、 归纳总结使学生了解 二次根式除法法则, 培养学生参与意识、 实践水平。 师生活动 设计意图
25 36
81 49 121 4
思考:如何化简:
1 2 , ? 7 3
总结归纳:把分母中的根号化去,叫 做分母有理化。
二、总结归纳
1、总结归纳: 【二次根式除法法则】
学生自主归纳, 教师巡
a = b
a 反之, = b
三、例题讲解
视, 参与学生的探索, 之 后总结。 学生在归纳总结的 过程中享受 “做数学” 的乐趣,不同层次的 题目难度让学生均有
1.填空:
16 = 9 25 = 36
16 = 9 25 = 36
;
教学目标 知识与技能:掌握二次根式除法法则并熟练应用;能将二次根式化简为最简二次根式;熟练 掌握分母有理化的过程。 过程与方法:通过实践,观察,类比总结出二次根式的除法法则,发展学生小组合作、自主 归纳问题的水平;化简为最简二次根式的过程,让学生回顾旧知应用新知;通过学生自主探 究分母有理化的过程,使他们利用新知识解决相关问题,提升分析问题、解决问题水平。 情感态度与价值观:在实践中激发学生的学习兴趣,体验小组合作的乐趣,从而增强学生 学数学、用数学解决问题的意识。 教学重点和难点 教学重点:二次根式除法法则的探究及应用。 教学难点:二次根式除法的应用过程及分母有理化。 教学方式和教学手段 (一)教学方式:自主探究,启发引导、讲练结合。 (二)教学手段:多媒体辅助教学。 教学过程 问题与情境 一、知识回顾 (学生活动)请同学们完成下列各 题: 1、二次根式的定义. 2、二次根式的乘法公式 二、创设情景,引入新知 学生利用旧知填空, 教师板书课题。 学生观察四组计算 通过动手计算、 归纳总结使学生了解 二次根式除法法则, 培养学生参与意识、 实践水平。 师生活动 设计意图
25 36
81 49 121 4
思考:如何化简:
1 2 , ? 7 3
总结归纳:把分母中的根号化去,叫 做分母有理化。
二、总结归纳
1、总结归纳: 【二次根式除法法则】
学生自主归纳, 教师巡
a = b
a 反之, = b
三、例题讲解
视, 参与学生的探索, 之 后总结。 学生在归纳总结的 过程中享受 “做数学” 的乐趣,不同层次的 题目难度让学生均有
1.填空:
16 = 9 25 = 36
16 = 9 25 = 36
;
16.2二次根式的乘除
知识要点
这样的二次根式,叫做最简二次根式。
最简二次根式的特点
被开方数不含分母。 被开方数中不含能开得尽方的因数或因式。
在二次根式的运算中, 最后结果 的一般要求
2 分母中不含二次根式。 如: × 2 1 被开方数不能含有小数或分数。如: 或 0.2 × 2 2x y 分子分母不能约分。 如: 2 × 3x
a b
2 a ( a a 0) 3.将平方式(或平方数)应用 把这个因式(或因数)开出来,将二次根式 化简。
课堂小结
1. 二次根式的乘法:
a b ab a 0, b 0 ab a b a 0, b 0
2. 二次根式的除法有两种常用方法:
(1)利用公式: a b
新课导入
1. 一个平行四边形的底为 5,高为 3 ,求 这个平行四边形的面积。
提示 根据平行四边形的面积公式 S = ah 求解。
3 5
S=
5
3
这是最终结果吗? 这个结果能否继续化简? 如何化简?
2. 如果矩形的面积是 20 ,长为 5 ,求宽。
提示 根据矩形的面积公式 S = ab 求解。
20
?
5
b=
20 5
这是最终结果吗? 这个结果能否继续化简? 如何化简?
16.2二次根式的乘除
探究
有什么 规律?
1. 计算:
4 ? 25
2 ?
2
5
5
2? 5 10
4? 25
1 ? 9 1 16
100 = 102 = 10
骣 骣 1 1 鼢 珑 ? 鼢 珑 鼢 珑 桫 桫 3 4
2 2
有什么 规律?
1 1 ? 3 4
