一种改进的多谓诃归并连接算法
基于MapReduce的多元连接优化方法

基于MapReduce的多元连接优化方法李甜甜;于戈;郭朝鹏;宋杰【摘要】多元连接是数据分析最常用的操作之一,MapReduce是广泛用于大规模数据分析处理的编程模型,它给多元连接优化带来新的挑战:传统的优化方法不能简单地适用到MapReduce中;MapReduce连接执行算法尚存优化空间.针对前者,考虑到I/O代价是连接运算的主要代价,首先以降低I/O代价为目标提出一种启发式算法确定多元连接执行顺序,并在此基础上进一步优化,最后针对MapReduce设计一种并行执行策略提高多元连接的整体性能.针对后者,考虑到负载均衡能够有效减少MapReduce的“木桶效应”,通过任务公平分配算法提高连接内部的并行度,并在此基础上给出Reduce任务个数的确定方法.最后,通过实验验证本文提出的执行计划确定方法以及负载均衡算法的优化效果.该研究对大数据环境下MapReduce 多元连接的应用具有指导意义,可以优化如OLAP分析中的星型连接、社交网络中社团发现的链式连接等应用的性能.【期刊名称】《计算机研究与发展》【年(卷),期】2016(053)002【总页数】12页(P467-478)【关键词】多元连接;执行计划;I/O代价;性能优化;MapReduce编程模型;负载均衡【作者】李甜甜;于戈;郭朝鹏;宋杰【作者单位】东北大学计算机科学与工程学院沈阳 110819;东北大学计算机科学与工程学院沈阳 110819;东北大学软件学院沈阳 110819;东北大学软件学院沈阳110819【正文语种】中文【中图分类】TP393连接运算根据连接条件把2个或多个关系中的记录组合为一个结果数据集,包含连接运算的查询简称为连接查询.连接查询在数据分析中很常见,TPC-H提供的22个查询用例中有16个涉及到此类查询[1].当一个连接查询涉及n个关系时,称为n元连接;当n>2时,称为多元连接,多元连接是数据分析中最常用的操作之一.此外,在当今的大数据环境下,MapReduce[2]编程模型被广泛用于大规模数据集的分析处理.目前,MapReduce中数据分析的优化工作包括索引、数据布局、查询优化、迭代处理、公平负载分配以及交互式处理等方面[3].基于此,我们分析MapReduce给多元连接的优化带来的新挑战.首先,多元连接查询依赖良好的执行计划.传统的执行计划确定方法[4]不满足MapReduce特性,无法通过简单的适应性更改应用到现有的优化中.另外,现有基于MapReduce的执行计划确定方法[5-6]复杂度较高,应用范围受限.因此,亟需提出一种新的满足MapReduce特性且复杂度较低的执行计划确定方法.此外,我们还注意到,无论是传统研究还是现有研究,其执行计划都只确定了连接的执行顺序,并未考虑无依赖关系的连接操作间的并行执行策略.其次,良好的执行计划固然重要,对执行框架的优化同样可以有效地提高多元连接的性能,这一点在分布式环境中尤为重要.一种公平的并行任务负载分配方法可以有效地减少MapReduce中的“木桶效应”,从而提高连接操作内部的并行度.然而,就我们所知,目前没有针对连接运算的MapReduce负载均衡方法,且现有的通用方法[7-9]仅考虑了任务的输入代价,不适用于连接运算,因为它的输出代价也不可忽略.本文研究MapReduce环境下多元连接的优化方法,基于上述分析提出以下问题:1)多元连接执行计划的解空间很大,短时间内很难找到最优解,那么能否通过某个复杂度较小的算法快速找到一个近似最优解;2)连接运算属于I?O密集型运算,I?O为主要代价,那么能否针对MapReduce特性提出I?O代价模型,并选择代价最小的执行计划;3)连接顺序确定后,不存在依赖关系的连接操作可以并行执行,那么当存在多个满足并行执行的连接操作时该如何选择;4)执行框架的优化中,负载均衡能够有效地减少“短板效应”,那么此处的连接负载又该如何定义.这些问题的求解存在一定程度的挑战,就我们目前所知,尚未发现能够完全解决上述问题的研究工作.本文首先通过分析多元连接执行计划解空间的缩减方法、MapReduce连接算法的I?O代价模型、Replicated Join①的优劣以及MapReduce作业的并行执行特性,最终确定了执行计划的优化方法;接着,结合MapReduce框架分析连接运算的特性,提出负载均衡模型及其对应的均衡算法,并在此基础上提出Reduce任务个数的确定方法.大量实验验证了本文提出的优化方法的有效性.现有多元连接的优化研究可归为以下3类:执行计划的优化、连接算法的优化和执行框架的优化.对于第1类研究,文献[4]将n元连接拆分为n-1个2元连接,每个2元连接对应一个MapReduce作业(后文如不特殊指明,作业均为MapReduce作业),然而该方法针对的是传统的多处理器计算环境,不适用于MapReduce,且该方法在n较大时会导致较高的作业初始化代价以及中间结果的存储代价.文献[10]针对链式连接提出使用平衡二叉树的方式来执行多元连接,但其并未给出平衡二叉树的构建规则.文献[11]在一个作业中完成所有的连接运算,然而该方法在n较大时会因为数据需要传输①Replicated Join:在一个MRJ中执行多个连接操作.此时,同一个Key-Value对需要被复制到多个Reducer上,因此称为Replicated Join.该算法牺牲部分网络I?O代价来换取MRJ的初始化以及HDFS读写代价.到多个Reducer而导致较高的网络I?O代价.文献[5-6]将n元连接划分为若干个组,每组涉及若干个关系并由一个作业完成,而后采用Replicated Join连接所有组生成的中间结果,然而该方法因为要穷举所有可能的m(m<n)元连接作为候选集而导致算法复杂度较高,从而使其应用范围较窄.此外,上述所有研究确定的执行计划都只确定了连接的执行顺序,并未考虑无依赖关系的连接操作间的并行执行策略.本文首先基于MapReduce特性提出多元连接顺序的确定方法,该方法复杂度较低且能够很好地均衡中间结果的存储代价与网络传输代价.确定连接顺序后,本文还给出一种算法来确定无依赖关系的连接操作间的并行执行顺序,该算法通过对节点资源的充分利用来提高多元连接的执行效率.对于第2类研究,文献[12]针对theta-join提出一种随机算法1-Bucket-Theta以及它的一个扩展算法M-Bucket;文献[13]对文献[12]中提出的算法进行下界分析,并通过聚类方法提高了M-Bucket算法的效率.文献[14-15]总结现有实现算法为Map Join,Reduce Join,Semi Join等,这些算法分别适用于不同的查询场景,如Map Join仅适用于数据量较小的关系能够装入内存的查询.MapReduce连接算法的优化研究相对比较成熟,不在本文的研究范围之内.因此,不失一般性,本文采用没有任何约束条件的通用的Reduce Join作为研究对象.连接运算的执行效率依赖于实现算法和运行环境,由此衍生出第3类研究.文献[16]基于MapReduce提出一个改进的执行框架Map-Reduce-Merge,新添加的Merge阶段为Reduce Join的执行节省了一次作业.文献[17]对MapReduce框架进行修改,允许不同操作间的数据管道式传输,支持在线聚集以及持续查询,然而改进后的框架使得失效恢复(fail recovery)机制变得非常复杂,且对于批处理性能的提高也很不明显.文献[7-9]给出了通用的MapReduce负载均衡方法,但他们都只考虑了任务的输入代价,不适用于连接运算,因为它的输出代价也不可忽略.本文提出的MapReduce负载均衡方法着重考虑连接任务的负载特性,与传统的负载均衡方法有所不同.具体来讲,本文提出的负载均衡方法基于的Reduce Join的Map阶段仅负责将参与连接的数据表中的记录解析成Key-Value对(此时I?O操作很少),并通过Shuffle阶段传输到对应的Reduce任务中,而真正的连接操作是在Reduce阶段中完成的(此时会产生大量I?O操作).考虑到I?O代价是影响连接查询的主要因素,我们对产生大量I?O 操作的Reduce阶段进行读写分析,综合考虑Reduce任务的输入和输出代价及其对应的读写权重,最终基于这一综合代价给出了Reduce任务的负载均衡方法.文献[18]中实现的负载均衡是通过均衡数据块实现的,本文与其有本质上的区别.多元连接执行计划的解空间很大,短时间内很难找到最优解.本节首先通过查询树模型确定解的一个子空间,而后通过复杂度较小的启发式算法从中找到一个近似最优解,并在此基础上做进一步的优化以均衡中间结果的存储代价与网络传输代价.最后,根据MapReduce框架特性给出一种算法来确定无依赖关系的连接操作间的并行执行顺序,该算法通过对节点资源的充分利用来提高多元连接的效率.2.1 查询树模型多元连接可以用一个查询图G=(V,E)来表示[46],其中V是节点的集合,每个节点代表一个关系(记为Ri),E是边的集合,每条边?Ri,Rj?连接2个之间存在连接属性(A,B,C等)的关系,如图1所示.图1(a)所示的查询图包含6个关系,为6元连接;同理,图1(b)所示的查询图为8元连接.多元连接执行计划的最优解确定是个P完全问题[6],传统优化方法通常采用查询树模型限定解的一个子空间,并设计算法从中获取一个最优解.如图2所示,主流的查询树模型有Left-deep Tree,Right-deep Tree,Zigzag Tree,Bushy Tree[19]四种,其中前3种为顺序执行,最后1种为并行执行.很多研究工作[4-5]显示,并行执行的Bushy Tree更适用于分布式环境.从图2也可以看出,只有基于Bushy Tree确定的连接顺序中不同连接操作间不是完全的依赖关系,是可以并行的.因此,本文选取Bushy Tree作为MapReduce多元连接的查询树模型.2.2 查询树模型一个n元连接的执行方式有2种:1)将其拆分为n-1个2元连接分别执行,每个2元连接对应一个作业;2)在一个作业中执行所有连接操作.然而,当n较大时,第1种执行方式的作业初始化代价以及中间结果的存储代价也随之增大,第2种执行方式也因为数据的多次传输而产生较大的网络代价.为解决该问题,本文首先基于Bushy Tree初步确定多元连接的执行顺序,而后根据是否受益将部分2元连接合并成多元连接.1)基于I?O代价的连接顺序确定方法通过Bushy Tree确定多元连接的执行顺序首先需要给出树的构建规则.考虑到连接运算属于I?O密集型计算,连接代价以I?O代价为主,本文针对MapReduce 特性给出连接运算的I?O代价模型,并选择I?O代价最小的连接顺序.正如第1节中的描述,本文选择Reduce Join作为连接算法,下面以2元连接为例对其进行简单介绍.Reduce Join由Map阶段和Reduce阶段组成.Map阶段主要完成如下操作:①Map任务读取(通常为本地读)参与连接的2个关系;②以连接属性为键、记录为值,按键排序后输出键值对到本地磁盘;③将中间结果通过网络传输给Reduce任务.Reduce阶段主要完成如下操作:①接收来自Map任务的键值对并按键排序;②执行连接操作,并将结果写入分布式文件系统(HDFS).基于该分析,我们给出关系Ri和Rj进行Reduce Join的I?O代价计算方法,见式(1):其中,C1,C2,C3分别为本地、网络和HDFS的I?O代价权重,三者均与系统硬件相关(其中C3还与HDFS的副本个数设置有关),其值均可事先通过文件读写实验测出(在本文的实验环境中,副本个数为3,通过实验测得3个参数的值分别为C1=3.67s?GB,C2=8.93s?GB,C3=13.37s?GB,三者之间的比值为1:2.4:3.6);|Ri|代表关系的基数.另外,Map阶段操作②首先需要溢出写文件,而后读取并排序输出,因此共需3次读写操作;Reduce阶段的操作①使用内存和磁盘进行混合式排序,因此我们用参数λ表示该混洗比例,其值可通过经验设定.通过Bushy Tree确定连接顺序时,我们每次从查询图G=(V,E)中选择I?O 代价最小的连接操作执行,而后更新图G及其对应的关系的特征参数,直到执行完所有连接运算(见算法1).算法1的复杂度为O(log(|V||E|)),小于文献[5-6]的复杂度O(log(|V|2|E|)).算法1.PMC算法.?*基于MC(minimal cost)的执行计划(plan)确定算法*?输入:G=(V,E),query profile;?*包括关系的基数、连接属性的基数等相关参数*?输出:Bushy Tree.PMC算法中计算最小代价时,|Ri|和|Rj|均已知,|RiRj|未知,需要我们计算.目前关于|RiRj|的计算方法通常假设Ri和Rj在连接属性A上均匀分布[4,9],具体计算方法见式(2):其中,|A|为连接属性的基数.然而,事实上Ri和Rj通常不满足均匀分布这一假设,因此在实际应用中,我们应该考虑数据倾斜因素.设Fi和Fj为A在Ri和Rj中出现的频数分布,则定义倾斜度如下:定义1.倾斜度.定义倾斜度δ为频数分布Fi和Fj偏离均匀分布的程度,表达式见式(3):在实际计算中,倾斜度可以通过采样获取.有了倾斜度,|RiRj|的计算方法见式(4):因为考虑倾斜度因素计算出的|RiRj|更精确,同时基于最小代价的PMC算法确定的连接顺序也更优.2)基于Replicated Join的优化通过Bushy Tree确定的执行顺序仅包含2元连接,这样的执行计划会导致较高的作业初始化代价和中间结果的存储代价.考虑到算法1在复杂度上的优越性,我们保留由它确定的执行顺序,并在此基础上做进一步的优化.解决上述问题的直观想法为减少作业个数,也即增加每个作业执行的连接操作个数.Replicated Join满足该需求,但该算法中同一个键值对需要被复制到多个Reduce任务上,网络代价较高.为此,本文分别计算查询图采用Replicated Join以及采用多个2元连接这2种执行方法的I?O代价,定义“受益(benefit)”为二者的代价差.当受益为正时,合并这些2元连接,如图3所示.2元连接的I?O代价见式(1),下面给出Replicated Join的I?O代价计算方法.设查询图G=(V,E),关系集合V={R1,R2,…,Rn},E关联的连接属性集合为E-,Ri关联的连接属性集合为E-i,Replicated Join的I?O代价计算见式(5):基于Replicated Join的优化需要对PMC算法确定的Bushy Tree进行遍历,以合并所有可能的2元连接.然而,这样做的代价很高,本文考虑到对无依赖关系的连接操作执行Replicated Join明显会导致较高的网络I?O代价,因此仅判定具有依赖关系的连接操作(也即图3(a)中只能顺序执行的子树).另外,如果一个顺序执行的子树进行Replicated Join时受益为负,那么包含该子树的顺序执行子树的受益也为负.通过以上方法能够大大降低树的遍历代价.基于Replicated Join的优化算法见算法2.OPTB的算法复杂度小于PMC算法确定的Bushy Tree中所有最大顺序执行子树的高度之和.又考虑到顺序执行子树的最大高度为n-1,故OPTB的算法复杂度为O(n).2.3 并行执行顺序很多关于多元连接执行计划的优化研究[4-6]都只确定了连接的执行顺序,并未考虑MapReduce环境下无依赖关系的连接操作间的并行执行策略.若图3(b)为2.2节中最终优化的多元连接顺序,那么连接操作R2R7,R4R8,R3R5R6之间无依赖关系,可以并行执行.下面结合MapReduce特性对并行执行的优势进行分析.MapReduce集群中每个节点最多可执行的Map任务个数是预设的,因此最多可并行执行的Map任务数也是确定的.对于连接运算,Reduce Join中的Map任务负责将关系中的元组按照连接属性值进行分区,其执行时间仅取决于处理数据量.又因为每个Map任务处理一个固定大小的分片,我们可以认为同时分配的Map任务同时结束.设MapReduce每次最多可并行的Map任务个数为M,M个任务的并行执行称为一轮[2,20-21].若每轮Map任务的执行时间为T,作业Ji需要的Map任务个数Mi=ai×M+bi,其中ai,bi∈NN,bi∈[0,M),那么可以认为Ji的执行时间为(ai+ bi?M )T.若作业Jj需要的Map任务个数Mj=aj×M+bj,那么当bi+bj≤M时,2个作业的并行执行时间为(ai+aj+1)T,而串行执行时间为(ai+aj+2)T,此时并行执行可节省T时间;当bi+bj>M时,并行执行时间和串行执行时间同为(ai+aj+2)T.综上,当bi+bj≤M 时,作业Ji和Jj并行执行的效率高于串行.当有多个作业满足这一条件时,我们选取bi+bj最大的2个作业并行执行,从而充分利用计算资源.下面给出具体的算法实现:2.4 小结通过2.2节和2.3节给出的优化算法,我们最终动态确定多元连接的执行计划.图4以流程图的方式描述了执行计划的优化步骤.给定查询图G,首先通过PMC算法初步确定Bushy Tree,而后分别通过算法OPTB和PEE进行优化,直到更新后的树中叶子节点的个数小于3.良好的执行计划固然重要,但对执行框架的优化同样可以有效地提高多元连接的执行效率,这一点在分布式环境中尤为重要.一种公平的并行任务负载分配方法可以有效地减少MapReduce中的“短板效应”,从而提高连接操作内部的并行度.连接运算的MapReduce实现算法有很多,分别适用于不同的查询场景.不失一般性,本文选择没有任何约束条件的Reduce Join作为连接执行算法.该算法包括Map和Reduce 2个阶段,Map阶段只负责将关系中的元组按照连接属性值进行分区以输出到不同的Reduce任务,运算完全相同,因此Map任务的负载完全取决于处理数据量.又因为MapReduce中每个Map任务只负责处理一个数据分片(split,默认64MB),所以Map阶段各个Map任务是负载均衡的.很多研究工作也都作出Map任务均衡的假设,如文献[6,22].因此,本文仅研究连接运算的Reduce任务负载均衡.Reduce Join算法在Reduce阶段执行连接运算,连接属性值的不均匀分布将会导致由默认Hash分区函数确定的Reduce任务负载不均衡.为提高Reduce任务间的并行度,本节给出一种针对连接运算的负载均衡优化方法.3.1 负载均衡模型设R1和R2为参与连接的2个关系,连接属性值的集合记为A,A在R1和R2中的频数分布分别为F1和F2.在计算Reduce任务的负载之前,我们先给出连接属性值a∈A的负载贡献定义如下:定义2.负载贡献.连接属性值a∈A的负载贡献(LCa)是指执行该连接操作的代价,见式(6):LCa=ω1(f1a+f2a)+ω2(f1a×f2a),(6)其中,f1a和f2a分别为R1和R2中连接属性值为a的元组个数;ω1和ω2为Reduce任务输入数据和输出数据的处理代价权重,输入数据为网络I?O,输出数据写到HDFS上,二者的比值是由运行多元连接的分布式集群系统决定的.此处,我们认为连接运算代价中I?O占主导地位,CPU处理代价可以忽略,文献[5-6]中也有同样结论.文献[8]给出的当前最好的负载均衡方法中采用的代价模型仅考虑输入数据对Reduce任务负载的影响,而事实上对于连接运算输出数据的代价不容忽略.通过对MapReduce运行机制的分析可知,Reduce任务的负载取决于分区函数.分区函数将连接属性值划分成若干个组,每组对应一个Reduce任务.设分区函数将连接属性值的集合A划分为A1,A2,…,AR一共R个组,那么组Ai的处理代价第i个Reduce任务的负载Load(Ri)=Load(Ai),Reduce任务负载均衡这一目标可以等价表示如下:负载均衡模型中最关键的是获取连接属性A在R1和R2中的频数分布F1和F2.获取这2个分布,最精确的方法是对不同键值进行频数统计[23],但当键值个数很多时,会耗费大量存储,且在汇总各个Map任务的统计信息时还会带来很高的网络传输代价.针对该问题,文献[5,7-9]对键值进行Hash从而降低统计信息的规模.然而,文献[9]在Map任务执行的同时对频数信息进行统计,这样会导致第2轮Map任务无法执行,还会造成数据到Reduce的传输延迟,因为必须等到根据频数信息确定Partition函数后才能进行传输.文献[5,7-8]则单独开启一个作业进行频数统计,避免了上述问题.基于以上分析,本文可以采用类似的方法获取连接属性值的频数信息,并据此确定Reduce任务的个数以及Partition函数.3.2 负载均衡算法文献[6]指出Reduce任务的负载均衡是一个NP难问题,不能够在多项式时间内获取最优解,因此我们仅专注于寻找尽可能接近最优解的近似解.由于连接属性值的不可分割性,拥有相同连接属性值的键值对必须发送到同一Reduce任务节点进行连接运算,Reduce任务的负载均衡问题可以转换成尽可能降低Reduce任务的最大负载max{Load(Ri)}.理想情况下,所有Reduce任务的负载完全相同,此时max{Load(Ri)}=Avg{Load(Ri)}.然而,这种情况不总发生,本文给出一种朴素的均衡算法来获取近似解.该算法首先对A中所有连接属性值的负载贡献值按降序排序,然后每次将连接属性值为a的键值对分配给当前负载最小的Reduce任务(详见算法4).为评估算法4,我们将由该算法获取的Reduce任务负载最大值Lmax与最优算法获取的最大值L*max进行对比,并得出Lmax的上界如下:Lmax≤1.5L*max.本文给出的负载均衡方法是以等值连接为例进行描述的,它还适用于其他连接,也可以扩展到连接以外的其他类型作业.例如,进行近似连接时,只需将连接属性值a(键值对中的键)替换为一个满足近似条件(如|a1-a2|≤δ)的2元组?a1,a2?,并将负载贡献值的计算公式中f1a和f2a分别替换为R1中连接属性值为a1的元组个数以及R2中连接属性值为a2的元组个数.执行Replicated Join时,键值对中的键将会变成多个连接属性构成的多元组.对于连接以外的其他作业,我们可以将Reduce任务输入数据的处理代价函数(频数的加和)以及输出数据的处理代价函数(频数的乘积)进行适应性的更改.3.3 Reduce任务个数的确定现有通用的Reduce端负载均衡的方法[7-9]均未考虑Reduce任务个数的确定方法,本文根据获取的键值频数统计信息给出一种简单的确定规则.设Map任务的输出中不同键值的个数为k,所有键值的负载贡献和为Sum,其中键值的最大负载贡献为LCmax,Reduce任务个数为R,通过优化算法获取的Reduce任务最大负载为Lmax.当LCmax≥Sum?R时,也即R≥Sum?LCmax时,Lmax的取值不再下降,始终为LCmax,这意味着作业的性能不再提高,而它的资源消耗却随着R的增加而增大.因此,有必要找到R的一个临界值使得连接的执行效率最高.另外,考虑到Lmax的取值还与Sum有关,本文给出均衡算法的度量函数g(Lmax,R)的表达式如下:其中,α是性能与能耗之间的权重比,度量值越小,均衡效果越好.函数g (Lmax,R)应该存在一个极小值点R0,使得在该点处性能与资源消耗达到一个很好的折中,且该值有可能比Sum?LCmax小.4.2节中通过大量实验得出,当α=0.05时,函数g(Lmax,R)的极小值点正好就是Lmax不再下降的临界值.另外,考虑到不同键值的个数可能会很大,这将导致频数统计信息不能存入内存,针对该问题,我们可以采用文献[8]中提出的optimal sketch packing算法,该方法通过Hash函数将键值(这里是负载贡献值)进行哈希后再进行均衡分配,从而降低键的规模,节省统计信息占用的内存.本质上,该方法是牺牲精确度来降低统计信息的存储空间.本节设计实验对提出的连接执行计划优化方法以及连接负载均衡方法进行验证和分析.其中,4.1节中的实验是依托图1中给出的查询图生成的虚拟数据表进行多元连接查询设计的,该实验能够很好地验证本文提出的执行计划的优化效果;4.2节中的实验则是依托TPC-H数据集中提供的逻辑数据表进行设计的,本文通过控制其数据的生成方式来设计实验以验证文中提出的连接负载均衡方法.实验的具体设置在4.1节和4.2节中均有对应的详细描述.。
第7章 减治法(《算法设计与分析(第3版)》C++版 王红梅 清华大学出版社)

比较对象,若 k 与中间元素相等,则查找成功;若 k 小于中间元素,则在中间元
算 法 设
计
素的左半区继续查找;若 k 大于中间记录,则在中间元素的右半区继续查找。不
与 分
析
断重复上述过程,直到查找成功,或查找区间为空,查找失败。
( 第
版 )
k
清 华
大
学
[ r1 … … … rmid-1 ] rmid [ rmid+1 … … … rn ] (mid=(1+n)/2)
Page 4
3
7.1.2 一个简单的例子——俄式乘法
【问题】俄式乘法(russian multiplication)用来计算两个正整数 n 和 m 的乘积
,运算规则:如果 n 是偶数,计算 n/2×2m;如果 n 是奇数,计算(n-1)/2×2m+
m;当 n 等于 1 时,返回 m 的值。
算
法
俄式乘法的优点?
与 分 析
2. 测试查找区间[low,high]是否存在,若不存在,则查找失败,返回 0;
( 第
3. 取中间点 mid = (low+high)/2; 比较 k 与 rmid,有以下三种情况:
版 )
3.1 若 k < rmid,则 high = mid - 1;查找在左半区进行,转步骤2;
清 华
3.2 若 k > rmid,则 low = mid + 1;查找在右半区进行,转步骤2;
Page 12
7.2.2 选择问题
【想法】假定轴值的最终位置是 s,则: (1)若 k=s,则 rs 就是第 k 小元素; (2)若 k<s,则第 k 小元素一定在序列 r1 ~ rs-1 中; (3)若 k>s,则第 k 小元素一定在序列 rs+1 ~ rn 中。
关联规则挖掘的两种改进算法

关联规则挖掘的两种改进算法
朱辉生;马常霞
【期刊名称】《计算机应用与软件》
【年(卷),期】2006(23)8
【摘要】针对Apriori算法的主要问题,提出了关联规则挖掘的两种改进算法:高维分解法通过遍历事务数据库形成高维频繁项目集和关联规则,然后直接分解高维关联规则得到低维关联规则;前缀广义链表法先通过对事务数据库的遍历形成前缀链表,然后再次扫描事务数据库,遍历其前缀链表,根据判断每个事务是否与其中的一条路径完全或部分重合而找到关联规则.这两种算法均能极大地减少事务数据库的遍历和大规模候选序列集的产生,提高挖掘算法的效率,使得关联规则的产生简单化.【总页数】3页(P117-119)
【作者】朱辉生;马常霞
【作者单位】淮海工学院计算机科学系,江苏,连云港,222005;淮海工学院计算机科学系,江苏,连云港,222005
【正文语种】中文
【中图分类】TP3
【相关文献】
1.两种基于关联规则的挖掘算法在电子商务中的改进 [J], 白连红;徐澍
2.商务智能系统中两种改进的关联规则挖掘算法 [J], 汤震
3.改进的关联规则挖掘算法及其在教育信息挖掘中的应用 [J], 曲春锦
4.基于改进的关联规则挖掘算法的用户兴趣挖掘 [J], 李珊;邵兰洁;孙丽云
5.商务智能系统中两种改进的关联规则挖掘算法 [J], 汤震
因版权原因,仅展示原文概要,查看原文内容请购买。
表连接优化
浓密树 它连接的两个输入可能都不是表,这种树的结构是完全自由的,查询优化 器只有在没有其他选择的情况下才会选择他。他常会出现在有无法合并的 视图或者子查询的时候。
连接的类型 两种写法 1、SQL-86 2、oracle9i开始支持SQL-92 我们下面来看看连接类型 1、交叉连接(笛卡尔连接) 将一张表的所有记录与另一张表的所有记录进行组合的操作。
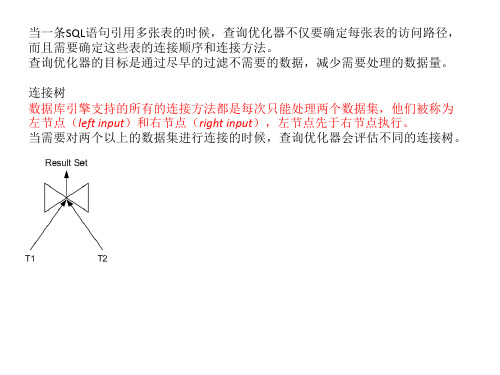
当一条SQL语句引用多张表的时候,查询优化器不仅要确定每张表的访问路径, 而且需要确定这些表的连接顺序和连接方法。 查询优化器的目标是通过尽早的过滤不需要的数据,减少需要处理的数据量。
连接树 数据库引擎支持的所有的连接方法都是每次只能处理两个数据集,他们被称为 左节点(left input)和右节点(right input),左节点先于右节点执行。 当需要对两个以上的数据集进行连接的时候,查询优化器会评估不同的连接树。
连接条件 限制条件
从实现的角度看,查询优化器误用限制条件与连接条件也是正常的,一 方面,连接条件可用来过滤数据,另一方面,为了最大程度的降低连接 使用的数据量,限制条件可能会在连接条件之前进行过滤。
首先执行的是限制条件 然后进行表连接
嵌套循环连接 嵌套循环连接处理的两个数据集被称为外部循环(outer loop,也就是驱动 数据源,driving row source)和内部循环(inner loop)。 外部循环作为左子节点,内部循环作为右子节点。 当外部循环执行一次的时候,内部循环需要针对外部循环返回的每条记录 执行一次。
注意:无法控制块预取功能的使用,如何以及是否使用块预取是数据库引擎自行 决定的。
其他可选的执行计划 只有当内部循环或者外部循环是 基于唯一索引扫描的时候才会使 用这种类型的执行计划。
基于Kriging模型的自适应多阶段并行代理优化算法

第27卷第11期2021年11月计算机集成制造系统Vol.27No.11 Computer Integrated Manufacturing Systems Nov.2021DOI:10.13196/j.cims.2021.11.016基于Kriging模型的自适应多阶段并行代理优化算法乐春宇,马义中+(南京理工大学经济管理学院,江苏南京210094)摘要:为了充分利用计算资源,减少迭代次数,提出一种可以批量加点的代理优化算法。
该算法分别采用期望改进准则和WB2(Watson and Barnes)准则探索存在的最优解并开发已存在最优解的区域,利用可行性概率和多目标优化框架刻画约束边界。
在探索和开发阶段,设计了两种对应的多点填充算法,并根据新样本点和已知样本点的距离关系,设计了两个阶段的自适应切换策略。
通过3个不同类型算例和一个工程实例验证算法性能,结果表明,该算法收敛更快,其结果具有较好的精确性和稳健性。
关键词:Kriging模型;代理优化;加点准则;可行性概率;多点填充中图分类号:O212.6文献标识码:AParallel surrogate-based optimization algorithm based on Kriging model usingadaptive multi-phases strategyYUE Chunyu,MA Yizhong+(School o£Economics and Management,Nanjing University of Science and Technology,Nanjing210094,China) Abstract:To make full use of computing resources and reduce the number of iterations,a surrogate-based optimization algorithm which could add batch points was proposed.To explore the optimum solution and to exploit its area, the expected improvement and the WB2criterion were used correspondingly.The constraint boundary was characterized by using the probability of feasibility and the multi-objective optimization framework.Two corresponding multi-points infilling algorithms were designed in the exploration and exploitation phases and an adaptive switching strategy for this two phases was designed according to the distance between new sample points and known sample points.The performance of the algorithm was verified by three different types of numerical and one engineering benchmarks.The results showed that the proposed algorithm was more efficient in convergence and the solution was more precise and robust.Keywords:Kriging model;surrogate-based optimization;infill sampling criteria;probabil让y of feasibility;multipoints infill0引言现代工程优化设计中,常采用高精度仿真模型获取数据,如有限元分析和流体动力学等E,如何在优化过程中尽可能少地调用高精度仿真模型,以提高优化效率,显得尤为重要。
八大行星排列顺序

八大行星排列顺序九大行星离太阳的远近排列顺序九大行星离太阳的远近排列顺序:水星、金星、地球、火星、木星、土星、天王星、海王星、冥王星水星:水星在九大行星中,他的体积排列倒数第二,但是它是离太阳最近的行星金星:金星按照距离太阳的远近次序是第二颗行星,在日落的任何时间里,在西方的上空看见一个发光的天体就是金星金星自己不会发光,它是反射了太阳的光才发亮的地球:地球按照距太阳由近到远的次序为第三颗行星,是九大行星中唯一适宜生命生存和繁衍的地方火星:火星按照距太阳由近到远的次序为第四颗行星,又叫”红色星行”,它一出现在天上,就可以看到他那淡淡的红色木星:木星按照距太阳由近到远的次序为第五颗行星,是太阳系中最大的一颗行星,它是地球半径的11倍,体积是地球的1316倍,质量是地球质量的318倍土星:土星按照距太阳由近到远的距离排列是第六颗,是太阳系里的第二大行星,它有七个美丽的光环,他的光环鲜艳夺目,因此有人把土星成为”星中美人”天王星:天王星按照距太阳由近到远的距离排列是第七颗,在太阳系的九大行星中他的体积位居第三,因为它的大气层中含有甲烷,因此天王星呈蓝绿色海王星:海王星是环绕太阳运行的第八可颗行星,他是一颗淡蓝色的行星他是典型的气体行星冥王星:冥王星是九大行星中离太阳平均距离最远,质量最小的行星一种奇序列并行排序算法第3卷第l期3513.3・计算机工程20年8月07Augt207us0No1.5ComputrEnnerngegiei软件技术与数据库・一文章编号:I_48I759_2文献1I32(J)—0每-JJ2I1J0标识码:A中围分类号:P0.T316种奇序列并行排序算法张建平,杜学东(山东科技大学信息科学与工程学院,青岛261)650摘要:提出了一种奇序列双调排序算法,过分析发现,算法对某些奇双调序列不能得到正确的排序结果在该算法的基础上,通该通过增加CIC操作,得到一种改进算法,改进后的算法能对任意奇双调序列进行正确排序,且不增加存储空间,计算复杂度级别也不变关健诃:双调序列;归并排序;双调排序PrllotngrtmfdeuneaalrigAloihodSqeceSOZHANGinpn,Ja-igDUednXu-og(lgfnomainlcecnniergSadncecnehooyUiesyQiga650ColeofrtaSinedEgnen,hnogSineadTcnlgnvri,ndo26)eIoait1IsrelTeeiaprllotlotmfdeuneByaayigtiagrhintorcfrodincsqecsTiAbtathrsaalragrhodsqec.nlz,hsloimsortomeodBtieune.hsesiontcesoagrhimeddbcesnCIoaeadcnioaltrhneoeaosadayodBincsqecaeoetotdbloimneyiraigC(mpnodtnliecag)prtn,nndtieunenbrclsrytsncriynioccyetemedelotm.tdeonraemeosaeColainoemedelotmosntcag.hndagrhiIosnticesm ̄pc.mpitftndagrhdeohnecohi[ywod!Btncsqec;rigsrBtncsrKersiieunemegno;iiootot16年Bthr]98acet提出了两个著名的排序算法:n奇偶排序和双调(i)i排序算法由于该类算法在开关网络、并行Btnc【)处理系统、多访问存储系统等方面都有着重要的应用价值,或者()2此序列能够循环旋转使得条件()1满足例如,(3,,5,是一个双调序列,该序列向右旋转1,7,4),68,2循环两位,得到(,1,7,也是双调序列4,3,8)2,6,5定义2布尔对称函数)对于n个不使用取补形式的变(量…,其所有积之和的形式所构成的函数称为布尔对将ab定义为a和b的最小值,即a=nab;而abbmi(,)+定义为ab的最大值,即abma(,)和+=xab称函数(olayboensmmeifntn,记之为S(,tcuco)ri ̄x…)zI,in因此数10年来,人们在此基础上进行了大量的后续性应用研究工作,并且取得了许多重要的研究成果】使得该算法的,应用可靠性不断提高,延迟级数越来越少近10余年来,些文献对双调归并网络及其改进算法进一行了研究1899年Nktiaan等人在两路归并排序算法的a基础上,提出了k路Btnc并行归并排序的思想;19一iio95年来智勇提出了一种并行归并排序算法,在保持效率为o1()的情况下,算法的并行度达到Ono,)99年胡珥等人(gn;19l将Btnc排序思想进行了扩充,出了kin排序算法iio提-tiBoc…,它可以在O1,.gn步内将k个单调序列合并成一个有序(gk1,)oo序列,其中n为问题规模,k为任意正整数求解排序问题的基本操作是两个数之间的“比较和条件交换”(opradcnioalitrhnec)cmaenodtnlecag,Cz操作iyn定理lBthr定理)给定一个双调序列aa…l:,(ace…,:I,a对于所有的1n,执行a和a的比较交换得:i,b=iaalmn),Cmx,)所形成的两个子序列:(,+iaaa=(,Mn{,:b)Mx【l:均是双调序列,且对所有的ibb,~,a=cc,)=,1…c1inJ足bC≤≤,n,1,.对并行排序算法的研究,多数是基于序列长度为2的幂次方的而在实际应用中并非所有的序列长度都是2的幂次方,所以在按Bteahr定理进行并行排序的过程中,有可能c出现奇数长度的子序列(或待排序序列本身就是奇数长度)文献【]2给出了一个奇序列的归并排序网络,通过分析发现,这种归并排序网络算法,并不能对所有的奇双调序列进定理2求找最小成本的排序网络问题等效于计算具有最少与或门的对称函数问题,而S(1,的值就是输入集nX)…合的逆序序列中第个值Bthr比较交换器的定义如图1ace所示行正确排序因此,本文在该算法的基础上,通过增加CIC操作,得到了一种改进的归并排序算法,使之能对任意奇双调序列进行正确排序,且不增加存储空间,计算复杂度级别也不变=l双调排序的基本思想双调排序算法利用了双调序列的特性,该特性又称为Bthrace定理…,下面给出相关的定义和定理二()b图1Bthrace比较器定义l双调序列)一个序列a,,.是双调序列(…l2.aa.,(incsqec)Btieune,如果o()1存在着一个a1kn,使得a≥.a≤≤k≤≤)(,≥…a成立;一作者筒介:张建平(91,男,17一)硕士研究生,主研方向:入式系嵌统;杜学东,教授、博士收稿日期:20—81060—0Ema:zjn136.m-ihig6@13olpc96一维普资讯http://图1a所示为Bthr比较器,()ace其功能是将2个输入量进列,递归使用CIC操作{i(ik,aa1≤_k为正整数):)】来完成奇序列双调归并排序行比较,小者从上端输出,大者从下端输出,简称CIC操作图1b是Bte比较器的简便画法()ahrcBthrace定理直接给出了如图2所示的双调归并网络的递算法1()1通过调用CI操作{.)1k,Caf(di一k为正整数)1,得到Mi{1b)和Ma=c,,'nb’=bkx{12.cc.¨)两个双调序列,且1bc(ik1≤k1j1,1J-);归构造方法一个2个数的双调归并网络可以遵循Bthrace定理,首先并行地进行两两比较,分别形成两个大小为n的Min和Ma列;因为MiMax序n和x都是双调序列,它们可继续按Bthrace定理形成4个大小为n2的MiMa双调/n和x序列,此过程一直重复下去,到各MiMa序列中都只直n和x有2个数为止显然,2个数的双调归并网络就是图1所示()归地对MiMa2递n和x这两个双调序列调用()1,直到Min和Max的长度为2但这种算法存在缺陷,不能对所有的奇双调序列进行正确的排序,对于中间元素是最大(或最小)的序列,按图3值的方法就不能得到正确的结果如对7个元素的双调序列{2,6,)l,7,4用算法1,3,5进行排序,到的结果是{2,4,,得l,7,6,3,5)并不是希望得到的结果之所以出现这种情况,是因为序列的中间元素既可以作为前半个序列的最大元素,也可以作为后半个序列的最大元素在作为前半个序列的最大元素时,在比较过程中没有与后半个序列的任何元素进行比较,使得它不能到达最终排序的正确位置的Bthrace比较器双调归并排序网络中比较器的数目为c()(gno2)n4n=I2+lgn・/o所需的网络延迟级数为DsBrr(=o ̄l2,n(g+g))Inon2其中,n2;n为待排序的元素个数;t=为正整数aIa叶I对上述存在的问题,本文在算法1的基础上,每个奇数子序列(包括原序列)都增加一个比较器,使奇序列中间的元甜素和最后一个元素进行比较,得到一种能对任何奇序列进行d2a叶2正确排序的算法改进后的奇序列双调归并网络如图4所示,即算法2图2双调归并网络的递归构造2奇序列双调排序算法对于长度为nn不为2的幂次方)(的序列,可用补充元素的方法进行排序在序列的后面补充若干个相同的元素,其值大于序列中所有的元素,使得序列的长度为|(中Ⅳ其2=,k为正整数)nN2,对补充元素后的序列采用双调归并排序算法,得到一个有序序列,再取有序序列的前n个元素,即为原序列的有序序列(若需逆序排序,可补充M个相同的元素,其值小于原序列中所有的元素,待排序好后,再取前n元素即可)但这种方法对于远小于2的序列,…需要补充近2个元素,浪费近2个存储空间如n200=5,则N406=9,需补充24个元素60陈国良在文献【】2中给出了如图3所示的一个奇序列的排序归并网络,即算法1图4改进后序列长度为7的双调归并网络设a,a(为正整数):,.k.是一个长度为奇数的双调序列,归使用CI递C操作a(≤≤,)1ikk为正整数)1来完成奇序列双调归并排序a口算法2()过调用CI操作{.(≤≤-,1通Caa)1ik1k为正整数)和{k)则得到Mi{12.k和Ma=c,,,_两个双调序列,a:a,nb,,,)=b.b.x{l2.1c.c)k且b≤j1≤k1≤k1.c(≤i,≤j-);()2然后再递归地对Min和Max这两个双调序列调用()1,直到MiMan和x的长度为23算法分析为了检验改进后的算法的正确性,本节通过实例进行了分析和验证,如下所示通过定理2可以对改进后的算法进行验证,算法的输出与布尔对称函数的输出相对应,因此改进算法是正确的c=12n口口口c=;,,a口口)lsn口,,,,)2s(口,,,,(,,4567q2456c3=;1234567C::12口口,)(,,,,,,)4(,,45口口口口口口口口口,,,7;1234567C:6a口,,,,,)(,,,,,,)6¥(,nn口口口口口口口口口口71234567c5=c7=;1234567(,,,,,,)口口n口口口n图3序列长度为7的双调归并网络用序列{3,4,做实例验证如下:5,1,7,2,6){,,,,,,)÷f432,,567)÷f4321,567)5321467_{,,)1{,,)_{,,,){,,)设a(为正整数),,…aka是一个长度为奇数的双调序{’,’’){’’){{’,’))’’,(下转第10页)0一97一维普资讯http://原尉3符合语法规则切分结果必须符合语法规则,不允许出现诸如“形容词+动词”的情况原则4符合语义规则切分结果必须符合语义规则,不允许出现明显的语义错误轮的检测,用现代汉语语法信息词典通过语法约束矩阵进行约束,如合适,则进入下一轮,否则重新进行切分在下一轮用《现代汉语语义词典通过语义约束矩阵进行约束,如合适,则进入下一轮,否则重新进行切分如果都符合规则的话,通过新词词典进行未登录词识别,识别完之后即完成一次切分,得到切分结果实践证明,分词处理效果显著,从实验结果看,准确率能提高1%左右0原则5正向最大匹配优先,用于出现几种合理切分结果的情况虽然这些原则并不严格,有时候必须视情况而定,在处理歧义字段时也会出现多个原则同时可用的情况,这使得系统实现比较灵活,也便于以后使用处理不确定性的方法改进规则5总结分词是计算机处理信息的基础,无论是在信息检索,还是在文本分类中都离不开分词本文采用《现代汉语语法信息词典和现代汉语语义词典来对汉语进行分词处理,4系统分词流程利用语法和语义在理解的基础上对分词结果进行检验,提高歧义消除能力,另外系统引入了约束矩阵,提高了分词系统的精度,对于进一步中文信息处理和信息挖掘具有参考价值参考文献1佘莉,符红光,方海光.几何命题处理中的中文分词技术fl计J1算机工程,053(8:-.20,l1)132汤洪燕,李晓军,王洪利.两种典型的中文分词方法的分析和比较f.J高性能计算技术,052()-.]20,88:323李庆虎,陈玉健,家广.种中文分词词典新机制——双字哈孙一希机制[.中文信息学报,0341)1.J120,(:-734曹勇刚,曹羽中,金茂忠,等.面向信息检索的自适应中文分词系统[l软件学报,051()34J120,8:-.8图1分词系统及各切分功能模块5张滨,李文翔,夏德麟,.等基于汉语句模的中文分词算法[lJ1系统分词的基本流程如图1所示首先对文本流用有限自动机(S进行预处理,FA)识别其中有明显特征的中英文数字(包括基数词、序数词、分数、小数、百分数等)、域名、日期、计算机工程,043()1.20,01-:36张茂元,卢正鼎,邹春燕.一种基于语境的中文分词方法研究flJ1小型微型计算机系统,052()1320,61:-.人名等;然后将进行过预处理的待切分文本输入,通过核心字典进行交叉歧义检测,得到进一步的切分结果,进入下一7余战秋.中文分词技术及其应用初探[.究与开发,043(:J研120,2)623—.(上接第97页)令cn(=k,(n2-k为正整数))1为使用改进算法进行排序所需的比较器个数,()cN为使用双调归并算法对N2(是=kSrnoitmptrneec.16.pgJniCoueCofrne982陈国良.并行算法排序和选择[.合J:中国科学技术大学出版M]IE社,9019.3AaodmdtA,PizaE.CaeBaeaoig:FudtnlIse,azssdResnnonaiasuso使Nn的最小正整数)>的序列进行排序所使用的比较器个数,在最坏情况下,c)(,(:N所以cn(g+g)/Tc)n(≤1al:・4)oNoNN令D(为网络延迟级数,在最坏情况下,每一次归并n)都比N2=的序列多一级延迟,则D(sD2),即sn()2MehdlgclaitnnytmprahsJ.mmuitoooiaVrisdSsaoaeApoce[AI]Con-ctn,9471:95.ais19,()3—9o4KodeLCsaeesnn[.raafn93lnr.aeBsdRaoigM]MognKuman19.J5OsobmeH,BreD.SmirtMerc:AomaictfidgiliyatsifrlUnfaioionDnlal,所以复杂度级别不变(≤gnon)o+g4结束语本文依据双调排序的基本思想,文献【】出的奇序列对2提CadnlnNo—adnlilryriaadnciaSmiiMesrsC]Po.ohrataue[/rcfte/ItrtoaneecnCaebaeaonn.19.nenainlCofrneos—sdResig97并行排序算法,通过增加CIC操作进行了改进,使之能对任意奇双调序列都能够进行正确排序,且具有下列优点:()1改进后的算法可对任意奇序列可以并行处理,而且不增加存储空问6NaaaiHun,dnBea.watoio[.EEktnT,agSAre,t1K・yBitSrJIEnct]Tasooues18,82:8—8.rn.nCmptr,993()23287BrhfateTer[.rdAmecnMaetaSceyioLLtchoyM]3de.kiiratmailoit,hcl697.()法的比较器个数c(2算n)不超过c2)(中(其2<<,n2k为正整数)8来智勇.并行归并算法[1计算机研究与发展,953()4.9J.19,26:64.算法的延迟级数DnsD2)((,数量级不变,系数略)2有增加9王文义,邱涌.一种新的并行归并排序算法[_算机研究与J计1发展,054()7-220,l5:17.10胡明,庆狮,高刘志勇.—inKBtioc排序[.国科学(辑)J中1E,参考文献1BteESrntrsadTepiain[]Po.facrK.otgNewoknhiApltsC/rcohirco/19,92:1512992()5—6.五大天启灾难:行星排成一列五大天启灾难:行星排成一列玛雅末日预言源自对古代玛雅人长历法的误解,该历法中一个历时约400年的周期“伯克盾”(baktun)将于2012年12月21日(也是冬至日)结束这是玛雅历法中的第13个伯克盾,只是一个完整的时间周期参照点而已换句话说,玛雅人的时间观念是具有周期性的,他们所用历法中某个周期的结束并不意味着世界的末日直到过去二十年间,西方人开始重新解释玛雅历法的时候,有关其预言世界末日的说法才逐渐出现玛雅世界末日的流言还在网络上扩散着,有的说12月21日之后世界将迎来一个和平的新纪元,更多的则是预测灾难性天文事件的发生世界和平当然是我们共同的愿望,但对于行星碰撞之类的预言,大可不必担心预言1:太阳将把我们全部杀死玛雅末日预言中说的较多的一个话题是,太阳目前正进入最活跃的时期太阳活动的强度具有周期性,大约为11年活跃的程度可以从太阳风暴和耀斑是否增加来判断有些太阳耀斑确实能够影响地球耀斑等太阳活动释放的电磁颗粒会与地球的大气层相互作用,太阳风暴能干扰电磁通讯,但我们已经有方法来保护卫星和其他电子设备这些带电粒子也是南北极极光出现的原因美国航空航天局的科学家称,有关太阳风暴将摧毁地球的说法没有事实依据所谓的太阳活动峰值与近期的历史纪录相比,只能算是毫不起眼也就是说,科学家并不认为太阳风暴能够影响我们的社会运作预言2:地球磁极将翻转玛雅启示与电磁学也有关系?该流言认为,地球南北极将出现灾难性的调转其实这也不是空穴来风:地球的磁场确实会偶尔翻转,但不是在一天之内美国航空航天局的科学家称,地球南北磁极的变换需要数百到数千年的时间磁极调转可能会导致宇宙辐射的少量增加,但从化石记录来看,之前的调转并未对生物产生影响预测磁极调转也是相当困难的上一次调转还是发生在大约78万年前,用了数千年的时间不过,在地球历史上,至少有一个时期磁极在3千万年时间里保持稳定预言3:未知行星将撞击地球行星X,有时候被称为Nibiru,实际上并不存在然而,一些末日理论者还是预言道,这一“流氓行星”将撞向地球,消灭所有生命有关行星X的流言始于1976年,当时已故作家Zecharia Sitchin宣称,他在自己翻译的闪族文本中重新发现了失落的行星Nibiru据传该行星围绕太阳运行一圈的时间为3600年,这也解释了为何现代人和天文望远镜都没能观察到这个行星邻居2003年,自称是灵媒兼外星人传语者的南希·莱德(Nancy Lieder)警告说,这颗行星将与地球相撞但撞击并未发生,于是预言日期又被推到了2012年,与玛雅预言合二为一显然,如果一颗行星将在数日之内与地球相撞的话,我们的肉眼都应该可以看得很清楚了事实上,如果Nibiru存在的话,在2012年4月的夜空,它就应该与火星一样明亮了以美国航空航天局的深空探测能力,如果有行星向地球飞来,势必逃不出探测器的法眼预言4:行星将排成一列关于另一个恐慌是行星将排成一条直线,从而影响地球这个流言比较容易破解,美国航空航天局的网页如是说:“行星对齐的现象在未来数十年内都不会出现,即使出现了,对地球的影响也几乎可以忽略不计”在1962年、1982 年和2000年,都曾经出现过行星排成一列的现象,但我们还是安然无恙预言5:地球大停电这则流言是在垃圾邮件中循环传播的邮件宣称,地球将全部陷入停电之中,有些电子邮件甚至宣称,这次停电是太阳和地球首次直线排列的结果,另外一些则更夸张,宣称地球将进入一个“静止环”美国航空航天局称,无论是什么原因,大停电都是不可能发生的有序的排列有序的排列例1:从甲地到乙地,可以乘汽车,也可以成火车,一天中,汽车有3班,火车有4班,一天中从甲地到乙地有多少种不同的走法?例2:艺术团的张叔叔有黄白两顶不同的演出带的帽子和黑白两种黑红两种颜色的鞋子,他每次出场演出都要戴一顶帽子,穿一双鞋,张叔叔的帽子和鞋子可以有哪几种不同的搭配?例3:旗杆上最多可挂两面信号旗,现在有红、黄、绿三种颜色的信号旗各一面,如果用挂信号旗表示信号,最多能表示多少种不同的信号?例4:从甲地到乙地有4条路,从乙地到丙地有两条路,从甲地经过乙地到丙地一共有多少种不同的走法?基础训练:1、一件工作可以用两种方法完成,有5人会用第一种方法,另外有4人会用第二种方法完成,要选出1人来完成这种工作,可以有多少种不同的选法?2、兰兰有2件上衣,3条裙子,她最多能在几天内保证每天穿的衣服不完全一样?3、婷婷、芳芳、晓晓站成一竖行排队,有多少种不同的排法?4、从A村到B村有5条路,B村到C村有3条路,如果从A村到C村,经过B村,一共有多少种不同的路线?八大行星之木星木星是太阳系中最大的行星,966木星是一个巨大的气态行星最外层是一层主要由分子氢构成的浓厚大气万巴的高压和由于木星快速的自转,大红斑”八大行星之木星太阳系中最大的行星——木星它的体积超过地球的一千倍,与其他巨行星一样,木星没有固态的表面,通过望远镜观测,这些云层就象是木星上的一条条绚丽的彩带在离木星大气云顶一万公里处,6000K 的高温下成为液态金属氢它有一个复杂多变的天气系统,木星云层的图案每时其中最著名的风暴是已经在木星大气层中存在其外围的云系每四到六天即运动一周,由于木星的大气运动剧烈,而是覆倍风1 质量超过太阳系中其他八颗行星质量的总和盖着公里厚的云层随着深度的增加,氢逐渐转变为液态液态氢在100木星的中央是一个由硅酸盐岩石和铁组成的核,核的质量是地球质量的10 每刻都在变化我们在木星表面可以看到大大小小的风暴,“这是一个朝着顺时针方向旋转的古老风暴,了几百年大红斑有三个地球那么大,暴中央的云系运动速度稍慢且方向不定致使木星上也有与地球上类似的高空闪电木星的两极有极光,这似乎是从木卫一上火山喷发出的物质沿着木星的引力线进入木星大气而形成的木星有光环光环系统是太阳系巨行星的一个共同特征,主要由小石块和雪团等物质组成木星的光环很难观测到,它没有土星那么显著壮观,但也可以分成四圈木星环约有6500公里宽,但厚度不到10公里质量+27 kg赤道半径71,492 km平均密度gm/cm平均日距778,330,000 km自转周期天公转周期天赤道地表重力m/sec赤道逃逸速度km/sec平均云层温度-121°C大气压力bars大气组成氢90%氦10%2八大算法排序排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等本文将依次介绍上述八大排序算法算法一:插入排序插入排序示意图插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入算法步骤:1)将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列2)从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)算法二:希尔排序希尔排序示意图希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本但希尔排序是非稳定排序算法希尔排序是基于插入排序的以下两点性质而提出改进方法的:●插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率●但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序算法步骤:1)选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;2)按增量序列个数k,对序列进行k 趟排序;3)每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度算法三:选择排序选择排序示意图选择排序(Selection sort)也是一种简单直观的排序算法算法步骤:1)首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置2)再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾3)重复第二步,直到所有元素均排序完毕算法四:冒泡排序冒泡排序示意图冒泡排序(Bubble Sort)也是一种简单直观的排序算法它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成这个算法的名字由来是因为越小的元素会经由交换慢慢”浮”到数列的顶端算法步骤:1)比较相邻的元素如果第一个比第二个大,就交换他们两个2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对这步做完后,最后的元素会是最大的数3)针对所有的元素重复以上的步骤,除了最后一个4)持续每次对越来越少的元素重复上面的步骤,直到。
基于RRT的运动规划算法综述
基于RRT的运动规划算法综述1.介绍在过去的十多年中,机器人的运动规划问题已经收到了大量的关注,因为机器人开始成为现代工业和日常生活的重要组成部分。
最早的运动规划的问题只是考虑如何移动一架钢琴从一个房间到另一个房间而没有碰撞任何物体。
早期的算法则关注研究一个最完备的运动规划算法(完备性指如果存在这么一条规划的路径,那么算法一定能够在有限时间找到它),例如用一个多边形表示机器人,其他的多边形表示障碍物体,然后转化为一个代数问题去求解。
但是这些算法遇到了计算的复杂性问题,他们有一个指数时间的复杂度。
在1979年,Reif则证明了钢琴搬运工问题的运动规划是一个PSPACE-hard问题[1]。
所以这种完备的规划算法无法应用在实际中。
在实际应用中的运动规划算法有胞分法[2],势场法[3],路径图法[4]等。
这些算法在参数设置的比较好的时候,可以保证规划的完备性,在复杂环境中也可以保证花费的时间上限。
然而,这些算法在实际应用中有许多缺点。
例如在高维空间中这些算法就无法使用,像胞分法会使得计算量过大。
势场法会陷入局部极小值,导致规划失败[5],[6]。
基于采样的运动规划算法是最近十几年提出的一种算法,并且已经吸引了极大的关注。
概括的讲,基于采样的运动规划算法一般是连接一系列从无障碍的空间中随机采样的点,试图建立一条从初始状态到目标状态的路径。
与最完备的运动规划算法相反,基于采样的方法通过避免在状态空间中显式地构造障碍物来提供大量的计算节省。
即使这些算法没有实现完整性,但是它们是概率完备,这意味着规划算法不能返回解的概率随着样本的数量趋近无穷而衰减到零[7],并且这个下降速率是指数型的。
快速扩展随机树(Rapidly-exploring Random Trees,RRT)算法,是近十几年得到广泛发展与应用的基于采样的运动规划算法,它由美国爱荷华州立大学的Steven M. LaValle 教授在1998年提出,他一直从事RRT算法的改进和应用研究,他的相关工作奠定了RRT算法的基础。
一种奇序列并行排序算法
[ ywod !Btncsq e c ; rigsr Btncsr Ke r s i i eu n e megn o ; i i o o t o t
16 年 B thr ] 98 acet提出了两个著名的排序算法 : n 奇偶排序 和双调( i)i 排序 算法 。由于该 类算法在 开关 网络 、并行 B tnc 【 )
t e me de l o t m . td e o n r a e me o s a e Co l a i n o e me de l o t m o sn tc a g . h n dag r h i I o sn ti c e s m  ̄ p c . mp i t ft n d a g r h d e o h n e c o h i
ZHANG in pn , Ja - ig DU e d n Xu -o g
( l g fnomain l cec n n ier g S a d n ce c n eh oo yU ies yQig a 6 5 0 Col eo fr t a Sin e dE gn e n , h n o gS ineadT c n lg nvri , n d o2 6 ) e I o a i t 1
序 列,其 中 n为 问题规模 ,k为任意正整数 。
求解排序 问题 的基 本操作 是两个数之间的 “ 比较和条件
交换”(o p r a dcn io al itrhn e c ) c m ae n o dt nl eca g ,C z操作 。 i yn
定理 lB thr定理) 给定一 个双 调序 列 aa…l:, ( ace … ,: I , a
ag r h i me d db ce sn CI o aea d c n i o al tr h n e o ea o s a da yo dBi ncsq e c a e o e t otdb lo i m n e y i r a igC ( mp n o dt n l i ec a g ) p rt n , n n d t i e u n e nb r cl s r y t s n c r i yn i o c c y e
GBFT:一种实用拜占庭容错算法改进方案
GBFT:一种实用拜占庭容错算法改进方案
李彬;张新有
【期刊名称】《计算机与数字工程》
【年(卷),期】2024(52)1
【摘要】区块链技术近年来成为研究热点,在金融、物流等行业已经有联盟链的落地案例。
共识算法作为区块链的核心技术,将对区块链的整体性能产生直接影响。
应用于联盟链的实用拜占庭容错算法(Practical Byzantine Fault Tolerance,PBFT)仍然存在着交易确认时间长、吞吐量低等问题。
面向联盟链应用场景,基于PBFT 算法,引入了非拜占庭容错协议,结合基于节点行为的选举机制,提出了三级共识机制的PBFT:GBFT。
最后从吞吐量、交易确认时延、容错性等方面对GBFT方案和原始PBFT算法进行了对比实验与分析。
实验结果表明,GBFT保持了PBFT算法1/3的容错性,有效提高了吞吐量,降低了交易确认时延。
【总页数】7页(P87-93)
【作者】李彬;张新有
【作者单位】西南交通大学信息科学与技术学院
【正文语种】中文
【中图分类】TP301
【相关文献】
1.一种区块链实用拜占庭容错算法的改进
2.一种基于积分制的改进实用拜占庭容错算法
3.一种改进的实用拜占庭容错算法
4.一种改进的实用拜占庭容错共识算法
5.一种改进的实用拜占庭容错算法
因版权原因,仅展示原文概要,查看原文内容请购买。
基于改进鲸鱼优化算法的多目标信号配时优化
2021年2月第1期第46卷昆明理工大学学报(自然科学版)Joernai of Kunming University of Science and Techuoloyy(Natural Sciences)Feb.2021No.1Vol.46doi:12.16112/1-chdi-53-1223/1-2221.21.20基于改进鲸鱼优化算法的多目标信号配时优化吴小龙4胡松6,成卫6(1-昆明阡陌交通工程咨询有限公司,云南昆明654028;9-昆明理工大学交通工程学院,云南昆明654540)摘要:为了使交叉口的通行效益最大化,构建以交叉口平均延误、平均停车次数最小以及最大通行能力最大化为优化目标的多目标函数模型,并提出一种基于自适应权重和levy飞行的改进鲸鱼优化算法(ALWOA)对信号控制交叉口进行配时方案优化.结合实际算例,将求解后的结果与现有方案、使用传统的Webster算法求解的方案、使用GA和标准WOA得到的方案进行对比.结果表明,使用ALWOA 得到的配时方案明显优于其他方法,从而证明了改进后的鲸鱼优化算法以及函数模型在交叉口信号配时方案优化上的有效性.关键词:交叉口信号控制;鲸鱼优化算法;信号配时优化;levy飞行中图分类号:U491.2文献标志码:A文章编号:O26-855X(222021-204-28Multi-Objective Signai Timing Optimization Based on ImpreveCWhale Optimization AlgoritUmWU Xiaolong1,HU Song2,CHENG Wei2(1.Kunming Qiasmo Tr—fic Engiueering Coxsul/ng Co.Ltd.,Kunming655428,China;2.Facalty of Transporiatiox Engiueering,Kunminy University of Science and Techuolopy,Kunmine650540,China) Abstrect:In order te yet tUo maximum benefiis of tUo comprebensive traffic intersection,wo constructeb a mulii 一okjective function mokei te achieve tUo minimum averayo delay,tUo smallest averayo nnmbyr of parking and tUo maximum capacity-Wo alse proposeb an Adaptive Wight and Lxy Flight Improveb Whaio Optimization Ai-OoritUm(ALWOA)to optimiao tUo timiny schemo io tUo sipnal control intersection-Combineb witU tUo actual x-amplos,tUo resulis and tUo schem were cempareb witU tUo schemo ixu UX Uom tUo conventional Webstor Alyo-rithm,GA and standard WOA-Tho ixu/s show that tUo ALWOA timing schemo is supxO/te otUor metUoks, which has proveb tUo ePectiveness of ALWOA and tUo function mokei on tUo intersection sipnal timing optimization-Key wcras:zntxsxtion sipnal control-Whalo optimization alyoritUm;timing of intersections,leve Uyo引言我国经济的高速发展大大刺激了国民的物质需求,私家车出行因为其灵活性和方便性也因此被越来越多的人选择.由于城市化的推进和私家车保有量的快速提高,城市交通问题已成为影响城市经济发展的一个重要因素•我国的早期交通规划化与和现有的通行能力需求并不成正比,城市路网负荷超标严重,导致大量城市出现了拥堵的情况•为了在现有的交通条件下尽可能提升交通效益、减少城市的拥堵状况,对收稿日期:2019-12-30基金项目:国家自然科学基金项目(6136400)作者简介:吴小龙(082-),男,硕士,高级工程师.主要研究方向:交通系统工程.E-mail:9362648l@通信作者:成卫(1277-)-男,博士,教授,博士生导师.主要研究方向:智能交通管理系统关键技术与理论方法.E-mail:C69948233@第1期吴小龙,胡松,成卫,:基于改进鲸鱼优化算法的多目标信号配时优化06交叉口信号控制进行优化是最有效的途径之一.交叉口信号配时优化要考虑多方面的综合因素来进行交叉口信号控制方案设计以达到交叉口的交通效益最优的目的.在评价交叉口通行效益时通常用停车延误、停车率、车辆排放、通行能力等指标来进行.国内外学者在交叉口配时优化上做出了很多研究:Webster配时法是以交叉口车辆延误的估计为基础,通过对周期长度的优化计算,确定相应的一系列配时参数的经典配时算法[1];国内外还开发了许多有关信号控制的软件系统如Syychrv等⑵;文献[3]针对交通流的时变特性,建立了以延误、排队长度和停车次数最小为目标的交叉口多目标信号配时优化模型,并结合实例证明了模型的有效性;文献[4]使用解析法来构建函数模型,并引入了基于排队论的理论模型,结合人工操作经验来完成交叉口的信号控制,但是该方式在情况复杂和波动性较大的城市交通中适用性不高.近年来,各种启发式算法的兴起使得交叉口配时的方法有了新的发展方向,已经有大量将启发式算法应用于交叉口配时优化的研究:文献[5]构建了车辆和行人总延误最小的信号配时模型,使用遗传算法寻优获得交通实体产生的平均交通延误达到最小的方案;文献[6]改善了过饱和条件下的信号配时优化模型,以延误最小和通行量最大为目标,使用遗传算法(GA)获得更优的配时方案;文献[7]基于TSTM结合GA算法提出的GATSTM系统能够通过校准系统参数来处理和管理交通网络状况的动态变化;文献[8]通过使用改进的微粒群算法对构建的函数模型求解,获得比传统Webster算法更优的配时方案;文献[9]将模拟退火算法引入自适应控制交叉口中,证明了该方法可以明显提升交叉口的通行能力-鲸鱼优化算法(W0A)作为一种新兴的元启发式搜索算法,在2217年由澳大利亚的mirjaPli等[12]根据观察海洋中座头鲸独特的捕食方式提出,算法通过模拟鲸鱼一系列的捕食行为实现目标函数的求解寻优.W0A算法因其操作简单、参数少而且性能好的特点被大量研究人员所关注并作出了许多相关研究.当前对WOA的研究主要集中在应用和改进两方面.文献:D-17]分别通过引入自适应权重和柯西变异以及随机自适应权重和模拟退火的策略对W0A进行改进,并使用测试函数表明了改进后算法的优越性;文献[13]对WOA进行改进并将其应用到充电站选址的项目上,证明了该算法在工程应用上的有效性.文献[14]使用WOA进行水资源的配置优化,验证WOA在该领域的适用性.文献[0]则通过对WOA进行电网无功优化调度,实例验证了WOA在解决该问题上的鲁棒性和有效性-文章提及的遗传算法、模拟退火算法和WOA等在进行求解时都存在着传统启发式算法通有的易陷入局部最优解、收敛精度低等缺陷•本文首先通过使用自适应权重和levy飞行策略对WOA进行改进,提升了WOA的全局寻优能力、局部寻优能力以及收敛精度,并把改进后的算法应用到交叉口信号配时优化中,然后通过构造多目标寻优函数模型并使用ALWOA对其进行寻优求解,获得综合通行效益最高的配时方案-1多目标信号配时优化的数学模型描述进行交叉口配时优化时,优化效果的评价指标主要包括延误时间、停车次数、道路通行能力、饱和度、油耗、尾气排放等•本文选取交叉口的车辆平均延误、平均停车次数以及最大通行能力这三个参数作为优化目标,利用加权的方法将这三个优化目标联合起来构造目标函数并进行寻优,以获取交叉口的最大交通效益-12交叉口平均延误时间车辆延误由均匀延误和随机延误组成,本文运用韦伯斯特(Webster)提出的延误时间的计算方法来计算车辆的平均延误时间.由Webster延误计算公式可得相位i的车辆平均延误仏如下:必=c(]-扎)0殆2(1-打)*2伽(1-切)(0式中:第一部分表示均匀延误,第二部分为随机延误;9表示周期9是绿信比,表示第i相位有效绿灯时间与信号周期的比值;9i为第i相位第J进口道的流量比;切为第i相位第丿进口道的饱和度为第i相位第j进口道的实际到达的当前交通量jcu/h.由式(1)可知交叉口的所有车辆的平均延误表示为:136昆明理工大学学报(自然科学版)第46卷d=丫也/丫%⑵1.2交叉口平均停车次数进入交叉口的车辆在信号控制的情况下会产生停车的总次数如式(3)所示:h=X仏%/》弘3)i i式中:,表示第i相位的车辆平均停车次数.由式(3)可得一个信号周期内的交叉口的车辆平均停车次数表示为:h=X也/X弘(4)i i1.3交叉口通行能力计算计算交叉口通行能力的方法:首先将交叉口各进口道划分为若干车道组,然后计算各车道组的通行能力,再将各相位的通行能力加起来,最后得到该交叉口一个周期的通行能力,表达式如下:q=X a=X s入⑸i i式中:Q,表示第i相位的通行能力,血为车道组i的饱和流率.13目标函数根据实际到达交通量,通过加权的方式将信号周期内交叉口车辆的平均停车次数、平均延误以及交叉口通行能力联合转化为交叉口信号控制优化目标函数,以控制周期内的有效绿灯时间作为自变量.考虑到路口交通量的变换,对模型在设置权重时要根据实际交通流率进行分配,权重设置为«3=2|3-y|;2=3.5|3-y=0.5 y(y为交叉口各相位关键流率比之和),目标函数如下:r d h Q o(6)约束条件包括以下几点:X((■“+4)邑*⑸5m女=gm m W&W&m*(8)式中:g a为相位i有效绿灯时间,厶为相位i损失时间,g lmin为相位i的最小绿灯时间,gm#为相位i的最大绿灯时间,5m为最小信号周期长度,5#为最大信号周期长度•由目标函数构成可知,要使目标函数取得最小值,就要求在约束条件下尽可能减小车辆的平均延误和停车次数而通行能力则尽量增大.2鲸鱼优化算法鲸鱼优化算法是一种新兴的群智能优化算法,鲸鱼优化算法具有简单、调整参数少、性能高效的特点.算法的主要思路是通过模拟海洋中的座头鲸的觅食行为得到的,把食物位置作为寻优目标通过包围捕食、气泡网攻击及随机游走等方式获得最优解•2.3包围捕食策略鲸鱼个体能识别猎物的位置区域.由于位置的优化设计在搜索空间不是预先确定的,WOA假定当前的最佳解决方案是目标位置或接近目标最优个体位置.在定义了最佳搜索位置之后,个体开始按照一定的策略朝着当前最优位置进行游动.此行为表示如下:D=\C•云⑸)-壬⑸)(9)X⑸+1)=十⑸)-A•D(10)式中/表示个体位置和最优个体间的距离丿表示当前迭代次数,丈表示当前最优个体位置向量,X表示其余个体位置向量,A和c表示系数向量,A、的计算方法如下:第1期吴小龙,胡松,成卫,:基于改进鲸鱼优化算法的多目标信号配时优化07A(11)C=2-r(12)式中&随着迭代次数增加从2到2线性递减的向量,表示一个2到1之间的随机向量.2.2气泡袭击阶段描述气泡网攻击行为的数学模型用如下两种方式设计实现:1)收缩包围机制:这种行为是通过降低式(11)中r的值来实现的,这时候A的值也会随之变化•换句话说,A是区间[-a,a]内的一个随机值,在这个区间内,呈现从2到2的线性递减迭代过程•如果A的随机值在[-1,0之间时,个体会朝着最优位置更新自身位置,更新方式通过式(0)实现.2)螺旋更新位置:此方法首先计算鲸鱼之间的距离,个体从当前位置朝着最优个体位置进行螺旋式移动,用一个螺旋方程来模拟鲸鱼的螺旋形运动如下:壬(+0=可•e"•cos(2n)+X*()(13)式中:o7=IX*()-x()1是鲸鱼个体与最优个体之间的距离向量,e是对数螺线形状常数S是[-1,0中的随机数•鲸鱼个体在猎物周围游动收缩包围和沿螺旋形的路径游走是同时进行的•这时为了模拟这两种同时进行的机制,使用2.0的阀值来决定是选择缩小包围机制还是螺旋模型更新个体的位置,数学模型如下:X(t)-A•D:P<2.5X(+0={一“一(14)[D'•e•cvs(2tt/)+X*()j MO.52.3搜寻猎物阶段该阶段同样基于向量A的变化方法来寻找猎物,个体会根据彼此的位置进行随机搜索.因此,我们使用A在大于1或小于-1的范围的随机值来偏离目标位置进行随机搜索,从而扩大搜索范围,这时就是迫使WOA执行全局搜索,从而表现出一定的全局寻优能力•数学模型如下:D=iC・X n()-X()I(15)X(+0=X Ud()-A•D(16)式中:X Vd是种群中随机一个个体的位置.3改进的鲸鱼优化算法为了避免传统的WOA在求解后期容易陷入局部最优导致的算法早熟从而收敛使进度不高的问题,本文改进WOA的思路从以下两个方法入手:一是使用自适应权重方法,使得WOA的局部寻优能力得到提升;另一方法是通过引入levy飞行策略对鲸鱼位置进行更新,以提升WOA的全局寻优能力-32自适应权重方法由于WOA的局部搜索实现方式是以公式(17)和公式(13)进行的,当个体以公式(14)的更新方式进行局部搜索时,这种方式只能在局部最优解附近徘徊,而不能实现更好的局部寻优•惯性权重是可以用来平衡算法局部搜索能力和全局搜索能力的重要参数•本文使用了一种呈指数改变的自适应权重方法,算法前期使用较大的权重实现较强的全局搜索性能:保证搜索范围:随着迭代次数的增长,接近最优解时:权重值呈现指数减小:使得算法的局部寻优能力大大提升.自适应权值公式如(17)所示,改进后的位置更新公式如(18所示:5J=e-(12!/T)6(0)138昆明理工大学学报(自然科学版)第46卷r®•0()-A-D,p<0.5(18)•X*()+D'•e b l•cos(2n/),pM0.5式中:表示当前迭代次数,T表示最大迭代次数.3.2levy飞行策略levy飞行这个概念的正式定义是“步长具有重尾概率分布的随机行走”.我们可以说这是一个随机游动,它的特殊性在于它表现出较大的跳跃,因为这个过程的步长来自于一个具有无限方差的分布•与任何随机过程一样,levy飞行起源于扩散过程.正因为如此,它们在随机测量和随机或伪随机自然现象的模拟中很有用,特别是表现出一种反常的扩散,系统中存在一种“微观结构”,与混沌理论有关.levy飞行的过程是实体在进行运动的过程中进行大量的小步长移动,同时还有少量跨越式大步长移动的过程•在Matlab图1Levy飞行二维平面示意图Fig.2Two-dimensional diagram of Lvvy flight研究发现许多生物的觅食行为符合levy飞行模式,目前也有大量的研究将其应用到一些仿生算法中,并取得了不错的效果•受文献[16-87]启发,本文将levy飞行应用于鲸鱼的位置更新中,在算法进行更新后再进行一次levy飞行更新个体位置,可以实现跳出局部最优解,扩大搜索能力的效果.位置更新的方式为:X(+8)=X()+a©levy(A)(19)式中:a是步长缩放因子,levy(X)就是随机步长,㊉就是'•*'运算.2009年,Yang X Y[18_18]把levy分布函数经过简化和傅立叶变换后得到其幕次形式的概率密度函数,使用Mantegna方法生成levy分布随机步长.levy飞行概率密度函数及生成随机步长的公式如下:levy::二)f,lw入W3(22)S(28)即进行更新时levy。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
。开发 究与设计技术 本栏目责任编辑:谢媛媛 一种改进的多谓诃归并连接算法
, 冯林。熊海灵。吴玲丽 (西南大学计算机与信息科学学院,重庆400715)
摘要:结构连接操作是XML数据库查谭的主要操作,结构连接算法优化是XML查询优化的核心。通过把扩展的oB 编码和Suffindex后缀树引、入MPMG3N算法,提出了Advance MPMG3『N算法。实验证明。该算法在降低时间复杂度,减少 冗余连接等方面有优良的性能 关键词:.X2ML查询优化;结构连接:Advance MPMG|N算法 中图法分类号:TP311 文献标识码:A 文章编号:1009—3044(2007)21—40736—03 An Advance lMulti-Predicate Merge Join Algorithm FENG Lin,XIONG Hai—ling,WU Ling—li (Faculty of Computer and Information Science,Southwest China University,Chongqing 400715,China) Abstract:Sb cturalqeoHnection operation【is the core for XML database query。structural connection order selection is the cen. tral order optimization problems.In this pape‘r,extended QB code and Suffix tre6 were inducted in MPMGJN algorithm.The expefi ment showed that the arithmetic has good performance:in reducing time complicacy and in decreasing redundant connection. Key words:XML query optimization:structural connection:advance MPMGJN algorithm
目前XML已经成为Imemet以及电子商务中进行数据 表示和数据交换事实上的标准. 越来越多的信息开始采用 XML进行存储、交换和表示 XML数据的查询成为当前的 一个研究热点.其中的结构连接操作是XML数据库查询的 主要操作。目前有很多结构连接算法,而其中较为常用的是 MPMGJN算法fn.与商业数据库系统中实现的标准归并连 接相比较.MPMGJN算法大大减少了连接次数.具有很强的 实用价值。但是.MPMCJN算法还是存在重复扫描的问题. 占用了大量的I/0资源。 为了进一步提高查询效率。本文把 扩展的QB编码和SufI1ndex引入MPMGJN算法.提出了一 种改进的结构连接算法.即Advance MPMGJN算法.并且通 过实验验证了在规模较大的XML查询中能够有效缩减搜 索空间.提高查询效率 1背景知识 本节主要介绍了与结构连接算法相关的理论知识 1.1 XML查询的结构连接 结构连接是路径查询处理中的核心操作陶 给定一个潜 在祖先(父亲)元素节点:的集合A和一个潜在后代(孩子) 节点的集合D.结构连接操作的任务是找到所有的节点对 (ai,dj),ai∈A,di∈D,ai是 的祖先(父亲)节点。 目前,已经提出的结构连接算法有两种:排序合并[3,5,61 和划分方法 。文献『3忡提出了k'e-jion算法,该算法需要多 次扫描数据集。文献f51提出了两类算法:树合并(Tree Merge) 算法和堆栈合并(Stack Tree)算法。文献『61对Stack Tree算 法作了改进.利用索引辅助跳过不需要参加连接的元素 此 外,文献r71中还针对它提出的PBiTree编码提出了基于划 分的结构连接算法.其划分策略有两种:水平划分和垂直划 分.分别按元素在树中的高度和所在分支对数据集合的划 分 本文将主要对MPMG-TN算法进行介绍。 l2 MPMGJN算法 C.zhang和J.Naughton提出了基于包含连接的MP= MGJN(multi—predicate merge join)算法ll】。算法的基本思想 是:设参加连接的两个关系表B和T。则对外表B中第一个 元组b。,首先在内表T中顺序搜索到可能与元组b。进行连 接的第一个元组.作为扫描起点.然后从扫描起点开始顺序 扫描,将满足连接条件的元组t 逐条与元组b。进行连接,产 生连接结果:继而对外表B中的其它元组依次重复上面的 步骤.但每次搜索时不必从内表T的第一个元组开始,而是 从上一次的扫描起点开始 MPMGJN算法中。考虑到可能存在同名的嵌套元素。
一个外表元组需从上一个外表元组在内表中的扫描起点开 始搜索.但是同名的嵌套元素毕竟只是少数.大量的搜索和 扫描是不必要的。另一方面.MPMGJN算法要对外表中的每 个元组到内表中进行搜索扫描.但在实际查询中。参加连接 内表和外表中的元组往往已经过筛选.很多的扫描是无意 义的。这样就占用了大量的I/O资源,影响了查询速度。因 此.本文主要对MPMGJN算法进行改进.提出了改进的 MPMGJN算法 1.3 Sumndex Sumndex是一种基于后缀树的索引结构 对OEM数据
图中的所有节点.构造一棵包含每个节点语义路径串的所 有后缀串之聚合后缀树(即共享语义路径的后缀树),则称 该后缀树为对应OEM数据图的后缀索引树。下面给出 Sumndex的形式化定义 设盯(To)={s ,s ,…,s }为V。中所有节点在V。的数据路径 串集合。对所有si =l,2,…,L1,取其语义路径串构造后缀树
收稿日.期:2007—09—12 作者简介: ̄dk(-1982一),男,四川南充市人,硕士研究生,研究方向:XML数据库;熊海灵(1973一),男 副教授,博士,研 究方向:XML数据库;吴玲丽(1983一),女,硕士研究生,研究方向:计算机应用。
736 电脑知识与技术
维普资讯 http://www.cqvip.com 本栏目责任编辑:谢媛媛 开发研究与设计技术 L ={V  ̄-,root ,TmE 幽∑0,F}。其中V root T ,E 分别 为树的节点集合、根节点、叶节点以及边集合,∑。来自T。。F (v’)=v I v∈Vo八v’∈V 八Vpafi ̄=v’ },v砌,v’ 分别为节点 v.v’的语义路径、 在构造Suff1ndex时.由于所有内节点的路径是叶节点 路径的子串.所以只需对OEM图中的所有叶节点路径进行 即可。也就是说盯(Tn1只需包含OEM图中所有叶节点的路 径即cr(T0)=ls ,s2,…,s },l为叶节点个数。 2优化的结构连接算法 . 该部分主要把扩展的QB编码和Sufflndex后缀树引入 MPMGJN算法.提出了改进的MPMGJN算法——Advan(:e MPMGJN.并且设计实验来比较了改进的MPMGJN算法和 MPMGJN算法 2.1扩展的QB编码方式 在本节中,我们对OB编码进行了扩展,在保留标志节 点范围的forder,size1对外.还加入了level来标志节点所处 XML文档树结构的层次和doclD来表示文档号 因此每个 节点被泽码为四元组fdoclD,order,size leve1)。AList、DList分 别表示祖先(或双亲)元素列表、后裔(或孩子)元素列表,并 将AList、DList分别记为A、D:每个列表都按(docID,order)有 序存储或索引聚集存储 那么 包含关系(祖先/后裔关系、 双亲/孩子关系)结构连接的条件分别是: A.docID=D.docID and A.order<D.order and D.order<A.size f2一l1 A.docID=D.docID and A.order<D.order and D.order<A. size and A.1evel=D.1evel—l (2-2) 条件f2一l1可以简记为A c0ntains D,条件f2—2)可以简 记为A directly contains D. 如果列表List按(docID,order1有序.任意给定一个 则 节点r在列表List中的所有后裔节点将是在列表List中紧 接着节点r的一串连续节点:假设列表List按(doclD,order1 有序.任意给定一个节点r.则节点r在列表List中的第一 个可能后裔节点是满足0rder>r.order的第一个节点(同时 还必须满足0rder<r.size.否则说明节点r在列表List中不 存在后裔节点).即在列表List中满足order>r.order且order 取最小值的节点:并且节点r在列表List中的所有后裔节 点将是紧接着第一个后裔节点的一串连续节点,直到do— c1D=r.d0c1D and 0rder< ize条件不成立为止 也就是说.如果在列表List中的某一节点n的order超 出了节点r的f0rder,size1范围.即n.order>r.size,则节点n及 其后面的节点均不可能是节点r的后裔 2.2改进的MPMGJN算法 我们对MPMGJN算法进行如下扩充:先对XML文档 构造Sufflndex树.建立起基于XML的结构摘要索引:同时 对DTD采取扩展的QB编码 扩展后的MPMGJN算法的思想是:构造XML文档的 Sufflndex树.归并尽可能多的重复路径节点,简化路径信 息,然后对该XML的DTD文档采用扩展的QB编码。根据 包含关系结构连接的条件(2一1)(2—2),获得参加连接的两个 表AList和DList.则对外表AList中的第一个元组a ,首先 在内表DList中顺序搜索到可能与元组a.进行连接的第一 个元组(即0rder>a1,Order的第一个元组),称为扫描始点 (scan start D0int),然后在内表DList中从扫描始点开始顺 序扫描(由于采用了Sufflndex树,在实际扫描时并归相同 路径后只扫描一次),对满足order<a..size条件的所有元组 d ,再判断是否满足连接条件,若满足则产生连接结果元组 a .dj;继续对外表AList中的第二个元组a:,重复上面的步 骤.直到外表AList或内表DList中的元组连接完毕。 算法核心代码如下: 算法l:扩展的基于包含连接的MPMGJN算法 //P指向DTD文档 //采用扩展的QB编码方案初始化DTD文档生成AList 和Dlist列表 QB——P=construct(P); DList=DListrequire(QB—P); AList=AListrequire(QB—PJ; ContainmentMerge(AList,DList) set cursorl at beginning of AList set cursor2 at beginning of DList while fcursor!=end of AList and cursor2 1=end of DList1 if(cursor1.doclD<cursor2.doclD) cursorl++; else if(cursor2.doclD<cursor1.doclD) cursor2++; else mark=cursor2;//记录下一次搜索始点
