数学物理方法姚端正CH10作业解答
数学物理方法(5)答案

数学物理方法第五次作业一、单项选择题【 】1、函数()f z 以b 为中心的罗朗(Laurent )展开的系数公式为11().2()k k f A C d i b γζζπζ+=-⎰ ()().!k k f b B C k = 1().2k f C C d i b γζζπζ=-⎰ 1!().2()k k k f D C d i b γζζπζ+=-⎰ 【 】2、本征值问题()()0,(0)0,()0X x X x X X l λ''+===的本征函数是A .cosn x l π B .sin n x l π C .(21)sin 2n x l π- D .(21)cos 2n x lπ- 【 】3、点z =∞是函数cot z 的 A. 解析点 B. 孤立奇点 C. 非孤立奇点 D. 以上都不对【 】4、可以用分离变量法求解定解问题的必要条件是A. 泛定方程和初始条件为齐次B. 泛定方程和边界条件为齐次C. 初始条件和边界条件为齐次D. 泛定方程、初始条件和边界条件为齐次【 】5、设函数()f z 在单连通区域D 内解析,C 为D 内的分段光滑曲线,端点为A 和B ,则积分()C f z dz ⎰A. 与积分路径及端点坐标有关B. 与积分路径有关,但与端点坐标无关C. 与积分路径及端点坐标无关D. 与积分路径无关,但与端点坐标有关【 】6、 条件1z <所确定的是一个A .单连通开区域 B. 复连通开区域 C. 单连通闭区域 D. 复连通闭区域【 】7、条件210<-<z 所确定的是一个A .单连通开区域 B. 复连通开区域 C. 单连通闭区域 D. 复连通闭区域【 】8、积分2||1cos z z z dz ==⎰A .1B .12-C .12D .0 【 】9、函数1()1f z z =-在12z +>内展成1z +的级数为 A .102(1)n n n z ∞+=-+∑ B .101n n z ∞+=∑ C .10(1)2nn n z ∞+=+∑ D .0n n z ∞=∑ 【 】10、点0z =是函数11()sin f z z -⎛⎫= ⎪⎝⎭的A. 解析点B. 孤立奇点C. 非孤立奇点D. 以上都不对二、填空题1.复数231i -的三角形式为,其指数形式为.2.复数5cos 5sin ππi +的三角形式为,其指数形式为.3.的实部u =,虚部v =,模r =,幅角θ=.4. 复数22i +-的实部=u ,虚部=v ,模=r ,幅角 =θ .5. 014=--i z 的解为.6.积分dz zz cos ==⎰1. 7. 积分⎰==++1222z z z dz . 8. 积分⎰==13cos z zdz z . 9. 积分=⎰b a dz z z 2cos .10. 积分=⎰10sin zdz z . 11.积分=⎰202sin πdz z z 12.幂级数n n n z ∑∞=121的收敛半径为. 13.幂级数∑∞=-1)1(n nn z 的收敛半径为. 14.幂级数211-1n n z n ∞=∑()的收敛半径为.15.函数zz f -=11)(在2|1|<+z 上展成)1(+z 的泰勒级数为 . 16. 0=z 为3cos 1)(z z z f -=的.(奇点的类型,极点的阶数) 17. 0=z 为3sin )(z z z f =的.(奇点的类型,极点的阶数)。
数学物理方法123章作业解答

另:()y x u u ,=,()y x v v ,=,⎩⎨⎧==ϕρϕρsin ,cos y xϕϕρρρsin cos yu xu y y u x x u u ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂ρϕϕϕϕϕρϕρρϕϕρϕρ∂∂=∂∂+∂∂=∂∂+∂∂-=⎪⎪⎭⎫⎝⎛∂∂+-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂=∂∂u x u y u y v xv yv x v y y v x x v vcos sin cos sin cos )sin (111 ϕϕρρρsin cos yv xv y y v x x v v ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂ρϕϕϕϕϕρϕρρϕϕρϕρ∂∂-=∂∂-∂∂-=∂∂+∂∂-=⎪⎪⎭⎫⎝⎛∂∂+-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂=∂∂v xv y v yu xu yu x u y y u x x u ucos sin cos sin cos )sin (111所以,有⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂∂∂=∂∂ρϕρϕρρv u v u 11 第18页第2题第27页 指出下列多值函数的支点及其阶。
(1))(a z -解:根式的可能支点是∞点和根式内多项式的零点,现在来逐个考察这些点的性质。
①az =:在此点的邻域内任取一点111φρi ea z +=(11<<ρ),则有211)(φφρρii eea z ==-当保持1ρ不变 πφφ211+→(绕az =一周)时,有2121221)(φπφπφρρρiiie eea z ≠==-++,当保持1ρ不变 πφπφ4211+→+(再绕az =一周)时,有212212221)(φπφππφρρρii ieeea z ===-+++,因此az =是一阶支点。
②∞=z :令tz 1=,tat a z -=-1)(,在0=t邻域内任取一点222φρi e z =,(12<<ρ),2222222111)(φφφρρρii i ee ea tat a z -≈-=-=-当t 绕0=t 一周回到原点时,22222211φπφρρiiee-+-≠当t 再绕0=t一周回到原点时,22222211φππφρρiiee-++-=因此0=t即∞=z 是)(a z -的一阶支点。
数学物理方法第八章作业答案

P 175 8.1在0x =的邻区域内,求解下列方程: (1) 2(1)0x y''xy'y -+-= 解:依题意将方程化为标准形式2210(1)(1)x y''y'y x x +-=-- 2()(1)x p x x =-,21()(1)q x x =-- 可见0x =是方程的常点. 设方程的级数解为0()nn n y x c x∞==∑,则11()n n n y'x nc x∞-==∑,22()(1)n n n y''x n n c x ∞-==-∑代入原方程得222122102221(1)(1)0(1)(1)0n n n n n n n n n n n n n nnn n n n n n n n n n n c xxn n c x x nc xc x n n c xn n c x nc x c x ∞∞∞∞---====∞∞∞∞-====---+-=⇒---+-=∑∑∑∑∑∑∑∑由0x 项的系数为0有:202012102c c c c ⋅-=⇒=由1x 项的系数为0有:311313200 (0)c c c c c ⋅+-=⇒=≠ 由2x 项的系数为0有:4222420114321201224c c c c c c c ⋅-⋅+-=⇒== 由3x 项的系数为0有:533355432300c c c c c ⋅-⋅+-=⇒= 由4x 项的系数为0有:6444640316543401080c c c c c c c ⋅-⋅+-=⇒== 由5x 项的系数为0有:755577654500c c c c c ⋅-⋅+-=⇒= 由6x 项的系数为0有:866686025587656056896c c c c c c c ⋅-⋅+-=⇒== ……∴ 方程的级数解为246801000001115()22480896n n n y x c x c c x c x c x c x c x ∞===++++++⋅⋅⋅∑(2) 22(1)0x y''xy'n y --+=解:依题意将方程化为标准形式2220(1)(1)x n y''y'+y x x -=-- 2()(1)x p x x =--,22()(1)n q x x =- 可见0x =是方程的常点. 设方程的级数解为0()kk k y x c x∞==∑,则11()k k k y'x kc x∞-==∑,22()(1)k k k y''x k k c x ∞-==-∑代入原方程得22212221022221(1)(1)0(1)(1)0k k k k k k k k k k k k k kkk k k k k k k k k k k c xxk k c x x kc xnc x k k c xk k c x kc x n c x ∞∞∞∞---====∞∞∞∞-====----+=⇒----+=∑∑∑∑∑∑∑∑由0x 项的系数为0有:22202021021n c n c c c ⋅+=⇒=-⋅由1x 项的系数为0有:2231131(1)320321n c c n c c c -⋅-+=⇒=-⋅⋅由2x 项的系数为0有:22224222420(4)(4)432120124321n n n c c c n c c c c --⋅-⋅-+=⇒=-=⋅⋅⋅ 由3x 项的系数为0有:22225333531(9)(1)(9)5432302054321n n n c c c n c c c c ---⋅-⋅-+=⇒=-=⋅⋅⋅⋅由4x 项的系数为0有:222226444640(16)(4)(16)65434030654321n n n n c c c n c c c c ---⋅-⋅-+=⇒=-=-⋅⋅⋅⋅⋅由5x 项的系数为0有:222227555751(25)(1)(9)(25)765450427654321n n n n c c c n c c c c ----⋅-⋅--=⇒=-=-⋅⋅⋅⋅⋅⋅由6x 项的系数为0有:2222228666860(36)(4)(16)(36)8765605687654321n n n n n c c c n c c c c ----⋅-⋅-+=⇒=-=⋅⋅⋅⋅⋅⋅⋅……∴ 方程的级数解为2222222345010101022222222226701(1)(4)(1)(9)()21321432154321(4)(16)(1)(9)(25)(4)(16)(36)654321765432187654321kk k n n n n n n y x c x c c x c x c x c x c x n n n n n n n n n n c x c x c ∞=----==+--++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅∑80x +⋅⋅⋅222222012222222111(2)[(22)]{1(1)}(2)!(1)(3)[(21)]{(1)}(21)!kk k kk k n n n k c x k n n n n k c x x k ∞=∞+=-⋅⋅⋅--=+---⋅⋅⋅--++-+∑∑8.3在0x =的邻区域内求解方程: (1) 222(1)0x y''xy'x y -+-=解:依题意将方程化为标准形式221(1)022x y''y'+y x x --= 1()2p x x =-,22(1)()2x q x x-= 可见0x =是方程的正则奇点. 设方程的级数解为0()n s n n y x c x ∞+==∑,则1()()n s n n y'x n s c x∞+-==+∑,20()()(1)n s n n y''x n s n s c x ∞+-==++-∑代入原方程得22120000202()(1)()02()(1)()0n s n s n sn s n n n n n n n n n sn sn sn s n n n n n n n n xn s n s c xx n s c xc xxc x n s n s c xn s c xc xc x ∞∞∞∞+-+-++====∞∞∞∞+++++====++--++-=⇒++--++-=∑∑∑∑∑∑∑∑由sx 项的系数为0有:0002(1)0s s c sc c --+= (指标方程) 因00c ≠,解得11s s ==或212s s == 取11s s ==1s x +(即2x )项的系数为0有:111112(1)(1)0300s sc s c c c c +-++=⇒=⇒= 2s x +(即3x )项的系数为0有:2220202012(2)(1)(2)01025s s c s c c c c c c c ++-++-=⇒-=⇒=⋅ 3s x +(即4x )项的系数为0有:33313132(3)(2)(3)02100s s c s c c c c c c ++-++-=⇒-=⇒=4s x +(即5x )项的系数为0有:444242420112(4)(3)(4)0360362459s s c s c c c c c c c c ++-++-=⇒-=⇒==⋅⋅⋅ 5s x +(即6x )项的系数为0有:55535352(5)(4)(5)05500s s c s c c c c c c ++-++-=⇒-=⇒=6s x +(即7x )项的系数为0有:666464640112(6)(5)(6)0780782456913s s c s c c c c c c c c ++-++-=⇒-=⇒==⋅⋅⋅⋅⋅7s x +(即8x )项的系数为0有:77737372(7)(6)(7)010500s s c s c c c c c c ++-++-=⇒-=⇒=……∴ 方程的一个特解 (11s s ==)为13571000002460111()2524592456913111(1)2524592456913n n n y x c x c x c x c x c x c x x x x ∞+===++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅∑ 取212s s ==1s x+(即32x )项的系数为0有:11112(1)(1)00s sc s c c c +-++=⇒= 2s x +(即52x )项的系数为0有:2220202012(2)(1)(2)06023s s c s c c c c c c c ++-++-=⇒-=⇒=⋅ 3s x+(即72x )项的系数为0有:33313132(3)(2)(3)01500s s c s c c c c c c ++-++-=⇒-=⇒=4s x +(即92x )项的系数为0有:444242420112(4)(3)(4)028*******s s c s c c c c c c c c ++-++-=⇒-=⇒==⋅⋅⋅ 5s x +(即112x )项的系数为0有:55535352(5)(4)(5)04500s s c s c c c c c c ++-++-=⇒-=⇒=6s x+(即132x )项的系数为0有:666464640112(6)(5)(6)0660662346711s s c s c c c c c c c c ++-++-=⇒-=⇒==⋅⋅⋅⋅⋅7s x +(即152x )项的系数为0有:77737372(7)(6)(7)09100s s c s c c c c c c ++-++-=⇒-=⇒=……∴ 方程的另一个特解 (212s s ==)为11591322222200000124620111()2323472346711111(1)2323472346711n n n y x c xc x c x c x c x c x x x x ∞+===++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅∑ ∴ 原方程的级数解为2461201246202461124622111()()()(1)2524592456913111(1)2323472346711111(1)2524592456913111(12323472346711y x Ay x By x Ac x x x x Bc x x x x C x x x x C x x x x =+=++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+++++⋅⋅⋅⋅⋅⋅⋅⋅⋅)⋅⋅⋅ (2) 42(1)0xy''x y'y +--= 解:依题意将方程化为标准形式(1)1024x y''+y'y x x--= (1)()2x p x x -=,1()4q x x=- 可见0x =是方程的正则奇点. 设方程的级数解为0()n s n n y x c x ∞+==∑,则1()()n s n n y'x n s c x∞+-==+∑,20()()(1)n s n n y''x n s n s c x ∞+-==++-∑代入原方程得211000114()(1)2()2()04()(1)2()2()0n s n s n s n s n n n n n n n n n s n s n sn s n n n n n n n n x n s n s c xn s c xx n s c xc x n s n s c xn s c xn s c xc x ∞∞∞∞+-+-+-+====∞∞∞∞+-+-++====++-++-+-==++-++-+-=∑∑∑∑∑∑∑∑由1s x-项的系数为0有:0004(1)20(21)0s s c sc s s c -+=⇒-= (指标方程)因00c ≠,解得112s s ==或20s s ==取112s s ==1s x (即12x )项的系数为0有:11111100101014(1)2(1)206203s s c s c s c c c c c c +++--=⇒-=⇒=11s x +(即32x )项的系数为0有:1121211121210114(2)(1)2(2)2(1)02040553s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅12s x +(即52x )项的系数为0有:11313122323204(3)(2)2(3)2(2)04260117753s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅ 13s x+(即72x )项的系数为0有:11414133434304(4)(3)2(4)2(3)072801199753s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅⋅ 14s x+(即92x )项的系数为0有:11515144545404(5)(4)2(5)2(4)01101001111119753s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅⋅⋅ 15s x+(即112x )项的系数为0有:11616155656504(6)(5)2(6)2(5)01312120111313119753s s c s c s c c c c c c c ++++-+-=⇒⋅-=⇒==⋅⋅⋅⋅⋅ ……∴ 方程的一个特解(112s s ==)为11357922222210000000111322001111()35375397531111975313119753n n s n n n n y x c x c xc x c x c x c x c x c x c x ∞∞++=====++++⋅⋅⋅⋅⋅⋅++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅∑∑1234562023456111111(1)353753975311975313119753111111)3!!5!!7!!9!!11!!13!!c x x x x x x x c x x x x x x =++++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=++++++⋅⋅⋅取20s s ==2s x (即0x )项的系数为0有:22121200101014(1)2(1)20202s s c s c s c c c c c c +++--=⇒-=⇒=21s x +(即1x )项的系数为0有:22222211212104(2)(1)2(2)2(1)0123011442s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅ 22s x +(即2x )项的系数为0有:22323222323204(3)(2)2(3)2(2)03050116642s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅ 23s x +(即3x )项的系数为0有:22424233434304(4)(3)2(4)2(3)056701188642s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅⋅ 24s x +(即4x )项的系数为0有:22525244545404(5)(4)2(5)2(4)090901110108642s s c s c s c c c c c c c ++++-+-=⇒-=⇒==⋅⋅⋅⋅ 25s x +(即5x )项的系数为0有:22626255656504(6)(5)2(6)2(5)0132110111212108642s s c s c s c c c c c c c ++++-+-=⇒+=⇒==⋅⋅⋅⋅⋅ ……∴ 方程的另一个特解 (20s s ==)为2234200000056001111()24264286421110864212108642n s n n n n n y x c xc x c c x c x c x c x c x c x ∞∞+=====++++⋅⋅⋅⋅⋅⋅++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅∑∑23456023456111111(1)222!23!24!25!26!c x x x x x x =++++++⋅⋅⋅⋅⋅⋅⋅⋅ ∴ 原方程的级数解为234561223456023456111111()()())3!!5!!7!!9!!11!!13!!111111(1)222!23!24!25!26!y x Ay x By x Ac x x x x x x Bc x x x x x x =+=++++++⋅⋅⋅+++++++⋅⋅⋅⋅⋅⋅⋅⋅2345612345623456111111(1)3!!5!!7!!9!!11!!13!!111111)222!23!24!25!26!C x x x x x x C x x x x x x =++++++⋅⋅⋅+++++++⋅⋅⋅⋅⋅⋅⋅⋅。
数学物理方法第三版答案

数学物理方法第三版答案【篇一:数学物理方法试卷答案】xt>一、选择题(每题4分,共20分) 1.柯西问题指的是( b ) a.微分方程和边界条件. b. 微分方程和初始条件. c.微分方程和初始边界条件. d. 以上都不正确. 2.定解问题的适定性指定解问题的解具有( d)a.存在性和唯一性. b. 唯一性和稳定性. c. 存在性和稳定性. d. 存在性、唯一性和稳定性.??2u?0,?3.牛曼内问题 ??u 有解的必要条件是( c)??n?f??a.f?0.b.u??0.c.?fds?0. d.?uds?0.???x(x)??x(x)?0,0?x?l4.用分离变量法求解偏微分方程中,特征值问题??x(0)?x(l)?0的解是( b )n?n??n???n??x ).b.( ?x ). a.( ??,cos?,sinllll????(2n?1)?(2n?1)??(2n?1)???(2n?1)??x ).d.( ?x ). c.( ??,cos?,sin2l2l2l2l????22225.指出下列微分方程哪个是双曲型的( d )a.uxx?4uxy?5uyy?ux?2uy?0. b.uxx?4uxy?4uyy?0.c.x2uxx?2xyuxy?y2uyy?xyux?y2uy?0. d.uxx?3uxy?2uyy?0.二、填空题(每题4分,共20分)??2u?2u?2?2?0, 0?x??, t?0?t?x??1.求定解问题?ux?0?2sint, ux????2sint, t?0的解是(2sintcosx).??ut?0?0, utt?0?2cosx, 0?x????2.对于如下的二阶线性偏微分方程a(x,y)uxx?2b(x,y)uxy?c(x,y)uyy?dux?euy?fu?0其特征方程为( a(x,y)(dy)2?2b(x,y)dxdy?c(x,y)(dx)2?0). 3.二阶常微分方程y(x)?或0).4.二维拉普拉斯方程的基本解为( ln1().r1 ),三维拉普拉斯方程的基本解为r113y(x)?(?2)y(x)?0的任一特解y?( jx44x1(x) 3225.已知j1(x)?222sinx, j1(x)?cosx,利用bessel函数递推公式求??x?x23j3(x)?(221221dsinx(sinx?cosx)??x()()). ?xx?xdxx三、(15分)用分离变量法求解如下定解问题2??2u2?u??t2?a?x2?0, 0?x?l, t?0??u??u?0, ?0, t?0 ??xx?l??xx?0?u?x, utt?0?0, 0?x?l.?t?0?解:第一步:分离变量(4分) 设u(x,t)?x(x)t(t),代入方程可得x(x)t(x)x(x)t(t)?ax(x)t(t)??2x(x)at(x)2此式中,左端是关于x的函数,右端是关于t的函数。
数学物理方法(10)--期末考试试卷(4)答案
k 2
k 0
� w( z )
2c2 +
ᆬ
[(k + 2)(k +1)ck+2 - ck-1]zk
0
k 1
将代入方程
c2 0c,3ckkk+23kk((ck33kkk--+-33-12c)1)k-()1k + 1)
即亦即
c3k
c3k -3 3k(3k -1)
1 3k (3k
-1)
代换,有
f1
t -
e- pt dt
0
f1
e- p + d
0
f1 e-p d
0
f2
第e- p d1
页F(1共p F23 p页 )
f (x) lim
n e -nx2
n
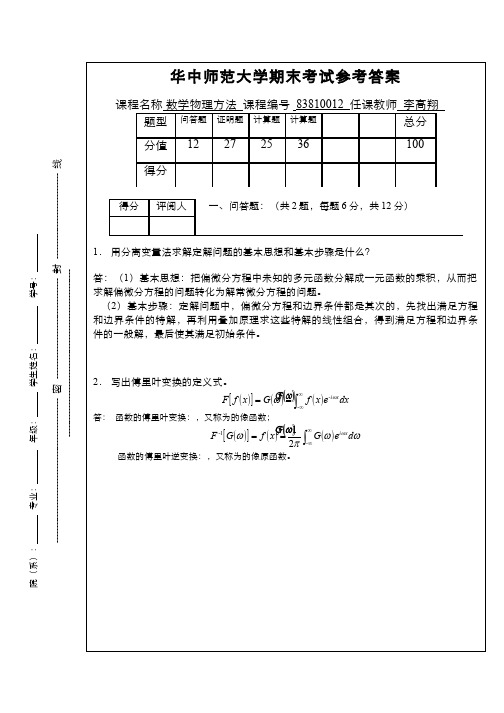
3. 试证明:是函数的一种表达式。
答: 函数的傅里叶变换:,又称为的像函数;
F -1 G
f
xGfx21
G eixd
-
函数的傅里叶逆变换:,又称为的像原函数。
专业:
院(系):
得分 评阅人 二、证明题:(共 3 题,每题 9 分,共 27 分)
1. 已知,试证明: ()
证明:将对 r 求导
ᆬ 1
1+ r2 - 2rx< 1)
(l +1)Pl+1(x) - (2l +l 1ᆬ)1xPl (x) + lPl-1(x) 0
ᆬ 1
1+ r2 - 2rx
ᆬ l0
Pl (x)rl
( x < 1)
15春福师《数学物理方法》在线作业二 答案

正确答案:B
C. C
D. D
正确答案:C
6.
如题
A. A
B. B
C. C
D. D
正确答案:B
7.
如题
A. A
B. B
C. C
D. D
正确答案:B
8.
如题
A. A
B. B
C. C
D. D
正确答案:D
9.
如题
A. A
B. B
C. C
D. D
正确答案:D
10.
如题
A. A
B. B
C. C
D. D
正确答案:A
11.
如题
正确答案:C
17.
如题
A. A
B. B
C. C
D. D
正确答案:D
18.
如题
A. A
B. B
C. C
D. D
正确答案:B
19.
如题
A. A
B. B
C. C
D. D
正确答案:C
20.
如题
A. A
B. B
C. C
D. D
正确答案:D
21.
如题
A. A
B. B
C. C
D. D
正确答案:A
22.
如题
A. A
福师《数学物理方法》在线作业二
一、单选题(共50道试题,共100分。)
1.
如题
A. A
B. BC. CD. D来自正确答案:C2.
如题
A. A
B. B
C. C
D. D
正确答案:C
3.
如题
A. A
数学物理方法习题解答

第八章习题P201:1,2,5,6,11,12,13,16,17,201.长为l 的弦,两端固定,弦中张力为T ,在距一端为0x 的一点以力0F 把弦拉开,然后突然撇除这力,求解弦的振动。
解:此题的定解问题为200000000,(0),(0,)(,)0,,(0),(,0)(),(),0.tt xx t t u a u x l u t u l t F l x x x x T l u x F x l x x x l T l u =⎧-=<<⎪==⎪⎪-⎧⎪<<⎪⎪⎨=⎨⎪⎪⎪-<<⎪⎩⎪⎪=⎩)4()3()2()1(令(,)()()u x t X x T t =代入泛定方程(1)中得X T X aTλ''''==- 可得20T a T X X λλ''⎧+=⎨''+=⎩ (0)()0X X l ==求解关于x 本征值问题,得到本征值和本征函数()2/n l λπ= (1,2,3,n =⋅⋅⋅⋅⋅⋅()sinn X x C x lπ= 将本征值代入关于t 的常微分方程,得到22220a n T T lπ''+= 其解为 ()cossin n n n n a n aT t A x B t l lππ=+ 1(,)()()cos sin sin n n n n a n a n u x t X x T t A t B t x l l l πππ∞=⎛⎫∴==+ ⎪⎝⎭∑将u 的级数解代入初始条件(4)得到001|sin cos sin t t n n t n n a n a n a n a n u A x B t xl l l l l πππππ∞===⎛⎫=-+ ⎪⎝⎭∑1sin 0nn n a n B x l lππ∞===∑ 0n B ∴=则1(,)cossin n n n a n u x t A t x l lππ∞=∴=∑ 根据初始条件(3)有0001000,(0),(,0)sin (),(),n n F l x x x x n T lu x A x F x l l x x x l T l π∞=-⎧<<⎪⎪==⎨⎪-<<⎪⎩∑02()sin l n n A d l l πϕξξξ=⎰ 000000022sin ()sin x l x F l x F x n n d l d l T l l l T l l ππξξξξξξ-=+-⎰⎰ 02000022222sin cos cos x lx F l x F x l n l n n l n l T l n l n l l T l n l ππξππξξξπππ⎧⎡⎤-⎪=--⎨⎢⎥⎣⎦⎪⎩020022sin cos lx F x l n n n T l n l l l ππξπξξπ⎫⎪⎡⎤--⎬⎢⎥⎣⎦⎪⎭000000000220()2sin cos cos cos xF l x l n x n x n x F x n x n l T n l l l T n l πππππππ⎧-⎪⎡⎤⎡⎤=---⎨⎢⎥⎢⎥⎣⎦⎣⎦⎪⎩0000022cos sin cos F x l n x n x n x n n T n l l l ππππππ⎫⎡⎤---+⎬⎢⎥⎣⎦⎭ 002221sin F l n x T n lππ=∴ 00221121(,)cos sin sin cos sin n n n F l n x n a n n a n u x t A t x t x l l T n l l l ππππππ∞∞==∴==∑∑2.求解细杆热传导问题,杆长l ,两端保持为零度,初始温度分布20/)(l x l bx u t -==。
数学物理方法习题及解答

2. 试解方程:()0,044>=+a a z44424400000,0,1,2,3,,,,i k iiz a a e z aek ae z i i ππππωωωωω+=-=====--若令则1.计算:(1)iii i 524321-+-+ (2)y =(3)求复数212⎛⎫+ ⎪ ⎪⎝⎭的实部u 和虚部v 、模r 与幅角θ(1) 原式=()()()123425310810529162525255i i i i i i +⋅+-⋅+-++=+=-+--(2) 332()102052(0,1,2,3,4)k i e k ππ+==原式(3)2223221cos sin cos sin ,3333212u v 1,2k ,k 0,1,2,223i i i e r ππππππθπ⎛⎫==+=+==- ⎪⎝⎭⎝⎭=-===+=±±原式所以:,3.试证下列函数在z 平面上解析,并分别求其导数.(1)()()y i y y ie y y y x e x x sin cos sin cos ++-3.()()()()()()()()cos sin ,cos sin ,cos sin cos ,sin sin cos ,cos sin sin sin ,cos sin cos ,,,x x x x x x x x u e x y y y v e y y x y ue x y y y e y x ue x y y y y y ve y y x y e y y x ve y y y x y yu v u v x y y x u v z f z u iv z u f z =-=+∂=-+∂∂=---∂∂=++∂∂=-+∂∂∂∂∂==-∂∂∂∂=+∂'=∂证明:所以:。
由于在平面上可微所以在平面上解析。
()()()cos sin cos cos sin sin .x x x x vi e x y y y e y i e y y x y e y x x∂+=-++++∂由下列条件求解析函数()iv u z f += (),1,22i i f xy y x u +-=+-=解:()()()()()()()222222222212,2,212,2,,,2112,22111,0,1,1,,221112.222u v x y v xy y x x y v u v y x y x x x x x c x y x f z x y xy i xy y x c f i i x y c c f z x y xy i xy x y ϕϕϕϕ∂∂==+∴=++∂∂∂∂∂''=+=-=-+∴=-=-+∂∂∂⎛⎫=-+++-+ ⎪⎝⎭=-+==+==⎛⎫=-++-++ ⎪⎝⎭而即所以由知带入上式,则则解析函数2. ()21,3,,.ii i i i i e ++试求()()(((()()()2(2)Ln 144(2)4ln32Ln32ln32ln1222Ln 21cos sin ,0,1,2,3cos(ln 3)sin(ln 3),0,1,2,i i k k i ii i k i i k i i k i k i k i i i i i eeeei k e e e e i k i e eeππππππππππππ⎛⎫⎛⎫+ ⎪⎪-+++⎝⎭⎝⎭-++-+-⎛⎫⎛⎫++-+ ⎪⎪⎝⎭⎝⎭+====+=±±====+=±±===解:()222,0,1,2,cos1sin1.k i i k e e e e i π⎛⎫ ⎪⎝⎭+=±±=⋅=+3. 计算 2,:122c dzc z z z =++⎰()2222220110,1,1,11,220,022z z z z i z i z c z z z c z z ++=++=+==-+=≤++≠=++解:时,而在内,故在内解析,故原式 1.计算221(1),21c z z dz c z z -+=-⎰: ()2221(2),21cz z dz c z z -+=-⎰:(1)212(21)=4 z i z z i ππ==-+解:原式 (2)2112(21)=2(41)6z z i z z i z i πππ=='=-+-=解:原式. 计算2sin()114,(1):1,(2):1,(3): 2.122c z dz c z c z c z z π+=-==-⎰其中1sin (1)sin 442.11c z z z z i i z z πππ=-⎡⎤-⎢⎥===⎢⎥+-⎢⎥⎣⎦⎰解:(1)原式1sin (1)sin 442.112c z z z z i i z z πππ=⎡⎤+⎢⎥===⎢⎥-+⎢⎥⎣⎦⎰(2)原式 12(3):2,1,11,.c z z z c c ===-以分别以为中心,为半径,做圆1222sinsin44.1122c c z zdz dz i i i z z ππ=+=+=--⎰⎰原式 3、将下列函数按()1-z 的幂级数展开,并指明收敛范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学物理方法姚端正CH10作业解答
题目1
题目描述
求解一维无限深势阱中的薛定谔方程。
解答过程
薛定谔方程为:
$$ -\\frac{{\\hbar}^2}{2m}\\frac{{d^2}\\psi}{{dx^2}} + V(x)\\psi = E\\psi $$
对于一维无限深势阱,即势能为零的区域内,薛定谔方程简化为:
$$ -\\frac{{\\hbar}^2}{2m}\\frac{{d^2}\\psi}{{dx^2}} = E\\psi $$
可以将上式改写为标准形式:
$$ \\frac{{d^2}\\psi}{{dx^2}} = -k^2\\psi $$
其中,$k = \\frac{\\sqrt{2mE}}{{\\hbar}}$。
上述方程为一个二阶常微分方程,可以通过分离变量的方法进行求解。
假设解为$\\psi(x) = A\\sin(kx) + B\\cos(kx)$,代入上式得到:
$$ (A\\sin(kx) + B\\cos(kx))'' = -k^2(A\\sin(kx) +
B\\cos(kx)) $$
化简上式可得:
$$ -Ak^2\\sin(kx) - Bk^2\\cos(kx) = -k^2(A\\sin(kx) +
B\\cos(kx)) $$
通过观察可以发现,上式两边的结果是相等的。
因此,我们只需对振幅因子A和B分别进行求解。
首先,将振幅因子A令为0,代入方程可得到:
$$ B\\cos(kx) = 0 $$
由于$\\cos(kx)$的周期为$2\\pi$,因此得到的解为$x = 0, \\pm \\pi, \\pm 2\\pi, \\cdots$。
接下来,将振幅因子B令为0,代入方程可得到:
$$ A\\sin(kx) = 0 $$
由于$\\sin(kx)$的周期也为$2\\pi$,因此得到的解为$x = \\pm \\frac{\\pi}{2}, \\pm \\frac{3\\pi}{2}, \\pm
\\frac{5\\pi}{2}, \\cdots$。
综上所述,满足一维无限深势阱的薛定谔方程的解为:
$$ \\psi(x) = A\\sin(kx) + B\\cos(kx) $$
其中,A和B分别为常数,k满足$k =
\\frac{\\sqrt{2mE}}{{\\hbar}}$。
题目2
题目描述
求解二维带电粒子在垂直于磁场方向上的运动。
解答过程
二维带电粒子在垂直于磁场方向上的运动可以描述为:
$$ m\\frac{{d^2}\\vec{r}}{{dt^2}} =
q\\vec{v}\\times\\vec{B} $$
其中,m为粒子的质量,q为粒子的电荷,$\\vec{v}$为粒子的速度,$\\vec{B}$为磁场。
对于垂直于磁场方向上的运动,我们可以假设粒子沿着垂直于磁场的方向匀速运动,即$\\vec{v} = v\\hat{j}$。
代入上述方程可得:
$$ m\\frac{{d^2}\\vec{r}}{{dt^2}} =
q(v\\hat{j})\\times\\vec{B} $$
化简上式可得:
$$ m\\frac{{d^2}\\vec{r}}{{dt^2}} = qvB\\hat{k} $$
由于$\\frac{{d^2}\\vec{r}}{{dt^2}}$是$\\vec{r}$对时间的二阶导数,因此可以将上式拆分为x和x两个方向上的二阶微分方程。
对于x方向:
$$ m\\frac{{d^2}x}{{dt^2}} = 0 $$
对于x方向:
$$ m\\frac{{d^2}y}{{dt^2}} = qvB $$
上述方程可以分别进行求解,得到:
x(x)=xx+x
$$ y(t) = \\frac{1}{2}\\frac{q}{m}vBt^2 + Ct + D $$
其中,A、B、C、D为常数。
综上所述,二维带电粒子在垂直于磁场方向上的运动可以由以下方程描述:
x(x)=xx+x
$$ y(t) = \\frac{1}{2}\\frac{q}{m}vBt^2 + Ct + D $$
其中,A、B、C、D为常数。
题目3
题目描述
解析循环数求原点数密度。
解答过程
解析循环数是描述复杂度的一个重要概念,原点数密度是指单位长度上的原点数量。
解析循环数的定义为:
$$ \\alpha =
\\frac{{\\log(\\frac{1}{\\lambda})}}{{\\log(r_0)}} $$
其中,$\\lambda$为分形曲线的缩放因子,x0为分形曲线的曲率半径。
原点数密度的定义为:
$$ \\gamma = \\frac{{\\text{原点数量}}}{{\\text{总长度}}} $$
要求解析循环数求原点数密度,首先需要计算出原点数量和总长度。
对于一个给定的分形曲线,总长度为已知的,因此只需要计算出原点数量即可。
原点数量可以通过对曲线进行采样并统计采样点中曲线经过原点的个数来计算。
综上所述,要求解析循环数求原点数密度,首先需要计算曲线的总长度,然后通过采样计算出原点的数量,最后计算原点数密度。
题目4
题目描述
求解偏微分方程$\\frac{{\\partial u}}{{\\partial t}} =
a\\frac{{\\partial^2u}}{{\\partial x^2}}$。
解答过程
对于偏微分方程$\\frac{{\\partial u}}{{\\partial t}} =
a\\frac{{\\partial^2u}}{{\\partial x^2}}$,其中a为常数。
我们可以使用分离变量的方法进行求解。
设解为x(x,x)=x(x)x(x),代入上述方程得到:
x′(x)x(x)=xx″(x)x(x)
化简上式可得:
$$ \\frac{{T'(t)}}{T(t)} = a\\frac{{X''(x)}}{X(x)} = -
\\lambda^2 $$
得到两个常微分方程:
$$ T'(t) = -\\lambda^2T(t) $$
$$ X''(x) + \\lambda^2X(x) = 0 $$
第一个方程的解为$T(t) = Ae^{-\\lambda^2t}$,第二个方
程的解为$X(x) = B\\sin(\\lambda x) + C\\cos(\\lambda x)$,其中A、B、C为常数。
假设有一个初始条件x(x,0)=x(x),代入解的表达式可得到:
$$ f(x) = X(x)T(0) = (B\\sin(\\lambda x) +
C\\cos(\\lambda x))T(0) $$
根据傅里叶级数展开定理的相关知识,我们知道:
$$ f(x) = \\sum_{n=0}^{\\infty}(a_n\\sin(nx) +
b_n\\cos(nx)) = \\sum_{n=1}^{\\infty}c_n\\sin(nx +
\\varphi_n) $$
将上述傅里叶级数展开形式与初始条件进行比较可以得到:$$ B\\sin(\\lambda x) + C\\cos(\\lambda x) = c_n\\sin(nx + \\varphi_n) $$
由于等式左右两边都是关于x的函数,因此可以得到:
$$ B = c_n\\sin(\\varphi_n) $$
$$ C = c_n\\cos(\\varphi_n) $$
综上所述,对于偏微分方程$\\frac{{\\partial
u}}{{\\partial t}} = a\\frac{{\\partial^2u}}{{\\partial x^2}}$,可以通过分离变量的方法求得解的形式为:
$$ u(x, t) = \\sum_{n=1}^{\\infty}(c_n\\sin(nx +
\\varphi_n))e^{-n^2a^2t} $$
其中,x x和$\\varphi_n$为常数。
总结
本文主要解答了数学物理方法姚端正第10章的作业。
通过求解一维无限深势阱中的薛定谔方程,我们得到了该方程的解析解。
此外,我们还讨论了二维带电粒子在垂直于磁场方向上的运动、解析循环数求原点数密度以及偏微分方程
$\\frac{{\\partial u}}{{\\partial t}} =
a\\frac{{\\partial^2u}}{{\\partial x^2}}$的求解方法。
希望本文对读者们在学习数学物理方法时有所帮助。
