方格作图 -
初中数学-网格作图题

专题复习(三)网格作图题1.(2016·合肥模拟)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.(1)以A为旋转中心,将四边形ABCD顺时针旋转90°,得到四边形AB1C1D1;(2)以A为位似中心,将四边形ABCD作位似变换,且放大到原来的两倍,得到四边形AB2C2D2.2.(2016·蜀山区二模)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).(1)画出△ABC关于x轴对称的△A1B1C1,写出B1点的坐标;(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,写出B2点的坐标.3.(2016·安徽二模)如图,已知A(2,3),B(1,1),C(4,1)是平面直角坐标系中的三点.(1)请画出△ABC关于y轴对称的△A1B1C1;(2)画出△A1B1C1向下平移3个单位得到的△A2B2C2;(3)若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标.解:(1)如图所示,△A1B1C1即为所求.(2)如图所示,△A2B2C2即为所求.(3)根据题意,可得P的对应点P2的坐标为(-x,y-3).4.(2016·芜湖模拟)如图,在9×7的小正方形网格中,△ABC的顶点A,B,C在网格的格点上.将△ABC向左平移3个单位,再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转:第1次,将△ABC绕点B 顺时针旋转90°得到△A1BC1;第2次,将△A1BC1绕点A1顺时针旋转90°得到△A1B1C2;第3次,将△A1B1C2绕点C 2顺时针旋转90°得到△A 2B 2C 2;第4次,将△A 2B 2C 2绕点B 2顺时针旋转90°得到△A 3B 2C 3,依次旋转下去.(1)在网格中画出△A′B′C′和△A 2B 2C 2;(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.解:(1)△A′B′C′和△A 2B 2C 2的图象如图所示.(2)通过画图可知,△ABC 至少在第8次旋转后得到△A′B′C′.5.如图,△ABC 的三个顶点和点O 都在正方形网格的格点上,每个小正方形的边长都为1.(1)将△ABC 先向右平移4个单位,再向上平移2个单位得到△A 1B 1C 1,请画出△A 1B 1C 1;(2)请画出△A 2B 2C 2,使△A 2B 2C 2和△ABC 关于点O 成中心对称;(3)在(1)、(2)中所得到的△A 1B 1C 1与△A 2B 2C 2成轴对称吗?若成轴对称,请画出对称轴;若不成轴对称,请说明理由.解:(1)如图所示,△A 1B 1C 1,即为所求.(2)如图所示,△A 2B 2C 2,即为所求.(3)如图所示,△A 1B 1C 1与△A 2B 2C 2成轴对称,直线a ,b 即为所求.6.(2016·阜阳校级二模)如图所示,在边长为1个单位长度的小正方形组成的网格中,△ABC 的顶点A ,B ,C 在小正方形的顶点上.将△ABC 向下平移2个单位得到△A 1B 1C 1,然后将△A 1B 1C 1绕点C 1顺时针旋转90°得到△A 2B 2C 1.(1)在网格中画出△A 1B 1C 1和△A 2B 2C 1;(2)计算线段AC 在变换到A 2C 1的过程中扫过区域的面积.(重叠部分不重复计算)解:(1)如图,△A 1B 1C 1和△A 2B 2C 1为所作.(2)线段AC 在变换到A 2C 1的过程中扫过区域的面积S =2×2+90·π·(22)2360=4+2π.7.(2016·昆明)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.解:(1)如图所示.(2)如图所示.(3)找出A关于x轴的对称点A′(1,-1),连接BA′,与x轴交点即为P.如图所示,点P坐标为(2,0).8.(2016·濉溪县模拟)如图,已知△ABC的三个顶点的坐标分别为A(3,3),B(-1,0),C(4,0).(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C 的对应点C1坐标;(不必画出平移后的三角形)(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△AB2C2.解:(1)∵经过平移,可使△ABC的顶点A与坐标原点O重合,∴A点向下平移3个单位再向左平移3个单位,故C1坐标为(1,-3).(2)如图所示,△A′BC′即为所求,A′点的坐标为(-4,4).(3)如图所示,△AB2C2即为所示.。
阅卷人五操作与实践(共10分)1.按要求在方格纸中作图(6分
阅卷人五操作与实践(共10分)1.按要求在方格纸
中作图(6分
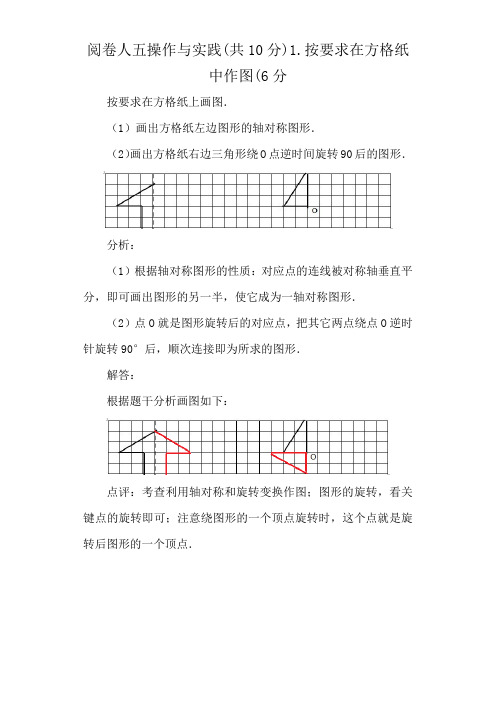
按要求在方格纸上画图.
(1)画出方格纸左边图形的轴对称图形.
(2)画出方格纸右边三角形绕O点逆时间旋转90后的图形.
分析:
(1)根据轴对称图形的性质:对应点的连线被对称轴垂直平分,即可画出图形的另一半,使它成为一轴对称图形.(2)点O就是图形旋转后的对应点,把其它两点绕点O逆时针旋转90°后,顺次连接即为所求的图形.
解答:
根据题干分析画图如下:
点评:考查利用轴对称和旋转变换作图;图形的旋转,看关键点的旋转即可;注意绕图形的一个顶点旋转时,这个点就是旋转后图形的一个顶点.。
2017中考网格作图

中考网格专练1.如图,在边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,请按要求完成下列各题:(1)画线段AD ∥BC 且使AD=BC ;(2)连接CD ,请直接写出四边形ABCD 的面积。
CAB2如图,每个小正方形的边长均为1个单位长度的网格中,有一个△个单位长度的网格中,有一个△ABC ABC ABC,三角形的三个,三角形的三个顶点均在网格的顶点上(1)在图中画线段CD CD,使,使CD=CB CD=CB,点,点D 在网格的格点上在网格的格点上; ; (2)连接AD 请求出四边形ABCD 的面积的面积. .3、如图,在边长为1的小正方形组成的网格中,A 、B 均在格点上,请按要求完成下列各题:(1)将线段AB 向右平移6个单位,得线段DC ,画出四边形ABCD. (2)求四边形ABCD 的面积. BA C4.图(a )、图(b )、是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a )、图(b )、图(c )中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.形各顶点必须与方格纸中的小正方形顶点重合.5、如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.顶点分别按下列要求画三角形.①使三角形三边长分别为3、22、5(在图1中画一个即可). ②使三角形为轴对称的钝角三角形且面积为4 (在图2中画一个即可).6.如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T (1,1)、A (2,3)、 B (4,2).). (1)把△TAB 绕点T 逆时针旋转90°得到△TA 1B 1,画出△TA 1B 1.(2)以点T (1,1)为位似中心,按比例尺(T A′∶TA )3∶1在位似中心的同侧将△TAB 放大为△T A′B′,放大后点A 、B 的对应点分别为A′、B′.画出△T A′B′,并写出点A′、B′的坐标;的坐标;第22题图题图T OBA xy7. 7. 如图所示,在△如图所示,在△如图所示,在△OAB OAB 中,点B 的坐标是(的坐标是(00,4),点A 的坐标是(的坐标是(33,1). (1)画出△)画出△OAB OAB 向下平移4个单位长度、再向左平移2个单位长度后的△个单位长度后的△O O 1A 1B 1. (2)画出△)画出△OAB OAB 绕点O 逆时针旋转9090°后的△°后的△°后的△OA OA 2B 2,并求出点A 旋转到A 2所经过的路径长(结果保留p )8. 8. 如图,在方格纸中,△ABC 如图,在方格纸中,△ABC 的三个顶点和点P 都在小方格的顶点上,按要求画一个三角形,使它的顶点在方格的顶点上.角形,使它的顶点在方格的顶点上. (1)将△ABC 平移,使点P 落在平移后的三角形内部,在图甲中画出示意图;落在平移后的三角形内部,在图甲中画出示意图;(2)以点C 为旋转中心,将△ABC 旋转,使点P 落在旋转后的三角形内部,在图乙中画出示意图.出示意图.9.9.如图,如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫做格点,以格点为顶点分别按下列要求画三角形;点为顶点分别按下列要求画三角形;(1)使三角形的三边长分别为3、22、5(在图((在图(11)中画一个即可);)中画一个即可); (2)使三角形为钝角三角形且面积为4(在图((在图(22)中画一个即可).)中画一个即可).((1) ((2)xy BAO1010.如图,在.如图,在9×5的网格中,每个小正方形的边长的网格中,每个小正方形的边长均为l ,线段AB AB、、BC 的端点A 、B 、C 均在小正均在小正 方形的顶点上.方形的顶点上. (1)(1) 在图中以AB AB、、BC 为边作四边形ABCD(ABCD(点点D 在小正方形的顶点上小正方形的顶点上)),使其为中心对称图形,使其为中心对称图形(2) (2)直接写出四边形直接写出四边形ABCD 的周长和面积.的周长和面积.11. 如图,点O A B 、、的坐标分别为(00)(30)(32)-,、,、,,将O A B △绕点O 按逆时针方向旋转90°得到OA B ¢¢△. (1)画出旋转后的OA B ¢¢△; (2)求B B ¢的长. 12. 12. 如图,在边长为如图,在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD 在直线l 的左侧,其四个顶点A 、B 、C 、D 分别在网格的格点上.点上.(1)请你在所给的网格中画出四边形A ′B ′C ′D ′,使四边形A ′B ′C ′D ′和四边形ABCD 关于直线L 对称,其中点A ′、′、B B ′、′、C C ′、′、D D ′分别是点A 、B 、C 、D 的对称点;的对称点; (2)在()在(11)的条件下,结合你所画的图形,直接写出四边形AA AA′′B ′B 的周长.的周长.ByxAO13. 13. 在平面直角坐标系中,四边形在平面直角坐标系中,四边形ABCD 的位置如图所示,解答下列问题:的位置如图所示,解答下列问题:(1)将四边形ABCD 先向左平移4个单位,再向下平移6个单位,得到四边形A 1B 1C 1D 1,画出平移后的四边形A 1B 1C 1D 1;(2)将四边形A 1B 1C 1D 1绕点A 1逆时针旋转90°,得到四边形A 1B 2C 2D 2,画出旋转后的四边形A 1B 2C 2D 2,并写出点C 2的坐标.的坐标.14.14. 如图,在正方形网格中,△ABC 各顶点都在格点上,点A ,C 的坐标分别的坐标分别 为(﹣为(﹣55,1)、(﹣(﹣11,4),结合所给的平面直角坐标系解答下列问题:,结合所给的平面直角坐标系解答下列问题:(1)画出△ABC 关于y 轴对称的△A 1B 1C 1; (2)画出△ABC 关于原点O 对称的△A 2B 2C 2;15.如图,正方形网格中每个小正方形的边长均为l ,△ABC 的三个顶点都在格点上,现将△ABC 绕着格点D 顺时针旋转900(1)画出△ABC 旋转后的△A 1B 1C 1: (2)求点C 旋转过程中所经过的路径长.旋转过程中所经过的路径长.16.如图,图l 和图2都是7×7×44正方形网格,每个小正方形的边长为l ,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.列图形,所画图形的各个顶点均在所给小正方形的顶点上. (1)在图1中画出一个等腰直角三角形ABC ;(2)在图2中画出一个钝角三角形ABD ,使△ABD 的面为3. 17.17.如图,正方形网格中的每个小正方形边长都是如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫做格点,以格点为顶点分别按下列要求画三角形;格点为顶点分别按下列要求画三角形;(1)使三角形的三边长分别为3、22、5(在图((在图(11)中画一个即可);)中画一个即可); (2)使三角形为钝角三角形且面积为4(在图((在图(22)中画一个即可).)中画一个即可).18.图l、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均在小正方形的顶点上.为1,点A、B在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC的面积为5.且△ABC 45°((画一个即可) ;中有一个角为45°且∠ ADB (2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD的面积为5,且∠90°((画一个即可).=90°19.图l、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均小正方形的顶点上.为1.点A和点B在小正方形的顶点上.画一个 即(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可);20.如图,在9×6的正方形网格中有一条线段AB(网格中每个小正方形的边长均为1个单位),其端点A、B均在小正方形的顶点上. (1)将点A、B分别向右平移3个单位,得到点D、C,请画出四边形ABCD;(2)过(1)中四边形ABCD的顶点A画一条直线,使其将四边形ABCD分成两个图形,要求这两个图形都是轴对称图形. 21. 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上. (1)在图1中画出等腰三角形△ABP(点P在小正方形的顶点上),△ABP的面积为6(画一个即可);(2)在图2中画出等腰梯形ABCD(点C、D在小正方形的顶点上),AB∥CD,且等腰梯形ABCD的面积为6(画一个即可). 22.如图,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在小正方形的顶点上. (1)以AB为腰的锐角等腰三角形为腰的锐角等腰三角形(2)以AB为一边的钝角三角形且面积等于4. 23.图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上. (1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;为钝角三角形;(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形且∠ABD=45°. 24.请在下列两个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画三角形的顶点与方格中的小正方形的顶点重合,在图中标出对称轴所在位置并将所画三角形涂上阴影(注:所画的三个图形不能重复) 25.如图,图1和图2都是7×4正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上. (1)在图1中画出一个等腰直角三角形ABC;(2)在图2中画出一个钝角三角形ABD,使△ABD的面为3. 26.图1、图2分别是12×12的网络,网络中的每个小正方形的边长为1.请在图1、图2中各画一个图形,分别满足以下要求:中各画一个图形,分别满足以下要求:(1)在图1中画出面积为24的矩形ABCD,所画矩形各顶点必须在小正方形的顶点上; (2)在图2中画出周长为26,面积为24的平行四边形EFGH,所画平行四边形各顶点必须在小正方形的顶点上. 27.正方形网格中的每个小正方形边长都是1,每个小格的顶点叫作格点,以格点为顶点分别按下列要求画三角形. (1)在图1中画△ABC,使△ABC的三边长分别为3、22、5;(2)在图2中画△DEF,使△DEF为钝角三角形且面积为2. 28.如图,网格中每个小方格都是边长为1个单位长度的小正方形,小正方形的顶点叫格点将△OAB放置在网格中的平面直角坐标系中,三角形顶点的坐标分别为O(0,0)、A(1,3)、B(5,0). (1)画出△OAB绕原点O顺时针旋转180°后得到的△OCD(其中点A与C对应,);点B与点D);(2)连接AD、BC得到四边形ABCD,过四边形ABCD边上的格点画一条直线,将四边形ABCD分成两个图形,并且使得所画直线两边的图形全等. 29. 图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上. (1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC为轴对称图形;为轴对称图形; (2)在图b中画出四边形ABCD(点C、D都在小正方形的顶点上),使四边形ABCD为中心对称图形且面积为5. 30.如图,正方形网格中的每个小正方形边长都为1,以每个小正方形的顶点为顶点按下列要求在图1和图2中分别画三角形和平行四边形. (1)使三角形三边长为2、3、13; (2)使平行四边形有一锐角为45°,且面积为4. 31.图1、图2分别是10×8的正方形网格,网格中的每个小正方形的边长都是1,线段AB的端点都在小正方形的顶点上请在图1、图2中各画一个图形,分别满足下列要求:(1)在图1中,画出一个以线段AB为一边的菱形ABCD(非正方形),所画的菱形的各顶点必须在小正方形的顶点上;点必须在小正方形的顶点上;(2)在图2中,画出一个以线段AB为腰的等腰梯形ABEF,所画等腰梯形的各顶点必须在小正方形的顶点上,且其周长为10+310. 图1 图2 32.图a、图b是8×6的网格,网格中每个小正方形的边长均为1,点A、B在小正方形的顶点上. (1)在图a中画一个直角梯形ABCD(点C、D在小正方形的顶点上),使所画的直角梯形的面积为6;(2)在图b中画一个直角三角形ABE(点E在小正方形的顶点上),使所画的直角三角形ABE 的面积为2. (图a) (图b) 33.图1、图2分别是10×10×88的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,使以A、B、C为顶点的三角形分别满足以下要求:为顶点的三角形分别满足以下要求:⑴请在图中各取一点C(点C必须在小正方形的顶点上),使△ABC为钝角等腰三角形.......;⑵通过计算,直接写出△ABC的周长.的周长.34.如图,在每个小正方形的边长均为1个单位长度的方个单位长度的方 A B (第22题图)题图)格纸中,有一个△ABC ,△ABC 的三个顶点均与小正方的三个顶点均与小正方 形的顶点重合。
5格点作图+模型题

第5章专题5 格点作图+几何模型1、如图,在方格纸中,每个小正方形的边长均为1个单位长度,有一个△ABC,它的三个顶点均与小正方形的顶点重合.(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应)请在方格纸中画出△DEF;(2)在(1)的条件下,连接AE和CE,请求出△ACE的面积S.2、如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).(1)利用图①中的网格,过P点画直线MN的平行线和垂线.(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是多少?3.如图1,BD∥AC,BE平分∠ABD,交AC于点E.若∠A=50°,则∠1的度数为___________ 4.如图2,BE平分∠ABC,DE∥BC,图中相等的角共有___________5.如图3,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为_____________6.如图,长方形ABCD,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=800,求∠BCE的度数.AD CBEFG7.把一张对边互相平行的纸条(AC′∥BD′)折成如图1所示,EF是折痕,若折痕EF 与一边的夹角∠EFB=32°,则∠AEG= .8.如图2,将一张矩形纸片按图中方式折叠,若∠1=63°,则∠2为度.9.如图3,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′、D′处,C′E交A于点G,若∠BEG=50°,则∠GFE=10.如图,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.试说明直线AD与BC垂直.11.已知:如图,AB∥DE,CM平分∠BCE,CN⊥CM.求证:∠B=2∠DCN.12.已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.。
绘画方格纸(A4纸打印)

绘画方格纸(A4纸打印)概述本文档提供了绘画方格纸的设计和打印指南,适用于A4纸打印。
设计要求- 方格大小应合适,以便绘图时方便使用。
- 方格线应清晰可见,但不会干扰绘图。
- 方格纸应具有明显的边界,以便在需要时进行裁切。
设计规格- 页面大小:A4纸(210mm x 297mm)- 方格大小:建议选择适合绘图需求的方格大小。
常用选项包括:- 5mm x 5mm:适用于绘制图表和简单的草图。
- 10mm x 10mm:适用于绘制图表、平面设计和建筑图纸等。
- 20mm x 20mm:适用于绘制大型图表和平面设计。
- 方格线颜色:建议选择灰色或浅灰色,以确保方格线在绘图中不太突出,但又清晰可见。
打印指南1. 打开你通常用于打印的应用程序(如Microsoft Word)。
2. 创建一个新文档并设置页面大小为A4纸。
3. 输入所需的方格大小和间距,以创建一个方格模板。
你可以通过绘制水平和垂直线来实现方格效果,或者使用应用程序中的网格工具。
4. 确保方格线颜色与设计规格一致。
5. 根据需要复制和粘贴方格模板,以适应所需绘图的数量。
6. 检查整个文档的布局和方格线的清晰度。
7. 如果需要,可以对文档进行调整,以确保边界线和方格线的位置正确。
8. 在打印之前,预览整个文档,确保绘制方格纸的效果符合预期。
9. 使用打印机打印方格纸。
注意事项- 在打印之前,检查打印设置以确保选择了正确的纸张类型和尺寸。
- 如果你需要更多或更少的方格数量,请相应地调整文档。
- 对于更复杂的绘图需求,可以考虑使用专业的绘图软件或工具。
以上是关于绘画方格纸(A4纸打印)的设计和打印指南。
根据你的绘图需求,选择适合的方格规格和打印设置,并确保方格纸的清晰可见和方便使用。
方格作图范例图解课件

本课程介绍方格作图范例图解,涵盖以下内容: - 方格作图的基本概念 - 方格图的讲解方法 - 方格作图的应用示例
方格作图的基本概念
方格作图是一种用方格图形来展示和解释数据的方法。它包括方格图的定义、 用途和优点,以及使用方格作图的基本原则和图的步骤简单易懂,通过例图分析可以更好地理解如何使用方格作图。 此外,我们还将探讨如何创新使用方格作图来展示数据。
方格作图的应用示例
方格作图可以在统计学、市场营销和教学等领域中得到广泛应用。我们将分 享一些真实案例,展示方格作图在不同场景下的实际应用。
总结
方格作图在数据可视化中具有一定的优点和不足之处。了解方格作图的应用场景和发展趋势,有助于更 好地利用方格作图来展示和解释数据。
参考资料
- 方格作图的基本原理与应用,张三,2018 - How to Create a Grid Chart,John Smith,2019
小学数学六年级上册数学作业(作图)

小学数学六年级上册数学作业(作图)学校:___________姓名:___________班级:___________一、作图题1.在如图长方形中画图表示出12×35的计算过程。
2.画图表示算式35÷4的意义。
3.小鸭子想去河里洗澡,它先从家出发,沿南偏东35°方向走60m,再沿东偏北45°方向走90m就到河边了。
请你将小鸭子的行走路线画出来。
4.彤彤在操场玩,她先向南偏东30°方向走了60m,接着向东偏北45°方向走了80m,最后再向东偏南40°方向走了50m。
请根据以上描述,画出彤彤运动的路线图。
5.画一个直径为2厘米的圆,并标出半径数据和单位。
6.画一画。
(1)在方格图中画一个最大的圆,标出圆心O;(2)在圆中画一个图形,使所画图形和圆组成的图形只有1条对称轴。
二、解答题分表示种百合的公顷数。
(整个方格图表示1公顷)参考答案:【详解】【详解】60÷30=2(格)90÷30=3(格)如图所示:【点睛】本题考查方向和位置,明确“上北下南,左西右东”及角度信息是解题的关键。
4.见详解【分析】以图上的“上北下南,左西右东”为准,图例表示图上1cm相当于实际距离20m。
以彤彤玩的地方为观测点,先在此处的南偏东30°方向上画60÷20=3cm长的线段;接着在此处东偏北45°方向上画80÷20=4cm长的线段;最后在此处东偏南40°方向上画50÷20=2.5cm长的线段即可;据此画出彤彤运动的路线图。
【详解】如图:【点睛】本题考查位置和方向的相关知识,掌握根据方向、角度和距离画路线图是解题的关键。
5.见详解【分析】已知圆的直径是2厘米,根据d÷2=r,求出圆的半径;先确定圆心O的位置,圆规两脚间的距离等于圆的半径,用圆规画圆,标出半径即可。
【详解】如图:(以实际测量为准)【点睛】掌握画圆的作图方法是解题的关键,明确圆规两脚间的距离就是圆的半径。
方格纸_精品文档

方格纸简介方格纸,又称网格纸,是一种由等距离的平行线和垂直线组成的纸张。
它通常被用于绘图和作图,以方便绘制和计算。
用途方格纸在各个领域有着广泛的应用,以下是方格纸的主要用途:绘制图表方格纸的一大用途是绘制各种图表。
例如,数学课上的坐标轴图、物理实验中的数据采集图、工程设计中的平面图等等,都可以利用方格纸的坐标系和网格线来精确绘制。
数据整理方格纸的网格线可以帮助整理数据。
在进行统计、记录和比较时,方格纸的对齐特性可以使数据更加清晰易读,减少错误。
导航和规划方格纸可以用于制作导航地图和规划布局。
例如,在户外探险中可以利用方格纸绘制地图,规划行程;在室内装修时可以使用方格纸描绘房屋布局,安排家具等。
常见类型普通方格纸普通方格纸由等距离的平行线和垂直线组成,构成了一个等边的方格网。
每个小方格的边长可以根据需要进行选择,常用的有1mm、2mm、5mm等。
比例方格纸比例方格纸是一种在普通方格纸上标定了比例的特殊方格纸。
它能够根据预定比例缩放,用于绘制按比例缩小的图形和模型。
比例方格纸常用于建筑、工程和设计领域。
等距方格纸等距方格纸是一种在普通方格纸上额外添加正六边形的特殊方格纸。
这样可以使图形保持等角度的特性,常用于绘制三角图、六边形布局等。
如何使用使用方格纸可以遵循以下步骤:1.准备一张合适尺寸的方格纸。
2.根据需要选择方格纸的类型和尺寸。
3.使用铅笔或者细线笔,在方格纸上按照需要绘制图形或者记录数据。
4.注意保持手的稳定,以确保绘制的准确性。
5.结合方格纸上的坐标系和网格线,绘制、计算和分析相关内容。
总结方格纸是一种实用的纸张,可以用于绘图、数据整理和规划等多个领域。
它的使用简单方便,并且能够提供准确和清晰的结果。
不同类型的方格纸适用于不同的需求,使用者可以根据自己的具体情况选择合适的类型和尺寸的方格纸。
希望本文对你了解方格纸有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光明南校七年级数学导学案 班级 姓名 课题:轴对称、平移、旋转(方格)作图专题 主备人:黄山 1.ABC 在网格中的位置如图所示,将ABC 沿y 轴翻折得到111A B C ,再将111A B C 绕点O 旋转180得到222A B C . 请依次画出111A B C 和222A B C .
2、平移方格纸中的图形(如图),使点A 平移到点A ′处,画出平移后的图形.
3.如图,平移正方形网格中的阴影图案,使AB 移动到 的位置.然后再向左平移6个单位.
4.如图,网格中的房子图案正好处于网格右下角的位置.平移这个图案,使它正好位于左上角的位置(不
能出格).
y
x
C
B
A
O 第1题
5、如图是将大定写字母N绕它右下侧的顶点按顺时针议程旋转90°,再作以右下侧的顶点按顺时针旋转90°后的图形。
6.把下面几个图形中左上角的图案绕着中心旋转90°,180°,270°,画出所得图案。
7、(1)现把四边形ABCD绕D点按顺时针方向旋转90°,画出相应的图形A1B1C1D1,
(2)若四边形ABCD平移后,与四边形A′B′C′D′成轴对称,写出满足要求的一种平移方法,并画出平移后的图形A2B2C2D2.
8、(2009•哈尔滨)如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC和一点O,△ABC的顶点和点O均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移5个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)在方格纸中,将△ABC绕点O旋转180°得到△A2B2C2,请画出△A2B2C2.
9、(2008•来宾)如图,已知△ABC关于直线MN的对称图形是△A1B1C1,将△A1B1C1绕点A1逆时针旋转90°得到△A1B2C2.请在图中分别画出△A1B1C1和△A1B2C2,并正确标出对应顶点的字母.(不要求写出画法)
光明南校七年级数学导学案 班级 姓名
10、在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,ABC △的三个顶点都在格点上(每个小方格的顶点叫格点).画出ABC △关于点O 的中心对称图形A B C '''△.
小组评价:1、作业等级 甲 乙 丙 丁
2、完成检测指标成绩( ) _______月________日。
