绝对值与数轴专项培优资料讲解
1.4与绝对值有关的十种常见题型与解法(新教材,重难点分层培优提升)(解析版)

1.4与绝对值有关的十种常见题型与解法(新教材,重难点分层培优提升)类型一、绝对值的有关概念1.(23-24·吉林延边·阶段练习)在下列数中,绝对值最大的数是()A.0B.1-C.2-D.1【答案】C【分析】本题考查的是绝对值与有理数的大小比较,熟练掌握上述知识点是解题的关键.先计算出各选项的绝对值,再进行大小比较即可.=-=-==,【详解】解:∵|0|0,|1|1,|2|2,|1|1而210>>,∴->-=>,|2||1||1|0故选:C.-,那么a=.2.(23-24七年级上·甘肃定西·阶段练习)如果a的相反数是0.74【答案】0.74【分析】本题主要考查了绝对值和相反数的知识,根据“只有符号不相同的两个数互为相反数;互为相反数3.(23-24七年级上·全国·课后作业)化简下列各数:(1)34--;(2)()0.5-+-⎡⎤⎣⎦;(3)6217⎡⎤⎛⎫-++ ⎪⎢⎥⎝⎭⎣⎦;(4)()2-+.4.(2024·辽宁抚顺·三模)下列各数在数轴上表示的点距离原点最远的是()A .2-B .1-C .3D .05.(23-24七年级上·四川宜宾·期中)若有理数m 在数轴上的位置如图所示,则化简3m m ++结果是.6.(23-24七年级上·四川成都·阶段练习)已知|2||1|6a a ++-=,则=a ;7.(23-24七年级下·河南南阳·期末)已知3535x x -=-,则x 的取值范围是.8.(24-25七年级上·全国·随堂练习)如果0a b c ++=且c b a >>.则下列说法中可能成立的是()A .a 、b 为正数,c 为负数B .a 、c 为正数,b 为负数C .b 、c 为正数,a 为负数D .a 、b 、c 为正数9.(23-24·黑龙江哈尔滨·期中)已知a 为有理数,则24a -+的最小值为.10.(24-25七年级上·全国·随堂练习)比较大小:76-65--.11.(24-25七年级上·全国·假期作业)比较下列各对数的大小:①1-与0.01-;②2--与0;③0.3-与13-;12.(23-24七年级上·湖南怀化·期末)已知下列各数,按要求完成各题:4.5+,142--,0, 2.5-,6,5-,()3+-.(1)负数集合:{......};(2)用“<”把它们连接起来是;(3)画出数轴,并把已知各数表示在数轴上.大于负数,两个负数比较大小绝对值越大其值越小进行求解即可;13.(23-24七年级上·海南省直辖县级单位·期末)如果21(2)0a b ++-=,则a b +的值为()A .1B .3C .1-D .3-14.(23-24·黑龙江哈尔滨·开学考试)已知|3||5|0x y -++=,求||x y +的值.15.(21-22七年级上·陕西·期中)已知(a +2)2+|b ﹣3|=0,c 是最大的负整数,求a 3+a 2bc ﹣12a 的值.二、填空题16.(23-24七年级上·四川南充·阶段练习)若12x <<,求代数式2121x x xx x x---+=.17.(23-24·上海杨浦·期末)12345x x x x x -+-+-+-+-的最小值为.18.(2024七年级下·北京·专题练习)已知112x -<<,化简|||2|3x x ---=.三、解答题19.(24-25七年级上·全国·随堂练习)在数轴上,a ,b ,c 对应的数如图所示,b c =.(1)确定符号:a ______0,b ______0,c _____0,b c +_____0,a c -______0;(2)化简:a c b +-;(3)化简:a a c --.20.(23-24·北京海淀·期中)有理数a ,b ,c 在数轴上的位置如图所示.(1)用“>”“<”或“=”填空:a b +______0,c a -______0,2b +______0.(2)化简:22a b c a b ++--+.【答案】(1)>,<,>(2)322a c --21.(23-24七年级下·河南周口·阶段练习)求解含绝对值的一元一次方程的方法我们没有学习过,但我们可以采用分类讨论的思想先把绝对值去除,使得方程成为一元一次方程,这样我们就能轻松求解了.比如,求解方程:32x -=.解:当30x -≥时,原方程可化为32x -=,解得5x =;当30x -<时,原方程可化为32x -=-,解得1x =,所以原方程的解是5x =或1x =.请你依据上面的方法,求解方程:3270x --=,得到的解为.22.(23-24七年级下·甘肃天水·期中)阅读下列材料:我们知道x 表示的是在数轴上数x 对应的点与原点的距离,即0x x =-,也就是说,x 对表示在数轴上数x 与数0对应点之间的距离.这个结论可以推广为12x x -表示在数轴上数1x ,2x 对应点之间的距离.例1:解方程6x =.解:∵06x x =-=,∴在数轴上与原点距离为6的点对应的数为6±,即该方程的解为6x =±.例2:解不等式12x ->.解:如图,首先在数轴上找出12x -=的解,即到1的距离为2的点对应的数为1-,3,则12x ->的解集为到1的距离大于2的点对应的所有数,所以原不等式的解集为1x <-或3x >.参考阅读材料,解答下列问题:(1)方程53x -=的解为______;(2)解不等式2219x ++<;(3)若123x x -++=,则x 的取值范围是_______;故答案为:8x =或2x =.(2)2219x ++<(3)123x x -++=,表示到1的点与到2-的点距离和为3,故答案为:21x -£<.23.(24-25七年级上·全国·假期作业)数学实验室:点A 、B 在数轴上分别表示有理数a ,b ,A 、B 两点之间的距离表示为AB ,在数轴上A 、B 两点之间的距离||AB a b =-.利用数形结合思想回答下列问题:(1)数轴上表示x 和3-的两点之间的距离表示为.(2)若34x +=,则x =.(3)32x x --+最大值为,最小值为.24.(23-24七年级上·四川南充·阶段练习)我们知道,a 可以理解为0a -,它表示:数轴上表示数a 的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点A ,B ,分别用数a ,b 表示,那么A ,B 两点之间的距离为AB a b =-,反过来,式子a b -的几何意义是:数轴上表示数a 的点和表示数b 的点之间的距离,利用此结论,回答以下问题:(1)数轴上表示数8的点和表示数3的点之间的距离是_________,数轴上表示数1-的点和表示数3-的点之间的距离是_________.(2)数轴上点A 用数a 表示,则①若35a -=,那么a 的值是_________.②36a a -++有最小值,最小值是_________;③求123202*********a a a a a a ++++++++++++ 的最小值.25.(23-24·黑龙江哈尔滨·期中)出租车司机李师傅某日上午一直在某市区一条东西方向的公路上营运,共连续运载八批乘客,若按规定向东为正,李师傅营运八批乘客里程数记录如下(单位:千米):8+,6-,3+,4-,8+,4-,5+,3-.(1)将最后一批乘客送到目的地后,李师傅位于第一批乘客出发地多少千米?(2)若出租车的收费标准为:起步价10元(不超过5千米),超过5千米,超过部分每千米2元,不超过5千米则收取起步价,求李师傅在这期间一共收入多少元?26.(23-24·黑龙江哈尔滨·阶段练习)刚刚闭幕的第33届“哈洽会”,于2024年5月16日至21日在哈尔滨市举办,中外宾客齐聚冰城.为确保全市道路交通安全有序,哈尔滨市公安交通管理局在开幕式当日对会展中心周边区域,以及部分道路进行交通管制和诱导分流.萧萧作为哈市青年当日也贡献了自己的一份力量.如图是某一条东西方向直线上的公交线路的部分路段,西起A 站,东至L 站,途中共设12个上下车站点,“哈洽会”开幕式当日,萧萧参加该线路上的志愿者服务活动,从C站出发,最后在某站结束服务活动,如果规定向东为正,向西为负,当天的乘车站数按先后顺序依次记录如下(单位:站):5,3,4,5,8,2,1,3,4,1+-+-+-+--+.(1)请通过计算说明结束服务的“某站”是哪一站?(2)若相邻两站之间的平均距离约为2.5千米,求这次萧萧志愿服务期间乘坐公交车行进的总路程约是多少千米?(3)已知油箱中要保持不低于10%的油量才能保证汽车安全行驶,若萧萧开始志愿服务活动时该汽车油量占油箱总量的1170,每行驶1千米耗油0.2升,活动结束时油量恰好能保证汽车安全行驶,则该汽车油箱能存储油多少升?一、单选题1.(22-23七年级上·云南保山·期末)有理数a ,b ,c 在数轴上的位置如图所示,在下列结论中:①0a b ->;②0ab <;③a b a b +=--;④()0b a c ->,正确的个数有()A .4个B .3个C .2个D .1个2.(23-24七年级上·浙江台州·期末)有理数a ,b 在数轴上的对应点的位置如图所示,下列结论中正确的是()A .0ab >B .4b a ->C .2a b a b +=D .()()230a b +-<3.(23-24七年级上·山东德州·期末)有理数a 、b 、c 在数轴上的位置如图所示,则b a b c a c --+--的化简结果为()A .2c-B .2a C .2b D .22b c+4.(18-19七年级上·北京海淀·期末)如图,数轴上点A ,M ,B 分别表示数a a bb +,,,若AM BM >,则下列运算结果一定是正数的是()A .a b +B .a b -C .abD .a b -5.(23-24七年级上·江西抚州·期末)适合|5||3|8a a ++-=的整数a 的值有()A .5个B .7个C .8个D .9个二、填空题6.(23-24七年级上·浙江绍兴·阶段练习)已知a 、b 为整数,202320a b +--=,且b a <,则a 的最小值为.7.(23-24七年级上·湖北省直辖县级单位·阶段练习)若0a b c ++=,且a b c >>,以下结论:①0a >,0c >;8.(23-24七年级上·河南南阳·阶段练习)已知x a b ,,为互不相等的三个有理数,且a b >,若式子||||x a x b -+-的最小值为2,则2023a b +-的值为.三、解答题9.(23-24七年级上·江苏南京·阶段练习)出租车司机小王某天下午营运全是东西走向的玄武大道进行的,如果规定向东为正,向西为负,他这天下午的行驶记录如下:(单位:千米)15+,3-,13+,11-,10+,12-,4+,15-,16+,19-(1)将最后一名乘客送到目的地时,小王距下午出车地点的距离是多少千米?(2)若汽车耗油量为a 升/千米,这天下午汽车共耗油多少升?(3)出租车油箱内原有5升油,请问:当0.05a =时,小王途中是否需要加油?若需要加油,至少需要加多少升油?若不需要加油,说明理由.10.(23-24七年级下·四川资阳·期末)(1)【阅读理解】“a ”的几何意义是:数a 在数轴上对应的点到原点的距离,所以“2a ≥”可理解为:数a 在数轴上对应的点到原点的距离不小于2,则:“2a <”可理解为:;我们定义:形如“x m ≤,≥x m ,x m <,x m >”(m 为非负数)的不等式叫做绝对值不等式,能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集.(2)【理解应用】根据绝对值的几何意义可以解一些绝对值不等式.例如:315x x -≤+我们将x 作为一个整体,整理得:315x x -≤+3x ≤再根据绝对值的几何意义:表示数x 在数轴上的对应点到原点的距离不大于3,可得:解集为33x -≤≤仿照上述方法,解下列绝对值不等式:①254x x -<-②1312313x x -+<-.11.(23-24六年级下·黑龙江绥化·期中)数轴上表示数m 和数n 的两点之间的距离等于||m n -.例如数轴上表示数2和5的两点距离为|25|3-=;数轴上表示数3和1-的两点距离为|3(1)|4--=;由此可知|63|+的意义可理解为数轴上表示数6和3-这两点的距离;|4|x +的意义可理解为数轴上表示数x 和4-这两点的距离;(1)如图1,在工厂的一条流水线上有两个加工点A 和B ,要在流水线上设一个材料供应点P 往两个加工点输送材料,材料供应点P 应设在_________时,才能使P 到A 的距离与P 到B 的距离之和最小?(2)如图2,在工厂的一条流水线上有三个加工点A B C ,,,要在流水线上设一个材料供应点P 往三个加工点输送材料,材料供应点P 应设在_________时,才能使P 到A B C ,,三点的距离之和最小?(3)如图3,在工厂的一条流水线上有四个加工点A B C D ,,,,要在流水线上设一个材料供应点P 往四个加工点输送材料,材料供应点P 应设在_________时,才能使P 到A B C D ,,,四点的距离之和最小?(4)①|3||4|x x ++-的最小值是_________,此时x 的范围是_________;②|6||3||2|x x x ++++-的最小值是_________,此时x 的值为_________;③|7||4||2||5|x x x x ++++-+-的最小值是_________,此时x 的范围是_________.(3)①根据(1)的结论即可得出答案;②根据(2)的结论即可得出答案;③根据(3)的结论即可得出答案.【详解】(1)解:当点P 在点A 左边时,2PA PB PA PA AB PA AB +=++=+,当点P 在A 、B 之间时,PA PB AB +=,当点P 点点B 的右边时,2PA PB AB PB PB AB PB +=++=+,∴当点P 在A 、B 之间时,才能使P 到A 的距离与P 到B 的距离之和最小;(2)解:当点P 在点A 左边时,2PA PB PC PA PA AC PB PA PB AC ++=+++=++,当点P 在A 、B 之间时,PA PB PC PB AC ++=+,当点P 在B 点时,PA PB PC AC ++=,当点P 在B C 、之间时,PA PB PC PB AC ++=+,当点P 在点C 的右边时,2PA PB PC PC PB AC ++=++,∴当点P 在B 点时,才能使P 到A B C ,,三点的距离之和最小(3)解:当点P 在点A 左边时,42PA PB PC PD PA AB CB AD +++=+++,当点P 在A 、B 之间时,2PA PB PC PD PB CB AD +++=++,当点P 在B C 、之间时,PA PB PC PD BC AD +++=+,当点P 在C D 、之间时,2PA PB PC PD BC AD PC +++=++,当点P 在点D 的右边时,24PA PB PC PD BC AD DC PD +++=+++,∴当点P 在B C 、之间时,才能使P 到A B C D ,,,四点的距离之和最小;(4)解:①由(1)可得:当34x -≤≤时,有最小值,最小值为()437--=,∴|3||4|x x ++-的最小值7,此时x 的范围是34x -≤≤;②由(2)可得:这是在求点x 到6-,3-,2三点的最小距离,∴当3x =-时,有最小值,最小值为|6||3||2||36||33||32|8x x x ++++-=-++-++--=;③由(3)可得:这是在求点x 到7-,4-,2,5四点的最小距离,∴当42x -≤≤时,由最小值,最小值为|7||4||2||5|742518x x x x x x x x ++++-+-=++++-+-=.12.(23-24七年级上·安徽安庆·期中)有数a b c 、、在数轴上的大致位置如图所示:(1)a c +__________0,b c -__________0,a b -__________0(用“>”、“<”、“=”);(2)化简||||||a c b c a b ++---.13.(23-24七年级上·江西上饶·期中)如图所示,数轴上从左到右的三个点A ,B ,C 所对应的数分别为a ,b ,c .其中点A 、点B 两点间的距离AB 的长是2021,点B 、点C 两点间的距离BC 的长是1000.(1)若以点C 为原点,直接写出点A ,B 所对应的数;(2)若原点O 在A ,B 两点之间,求a b b c ++-的值;(3)若O 是原点,且18OB =,求a b c +-的值.【答案】(1)点A 所对应的数a 为3021-,点B 所对应的数b 为1000-(2)3021(3)a b c +-的值为3003-或3039-【分析】本题考查了数轴与绝对值的意义,理解绝对值的意义是解答本题的关键.(1)根据题意先求解AC 的长,结合数轴的定义可求解点A ,B 所对应的数;(2)根据数轴上点的特征可得a<0,0b >,0c >,0b c -<,结合绝对值的性质化简可求解;,14.(22-23七年级上·北京·期中)已知a ,b 在数轴上的位置如图所示:(1)用“>”、“<”或“=”填空:____0a ,____0a b +,____0b a -;(2)化简:||||2||a b a a b +--+;(3)若21a b =-=,,x 为数轴上任意一点所对应的数,则代数式||||x a x b -+-的最小值是______;此时x 的取值范围是______.。
七年级上册数学培优讲义(绝对值)第三讲

绝对值的几何意义:一个数a 的绝对值就是数轴上表示数a 的点与原点的距离.数a 的绝对值记作a .绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.注意:①取绝对值也是一种运算.运算符号是“”.求一个数的绝对值.就是根据性质去掉绝对值符号.②绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.③绝对值具有非负性.取绝对值的结果总是正数或0.④任何一个有理数都是由两部分组成:符号和它的绝对值.如:5-符号是负号.绝对值是5.求字母a 的绝对值:①(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩②(0)(0)a a a a a ≥⎧=⎨-<⎩ ③(0)(0)a a a a a >⎧=⎨-≤⎩ 利用绝对值比较两个负有理数的大小:两个负数.绝对值大的反而小.绝对值非负性:如果若干个非负数的和为0.那么这若干个非负数都必为0. 例如:若0a b c ++=.则0a =.0b =.0c =绝对值的其它重要性质:(1)任何一个数的绝对值都不小于这个数.也不小于这个数的相反数.即a a ≥.且a a ≥-;(2)若a b =.则a b =或a b =-;(3)ab a b =⋅;a a b b =(0)b ≠; (4)222||||a a a ==;a 的几何意义:在数轴上.表示这个数的点离开原点的距离.a b -的几何意义:在数轴上.表示数a 、b 对应数轴上两点间的距离.绝对值【经典例题1】到数轴原点的距离是2的点表示的数是()A、±2B、2C、-2D、4【题目难度】★【解题思路】此题要全面考虑.原点两侧各有一个点到原点的距离为2.即表示2和-2的点.【题目答案】根据题意.知到数轴原点的距离是2的点表示的数.即绝对值是2的数.应是±2.故选A.【考点难点】利用数轴可以直观地求出两点的距离或解决一些与距离有关的问题.体现了数形结合的数学思想.【经典例题2】下列说法正确的有()①有理数的绝对值一定比0大;②如果两个有理数的绝对值相等.那么这两个数相等;③互为相反数的两个数的绝对值相等;④没有最小的有理数.也没有绝对值最小的有理数;⑤所有的有理数都可以用数轴上的点来表示;⑥符号不同的两个数互为相反数.A、②④⑤⑥B、③⑤C、③④⑤D、③⑤⑥【题目难度】★★【解题思路】分别根据有理数、绝对值、相反数的定义及数轴的特点对各小题进行逐一判断.【题目答案】①0是有理数.|0|=0.故本小题错误;②互为相反数的两个数的绝对值相等.故本小题错误;③互为相反数的两个数的绝对值相等.故本小题正确;④有绝对值最小的有理数.故本小题错误;⑤由于数轴上的点和实数是一一对应的.所以所有的有理数都可以用数轴上的点来表示.故本小题正确;⑥只有符号不同的两个数互为相反数.故本小题错误.所以③⑤正确.故选B.【考点难点】本题考查的是有理数、绝对值、相反数的定义及数轴的特点.熟知以上知识是解答此题的关键.【经典例题3】如果a的绝对值是2.那么a是()A、2B、-2C、±2D、【题目难度】★【解题思路】根据题意可知:绝对值等于2的数应该是±2.【题目答案】2的绝对值是2.-2的绝对值也是2.所以a的值应该是±2.故选C.【考点难点】本题考查了绝对值的概念.学生要熟练掌握.【经典例题4】若a<0.则4a+7|a|等于()A、11aB、-11aC、-3aD、3a【题目难度】★★【解题思路】:本题考查有理数的绝对值问题.如果用字母a表示有理数.则数a 绝对值要由字母a本身的取值来确定:①当a是正有理数时.a的绝对值是它本身a;②当a是负有理数时.a的绝对值是它的相反数-a;③当a是零时.a的绝对值是零【题目答案】:解:∵a<0.∴|a|=-a.4a+7|a|=4a+7|-a|=4a-7a=-3a.选C.【经典例题5】一个数与这个数的绝对值相等.那么这个数是()A、1.0B、正数C、非正数D、非负数【解题思路】:根据绝对值的性质进行解答即可.【题目答案】解:因为一个正数的绝对值是它本身.一个负数的绝对值是它的相反数.0的绝对值是0.所以一个数与这个数的绝对值相等.那么这个数是非负数.故选D .【经典例题6】已知|x|=5.|y|=2.且xy >0.则x-y 的值等于( )A 、7或-7B 、7或3C 、3或-3D 、-7或-3【题目难度】★★【解题思路】先根据绝对值的定义求出x 、y 的值.再由xy >0可知x 、y 同号.根据此条件求出x 、y 的对应值即可. 【题目答案】解:∵|x|=5.|y|=2.∴x=±5.y=±2.∵xy >0.∴当x=5时.y=2.此时x-y=5-2=3;当x=-5时.y=-2.此时x-y=-5+2=-3.故选C .【考点难点】本题考查的是绝对值的性质及有理数的加减法.熟知绝对值的性质是解答此题的关键.【经典例题7】若1-=x x.则x 是( )A 、正数B 、负数C 、非负数D 、非正数【解题思路】本题作为选择题可用排除法进行解答.由于是分式.所以x≠0.故可排除C、D;再根据x的取值范围进行讨论即可.【题目答案】:解:∵是分式.∴x≠0.∴可排除C、D.∵当x>0时.原式可化为=1.故A选项错误.故选B.【考点难点】本题考查的是绝对值的性质.即一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.【经典例题8】已知:a>0.b<0.|a|<|b|<1.那么以下判断正确的是()A、1-b>-b>1+a>aD、1-b>1+a>-b>aC、1+a>1-b>a>-bB、1+a>a>1-b>-b【题目难度】★★★【解题思路】根据绝对值的定义.可知a>0.b<0时.|a|=a.|b|=-b.代入|a|<|b|<1.得a<-b <1.由不等式的性质得-b>a.则1-b>1+a.又1+a>1.1>-b>a.进而得出结果.【题目答案】∵a>0.∴|a|=a;∵b<0.∴|b|=-b;又∵|a|<|b|<1.∴a<-b<1;∴1-b>1+a;而1+a>1.∴1-b>1+a>-b>a.故选D.【考点难点】本题主要考查绝对值的定义:一个正数的绝对值是它本身;一个负数的绝对值是是它的相反数;0的绝对值是0;互为相反数的绝对值相等.【经典例题9】已知a、b互为相反数.且|a-b|=6.则|b-1|的值为()A、2B、2或3C、4D、2或4【题目难度】★★【解题思路】根据互为相反数的两数和为0.又因为|a-b|=6.可求得b的值.代入即可求得结果判定正确选项.【题目答案】∵a、b互为相反数.∴a+b=0.∵|a-b|=6.∴b=±3.∴|b-1|=2或4.故选D.【考点难点】此题把相反数和绝对值的运算结合求解.先根据相反数求出b的值.再确定绝对值符号中代数式的正负.去绝对值符号.【经典例题10】a<0.ab<0.计算|b-a+1|-|a-b-5|.结果为()A、6B、-4C、-2a+2b+6D、2a-2b-6【题目难度】★★【解题思路】:根据已知条件先去掉绝对值即可求解.【题目答案】解:∵a<0.ab<0.∴b-a+1>0.a-b-5<0.∴|b-a+1|-|a-b-5|=b-a+1+a-b-5=-4.故选A.【经典例题11】若|x+y|=y-x.则有()A、y>0.x<0B、y<0.x>0C、y<0.x<0D、x=0.y≥0或y=0.x≤0【题目难度】★★★★【解题思路】根据绝对值的定义.当x+y≥0时.|x+y|=x+y.当x+y≤0时.|x+y|=-x-y.从中得出正确答案.:【题目答案】解:∵|x+y|=y-x.又当x+y≥0时.|x+y|=x+y.可得x=0.y≥0或者y=0.x≤0又当x+y≤0时.|x+y|=-x-y.可得y=0.x≤0或x=0.y≥0∴x=0.y≥0或y=0.x≤0选D.【考点难点】此题主要考查了绝对值的性质.能够根据已知条件正确地判断出x.y的值是解答此题的关键.【经典例题12】已知:x<0<z.xy>0.且|y|>|z|>|x|.那么|x+z|+|y+z|-|x-y|的值()A、是正数B、是负数C、是零D、不能确定符号【题目难度】★★★★【解题思路】:先根据已知条件确定x、y、z的符号及其绝对值的大小.再画出数轴确定出各点在数轴上的位置.根据绝对值的性质即可去掉原式的绝对值.使原式得到化简.【题目答案】:解:由题意可知.x、y、z在数轴上的位置如图所示:所以|x+z|+|y+z|-|x-y|=x+z-(y+z)-(x-y)=0【经典例题13】给出下面说法:(1)互为相反数的两数的绝对值相等;(2)一个数的绝对值等于本身.这个数不是负数;(3)若|m|>m.则m<0;(4)若|a|>|b|.则a>b.其中正确的有()A、(1)(2)(3)B、(1)(2)(4)C、(1)(3)(4)D、(2)(3)(4)【题目难度】★★★【解题思路】:分别根据绝对值的性质、相反数的定义进行解答.【题目答案】解:(1)正确.符合绝对值的性质;(2)正确.符合绝对值的性质;(3)正确.符合绝对值的性质;(4)错误.例如a=-5.b=2时.不成立.故选A.(1)相反数的定义:只有符号不同的两个数.叫互为相反数;(2)绝对值的性质:一个正数的绝对值是它本身.一个负数的绝对值是它的相反数.0的绝对值是0.【经典例题14】已知a.b.c为三个有理数.它们在数轴上的对应位置如图所示.则|c-b|-|b-a|-|a-c|= _________【题目难度】★★★【解题思路】:根据图示.可知有理数a.b.c的取值范围b>1>a>0>c>-1.然后根据它们的取值范围去绝对值并求|c-b|-|b-a|-|a-c|的值.【题目答案】:解:根据图示知:b>1>a>0>c>-1.∴|c-b|-|b-a|-|a-c|=-c+b-b+a-a+c=0故答案是0.【考点难点】本题主要考查了关于数轴的知识以及有理数大小的比较.【经典例题15】若x<-2.则|1-|1+x||=______若|a|=-a.则|a-1|-|a-2|= ________【题目难度】★★★【解题思路】根据已知x<-2.则可知1+x<0.x+2<0;再根据绝对值的定义|1-|1+x||逐步去掉绝对值可转化为-2-x根据已知|a|=-a与绝对值的定义.那么a≤0.则|a-1|-|a-2|可去掉绝对值后【题目答案】∵x<-2.∴1+x<0.x+2<0.则|1-|1+x||=|1-[-(1+x)]|=|2+x|=-2-x;∵|a|=-a.∴a≤0.∴a-1<0.a-2<0..则|a-1|-|a-2|=1-a-(2-a).=1-a-2+a.=-1.故答案为:-2-x.-1.【考点难点】此题主要考查了绝对值的性质.能够根据已知条件正确地判断出1+x<0、x+2<0、a≤0进而得出a-1<0、a-2<0.这些是解答此题的关键.【经典例题16】()2120a b++-=.分别求a b,的值【题目难度】★★★【解题思路】根据平方和绝对值的非负性解决.【题目答案】()02,012≥-≥+ba可得02,01=-=+ba;所以2,1=-=ba所以|x+1|+|x-5|+4的最小值是10.故答案为:10.【考点难点】本题主要考查了绝对值的定义.如何去掉绝对值是解决本题的关键.因而采用了对x的取值讨论.去掉绝对值.进而确定式子的最小值.【经典例题18】计算=【题目难度】★★★★【解题思路】根据绝对值的定义.去掉绝对值符合.化简求值.【题目答案】= ===故答案为【考点难点】解决本题的关键是去掉绝对值符号后.部分数值恰好是互为相反数.其和等于0.【经典例题19】若|a|+a=0.|ab|=ab.|c|-c=0.化简:|b|-|a+b|-|c-b|+|a-c|= ________ 【题目难度】★★★★【解题思路】根据绝对值的性质进行化简:正数的绝对值是它本身.负数的绝对值是它的相反数.0的绝对值是0.【题目答案】∵|a|+a=0.|ab|=ab.|c|-c=0.∴a≤0.b≤0.c≥0.∴a+b≤0.c-b≥0.a-c≤0.∴原式=-b+a+b-c+b-a+c=b.故答案为b.【考点难点】此题考查了绝对值的性质.同时注意根据有理数的运算法则正确判断含有字母的式子的符号.【经典例题20】已知:abc≠0.且M= .当a.b.c取不同值时.M有 ____种不同可能.当a、b、c都是正数时.M= ______;当a、b、c中有一个负数时.则M= ________;当a、b、c中有2个负数时.则M= ________;当a、b、c都是负数时.M=__________ .【题目难度】★★★★【解题思路】:根据abc≠0.可以知道.a、b、c一定不可能是0.可以分三个中都是正数.只有一个负数.有2个负数.3个都是负数.4种情况进行讨论即可.【题目答案】当a、b、c中都是正数时.M=1+1+1=3;当a、b、c中有一个负数时.不妨设a是负数.则M=-1+1+1=1;当a、b、c中有2个负数时.不妨设a.b是负数.则M=-1-1+1=-1;当a、b、c都是负数时.M=-1-1-1=-3;故M有4种不同结果.课堂检测练习1. 若a的绝对值是.则a的值是()A、2B、-2C、D、【题目难度】★【解题思路】:根据绝对值的意义可知:表示数a的点与原点的距离为.这样的点有两个.分别在原点的左右两侧.求出即可.【题目答案】解:∵|a|= .∴a= .故选D.【考点难点】此题注意考查绝对值的意义.应多让学生借助数轴.直观的观察、总结、归纳结论.2. 若|x|=-x.则x一定是()A、负数 B、负数或零 C、零 D、正数【题目难度】★【解题思路】:根据绝对值的性质进行解答即可.【题目答案】:解:A、错误.例如x=0时不成立;B、正确.符合绝对值的性质;C、错误.x<0时原式仍成立;D、错误.例如|5|≠-5.故选B.【考点难点】本题考查的是绝对的性质.根据已知条件判断出x的取值范围是解答此题的关键.练习2. 如果|x-1|=1-x.那么()A、x<1B、x>1C、x≤1D、x≥1【题目难度】★【解题思路】:根据|x-1|=1-x可确定x-1的符号.再根据不等式的性质解答即可.【题目答案】:解:∵|x-1|=1-x.∴x-1≤0.∴x≤1.故选C.【考点难点】绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.在确定x与1的大小关系时要利用不等式的相关性质.练习3. 若|a-3|=2.则a+3的值为()A、5 B、8 C、5或1 D、8或4 【题目难度】★★【解题思路】:先根据绝对值的性质去掉绝对值符号.求出a的值.再把a的值代入a+3进行计算即可.【题目答案】:解:当a-3≥0.即a≥3时.原不等式可化为a-3=2.a=5.故a+3=5+3=8;当a-3<0.即a<3时.原不等式可化为-a+3=2.a=1.故a+3=1+3=4.故a+3=8或4.故选D.【考点难点】本题考查的是绝对值的性质.解答此题题目是要注意分类讨论.不要漏解.练习4.若x<2.则|x-2|+|2+x|=________________【题目难度】★★【解题思路】:已知x<2.可得x-2<0.先分类讨论.然后根据绝对值的性质进行求解.【题目答案】:解:∵x<2.∴x-2<0.①若-2≤x<2.∴|x-2|+|2+x|=-(x-2)+2+x=4;②x<-2.∴x+2<0.∴|x-2|+|2+x|=2-x-2-x=-2x.故答案为:4或-2x.【考点难点】此题主要考查绝对值的性质.当x>0时.|x|=x;当x≤0时.|x|=-x.解题的关键是如何根据已知条件.去掉绝对值.还考查了分类讨论的思想.是一道好题.练习5. 绝对值小于6的所有整数的和与积分别是__________【题目难度】★★【解题思路】根据绝对值的概念.即数轴上表示数的点到原点的距离叫这个数的绝对值.结合数轴.知绝对值小于6的所有整数分别是±1.±2.±3.±4.±5.0.进一步求得其和与积.【题目答案】绝对值小于6的所有整数分别是±1.±2.±3.±4.±5.0.则它们的和是0.积是0.故答案为0.0.【考点难点】此题考查了绝对值的意义以及有理数的加法和乘法运算.互为相反数的两个数的和是0;几个数相乘.若其中一个因数为0.则积为0.练习6.如图所示.a、b是有理数.则式子|a|+|b|+|a+b|+|b-a|化简的结果为 __________【题目难度】★★★【解题思路】先根据a、b两点在数轴上的位置判断出其取值范围.再根据绝对值的性质进行解答即可.【题目答案】∵由数轴上a、b两点的位置可知.-1<a<0.b>1.∴a+b>0.b-a>0.∴原式=-a+b+a+b+b-a=3b-a.故答案为:3b-a.【考点难点】本题考查的是绝对值的性质及数轴的特点.能根据a、b两点在数轴上的位置判断出其取值范围是解答此题的关键.练习7. 已知|x|=2.|y|=3.且xy<0.则x+y的值为 _________【题目难度】★★★【解题思路】若|x|=2.|y|=3.则x=±2.y=±3;又有xy<0.则xy异号;故x+y=±1.∴x=±2.y=±3.∵xy<0.∴xy符号相反.①x=2.y=-3时.x+y=-1;②x=-3.y=3时.x+y=1.故答案为:±1.【考点难点】本题考查绝对值的化简.正数的绝对值是其本身.负数的绝对值是它的相反数.0的绝对值是0.课后练习练习1.-19的绝对值是________【题目难度】★【解题思路】直接根据绝对值的性质进行解答即可.∴|-19|=19.故答案为:19.【考点难点】本题考查的是绝对值的性质.用到的知识点为:负数的绝对值是它的相反数.练习2. 如果|-a|=-a.则a的取值范围是(A、a>OB、a≥OC、a≤OD、a<O【题目难度】★【解题思路】:根据绝对值的性质:一个负数的绝对值是它的相反数.0的绝对值是0.若|-a|=-a.则可求得a的取值范围.注意0的相反数是0.【题目答案】:解:因为一个负数的绝对值是它的相反数;0的绝对值是0或相反数.所以如果|a|=-a.那么a的取值范围是a≤0.故选C.【考点难点】此题考查的知识点是绝对值.关键明确绝对值规律总结:一个正数的绝对值是它本身.一个负数的绝对值是它的相反数.0的绝对值是0.练习3. 对值大于1且不大于5的整数有 __________个.【题目难度】★★【解题思路】先根据题意列出不等式组.求出x的取值范围.在x的取值范围内找出符合条件的x的整数值即可.【题目答案】由题意得.解得1<x≤5或-5≤x<-1.所以x的值可以是2、3、4、5或-2、-3、-4、-5共8个.故答案为:8.【考点难点】本题考查的是绝对值的性质及一元一次不等式组的特殊解.根据题意列出不等式组是解答此题的关键.练习4.绝对值最小的有理数是 _________.绝对值等于本身的数是________.【题目难度】★【解题思路】根据绝对值的定义及性质来解答.【题目答案】绝对值等于本身的数是非负数.绝对值最小的有理数是0.故答案为:0、非负数.【考点难点】本题考查了绝对值的定义.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.练习5. 当x __________时.|2-x|=x-2.【题目难度】★★【解题思路】因为x-2和2-x互为相反数.即一个数的绝对值等于它的相反数.所以2-x≤0.即可得到答案.【题目答案】∵x-2=-(2-x)..|2-x|=x-2.∴2-x≤0.解得:x≥2.故答案为:x≥2.【考点难点】本题考查对绝对值和相反数的理解和掌握.知一个数的绝对值等于它的相反数.这个数是负数是解此题的关键.练习6.如图.有理数x.y 在数轴上的位置如图.化简:|y-x|-3|y+1|-|x|= ________【题目难度】★★★【解题思路】依据x.y 在数轴上的位置比较大小.在此基础上化简给出的式子.【题目答案】根据数轴图可知:x >0.y <-1.∴|y-x|=x-y.|y+1|=-1-y.|x|=x ;∴|y-x|-3|y+1|-|x|=x-y+3(1+y )-x=2y+3.【考点难点】考查绝对值的运算.先确定绝对值符号中代数式的正负再去绝对值符号.借助数轴化简含有绝对值的式子.比较有关数的大小有直观、简捷.举重若轻的优势.练习7. 若3230x y -++=.则y x的值是多少? 【题目难度】★★★【解题思路】根据绝对值的非负性来解决.【题目答案】由03,02≥+≥-y x 可得:03,02=+=-y x 所以3,2-==y x 所以y x =23-。
走进重高培优讲义北师大七年级上第3讲:数轴和绝对值(概况难点,题型新颖,能力提高,启迪思维)
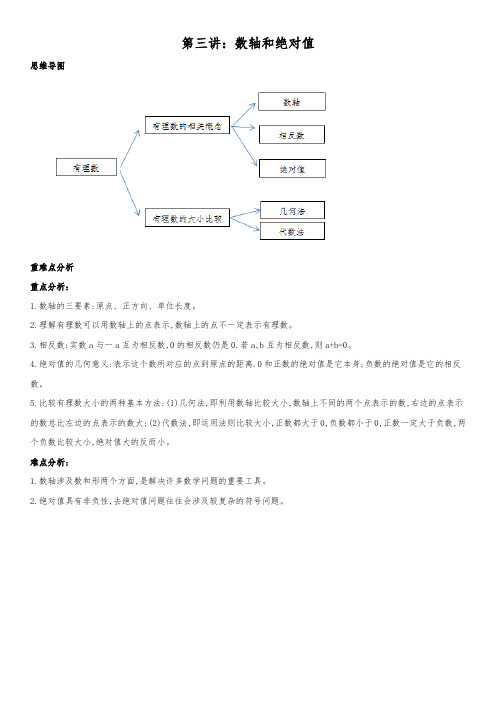
第三讲:数轴和绝对值思维导图重难点分析重点分析:1.数轴的三要素:原点、正方向、单位长度。
2.理解有理数可以用数轴上的点表示,数轴上的点不一定表示有理数。
3.相反数:实数a与一a互为相反数,0的相反数仍是0.若a,b互为相反数,则a+b=0。
4.绝对值的几何意义:表示这个数所对应的点到原点的距离.0和正数的绝对值是它本身;负数的绝对值是它的相反数。
5.比较有理数大小的两种基本方法:(1)几何法,即利用数轴比较大小,数轴上不同的两个点表示的数,右边的点表示的数总比左边的点表示的数大;(2)代数法,即运用法则比较大小,正数都大于0,负数都小于0,正数一定大于负数,两个负数比较大小,绝对值大的反而小。
难点分析:1.数轴涉及数和形两个方面,是解决许多数学问题的重要工具。
2.绝对值具有非负性,去绝对值问题往往会涉及较复杂的符号问题。
例6:如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合。
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为______cm.(2)由题(1)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要34年才出生;你若是我现在这么大,我已经116岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?探究提升观察下列每对数在数轴上的对应点间的距离4与−2,3与5,−2与−6,−4与3.并回答下列各题:(1)你能发现所得距离与这两个数的差的绝对值有什么关系吗?答:______;(2)若数轴上的点A表示的数为x,点B表示的数为−1,则A与B两点间的距离可以表示为______;(3)结合数轴求得|x−2|+|x+3|的最小值为______,取得最小值时x的取值范围为______;(4)满足|x+1|+|x+4|>3的x的取值范围为______.拓展训练A 组1、如图,数轴上点A 所表示的数的相反数的倒数是( )。
数轴绝对值培优

.初一数学培优竞赛数轴与绝对值知识要点:数轴上的点与有理数的关系 2、利用数轴比较有理数的大小1、 3、去绝对值的符号法则0)?(aa??0)?0(a|a|???0)?(a?a?|ab|=|a||b| 5、绝对值的几何意义:;4、绝对值的基本性质非负性:|a|≥0 二、例题选讲:,则a 0引例:|a|=-a的值a+1)+|b-2|=0,求a、例题1:已知:(1)(2 b的值,|b|=2,且a<b,求 a-b (2)|a|=5cba的值?c均为非零有理数,求?若a、b、 2 例题cba互为相反数,试求代数式与|b-1|例题3 已知|ab-2|1111????的值(a?2)(?b?2)2011)(b?2011)?ab(a1)(b?1)(a例题4 有理数a,b,c 在数轴上的位置如图所示:cab10 1-c│,│a-c│-?│-m=若│a+b│-│b-1│1000m=则在数轴上的位置如图所示,练习:如图:a , b , coabc a-b|+|-2c|+|c+b|+|3b|试化简:︳ b)|ab|+|a+b|=1的所有整数对(a,例题6 已知求满足【基础夯实】一、选择题a,b,c在数轴上的位置如图所示,则a,b, -c由小到大的顺序是 1.数()A. a,-c,bB. b,a,-cC. a, b,-cD. b,-c,a2.四个互不相等的整数的积是9,那么这四个整数的和等于()A.27B.0C.9D.以上答案都不对?a=-a,那么 ( )3.如果A.-a一定是负数; ;一定非负数B.-a;...aa.D.- 不能是零C.一定是正数;( )成立的是4.下列各式的结论,nmnm A.则若若m>n,> = ,则m=n B.nmmn.若m<n<0,则>>,则m>n 若 C.D.()a+b>0,则a-b的值是,且5.若|a|=8,|b|=5-13 或-3 D.-3或A.3或13 B.13或 -13 C.3 二、解答题 c-b│.│a+c│+│6.设有理数在数轴上对应点如图所示,化简│b-a│+|2x-1|+|x-2| .化简7【能力拓展】a?3?2a?4,?0?a()的最大值等于1、已知那么A. 1B. 5C. 8D. 3) 2、满足|a-b|=|a|+|b|成立的条件是(1??0D.abCabA.?0B.ab?1.ab绝对有理数运算及后续二次根式的基础.绝对值是我们初中代数中的一个基本概念,是学习相反数、、函数中距离等问题、解不等(组))值又是初中代数中的一个重要概念,在解代数式化简求值、解方程(组有着广泛的应用,全面理解、掌握绝对值这一概念,应从以下方面人手:)a?0_____(??)0?a?_____(a l.绝对值的代数意义:??)0_____(a??a;长度,非负表示_____________________的距离() 2.绝对值的几何意义从数轴上看,ba?.表示__________________________ 3.绝对值基本性质;...aa222baa?0ab??)0?(b?aaa??;③;④①非负性:;②.bb培优讲解(一)、绝对值的非负性问题??zx?y05?x?3?y?1?z?】若。
培优专题一绝对值

专题一 绝对值题型一、基本定义化简【典型例题】例1、(1)已知数a 、b 、c 在数轴上的位置如图所示,化简a b a b b c +++-- (2)已知有理数a , b, c,在数轴上的位置如图所示,化简:a c c b b a ++--+.例2、已知00x z xy y z x <<>>>,,,那么x z y z x y +++--= 例3、已知0,>-<ba b a ,化简a b a b ab -+++【课后练习】 1、实数,,a b c 在数轴上的对应点如图,化简a c b a b a c +--++-0cb a2、已知有理数,,a b c 在数轴上的位置如图所示,化简a a b c b a c -++-++3、⑴若有理数a 、b 满足|a+4|+|b-1|=0,则a+b=_______⑵若|a|=5,|b|=3,且|a-b|=b-a ,则a+b=________.⑶若m 是有理数,则|m|-m 一定是( ) A.零 B.非负数 C. 正数 D 负数⑷如图,有理数b a 、在数轴上的位置如图所示,则在b a +,a b 2-,a b -,b a -,2+a ,4--b 中,负数共有( )A . 1个B .2个C .3个D .4个-232b a1-1题型二、绝对值零点分段化简【典型例题】例4、阅读下列材料并解决相关问题: 我们知道()()()0000x x x x x x >⎧⎪==⎨⎪-<⎩,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式12x x ++-时,可令10x +=和20x -=,分别求得12x x =-=,(称12-,分别为1x +与2x -的零点值),在有理数范围内,零点值1x =-和2x =可将全体有理数分成不重复且不易遗漏的如下3中情况:·⑴当1x <-时,原式()()1221x x x =-+--=-+⑵当12x -<≤时,原式()123x x =+--=⑶当2x ≥时,原式1221x x x =++-=-综上讨论,原式()()()211312212x x x x x -+<-⎧⎪=-<⎨⎪-⎩≤≥通过阅读上面的文字,请你解决下列的问题: ⑴分别求出2x +和4x -的零点值 ⑵化简代数式24x x ++-【课后练习】化简: ⑴3x- ⑵12x x +++⑶523x x ++- ⑷212x x ---⑸12m m m +-+- ⑹121x x --++(7)3243m m m ++-+- (8)32264m m m ++-+-题型三、关于aa的探讨应用【典型例题】 例5、已知a b c abc x a b c abc =+++,且a b c ,,都不等于0,求x 的所有可能值。
第一讲、七年级数轴与绝对值专题

第一讲 数轴与绝对值专题绝对值是初中代数中的一个基本概念,是学习相反数、有理数运算及后续算术根的基础.绝对值又是初中代数中的一个重要概念,在解代数式化简求值、解方程(组)、解不等(组)等问题有着广泛的应用,全面理解、掌握绝对值这一概念,应从以下方面人手l .去绝对值的符号法则:⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a2.绝对值基本性质 ①非负性:0≥a ;②b a ab ⋅=;③)0(≠=b ba b a ;④222a a a ==. 3.绝对值的几何意义 从数轴上看,a 表示数a 的点到原点的距离(长度,非负);b a -表示数a 、数b 的两点间的距离.例1、(1)已知321===c b a ,,,且c b a >>,那么c b a -+=________. (2)已知d c b a 、、、是有理数,169≤-≤-d c b a ,,且25=+--d c b a , 那么=---c d a b ________.例2、如果是非零有理数,且0=++c b a ,那么abc abc c c b b a a +++的所有可能的值为( ).A .0B . 1或一lC .2或一2D .0或一2例3、已知12--b •ab 与互为相反数,试求代数式:)2002)(2002(1)2)(2(1)1)(1(11++++++++++b a b a b a ab 的值.c b a 、、变式: 设999727525323124932⨯++⨯+⨯+⨯= S ,992725231482++++= T ,则T S -=( ). A .99249 B .992149- C .199249- D .199249+ 例4、化简(1)12-x (2)31-+-x x ;例5、已知a 为有理数,那么代数式4321-+-+-+-a a a a 的取值有没有最小值?如果有,试求出这个最小值;如果没有,请说明理由.例6、(新加坡数学竞赛题)如果4个不同的正整数q p n m 、、、满足4)7)(7)(7)(7(=----q p n m ,那么,q p n m +++等于( ).A .10B .2lC .24D .26E .28能力拓展A (数轴)1.c b a 、、在数轴上的位置如图所示,则ca b c b a ---111、、中最大的是________.2.有理数c b a 、、在数轴上的位置如图所示,若c c a b b a m ------+=11,则,则1000m =________. (“希望杯”邀请赛试题)3.11-++x x 的最小值是_________.4.有理数b a 、满足0>a ,0<b ,b a <,用“<”将b a b a --、、、连接起来.5.若00<>b a ,,则使b a b x a x -=-+-成立的x 取值范围是________.6.不相等的有理数c b a 、、在数轴上对应点分别为A 、B 、C ,若c a c b b a -=-+-,那么点B( ).A .在A 、C 点右边B .在A 、C 点左边 C .在A 、C 点之间D .以上均有可能 能力拓展B (绝对值)1.若有理数x 、y 满足2002(x 一1)2 +0112=+-y x ,则=+22y x ________.2.已知3,5==b a ,且a b b a -=-,那么b a +=________.3.已知有理数c b a 、、在数轴上的对应位置如图所示: 则b a c a c -+-+-1化简后的结果是________.4.若为有理数,那么,下列判断中:(1)若b a =,则一定有b a =; (2)若b a >,则一定有b a >; (3)若b a >,则一定有b a >;(4)若b a =,则一定有22)(b a -=.正确的是 (填序号)5.已知数轴上的三点A 、B 、C 分别表示有理数a ,1,一l ,那么1+a 表示( ).A .A 、B 两点的距离 B .A 、C 两点的距离C .A 、B 两点到原点的距离之和D . A 、C 两点到原点的距离之和6.已知a 是任意有理数,则a a --的值是( ).A .必大于零B .必小于零C 必不大于零D .必不小于零7.若1++b a 与2)1(+-b a 互为相反数,则a 与b 的大小关系是( ).A .b a >B .b a =C .b a <D .b a ≥8.如图,有理数在数轴上的位置如图所示,则在4,2,,,2,--+---+b a b a a b a b b a 中,负数共有( )A . 1个B .2个C .3个D .4个12.使代数式x x x 43-的值为正整数的x 值是( ).A .正数B .负数C .零D .不存在的13.如果02=+b a ,则21-+-ba b a 等于( ).A .2B .3C .4 或2D .514.如果150<<p ,那么代数式1515--+-+-p x x p x 在15≤≤x p 的最小值是().b a 、b a、A .30B .0C .15D .一个与p 有关的代数式15.有理数c b a 、、均不为零,且0=++c b a ,设b a ca c bc b ax +++++=,试求代数式20029919+-x x的值.16.(1)已知c b a 、、都不等于零,且abc abc c c b b a a +++的最大值是m ,最小值为n ,求mnn m的值.17.若c b a 、、为整数,且19919=-+-a c ba ,求cb b a ac -+-+-的值.18.已知1,1≤≤y x ,设421--++++=x y y y x M ,求M 的最大值与最小值.19.已知02003200232120032002321=-+-++-+-+-x x x x x ,求代数式20032002212222x x x x +--- 的值.。
第一讲-数轴与绝对值

课题第一讲:数轴与绝对值复习教学目标1、理解数轴的概念,掌握数轴的三要素,会画数轴;2、会用数轴上的点表示有理数,能说出数轴上的点表示的有理数;3、利用数轴理解相反数的意义,会求一个数的相反数。
4、理解绝对值的意义,会求一个数的绝对值;5、能熟练运用法则结合数轴比较有理数的大小,特别是应用绝对值概念比较两个负数的大小,能利用数轴对多个有理数进行有序排列重点、难点重点:1、理解数轴上的点与有理数之间的关系2、绝对值的概念和求一个数的绝对值;难点:1、从数形结合的观点出发认识相反数。
2、绝对值的几何意义及求绝对值等于某一个正数的有理数;考点及考试要求1、用数轴上的点表示有理数以及有理数的相反数2、求一个数的绝对值3、利用数轴比较有理数的大小教学内容知识框架1、数轴的概念及画法2、数轴上的点与有理数之间的关系3、绝对值的几何意义4、绝对值的代数意义5、绝对值的性质知识点一:数的分类1、正数和负数的概念比0大的数叫做正数;在正数前面加上“-”号的数叫做负数;0既不是正数,也不是负数.为了突出数的符号,可以在正数前面加“+”号,一般地“+”号往往省略不写,但负数前面的“-”号不能省略.对于正数和负数的概念,不能简单地理解为:带“+”号的数是正数,带“-”号的数是负数.2、有理数的概念及分类整数和分数统称为有理数:正数、负数和零也统称为有理数.整数包括正整数、零和负整数、分数包括正分数和负分数;正数包括正整数和正分数;负整数包括负整数和负分数.到目前为止,我们学过的数细分有五类:正整数、正分数、零、负整数、负分数,因为有限小数和无限循环小数可以化为分数,所以把有限小数和无限循环小数都看作分数.有时为了研究的需要,整数也可以看作是分母为 1的分数,但本章中的分数是指不包括分母是1的分数.通常把正整数和零统为非负数;负数和零统称为非正数;正整数和零统称为非负整数,即为自然数;负整数和零统称为非正整数.【题型一】例1.把下列各数分别填入相应的集合:-3.5,-12,3.2,8.1,0,.1.3,-20%,5,14,-7.整数集:{ …};分数集:{ …}; 自然数集:{ …}; 非负数集:{ …}; 非正数集:{ …}.变式1:把下列各数填入相应的数集圈:-2.1,0,-2,15,10,-52,+5.8,.6.2,50%.变式2:下列既不是正数又不是负数的是( )A 、-1B 、+3C 、0.12D 、0例2. 下列各数-5,31,71_,0,-212,314,-m(m 是有理数)中,一定是负数的有()。
七年级培优讲义第二讲-数轴、绝对值

第二讲 数轴、绝对值知识导航像8,1.8, 21…这样的数叫做正数,它们都比0大. 在正数前面加上“-”号的数叫做负数,如-8,-5,…0既不是正数,也不是负数.数的分类如下:规定了原点、正方向和单位长度的直线叫做数轴.一个数a 的绝对值就是数轴上表示数a 的点与原点的距离,数a 的绝对值记作a 用式子表示为重点:理解有理数及有理数的大小比较、数轴、绝对值的概念.难点:数轴、绝对值的应用问题,点燃思维点燃1:实数c b a ,,在数轴上的对应点如图2.1-1,化简: =+--++c b c b a a点燃2:若0,0,<>>b a b a ,把b a b a --,,,按由小到大的顺序排列.点燃3:如图2.1—3,在数轴上有六个点,且EF DE CD BC AB ====,则与点C 所表示的数最接近的整数是 ( )(A)-1; (B)0; (C)-1; (D)2.点燃4:已知数轴上有AB 两点,AB 之间的距离为1,点A 与原点O 的距离为3,那么所有满足条件的点B 与原点O 的距离之和等于多少?点燃5:已知,3,2,1===c b a 且c b a >>,那么=-+c b a点燃6:如果c b a ,,均为非零有理数,试求c c b b a a ++的值中考考点热点直击与中考真题欣赏1、如图—5,若数轴上的两点AB 表示的数分别为b a ,,则下列结论正确的是( )(A) 021>-a b (B) 0>-b a ;(C) 02>+b a ; (D) 0>+b a . 2、一2的相反数是( )(A) 21-; (B) 21; (C)2; (D)-2.3、21的相反数是( ) (A) 21-; (B) 21; (C)2; (D)-2.4、31-的倒数是( ) (A) 31-; (B) 31; (C)3; (D)-3. 5、数轴上表示21-的点到原点的距离是( ) (A) 21-; (B) 21; (C)2; (D)-2. 创新思维与赛题探究1:观察依次排列的一列数,它的排列有什么规律?你能说出这列数的第50个数,第100个数,第2010个数是什么吗?2:如图2. 1 -6,数轴上标出了若干个点,每相邻两点相距1个 单位,数轴上还标出了四个点D C B A ,,,,它们对应的数分别是d c b a ,,,且102=-a d ,那么数轴的原点应是 ( )(A) A 点; (B) B 点; (C)C 点; (D)D 点.2:电子跳蚤从数轴上的某点0M 开始跳动,第1步从0M 向左跳1个单位到1M ,第2步从1M 向右跳2个单位到2M ,第3步从2M 向 左跳了 3个单位到3M ,第4步从3M 向右跳4个单位到4M ,…,按以上规律跳了 160步时,电子跳蚤落在数轴上的点160M 所表示的数为,试 求电子跳蚤的初始位置0M 点所表示的数.3:已知c b a ,,都是负数,并且0=-+-+-c z b y a x ,则xyz 是( )(A) 负数; (B) 非负数; (C)正数; (D)非正数.4:已知15,150≤≤<<x p p ,求1515--+-+-p x x p x 的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝对值与数轴专项培
优
数轴与绝对值专项培优
(一)数轴的应用
一、利用数轴直观地解释相反数;
例1:如果数轴上点A 到原点的距离为3,点B 到原点的距离为5,那么A 、B 两点的距离为 。
拓广训练:
1、在数轴上表示数a 的点到原点的距离为3,则._________3=-a
2、已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么所有满足条件的点B 与原点O 的距离之和等于 。
(北京市“迎春杯”竞赛题)
二、利用数轴比较有理数的大小;
例2:已知有理数a 在数轴上原点的右方,有理数b 在原点的左方,那么( )
A .b ab <
B .b ab >
C .0>+b a
D .0>-b a
拓广训练:
1、如图b a ,为数轴上的两点表示的有理数,在a b b a a b b a ---+,,2,中,负数的个数有( )(“祖冲之杯”邀请赛试题)
A .1
B .2
C .3
D .4
2、把满足52≤<a 中的整数a 表示在数轴上,并用不等号连接。
例3:已知0,0<>b a 且0<+b a ,那么有理数b a b a ,,,-的大小关系
是 。
(用“<”号连接)(北京市“迎春杯”竞赛题)
拓广训练:
1、若0,0><n m 且n m >,比较m n n m n m n m --+--,,,,的大小,并用“>”号连接。
三、利用数轴解决与绝对值相关的问题。
例4: 有理数c b a ,,在数轴上的位置如图所示,式子c b b a b a -++++化简结果为( )
A .c b a -+32
B .c b -3
C .c b +
D .b c - (二)绝对值问题
一、去绝对值符号问题
例1:已知3,5==b a 且a b b a -=-那么=+b a 。
拓广训练:
1、若5,8==b a ,且0>+b a ,那么b a -的值是( )
A .3或13
B .13或-13
C .3或-3
D .-3或-13
二、恰当地运用绝对值的几何意义
例2: 11-++x x 的最小值是( )
拓广训练:
1、 已知23++-x x 的最小值是a ,23+--x x 的最大值为b ,求b a +的值。
2、(1)当x 取何值时,3-x 有最小值?这个最小值是多少?(2)当x 取何值时,25+-x 有最大值?这个最大值是多少?(3)求54-+-x x 的最小值。
(4)求
987-+-+-x x x 的最小值。
三、培优训练
1、如图,有理数b a ,在数轴上的位置如图所示: 则在4,2,,,2,--+---+b a b a a b a b b a 中,负数共有( )(湖北省荆州市竞赛题)
A .3个
B .1个
C .4个
D .2个
2、若m 是有理数,则m m -一定是( )
A .零
B .非负数
C .正数
D .负数
3、已知a a -=,则化简21---a a 所得的结果为( )
A .1-
B .1
C .32-a
D .a 23-
4、已知40≤≤a ,那么a a -+-32的最大值等于( )
A .1
B .5
C .8
D .9。
