21.6波函数
波函数

结论: 结论:3)波函数所代表的波是几率波. 波函数所代表的波是几率波. 微观粒子出现在|Ψ 大的地方, Ψ 微观粒子出现在 Ψ|2大的地方,|Ψ|2小的 地方粒子出现少;粒子受波数所引导, 地方粒子出现少;粒子受波数所引导, 波函数按波的形式去分配粒子的出现的 几率. 几率. 例)求一个能量为E,动量为 的自由粒子的几率 求一个能量为 ,动量为P的自由粒子的几率 i 密度. 密度. ( EtPr ) 解: 波函数为 Ψ = Ψ e 0
∞→∞
因为粒子在全空间出现是必然事件
例1: 设粒子在一维空间运动,其状态可用波函 : 设粒子在一维空间运动, 数描述为: 数描述为:
ψ ( x, t ) = 0
( x ≤ b / 2), x ≤ b / 2)
其中A为任意常数, 和 均为确定的常数. 均为确定的常数 其中 为任意常数,E和b均为确定的常数. 为任意常数 归一化的波函数;几率密度W? 求:归一化的波函数;几率密度W? 解:由归一化条件,有: 由归一化条件,
nπ 其最大值对应于 sin = ±1 4
L 2 2 nπ ω n = Ψ ( ) = sin 4 L 4
,于是有: 于是有:
∴ n = 2(2k + 1)
π nπ = ( 2k + 1) (k = 0,1,2, ) 4 2
(k = 0,1,2, )
�
cos (
2
πx
b
)dx = 1
b ∴ A =1 2
2
∴ A =
2 b
由此可求出归一化的波函数和几率密度 几率密度为: 几率密度为:
W ( x, t ) = ψ 2 ( x, t ) = 0 ( x ≤ b / 2), x ≤ b / 2) 2 2 π x 2 W ( x, t ) = ψ ( x, t ) = cos ( ) ( b / 2 ≤ x ≤ b / 2) b b
量子力学的波函数解析

量子力学的波函数解析量子力学是一门研究微观世界的科学,波函数是其核心概念之一。
本文将介绍量子力学的波函数解析。
一、波函数的定义和物理意义波函数是量子力学描述微观粒子状态的数学函数。
通常用Ψ来表示波函数,其一般形式为Ψ(x, t),其中x表示位置,t表示时间。
波函数的平方乘以一个常数就是粒子在该位置出现的概率密度。
二、波函数的波动性根据量子力学的原理,粒子在某一位置的运动具有波动性。
这是波函数的一大特征。
当波函数呈现波动性时,可以使用波动方程来描述其演化。
三、波函数的波动方程波函数的演化可以由薛定谔方程描述。
薛定谔方程是一个偏微分方程,描述了波函数随时间变化的规律。
该方程对于理解量子力学的基本性质至关重要。
四、波函数的归一化条件波函数必须满足归一化条件,即波函数的平方在整个空间积分等于1。
这保证了粒子在所有可能位置出现的概率之和等于1。
五、波函数的例子1. 粒子在一维无限深势阱中的波函数:无限深势阱是量子力学中的简化模型,其波函数为正弦函数和余弦函数的线性组合。
这个例子展示了粒子在特定能级上的定态波函数。
2. 粒子在一维谐振子中的波函数:谐振子是量子力学中的经典模型,其波函数为厄密多项式的高斯函数。
这个例子展示了粒子在谐振子势场中的概率分布。
3. 电子双缝干涉的波函数:双缝干涉实验证明了波粒二象性的存在。
电子双缝干涉的波函数可以通过叠加两个点源的波函数得到。
这个例子展示了波函数在干涉实验中的应用。
六、波函数的测量与实验在实验中,波函数的测量通常通过观察粒子的位置、动量或其他物理量得出。
根据波函数坍缩的原理,测量结果将会使波函数发生坍缩,粒子出现在某一确定的状态。
七、波函数的解析解与近似解对于简单的系统,可以通过求解薛定谔方程得到波函数的解析解。
然而,对于复杂的系统,通常需要使用数值计算方法或近似解来描述波函数。
总结:本文介绍了量子力学的波函数解析。
波函数是量子力学中描述微观粒子的数学函数,具有波动性和粒子分布概率的特征。
波函数PPT课件

作代换:px x,px x0,则
(
px
px )
1
2
e dx i (
p
x
px
)
x
13
(4)平面波归一化 I Dirac —函数
定义:
0 ( x x0 )
x x0 x x0
x0 x0
(x
x0 )dx
( x x0 )dx 1
( 0)
或等价的表示为:对在x=x0 邻域 连续的任何函数 f(x)有:
—函数 亦可写成 Fourier 积分形式: 令 k=px/ , dk= dpx/ , 则 性质: ( x) ( x)
0
x0
x
(x
x0 )
1
2
dk
e ik ( x x0 )
(x
x0 )
1
2
e dp i
p
x
(
x
x0
)
x
(ax) 1 ( x)
|a|
f ( x) ( x x0 ) f ( x0 ) ( x x0 ) .
p(r )
i [ p•r]
Ae
px ( x) py ( y) pz (z)
A e A e A e i [
p
x
x
]
i[
p
y
y
]
i[
pz
z
]
1
2
3
考虑一维积分
px * ( x, t )px ( x, t )dx
ei[
E
x
E
x
]t
px * ( x) px ( x)dx
(
px
2
2
C(r1 , t ) (r1 , t )
波函数公式
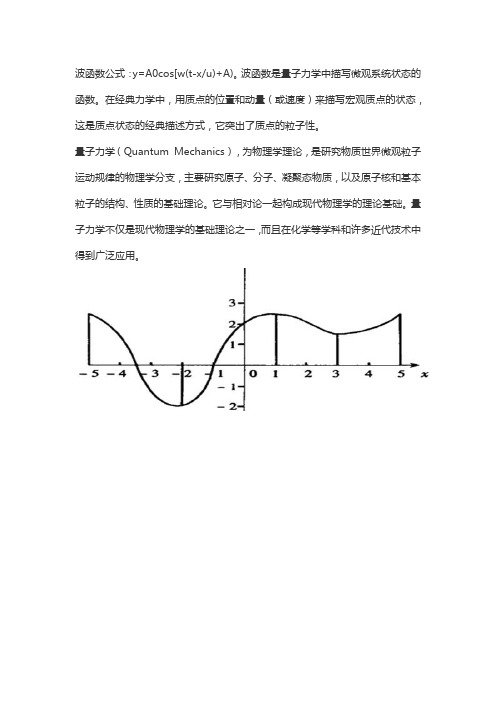
波函数公式:y=A0cos[w(t-x/u)+A)。
波函数是量子力学中描写微观系统状态的函数。
在经典力学中,用质点的位置和动量(或速度)来描写宏观质点的状态,这是质点状态的经典描述方式,它突出了质点的粒子性。
量子力学(Quantum Mechanics),为物理学理论,是研究物质世界微观粒子运动规律的物理学分支,主要研究原子、分子、凝聚态物质,以及原子核和基本粒子的结构、性质的基础理论。
它与相对论一起构成现代物理学的理论基础。
量子力学不仅是现代物理学的基础理论之一,而且在化学等学科和许多近代技术中得到广泛应用。
波函数、势井中的粒子、氢原子(公式讲解).ppt

2 2m
2x x 2
E x x
一维自由粒子薛定谔方程
2 2 U E
2m
三维势场粒子的薛定谔方程
U E 是 x y z 的函数
12
例:已知氢原子中电子的径向波函数为
r
Ae a
A、ar为常数,求 r r dr
之间电子出现的概率。在何处这个 概率最大?
解:先归一化求出常数A
4r 2r
2
dr
4
A
2
r
2e
2r a
dr
1
0
0
13
A
a3
1 2
归一化波函数
r
1
r
ea
a3
在 r r dr之间出现的概率
Wr
r
2 4r 2dr
4 a3
e
2r a
r
2dr
wrdr
14
dwr dr
4 a3
2re 2r / a 1 r 0 a
d2wr 0 dr 2 r a 处出现的概率密度最大
等于零(否则 x 0 )。系数行列式必须
等于零。
eika eika
eika =0 eika
18
用欧拉公式展开 sin2ka=0
2ka n
kn 2a n
n 1,2,
n 不能取零,n=o,k=0 , x 在 x
a
区间内是一常数,无物理意义
将kn En
2a 2kn2
2m
n回代k 2
2 2
8ma 2
n2
2mE 2
n
得
1,2,
19
将 kn 代入 Aeika Be ika 0
i n
21.6波函数

4π p h
2
2
2
Ψ
Ψ t
E Ek
h
2 2 2
p
i2 π h
2
EΨ
k
(v c )
2 mE
一维运动自由粒子 的含时薛定谔方程
Ψ
2
8 π m x
i
h Ψ 2 π t
21.6波函数
薛定谔方程
第21章 量子物理
若粒子在势能为 E p 的势场中运动
E Ek Ep
如果把波函数在空间各点的振幅同时增大一倍, 并不影响粒子在空间各点的几率。所以将波函数乘 上一个常数后,所描写的粒子的状态并不改变。
21.6波函数
薛定谔方程
第21章 量子物理
以一维波函数为例,在下述四种函数曲线中,只 有一种符合标准条件
符合
不符合
不符合
不符合
21.6波函数
薛定谔方程
第21章 量子物理
2
2 a
sin
2
21.6波函数
薛定谔方程
nπ a
y
n
第21章 量子物理
2
y ( x ) A sin
x
y (x)
2 a
y
sin
2 n
2
nπ a
x
n4
16 E 1
n3 n2
n 1 x0
a 2
9 E1
4 E1
a
x0
a 2
a
E1
Ep 0
一维运动粒子的含时薛定谔方程 2 2 h Ψ h Ψ E p ( x , t )Ψ i 2 2 8π m x 2 π t
粒子在恒定势场中的运动
波函数

写成分量形式
p(r )
i [ p•r]
Ae
px
( x) py ( y) pz
(z)
A e A e A e i [
px
x
]
i[
p
y
y
]
i[
pz
z
]
1
2
3
考虑一维积分
px * ( x, t )px ( x, t )dx
(
px
px )
1
2
e dx i (
p
x
px
)
x
e i [
2. 粒子由波组成
电子是波包。把电子波看成是电子的某种实际结构,是三维空间中连
续分布的某种物质波包。因此呈现出干涉和衍射等波动现象。波包的 大小即电子的大小,波包的群速度即电子的运动速度。
什么是波包?波包是各种波数(长)平面波的迭加。
平面波描写自由粒子,其特点是充满整个空间,这是因为平面波 振幅与位置无关。如果粒子由波组成,那么自由粒子将充满整个空间, 这是没有意义的,与实验事实相矛盾。
电子一个一个的通过小孔,但只要时间足够长,底片上增 加呈现出衍射花纹。这说明电子的波动性并不是许多电子在空间聚 集在一起时才有的现象,单个电子就具有波动性。
事实上,正是由于单个电子具有波动性,才能理解氢原子 (只含一个电子!)中电子运动的稳定性以及能量量子化这样一 些量子现象。
波由粒子组成的看法夸大了粒子性的一面,而抹杀 了粒子的波动性的一面,具有片面性。
(ax) 1 ( x)
作代换:px x,px x0,则
|a|
f ( x) ( x x0 ) f ( x0 ) ( x x0 )
(
px
波函数公式推导

波函数公式推导
波函数是用来描述物理系统中的波动现象的函数,它可以用来描述电磁波、声波、热波等。
波函数的一般形式为:
$$f(x)=A\sin(kx-\omega t+\phi)$$
其中,A为振幅,k为波数,ω为角速度,t为时间,φ为相位。
推导过程:
首先,我们考虑一个物理系统,它的位置可以用x来表示,它的运动可以用一个函数来描述:
$$x=f(t)$$
其中,t为时间。
假设这个物理系统的运动是周期性的,即:
$$f(t+T)=f(t)$$
其中,T为周期。
我们可以将这个函数写成如下形式:
$$f(t)=A\sin(kx-\omega t+\phi)$$
其中,A为振幅,k为波数,ω为角速度,t为时间,φ为相位。
由于这个函数是周期性的,所以我们可以得到:
$$f(t+T)=A\sin(kx-\omega (t+T)+\phi)=A\sin(kx-\omega t+\phi)=f(t)$$
从而得到:
$$\omega T=2\pi$$
即:
$$\omega=\frac{2\pi}{T}$$ 这就是波函数的一般形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4π p h
2
2
2
Ψ
Ψ t
E Ek
h
2 2 2
p
i2 π h
2
EΨ
k
(v c )
2 mE
一维运动自由粒子 的含时薛定谔方程
Ψ
2
8 π m x
i
h Ψ 2 π t
21.6波函数
薛定谔方程
第21章 量子物理
若粒子在势能为 E p 的势场中运动
E Ek Ep
21.6波函数
薛定谔方程
第21章 量子物理
薛定谔方程是量子力学的一个基本假设,它既不 可能从已有的经典规律推导出来,也不可能直接从实 验事实总结出来(因为波函数本身是不可观测的).实际 上是“猜” 加“凑”出来的.方程的正确性只能靠实 践检验.到目前为止,实践检验它是正确的. 下面不是推导,而是作为便于初学者接受的一种引导.
21.6波函数
薛定谔方程
第21章 量子物理
薛定谔,奥地利人,是著名的 理论物理学家,量子力学的重要奠 基人之一。他同时在固体的比热、 统计物理、原子光谱及镭的放射性 等方面的研究都有很大成就。
薛定谔对分子生物学的发展也做过工作。由于他 的影响,不少物理学家参与了生物学的研究工作,使 物理学和生物学相结合,形成了现代分子生物学的最 显著的特点之一。
如果把波函数在空间各点的振幅同时增大一倍, 并不影响粒子在空间各点的几率。所以将波函数乘 上一个常数后,所描写的粒子的状态并不改变。
21.6波函数
薛定谔方程
第21章 量子物理
以一维波函数为例,在下述四种函数曲线中,只 有一种符合标准条件
符合
不符合
不符合
不符合
21.6波函数
薛定谔方程
第21章 量子物理
某一时刻在整个空间内发现粒子的概率为
归一化条件
Ψ
2
dV 1
21.6波函数
薛定谔方程
第21章 量子物理
4)波函数应满足的条件 ①标准条件 粒子在某一个时刻t,在空间某点上粒子出现的几 率应该是唯一的、有限的,所以波函数必须是单值的、 有限的;又因为粒子在空间的几率分布不会发生突变, 所以波函数还必须是连续的。 波函数必须满足“单值、有限、连续”的条件,称 为波函数的标准条件。也就是说,波函数必须连续可 微,且一阶导数也连续可微。 ②归一化条件 由于粒子必定要在空间中的某一点出现,所以任 意时刻,在整个空间发现粒子的总几率应是1。所以 2 应有: | | dV 1
a
a a 粒子在0到a/2区域内出现的概率
21.6波函数
二
薛定谔方程
第21章 量子物理
薛定谔方程(非相对论情形) 自由粒子薛定谔方程的建立
自由粒子平面波函数
Ψ ( x, t ) y 0e
Ψ
2
i
2π ( Et px ) h
上式取 x 的二阶偏导数和 t 的一阶偏导数得
x 自由粒子
2
d y
2 (x) 2
8π m h
2
2
dx
( E E p )y ( x ) 0
21.6波函数
y
2
薛定谔方程
2
第21章 量子物理
在三维势场中运动粒子的定态薛定谔方程
x
2
y y
2
y
2
z
2
8π m h
2
2
( E E p )y 0
2 2
拉普拉斯算子
定态薛定谔方程
21.6波函数
E p 0,
d y
2 2
薛定谔方程
0 xa
2
第21章 量子物理
E p , x 0 , x a y 0, ( x 0, x a )
Ep
2
8π
mE
2
y 0
k y 0
2
dx
k
h
mE
2
8π
d y
2
h
dx
2
o
a
x
y ( x ) A sin kx B cos kx
21.6波函数
一
薛定谔方程
第21章 量子物理
波函数 概率密度 1)经典的波与波函数 机械波
y ( x , t ) A cos 2π ( t x
)
电磁波
E ( x , t ) E 0 cos 2π ( t
H ( x,t) H
0
x
x
)
)
cos 2π ( t
i 2 π ( t x )
a
k 8 π mE h
2 2
E n
2
h
2 2
8 ma
o
a
基态能量 E 1
h
2 2
x
, ( n 1)
h
2 2
8 ma
2 激发态能量 E n n
, ( n 2 ,3 , )
8 ma
一维无限深方势阱中粒子的能量是量子化的 .
21.6波函数
y
2 2
薛定谔方程
y ( x ) A sin kx
2
sin
0
2
x
a
dx 1
0
2
dx
2 a
a/2
0
sin
2
x
a
dx
1 2
(3)概率最大的位置应该满足
2 a
解得
a 2
A
2
1
A
d dx
2
2 a
sin
2 x a
0
(2)粒子的概率密度为
2
2
sin
2
x
即当 2 x k , k 0 , 1 , 2 , 时,粒子出现的概率最大。因 为0<x<a,故得x=a/2,此处粒 子出现的概率最大。
经典波为实函数
y ( x , t ) Re[ A e
]
21.6波函数
薛定谔方程
第21章 量子物理
2)量子力学波函数(复函数)
描述微观粒子运动的波函数
微观粒子的波粒二象性
自由粒子能量 E 和动量 p 是确定的,其德布罗
意频率和波长均不变 , 可认为它是一平面单色波 .
Ψ( x, y, z, t ) h E p h
x,
(0 x a )
21.6波函数
波动方程
薛定谔方程
d y
2
第21章 量子物理
Ep
dx
2
8 π mE h
2
2
y 0
波函数
0, ( x 0, x a )
nπ a x, (0 x a )
y (x)
2 a
o
2 a
2
a
sin
x
概率密度 能量 量子数
y (x)
En n
2 2
E En y y n ( x )
能量本征值 能量本征函数
21.6波函数
薛定谔方程
第21章 量子物理
三 一维势阱问题 粒子势能 E p 满足的边界条件
0 x a
Ep
Ep
意义
0,
E p , x 0, x a
o
a
x
1)是固体物理金属中自由电子的简化模型; 2)数学运算简单,量子力学的基本概念、原理 在其中以简洁的形式表示出来 .
2
2
sin
nπ a
x
h
2 2
8 ma
n 1, 2 , 3 ,
21.6波函数
薛定谔方程
第21章 量子物理
结论: 1)能量量子化: 2 2 2
En n 2ma
2
(n 1,2,3)
2)能量的本征函数
y n ( x)
2 a sin nx a
n x a
3) 概率分布
P y n ( x) n
德布罗意波(概率波)不同于 经典波(如机械波、电磁波)
经 典 波
是振动状态的传播 波强(振幅的平方)代 表通过某点的能流密度
能流密度分布取决于空 间各点的波强的绝对值。
德布罗意波
不代表任何物理量的传播 波强(振幅的平方)代表粒 子在某处出现的概率密度
概率密度分布取决于空间各 点波强的比例,并非取决于 波强的绝对值。 因此,将波函数在空间各 因此,将波函数在空间各 点的振幅同时增大 C倍,则 个处的能流密度增大 C2 倍, 点的振幅同时增大 C倍,不影 响粒子的概率密度分布,即 变为另一种能流密度分布状 和C 所描述德布罗意波的状 态。 态相同。 波动方程无归一化问题。 波函数存在归一化问题。
21.6波函数
x 例:作一维运动的粒子被束缚在0<x<a x A sin 的范围内,已知其波函数为: a 求:(1)常数A;(2)粒子在0到a/2区域内出现的概率;(3)粒子在何处 出现的概率最大?
薛定谔方程
第21章 量子物理
解:(1)由归一化条件
a
a/2
2
dx A
2
2 a
sin
2
21.6波函数
薛定谔方程
nπ a
y
n
第21章 量子物理
2
y ( x ) A sin
x
y (x)
2 a
