第14章 稳恒磁场
14电磁感应2(自感互感、磁场能量)

I
一、自感 1.当一线圈中的电流变化时,它所激发的磁 场通过线圈自身的磁通量也在变化,使线 圈自身产生感应电动势。 这种因线圈中电流变化而在线圈自身所引 起的感应现象叫做自感现象,所产生的电 动势叫做自感电动势。
R
L
S2 S1
S
L
闭合开关, 2比S1先亮 S
断开开关,S闪一下熄灭
电流增大时,dI 0 , L 0 ,即 L与电流反
向,阻碍电流增大;
dI 电流减小时, 0 , L 0 ,即 L与电流同 dt dt
向,阻碍电流减小
I
例1 、 试计算长直螺线管的自感。 已知:匝数N,横截面积S,长度l ,磁导率
μ
l
自感的计算步骤:
S
LH dl I B H B H
单位长度导线内磁能为:
R
P
Wm wm dV
V
R
0
I 2 r 2 I 2 2rdr 2 4 8 R 16
§14-5 位移电流 麦克斯韦方程组
一、电磁场的基本规律 静电场:
D dS q
S
E dl 0
l
(对真空或电介质都成立)
稳恒磁场:
例、如图,求同轴传输线之磁能及自感系数 R2 I I 解: H B dV 2rldr R 1 2r 2r 1 W V wdV V H 2 dV 2 R2 1 I 2 ( ) 2rldr R1 2 2r I 2 l R2 ln( ) 4 R1 I 2 l R2 1 2 LI W ln( ) 4 R1 2 l R2 可得同轴电缆 L ln( ) 的自感系数为 2 R1
毕奥—萨伐尔定律
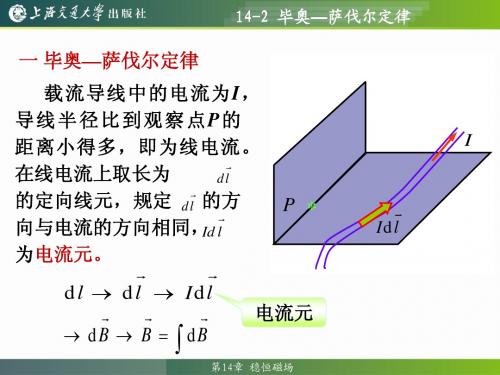
B = ∫ dBx = ∫ dB ⋅ cos θ
θ p yθ r
o x
dx
x
µ 0 Id x =∫ ⋅ cos θ 2π r a y cos θ = 2 2 2 2 r= x +y x +y
第11章 静电场 第14章 稳恒磁场
11-2 库仑定律 14-2 毕奥—萨伐尔定律 14- 11毕奥 萨伐尔定律
11-2 库仑定律 14-2 毕奥—萨伐尔定律 14- 11毕奥 萨伐尔定律
一个圆环之磁矩
r r 2 dm = π r dIen
m = ∫ dm
= ∫ π r ωσ rdr
2 0 R
r R
dr
1 2 = ω qR 4
第11章 静电场 第14章 稳恒磁场
=
=
µ0 I dl sin α
∫ 4π
µ0 I
r Idl
2 2 3 2
r
2
2π R
x
4π r
sin α ∫ 2
0
dl =
µ0 IR
2
第11章 静电场 第14章 稳恒磁场
2( R + z )
11-2 库仑定律 14-2 毕奥—萨伐尔定律 14- 11毕奥 萨伐尔定律
B=
µ0 IR
2
2 2 3 2
2( R + z )
θ2
1
x
C
o
r0
=
(cos θ1 − cos θ 2 )
第11章 静电场 第14章 稳恒磁场
11-2 库仑定律 14-2 毕奥—萨伐尔定律 14- 11毕奥 萨伐尔定律
推论
0
无限长载流长直导线的磁场。 无限长载流长直导线的磁场。
大学物理稳恒磁场解读

2018/9/27
24
r the displacement from
I dl
I
Idl toward P.
dB
the contribution of Idl to the magnetic induction at point P.
r
P
B
the magnetic field of I at point P.
I
S
2018/9/27 5
I
Magnetic field lines surrounding a long and straight wires
2018/9/27
6
I
Magnetic field lines for a tightly wound solenoid of finite length carrying a steady current.
Gauss’ theorem
B dS 0
Ampere’s circulation theorem (Ampere’s Law) L B d l 0 Ii
i
11
2018/9/27
Affect of magnetic field force on currents
right hand rule
26
Superposition Principle of Magnetic Induction
B d B
L
B Bi
u Idl r B d B= 4 r
L
0
L
3
2018/9/27
27
DISCUSSION
《大学物理》稳恒磁场

第四节 安培环路定理
Bdl L
0 (I1 I2 )
(0 I1
I
)
2
I1
I2 I3
I1
L
I1
问(1)B 是否与回路 L 外电流有关?
(2)若
LB d l 0 ,是否回路 L 上各处
B
0
?
是否回路 L 内无电流穿过?
43
第四节 安培环路定理
安培环路定理的应用
例题 无限长载流圆柱体的磁场
33
第三节 磁通量 磁场的高斯定理
例题 如图载流长直导线的电流为 I, 试求通过矩形面积的磁通量.
B
I
l
d1 d2
o
x
解
B 0I
2π x
dΦm
BdS
0I
2πx
ldx
Φm
B dS 0Il
S
2π
d2 dx x d1
Φm
0 Il
2π
ln
d2 d1
34
第三节 磁通量 磁场的高斯定理 磁场的高斯定理
d
I
B1
r1
dl1
B2 dl2
r2
l
B1
0I ,
2 π r1
B2
0 I
2 π r2
B1
dl1
B2
dl2
0 I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
40
第四节 安培环路定理
多电流情况
I1
I2
I3
l
B B1 B2 B3
Bdl
l
0(I2 I3)
推广:
➢ 安培环路定理
第13章
1稳恒磁场

稳恒磁场
电与磁
密切联系
11世纪我国——指南针 电场一样,
运动电荷
电场 磁场
14-1 磁场的描述
一、基本磁现象 天然磁石 同极相斥 异极相吸
SN
S
N
电流的磁效应 1820年 奥斯特
I
SN
通电导线周围有磁场
I
F F I
地磁为生命创造条件,也对生命起保护作 用,生命与地磁是紧紧联系在一起的
最近几个世纪科学家经过观测,发现地磁 场在减弱
十年前,美国科学家测出减弱的速度,
如果按此速度减弱,在公元32 世纪,地 磁为零——颠倒
有关地磁的起源一直是科学家们力图探明 的基本课题
根据安培提出的磁性源于分子电流的假设, 地球核心内部存在一个巨大的环形电流, 但此电流怎样形成的呢?又是什么机制促 使如此巨大的环形电流周期性换向呢?
小磁针静止时与水平面的夹角——磁倾角 地磁赤道上,磁倾角为零,磁南极和磁北 极,磁倾角为90度
磁场强度的水平分量,磁偏角,磁倾角— —地磁三要素
北京,地磁场 B 0.5104T 磁偏角 60
磁倾角 5701'
不同地点三要素不同,根据三要素可画地 磁图
人们发现地磁场的方向在过去的4百万年 中已经循环颠倒9次
通电导线之间有力的作用
电子束
S
+
N
磁场能使电子束偏转
产生 电流(运动电荷)
磁场
力 安培指出:
电荷的运动是一切磁现象的根源。
二 、磁 感 强 度 B 的 定 义
1、 磁感强度 B的方向
SN
该点小磁针静止时, N极指向
2、磁感强度大小 运动电荷在磁场中受力
F
稳恒磁场知识点复习

解: RA mAvA 1 2 1 : 2 TA mA 1mB
(2)
例2: 如图所示,在均匀磁场中,半径为R的薄圆盘以角速
度绕中心轴转动,圆盘电荷面密度为。求它的磁矩、
所受的磁力矩以及磁矩的势能。
解:取半径为r的环状面元,圆盘转动时, 它相当于一个载流圆环,其电流:
计,电流I均匀分布,与铜片共面到近边距离为b 的一点 P的磁感应强度 B 的大小为________。
解:
dB 0dI 0 Idr 2r 2ar
dI I dr a
Ia dr
bB
rP
B dB 0I ab dr 0I ln a b
2a b r 2a b
(6)
例5: 如图, 一扇形薄片, 半径为R, 张角
5. 均匀磁场中载流线圈受到的力矩: 6. 均匀磁场中载流线圈的磁矩势能:
M
pm
B
Wm pm B
7. 带电粒子在磁场中的运动
回转半径: R mv qB
回转周期: T 2m
qB
例1: A、B为两个电量相同的带电粒子,它们的质量之比 mA:mB=1/4,都垂直于磁场方向射入一均匀磁场而作圆 周运动。A粒子的速率是B粒子速率的两倍。设RA,RB 分别为A粒子与B粒子的轨道半径;TA、TB分别为它们 各自的周期。则RA∶RB=? TA∶TB=?
F dF 0I1I2 dl 2d
例3:一弯曲的载流导线在同一平面内,形状如图(O点
是半径为R1和R2的两个半圆弧的共同圆心,电流自无穷 远来到无穷远去),则O点磁感应强度
的大小是______________。
解: B 0I 0I 0I 4R1 4R2 4R2
I
R1
O
R2
稳恒磁场

磁场 磁感应强度 基本磁现象1、通有电流的导线周围,小磁针会发生偏转。
2、磁铁附近的载流导线及载流线圈会受到力的作用。
3、载流导线之间或载流线圈之间有相互作用力。
4、电子射线束在磁场中路径发生偏转。
一切磁现象的根源是电流。
任何物质的分子中都存在有圆形电流,称为分子电流.分子电流相当于一个基元磁铁。
当物体不显示磁性时,各分子电流作无规则的排列, 它们对外界所产生的磁效应互相抵消。
在外磁场的作用下,与分子电流相当的基元磁铁将趋向于沿外磁场方向取向,从而使整个物体对外显示磁性。
磁感应强度磁现象中,电流与电流之间,电流与磁铁之间以及磁铁与磁铁之间的相互作用是通过一种叫磁场的特殊物质来传递的。
磁场对外的重要表现:1、磁场对进入场中的运动电荷或载流导体有磁力的作用;2、载流导体在磁场中移动时,磁场的作用力将对载流导体作功,表明磁场具有能量。
引入磁感应强度矢量B 来描述磁场的强弱和方向。
试验线圈(线度必须小,其引入不影响原有磁场的性质)的面积为 S ∆,线圈中电流为0I ,则定义试验线圈的磁矩为 n S I P m ∆0= 磁矩是矢量,其方向与线圈的法线方向一致,n 表示沿法线方向的单位矢量,法线与电流流向成右螺旋系。
(附图)线圈受到磁场作用的力矩(称为磁力矩)使试验线圈转到一定的位置而稳定平衡。
此时,线圈所受的磁力矩为零,此时线圈正法线所指的方向,定义为线圈所在处的磁场方向。
如果转动试验线圈,只要线圈稍偏离平衡位置,线圈所受磁力矩就不为零。
当试验线圈从平衡位置转过090时,线圈所受磁力矩为最大。
在磁场中给定点处,比值m P M max 仅与试验线圈所在位置有关,即只与试验线圈所在处的磁场性质有关。
规定磁感应强度矢量B 大小为m P M B max =磁场中某点处磁感应强度的方向与该点处试验线圈在稳定平衡位置时的法线方向相同;磁感应强度的量值等于具有单位磁矩的试验线圈所受到的最大磁力矩。
单位:磁感应强度的国际单位为特斯拉,简称特。
稳恒磁场的定义和作用机理

dF21
方向向下
k
I1I2dl1dl2 r221
律,实际中,不存在孤立的稳恒电 流元。沿回路积分,回路作用力总 与反作用力大小相等,方向相反。
电流强度单位:安培的定义的绝对测量
dFr12kI1I2dlr2r1(22dlr1rrˆ12)
r I 1 d l1
k 0 4
0 4107
r r1 2
r d F 21
r L 1对 I2dl2 的 作 用 力 :
Ñ dF r24 0 L1I1I2dlr2r1(2 2dlr1rrˆ12)
Ñ r
L 1对 I2dl2 的 作 用 力 :
dF r24 0 L1I1I2dlr2r1(2 2dlr1rrˆ12)
Ñ dF r240I2dlr2L 1I1dlrr 1 1 2 2 r rˆ12I2dlrB r
• 十一世纪:北宋:沈括《梦溪笔谈》明确 记载指南针:“方家以磁石磨针锋,则能 指南,然常微偏东,不会南也。”
• 十二世纪:以指南针航海 • 十三世纪:西方在北宋200年后才有类似记
载
• 近代:铁磁物质充磁(励磁),冰箱封条 • 磁铁两端引铁屑,中部不引 • 两端:磁极,中部:中性区
两端吸引,中部不吸
十九世纪 :重要发现:认识到两开者不可分
奥斯特实验
无电流:沿南北取向 有电流:偏转 电流方向不同,偏转方向也不同 磁铁对电流有作用力?
磁铁对电流也有作用力!
电流对磁铁有作用力
电流与电流间是否有作用力?
有作用力!
同向相吸, 异向相斥
螺线管:
通电螺线管类似磁铁 右手定则:弯曲四指 沿电流环绕方向,拇 指指向为N极。
毕奥-萨伐尔定律
Ñ r
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x dB
I
0 Idl cos Bp dB// dB cos 2 4 r
R cos r R (R2 x )
1 2 2
由于圆电流对称性,整个圆电流在P点的场沿Ox方向
0 Bp 4
IR (R2 x )
3 2 2
dl
L
电流产生的磁感应线既没有起始点,也没有终止点,即 磁场线既没有头,也没有尾。磁场是无源场。
静电场 29
例 如图载流长直导线的电流为I,试求通过矩形面积的磁通量.
B
I
解:先求dФm,然后积分求Фm
l
d1 d2
0 I B 2π x
dΦm BdS
Φm B dS
S
B // S
y
Idl
I
a
r
dB
dB
解:取 Idl ( Idl r )
dB
x
dB ( Idl , r )
dB
P
0 Idl 4 r 2
z
当 Idl 的位置发生变化时 ,它所激发的磁场 dB 矢 量构成了一个圆锥面。
Idl
y
dB
a
x z
静电场
16
IdlR r源自O xP dB
P
B
了电现象和磁现象的本质。 一切磁现象起源于电荷运动
1822年:法国的安培提出了分子电流假说。
稳恒磁场 2
通电导线受马蹄形磁铁 作用而运动
螺线管与磁铁相互作 用时显示出N极和S极
稳恒磁场
3
相关实验
稳恒磁场
4
地磁场与指南针
地磁场线
指南针成就了航海, 航海催生了地磁图, 地磁图吸引了Gauss… Gauss创立了磁学基础
任一载流导线均可看作由无数电流元首尾相接而成
B dB
稳恒磁场
?
10
二 毕-萨定律
dB
7
0 Idl sin
4π
2
P
r
2
0 4 10 N A ——真空中的磁导率
方向:dB Idl r
4π
Id l
r
1
dB
(右手螺旋法则)
r 4π r
0 Idl r 0 Idl r 0 矢量形式: dB 3 2
0 I
2π x
2π
ldx
dx x
0 Il
o
d2
d1
x
Φm
静电场
0 Il
2π
ln
d2 d1
30
§9.4 安培环路定理 内容回顾:
L E dl 0 稳恒磁场: B dl 0? L
静电场:
例:无限长载流直导线的磁场 则 若取闭合磁力线为积分回路L, 对回路中任一线元:
稳恒磁场 5
太阳风与地磁场
稳恒磁场
6
自然界中的磁现象
——极光( polar light ,学名aurora,取自罗马的曙光女神)
加拿大育空地区的极光现象
稳恒磁场
美国阿拉斯加地区极光现象
7
结论: 磁场不是凭空想象出来的,是确确实实存在的一种 物质。 磁现象广泛存在于自然界中。
二、磁场的基本性质
(3)
x R
2
B
0 IR 2
2( R 2 x 2 )3/ 2
0 IR 0 IS B 3 2x 2x 3
定义
pm
n
S I
静电场 19
B
pm ISn 磁矩 0 pm
2 x 3
四、运动电荷的磁场
0 Idl r0 dB 4 r 2
P
电荷密度
4a
稳恒磁场
2
P
r
a
I
1
13
0 I
(3) 无限长载流平板 解
Idx dI b
dB
2by sec
y
P
dB
0dI
2r
0 Idx
d Bx
dB
O
r
BP Bx dBx dB cos
2
2
b 2 0
dx 2by sec 2
0 I
x
b I dx
静电场是保守场 是否保守场?
I
L
B
B dl 0
L B dl 0
(不恒为零)
稳恒磁场
31
一、安培环路定理的内容
在稳恒电流的磁场中,磁感应强度沿任何闭合环路L的 线积分,等于穿过这环路的所有电流强度代数和的μ0倍。 数学表达式:
Ii 内 L B dl o i
I
B ——回路上的总磁感应强度 L ——在场中任取的一闭合线 电流为正 dl ——L绕行方向上的任一线元 0 ——真空中的磁导率 0 4 107 N A2
0 (nsqv )dl r0 dB 4 r2
n sdl q dQ nsqv I dt dt
Idl
r
S
Idl
电流元内总电荷数 dN nsdl
dB
0 dN qv r0
4 r2
q +
dB 0 qv r0 一个电荷产生的磁场 B dN 4 r 2
Fmax B qv
方向:该点处小磁针N极的指向 单位:特斯拉(T)
磁感应强度描述场的性质,是空间位置的单值函数。
稳恒磁场 9
§9.2 毕奥—萨伐尔定律 一 磁场的叠加原理
1. 当空间同时存在多个电流时,它们共同激发的磁场 是各个电流单独存在时激发磁场的叠加。
B Bi
i
2. 电流元 Idl —— 磁场中的理想化模型, 在场中只占据一个点的位置。 大小:Idl 方向:沿载流方向
0 I (cos 1 cos 2 ) 4a
稳恒磁场 12
0 I (cos 1 cos 2 ) 讨论 B 4a
(1) 无限长直导线
B
I
2
B
P
1 0 2
1
0 I
2a
方向:右螺旋法则
(2) 任意形状直导线 B1 0
0 I B2 (cos 900 cos1800 ) 4a
静电场
25
I S I
S
N
N
S
B
N B S
磁场中某点处垂直 B矢量的单 位面积上通过的磁感线数目等 于该点B 的数值。
静电场 26
2.磁场线性质 (1) 磁场线不会相交; (2) 无头无尾的闭合曲线,且每条闭合的磁 场线都与闭合的载流回路互相套合; 3.磁通量Фm 通过某一曲面的磁场线条数,即为通过该曲面的磁通量。
1、磁场是一种物质,具有质量、动量、能量。 2、磁场的产生源: 运动电荷(电流) 3、磁场的存在使场中电流受到磁场力的作用,这种 作用通过磁场来实现。
稳恒磁场
8
三. 磁感应强度
运动电荷在磁场中的受力特点: (1) 电荷在磁场中的运动方向不同,
受力也不同;
(2) 总存在一个方向,当电荷沿该 方向运动时,受到的磁场力最大; 定义 磁感应强度的大小
4
a
3
0 b 同理 B4 In 线段4:
4
2
a
B B1 B2 B3 B4
1 1 b (1 In ) 0 2 a
静电场 24
§9.3 磁通量 磁高斯定理 一 磁场线 磁通量
1. 磁场线 规定:曲线上每一点的切线方向就是该点的磁感强度的方向, 曲线的疏密程度表示该点的磁感强度的大小. I I I
源电流分布的空间
4
0 Idl sin
r
2
I
由叠加原理:B dB 统一变量:
0 Idl sin
r
2
Idl
a
r
P
dB
l a cot a cot
r a csc
1
dl a csc 2 d
B 4a θ 1
0 I
θ2
sin d
m 0 m 0
静电场
Φe E dS
s
28
二
磁场中的高斯定理
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
S
B
B2
dS1
1 B1
S
B cos dS 0
2
dS2
S
B d S 0
——磁场高斯定理
物理意义:通过任意闭合曲面的磁通量必等于零
1 r 2 dr 2
1 3 3 ( a l ) a 6
静电场
23
例5 如图的导线,已知电荷线密度为 ,当绕 O 点以 转动时 求: O 点的磁感应强度
解: 线段1: B1
同理
1 b 0 2b 2 4
0
1
b O
1 B2 0 线段2: 4 0 b B In 线段3: 3 4 a
2 3 dPm dI S rdr r r dr
O
dr
Pm dPm
R
0
1 r dr R 4 4
3
静电场
22
例4 求:O点磁感应强度和磁矩。 解: 在r处取长为dr的线元
dr r
dq dr
经旋转形成小圆电流dI
O
分析: B p
b arctan (ii) y b 2y 2 I 0 I 1 BP 0 0 j 2b 2b 2
