角的和差倍分1
人教版七年级数学课件《角的和、差、倍、分》
达标检测
人教版数学七年级上册
3.如图所示，∠AOB=∠ COD=90°， ∠AOD=146°， ∠BOC=_3_4__°__.
4.如果∠AOB＝34°，∠BOC＝18°，那么∠AOC的度数是( C )
A.52°
B.16°
C.52°或16° D.52°或18°
1.如图①，若∠AOC=35°，∠BOC＝40°，则 ∠AOB＝ 75 °．
2.如图②，若∠AOB= 60°，∠BOC＝40°，则∠AOC＝ 20 °． 3.若∠AOB ＝60°，∠AOC ＝30°，则∠BOC＝ 90或30 °．
B C
A C
A C
O
A
O
BO
B
图①
图②
C
知识精讲
人教版数学七年级上册
5. 已知∠AOB=38°，∠BOC=25°，那么∠AOC 的度数是13°或63° .
达标检测
人教版数学七年级上册
6.图中∠1=∠2, 试判断∠BAD和∠EAC的大小, 并说明理由.
解： ∠BAD=∠EAC
理由：∵∠1=∠2 ∴∠1＋∠DAC ＝∠２＋∠DAC，
E D
∴∠BAD＝∠EAC.Fra bibliotek1C
2
B
知识精讲
人教版数学七年级上册
如图所示： (1) ∠AOC是哪两个角的和？
∠AOC =∠AOB +∠BOC.
(2) ∠AOB是哪两个角的差？
∠AOB =∠AOC －∠BOC =∠AOD－∠BOD.
(3) 如果∠AOB=∠COD，则∠AOC与∠BOD 的大小关系如何？
O
∠AOC =∠BOD.
D C
重庆中考复习重庆中考几何题分类汇编含答案
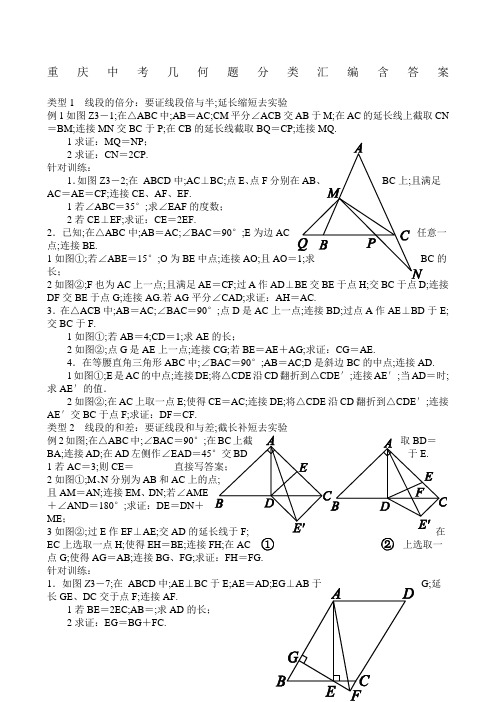
重庆中考几何题分类汇编含答案类型1线段的倍分：要证线段倍与半;延长缩短去实验例1如图Z3－1;在△ABC中;AB＝AC;CM平分∠ACB交AB于M;在AC的延长线上截取CN ＝BM;连接MN交BC于P;在CB的延长线截取BQ＝CP;连接MQ.1求证：MQ＝NP；2求证：CN＝2CP.针对训练：1．如图Z3－2;在ABCD中;AC⊥BC;点E、点FAC＝AE＝CF;连接CE、AF、EF.1若∠ABC＝35°;求∠EAF的度数；2若CE⊥EF;求证：CE＝2EF.2．已知;在△ABC中;AB＝AC;∠BAC＝90°;E为边AC点;连接BE.1如图①;若∠ABE＝15°;O为BE中点;连接AO;且AO的长；2如图②;F也为AC上一点;且满足AE＝CF;过A作AD⊥连接DF交BE于点G;连接AG.若AG平分∠CAD;求证：AH＝AC.3．在△ACB中;AB＝AC;∠BAC＝90°;点D是AC上一点;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点G是AE上一点;连接CG;若BE＝AE＋AG;求证：CG＝AE.4．在等腰直角三角形ABC中;∠BAC＝90°;AB＝AC;D是斜边BC的中点;连接AD.1如图①;E是AC的中点;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′;当AD＝时;求AE′的值．2如图②;在AC上取一点E;使得CE＝AC;连接DE;将△CDE沿CD翻折到△CDE′;连接AE′交BC于点F;求证：DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2如图;在△ABC中;∠BAC＝90°;BA;连接AD;在AD左侧作∠EAD＝451若AC＝3;则CE＝________2如图①;M、N分别为AB和AC且AM＝AN;连接EM、DN;若∠AME＋∠AND＝180°;求证：DE＝DN＋ME；3如图②;过E作EF⊥AE;交ADEC上选取一点H;使得EH＝BE;连接FH;在AC上选取一点G;使得AG＝AB;连接BG、FG;求证：FH＝FG.针对训练：1．如图Z3－7;在ABCD中;AE⊥BC于E;AE＝G;延长GE、DC交于点F;连接AF.1若BE＝2EC;AB＝;求AD的长；2求证：EG＝BG＋FC.2．如图;在正方形ABCD中;点P为AD延长线上一点;连接AC、CP;过点C作CF⊥CP 于点C;交AB于点F;过点B作BM⊥CF于点N;交AC于点M.1若AP＝AC;BC＝4;求S△ACP；2若CP－BM＝2FN;求证：BC＝MC.3．如图;在△ABC中;AB＝BC;以AB为一边向形ABDE;连接DC;EB并延长EB交AC于F;且AE 于G.1若∠EBG＝20°;求∠AFE；2试问线段AE;AF;CF之间的数量关系并证明．类型3倍长中线：三角形中有中线;延长中线等中线例3如图Z3－10①;在Rt△ABC中;∠ABC＝90°;D为斜边AC上两点;且AD＝AB;CE＝CB;连接BD、1求∠EBD的度数；2如图Z3－10②;过点D作FD⊥BD于点D;交BEF;在AB上选取一点H;使得BH＝BC;连接CH;在一点G;使得GD＝CD;连接FH、FG;求证：FH＝FG.针对训练：1．如图;已知在ABCD中;G为BC的中点;点E在AD边上;且∠1＝∠2.1求证：E是AD中点；2若F为CD延长线上一点;连接BF;且满足∠3＝∠2;求证：CD＝BF＋DF.2．如图Z3－12;在菱形ABCD中;点E、F分别是BC、CD上的点;连接AE;AF;DE、EF;∠DAE＝∠BAF.1求证：CE＝CF；2若∠ABC＝120°;点G是线段AF的中点;连接DG;EG.求证：DG⊥GE.3．在Rt△ABC中;∠ACB＝90°;点D与点B在;∠ADC＞∠BAC;且DA＝DC;过点B作BE∥DA交于点E;M为AB的中点;连接MD;ME.1如图①;当∠ADC＝90°时;线段MD与ME________；2如图②;当∠ADC＝60°时;试探究线段MD数量关系;并证明你的结论；3如图③;当∠ADC＝α时;求的值．4．如图①;等边三角形ABC中;CE平分∠ACB;D为BC边上一点;且DE＝CD;连接BE.1若CE＝4;BC＝6;求线段BE的长；2如图②;取BE中点P;连接AP;PD;AD;求证：AP⊥PD且AP＝PD；3如图③;把图Z3－14②中的△CDE绕点C顺时针旋转任意角度;然后连接BE;点P为BE中点;连接AP;PD;AD;问第2问中的结论还成立吗若成立;请证明；若不成立;请说明理由．5．在△ABC中;以AB为斜边;作直角三角形ABD;使点D落在△ABC内;∠ADB＝90°.1如图①;若AB＝AC;∠BAD＝30°;AD＝6;点P、M分别为BC、AB边的中点;连接PM;求线段PM的长；2如图②;若AB＝AC;把△ABD绕点A逆时针旋转一定角度;得到△ACE;连接ED并延长交BC于点P;求证：BP＝CP；3如图③;若AD＝BD;过点D的直线交AC于点E;交BC于点F;EF⊥AC;且AE＝EC;请直接写出线段BF、FC、AD之间的关系不需要证明．类型4中位线：三角形中两中点;连接则成中位线例42017·河南如图①;在Rt△ABC中;∠A＝90°;AB＝AC;点D;E分别在边AB;AC上;AD＝AE;连接DC;点M;P;N分别为DE;DC;BC的中点．1观察猜想：图①中;线段PM与PN的数量关系是__________;位置关系是__________；2探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置;连接MN;BD;CE;判断△PMN 的形状;并说明理由；3拓展延伸：把△ADE绕点A＝10;请直接写出△PMN面积的最大值．针对训练：1．如图①;在任意的三角形ABC以AB和AC为一边作等腰三角形ABE和等腰三角形ACD;AB＝AE;AC＝AD;且∠BAE＋∠CAD＝180°;连接DE;延长CA交DE于F.1求证：∠CAB＝∠AED＋∠ADE；2若∠ACB＝∠BAE＝∠CAD＝90°;如图②;求证：BC＝2AF；3若在△ABC中;如图③所示;作等腰三角形ABE和等腰三角形ACD;AB与DE交于点F;F为DE的中点;请问2中的结论还成立吗若成立;请给出证明;若不成立;请说明理由．2．如图;在△ABC和△ADE中;AB＝AC;AD＝AE;∠BAC＋∠EAD＝180°;△ABC不动;△ADE绕点A旋转;连接BE、CD;F为BE的中点;连接AF.1如图①;当∠BAE＝90°时;求证：CD＝2AF；2当∠BAE≠90°时;1的结论是否成立请结合图②说明理由．3．如图①;在等腰三角形ABC中;AB＝AC;在底边BC上取一点D;在边AC上取一点E;使AE＝AD;连接DE;在∠ABD的内部作∠ABF＝2∠EDC;交AD于点F.1求证：△ABF是等腰三角形；2如图②;BF的延长交AC于点G.若∠DAC＝∠CBG;延长AC至点M;使GM＝AB;连接BM;点N是BG的中点;连接AN;试判断线段AN、BM之间的数量关系;并证明你的结论．类型5角的和差倍分图中有角平分线;关系现．角平分线平行线;;三线合一试试看．例5．如图;把△EFP放置在菱形ABCD中;顶点E;F;P分别在线段AB;AD;AC上;EP＝FP＝6;EF＝6;∠BAD＝60°;且＞6.1求∠EPF的大小；2若AP＝10;求AE＋AF的值．针对训练：1．已知：如图①;AD平分∠BAC;∠B＋∠C＝180°°;易知：DB＝DC.探究：如图②;AD平分∠BAC;∠ABD＋∠ACD;∠ABD＜90°;求证：DB＝DC.2．在△ACB中;AB＝AC;∠BAC＝90°;点D;连接BD;过点A作AE⊥BD于E;交BC于F.1如图①;若AB＝4;CD＝1;求AE的长；2如图②;点P是AC上一点;连接FP;若AP＝CD;求证：∠ADB＝∠CPF.3．已知;在ABCD中;∠BAD＝45°;AB＝BD;E为BC上一点;连接AE交BD于F;过点D 作DG⊥AE于G;延长DG交BC于H.1如图①;若点E与点C重合;且AF＝;求AD的长；2如图②;连接FH;求证：∠AFB＝∠HFB.4．如图;将正方形纸片ABCD沿EF折叠点E、F分别在边AB、CD上;使点B落在AD边上的点M处;点C落在点N处;MN与CD交于点P;连接EP.当点M在边AD上移动时;连接BM、BP.1求证：BM是∠AMP的平分线；2△PDM的周长是否发生变化证明你的结论．类型6旋转型全等问题：图中若有边相等;可用旋转做例6．△ABC中;∠BAC＝90°;AB＝AC;点D为直线点点D不与B;C重合;以AD为边在AD右侧作正方形ADEF;连接CF.1观察猜想：如图①;当点D在线段BC上时;①BC与CF关系为：________．②BC;CD;CF之间的数量关系为：___________；将结写在横线上2数学思考：如图Z3－25②;当点D在线段CB的延长线上时;结论①;②是否仍然成立若成立;请给予证明；若不成立;请你写出正确结论再给予证明．3拓展延伸：如图Z3－25③;当点D在线段BC的延长线上时;延长BA交CF于点G;连接GE.若已知AB＝2;CD＝BC;请求出GE的长．针对训练：1．在四边形ABCD中;∠B＋∠180°;对角线AC平分∠BAD.1如图①;若∠DAB＝120°;且∠B＝90°;试探究边AD、AB与对角线AC2如图②;若将1中的条件“∠B＝去掉;1中的结论是否成立请说明理由．3如图③;若∠DAB＝90°;探究边AD、AB与对角线AC的数量关系并说明理由．2．如图①;在正方形ABCD中;点E为边BC上一点;将△ABE沿AE翻折得△AHE;延长EH交边CD于F;连接AF.1求证：∠EAF＝45°；2延长AB;AD;如图②;射线AE、AF分别交正方形两个外角的平分线于M、N;连接MN;若以BM、DN、MN为三边围成三角形;试猜想三角形的形状;并证明你的结论．3．如图①;在正方形ABCD内有一点P;PA＝;PB＝;PC＝1;求∠BPC的度数．分析问题根据已知条件比较分散的特点;我们可以通过旋转变换将分散的已知条件集中在一起;于是将△BPC绕点B逆时针旋转90°;得到了△BP′A如图Z3－28②;然后连接PP′.1请你通过计算求出图Z3－28②中∠BPC的度数；2如图③;若在正六边形ABCDEF内有一点P;且PA＝2;PB＝4;PC＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1.证明：1∵AB＝AC;∴∠ABC＝∠ACB.∵∠MBQ＋∠ABC＝180°;∠ACB＋∠PCN＝180°;∴∠MBQ＝∠PCN.在△QBM和△PCN中;∴△QBM≌△PCNSAS．∴MQ＝NP.2过M作MG∥AC交BC于G;∵MG∥AC;∴∠MGB＝∠ACB;∠MGC＝∠PCN;∵由1知;∠ABC＝∠ACB;∴∠ABC＝∠MGB;∴MB＝MG;∵MB＝CN;∴MG＝CN.在△MGP和△NCP中;∴△MGP≌△NCPAAS．∴PG＝CP;∴CG＝CP＋PG;即CG＝2CP.∵CM平分∠ACB;∴∠BCM＝∠MCA;∵MG∥AC;∴∠MCA＝∠GMC;∴∠BCM＝∠GMC;∴MG＝CG;∵MG＝CN;∴CN＝CG;∴CN＝2CP.针对训练1.解：1∵AC⊥BC;∴∠ACB＝90°;又∵AC＝CF;∴∠45°;∵∠ABC＝35°;∴∠EAF＝10°；2证明：方法1：取CF的中点M;连接EM、AM;∵CE⊥EF;∴EM＝CM＝FM＝CF;又∵AC＝AE;∴AM为EC的中垂线;∴∠CAM＋°; 又∵∠ECF＋∠ACE＝90°;∴∠CAM＝∠FCE;又∵∠CEF＝∠ACM＝90°;∴△ACM∽△CEF;∴＝;又∵CF＝AC＝2CM;∴＝＝;即CE＝2EF；方法2：延长FE至M;使EF＝EM;连接CM;∵CE⊥EF;∴△CMF为等腰三角形;又∵AC＝AE＝CF;且∠ACE＝∠CFE易证;∴△CMF≌△CEA;∴FM＝CE＝2EF.2.解：1如图①;在AB上取一点M;使得BM＝ME;连在Rt△ABE中;∵OB＝OE;∴BE＝2OA＝2;∵MB＝ME;∴∠MBE＝∠MEB＝15°;∴∠AME＝∠MBE＋∠MEB＝30°;设AE＝x;则ME＝BM＝2x;AM＝x;∵AB2＋AE2＝BE2;∴2x＋x2＋x2＝22;∴x＝负根舍弃;∴AB＝AC＝2＋·;∴BC＝AB＝＋1.2证明：如图②;作CP⊥AC;交AD的延长线于P;GM⊥AC 于M.∵BE⊥AP;∴∠AHB＝90°;∴∠ABH＋∠BAH＝90°;∵∠BAH＋∠PAC＝90°;∴∠ABE＝∠PAC;又∵AB＝AC;∠BAE＝∠ACP＝90°;∴△ABE≌△CAP;∴AE＝CP＝CF;∠AEB＝∠P;在△DCF和△DCP中;∴△DCF≌△DCP;∴∠DFC＝∠P;∴∠GFE＝∠GEF;∴GE＝GF;∵GM⊥EF;∴FM＝ME;∵AE＝CF;∴AF＝CE;∴AM＝CM;在△GAH和△GAM中;∴△AGH≌△AGM;∴AH＝AM＝CM＝AC.3.解：1∵AB＝4;∴AC＝AB＝4.∵CD＝1;∴AD＝AC－CD＝3.∵在Rt△ABD中;∠BAC＝90°;∴BD＝＝5;∵S＝AB·AD＝AE·BD;∴AE＝2.4.△ABD2证明：如图;在线段EB上截取EH＝AE;并连接∵AE⊥BD;EH＝AE;∴AH＝AE.∵BE＝AE＋AG;∴BH＝BE－HE＝AG.∵∠BAD＝∠BEA＝90°;∴∠ABE＋∠BAE＝∠CAG＋∠BAE＝90°;∴∠ABE＝∠CAG.∵BA＝AC;∴△ABH≌△CAG;∴CG＝AH＝AE.4.解：1∵∠BAC＝90°;AB＝AC;D是斜边BC的中点;∴∠ADC＝90°;∠ACD＝45°.在Rt△ADC中;AC＝AD÷sin45°＝2.∵E是AC的中点;∴CE＝AC＝.∵将△CDE沿CD翻折到△CDE′;∴CE′＝CE＝;∠ACE由勾股定理;得AE′＝＝.2证明：如图;过B作AE′的垂线交AD于点G;交AC于点∵∠ABH＋∠BAF＝90°;∠CAF＋∠BAF＝90°;∴∠ABH＝∠CAF.又∵AB＝AC;∠BAH＝∠ACE′＝90°;∴△ABH≌△CAE′.∴AH＝CE′＝CE;∵CE＝AC;∴AH＝HE＝CE.∵D是BC中点;∴DE∥BH;∴G是AD中点．在△ABG和△CAF中：AB＝AC;∠BAD＝∠ACD＝45°;∠ABH＝∠CAF; ∴△ABG≌△CAF.∴AG＝CF.∵AG＝AD;∴CF＝AD＝CD.∴DF＝CF.类型2线段的和差：要证线段和与差;截长补短去实验例2：解：132证明：延长DN到K;使得NK＝ME;连接AK;如图①;因为∠1＋∠3＝180°;∠1＋∠2＝180°;∴∠2＝∠3.在△AME和△ANK中;∴△AME≌△ANK SAS．∴AE＝AK;∠4＝∠5;∴∠4＋∠EAC＝90°;∴∠5＋∠EAC＝90°;即∠EAK＝∵∠EAD＝45°;∴∠KAD＝∠EAK－∠EAD＝90°－45∴∠EAD＝∠KAD.在△EAD和△KAD中;∴△EAD≌△KAD SAS;∴ED＝KD.∵DK＝DN＋KN;∴ED＝DN＋KN;又NK＝ME;∴ED＝DN＋ME.3证明：延长AE到J;使得EJ＝AE;连接JH;JF.如图②;在△ABE和△JHE中;∴△ABE≌△JHESAS;∴JH＝AB;∠1＝∠2;∵AB＝AG;∴JH＝AG;∵AE＝EJ;EF⊥AJ;∴AF＝JF;∴∠JAF＝∠AJF＝45°;即∠2＋∠3＝45°;∵∠BAC＝90°;∴∠1＋∠EAD＋∠4＝90°;∴∠1＋∠4＝90°－∠EAD;＝90°－45°＝45°;∵∠1＝∠2;∴∠3＝∠4;在△JHF和△AGF中;∴△JHF≌△AGFSAS;∴FH＝FG.针对训练：1.解：1∵四边形ABCD是平行四边形;∴AD＝BC.∵BE＝2EC;设CE＝x;BE＝2x;∴BC＝AD＝AE＝3x.又∵EG⊥AB;∴∠AEB＝90°;∴AB2＝AE2＋BE2;即13＝9x2＋4x2;∴x＝1;∴AD＝3x＝3.2证明：如图;过C作CH⊥AB于H;则四边形CHGF为矩形．∴CF＝HG;∠CHB＝90°;GF＝CH.∵AE⊥BC;EG⊥AB;∴∠AEB＝∠CHB＝90°;∠BCH＋∠B＝90°;∠BAE＋∠B＝90°;∴∠BCH＝∠BAE.又∵AE＝BC;∴△AGE≌△CHB;∴GE＝BH;AG＝GF;∴GE＝BH＝BG＋GH＝BG＋CF.2.解：1∵四边形ABCD是正方形;BC＝4;∴AB＝AD＝CD＝BC＝4;∠ADC＝∠ABC＝90°.∵在Rt△ABC中;AC＝＝4;∴AP＝AC＝;∴S＝AP·CD＝7.△ACP2证明：方法一：如图①;在NC上截取NK＝NF;连接BK.∵四边形ABCD是正方形;∴AB＝BC＝DC;∠ABC＝∠BCD＝∠ADC＝90°.∵∠BCD＝90°;CF⊥CP;∴∠1＋∠DCF＝∠2＋∠DCF＝90°;∴∠1＝∠2;∵在△FBC和△PDC中;∴△FBC≌△PDCASA;∴CF＝CP;∵CP－2FN＝BM;∴CF－FK＝BM;即CK＝BM;∵∠FBC＝90°;BM⊥CF;∴∠1＋∠NBC＝∠4＋∠NBC; ∴∠1＝∠4;∵在△ABM和△BCK中;∴△ABM≌△BCKSAS;∴∠7＝∠6.∵BM⊥CF;NK＝NF;∴BF＝BK;∵BF＝BK;BM⊥CF;∴∠4＝∠∴∠4＋∠7＝∠5＋∠6;∵∠8＝∠4＋∠7;∴∠8＝∠MBC;∴BC＝MC.解：方法二：如图②;延长BM交AD于点G;过A作AE⊥BGE先证△AEB≌△BNCAAS;∴AE＝BN;又证△AEG≌△BNFAAS;∴EG＝NF;再证四边形BCPG为平行四边形;∴BG＝CP;∵CP－BM＝2FN;∴BG－BM＝2EG;∴MG＝2EG;∴点E为MG中点;∵AE⊥MG;EM＝EG;∴AM＝AG;∴∠3＝∠4;∵∠2＝∠3;∠1＝∠4;∴∠1＝∠2;∴BC＝MC.3.解：1∵∠EBG＝20°;CB⊥AE;∴∠BEG＝70o;∠CBF＝∠EBG＝20°;∵四边形ABDE是菱形;∴∠ABE＝∠BEG＝70°;∴∠ABG＝50°;∵AB＝BC;∴∠FCB＝25°;∴∠AFE＝∠CBF＋∠FCB＝45°；2AE;AF;CF之间的数量关系是AF2＋CF2＝2AE2;证明如下：连接DF;∵四边形ABDE是菱形;∴AB＝DB;∠DBE＝∠ABE;∴∠DBF＝∠ABF;∵BF＝BF;∴△DBF≌△ABFSAS;∴DF＝AF;∠BDF＝∠BAF;∵∠BCF＝∠BAF;∴∠BCF＝∠BDF; ∵CB⊥AE;AE∥DB;∴DB⊥CB;∵CB＝AB＝BD;∴△DBC是等腰直角三角形;∴DC＝BD＝AE;∵∠DPB＝∠CPF;∴∠CFP＝∠DBP＝90°;∴DF2＋CF2＝DC2; 即有：AF2＋CF2＝2AE2.类型3倍长中线：三角形中有中线;延长中线等中线例3解：1设∠BEC＝α;∠BDA＝β;则∠C＝180°－2α;∠A＝180°－2β.∵在Rt△ABC中;∠ABC＝90°;∴∠A＋∠C＝90°;即180°－2α＋180°－2β＝90°;∴α＋β＝135°;∴∠EBD＝45°.2证明：法一：如图①;延长BD至点B′;使得DB′＝在△GDB′和△CDB中;∴△GDB′≌△CDB.∴GB′＝BC＝BH;∠GB′D∵FD⊥BD;BD＝DB′;∴FB＝FB′.∵∠FB′G＝45°－∠GB′D;∠HBF＝90°－45°－∠CBD＝45°－∠CBD;∴∠FB′G＝∠HBF.在△FHB和△FGB′中;∴△FHB≌△FGB′;∴HF＝GF.法二：如图②;延长FD至点F′;使得DF′＝DF;先证△DGF≌△DCF′;再证△BHF≌△BCF′;∴HF＝GF.针对训练1.证明：1∵四边形ABCD是平行四边形;∴AB＝CD;AD＝BC;∠A＝∠C.又∵∠1＝∠2;∴△ABE≌△CDG ASA;∴AE＝CG.∵G为BC中点;∴CG＝BC;∴AE＝CG＝BC＝AD;∴E是AD中点．2如图;延长BE;CD交于点H.∵四边形ABCD是平行四边形;∴AB綊CD;∴∠A＝∠ADH;∠1＝∠4;又∵∠1＝∠2;∠3＝∠2;∴∠1＝∠2＝∠3＝∠4;∴FH＝FB.由1;E是AD中点;∴AE＝DE;∴△ABE≌△DHEAAS;∴AB＝DH;∴CD＝AB＝DH＝DF＋FH＝DF＋BF;即CD＝BF＋DF.2.证明：1在菱形ABCD中;AB＝BC＝CD＝AD;∠ADF＝∠ABE; ∵∠DAE＝∠BAF;∴∠DAE－∠EAF＝∠BAF－∠EAF;即∠DAF＝∠BAE.∴△DAF≌△BAE;∴BE＝DF.又∵BC＝CD;∴CE＝CF2如图;延长DG交AB于H;连接EH;∵在菱形ABCD中;AB∥CD;∴∠DFA＝∠GAH.∵G为AF中点;∴AG＝GF.又∵∠DGF＝∠AGH;∴△DGF≌△HGA.∴DG＝又∵AB＝CD;∴BH＝CF.又∵AB∥CD;∠ABC＝120°;∴∠C＝60°.又∵CE＝CF;∴△CEF为等边三角形;∴CF＝EF;∠CFE＝60°;∴EF＝BH;∠DFE＝∠ABC＝120°.又∵BE＝DF;∴△EFD≌△HBE;∴HE＝ED;又∵HG＝DG;∴DG⊥GE.3.解：1MD=ME2MD＝ME.理由如下：如图①;延长EM交DA于点F.∵BE∥DA;∴∠FAM＝∠EBM.又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.∵DA＝DC;∠ADC＝60°;∴∠BED＝∠ADC＝60°;∠ACD＝60°.∵∠ACB＝90°;∴∠ECB＝30°;∴∠EBC＝30°;∴CE＝BE;∴AF＝EC;∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∴∠MDE＝30°.在Rt△MDE中;tan∠MDE＝＝.∴MD＝ME.3如图②;延长EM交DA于点F;∵BE∥DA;∴∠FAM＝∠EBM;又∵AM＝BM;∠AMF＝∠BME;∴△AMF≌△BME;∴AF＝BE;MF＝ME.延长BE交AC于点N;∴∠BNC＝∠DAC.∵DA＝DC;∴∠DCA＝∠DAC;∴∠BNC＝∠DCA;∵∠ACB＝90°;∴∠ECB＝∠EBC;∴CE＝BE;∴AF＝CE.∴DF＝DE;∴DM⊥EF;DM平分∠ADC;∵∠ADC＝α;∴∠MDE＝.∴在Rt△MDE中;＝tan∠MDE＝tan.4.解：1如图①;作EH⊥BC于点H.∵△ABC是等边三角形;∴∠ACB＝60°.∵CE平分∠ACB;∴∠ECH＝∠ACB＝30°;∵EC＝4;∠ECH＝30°;∴EH＝2;HC＝2.∵BC＝6;∴BH＝6－2＝4.在Rt△BHE中;BE2＝42＋22＝52;∴BE＝2.2如图②;延长DP至M;使DP＝PM;连接BM、AM.在△PDE和△PMB中;∴△PDE≌△PMB SAS．∴BM＝DE;∠1＝∠2.∴BM∥DE.∴∠MBD＋∠BDE＝180°.∵CE平分∠ACB;DE＝CD;∴∠BDE＝30°＋30°＝60∴∠MBD＝120°.∵△ABC是等边三角形;∴∠ABC＝60°;∴∠3＝60°.∵BM＝DE;DE＝CD;∴BM＝CD.在△ABM和△ACD中;∴△ABM≌△ACD SAS．∴AD＝AM;∠4＝∠5.∵PD＝PM;∴AP⊥PD.∵∠4＝∠5;∠BAD＋∠5＝60°;∴∠4＋∠BAD＝60°;即∠MAD＝60°.∴∠PAD＝∠MAD＝30°.∵在Rt△APD中;tan30°＝;∴AP＝PD.3第2问中的结论成立;理由如下：如图③;延长DP至使DP＝PN;连接BN、AN;取BE、AC交于点O.在△PDE∴△PDE≌△PNBSAS．∴BN＝DE;∠1＝∠2.∵DE＝CD;∴BN＝CD.∵∠AOB＝∠EOC;∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO＝60°;∠DEC＝∠DCE＝30°;∴∠1＋∠3∴∠3＝∠4.在△ABN和△ACD中;∴△ABN≌△ACDSAS．∴∠5＝∠6;AN＝AD.∵PD＝PN;∴AP⊥PD.∵∠NAC＋∠5＝60°;∴∠NAC＋∠6＝60°;即∠NAD＝60°.∴∠PAD＝∠NAD＝30°; ∵在Rt△APD中;tan∠PAD＝;∴AP＝PD.5.解：1∵∠ADB＝90°;∠BAD＝30°;AD＝6;∴cos∠BAD＝;∴＝;∴AB＝12.又∵AB＝AC;∴AC＝12;∴PM为△ABC的中位线;∴PM＝AC＝6.2证明：方法一：如图①;在截取ED上截取EQ＝PD;∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4.在△BDP和△CEQ中;PD＝QE;∠1＝∠4;BD＝CE;∴△BDP≌△CEQ.∴BP＝CQ;∠DBP＝∠QCE;又∵∠5＝∠1＋∠DBP;∠6＝∠4＋∠QCE;∴∠5＝∠6;∴PC＝CQ;∴BP＝CP.方法二：如图②;过点B作EP的垂线交EP的延长线于点M;过C EP的垂线交EP于点N.∵∠ADB＝90°;∴∠1＋∠2＝90°;又∵AD＝AE;∴∠2＝∠3;又∵∠3＋∠4＝90°;∴∠1＝∠4;在△BMD和△CNE中;∠1＝∠4;∠BMD＝∠CNE＝90°;BD＝CE;∴△BMD≌△CNE.∴BM＝CN.在△BMP和△CNP中;∠5＝∠6;∠BMP＝∠CNP;BM＝CN;∴△BMP≌△CNP;∴BP＝CP.方法三：如图③;过点B作BM∥CE交EP略证△BMP≌△CEP;∴BP＝CP.3BF2＋FC2＝2AD2.类型4中位线：三角形中两中点;连接则成中位线例4:解：1PM=PN;PM⊥PN2△PMN为等腰直角三角形;理由如下：由题意知△ABC和△ADE均为等腰直角三角形;∴AB＝AC;AD＝AE;∠BAC＝∠DAE＝90°;∴∠BAD＋∠DAC＝∠CAE＋∠DAC;∴∠BAD＝∠CAE;∴△BAD≌△CAE;∴∠ABD＝∠ACE;BD＝CE.又∵M、P、N分别是DE、CD、BC的中点;∴PM是△CDE的中位线;∴PM∥CE且PM＝CE;∠MPD＝∠ECD＝∠ACD＋∠ACE.同理;PN∥BD且PN＝BD;∠DBC＝∠PNC;又∵BD＝CE;∠ABD＝∠ACE;∴PM＝PN;∴∠MPN＝∠MPD＋∠DPN＝∠ECD＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°;∴PM⊥PN;∴△PMN为等腰直角三角形；3△PMN面积的最大值为.提示：在旋转的过程中;由2中的结论知△PMN为等腰直角三角形;S＝PN2＝BD2;当S△PMN有最大值时;则BD的值最大;由三角形三边关系可推断出当B、A、D三△PMN点共线时;BD的值最大;其最大值为14;此时S△PMN＝PN2＝BD2＝×14×14＝.针对训练：1.解：1证明：延长DA交BE于G点．∵∠BAE＋∠CAD＝180°;即∠EAG＋∠GAB＋∠CAD＝180°;∵∠GAB＋∠BAC＋∠CAD＝180°;∴∠EAG＝∠CAB.∵∠EAG＝∠AED＋∠ADE;∴∠CAB＝∠AED＋∠ADE.2证明：如图①;过E点作DA延长线的垂线;垂足为H.∴∠AHE＝∠ACB＝90°;由1可知;∠EAH＝∠BAC;又∵AE＝AB;∴△AHE≌△ACB;∴EH＝BC;AH＝AC.∵AC＝AD;∴AH＝AD.∵∠EHA＝∠FAD＝90°;∴AF∥EH.∵A为DH中点;∴AF为△DHE中位线;∴EH＝2AF;∴BC＝2AF.3成立．证明如下：如图②;延长DA至M点;使AM＝DA;连接EM;∵∠BAE＋∠CAD＝180°;∠CAD＋∠CAM＝180°;∴∠BAE＝∠CAM;∴∠BAE＋∠CAC＝∠CAM＋∠EAC;即∠BAC＝∠CAM.∵AM＝AD;AD＝AC;∴AM＝AC.又∵AB＝AE;∠BAC＝∠EAM;∴△BAC≌△EAM;∴BC＝EM.∵F、A分别为DE、DM中点;∴AF为△DEM中位线;∴EM＝2AF;∴BC＝2AF.2.解：1证明：∵∠BAC＋∠EAD＝180°;∠BAE＝90°;∴∠DAC＝90°;在△ABE与△ACD中;AE＝AD;∠BAE＝∠CAD＝90°;AB＝AC;∴△ABE≌△ACDSAS;∴CD＝BE;∵在Rt△ABE中;F为BE的中点;∴BE＝2AF;∴CD＝2AF.2成立;证明：如图;延长EA交BC于G;在AG上截取AH＝∵∠BAC＋∠EAD＝180°;∴∠EAB＋∠DAC＝180°;∵∠EAB＋∠BAH＝180°;∴∠DAC＝∠BAH;在△ABH与△ACD中;AH＝AD;∠BAH＝∠CAD;AB＝AC;∴△ABH≌△ACDSAS;∴BH＝DC;∵AD＝AE;AH＝AD;∴AE＝AH;∵EF＝FB;∴BH＝2AF;∴CD＝2AF.3.解：1证明：∵AB＝AC;∴∠ABD＝∠ACD;∵AE＝AD;∴∠ADE＝∠AED;∵∠BAD＋∠ABD＝∠ADE＋∠EDC;∠EDC＋∠ACD∴∠BAD＝2∠EDC;∵∠ABF＝2∠EDC;∴∠BAD＝∠ABF;∴△ABF是等腰三角形；2方法一：如图①;延长CA至点H;使AG＝AH;连接BH;∵点N是BG的中点;∴AN＝BH;∵∠BAD＝∠ABF;∠DAC＝∠CBG;∴∠CAB＝∠CBA;∴△ABC是等边三角形．∴AB＝BC＝AC;∠BAC＝∠BCA＝∵GM＝AB;AB＝AC;∴CM＝AG;∴AH＝CM;在△BAH和△BCM中;∴△BAH≌△BCMSAS;∴BH＝BM;∴AN＝BM;方法二：如图②;延长AN至K;使NK＝AN;连接KB;同方法一;先证△ABC是等边三角形;再证△ANG≌△KNB SAS;所以BK＝AG＝CM;然后可以证得∠ABK＝∠BCN＝120°;最后证△ABK≌△BCN SAS;所以BM＝AK＝2AN.类型5角的和差倍分例5：解：1如图;过点P作PG⊥EF于G.∵PE＝PF＝6;EF＝6;∴FG＝EG＝3;∠FPG＝∠EPG＝∠EPF.在Rt△FPG中;sin∠FPG＝＝＝.∴∠FPG＝60°;∴∠EPF＝2∠FPG＝120°.2如图;作PM⊥AB于M;PN⊥AD于N.∵AC为菱形ABCD的对角线;∴∠DAC＝∠BAC;AM＝AN;PM＝PN.在Rt△PME和Rt△PNF中;PM＝PN;PE＝∴Rt△PME≌Rt△PNF;∴NF＝ME.又∵AP＝10;∠PAM＝∠DAB＝30°;∴AM＝AN＝AP cos30°＝10×＝5.∴AE＋AF＝AM＋ME＋AN－NF＝AM＋AN针对训练：1.证明：如图;过D作DE⊥AB于E;过D作DF⊥AC于F;∵DA平分∠BAC;DE⊥AB;DF⊥AC;∴DE＝DF;∵∠B＋∠ACD＝180°;∠ACD＋∠FCD＝180°∴∠B＝∠FCD;在△DFC和△DEB中;∴△DFC≌△DEB;∴DC＝DB.2.解：1∵AC＝AB＝4;且CD＝1;∴AD＝AC－CD＝3.在Rt△ABD中;∠BAD＝90°;∴BD＝＝5;＝AB·AD＝AE·BD;∵S△ABD∴AE＝2.4.2证明：如图;取BC的中点M;连接AM交BD于点N.∵∠BAC＝90°;AB＝AC;点M为BC的中点;∴AM＝BM＝CM;AM⊥BC;∠NAD＝∠FCP＝45°;∴∠AMF＝∠BMN＝90°.∵AE⊥BD;∴∠MAF＋∠ANE＝∠MBN＋∠BNM＝90°;又∠ANE＝∠BNM;∴∠MAF＝∠MBN;∴△AMF≌△BMN;∴MF＝MN;∴AM－MN＝CM－MF;即AN＝CF.∵AP＝CD;∴AC－CD＝AC－AP;即AD＝CP.∴△ADN≌△CPF;∴∠ADB＝∠CPF.3.解：1∵AB＝BD;∠BAD＝45°;∴∠BDA＝45°;即∠ABD＝90°.∵四边形ABCD是平行四边形;∴当E、C重合时;BF＝BD＝AB.∵在Rt△ABF中;AB2＋BF2＝AF2;∴2BF2＋BF2＝2;∴BF＝1;AB＝2.在Rt△ABD中;AD＝＝＝2.2证明：如图;在AF上截取AK＝HD;连接BK.∵∠AFD＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°; ∴∠2＝∠3.在△ABK与△DBH中;∴△ABK≌△DBH;∴BK＝BH;∠6＝∠5.∵四边形ABCD是平行四边形;∴AD∥BC;∴∠5＝∠4＝45°;∴∠6＝∠5＝45°;∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK与△BFH中;∴△BFK≌△BFH.∴∠BFK＝∠BFH;即∠AFB＝∠HFB.4.解：1证明：由折叠知∠EMN＝∠ABC＝90°∴∠EMB＝∠EBM;∴∠EMN－∠EMB＝∠ABC－∠EBM;即∠BMP＝∠MBC.∵在正方形ABCD中;AD∥BC;∴∠AMB＝∠MBC;∴∠AMB＝∠BMP;∴BM是∠AMP的平分线．2△PDM的周长没有发生变化．证明如下：如图;过B作BQ∵∠A＝90°;且由1知BM是∠AMP的平分线;∴BA＝BQ;∵∠A＝∠MQB＝90°;∠AMB＝∠BMP;MB＝MB;∴△AMB≌△QMB AAS．∴MA＝MQ.∵BA＝BC;∴BQ＝BC;又∵∠BQP＝90°＝∠C;BP＝BP;∴Rt△BPC≌Rt△BPQ HL．∴PC＝PQ;∴△PDM的周长＝MD＋MP＋DP＝MD＋MQ＋QP＋PD＝MD＋MA＋PC＋PD＝AD＋DC＝2AD.∴△PDM的周长没有发生变化．类型6旋转型全等问题：图中若有边相等;可用旋转做实验例6：解：1①∵四边形ADEF是正方形;∴AD＝AF;AB＝AC;∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠B＝∠ACF;∴∠ACB＋∠ACF＝90°;即CF⊥BC；②∵△DAB≌△FAC;∴CF＝BD;∵BC＝BD＋CD;∴BC＝CF＋CD.2结论①成立;结论②不成立．∵四边形ADEF是正方形;∴AD＝AF;AB＝AC.∵∠BAC＝∠DAF＝90°;∴∠BAD＝∠CAF;∴△DAB≌△FAC;∴∠ABD＝∠ACF;CF＝BD;∴∠BCF＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°;即CF⊥BC；∵BC＝CD－BD;∴BC＝CD－CF.3如图;过A作AH⊥BC于H;过E作EM⊥BD于M;EN∵∠BAC＝90°;AB＝AC;∴BC＝AB＝4;AH＝CH＝BC∴CD＝BC＝1;∴DH＝3;同2证得△BAD≌△CAF;∴∠ABD＝∠ACF＝45°;∴∠BCF＝∠ACB＋∠ACF＝∴BC⊥CF;CF＝BD＝5.∵四边形ADEF是正方形;∴AD＝DE;∠ADE＝90°;∵BC⊥CF;EM⊥BD;EN⊥CF;∴四边形CMEN是矩形;∴NE＝CM;EM＝CN;∵∠AHD＝∠ADE＝∠EMD＝90°;∴∠ADH＋∠EDM＝∠EDM＋∠DEM＝90°;∴∠ADH＝∠DEM;∴△ADH≌△DEM;∴EM＝DH＝3;DM＝AH＝2;∴CN＝EM＝3;EN＝CM＝3;∵∠ABC＝45°;∴∠BGC＝45°;∴△BCG是等腰直角三角形;∴CG＝BC＝4;∴GN＝1;∴EG＝＝.针对训练：1.解：1AC＝AD＋AB.证明如下：∵∠B＋∠D＝180°;∠B＝90°;∴∠D＝90°.∵∠DAB＝120°;AC平分∠DAB;∴∠DAC＝∠BAC＝60°;∵∠B＝90°;∴AB＝AC;同理AD＝AC.∴AC＝AD＋AB.21中的结论成立;理由如下：如图①;以C为顶点;AC为一边作∠ACE＝60°;∠ACE的另一边交AB的延长线于点E;∵∠BAC＝60°;∴△AEC为等边三角形;∴AC＝AE＝CE;∠E＝60°;∵∠ABC＋∠D＝180°;∠DAB＝120°;∴∠DCB＝60°;∴∠DCA＝∠ECB.在△DAC和△BEC中;∴△DAC≌△BEC;∴AD＝BE;∴AC＝AE＝AD＋AB.3AD＋AB＝AC.理由如下：如图②;过点C作CE⊥AC交AB的延长于点E;∵∠ABC＋∠D＝180°;∠DAB＝90°;∴∠DCB＝90°;∵∠ACE＝90°;∴∠DCA＝∠BCE;又∵AC平分∠DAB;∴∠CAB＝45°;∴∠E＝45°;∴AC＝CE.∴△CDA≌△CBE;∴AD＝BE;∴AD＋AB＝AE.∵在Rt△ACE中;∠CAB＝45°;∴AE＝＝AC;∴AD＋AB＝AC.2.解：1证明：∵四边形ABCD是正方形;∴∠B＝∠D＝∠BAD＝90°;AB＝AD;∵△ABE沿AE翻折得到△AHE;∴△ABE≌△AHE;∴AH＝AB＝AD;BE＝EH;∠AHE＝∠AHF＝∠B＝∠D＝90°.在Rt△AHF和Rt△ADF中;∴Rt△AHF≌Rt△ADFHL;∴∠HAF＝∠DAF;∴∠EAF＝∠EAH＋∠FAH＝∠BAH＋∠HAD＝∠BAD＝45°;2以BM;DN;MN为三边围成的三角形为直角三角形．证明如下：如图;过点A作AH⊥AN并截取AH＝AN;连接BH、HM;∵∠1＋∠BAN＝90°;∠3＋∠BAN＝90°;∴∠1＝∠3;在△ABH和△ADN中;∴△ABH≌△ADN SAS;∴BH＝DN;∠HBA＝∠NDA＝135°;∵∠HAN＝90°;∠MAN＝45°;∴∠1＋∠2＝∠HAM＝∠MAN＝45°;在△AHM和△ANM中;∴△AHM≌△ANM SAS;∴HM＝NM;∴∠HBP＝180°－∠HBA＝180°－135°＝45°;∴∠HBP＋∠PBM＝45°＋45°＝90°;∴△HBM是直角三角形;∵HB＝DN;HM＝MN;∴以BM;DN;MN为三边围成的三角形为直角三角形．3.解：1如图①;将△PBC绕点B逆时针旋转90°得△P△AP′B≌△CPB;∴P′B＝PB＝;P′A＝PC＝1;∠1＝∠2;∠AP′B＝∠BPC.∵四边形ABCD是正方形;∴AB＝BC;∠ABC＝90°;∴∠2＋∠3＝90°;∴∠1＋∠3＝90°;即∠P′BP＝90°;∴∠BP′P＝45°.在Rt△P′BP中;由勾股定理;得PP′2＝ 4. ∵P′A＝1;AP＝∴P′A2＝1;AP2＝5;∴P′A2＋PP′2＝AP2;∴△P′AP是直角三角形;∴∠AP′P＝90°;∴∠AP′B＝45°＋90°＝135°;∴∠BPC＝135°.2仿照分析中的思路;将△BPC绕点B逆时针旋转120°;得到了△BP′A;连接PP′;如图②.则△PBC≌△P′BA;∴P′B＝PB＝4;P′A＝PC＝2;∠BPC＝∠BP′A;∴△BPP′为等腰三角形;∵∠ABC＝120°;∴∠PBP′＝120°;∴∠BP′P＝30°;过点B作BG⊥PP′于G;则∠P′GB＝90°;∴PP′＝2P′G.∵P′B＝PB＝4;∠BP′P＝30°;∴BG＝2;∴P′G＝2.∴PP′＝4;在△APP′中;∵PA＝2;P′A＝2;PP′＝4;∴P′A2＋P′P2＝PA2;∴△PP′A是直角三角形;∴∠AP′P＝90°;∴∠BPC＝∠BP′A＝∠PP′B＋∠AP′P＝30°＋90°＝120°.。
线段与角的和差倍分计算
线段与角的和差倍分计算
在几何学中，我们经常遇到线段与角之间的和、差和倍分计算问题。
这些计算方法是为了帮助我们更好地理解图形的性质和关系。
本文将详细
介绍线段与角之间的和、差和倍分计算方法。
一、线段的和、差计算
1.线段的和计算：给定线段AB和线段BC，我们需要计算出两个线段
的和，即线段AB+BC。
计算方法是将线段AB和BC的长度相加，即AB+BC。
2.线段的差计算：给定线段AB和线段BC，我们需要计算出两个线段
的差，即线段AB-BC。
计算方法是将线段AB的长度减去线段BC的长度，
即AB-BC。
二、角的和、差计算
1.角的和计算：给定角α和角β，我们需要计算出两个角的和，即
角α+角β。
计算方法是将两个角的度数相加，即α+β。
2.角的差计算：给定角α和角β，我们需要计算出两个角的差，即
角α-角β。
计算方法是将角α的度数减去角β的度数，即α-β。
三、线段与角的倍分计算
1.线段的倍分计算：给定线段AB，我们需要计算出线段AB的一半或
一四分之一的长度。
计算方法是将线段AB的长度除以2或4，即AB/2或AB/4
2.角的倍分计算：给定角α，我们需要计算出角α的一半或一四分
之一的度数。
计算方法是将角α的度数除以2或4，即α/2或α/4
以上是线段与角的和、差和倍分计算的基本方法。
在实际应用中，我们还可以利用一些几何定理和性质来简化计算，例如角的补角、互补角和对应角等关系。
人教版七年级数学下册8.3.1《和差倍分问题》教学设计
人教版七年级数学下册8.3.1《和差倍分问题》教学设计一. 教材分析《和差倍分问题》是人教版七年级数学下册第八章第三节的第一课时，主要内容是引导学生掌握和差、倍数关系的解法，培养学生解决实际问题的能力。
本节课的内容在学生的知识体系中占有重要地位，为其后续学习方程、比例等知识打下基础。
二. 学情分析学生在之前的学习中已经掌握了整数的加减乘除运算，对数学问题有一定的分析能力。
但他们在解决实际问题时，还存在着对和差、倍数关系的理解不够深入，解题方法不够灵活等问题。
因此，在教学过程中，需要关注学生的学习需求，引导他们通过实例感受和差、倍数关系，培养他们的解决问题的能力。
三. 教学目标1.理解并掌握和差、倍数关系的解法。
2.能够运用和差、倍数关系解决实际问题。
3.培养学生的数学思维能力和解决问题的能力。
四. 教学重难点1.重点：和差、倍数关系的解法。
2.难点：运用和差、倍数关系解决实际问题。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过实例引导学生感受和差、倍数关系，培养学生解决实际问题的能力。
六. 教学准备1.准备相关案例和实际问题。
2.准备课件和教学道具。
七. 教学过程1.导入（5分钟）通过一个实际问题引入本节课的主题：“小明有5个苹果，小华比小明多2个苹果，小丽比小华少3个苹果，请问小丽有几个苹果？”引导学生思考和差、倍数关系。
2.呈现（10分钟）呈现一系列和差、倍数关系的例子，让学生观察、分析并总结解题方法。
如：（1）甲有10个苹果，乙比甲多5个苹果，丙比乙少3个苹果，请问丙有几个苹果？（2）一家有3个孩子，老大比老二大3岁，老二比老三大2岁，请问老三大几岁？3.操练（10分钟）让学生分成小组，运用和差、倍数关系解决实际问题。
如：某班有40名学生，其中男生比女生多20%，请问男生和女生各有多少名？4.巩固（10分钟）通过一些练习题，巩固学生对和差、倍数关系的理解和掌握。
如：（1）甲有20个苹果，乙比甲多1/5，丙比乙少1/4，请问丙有几个苹果？（2）一家有5个孩子，老大比老二大2岁，老二比老三大1岁，请问老五大几岁？5.拓展（10分钟）引导学生思考和差、倍数关系在实际生活中的应用，如购物、分配等。
角的单位及和差倍分
角的单位及和差倍分（总第71课时）执笔人：鲁贤聪教学目标1.了解角的单位的意义，并能进行角的单位之间换算2.经历角的单位的换算过程，理解角的单位互化的程序（分段进行）3.通过角的单位的互化和角的四则运算，提高计算能力，培养学生一丝不苟的学习精神。
教学重难点重点：角的度量单位及角的单位之间的换算，角的四则运算难点：角的减法、除法运算教学过程1.角的度量单位——度、角、分角的度量单位是“度、分、秒”。
把1个周角360等分，每一等分是1度的角，1度记作1°；把1°的角60等分，每一等分就是1分的角，1分记作1′；把1′的角60等分，每一等分就是1秒的角，1秒记作1″。
即1°=60′， 1′=60″1′=︒⎪⎭⎫ ⎝⎛601 '⎪⎭⎫ ⎝⎛="6011 注：要类比时间单位记忆2.角的单位的互换例1 （1）用度、分、秒表示°解：因为°=60′×=′ （度 退位 分）′=60″×=36″ （分 退位 秒）所以°=30°15′36″（2）42°18′15″等于多少度'=⨯'⎪⎭⎫⎝⎛="25.01560115 （秒进位 分）︒≈⨯︒⎪⎭⎫ ⎝⎛='304.025.1860125.18 （分进位 度） 所以42°18′15″≈42°＋°≈°注：（1）是将高级单位化为低级单位，乘以60（退位×60）（2）是将低级单位化为高级单位，除以60（进位÷60）P145练习13.角的四则运算例2计算（1）25°23′17″＋46°53′43″解：25°23′17″＋46°53′43″=71°76′60″=72°17′（2）19°20′24″×4解：19°20′24″×4=76°80′96″=77°21′36″（3）75°23′12″－46°53′43″解：75°23′12″－46°53′43″=74°83′12″－46°53′43″=74°82′72″－46°53′43″=28°29′29″分析：被减数的分不够减，向度借1算60分；被减数的秒不够减，向分借1算60秒.（4）把一个周角17等分，每份是多少（精确到1′）解：360°÷17=21°＋3°÷17=21°＋180′÷17≈21°11′.思考：若精确到1″，答案约为多少（21°10′35″）练习2第3小题角的运算总结：1.加法、乘法：加法、乘法按度、分、秒分别计算，再由低级单位向高级单位进位（逢60进1）2.减法：先看要不要退位，够不够减，如要退位应先退位，再相减（退1算60）3.除法：由高级单位向低级单位逐级计算，余数要退位（退1算60）再相除作业习题第3题（1）（2）（3）（4）。
初中数学《角》单元教学设计以及思维导图
3.初步会用运动、变化的观点看待几何图形。 情感态度与价值观： 培养学生勇于探索创新的精神;增强学生的自主性和合作精神;增强学 生学习的兴趣。
对应课标（说明：学科课程标准对本单元学习的要求）
1. 通过丰富的实例，进一步认识角的概念 2. 会比较角的大小，认识角的和、差、倍、分，理解角平分线的 概念。 3. 认识度、分、秒，会进行角的和、差的简单计算。了解直角、 锐角、钝角、余角的概念，知道同角或等角的余角、补角相等。 4. 了解对顶角概念，知道对顶角相等 5. 了解垂线、垂线段的概念，知道过一点能画并且只能画一条直 线与已知直线垂直，会用三角尺或量角器过一点画一条已知直线的垂 线，了解垂线段最短的性质和点到直线距离的意义。
所需教学环境和教学资源(说明：在此列出本专题所需要的教学环境 和学习过程中所需的信息化资源、常规资源等和各种支持资源)
教学环境：配有电子白板的教室 信息化资源：电脑、实物投影仪、网络及相关应用软件 常规资源：三角尺、圆规、量角器
学习活动设计
第一课时 活动一：创设情境 合作探究 1.观察有关角的图片，让学生总结角的特点。
主题单元问 题设计
1.角是怎样形成的？如何度量与比较角的大小呢？ 2.角按照大小怎样进行分类？ 3.对顶角与什么有关系呢，是大小还是位置？
专题划分
专题一：角的比较与度量
（ 4 课时）
专题二：角的和、差、倍、分 （ 1 课时）
专题三：对顶角
（ 1 课时）
其中，或专题 一 中的活动 第二课时作为研究性学 习）
3. 怎 样用 叠合 法比 较角 的大 小？ 什么 是角 的平 分源自线？专题问题设 计
4.角的度量单位是什么？度、分、秒之间是怎样转化 的？ 5.直角、锐角、钝角是怎样定义的？当两个角满足怎
角的比较大小 角的比较
角的比较大小角的比较教学建议一、知识结构二、重点、难点分析本节教学的重点是角的大小比较，角平分线的意义，两个角的和、差、倍、分的意义．难点是空间观念，几何识图能力的培养．角的比较的相关知识是进一步学习角的度量和画法，以及进一步研究平面几何图形的基础.1﹒角的大小的比较有两种方法：（1）重合法：即把要比较的两个角的顶点和一条边重合，再比较另一条边的位置；（2）度量法；即比较两个角的度数．两种方法的比较结果是一致的．2．利用比较角大小的上述两种方法，就可以画出角的和、差、倍、分，并进而比较角的和、差、倍、分的大小．3．对于角平分线的概念，要注意以下两点：（1）它是角的内部的一条射线，并且是一条特殊的射线，它把角分成了相等的两部分．（2）要掌握角平分线的数学表达式：若OC 是的平分线，则或4．在比较角的大小时，应注意角的大小只与开口的大小有关，而与角的边画出部分的长短无关．这是因为角的边是射线而非线段．若用射线旋转成角的定义，也可以说转得较多的角较大．三、教法建议1．本节教材，完全可以对照线段的比较，线段的和差倍分，以及中点的意义来进行．两者是十分相似的．2．比较两个角的大小时，把角叠合起来，一定要使两个角的顶点及一边重合，另一边落在第一条边的同旁，否则不能进行比较．这可以通过叠合两块三角尺比较角的大小的实例来说明．这和线段大小比较十分相似．3．由于前面学过线段的大小比较和线段的和、差、倍、分．本课教学的指导思想就是运用类比联想的思维方法，引导学生利用旧知识，解决新问题．4．在本课的练习中，在可能的情况下，将以后经常遇到的图形，提前让学生见到，为以后的学习奠定了基础．5．在角的和、差、倍、分的计算中，由于度、分、秒的四则运算还没有讲到，因此只进行度的加、减．教学设计示例一、素质教育目标（一）知识教学点1．理解两个角的和、差、倍、分的意义．2．掌握角平分线的概念3．会比较角的大小，会用量角器画一个角等于已知角．（二）能力训练点1．通过让学生亲自动手演示比较角的大小，画一个角等于已知角等，培养训练学生的动手操作能力．2．通过角的和、差、倍、分的意义，角平分线的意义，进一步训练学生几何语言的表达能力及几何识图能力，培养其空间观念．（三）德育渗透点通过具体实物演示，对角的大小进行比较这一由感性认识上升到理性认识的过程，培养学生严谨的科学态度，对学生进行辩证唯物主义思想教育．（四）美育渗透点通过对角的大小比较，提高学生的鉴赏力，通过学生自己作角及角平分线，使学生进一步体会几何图形的形象直观美．二、学法引导1．教师教法：直观演示、尝试、指导相结合．2．学生学法：主动参与、积极思维、动手实践相结合．三、重点·难点·疑点及解决办法（一）重点角的大小比较，角平分线的意义，两个角的和、差、倍、分的意义．（二）难点空间观念，几何识图能力的培养．（三）疑点角的和、差、倍、分的意义．（四）解决办法通过学生主动参与，在自觉与不自觉中掌握知识点，再经过练习，解决难点和疑点．四、课时安排1课时五、教具学具准备投影仪或电脑、一副三角板、自制胶片（软盘）、量角器．六、师生互动活动设计七、教学步骤（一）明确目标通过教学，使学生在角的比较中掌握方法，理解相应概念，并掌握角平分线的概念．（二）整体感知通过现代化教学手段与学生的画图相结合，完成本节教学任务．（三）教学过程创设情境，引出课题师：请同学们拿出你的一副三角板，你能说出这几个角的大小吗？学生基本知道一副三角板各角的度数，他们可能利用度数比较，也可能通过观察，也会有同学用叠合法．这里可以让学生讨论，说出采用的比较方法，但叙述可能不规范．教师既不给予肯定也不否定，只是再提出新问题．投影显示：两个度数相差1度以内的角，不标明度数，只凭眼观察不能确定两个角的大小．师：对于这两个角你能说出它们哪一个大？哪一个小吗？（学生困惑时教师点出课题．）这节课我们就学习角的比较．同学们提出的比较一副三角板各角的方法有些很好，但不规范．希望同学们认真学习本节内容，掌握角的比较等知识，为以后的学习打好基础．（板书课题）［板书］ 1.5 角的比较【教法说明】由学生熟知的三角板各角的比较入手，把学生带入比较角的大小的意境．但问题一转，出现了不标度数，观察又不能确定大小的角，当学生束手无策时，教师提出这就是我们要学习的新内容，调动学生的积极性，吸引其注意力．探究新知1．角的比较（1）叠合法教师通过活动投影演示：两个角设计成不同颜色，三种情况：，，，如图1所示．图1演示：移动，使其顶点与的顶点重合，一边和重合，出现以下三种情况，如图2所示．图2师：请同学们观察的另一边的位置情况，你能确定出两个角的大小关系吗？学生活动：观察教师演示后，同桌也可以利用两副三角板演示以上过程，帮助理解比较两角的大小，回答教师提出的问题．教师根据学生回答整理板书．［板书］① 与重合，等于，记作．② 落在的内部，小于，记作．③ 落在的外部，大于，记作．【教法说明】通过直观的实物演示和投影（电脑）显示，既加强了角的比较的直观性，又可提高学生的兴趣．注意再次强调角的大小只与开口大小有关，与边的长短无关，以及角的符号与小于号、大于号书写时的区别．（2）测量法师：小学我们学过用量角器测量一个角，角的大小也可以按其度数比较．度数大的角则大，度数小的则小．反之，角大度数大，角小度数小．学生活动：请同桌分别画两个角，然后交换用量角器测量其度数，比较它们的大小．【教法说明】测量前教师可提问使用量角器应注意的问题．即三点：对中；重合；读数．让学生动手操作，培养他们动手能力．反馈练习：课本第32页习题1.3A组第3题，用量角器测量、、的大小，同桌交换结果看是否准确．2．角的和、差、倍、分投影显示：如图1，、．图1提出问题：如图1，，把移到上，使它们的顶点重合，一边重合，会有几种情况？请同学们在练习本上画出．你如何把移到上，才能保证的大小不变呢？学生活动：讨论如何移到上，移动后有几种情况，在练习本上画出图形．（有小学测量的基础，学生不会感到困难，可放手让学生自己动手操作．）教师根据学生回答小结：量角器可起移角的作用，先测量的度数，然后以的顶点为顶点，其中一边为作作一个角等于，出现两种情况．如图2及图3所示：（1）在内部时，如图2，是与的差，记作：．（2）在外部时，如图3，是与的和，记作：．【教法说明】在以上教学过程中，一定要注意训练学生的看图能力和几何语句表达能力，如与的和差所得到的两个图形中，还可让学生观察得到图2中是与的差，记作：，或与的和等于，记作：，图3中是与的差，记作：等进行看图能力的训练．图2 图3反馈练习：学生在练习本上完成画图．已知如图4，，画，使．师：两个的和是，那么是的2倍，记作，或是的，记作：．同样，有角的3倍和等等．角的和、差、倍、分的度数等于它们的度数的和、差、倍、分．图43．角平分线学生观察以上反馈练习中的图形，，也就是把分成了两个相等的角，这条射线叫的平分线．［板书］定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线．几何语言表示：是的平分线，（或）．说明：若，则是的平分线，同样有两条三等分线，三条四等分线，等等．变式训练，培养能力投影显示：1．如图1填空：图1①②2．是的平分线，那么，①②图23．如图2：是的平分线，是的平分线①若，则② ，，则度【教法说明】练习中的第1、2题可口答，第3题在教师引导下写出过程，初步渗透推理过程，培养学生的逻辑推理能力，推理过程由已知入手，联想得出结论．（四）总结、扩展找学生回答：今天学习了哪些内容？教师归纳得出以下知识结构：八、布置作业课本第33页B组第1、2题．作业答案1．解：，若，那么，2．解：∵ 是的平分线，∴ ．又∵ 是的平分线，∴ ．又∵ ，∴ ．说明：学生作业或回答问题，尽量要求用“∵ ∴”的形式，为以后解证明题打好基础．九、板书设计同七、（四）的格式．。
角的比较和运算教案
教学过程：一：创设情境，提出问题，引入新课（动）（一）、从实际生活中建立角的概念1．类比联想，提出问题前面学习了线段的概念之后，紧接着就学习了比较线段的大小以及线段的和、差、倍、分的画法问题．上节课我们已经学习了角的概念，类似的，今天我们也要学习如何比较角的大小，以及角的和、差、倍、分的画法问题．(板书课题)2．类比联想，探索解决问题的方法(1)师生共同回忆线段大小比较的方法，以及和、差、倍、分的画法．(2)分组讨论，发现方法．提出问题：如图1-26(a)，试比较∠AOB和∠COD的大小并画出∠AOB+∠COD．1．习角的有关概念二：引入新课（动）三：新课：((板书))2：角的大小可以有两种比较方法：重叠比较法和度量法．(1)重叠比较法：由线段的重叠比较法知，将要比较的两条线段一端重合，再看另一端的位置．角的比较也类似，提问谁能用两个三角板演示一下，然后总结，在比较角的大小的过程中，要让角的顶点和角的一条边都重合，看另一条边落在角内还是角外．(让学生自己总结出三种不同的结论，并让学生在黑板上画出图形，量角器可起移角的作用，先测量的度数，然后以的顶点为顶点，其中一边为边作一个角等于．)记作：∠AOB=∠COD记作：∠AOB＞∠COD记作：∠AOB＜∠COD(2)度量法：因为角可以用量角器来量出度数，度数大的角大于度数小的角，通过角的度数来比较角的大小．(注意写法)例1如图4.6。
8，比较∠AOB与∠CDE的大小．(书上的154页的3图)因为量得∠AOB=35°，∠CDE=65°．所以∠CDE＞∠AOB．(当然，书上的角不能剪下来，我们可以把一个角画到一张描图纸上，放在另一个角上面比较比较角的大小，也可以用量角器分别量出角的度数，然后加以比较.1：画角(做一做)3；画特殊的角30；45；60；75 ；15；105；(角的运算的一种)提出问题：如图1-26(a)，试比较∠AOB和∠COD的大小并画出∠AOB+∠COD．4：角的运算(和差)我们可以对角进行简单的加减运算，如：(1) 34°34′+21°51′=55°85′=56°25′(2) 180°-52°31′=179°60′-52°31′=127°29′(如图并列式子)4．角的和、差、倍、分也可以有两种方法：作图法和度量计算法．(1)作图法：在图中作出两个角的和、差、倍、分．例2 已知∠AOB ，∠CED 且∠AOB ＞∠CED ，如图1-28．求作(i)∠AOB 与∠CED 的和；(ii)∠AOB 与∠CED 的差；(iii)∠CED 的二倍．教师在黑板上以草图的形式为学生演示，依照线段的和、差、倍、分的作法，从而发现作图中的问题，怎样做一个角等于已知角．由于这个基本作图没学，因此作图法暂时不能具体操作，所以目前切实可行的方法只有度量计算法．(2)度量计算法．依然选用例2，解法如下解：量得∠AOB=50°，∠CED=20°，∠AOB 与∠CED 的和是70°． ∠AOB 与∠CED 的差是30°．∠CED 的二倍是40°．6：例子练习(1)如图1-29，∠AOB=130°，∠AOE=50°，∠OEA=60°，求∠BOE ，∠OEB ．(2)如图1-30，量出∠BAC ，∠ABD ，∠BDC ，∠ACD 的度数，并求出四个角的和，∠BAC 与∠ACD 的和．(3)如图1-31，已知∠A=∠B=25°，若∠A+∠B+∠BCA=180°，求∠ACE ．2．如图1-35，1-36，∠AOD=∠BOC=90°，∠COD=42°，求∠AOC ，∠AOB ．二、角平分线的概念(由)教师提问：1．回忆怎样求线段的中点．2．怎样平分一个角．总结：在现阶段只能用度量法解决这两个问题，由于在求一个角的几分之几的情况中，最特殊的就是求一个角的二分之一，它的地位相当于求线段的中点，因此我们下面重点研究角的二等分．将线段二等分的点，叫做线段的中点，由此，我们得一个新的概念——角平分线．(由4的和差引入一个特殊关系；做一做)角平分线定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线．对这个定义的理解要注意以下几点：1．角平分线是一条射线，不是一条直线，也不是一条线段．如图1-32，它是由角的顶点出发的一条射线，这一点也很好理解，因为角的两边都是射线．2．当一个角有角平分线时，可以产生几个数学表达式．如图1-32，可写成因为 OC 是∠AOB 的角平分线，所以 ∠AOB=2∠AOC=2∠COB(1)∠AOC=∠COB(2)反过来，只要具备上述的式子之一，就能得到OC 为∠AOB 的角平分线．这一点学生要给以充分的注意． (在角的比较中有一个好题)练习：1．画一个三角形ABC ，然后作出这三个角的平分线．观察它们是否交于一点，如果交于一点，则交点的位置在哪里？2．如图1-33，若∠AOB=∠COB=∠DOC ，进行下列填空．(1)∠AOD=( )+( )+( )；(2)∠AOB=( )∠AOD ；(3)∠AOD=( )∠COB ；(4)∠DOB=( )=( )+( )．3．如图1-37，OC 是∠AOB 的角平分线，∠CAO=90°，∠CBO=90°，比较∠ACO 与∠BCO 的大小．（三）、总结教师提问：这节课我们都学习了哪些内容和主要的思维方法？学生的回答可能不够全面，或者比较零散，教师最后给以归纳．1．学习的内容有三个：(1)比较角的大小．(2)角的和、差、倍、分．(3)角平分线的概念．2．学习了类比联想的思维方法．七、练习设计1． 156页的中1,2。
第十二讲两角和与差的三角公式及三角恒等变换
第十二讲 两角和与差的三角公式及三角恒等变换一、知识要点：1、两角和与差的正弦、余弦、正切公式及倍角公式（找准核心记忆）：()sin sin cos cos sin sin 22sin cos 令αβαβαβαβααα=±=±−−−→=()()2222222cos cos cos sin sin cos 2cos sin 2cos 112sin tan tan 1+cos2tan cos 1tan tan 21cos2sin 22tan tan 21tan 令 ＝ ＝ αβαβαβαβααααααβααβααβααααα=±=−−−→=-↓=-=-±±=⇒-↓=-2、三角函数的化简、计算、证明的恒等变形的基本思路是：一角二名三结构.即首先观察角与角之间的关系，注意角的一些常用变式，角的变换是三角函数变换的核心！第二看函数名称之间的关系，通常“切化弦”；第三观察代数式的结构特点. 基本的技巧有:⑴ 巧变角（已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如:()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，22αβαβ++=⋅，()()222αββααβ+=---等）(2)三角函数名互化(切割化弦)(3)公式变形使用（tan tan αβ±()()tan 1tan tan αβαβ=± .(4)三角函数次数的降升降幂公式：21cos 2cos 2αα+=，21cos 2sin 2αα-= 升幂公式：21cos 22cos αα+=，21cos 22sin αα-=(5)式子结构的转化(对角、函数名、式子结构化同). (6)常值变换主要指“1”的变换（221sin cos x x =+22sec tan tan cot x x x x =-=⋅tan sin 42ππ=== 等）.3、辅助角公式中辅助角的确定()sin cos a x b x x θ+=+(其中θ角所在的象限由a , b 的符号确定，θ角的值由tan baθ=确定)在求最值、化简时起着重要作用. 二、典例分析：题根分析： 先通过诱导公式转化为求已知两个角的和的余弦值问题．变式网络：分析与解：此时的两角均为锐角，容易求得33cos 65C =.变式 3 ：( 2009 全国）已知()1tan 4,cot ,tan 3αβαβ==+=则 .变式8：:2012年江苏理设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则)122sin(π+a 的值为 ▲ ．解析：∵α为锐角，即02<<πα，∴2=66263<<πππππα++. ∵4cos 65απ⎛⎫+= ⎪⎝⎭，∴3sin 65απ⎛⎫+= ⎪⎝⎭.3424sin 22sin cos =2=3665525αααπππ⎛⎫⎛⎫⎛⎫+=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ . ∴7cos 2325απ⎛⎫+=⎪⎝⎭. ∴sin(2)=sin(2)=sin 2cos cos 2sin 12343434a a a a πππππππ⎛⎫⎛⎫++-+-+ ⎪ ⎪⎝⎭⎝⎭247=252252- 题根2：（2006北京）已知函数1)4()cos x f x xπ-=. （Ⅰ）求()f x 的定义域；（Ⅱ）设α的第四象限的角，且tan α43=-，求()f α的值. 分析：因为正、余弦函数的定义域为以R ，因此只要考虑分母不为零就可以了.解：（Ⅰ）由 cos 0x ≠得()2x k k Z ππ≠+∈， 故()f x 在定义域为},,2x x k k Z ππ⎧≠+∈⎨⎩（Ⅱ）因为4tan 3α=-，且α是第四象限的角, 所以43sin ,cos ,55αα=-=故1)4()cos f x παα--=12(2cos 2)22cos ααα-=1sin 2cos 2cos ααα-+=22cos 2sin cos cos αααα-=2(cos sin )αα=- .变式网络：变式1.2：若2,3ππθ<<cos 2θ=-.则θ的取值范围是 .三、练习：5、（2010全国卷1理数17）已知∆ABC 的内角A ,B 及其对边a ,b 满足cot cot ,a b a A b B +=+求内角C .参考答案：6、（2012高考真题辽宁理7）已知sin cos αα-=，α∈(0，π)，则tan α=(A) -1 (B) 2- (C) 2(D) 1解析一：sin cos )sin()144ππαααα-=-=∴-=3(0),,tan 14παπαα∈∴=∴=- ，，故选A解析二：2sin cos (sin cos )2,sin 21,ααααα-=∴-=∴=-33(0,),2(0,2),2,,tan 124ππαπαπααα∈∴∈∴=∴=∴=- ，故选A 点评：本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和运算求解能力，难度适中.7、（2012高考真题江西理4）若tan θ+1tan θ=4,则sin2θ= A ．15 B. 14 C. 13 D. 12【命题立意】本题考查三角函数的倍角公式以及同角的三角函数的基本关系式.解析：由4tan 1tan =+θθ得：4cos sin cos sin sin cos cos sin 22=+=+θθθθθθθθ，即42sin 211=θ，所以212sin =θ，选D. 8、（2012高考真题全国卷理7）已知α为第二象限角，33cos sin =+αα，则cos2α=(A) （B ） (C)解析：因为33cos sin =+αα所以两边平方：31cos sin 21=+αα22sin cos 03αα⇒=-<， 因为已知α为第二象限角，所以0cos ,0sin <>αα，31535321cos sin 21cos sin ==+=-=-αααα， 所以)sin )(cos sin (cos sin cos 2cos 22ααααααα+-=-==3533315-=⨯-，选A 9、（2012高考真题重庆理13）设ABC ∆的内角,,A B C 的对边分别为,,a b c ，且53c o s =A ，135cos =B ,3=b 则c = 解析：因为53cos =A ,135cos =B ,所以54sin =A ，1312sin =B ， 655653131213554)sin(sin =⨯+⨯=+=B A C ,根据正弦定理C c B b sin sin =得655613123c =,解得514=c .。
线段及角的和差倍分计算
线段及角的和差倍分计算
首先我们来介绍线段的和、差计算方法。
1.线段的和计算：
设线段AB的长度为a，线段BC的长度为b，那么线段AC的长度为
a+b。
2.线段的差计算：
设线段AB的长度为a，线段BC的长度为b，那么线段AC的长度为，
a-b，即两个线段长度的差的绝对值。
接下来我们来介绍角的和、差计算方法。
1.角的和计算：
设角A的度数为α，角B的度数为β，那么角A和角B的度数和为
α+β。
2.角的差计算：
设角A的度数为α，角B的度数为β，那么角A和角B的度数差为，α-β，即两个角度数的差的绝对值。
--------------------------------------------
下面我们来介绍线段和角的倍数计算方法。
1.线段的倍数计算：
设线段AB的长度为a，倍数为n，那么线段AB的n倍长度为na。
2.角的倍数计算：
设角A的度数为α，倍数为n，那么角A的n倍度数为nα。
需要注
意的是，角度的n倍有时候不是一个具体的度数，而是一种表示角度大小
关系的相对概念。
线段和角的等分计算方法：
1.线段的等分计算：
设线段AB的长度为a，要将其等分成n份，那么每一份的长度为a/n。
例如，要将线段AB等分成3份，那么每一份的长度为a/3
2.角的等分计算：
设角A的度数为α，要将其等分成n份，那么每一份的度数为α/n。
例如，要将角A等分成2份，那么每一份的度数为α/2。
【初三】线段、角的和差倍分
初中数学竞赛专题选讲线段、角的和差倍分一、内容提要证明线段、角的和，差，倍，分，常用两种方法：一是转化为证明线段或角的相等关系；一是用代数恒等式的证明方法。
一.转化为证明相等的一般方法㈠通过作图转化1.要证明一线段（角）等于两线段（角）的和（用截长补短法）⑴分解法――把大量分成两部分，证它们分别等于两个小量⑵合成法――作出两个小量的和，证它与大量相等2.要证明一线段（角）等于另一线段（角）的2倍⑴折半法――作出大量的一半，证它与小量相等⑵加倍法――作出小量的2倍，证它与大量相等㈡应用有关定理转化1.三角形中位线等于第三边的一半，梯形中位线等于两底和的一半2.直角三角形斜边中线等于斜边的一半3.直角三角形中，含30度的角所对的直角边等于斜边的一半4.三角形的一个外角等于和它不相邻的两个内角和5.等腰三角形顶角的外角等于底角的2倍6.三角形的重心（各中线的交点）分中线为2∶17.有关比例线段定理二.用代数恒等式的证明1.由左证到右或由右证到左2.左右两边分别化简为同一个第三式3.证明左边减去右边的差为零4.由已知的等式出发，通过恒等变形，到达求证的结论二、例题例1.已知：△ABC中，∠B＝2∠C，AD是高求证：DC＝AB＋BD分析一：用分解法，把DC分成两部分，分别证与AB，BD相等。
可以高AD为轴作△ADB的对称三角形△ADE，再证EC＝AE。
∵∠AEB＝∠B＝2∠C且∠AEB＝∠C＋∠EAC，∴∠EAC＝∠C辅助线是在DC上取DE＝DB，连结AE。
分析二：用合成法，把AB，BD合成一线段，证它与DC相等。
---------------------------------------------------------------------------------------------------------------------------------仍然以高AD为轴，作出DC的对称线段DF。
《角的和与差》
问题中具有广泛的应用。
03
角的和与差的应用
在几何学中，角的和与差的概念和性质被广泛应用于证明定理、求解
几何图形等问题。例如，在证明勾股定理时，就需要使用角的和与差
的概念和性质。
对几何学中角的和与差的应用的展望
要点一
角的和与差在几何学中的应用将 继续发挥重要作用
随着几何学的发展，角的和与差的概念和性质将继续被 广泛应用于证明定理、求解几何图形等问题。例如，在 证明更高级的定理时，可能需要使用更复杂的角的和与 差的概念和性质。
05
总结与展望
对角的和与差的认识与理解
01
角的和与差的概念
角的和与差是指两个角之间的和或差值，是几何学中最基本的概念之
一。通过对角的和与差的学习，可以更好地理解几何学中的基本概念
和原理。
02
角的和与差的性质
在几何学中，角的和与差具有一些基本的性质，例如两个角的和或差
值等于它们在同一三角形中的对角之和或差值。这些性质在解决几何
02
角的和与差
角的和的定义
角的和是指两个或两个以上的角通过加法运算得到的和。
角的和在几何学中有着重要的应用，如在证明几何定理、求解几何问题时常常需 要用到角的和的概念。
角的和可以用数学公式表示，如A+B=C，其中A、B、C分别代表不同的角。
角的差的定义
角的差是指两个或两个以上的 角通过减法运算得到的差。
[2] 王晓丽. 角的和与差在几何问 题中的应用[J]. 数学学习与研究,
2019(11): 123-125.
[3] 李明. 从角的和与差谈数学思 维的培养[J]. 教育研究, 2020(3):
56-58.
感谢您的观看
人教七下数学角的和差倍分计算专题
角的和差倍分计算
1、如图∠AOB 和∠BOC 的和是表示为=______+______∠AOB 和∠BOD 的和是表示为=______+______∠AOD 和∠BOD 的差是表示为=_____-______∠AOD 和∠AOC 的差是表示为=_____-______
2.如图，若∠AOC ＝50º，∠AOB ＝30º，求∠BOC
的度数。
3.如图，若∠AOB ＝50º，∠BOC ＝20º，求∠AOC
的度数。
例如图，O 是直线AB 上一点，∠AOC ＝53º17′，求∠BOC
的度数.
角的平分线
如果从一个角的_________引出的一条_____把这个角分成的两个角相等，那么这条射线叫做这
个角的平分线。
1.如图，已知∠AOB ＝90º，∠BOC ＝60º，OD 是∠AOC 的平分线，求∠BOD 的度数
.
几何语言：
2.如图，∠AOB=135°，∠BOC=80°，OD平分∠BOC，求∠AOD的度数
3.如图，点0是直线AB上一点，已知∠BOD=30°0E平分∠AOD，求∠AOE的度数
4.如图所示，OE平分∠AOB，OD平分∠BOC，∠AOB=90°，∠EOD=80°，求∠BOC的度数.
5.如图，∠AOB=120°，∠AOC是直角，0D为∠AOB的平分线，OC平分∠BOD吗？
6.如图，∠COB=2∠AOC，OD平分，∠AOB，且∠COD=19°，求∠AOB.。
二次函数与角度和差倍分
二次函数与角度和差倍分1.引言1.1 概述二次函数与角度和差倍分是数学领域中的重要概念和理论。
二次函数是一种特殊的函数形式，其解析式可以表示为一个变量的二次多项式形式。
二次函数具有独特的性质和特点，其图像通常呈现出抛物线的形状，对于解决实际问题和分析数学模型具有广泛的应用。
角度和差则是指两个角度之间的加法和减法运算。
在三角函数中，角度和差公式是一组重要的等式，用于求解两个角度的和与差的三角函数值。
通过角度和差公式，可以将一个三角函数表达式化简为另一种形式，从而使计算更加简便。
本文旨在探讨二次函数与角度和差之间的关系，以及它们在实际问题中的应用和意义。
首先，我们将介绍二次函数的定义和特点，包括二次函数的一般形式、顶点坐标、对称轴等内容。
然后，我们将深入讨论角度和差的定义及其常见的倍分公式，包括正弦、余弦和正切函数的角度和差倍分公式。
最后，我们将总结二次函数与角度和差的关系，并探讨它们在实际问题中的应用和意义。
通过本文的阅读，读者将能够全面了解二次函数与角度和差的概念和理论，并能够运用它们解决实际问题。
无论是在科学研究还是日常生活中，这些知识都是非常有用的，能够帮助我们更好地理解数学的本质和应用。
1.2文章结构文章结构部分的内容可以包括以下几个方面：1. 章节划分：介绍本文的章节划分和内容安排，即明确说明文章包含哪些主要章节和各个章节的主题。
2. 二次函数部分：简要介绍文章中关于二次函数的内容，包括定义和特点以及图像和性质。
可以提及二次函数的标准形式、顶点形式和一般式，以及二次函数图像的开口方向、对称轴和顶点位置等基本性质。
3. 角度和差倍分部分：概述文章中关于角度和差倍分的内容，包括角度和差的定义和角度和差的倍分公式。
可以提及如何计算角度和差以及如何利用倍分公式得出特定角度的倍分值。
4. 结构关联：指出二次函数和角度和差倍分之间的关系，即通过二次函数的性质可以推导出角度和差倍分的公式。
可以说明角度和差倍分在解决二次函数问题中的应用价值。
人教版七年级数学下册8.3.1和差倍分问题教案
此外，小组讨论环节，学生们表现得相当积极，但我也注意到有些小组在讨论过程中可能会偏离主题。针对这一点，我计划在下次的讨论中提供更明确的讨论指南，同时加强巡视指导，确保每个小组都能围绕核心知识点进行深入讨论。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解和差倍分的基本概念。和差倍分是解决数学中加减乘除问题的方法。它们在日常生活中有着广泛的应用，如购物、计算时间、分配物品等。
2.案例分析：接下来，我们来看一个具体的案例。比如，小华有10元钱，比小刚多3元，问小刚有多少钱。这个案例展示了如何运用和差知识解决问题。
-引导学生从实际问题中抽象出数学关系，构建数学模型，运用数学语言进行表达。
三、教学难点与重点
1.教学重点
-理解和差问题的求解方法，包括加法原理和乘法原理的应用。
-掌握倍分问题的解决策略，特别是如何建立倍数关系解决问题。
-能够将和差倍分知识应用于解决实际生活中的数学问题。
举例解释：
-在讲解和差问题时，重点强调如何将问题转化为数学表达式，例如“已知两个数的和与其中一个数，求另一个数”的类型，重点在于让学生掌握(a+b)-a=b的转换过程。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“和差倍分在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
角的和差倍分专项训练题1(含答案)
角的和差倍分专项训练题11.如图, OC平分∠AOD, OE是∠BOD的平分线, 如果∠AOB=130º, 那么∠COE是多少度？2.如图所示, 点O是直线AB上一点, OE, OF分别平分∠AOC和∠BOC, 若∠AOC＝68°, 则∠BOF和∠EOF是多少度？3.如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线.(1)求∠DOE的度数, (2)如果∠AOD=51°17′,求∠BOE的度数4.如图, 直线AB上有一点O, ∠AOD＝440, ∠BOC＝320, ∠EOD＝900, OF平分∠COD, 求∠FOD与∠EOB的度数5.如图, 从点O引出6条射线OA, OB, OC, OD, OE, OF, 且∠AOB＝1000, OF平分∠BOC, ∠AOE＝∠DOE, ∠EOF ＝1400, 求∠COD的度数6.如图, ∠AOD=80°,∠AOB=30°,OB是∠AOC的平分线, 求∠AOC及∠COD的度数7.已知∠AOB=3∠BOC, 若∠BOC=300, 求∠AOC的度数8.如图, ∠BAE =750, ∠DAE= 150, AC是∠BAD的平分线, 求∠CAD的度数9.如图, BD平分∠ABC, BE分∠ABC为2: 5两部分, ∠DBE=240, 求∠ABE的度数10.如图, ∠AOC+∠AOB=1800, OM、ON分别是∠BOC.∠AOB的平分线, ∠MON=600, 求∠AOC和∠AOB的度数11.已知∠AOB, 过O点作射线OC, 若∠AOC=0.5∠AOB, 且∠AOC=220, 求∠BOC的度数12.已知∠AOB=600, ∠BOC=1200, OD平分∠AOB, OE是∠BOC的一条三等分线, 求∠DOE的度数13.如图, 已知∠AOC=900, ∠DOC比∠DOA大280, OB是∠AOC的平分线, 求∠BOD的度数14.如图, 已知∠AOC=1500, OB是∠AOC的平分线, OE, OF分别是∠AOB, ∠BOC的平分线, 求∠EOF的度数15.直线AB.CD相交于点O, OE平分∠AOD, ∠FOC=900, ∠1=400, 求∠2与∠3的度数角的和差倍分专项训练题1参考答案1.分析: 直接利用角平分线的定义进而得出∠AOC=∠DOC, ∠BOE=∠EOD, 即可得出答案解:OC 平分∠AOD, 0E 是∠BOD 的平分线, ∴∠AOC=∠DOC, ∠BOE=∠DOE, ∴∠COE=∠COD+∠DOE=∠AOC+∠BOE=21∠AOB=21×1300=650. 2.分析: 由角平分线的定义, 结合平角的定义, 易求∠BOF 和∠EOF 的度数,解: 点O 是直线AB 上一点, 则∠AOB=180°.若∠AOC=68°, 则∠BOC=∠AOB-∠AOC=180°-68°= 112°, ∵OF 平分∠BOC, ∴∠BOF= ∠BOC= ×112°=56°；又∵OE 平分∠AOC, ∴∠EOF= ∠AOC+ ∠BOC=34°+56°=90, 故∠BOF 和∠EOF 分别是56°和90°.3.分析: (1)由∠AOC+∠COB=180°, 又知OD 是∠AOC 的平分线, OE 是∠COB 的平分线, 故知∠DOE=∠DOC+∠COE= (∠AOC+∠COB)=90°.(2)∵∠A0D+∠BOE=90°和∠AOD=51°17′,可以得到∠BOE 的度数.解: (1)∵∠AOC+∠COB=180°, 已知OD 是∠AOC 的平分线, OE 是∠COB 的平分线∴∠DOC= ∠AOC,∠COE= ∠COB, ∴∠DOE=∠DOC+∠COE= (∠AOC+∠COB)=90°.(2)∵∠AOD+∠BOE=90°,∠AOD=51°17′, ∴∠BOE=90°-∠A0D=38°43′, 故答案为90°, 38°, 43′.4.分析: 根据平角的定义及互补的性质, 解答出即可解:∵∠AOD=44°,∠BOC=32°, ∴∠C0D=104°.∵OF 平分∠COD, ∴∠FOD=52°, 又∵∠EOD=90°, ∴∠EOA=90°-44°=46°, ∴∠BOE=134°.5.分析: 设∠BOF=∠COF=x °, ∠AOE=∠DOE=y °, ∠COD=z °, 根据角的和差列出方程即可求解. 解: 设∠BOF=∠COF=x °,∠AOE=∠DOE=y °,∠COD=z °, 根据题意可得:100+140+x+y=360°, x+y+z=140°, 两式相减得:z=20, 即∠COD=20°.6.分析: 根据角平分线定义求出∠AOC, 代入∠COD=∠AOD-∠AOC 求出即可.解:∵OB 是∠AOC 的平分线,∠AOB=30°, ∴∠AOC=2∠AOB=60°, ∵∠AOD=80°, ∴∠COD=∠AOD-∠AOC=20°.7.分析: 此题需要分类讨论 , 共两种情况, 可以作图后计算.解：∵∠BOC=30°, ∠AOB=3∠BOC,∴∠AOB=3×30°=90°.当OC 在∠AOB 的外侧时, ∠AOC=∠AOB+∠BOC=90°+30°=120°, 当OC 在∠AOB 的内侧时, ∠AOC=∠AOB+∠BOC=90°-30°=60°, 所以 ∠AOC=120°或60°.8.分析:先利用∠BAD=∠BAE-∠DAE 求出∠BAD 的度数, 然后根据角平分线的定义计算∠CAD 的度数.解:∵∠BAE=75°,∠DAE=15°,∴∠BAD=∠BAE-∠DAE=60°,∵AC 是∠BAD 的平分线, ∴∠CAD= 21∠BAD=30°. 9.分析;由角平分线的定义, 则∠CBD=∠DBA, 根据BE 分∠ABC 为2:5两部分这一关系列出方程求解:设∠CBE=2x °,得2x+24=5x-24,解得x=16, ∴∠ABE=5x=5×16°=80°.10.分析: 由OM 、ON 分别是∠AOB 与∠AOC 的平分线, 得出∠AOM=∠BOM= ∠AOB, ∠AOM= ∠AOC ；再由∠AOB 与∠AOC 互补, 得出∠AOB+∠AOC=180°, 得出∠AOM+∠AON=90°, 再进一步结台∠MON=∠AON-∠AOM=40°, 求得∠AOM, 进一步求得结论.解: ∵OM 、ON 分别是∠AOB 与∠AOC 的平分线, ∴∠AOM=∠BOM= ∠AOB,∠AON= ∠AOC ；∵∠AOB +∠AOC=180°, ∴∠AOM+∠AON=90°, ∵∠MON=∠AON-∠AOM=40°, ∴∠AOM=25°∴∠AOB=50°,∠AOC=130°.11.分析: 此题需要分类讨论 , 分两种情况计算.解: 当OC 在∠AOB 的内部时, 根据∠AOC=0.5∠AOB, ∠AOC=220, 可以得出∠BOC=∠AOC=220；当OC在∠AOB的外部时, 根据∠AOC=0.5∠AOB, ∠AOC=220, 可以得出∠BOC=∠AOC+∠AOB=660. 12.分析: 此题需要分类讨论 , 分四种情况计算.(1)如图1, 当∠AOB+∠AOB=180°, 即∠AOC为平角时,OE为靠近OB的一条三等分线.∵∠AOB=60°, OD平分∠AOB, ∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE=40°∴∠OOE=∠DOB+∠BOE=30°+40°=70°；（2）如图2, 当∠AOB+∠AOB=180°, 即∠AOC为平角时,OE为靠近OC的一条三等分线.∵∠AOB= 60°, OD平分∠AOB, ∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE= 80°, ∴∠OOE=∠DOB+∠BOE=30°+80°=110°；（3）如图3, 当∠AOB 与∠BOC有公共边OB, ∠AOB的另一边OA在∠BOC内部时, OE为∠BOC内靠近OC边的一条三等分线.∵∠AOB=60°, ∠BOC=60°, ∴OA为∠BOC平分线上, ∵OD平分∠AOB,∴∠DOB=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°∴∠BOE=80°, ∴∠DOE=∠BOE-∠DOB=80°-30°=50°；（4）如图4, 当∠AOB 与∠BOC有公共边OB, ∠AOB的另一边OA在∠BOC内部时, OE为∠BOC内靠近OB边一条三等分线且更靠近∠AOB的平分线OD.∵∠AOB=60°, OD平分∠AOB, ∴∠DOA=30°, ∵OE是∠BOC的一条三等分线, ∠BOC=120°, ∴∠BOE=40°∴∠DOE=∠BOE+∠AOD-∠AOB=40°+ 30°-60°=10°.13.分析: 先由∠COD﹣∠DOA＝28°, ∠COD+∠DOA＝90°, 解方程求出∠COD与∠DOA的度数, 再由OB是∠AOC的平分线, 得出∠AOB＝∠AOC＝45°, 则∠BOD＝∠AOB﹣∠DOA, 求出结果. 解: ∵∠COD比∠DOA大28°, ∴∠COD＝∠DOA+28°, ∵∠AOC＝90°, ∴∠COD+∠DOA＝90°, ∴∠DOA+28°+∠DOA＝90°, 2∠DOA＝62°, 所以∠DOA＝31°, ∵OB是∠AOC的平分线, ∴∠AOB ＝∠BOC＝∠AOC＝45°, ∴∠BOD＝∠AOB﹣∠DOA＝45°﹣31°＝14°. 故答案为14°.14.分析: 根据角平分线定义得到∠AOB=∠BOC= ∠AOC, ∠AOE =∠BOE= ∠AOB, ∠BOF=∠COF= ∠BOC, 则有∠EOF＝∠EOB+∠BOF＝∠AOC=75°.解: ∵OB是∠AOC的角平分线, ∴∠AOB=∠BOC= ∠AOC, ∵OE、OF分别是∠AOB.∠COB的角平分线, ∴∠AOE =∠BOE= ∠AOB, ∠BOF=∠COF= ∠BOC, ∴∠EOF＝∠EOB+∠BOF＝∠AOB+ ∠BOC＝（∠AOB+∠BOC）＝∠AOC= ×150°=75°.规律: 从一个角的内部任意引一条射线, 这条射线把这个角分成的两个角的角平分线组成的角的度数等于这个角的一半.15.分析:根据平角为180度可得∠2＝180°﹣∠1﹣∠FOC, 根据∠AOD＝∠BOC可得∠AOD的度数, 再根据角平分线定义进行计算可得∠3.解：∵∠AOB＝180°, ∴∠1+∠2+∠COF＝180°, ∵∠FOC＝90°, ∠1＝40°, ∴∠2＝180°﹣∠1﹣∠FOC＝50°, ∠BOC＝∠1+∠FOC＝130°, ∴∠AOD＝∠BOC＝130°, ∵OE平分∠AOD, ∴∠3＝∠AOD＝65°．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学科：初中中数学教材版本：沪教版学员年级：六年级课时数：3课题角的和差倍分教学目标1、理解角的概念,掌握角的有关名称2、掌握角的大小比较方法3、理解两个角的和差倍的意义,并会用等式表示角的和差倍的关系，会画角的和差倍4、理解余角补角的概念教学内容知识点1：角的大小的比较方法（1）量角器（2）叠合法知识点2：角的和、差、倍（1）两个角可以相加，它们的和也是一个角，它的度数等于这两个角的度数的和。
（2）两个角可以相减，它们的差也是一个角，它的度数等于这两个角的度数的差。
知识点3：角平分线（1）定义：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。
（2）角平分线的作法【例题1】能用∠α、∠AOB、∠O三种方式表示同一个角的图形是（）A B C D【解析】A【检测1】如图,能用∠1、∠ABC、∠B三种方法,表示同一个角的是（）A B C D【解析】B【例题2】8点30分时,时钟的时针与分针所夹的锐角是（）A.70°B.75°C.80°D.60°【解析】解：钟面每份是30°，8点30分时针与分针相距2.5份，8点30分时，时钟的时针与分针所夹的锐角是30°×2.5=75°，故选：B．【检测2】时钟的时针在不停的旋转,时针从上午的6时到9时,时针旋转的旋转角是（）A.30°B.60°C.90°D.9°【解析】解：∵时针从上午的6时到9时共旋转了3个格，每相邻两个格之间的夹角是30°，∴时针旋转的旋转角=30°×3=90°．故选：C．【例题3】用一个放大镜去观察一个角的大小，正确的说法是（）A.角的度数扩大了B.角的度数缩小了C.角的度数没有变化D.以上都不对【解析】C【检测3】下列说法正确的是（）A.两点之间直线最短B.用一个放大镜能够把一个图形放大，也能够把一个角的度数放大C.将一个角分成两个角的射线叫角的平分线D.直线l经过点A,那么点A在直线l上【解析】解：（1）对于A选项，直线没长度，故A错误．（2）放大镜能够把一个图形放大，不能够把一个角的度数放大，故B错误．（3）对于C选项，没有提到所分角的相等，故C错误．（4）直线过A点，则A一定在直线上．综上可得只有D正确．故选：D．【例题4】如图,OC⊥AB,OE为∠COB的角平分线,∠AOE的度数为_________A.130°B.125°C.135°D.145°【解析】解：∵OC⊥AB，∴∠COB=∠AOC=90°，∵OE为∠COB的角平分线，∴∠COE=45°，∴∠AOE=∠AOC+∠COE=90°+45°=135°；【检测4】如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB=（）A.40°B.60°C.120°D.135°【解析】解：设∠AOC=x，则∠BOC=2x，则∠AOD=1.5x．∵∠AOD﹣∠AOC=∠COD，∴1.5x﹣x=20°，解得：x=40°．∴∠AOB=3x=120°．故选：C．【例题5】设一个锐角与这个角的补角的差的绝对值为α，则（）A.0°＜α＜90°B.0°＜α≤90°C.0°＜α＜90°或90°＜α＜180°D.0°＜α＜180°【解析】解：设这个角的为x且0＜x＜90°，根据题意可知180°﹣x﹣x=α，∴α=180°﹣2x，∴180°﹣2×90°＜α＜180°﹣2×0°，0°＜α＜180°．故选：D．【检测5】(1)下列说法中正确的个数是（）①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补;⑤如果互补的两个角相等;那么这两个角都是90°A.1B.2C.3D.4【解析】解：锐角的补角一定是钝角，①正确；钝角的补角小于这个角，②错误；如果两个角是同一个角的补角，那么它们相等，③正确；锐角和钝角不一定互补，④错误；如果互补的两个角相等，那么这两个角都是90°，⑤正确．故选：C．(2)如图所示,在三角形ABC中,点D是边AB上的一点.已知∠ACB=90°,∠CDB=90°,则图中与∠A互余的角的个数是__________【解析】解：∵∠ACB=90°，∴∠A+∠B=90°，∵∠CDB=90°，∴∠A+∠ACD=90°，∴∠A互余的角的个数是2．【例题6】已知∠AOB=α（90°＜α＜180°）,∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD(1)若∠COD=180°﹣α时,探索下面两个问题:①如图1,当OC在OD左侧,求∠MON的度数②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数（用含α的代数式表示）(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数（用含α、k的代数式表示）【解析】解：（1）①如图1，∵OM平分∠AOC，ON平分∠BOD，∴∠AOM=∠AOC，∠BON=∠BOD，∴∠AOM+∠BON=（∠AOC+∠BOD），∵∠AOB=α，∠COD=180°﹣α，∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣（180°﹣α）=2α﹣180°，∴∠AOM+∠BON=（2α﹣180°）=α﹣90°，∴∠MON=∠AOB﹣（∠AOM+∠BON）=α﹣（α﹣90°）=90°；②当OC在OD右侧，补全图形如图2所画，∵OM平分∠AOC，ON平分∠BOD，∴∠AOM=∠AOC，∠BON=∠BOD，∵∠AOB=α，∠COD=180°﹣α，∴∠AOC+∠BOD=∠AOB+∠COD=α+（180°﹣α）=180°，∴∠AOM+∠BON=×180°=90°，∴∠MON=∠AOB﹣（∠AOM+∠BON）=α﹣90°；（2）∠MON的度数为（1+k）α．理由：如图3，∵OM平分∠AOC，ON平分∠BOD，∴∠AOM=∠AOC，∠BON=∠BOD，∴∠AOM+∠BON=（∠AOC+∠BOD），∵∠AOB=α，∠COD=kα，∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα，∴∠AOM+∠BON=（α﹣kα）=α（1﹣k），∴∠MON=∠AOB﹣（∠AOM+∠BON）=α﹣α（1﹣k）=（1+k）α．【检测6】已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小(2)如图2,若∠BOC=20°,OM平分∠AOC，ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时求∠MON的大小(3)在(2)的条件下,若∠AOB=10°,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM:∠DON=2:3,求t的值【解析】解：（1）因为∠AOD=160°OM平分∠AOB，ON平分∠BOD所以∠MOB=∠AOB，∠BON=∠BOD即∠MON=∠MOB+∠BON=∠AOB+∠BOD=（∠AOB+∠BOD）=∠AOD=80°；（2）因为OM平分∠AOC，ON平分∠BOD所以∠MOC=∠AOC，∠BON=∠BOD即∠MON=∠MOC+∠BON﹣∠BOC=∠AOC+∠BOD﹣∠BOC=（∠AOC+∠BOD）﹣∠BOC=（∠AOD+∠BOC）﹣∠BOC=×180°﹣20°=70°；（3）∵射线OB从OA逆时针以2°每秒的旋转t秒，∠COB=20°，∴∠AOC=∠AOB+∠COB=2t°+10°+20°=2t°+30°．∵射线OM平分∠AOC，∴∠AOM=∠AOC=t°+15°．∵∠BOD=∠AOD﹣∠BOA，∠AOD=160°，∴∠BOD=150°﹣2t．∵射线ON平分∠BOD，∴∠DON=∠BOD=75°﹣t°．又∵∠AOM：∠DON=2：3，∴（t+15）：（75﹣t）=2：3，解得t=21．答：t为21秒．【测试1】已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是（）A.20°或50°B.20°或60°C.30°或50°D.30°或60°【解析】解：分为两种情况：如图1，当∠AOB在∠AOC内部时，∵∠AOB=20°，∠AOC=4∠AOB，∴∠AOC=80°，∵OD平分∠AOB，OM平分∠AOC，∴∠AOD=∠BOD=∠AOB=10°，∠AOM=∠COM=∠AOC=40°，∴∠DOM=∠AOM﹣∠AOD=40°﹣10°=30°；如图2，当∠AOB在∠AOC外部时，∠DOM=∠AOM+∠AOD=40°+10°=50°；故选：C．【测试2】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与O重合，直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒3°的速度沿顺指针方向旋转一周,设运动时间为t秒(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由(2)若在三角尺转动的同时,直线EF也绕点O以每秒9°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动①当t为何值时,EF平分∠AOB?②EF能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由【解析】解：（1）∵当直角边OB恰好平分∠NOE时，∠NOB=∠NOE=（180°﹣30°）=75°，∴90°﹣3t°=75°，解得：t=5．此时∠MOA=3°×5=15°=∠MOE，∴此时OA平分∠MOE．（2）①OE平分∠AOB，依题意有30°+9t﹣3t=90°÷2，解得t=2.5；OF平分∠AOB，依题意有30°+9t﹣3t=180°+90°÷2，解得t=32.5．故当t为2.5s或32.5s时，EF平分∠AOB②OB在MN上面，依题意有180°﹣30°﹣9t=（90°﹣3t）÷2，解得t=14；OB在MN下面，依题意有9t﹣（360°﹣30°）=（3t﹣90°）÷2，解得t=38．故EF能平分∠NOB，t的值为14s或38s．【练习1】一个角的补角比它的余角的4倍少30°，这个角的度数是【解析】解：设这个角为x，由题意得，180°﹣x=4（90°﹣x）﹣30°，解得x=50°．故答案为：50°．【练习2】如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是【解析】解：∵OA的方向是北偏东15°，OB的方向是北偏西40°∴∠AOB=40°+15°=55°∵∠AOC=∠AOB∴OC的方向是北偏东15°+55°=70°【练习3】将两块直角三角板的直角顶点重合，如图所示，若∠AOD=128°，则∠BOC的度数是_______【解析】解：∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣128°=52°．【练习4】如图,直线AB、CD相交于点O，OA平分∠EOC(1)若∠EOC=70°,求∠BOD的度数(2)若∠EOC:∠EOD=2:3,求∠BOD的度数【解析】解：（1）∵OA平分∠EOC，∴∠AOC=∠EOC=×70°=35°，∴∠BOD=∠AOC=35°；（2）设∠EOC=2x，∠EOD=3x，根据题意得2x+3x=180°，解得x=36°，∴∠EOC=2x=72°，∴∠AOC=∠EOC=×72°=36°，∴∠BOD=∠AOC=36°．【练习5】如图所示,OE、OD分别平分∠AOC和∠BOC(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数(2)如果∠AOB=α,∠BOC=β（α、β均为锐角，α＞β）,其他条件不变,求∠DOE(3)从(1)、(2)的结果中,你发现了什么规律,请写出来【解析】解：（1）∵∠AOB=90°，∠BOC=38°∴∠AOC=∠AOB+∠BOC=90°+38°=128°又∵OE，OD分别平分∠AOC和∠BOC，∴∠COE=∠AOC=×128°=64°∠COD=∠BOC=×38°=19°∴∠DOE=∠COE﹣∠COD=64°﹣19°=45°（2）∵∠AOB=α，∠BOC=β，∴∠AOC=∠AOB+∠BOC=α+β，又∵OE，OD分别平分∠AOC和∠BOC，∴∠COE=∠AOC=（α+β）∠COD=∠BOC=β∴∠DOE=∠COE﹣∠COD=（α+β）﹣β=α+β﹣β=α；（3）∠DOE的大小与∠BOC的大小无关．。