8..扭转
第六章-扭转

Me
g
AD BC
Me
f
根据圆筒横截面本身以及施加的力偶的极对称 性容易判明, 圆筒表面同一圆周线上各处的切应变均 相同。因此, 在材料为均匀连续这个假设条件下, 圆 筒横截面上与此切应变相应的切应力其大小在外圆 周上各点处必相等;至于此切应力的方向, 从相应的 切应变发生在圆筒的切向平面可知, 是沿外圆周的切 向。
M1 d
M3
M2
B
A
C
lAB
lAC
35
例题 8-2
M2
M1 d
M3
B
A
C
lAB
lAC
解: 由截面法得Ⅰ,Ⅱ两段内扭矩分别为T Ⅰ=
955 N·m, T Ⅱ= 637 N·m 。先分别计算B ,C截
面对A之扭转角fAB, fAC , 则可以假想此时A不
动。
f AB
T l AB GIp
, fAC
T l AC GIp
17
取微段dx分析: 得半径为r的任意圆杆面上的切应
变。
gr
tan g r
r df
dx
r(df )
dx
(1)
式中: d f/dx 是长度方向的变化率,按平面假设是常 量。这样,等直圆杆受扭时, gr 与r 成线性关系。
18
2. 物理方面 由剪切胡克定律: tr=Ggr ,在 t<tp 时,可把(1)
扭转变形演示
15
1. 几何方面 如下图,实验表明:
(1) 等直圆杆受扭时, 画在表面上的圆周线只是绕杆的 轴线转动, 其大小和形状都不改变;且在变形较小的 情况时, 圆周线间的相对纵向距离也不变。
16
(2) 平截面假设 等直圆杆受扭时, 它的横截面如同刚性的圆盘
工程力学--第八章_圆轴的扭转

利用t t ',经整理得
s a t sin 2a , ta t cos2a
s a t sin 2a , ta t cos2a
由此可知: (1) 单元体的四个侧面(a = 0°和 a = 90°)上切应力的 绝对值最大; (2) a =-45°和a =+45°截面上切应力为零,而正应 力的绝对值最大;
1)已知二轴长度及所受外力矩完全相同。若二轴截
面尺寸不同,其扭矩图相同否?
若二轴材料不同、截面尺寸相同, 各段应力是否相同? 相同
相同 不同 变形是否相同?
2)下列圆轴扭转的剪应力分布图是否正确?
MT
o
o
MT
o
MT
o
MT
8.3.3
扭转圆轴任一点的应力状态
研究两横截面相距dx的任一A处单位厚度微元,左右二边为
t
t′
s45
t dy
t′
纯剪应力
状态等价于转过 等值拉压应力状 态。
A
c dx
A
t
c
45
t45 45后微元的二向
t
s
dx
45斜截面上的应力: tdx+(t45dx/cos45)cos45+(s45dx/cos45)sin45=0 tdx-(t45dx/cos45)sin45+(s45dx/cos45)cos45=0 解得: s45=-t;t45=0。还有:s45=t; t45=0
第八章 圆轴的扭转
8.1 扭转的概念与实例 8.2 扭矩、扭矩图 8.3 圆轴扭转时的应力与变形 8.4 圆轴扭转的强度条件和刚度条件 8.5 静不定问题
8.1 扭转的概念与实例
传动轴
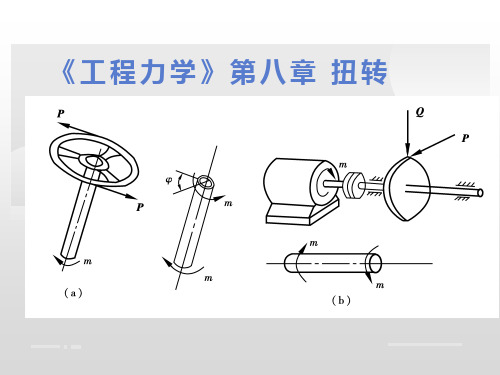
实际工程中,有很多产生扭转变形的构件。图示汽车操纵杆 ;机械中的传动轴等。
工程力学第八章圆轴的扭转详解

轴AB间的相对扭转角为:AB=TL/GIP
单位长度的扭转角为:q =AB/L=T/GIP
扭转刚度条件则为: qmax[q ] ---许用扭转角 机械设计手册建议:[q ]=0.25~0.5/m; 精度高的轴;
[q ]=0.5~1.0/m; 一般传动轴。
整理课件
32
3.扭转圆轴的设计
强度条件: t max T /WT [t ]
Mo
Mo
假想切面
取左边部分
Mo
外力偶
T 内力偶
由平衡方程: T M o 整理课件
平衡
4
返回主目录
Mo
Mo
T
取左边部分
Mo 假想切面
外力偶
扭矩
由平衡方程:
平衡
Mo
TMo T
取右边部分 T
T 和T 是同一截面上的内力, 应当有相同的大小和正负。
整理课件
扭矩
外力偶
平衡
5
扭矩的符号规定:
Mo
T
正
Mo
T
1)已知二轴长度及所受外力矩完全相同。若二轴截 面尺寸不同,其扭矩图相同否? 相同 若二轴材料不同、截面尺寸相同, 各段应力是否相同?相同 变形是否相同? 不同
2)下列圆轴扭转的切应力分布图是否正确?
T
o
o
o
o
T
T
T
整理课件
24
8.3.3 扭转圆轴任一点的应力状态
研究两横截面相距dx的任一A处单位厚度微元,左 右两边为横截面,上下两边为过轴线的径向面。
3) 计算扭转角AC
AC
TAB l AB GIPAB
+ T BC lBC GIPBC
整理课件
工程力学--第八章_圆轴的扭转

df /dx ,称为单位扭转角。
对半径为r的其它各处,可作类 似的分析。
1. 变形几何条件
MT
A
r
B r
rr
C
df
C O D
D
dx
对半径为r的其它各处,作类 似的分析。 同样有:
CC= dx=rdf
即得变形几何条件为:
rdf / dx --(1)
剪应变的大小与半径r成
2
TBC 2
B mx C
2 TBC
2
T
A
用假想截面2将圆轴切开 ,取左段或右段为隔离 体,根据平衡条件求得 :
TBC=-mx
(3)作扭矩图
2mx +
B
–
Cx mx
[例8-2]图示为一装岩机的后车轴,已知其行走的功率 PK=10.5kW,额定转速n=680r/min,机体上的荷载通过轴承 传到车轴上,不计摩擦,画出车轴的扭矩图
4.78
6.37
15.9
4.78
简捷画法:
MT图 10kN m 10kN m
FN图(轴力)
2kN 8kN
5kN
o
x
A
C B 20kN m
5kN 2kN 8kN
5kN
向 按右手法确定
向
MT / kN m
20
5kN
3kN
10
N图
5kN
A
B
C
在左端取参考正向,按载荷大小画水平线;遇集 中载荷作用则内力相应增减;至右端回到零。
G
df
dx
A
r 2dA
MT
3. 力的平衡关系
令:
民族舞基本功16个动作

民族舞基本功16个动作民族舞是各个民族文化的重要组成部分,也是中国文化的瑰宝之一。
随着时间的推移,民族舞逐渐发展出了独特而多样的风格。
在学习民族舞的过程中,掌握基本功是非常重要的一步。
下面将介绍民族舞的基本功16个动作。
1. 站立姿势(Standning Position)站立姿势是舞蹈的起始姿势,舞者要求双脚并拢,身体挺直,双手自然下垂,目光前视。
这个姿势需要保持稳定,以便开展后续的舞蹈动作。
2. 弓步(Bow Step)弓步是指一脚向前迈出,脚尖朝外,另一脚跟着并拢,同时双膝弯曲。
这个动作可以展示舞者的优美和灵动性。
3. 步点(Stamping)步点是民族舞中非常重要的动作之一,它要求舞者用力将一只脚重重地踩在地上,以产生清脆的声音效果。
这个动作能够增加舞蹈的节奏感。
4. 转身(Turn)转身是舞者在站立位置上以一定的技巧快速转动身体。
这个动作可以增加舞蹈的变化和视觉效果。
5. 跳跃(Jump)跳跃是指舞者用力腾空离地,然后再落下。
舞者可以通过跳跃来表达喜悦、兴奋等情感,同时也能展示出舞者的身体力量。
6. 双臂动作(Arm Movements)双臂动作是舞蹈中非常重要的一部分,它可以展示出舞者的柔韧性和舒展性。
舞者可以进行各种手臂的动作,如上扬、下降、划弧等。
7. 旋转(Spin)旋转是指舞者快速地围绕自己的轴心旋转。
这个动作可以给舞蹈增添一种飞舞的感觉,同时也要求舞者有良好的平衡能力。
8. 扭转(Twist)扭转是指舞者上半身沿着某个方向转动,可以是左右扭转或前后扭转。
这个动作可以增加舞蹈的动感,并且能够展示出舞者的柔韧性。
9. 下蹲(Squat)下蹲是指舞者屈膝,臀部下蹲,同时保持身体的平衡。
这个动作可以增加舞蹈的力度和稳定性。
10. 扭腰(Waist Twisting)扭腰是指舞者用力快速地扭动腰部,可以是左右扭动或者前后扭动。
这个动作可以表达出舞者的活力和韵律感。
11. 跳跃并双膝弯曲(Jump and Bend Knees)跳跃并双膝弯曲是指舞者在跳跃的过程中双膝弯曲,以增加舞蹈的变化和视觉效果。
扭转实验原理及目的

扭转实验原理及目的
扭转实验是一种经典的科学实验方法,通常用于探究物体在外力作用下的扭转行为以及相关的物理规律。
其原理基于扭转力矩和物体转动惯量之间的关系。
在扭转实验中,首先需要准备一个具有一定长度的杆状物体或轴,称为扭转杆。
扭转杆的一端固定,另一端可自由转动。
接着,在扭转杆上加上一个或多个力矩传感器,以测量施加到扭转杆上的力矩大小。
在实验中,可以改变施加到扭转杆上的力矩大小,记录下对应的扭转角度。
根据牛顿第二定律和扭转杆的几何形状特征,可以推导出扭转力矩与扭转角度之间的数学关系。
具体来说,扭转力矩正比于扭转角度,并且与扭转杆的几何形状参数有关,如杆长、横截面形状等。
扭转实验的目的包括但不限于以下几个方面:
1. 研究材料的机械性质:由于不同材料的力学性质不同,进行扭转实验可以研究不同材料的扭转刚度、弹性模量等参数,深入了解材料的性质。
2. 确定物体的转动惯量:通过扭转实验可以测量得到物体的转动惯量,这对于物体的旋转运动、惯性特性等的研究具有重要意义。
3. 验证物理定律或模型:扭转实验中,可以将得到的实验数据
与理论模型进行对比,从而验证相关的物理定律或模型的准确性和适用范围。
总之,扭转实验通过测量扭转力矩和扭转角度之间的关系,可以研究物体的转动行为和相关物理规律,具有重要的科学意义和应用价值。
20个坐立扭转体式

20个坐立扭转体式摘要:一、坐立扭转体式的简介1.坐立扭转体式的定义2.坐立扭转体式的功能二、20 个坐立扭转体式的具体动作1.基本坐立扭转2.高级坐立扭转3.瑜伽坐立扭转4.椅子坐立扭转5.站立坐立扭转6.桌子坐立扭转7.墙壁坐立扭转8.垫子坐立扭转9.平衡坐立扭转10.单腿坐立扭转11.双手抱膝坐立扭转12.半莲花坐立扭转13.瑜伽球坐立扭转14.倒立坐立扭转15.悬挂坐立扭转16.椅子辅助坐立扭转17.墙壁辅助坐立扭转18.垫子辅助坐立扭转19.平衡辅助坐立扭转20.单腿辅助坐立扭转三、坐立扭转体式的注意事项1.呼吸与动作的配合2.保持脊柱的挺直3.避免过度扭转4.适当调整难度正文:坐立扭转体式是一种非常受欢迎的瑜伽体式,它能够有效锻炼脊柱的柔韧性,提高身体的核心力量,同时还能缓解压力,改善身体姿势。
在这个练习中,你需要以坐姿为基础,通过扭转脊柱来完成各种不同的动作。
下面我们将详细介绍20 个坐立扭转体式的具体动作。
首先,我们来了解坐立扭转体式的基本动作。
这个动作要求练习者坐在地面上,双腿伸直,然后将一条腿弯曲,脚跟靠近另一条腿的大腿内侧。
接着,将弯曲的腿向外侧打开,同时用另一只手去触摸脚趾。
保持这个动作数个呼吸,然后换另一侧重复。
接下来的高级坐立扭转体式要求练习者在完成基本动作的基础上,将弯曲的腿进一步向侧边打开。
这个动作对于提高脊柱的柔韧性和髋关节的灵活性非常有帮助。
瑜伽坐立扭转体式则是在基本坐立扭转的基础上,用双手抱住弯曲的腿,使上半身更深入地扭转。
这个动作能够有效锻炼腰腹部肌肉,同时还能提高心肺功能。
除了以上几种常见的坐立扭转体式,还有许多其他的变体。
例如,在椅子坐立扭转中,练习者可以使用椅子作为辅助工具,使动作更加轻松。
在站立坐立扭转中,练习者需要站在瑜伽球上,通过球的不稳定性来增加动作的难度。
在练习坐立扭转体式时,需要注意以下几点:首先,要保持脊柱的挺直,避免塌腰或弓背;其次,在扭转时,要尽量保持自然、舒适的呼吸,不要憋气或急促;最后,根据自己的身体状况,适当调整动作难度和持续时间。
《工程力学》第八章 扭转
• 规定为负。因此,同一截面左右两侧的扭 矩,不但数值相等,而且符号相同。
• 3)扭矩图
• 为了显示整个轴上各截面扭矩的变化规律, 可用横坐标表示截面位置,纵坐标表示各 截面扭矩的大小,按适当比例尺绘出扭矩 图,以便确定最大扭矩数值及危险截面。
• §8-3 薄壁圆筒的扭转纯剪切
• 一、薄壁圆筒扭转时横截面上的应力
• 式中θmax和[θ]的单位为度/米(°/m)。
图8-21 *§8-6 圆轴扭转时的变形能
• 当轴扭转时,轴内将积蓄变形能。扭转实 验表明,在弹性范围内受扭圆轴端面的扭 转角φ与外力偶矩m成正比。如图8-22所 示,当等截面圆轴承受的外力偶矩从零逐 渐增到m时,其扭转角也从零增加到φ。
• 所以,外力偶矩所做的功 • 将 代入上式 • 于是得到扭转时的变形能为
即
上式表明:在互相垂直的两个平面上,剪应力必然 成对存在,且数值相等;二者都
• 垂直于两平面的交线,其方向则共同指向
• 或共同背离两平面的交线,这种关系称为 剪应力互等定理。在图8-9所示微体的四 个侧面上,只存在剪应力而无正应力,这种 受力状态称为纯剪切。
• 三、剪切虎克定律
• 薄壁圆筒的扭转实验表明(图8-10),当剪 应力不超过材料的比例极限τp时,剪应力τ 与剪应变γ成正比,即
为了保证圆轴扭转时不发生破坏,要求它在工作 时危险截面上的最大工作剪应力τmax不 超 过 材料的许用扭转剪应力[τ],所以扭转强度条件 为
• 三、圆轴扭转的刚度条件 • 在生产中要限制轴产生过大的扭转变形。
扭转变形过大,将会引起较大的扭转振动, 影响机器的正常运转和工件的加工质量。 为了保证轴的刚度,通常规定轴的最大单 位长度扭转角θmax不超过许用扭转角[θ], 即刚度条件为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2: 已知:N=7.5kW, n=100r/min,许用切应力=40MPa,
空心圆轴的内外径之比 = 0.5。 求: 实心轴的直径d1和空心轴的外径D2。
解: N 7.5 T=9549 = 9549 n 100
=716.2 N.m
T 16 T max= = =40 MPa 3 Wt AB BC 1.50102 rad -1.1710-2 rad 0.3310-2 rad
各段轴的扭转角的转向,由相应扭矩的转向而定。
2
刚度校核
AB段的扭矩最大,应校核该段轴的扭转刚度。AB段的扭转角变化率为:
d T1 180N m 180 0 0 . 43 /m θ 9 5 12 4 dx GI (8010 Pa)(3.0 10 10 m ) π
结论
横截面上各点的剪(切)应 力的方向必与圆周线相切。
分析判断:
1、各圆周线绕轴有相 对转动,但形状、大 小及两圆周线间的距 离不变。
:切应变
横截面上没有正应力。
直角的改变量
2、各纵向线仍为直线, 但都倾斜了同一角度 γ,原来的小矩形变 成平行四边形。
横截面上必有τ存在,其 方向垂直于圆筒半径。 每个小矩形的切应变都等于纵向线倾斜的角度γ,故圆筒 表面上每个小矩形侧面上的τ均相等。 <<2r,认为沿厚度均布。
dx
T
e
T
a dx
d
b
2、物理关系(剪切虎克定律)
G
d G G dx
d Ip dx
dA
d dx
3、力学关系
T dA G
A
d dx
A
2 dA G
O
r
Ip
2 A dA —极惯性矩
dA
T
T
l
GIp—抗扭刚度 表示杆抵抗扭转变形能力的强弱。 单位长度的扭转角: 刚度条件
Tmax 180 max [ ] GI
d T dx GI p
其中:[]—许用扭转角, 取值可根据有关设计标淮或规 范确定。
例 图示圆截面轴AC,承受扭力矩MA, MB与MC 作用,试计算该轴的总扭转角 φAC并校核轴的刚度。 已知MA=180N· m, MB=320 N · m, MC=140N· m, Iρ = 3.0×105mm4,l=2m,G=80GPa,[θ]=0.50/m。
第
扭
概 述
八
章
转
扭矩及扭矩图 薄壁圆筒的扭转 扭转时的应力、强度条件 扭转时的变形、刚度计算
F A
F/ MB
司机通过方向盘把力偶作用 于转向轴的A端,在转向轴 的B端受到来自转向器的约 束力偶作用。即转向轴受到 作用面位于横截面内的外力 偶的作用。
概
m述 A
mB
AB
外力偶作用平面和杆件横截面平行
mA
mB
mC
解:
1.扭转变形分析
l
l
AB段BC段的扭矩分别为:T1=180 N· m, T2=-140 N· m
设其扭转角分别为φAB和φBC,则:
T1l (180N m)(2m) 2 AB 1 . 50 10 rad 9 5 12 4 GI (8010 Pa)(3.0 10 10 m ) Tl (140N m)(2m) 2 BC 2 1 . 17 10 rad 9 5 12 4 GI (8010 Pa)(3.0 10 10 m )
d
d
x
dx
dx
d dx
G
d 2 G dA T dx A
Ip
G
T IP
dA T
A
d T dx GI P
截面的极惯性矩
T
dA dA
T IP
Tr max IP
IP WP r
由上式解出:d=46.9mm。
A空 ( D 2 D 2t 2 ) d 2 1 0 . 334 空实心轴的面积比为:A 4 4 3 实
故同样强度下, 空心轴较实心轴合理。
一、扭转时的变形
扭转时的变形 刚度条件
计算目的:刚度计算、为解超静定问题作准备。
T Tl 相对扭转角: d dx (rad ) 0 GI GI p p l
例
试绘制图示圆轴的扭矩图
薄壁圆筒的扭转 m
m
1
R0
δ<<R0
---薄壁圆筒
1
m
T
扭矩
对应
1 R0 10 为薄壁圆筒
切应力
薄壁圆筒的扭转时的应力—扭转实验
圆周线
纵线
扭转实验前
扭转实验后
加力后:表面扭转变形现象 1.各圆周线形状、大小、间距不变,相邻两圆周线绕 轴线相对转动。 2. 各纵向线均倾斜相同的角,仍为平行直线。 3. 纵向线和环向线所围成的曲面正方形,变形后成 为曲面菱形。 4.平面假设: 圆轴扭转时,其横截面似刚性平面绕 轴线转动(横截面仍保持平面,横截面内的半径仍保 持直线)。 相邻截面绕轴线作相对转动
I P 23d D 4 d 4 32 d
d D
2 D 2
D
d
IP
D 4
1 32
4
WP
D 3
16
1
4
三、强度条件
强度条件: max
Tmax [ ] Wp
[]—许用切应力
理论与试验研究均表明,材料纯剪切时的许用切应 力 [t] 与许用正应力[σ]之间存在下述关系:
平衡吗?
切应力互等定理
根据力偶平衡理论
y
(dydz)dx ( dxdz)dy
在相互垂直的两个平 面上,切应力必成对 出现,两切应力的数 值相等,方向均垂直 于该平面的交线,且 同时指向或背离其交 线。
dy dz
x
dx
z
因为切应力互等定理是由单元体的平衡条件导出的,与材料的性能无关 若单元体各个截面上只有切应力而无正应力,称为纯剪切状态。 不论单元体上有无正应力存在,切应力互等定理都是成立的。 所以不论材料是否处于弹性范围,切应力互等定理总是成立的。
扭转截面系数,单位m3
max
T WP
适用范围:
(1)圆轴、或截面变化缓慢的圆锥扭转。 (2)线弹性范围。
截面的极惯性矩与扭转截面系数
实心圆截面 3 2 2 2 d I P dA 2d
A
A
0
d 2
d
d
IP
d
4
32
WP
d 3
16
空心圆截面
杆件特征:杆件为等园截面的直杆。——圆杆
受力特征:在杆的两端垂直于杆轴的平面内, 作用着一对力偶,其力偶矩相等、方向相反。
——扭转外力偶。
变形特征:杆件的各横截面环绕轴线发生相对 的转动。其任意两个横截面会因为相对转动而 产生相对的角位移,称为——相对扭转角。
扭矩及扭矩图
Ⅰ m (a) Ⅰ A n n n m I
强度计算的三类问题 :
Tmax WP
(2)、截面设计
WP
Tmax
(3)、确定许用荷载
Tmax WP
例: 某汽车主传动轴钢管外径 D=76mm ,壁厚 t=2.5mm ,传递 扭矩T=1.98kN· m,[t]=100MPa,试校核轴的强度。 4 4 解:计算截面参数: I 77 . 1 10 m m p
例题
试根据切应力互等定理,判断图中所 示的各单元体上的切应力是否正确。
10 kN 20 kN 30 kN 50 kN 10 kN 20 kN 50 kN 30 kN 30 kN
扭转时的应力 强度条件
一、横截面上的应力
Me
a
b O2
1、变形几何关系M
3 3 W 20 . 3 10 m m p
由强度条件: max
Tmax 97.5MPa [ ] 故轴的强度满足要求 WP
max 97.5MPa
若将空心轴改成实心轴,仍使
则
max
Tmax 1.98103 97.5MPa 3 Wp d / 16
3
d1=
16 716. 2 =0.045 m=45 mm 40 106
对于塑性材料, [] =(0.5---0.577) [σ] 对于脆性材料,[] =(0.8---1.0) [σ] 式中, [σ]代表许用拉应力。
根据强度条件可进行:
强度校核; 选择截面; 计算许可荷载。
Tmax max= Wp
(1)、强度校核
注意:max产生于哪些截面的哪些点?危 险截面在哪里?危险点在哪里?
T
T+
I
外加力偶矩与功率和转速的关系
x
PkW M e 9.55 10 N .m nr / min
3 n
扭矩
扭矩图
Ⅰ m (a) Ⅰ A m I T n I n B n m
扭矩T的计算方法: 截面法x
mI T
I T
m
扭 矩 符 号 规 定 :
I mI T
T
I
I
T
m
T
I I
右手定则:右手四指内屈,与扭矩转向相 同,则拇指的指向表示扭矩矢的方向,若 扭矩矢方向与截面外法线相同,规定扭矩 为正,反之为负。
