量子化学程序Gaussian
gaussian标准态活化自由能
gaussian标准态活化自由能
在物理化学中，Gaussian标准态活化自由能是指在Gaussian分布中的一个分子或原子活化过程的自由能。
Gaussian分布是一
种常见的概率分布，被广泛用于描述分子和原子的能量分布。
活化自由能是指在化学反应中，从起始状态到过渡态的能量差异。
它是一个重要的物理量，用于描述化学反应的速率和反应动力学。
Gaussian标准态活化自由能通常使用Gaussian软件包计算得到。
该软件包使用量子化学方法来计算分子或原子的能量和结构。
计算Gaussian标准态活化自由能需要确定反应的过渡态结构，并对其进行优化计算以获得最稳定的过渡态结构。
然后，通过计算过渡态的能量和起始态的能量，可以得到活化自由能的差值。
Gaussian标准态活化自由能在许多化学领域中有重要的应用，
如催化剂设计、药物研发和材料科学等。
它可以帮助研究人员理解化学反应的机理，预测反应速率，并指导实验设计和合成化学品的选择。
《Gaussian培训》课件
Gaussian软件的发展历程
• Gaussian软件的发展历程可以追溯到上世纪80年代，自1980年代中期以来，Gaussian软件不断推出新的版本，并逐渐实 现了从单一的量子化学计算软件到计算化学综合平台的转变。目前，Gaussian软件已经成为全球使用最广泛的计算化学软 件之一。
Gaussian软件的主要功能和应用领域
06
参考文献
参考文献
Gaussian 09, Revision A.01, Mopac 2012, and associated
tutorials and examples.
Gaussian 09, Revision A.01, Mopac 2012, and associated
tutorials and examples.
依据。
金属表面的结构和性质研究
要点一
总结词
Gaussian软件可用于金属表面结构的研究，预测表面 形貌、电子结构以及化学反应活性等性质。
要点二
详细描述
借助Gaussian软件，科研人员可以模拟金属表面的电 子云分布、能带结构以及化学反应活性等性质，为催 化剂设计、能源存储与转化等应用提供理论支持。
Gaussian培训
2023-11-12
目录
• Gaussian软件概述 • Gaussian计算方法介绍 • Gaussian软件操作流程 • Gaussian软件应用实例 • Gaussian软件的优缺点及未来发展 • 参考文献
01
Gaussian软件概述
Gaussian软件简介
• Gaussian软件是一款广泛应用于计算化学领域的软件，由美国 Gaussian公司开发。它提供了一系列的计算化学工具，包括分 子建模、量子化学计算、分子动力学模拟等，被广泛应用于药 物设计、材料科学、能源研究等领域。
高斯的介绍和使用
AO轨 道
轨道系数 LUMO
注: • 输出的MO系数是未经归一化过的; • 1s, 2s等符号并非真正意义上的AO, 它与计算 所采用的基组 有关. 对于上例, 采用的是6-31G基组, 可知, 对于价层AO是 分裂为两组的, 故对于O原子, 输出的2s和3s 实际上均为价 轨道, 其它类推. • 当基函数较多时, 若只考察前线附近的轨道成 分, 可用关键 词: pop=regular, 此时只给出5个占据轨道和5 个空轨道组成.
距离矩阵
各原子的直角坐标
需核查!
注意:计算结果是以该坐标系为准
需核查!
MO初始猜测
迭代次数 收敛指标
自洽场迭代求解部分
迭代次数 收敛指标
自洽场迭代求解部分
偶极矩及多极矩
对主要计算结果进行总结
分子轨道系数的输出:关键词: pop=full说明: 有时为 了分析MO成分, 则需利用该关键词输出各MO的成 分, 以H2O为例:
Mulliken电荷分布
说明： 电荷的绝对值是没有意义的，其数值受到所用方法, 尤其是 基组的影响较大： 以H2O为例： 方法/基组 B3LYP/STO-3G B3LYP/3-21G B3LYP/6-31G HF/6-31G O H
-0.329 -0.637 -0.705
-0.795
0.165 0.318 0.353
二、安装高斯对计算机的要求
现在的 PC 速度非常快，成本低廉，是使用 Gaussian 的一 个经济实惠的平台。 对稍懂计算机的人我会建议组装一台 Linux 工作站，基本的配备应包括 64 位 Dual-Core CPU， 如 Intel P4 8xxD， 9xxD, Core Duo， 或 AMD Athlon 64X2 等， 2 GB DDR2 667 以上内存， 2 台 200 GB 以上 SATA 硬盘以 弹 性 使 用 Raid 0/1 。 Linux 操 作 系 统 可 选 择 免 费 下 载 之 Fedora Core 4 或 5，Suse 10 等，记得要使用 64 位的版本。 旧的 32 位 PC 也可以用，只是效能上会差很多。接下来要依 照你的系统种类选择适当的 Gaussian 03 版本，请参阅本站 首页。目前 Window XP 的版本 (G03W) 还不能发挥 64 位的 运算效能， 使用上的便利性及功能性也都不如 Linux 的版本
Gaussian程序常用计算方法
Gaussian程序常用计算方法Gaussian提供的常用计算方法：杨磊 131******** （1）半经验方法：关键词：AM1, PM3, CNDO, INDO, MINDO它们主要用于大的有机分子体系(由上百个原子组成)，一般对于含金属体系不适用。
这些方法只有在特殊场合适用。
（2) 从头算(ab initio)方法：HF方法：即基于Hartree-Fock原理的方法关键词：HF，RHF，UHF，ROHF说明：（i)当关键词为HF时，会自动根据自旋多重度选择RHF还是UHF；（ii)ROHF为限制性开壳层HF方法，与UHF区别在此时除了成单电子外，其余的α和β电子仍配对，通常该方法得到的能量要较UHF略高。
（iii)HF方法可以看作是最低级的从头算方法，该方法除了在构型优化时有使用外，不计算能量。
（3）密度泛函方法(DFT)：基于电荷密度自洽的方法关键词：B3LYP等根据所采用的相关和交换泛函，可以选择不同的DFT方法，具体参见gaussian的帮助文件。
其中B3LYP方法是使用最为广泛的DFT方法，由于DFT方法考虑了电子之间的相关作用，因此得到的能量要较HF来得精确，它是目前最常用的量子化学计算方法。
交换泛函: Slater(S)、X (XA)、Becke88(B)、Perdew-Wang 91(PW91)、PBE(PBE)等相关泛函: VWN、LYP、PW91、P86、PBE等组合形式如：BP86、SVWN、PW91PW91、PBEPBE等（4）MPn方法：关键词：MP2,MP3, MP4, MP5说明：（i) 这些方法在HF基础上，进一步根据MP微扰理论考虑电子相关作用，微扰项截至到二阶则为MP2，截至到三阶则为MP3，其它类推，理论上考虑的微扰项越多，得到的能量越精确，但将大大增加计算量，而且通常也无此必要，多数场合选取MP2即可。
（ii) 对于该类方法，硬盘和内存通常开销较大，应考虑具体的硬件考虑之，其中对于硬盘空间的设置见文件Default.Rou内容，另外，必须注意到由于受到操作系统的限制，中间文件不能超过2GB(32位系统)，此时需设置多个中间文件，具体见gaussian说明。
gaussian计算原子间距
一、介绍高斯计算方法高斯计算方法是一种基于量子力学的计算原子间距的方法，它通过求解薛定谔方程来模拟原子之间的相互作用。
这种方法广泛应用于化学、物理和材料科学领域，可以帮助科学家们理解原子之间的结构和相互作用。
二、高斯计算方法的原理1. 哈密顿量的构建在高斯计算方法中，首先需要构建系统的哈密顿量，它描述了系统的动力学性质和能量。
哈密顿量的构建需要考虑原子核和电子之间的相互作用，以及电子之间的库伦排斥和交换作用。
2. 薛定谔方程的求解构建好哈密顿量后，接下来需要求解薛定谔方程。
这一步通常采用数值求解的方法，计算机会对薛定谔方程进行离散化处理，然后利用数值方法求解得到原子间的距禿。
三、高斯计算方法的优势1. 精度高高斯计算方法能够精确地描述原子间的相互作用，可以提供非常精确的原子间距离。
2. 适用范围广高斯计算方法可以应用于各种原子体系和分子体系，不受体系大小和结构复杂程度的限制。
3. 可拓展性强高斯计算方法可以通过引入更复杂的理论和模型，进一步提高计算精度和适用范围，具有很强的可拓展性。
四、高斯计算原子间距的步骤1. 准备工作在进行高斯计算原子间距之前，需要准备好体系的结构信息、原子坐标、原子核电荷等参数。
2. 构建系统的哈密顿量根据体系的结构信息和哈密顿量构建的规则，建立系统的哈密顿量。
3. 求解薛定谔方程利用数值方法对构建好的哈密顿量进行求解，得到系统的波函数和能谱。
4. 计算原子间距根据系统的波函数和能谱，可以计算得到原子间的距离。
五、高斯计算原子间距的挑战1. 计算复杂度高高斯计算方法需要进行大量的哈密顿量构建和薛定谔方程求解，计算过程复杂，耗时较长。
2. 计算精度受限由于计算方法的近似性质以及计算参数的选择，高斯计算方法的精度仍然存在一定的误差。
3. 计算结果的验证高斯计算方法得到的原子间距需要进行实验验证，以保证计算结果的准确性和可靠性。
六、结语高斯计算方法是一种重要的计算原子间距的方法，它通过求解量子力学的薛定谔方程，可以为科学家们研究原子间的相互作用提供重要的参考。
G98w(Gaussian 98)程序及其应用
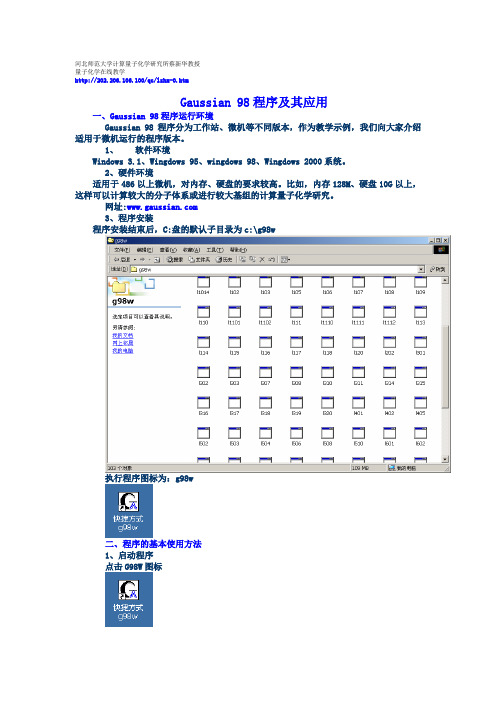
河北师范大学计算量子化学研究所蔡新华教授量子化学在线教学http://202.206.106.100/qc/lzhx-0.htmGaussian 98程序及其应用一、Gaussian 98程序运行环境Gaussian 98程序分为工作站、微机等不同版本，作为教学示例，我们向大家介绍适用于微机运行的程序版本。
1、软件环境Windows 3.1、Wingdows 95、wingdows 98、Wingdows 2000系统。
2、硬件环境适用于486以上微机，对内存、硬盘的要求较高。
比如，内存128M、硬盘10G以上，这样可以计算较大的分子体系或进行较大基组的计算量子化学研究。
网址:3、程序安装程序安装结束后，C:盘的默认子目录为c:\g98w执行程序图标为：g98w二、程序的基本使用方法1、启动程序点击G98W图标2、设置工作环境File-Preference指定执行文件目录、输入、输出数据文件目录3、建立分子数据输入文件File-New以水分子Hartree-Fock STO-3G基组的计算为例说明直接输入分子的直角坐标数据点击开始运行程序点击图标：指出计算结果输出文件名称后，程序开始运行。
4、计算结束后，用编辑器打开输出文件，分析计算结果。
Entering Link 1 = C:\g98w\l1.exe PID= 1072.Copyright (c) 1988,1990,1992,1993,1995,1998 Gaussian, Inc.All Rights Reserved.This is part of the Gaussian(R) 98 program. It is based onthe Gaussian 94(TM) system (copyright 1995 Gaussian, Inc.),the Gaussian 92(TM) system (copyright 1992 Gaussian, Inc.),the Gaussian 90(TM) system (copyright 1990 Gaussian, Inc.),the Gaussian 88(TM) system (copyright 1988 Gaussian, Inc.),the Gaussian 86(TM) system (copyright 1986 Carnegie MellonUniversity), and the Gaussian 82(TM) system (copyright 1983Carnegie Mellon University). Gaussian is a federally registered trademark of Gaussian, Inc.This software contains proprietary and confidential information, including trade secrets, belonging to Gaussian, Inc.This software is provided under written license and may beused, copied, transmitted, or stored only in accord with thatwritten license.The following legend is applicable only to US Governmentcontracts under DFARS:RESTRICTED RIGHTS LEGENDUse, duplication or disclosure by the US Government is subject to restrictions as set forth in subparagraph (c)(1)(ii) of theRights in Technical Data and Computer Software clause at DFARS252.227-7013.Gaussian, Inc.Carnegie Office Park, Building 6, Pittsburgh, PA 15106 USAThe following legend is applicable only to US Governmentcontracts under FAR:RESTRICTED RIGHTS LEGENDUse, reproduction and disclosure by the US Government is subjectto restrictions as set forth in subparagraph (c) of theCommercial Computer Software - Restricted Rights clause at FAR52.227-19.Gaussian, Inc.Carnegie Office Park, Building 6, Pittsburgh, PA 15106 USA---------------------------------------------------------------Warning -- This program may not be used in any manner thatcompetes with the business of Gaussian, Inc. or will provideassistance to any competitor of Gaussian, Inc. The licenseeof this program is prohibited from giving any competitor ofGaussian, Inc. access to this program. By using this program,the user acknowledges that Gaussian, Inc. is engaged in thebusiness of creating and licensing software in the field ofcomputational chemistry and represents and warrants to thelicensee that it is not a competitor of Gaussian, Inc. and thatit will not use this program in any manner prohibited above.---------------------------------------------------------------Cite this work as:Gaussian 98, Revision A.3,M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam,A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi,V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo,S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui,K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari,J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin,D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara,C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen,M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon,E. S. Replogle, and J. A. Pople,Gaussian, Inc., Pittsburgh PA, 1998.********************************************Gaussian 98: x86-Win32-G98RevA.3 2-Sep-199801-Jun-2000********************************************----------#HF/STO-3G----------1/38=1/1;2/17=6,18=5/2;3/11=9,25=1,30=1/1,2,3;4//1;5/5=2,32=1,38=4/2;6/7=2,8=2,9=2,10=2,28=1/1;99/5=1,9=1/99;------------WATER ENERGY------------Symbolic Z-matrix:Charge = 0 Multiplicity = 1O -0.46 0.18 0.H -0.46 1.14 0.H 0.44 -0.14 0.------------------------------------------------------------------------ Z-MATRIX (ANGSTROMS AND DEGREES)CD Cent Atom N1 Length/X N2 Alpha/Y N3 Beta/Z J ------------------------------------------------------------------------1 1 O 0 -0.460000 0.180000 0.0000002 2 H 0 -0.460000 1.140000 0.0000003 3 H 0 0.440000 -0.140000 0.000000------------------------------------------------------------------------ Z-Matrix orientation: ---------------------------------------------------------------------Center Atomic Atomic Coordinates (Angstroms)Number Number Type X Y Z---------------------------------------------------------------------1 8 0 -0.460000 0.180000 0.0000002 1 0 -0.460000 1.140000 0.0000003 1 0 0.440000 -0.140000 0.000000---------------------------------------------------------------------Distance matrix (angstroms):1 2 31 O 0.0000002 H 0.960000 0.0000003 H 0.955196 1.564736 0.000000Interatomic angles:H2-O1-H3=109.5731Stoichiometry H2O======================================================================= Framework group CS[SG(H2O)]Deg. of freedom 3Full point group CS NOp 2Largest Abelian subgroup CS NOp 2Largest concise Abelian subgroup C1 NOp 1Standard orientation:---------------------------------------------------------------------Center Atomic Atomic Coordinates (Angstroms)Number Number Type X Y Z---------------------------------------------------------------------1 8 0 0.000000 0.110436 0.0000002 1 0 0.782357 -0.445907 0.0000003 1 0 -0.782357 -0.437577 0.000000---------------------------------------------------------------------Rotational constants (GHZ): 926.0025221 409.6094525 283.9892074Isotopes: O-16,H-1,H-1Standard basis: STO-3G (5D, 7F)There are 6 symmetry adapted basis functions of A' symmetry.There are 1 symmetry adapted basis functions of A" symmetry.Crude estimate of integral set expansion from redundant integrals=1.000.Integral buffers will be 262144 words long.Raffenetti 1 integral format.Two-electron integral symmetry is turned on.7 basis functions 21 primitive gaussians5 alpha electrons 5 beta electronsnuclear repulsion energy 9.1799871566 Hartrees.One-electron integrals computed using PRISM.NBasis= 7 RedAO= T NBF= 6 1NBsUse= 7 1.00D-04 NBFU= 6 1Projected INDO Guess.Initial guess orbital symmetries:Occupied (A') (A') (A') (A') (A")Virtual (A') (A')Warning! Cutoffs for single-point calculations used.Requested convergence on RMS density matrix=1.00D-04 within 64 cycles.Requested convergence on MAX density matrix=1.00D-02.Requested convergence on energy=5.00D-05.Keep R1 integrals in memory in canonical form, NReq= 406338.Convergence on energy, delta-E=4.15D-05SCF Done: E(RHF) = -74.9603312992 A.U. after 4 cyclesConvg = 0.7155D-03 -V/T = 2.0050S**2 = 0.0000**********************************************************************Population analysis using the SCF density.**********************************************************************Orbital Symmetries:Occupied (A') (A') (A') (A') (A")Virtual (A') (A')The electronic state is 1-A'.Alpha occ. eigenvalues -- -20.23442 -1.26198 -0.62554 -0.44059 -0.38721Alpha virt. eigenvalues -- 0.59512 0.75717Condensed to atoms (all electrons):1 2 31 O 7.840531 0.267076 0.2673092 H 0.267076 0.591156 -0.0447433 H 0.267309 -0.044743 0.589028Total atomic charges:11 O -0.3749172 H 0.1865113 H 0.188406Sum of Mulliken charges= 0.00000Atomic charges with hydrogens summed into heavy atoms:11 O 0.0000002 H 0.0000003 H 0.000000Sum of Mulliken charges= 0.00000Electronic spatial extent (au): <R**2>= 17.8206Charge= 0.0000 electronsDipole moment (Debye):X= -0.0081 Y= -1.6911 Z= 0.0000 Tot= 1.6911Quadrupole moment (Debye-Ang):XX= -4.1948 YY= -5.4615 ZZ= -6.0900XY= -0.0077 XZ= 0.0000 YZ= 0.0000Octapole moment (Debye-Ang**2):XXX= -0.0061 YYY= -0.1783 ZZZ= 0.0000 XYY= 0.0045XXY= -0.5878 XXZ= 0.0000 XZZ= -0.0015 YZZ= -0.0071YYZ= 0.0000 XYZ= 0.0000Hexadecapole moment (Debye-Ang**3):XXXX= -6.5371 YYYY= -4.6977 ZZZZ= -3.2271 XXXY= 0.0086XXXZ= 0.0000 YYYX= 0.0075 YYYZ= 0.0000 ZZZX= 0.0000ZZZY= 0.0000 XXYY= -1.6959 XXZZ= -1.8089 YYZZ= -1.3490XXYZ= 0.0000 YYXZ= 0.0000 ZZXY= 0.0044N-N= 9.179987156624D+00 E-N=-1.969725142722D+02 KE= 7.458977663622D+01 Symmetry A' KE= 6.953231418420D+01Symmetry A" KE= 5.0574********D+001|1|UNPC-UNK|SP|RHF|STO-3G|H2O1|PCUSER|01-Jun-2000|0||#HF/STO-3G||WATER ENERGY||0,1|O,0,-0.46,0.18,0.|H,0,-0.46,1.14,0.|H,0,0.44,-0.14,0.||Version=x86-Win32-G98RevA.3|State=1-A'|HF=-74.9603313|RMSD=7.155e-004|Dipole=0.5440589,0.3829736,0.|PG=CS [SG(H2O1)]||@EDUCATION DOESN'T COST... IT PAYS!-- POSTMARK, UNIV. OF MISSISSIPPI, DEC 78Job cpu time: 0 days 0 hours 0 minutes 28.0 seconds.File lengths (MBytes): RWF= 10 Int= 0 D2E= 0 Chk= 5 Scr= 1 Normal termination of Gaussian 98.5、直接读入由其它程序建立的数据文件。
gaussian 溶剂介电常数
gaussian 溶剂介电常数Gaussian 溶剂介电常数引言：在化学领域中，溶剂介电常数是描述溶剂极性的重要物理量之一。
溶剂的极性对于溶解性、反应速率和化学平衡等过程都有重要影响。
本文将重点介绍常用的计算软件Gaussian中的溶剂介电常数模型，并探讨一些相关的应用和研究。
一、溶剂介电常数的定义和意义溶剂介电常数是描述溶剂对电场的响应能力的物理量。
它反映了溶剂中分子相互作用的强度和极性程度。
溶剂介电常数越大，说明溶剂分子间的相互作用越强，溶液中的离子间相互作用也会增强，从而影响溶解度、反应速率和反应平衡等化学过程。
因此，溶剂介电常数是研究溶液化学性质和反应机理的重要参数。
二、Gaussian 软件中的溶剂介电常数模型Gaussian是一款广泛应用于计算化学领域的量子化学计算软件。
在Gaussian中，可以通过使用连续介质模型来计算溶剂介电常数。
连续介质模型是一种简化的模型，将溶剂视为均匀分布的介质，并通过计算溶剂分子的极化能来估算溶剂介电常数。
三、Gaussian 中的溶剂模型Gaussian中使用的溶剂模型包括连续介质模型和离散模型。
连续介质模型假设溶剂是均匀的介质，通常使用连续介质的介电常数来表示溶剂的极性。
离散模型则将溶剂分子离散地放置在计算模型中，通过计算溶剂分子的极化能来估算溶剂介电常数。
四、Gaussian 中的溶剂介电常数计算在Gaussian中，可以使用不同的方法来计算溶剂介电常数。
其中，常用的方法有连续介质模型和离散模型。
连续介质模型可以使用常见的介电常数来表示溶剂的极性，如水的介电常数为78.4。
离散模型则需要将溶剂分子离散地放置在计算模型中，并通过计算溶剂分子的极化能来估算溶剂介电常数。
五、Gaussian 中溶剂介电常数的应用Gaussian中的溶剂介电常数模型可以应用于多个领域。
例如，在有机化学中，研究化合物在不同溶剂中的溶解度和反应速率可以通过计算溶剂介电常数来预测。
高斯使用指南.总结
2014年下学期城南中学人防应急疏散演练方案为增强中学生人民防空意识和国防观念，进一步加强师生安全教育，提高广大师生应对突发事件的能力，保障战时人民防空和平时应急救灾的组织指挥能力，避免在火灾、地震等突发事件来临时学生惊慌失措、盲目逃生。
由市人防办统一部署，结合10月31日防空警报试鸣，组织我校师生应急疏散演练。
一、指导思想为提高学校师生安全应急能力，增强师生安全防范意识，提高师生自我保护能力，确保师生人身安全，避免安全事故的发生，同时检验学校应急疏散意外事故处置能力，特制定本演练方案。
二、演练目的（一）、使师生进一步掌握在应急突发事件中疏散撤离的基本常识。
（二）、使师生熟悉疏散撤离的路线、方法，通过演练缩短疏散时间。
（三）、检验学校制定的“应急疏散预案”是否科学合理、具备可行性；检验学校在应急突发事件中的指挥、疏散、安保、救护工作是否及时迅速，准确到位。
三、演练时间：2014年10月31日上午10时,开始疏散， 10时20分演练结束。
四、演练集结地点：学校大操场五、组织机构和职责（一）、疏散安全工作领导小组组长：林庆根副组长：兰志雄成员：凌运秀钟竹年程国贵丁红来张志辉杨华辉成波勇张雄勇刘劲松各班班主任（二）、各疏散点指挥责任人：1、大操场：林庆根钟竹年成波勇张雄勇2、教学楼各楼层：各班班主任各下班老师(如教师在他班上课,可就地指挥学生疏散)各班主任和各下班老师应控制班级与班级之间撤离的时间，维持秩序，,防拥挤、防踩踏。
4、楼梯口：各楼梯口负责人需要控制学生通过速度，维持秩序，,防拥挤、防踩踏。
5、总协调：林庆根6、有关机构负责人（1）、指挥员（负责现场指挥并计时）：成波勇(指挥)、张雄勇(计时,协助指挥)（2）、与有关部门紧急联系或寻求救援负责人：张志辉（3）、临时救护负责人：刘劲松（4）、人数清点负责人：钟竹年六、疏散方案（一）、疏散具体步骤10时，预先警报信号响起，全体师生紧急疏散到操场等空旷地带；10时8分，空袭警报信号响起，全体师生隐蔽在操场等场所；10时21分,解除警报信号响起，演练结束，全体师生结束隐蔽恢复正常教学秩序。