多变量模糊神经网络控制器的研究
倒立摆论文

倒立摆系统的设计摘要倒立摆是一个非线性、强耦合、多变量和自然不稳定的系统。
通过它能有效地反映控制过程中诸如可镇定性、鲁棒性、随动性以及跟踪等多种关键问题,是检验各种控制理论的理想模型。
对倒立摆系统的研究不仅具有很重要的理论意义,而且在航天科技和机器人学领域中也有现实指导性意义。
本文以直线二级倒立摆模型为控制对象,阐述了倒立摆稳定控制的研究现状以及倒立摆系统的控制系统及机械结构组成。
在数学模型的基础上,重点分析基于Lagrange方程进行数学模型的方法,以及系统的能控性和能观测性。
接着进行了倒立摆系统的LQR控制方法研究。
运用最优控制理论,探讨了加权矩阵Q 和R的选取方法。
然后利用Matlab软件建立倒立摆系统模型,对二级倒立摆的LQR控制器进行了设计与仿真,利用Simulink建立了二级倒立摆的LQR控制模型,实现了二级倒立摆系统的稳定控制。
结果表明本文所给出的控制策略是有效的。
最后对倒立摆系统时滞问题进行了分析,给出了系统稳定性的判别公式。
关键词:倒立摆;Lagrange方程;数学模型;最优控制;SIMULINKDesign of Inverted Pendulum SystemABSTRACTInverted pendulum is a nonlinear,coupling,variable and natural unsteadiness system.During the controlprocess,pendulum can effectively reflect many pivotal problems such as equanimity, robust,follow-up and track.Therefore,it is a perfect model used to testing various control theories.Studying on inverted pendulum not only has a very important theory significance,but also has a realistic directory meaning in aerospace science and technology and robotics.In this paper,we establish mathematical models of double inverted pendulum system,and analyze the controllability and observability of these models.According to the theoretical analysis,this paper puts forward a solution that it is found by Linear Quadratic Optimal Control Theory.In the following,we design a double inverted pendulum’s controller based on the theory.Based on introducing the present established mathematical model,the method of the Mathematical model was done by analyzing the Lagrange equation. And the system characteristic was briefly analyzed.Next we do research on LQR control algorithm of inverted pendulum system.By using optimization control theory,the selection of matrix Q and R is dicussed.It is introduced how to realize the simulation of the inverted pendulum system by the Matlab.Double inverted pendulum LQR controller is designed and emulated.LQR control model is programmed by Simulink, control of double inverted pendulum hardware system is realized.And it indicates that the control strategy proposed in this paper is effctive.Finally,we analysis the time-delay problem of double inverted pendulum system, get the giscriminant formula of the Stability of the system.Keywords: inverted pendulum;Lagrange equation;mathematical model;optimization control theory;Simulink目录1绪论 (1)1.1倒立摆系统研究的意义和前景 (1)1.2倒立摆系统的研究现状 (1)1.3课题任务 (2)2倒立摆系统建模与性能分析 (3)2.1系统数学模型的建立 (3)2.1.1倒立摆系统的运动分析 (3)2.1.2模型建立的基本方法 (4)2.1.3模型的建立 (4)2.2倒立摆系统性能分析 (8)2.2.1系统稳定性原理 (8)2.2.2系统能控性和能观性 (9)2.2.3二级倒立摆系统性能 (9)3 倒立摆系统控制与仿真 (11)3.1 LQR理论基础 (11)3.1.1 线性二次型问题 (11)3.1.2无限时间状态调节器问题 (12)3.2矩阵黎卡提方程的求解 (12)3.3 Simulink概述 (12)3.4二级倒立摆最优控制器的设计 (13)3.4.1最优控制器的设计 (13)3.4.2二级倒立摆系统仿真 (14)4倒立摆系统的实时控制 (17)4. 1硬件在回路仿真技术 (17)4.2系统实现方案介绍 (17)4.3系统实时性分析 (18)4.4系统实现方案确定 (20)4.5本章小结 (20)5摆系统时滞问题 (21)5.1 系统的稳定性 (21)5.2小结 (23)6 结论 (24)谢辞 (25)参考文献 (26)附录A (27)附录B (34)1 绪论1.1倒立摆系统研究的意义和前景倒立摆系统是一个非线性程度严重的高阶不稳定系统,也是一个典型的多变量系统。
模糊控制技术现状及研究热点

模糊控制技术发展现状及研究热点摘要:综合介绍丁模糊控制技术的基本原理和发展状况,重点总结丁近年来该研究领域的热点问题,并对今后的发展前景进行了展望。
关键词:模糊控制结构分析稳定性白适应控制1模糊控制的热点问题模糊控制技术是一项正在发展的技术,虽然近年来得到了蓬勃发展,但它也存在一些问题,主要有以下几个方面:(1)还投有形成完挫的理论体系,没有完善的稳定性和鲁棒性分析,系统的设计方法(包括规则的获取和优化、隶属函数的选取等);(2)控制系统的性能小太高(稳态精度牧低,存在抖动及积分饱和等问题):(3)自适应能力有限。
目前,国内外众多专家学者围绕着这些问题展开了广泛的研究,取得了一些阶段性成果,下面介绍一下近期的主要研究热点。
2模糊控制系统的稳定性分析任何一个自动控制系统要正常工作,首先必须是稳定的。
由于模糊系统本质上的非线性和缺乏统一的系统描述,使得人们难以利用现有的控制理论和分析方法对模糊控制系统进行分析和设计。
因此,模糊控制理论的稳定性分析一直是一个难点课题,未形成较为完善的理论体系。
正因为如此,关于模糊系统的稳定性分析近年来成为众人关注的热点,发表的论文较多,提出了各种思想和分析方法。
目前模糊控制系统稳定性分析方法主要有以下几种:(1)李亚普诺夫方法(2)基于滑模变结构系统的稳定性分析方法(3)描述函数方法(4)圆稳定性判据方法模糊控制系统的稳定性分析还有相平面法、关系矩阵分析法、超稳定理论、Popov判据、模糊穴——穴映像、数值稳定性分析方法以及最近出现的鲁棒控制理论分析方法和LMI(矩阵不等式)凸优化方法等。
3自适应模糊控制器的研究为了提高模糊控制系统的自适应能力,许多学者对自适应模糊控制器进行了研究,研究方向主要集中在以下方面。
(1)自校正模糊控制器自校正模糊控制器是在常规模糊控制的基础上,采用加权推理决策,并引入协调因子,根据系统偏差e和偏差变化ec的大小,预测控制系统中的不确定量并选择一个最佳的控制参数或控制规则集,在线自动调整保守和大胆控制的混合程度,从而更全面确切地反映出入对诸因素的综合决策思想,提高系统的控制精度和鲁捧性能。
一种新型动态神经网络在多变量系统中的应用研究

1 基 于 新 型 神 经 网 络 控 制
维普资讯
第2卷第5 3 期
200 2 年 9 月
南方 金 学 院 学报 台
J U A O T E N T T T F ME A L RG O RN L OF S U H RN I S I U E O T L U Y
智 能 P D控 制 方 法 【¨ 些 方 法 实 质 是 利 用 神 经 网络 自整 定 P D参 数 , 产 生 的 控 制 信 号 u ) I 1. I这 I 而 仍 然 为 误 差 信 号 的 比例 、 分 、 分 的线 性 组 合 . 而 , 论 分 析 和 大 量 实 践 表 明 , 线 性 组 合 ” 积 微 然 理 “ 常 引起 快 速 性 与 超 调 量 的矛 盾 .有 些 学 者 尽 管 认 识 到 多 层 前 向神 经 网 络 可 以 实 现 任 意 函 数 逼
器 的 自适 应 控 制 系 统
如 图 1所 示 , I NN 是 四 层 P D— C
前 向 网络 , 由 并 列 的 多 个 子 网 络 组
成 .每 个 子 网 络 输 入 层 有 两 个 神 经
元 , 别 输 入 系 统 一 个 变 量 的 给定 值 分 和 输 出值 ,隐 含 层 有 3个 神 经 元 , 其
中 图 分 类 号 :P 9 . 文 献 标 识 码 : T 31 9 A
文 章 编 号 : 0 —12 (0 20 — 4 0 1 7 2 92 0 )5 4 — 4 0
基于FPGA多变量模糊神经网络控制器设计

基 于 F GA 多变 量 模 糊 神 经 网络 控 制器 设 计 P
靖 固, 刘璐杨 , 于晓洋
( 哈尔滨理工大学 计算机科学 与技术学 院,黑龙江 哈尔滨 10 8 ) 5 00
摘
要: 在对基 于 F G P A模糊神经网络控制的原理和设计 中使用的算法进行分析后 , 对糊神
速 度 , 可 以改善 传统 模糊 神 经 网络 控 制 器的控 制性 能 . 还 关键 词 :P A; 糊 神 经 网络 控 制 ;设 计综合 FG 模
中 图分 类号 : P3 T 27
文 献标 志码 :A
文章 编号 :t0 —28 (0 10 —04 — 5 07 63 2 1 )2 0 4 0
Ab t a t I n lsso e c n r l rn i l f u z e r ew r a e n F GA a d t ed sg g r h , sr c :n a ay i f h o to i cp e o zy n u a n t o k b s d o P n e i n a o t m t p f l h l i h e a e a e i f t e f z y n u a e w r o tolr i a re u . T e d sg n l d s f z i c t n mo u e ir r h d s l n g o h u z e r ln t o k c n r l s c r d o t h e i n i c u e u zf ai d l , e i i o c nr lr l d l ,n r lia in mo u e,w ih a a tr mo u e a d d f z i c t n mo u e T e p i cp e o o t u e mo u e oma z t d l o o e g tp r me e d l n e u zf ai d l . h r i l f i o n tp d w e i l w d i e d sg r c s ,e c d l e i a e n o t z d, n h n t e w o e s s o - o n d sg i f l e t e i p o e s a h mo u e d sg h sb e p i e a d t e h l y — n soo n h n n mi h tr e i n a d s n h ssi a re u . T e e p r n e u t h w te fa i i t ft e me h d Me n i h s e d sg n y t e i s c rid o t h x e me t s l s o h e sbl y o t o . n i r s i h a whl t i e d sg a c e tr p r r a c a e c s m u z e r ln t r o t l ra d t e s e d i q ik e i h a mu h b t ef m n e t n t u t f z y n u a ewo k c n r l n h p e s u c . n s e o h h o o e Ke r s F G ;f z y n u a e w r o to ;d sg y t e i y wo d : P A u z e r n t o k c n r l e i s n h ss l n
西安理工大学 自动化与信息工程 学院 届学生毕业设计(论文
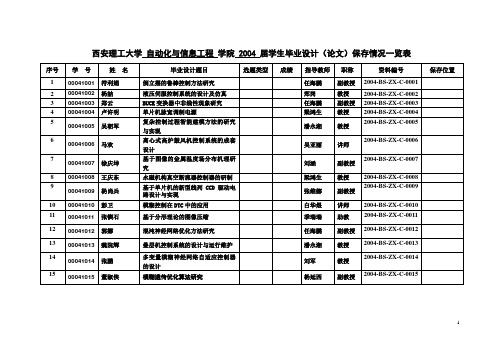
西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表西安理工大学自动化与信息工程学院 2004 届学生毕业设计(论文)保存情况一览表。
神经网络和模糊系统

05
CATALOGUE
应用案例
控制系统
神经网络在控制系统中主要用于优化 和预测控制策略。
通过训练神经网络来学习系统的动态 行为,可以实现对系统的精确控制。 例如,在机器人控制、航空航天控制 等领域,神经网络被用于提高系统的 稳定性和响应速度。
数据分类
模糊系统在数据分类中主要用于处理不确定性和不精确性。
练出最优的神经网络模型。
反向传播算法
根据输出层的误差,计算出每 层的误差梯度,然后根据梯度 下降法更新权重和偏差。
随机梯度下降法
在训练过程中,每次只使用一 部分数据来计算梯度,然后更 新权重和偏差,以提高训练效 率。
自适应学习率算法
根据误差梯度的变化情况,动 态调整学习率,以加快收敛速
度并避免陷入局部最小值。
自适应神经模糊系统
自适应神经模糊系统是在神经模糊系统的基础上,增加了 自适应调整能力。它能够根据系统的运行状态和输入数据 的特性,自适应地调整模糊规则和隶属函数的参数,以更 好地适应环境和任务的变化。
自适应神经模糊系统通过引入在线学习算法和自适应调整 策略,使得系统能够根据运行过程中的反馈信息,不断优 化模糊规则和参数,提高系统的实时性和准确性。
ቤተ መጻሕፍቲ ባይዱ
混合神经模糊系统
混合神经模糊系统是一种将不同类型的神经网络和模糊逻辑结合起来,形成一个 多层次、多模态的混合智能系统。它利用不同类型神经网络的优势,结合多种模 糊逻辑方法,实现对复杂系统的全面建模和控制。
混合神经模糊系统通过集成不同类型的神经网络和模糊逻辑方法,能够充分发挥 各自的优势,提高系统的整体性能。同时,它还能够处理不同类型的输入数据和 任务,具有更强的泛化能力和适应性。
应用前景
模糊控制――文献综述【范本模板】
模糊控制――文献综述摘要模糊控制理论是以模糊数学为基础,用语言规则表示方法和先进的计算机技术,由模糊推理进行决策的一种高级控制策。
模糊控制作为以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数字控制,它已成为目前实现智能控制的一种重要而又有效的形式尤其是模糊控制和神经网络、遗传算法及混沌理论等新学科的融合,正在显示出其巨大的应用潜力。
实质上模糊控制是一种非线性控制,从属于智能控制的范畴.模糊控制的一大特点是既具有系统化的理论,又有着大量实际应用背景。
本文简单介绍了模糊控制的概念,模糊控制系统的组成,模糊控制的算法,其中包含模糊控制系统的原理、模糊控制器的分类及其设计元素。
最后以模糊PID复合控制在锅炉汽包水位控制中的应用说明模糊控制系统的整体设计过程,通过仿真证明了模糊控制显示出的优势。
1. 模糊控制的基本思想模糊控制是模糊集合理论中的一个重要方面,是以模糊集合化、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制,从线性控制到非线性控制的角度分类,模糊控制是一种非线性控制;从控制器的智能性看,模糊控制属于智能控制的范畴[1][2]。
模糊控制是建立在人类思维模糊性基础上的一种控制方式,模糊逻辑控制技术模仿人的思考方式接受不精确不完全信息来进行逻辑推理,用直觉经验和启发式思维进行工作,是能涵盖基于模型系统的技术。
它不需用精确的公式来表示传递函数或状态方程,而是利用具有模糊性的语言控制规则来描述控制过程。
控制规则通常是根据专家的经验得出的,所以模糊控制的基本思想就是利用计算机实现人的控制经验[3].2. 模糊控制系统的组成及结构分析摸糊控制系统是采用计算机控制技术构成的一种具有反馈通道的闭环结构的数字模糊控制系统。
智能性的模糊控制器是模糊控制系统的核心,一个模糊控制系统性能的优劣,主要取决于模糊控制器的结构,所采用的模糊控制规则、合成推理算法以及模糊决策的方法等因素[6] [7]。
模糊控制系统组成原理如图1所示。
带有参数自调整机构的多变量系统模糊神经网络解耦控制
时滞 和惯性 都较 大 的对 象 , 用 这 种控 制 器 难 以获 采
得预期 的控 制效果 . 针对 这一 问题 , 文采 用 模糊 神 本
在 这 m 个 输 入 中 , 择 一 个 起 主 导 作 用 的输 选 入 , 为 n其 余看 作是 这 个 子 系 统 的外 来 干 扰 , 记 则
胡 慧 刘 国 荣 郭 鹏 , ,
(. 1 湖南 工程学院 电气信 息学 院 , 湖南 湘潭 4 10 ;. 1 1 1 2 湖南 工程学院 计算机与通信学 院 , 湖南 湘潭 4 10 ) 1 1 4
摘 要 :在文献[] 1 的基础上, 引入模糊神经网络和参数 自调整算法, 改善 系统的智能, 系统具有 自学 使
习和 自调整 模糊 规 则的能 力. 真结 果表 明 , 方 法能 实现 静 态解耦 , 仿 该 并提 高 了 系统 的抗 干 扰 能 力和 鲁
棒性 , 改善 了系统的性 能. 关键词 :解 耦控 制 ; 模糊 神 经 网络 ; 多变量 系统 中图分类 号 :T 2 3 文 献标识 码 :A 文 章编 号 :1 7 一I 9 2 0 ) 3 0 0 - 0 P7 6 1 1 X( 0 8 0 - 0 5 5
第 1 第 3期 8卷
20 0 8年 9月
湖 南 工 程 学 院 学 报 J u n l fHu a n tt t f gn e ig o r a n n I siu eo i e rn o En
v 1 1. . o . 8 No 3
S p. 0 8 e t2 0
带 有 参 数 自调 整 机 构 的 多 变 量 系 统 模 糊 神 经 网络 解 耦 控 制
变化 都会 影 响所 有 的输 出 , 输人 输 出之 间存 在耦 合. () 给 出的 mXm 维多 变量 系 统 可 以看 作为 m 个 1式 多输 入/ 输 出子系 统 , 单 其第 个 子 系统 为 :
风冷制冷机组的多变量模糊控制研究
蒸发 器 、 膨胀 阀 4个 基本 部 件组成 的制冷 系统 , 个 是 多输 入 多输 出( MO) 统. MO 系 统 通 常具 有 MI 系 MI 明显 的 非线性 热力 学 耦 合 特 性 , 因此 控 制 的难 点 在
程 中通过采样数据在线学习, 调整 网络结构 , 产生模糊控 制规 则并调 整规 则的参数 , 使得控制器具 有模糊控制的特点, 又有神经网络学习的能力. 通过对风冷制冷机组控制试验的结果表 明, 该控 制
器 能够 达到 同时控 制 蒸发 压 力和过 热度 的 目的. 关键 词 :制 冷机 组 ; 多输入 多输 出 ; 糊控 制 ; 经 网络 模 神 中图分 类号 :TK33 文献 标 识码 :A 文章 编号 :0 5—8X(0 60 —540 2 2 397 20 ) 50 1-4
s 控制 , o) 相关 研究 已有报 导 ¨ ]SS 1 . IO模 糊 控 制 规
则 生 成 简单 , 顾 及不 到整 个 系统参 数 之间 的耦 合 , 但
无法到达最佳运行工况. 文献[] 3采用复合模糊控制
器 解决 MI Mo 系统耦 合 问题 , 且 提 高 了其 控 制 特 并
( c o l f n r y a d P we n i e r g i nJa t n iest ,Xi n 7 0 4 ,C ia S h o e g n o rE gn e i ,X i o g Un v ri oE n a o y 10 9 hn ) a
Ab ta t sr c :Fo li n u l— u p t a d n n ie r c mp e y tm ,a s l o g nz d f z y r a mu t i p tmut o t u n o l a o lx s s e — i n ef r a ie u z -
数控珩磨机进给系统模糊神经网络控制研究
模糊 神 经 网络 ( u z e rl ew r ,N 结 F zyn ua nt okF N)
合 了神 经 网络 自学 习 、 自适 应 强 的特 点 和 模 糊 推 理 性 强 的优 点 ,成 为近 年 来 研 究 的 热 点 …。数 控
珩 磨 机 进 给 系统 的模 糊 神 经 网络 控 制 器 ,是 利 用 模 糊 推 理 来 训 练 神 经 网络 ,在 神 经 网络 进 行 学 习 时运 用 B P算法 来 修正 网络参 数 。这 两 者 的结合 对 于 复 杂 多 变 量 系统 ,有 助 于 提 高 学 习速 度 和 控 制
三通 电磁 阀分 别 进 入 高 、低 压 比例 减 压 阀 ,获 得 两 级 压 力 后 进 入 三 位 四通 比 例 换 向 阀。 粗 珩 时 ,
粗 珩 油 缸活 塞 下 移 ,通 过 连 杆 推 动珩 磨头 粗 珩 锥
体 下 移 ,实 现 粗珩 进 给 ;精 珩 时 ,精 珩 油 缸下 移 , 通 过 连 杆 推 动 精 珩 锥 体 下 移 实 现 精 珩 进 给 。珩 磨
层 3:规 则 层 。这 一 层 是 固定 结 点 ,它 首 先
作 所有输 入 信 号的积 ,并 归一 化激 励强 度 ;
云
”4 ’9
其 中 : f ^() (c ,j 1 … , = f e) = , 7 e
层4 输出 : 隶属函 数层。 4 , 云(eqc? 0, f i— - 9 eI) 一 i 1 +j-j i - "
2 f n ,te B )I e s iNB a d ciNM h nUi P . e s s
一
m一 外负载 质量 ,k ; g
一
研一传感器 的位移 / 电压转换 系数 , / V m;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 仿真实例
为了比较, 取文献 [ 2 ] 中所用的系统仿真对象。 设一个带时延的强耦合二变量非线性对象为
y 1 ( k + 1) =
1 [ 0. 8y 1 ( k ) + 1 + y2 1 (k )
图 2 模糊神经网络控制二变量对象的响应曲线
110
控 制 与 决 策
2001年
v 1 ( k - 2) + 0. 2v 2 ( k - 3) ] y 2 ( k + 1) =
作者简介: 李旭明 ( 1969—) , 男, 安徽安庆人, 助教, 硕士, 从事神经网络、 模糊控制等研究。
108
控 制 与 决 策
2001年
图 1 二变量模糊神经网络控制系统
子网络输出信号经规范化后作为单层神经网络的输 入信号, 单层神经网络通过自主学习调整网络权值, 并同时完成系统的解耦工作。 图 1 给出了一个二输入二输出的模糊神经网络 控制系统。 由图可知, 该多变量模糊神经网络包括两 个子网络, 一个单层神经网络, 输入神经元个数为 30, 输出神经元个数为 2。 各子网络相互独立, 分别 接受一个被控量的给定值和实际值。 各子网络在单 层神经网络中相互交叉相连, 该单层神经网络完成 控制规律的综合, 形成多变量对象的控制输入。
V ( K ) 按式 ( 1) 进行规范化处理。 即
(K ) = V′
V (K )
30
, K = 1, 2, …, 30
( 1)
∑
K= 1
V (K )
第 3 步: 单层神经网络计算。 该步是最关键的一 步, 前两步都是为它做准备。 它完成控制规律的综 合, 解模糊形成多变量对象的控制输入, 并通过在线 学习调整网络权值, 完成解耦控制工作。 单层神经网 络计算包括前向计算和反向计算。 1) 前向计算
k + 1, 返回 4) 。
阈值也可相应调整为 Η ′ ∆i ( k ) i ( k + 1) = Η i (k ) + Β
( 7)
式中 Β 和 Β′ 分别为权值和阈值的学习速率因子。 3. 2 多变量模糊神经网络初始值的确定 网络初始值直接关系到学习收敛速度和收敛方 向, 但初值的确定原则目前尚未有系统的理论指导。 一般说, 这些初值应根据被控对象的特点和人的经 验而定。 可在调试过程中用试探法来确定某些参数, 也可用一些优化算法进行寻优。 针对图 1 的控制系 统和所选取的被控对象的特点, 本文用试探法确定 出各变量偏差 ( e1 , e2 ) 论域范围为 ( - 0. 5, + 0. 5) , 偏 差变化率 ( ce1 , ce2 ) 论域范围为 ( - 0. 25, + 0. 25) 。 图 1 中单层神经网络初始权重和阈值的选取非 常重要。 它们的初始化可由计算机随机产生, 也可根 据先验知识人为地加以选择。 本文的做法是: 首先初 ( 步确定初始的权重范围 - 10, 10) , 由计算机随机 产生; 然后带入系统进行训练, 选取其中控制效果最
1 引 言
目前, 模糊神经网络控制系统所控制的对象通 常是 M ISO 系统, 因为操作者大多只能给出一组如 下的二维模糊控制规则: IF ( 偏差为 ei , 偏差变化率 为 ce i ) TH EN ( 控制量为 u i ) 。 若直接推广到多变量系 统, 会遇到很多困难。 首先, 难以建立一组比较完善 的多维 ( ≥ 4 维) 模糊控制规则; 其次, 用于多变量控 制的模糊查询表及关系矩阵 R 将占据大量计算机内 存空间和计算时间, 甚至难以用计算机实现。 由于 M ISO 系统是多变量系统的特殊情况, 并 且在工程实践中所遇到的许多控制对象都是多变量 系统, 因此对 M I M O 系统模糊控制方法的研究具有 重要意义。 目前, 多变量模糊控制系统的研究方兴未 艾, 已成为模糊控制领域研究的热点课题[ 1~ 3 ]。
1, 2。 如果能通过 e l ( k ) 推算得到网络的输出误差, 则
训练便可进行下去。 文献 [ 6 ] 针对多层网络, 通过在 线计算多变量对象输出对输入的偏导数而实现以上 过程。 本文把这种方法用于单层网络的训练, 则单层 网络权值可调整为
第 16 卷 第 1 期
李旭明: 多变量模糊神经网络控制器的研究
( 5)
109
u im ( k + 1) = u im ( k ) + Β∆i ( k ) h ′ m (k )
式中 ∆i ( k ) =
2
-
∑e (k )
l l= 1
∃ y l (k ) u′ u′ i (k ) [ 1 i (k ) ] ∃ u i (k )
( 6)
好的一次网络权值将其保存, 作为控制系统初始化 的权重。 这样便大大加快了网络训练速度, 保证了控 制系统的稳定性。 3. 3 控制算法设计 根据以上讨论, 按本文方法设计多变量自适应 模糊控制器的步骤如下: 1) 训练好 B P 网络; 2) 确定各变量偏差 ( e1 , e2 ) 和偏差变化率 ( ce1 , ce2 ) 论域, 并在其上定义相应的 模糊子集, 确定执行机构的动作范围, 确定单层神经 网络权值和阈值的初值, 设定相应的参数学习率因 子, 取 k = 4; 3) 求各变量值 e1 , e2 , ce1 , ce2 , 并将它们 模糊化; 4) 由 B P 网络求出各子网络输出层的输出 信号; 5) 规范化处理; 6) 按单层神经网络前向计算 方法求出网络的控制输出; 7) 按单层神经网络反向 计算方法在线调整单层网络的权值和阈值; 8) k =
本文提出一种自动完成 M I M O 系统解耦控制 的多变量系统模糊神经网络控制器, 该控制器具有 一定的通用性。 这种多变量模糊神经网络控制系统 在未知对象参数的情况下, 通过训练和学习可实现 系统的解耦控制, 使系统变量之间的相互耦合作用 基本消除。 给出的仿真实例证明了该方法的有效性。 与文献 [ 2 ] 结果相比, 本文方法网络收敛速度加快, 超调小, 系统稳定时间快, 实时性能好, 在过程控制 中具有广阔的应用前景。 参考文献:
摘 要: 提出一种 M I M O 系统的模糊神经网络控制器结构, 阐述了基本设计思想和具体算法过程。 应 用实例仿真结果表明, 它可用于控制强耦合带时延多变量系统, 并使系统具有良好的动态和静态性能。 关键词: 神经网络; 模糊控制; M I M O 系统; 解耦 中图分类号: T P 18 文献标识码: A
收稿日期: 1999211208; 修回日期: 2000203230
2 多变量模糊神经网络控制系统的
结构
设多变量被控对象为 N 输入 N 输出的 N 变量 系统。 本文提出的多变量模糊神经网络控制器的设 计思想是: 对于 N 变量系统, 首先构造 N 个 M ISO 系统并列且相同的子模糊神经网络, 各子网络结构 均为文献 [ 4 ] 给出的优化的 BP 网络: 2626215, 且相 互独立; 然后通过在线测量的系统给定值和输出值, 计算出各子网络的系统偏差 en 和偏差变化率 cen , 按 二输入一输出M ISO 系统模糊神经网络控制器的设 计方法[ 5 ] , 分别计算出各子网络输出的模糊量, 参照 重心法解模糊的思想, 对各子网络输出的模糊量进 行规范化; 最后构造一个单层神经网络 ( 输入层神经 元 个数为 15 ×N , 输出层神经元个数为N ) , 把各
( i) = u′
30
3 多变量模糊神经网络的计算方法
3. 1 计算Βιβλιοθήκη 程1 1 + em
oi + Η i
, i = 1, 2
( 2) ( 3)
oi =
∑v
m= 1
u im , i = 1, 2
本文的多变量模糊神经网络的计算过程分为 3 步。 现以图 1 所示的控制系统为例, 说明这种算法的 具体过程。 第 1 步: 计算各子网络输出层神经元的输出信 号。 设子网络 1 输出信号为 V 1 ( k ) , 子网络 2 输出信 号为 V 2 ( k ) , k = 1, 2, …, 15。 由图 1 可见, 各子网络 分别接受一个被控变量的给定值和实际值, 这样就 可分别计算出各子网络的系统偏差 e 和偏差变化率 ce; 然后将各子网络的 e 和 ce 模糊化, 作为各子网络 的输入信号, 通过已训练好的 B P 网络前向计算, 即 可计算出各子网络的输出信号。 以上过程具体实现 方法与文献 [ 5 ] 模糊神经控制器设计方法基本相 同, 只是省去了解模糊环节。 网络总的输出信号为 V ( K ) = [V 1 , V 2 ], K = 1, 2, …, 30 第 2 步: 规范化处理。 由于各子网络均省去了解 模糊环节, 因此子网络的输出信号为模糊量, 但最后 的控制量必须是精确量。 实际上, 最后一个单层神经 网络包含着解模糊功能, 只是采取的方法与前述解 模糊方法不同。 因此, 在进行单层神经网络计算之 前, 按照重心法的思想, 对各子网络总的输出信号
1 [ 0. 9y 2 ( k ) + 1 + y2 2 (k ) 0. 3v 1 ( k - 3) + v 2 ( k - 2) ]
式中 y i ( z ) 和 v i ( z ) ( i = 1, 2) 分别为对象输入量和 输出量的 z 变换。 给定输入激励为
R 10 = r1 ( k ) r2 ( k )
式中, Η i 为第 i 个输出神经元的阈值, u im 是连接第 i 个输出神经元的第 m 个权重, v m 是单层神经网络的 输入神经元信号。 ( i) 的变化范 由于式 ( 2) 采用 S 型函数, 因此 u ′ ( i) 得到实 围 为 ( 0, 1) 。 可通过适当的线性变换由 u ′ 际控制输出 u ( i) , 比如 ( i) × [ u ( i, m ax ) u ( i) = u ′ u ( i , m in ) ] + u ( i , m in ) , i = 1, 2 ( 4) 式中 u ( i, m ax ) 和 u ( i, m in ) 分别为执行机构所能动 作的最大、 最小值。 2) 反向计算 设 k 时刻单层网络的输入为 h ′ m ( k ) , m = 1, 2, …, 30; 相应的权重系数为 u im ( k ) , m = 1, 2, …, 30; 网络输出的控制作用为 u i ( k ) , i = 1, 2; 系统中能测 得的是对象的输出误差 el ( k ) = r l ( k ) - y l ( k ) , l =
