高考数学(理)必考考点自查清单教学内容
最新高考数学(理科)考点解析及考点分布表资料

2018年高考数学(理科)考点解析一、考核目标与要求数学科高考注重考查中学数学的基础知识、基本技能、基本思想方法(所谓三基),考查空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识、创新意识(五种能力、两种意识)。
具体考试内容根据教育部颁布的《普通高中数学课程标准(实验)》、教育部考试中心颁布的《普通高等学校招生全国统一考试大纲(理科·课程标准实验)》确定。
关于考试内容的知识要求和能力要求的说明如下:1.知识要求知识是指《课程标准》所规定的必修课程、选修课程中的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想方法,还包括按照一定程序与步骤进行运算,处理数据、绘制图表等基本技能。
各部分知识的整体要求及其定位参照《课程标准》相应模块的有关说明.对知识的要求由低到高分为了解、理解、掌握三个层次(分别用A、B、C表示),且高一级的层次要求包含低一级的层次要求.(1)了解(A):要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别、认识它。
“了解”层次所涉及的主要行为动词有:了解,知道、识别,模仿,会求、会解等。
(2)理解(B):要求对所列知识内容有较深刻的理性的认识,知道知识间的逻辑关系,能够对所列知识作正确的描述说明并用数学语言表达,能够利用所学的知识内容对有关问题进行比较、判断、讨论,具备利用所学知识解决简单问题的能力。
“理解”层次所涉及的主要行为动词有:描述,说明,表达、表示,推测、想象,比较、判别、判断,初步应用等。
(3)掌握(C):要求能够对所列的知识内容进行推导证明,能够利用所学知识对问题进行分析、研究、讨论,并且加以解决。
“掌握”层次所涉及的主要行为动词有:掌握、导出、分析,推导、证明,研究、讨论、运用、解决问题等。
2(1会运用图形与图表等手段形象地揭示问题的本质。
高考数学必考知识点总结_数学知识点总结

高考数学必考知识点总结_数学知识点总结2022高考数学必考知识点第一、高考数学中有函数、数列、三角函数、平面向量、不等式、立体几何等九大章节。
主要是考函数和导数,这是我们整个高中阶段里最核心的板块,在这个板块里,重点考察两个方面:第一个函数的性质,包括函数的单调性、奇偶性;第二是函数的解答题,重点考察的是二次函数和高次函数,分函数和它的一些分布问题,但是这个分布重点还包含两个分析就是二次方程的分布的问题,这是第一个板块。
第二、平面向量和三角函数。
重点考察三个方面:一个是划减与求值,第一,重点掌握公式,重点掌握五组基本公式。
第二,是三角函数的图像和性质,这里重点掌握正弦函数和余弦函数的性质,第三,正弦定理和余弦定理来解三角形。
难度比较小。
第三、数列。
数列这个板块,重点考两个方面:一个通项;一个是求和。
第四、空间向量和立体几何,在里面重点考察两个方面:一个是证明;一个是计算。
第五、概率和统计。
这一板块主要是属于数学应用问题的范畴,当然应该掌握下面几个方面,第一……等可能的概率,第二………事件,第三是独立事件,还有独立重复事件发生的概率。
第六、解析几何。
这是我们比较头疼的问题,是整个试卷里难度比较大,计算量的题,当然这一类题,我总结下面五类常考的题型,包括:第一类所讲的直线和曲线的位置关系,这是考试最多的内容。
考生应该掌握它的通法;第二类我们所讲的动点问题;第三类是弦长问题;第四类是对称问题,这也是2008年高考已经考过的一点;第五类重点问题,这类题时往往觉得有思路,但是没有答案,当然这里我相等的是,这道题尽管计算量很大,但是造成计算量大的原因,往往有这个原因,我们所选方法不是很恰当,因此,在这一章里我们要掌握比较好的算法,来提高我们做题的准确度,这是我们所讲的第六大板块。
第七、押轴题。
考生在备考复习时,应该重点不等式计算的方法,虽然说难度比较大,我建议考生,采取分部得分整个试卷不要留空白。
这是高考所考的七大板块核心的考点。
2021版高考理科数学人教通用版大一轮复习基础自查学案:6.6 数学归纳法

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
第六节数学归纳法知识体系必备知识数学归纳法一般地,证明一个与正整数n有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n取第一个值n0(n0∈N*)时命题成立.(2)(归纳递推)假设n=k(k≥n0,k∈N*)时命题成立,证明当n=k+1时命题也成立.只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.上述证明方法叫做数学归纳法.1.数学归纳法的两个注意点(1)数学归纳法证题时初始值n0不一定是1.(2)推证n=k+1时一定要用上n=k时的假设,否则不是数学归纳法. 2.易忽视“归纳—猜想—证明”问题的前若干具体项的计算解“归纳——猜想——证明”题的关键是准确计算出前若干具体项,这是归纳、猜想的基础,否则将会做大量无用功.基础小题1.给出以下对数学归纳法的描述,其中正确的个数是( )(1)用数学归纳法证明问题时,第一步是验证当n=1时结论成立.(2)所有与正整数有关的数学命题都必须用数学归纳法证明.(3)用数学归纳法证明问题时,归纳假设可以不用.(4)不论是等式还是不等式,用数学归纳法证明时,由n=k到n=k+1时,项数都增加了一项.(5)用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证n=1时,左边式子应为1+2+22+23.A.1B.2C.3D.4【解析】选A.第一步验证初始值n0不一定是n=1,故(1)错误;并不是所有与正整数有关的数学命题都必须用数学归纳法证明,故(2)错误;数学归纳法一定用归纳假设,故(3)错误;不论是等式还是不等式,用数学归纳法证明时,由n=k到n=k+1时,项数增加了不止一项,故(4)错误;(5)正确.2.(教材改编)用数学归纳法证明“1+2+22+…+2n-1=2n-1(n∈N*)”的过程中,第二步n=k时等式成立,则当n=k+1时,应得到( )A.1+2+22+…+2k-2+2k-1=2k+1-1B.1+2+22+…+2k+2k+1=2k-1+2k+1C.1+2+22+…+2k-1+2k+1=2k+1-1D.1+2+22+…+2k-1+2k=2k+1-1【解析】选D.由条件知,左边从20,21到2n-1都是连续的,因此当n=k+1时,左边应为1+2+22+…+2k-1+2k,而右边应为2k+1-1.3.某个命题与正整数有关,如果当n=k(k∈N*)时命题成立,那么可推得当n=k+1(k∈N*)时命题也成立.现已知当n=8时该命题不成立,那么可推得( )A.当n=7时该命题不成立B.当n=7时该命题成立C.当n=9时该命题不成立D.当n=9时该命题成立【解析】选A.根据逆否命题和原命题的真假一致性得,当n=k(k∈N*)时命题不成立,则n=k-1(k∈N*)命题也不成立,所以当n=8时命题不成立,则n=7时命题也不成立.4.(教材改编)用数学归纳法证明“1+a+a2+…+a n+1=(a≠1)”.当验证n=1时,上式左端计算所得为____________.【解析】当n=1时,左边=1+a+a2.答案:1+a+a25.设数列{a n}满足a1=2,a n+1=2a n+2,用数学归纳法证明a n=4·2n-1-2的第二步中,假设当n=k时结论成立,即a k=4·2k-1-2,那么当n=k+1时,________.【解析】因为a k=4·2k-1-2,所以a k+1=2a k+2=2(4·2k-1-2)+2=4·2(k+1)-1-2.答案:a k+1=2a k+2=4·2(k+1)-1-26.已知f(n)=+++…+,则f(k+1)=f(k)+________.【解析】因为f(n)=+++…+,所以f(k)=+++…+.f(k+1)=+++…+=+++…++=f(k)+-答案:-关闭Word文档返回原板块。
高考理科数学必考知识内容

高考理科数学必考知识内容高考理科数学的考点1.【数列】【解三角形】数列与解三角形的知识点在解答题的第一题中,是非此即彼的状态,近些年的特征是大题第一题两年数列两年解三角形轮流来, 20__、220__大题第一题考查的是数列,220__大题第一题考查的是解三角形,故预计220__大题第一题较大可能仍然考查解三角形。
数列主要考察数列的定义,等差数列、等比数列的性质,数列的通项公式及数列的求和。
解三角形在解答题中主要考查正、余弦定理在解三角形中的应用。
2.【立体几何】高考在解答题的第二或第三题位置考查一道立体几何题,主要考查空间线面平行、垂直的证明,求二面角等,出题比较稳定,第二问需合理建立空间直角坐标系,并正确计算。
3.【概率】高考在解答题的第二或第三题位置考查一道概率题,主要考查古典概型,几何概型,二项分布,超几何分布,回归分析与统计,近年来概率题每年考查的角度都不一样,并且题干长,是学生感到困难的一题,需正确理解题意。
4.【解析几何】高考在第20题的位置考查一道解析几何题。
主要考查圆锥曲线的定义和性质,轨迹方程问题、含参问题、定点定值问题、取值范围问题,通过点的坐标运算解决问题。
5.【导数】高考在第21题的位置考查一道导数题。
主要考查含参数的函数的切线、单调性、最值、零点、不等式证明等问题,并且含参问题一般较难,处于必做题的最后一题。
6.【选做题】今年高考几何证明选讲已经删除,选考题只剩两道,一道是坐标系与参数方程问题,另一道是不等式选讲问题。
坐标系与参数方程题主要考查曲线的极坐标方程、参数方程、直线参数方程的几何意义的应用以及范围的最值问题;不等式选讲题主要考查绝对值不等式的化简,求参数的范围及不等式的证明。
高考数学必考知识点归纳圆的标准方程(x-a)2+(y-b)2=r2注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0注:D2+E2-4F0抛物线标准方程y2=2pxy2=-2p__2=2pyx2=-2py直棱柱侧面积S=c__h斜棱柱侧面积S=c__h正棱锥侧面积S=1/2c__h正棱台侧面积S=1/2(c+c)h圆台侧面积S=1/2(c+c)l=pi(R+r)l球的表面积S=4pi__r2某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41__2+2__3+3__4+4__5+5__6+6__7+…+n(n+1)=n(n+1)(n+2)/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角圆的标准方程 (x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F0抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积 S=c__h 斜棱柱侧面积 S=c__h正棱锥侧面积 S=1/2c__h 正棱台侧面积 S=1/2(c+c)h圆台侧面积 S=1/2(c+c)l=pi(R+r)l 球的表面积 S=4pi__r2圆柱侧面积 S=c__h=2pi__h 圆锥侧面积 S=1/2__c__l=pi__r__l弧长公式 l=a__r a是圆心角的弧度数r 0 扇形面积公式 s=1/2__l__r 锥体体积公式 V=1/3__S__H 圆锥体体积公式 V=1/3__pi__r2h斜棱柱体积 V=SL 注:其中,S是直截面面积, L是侧棱长柱体体积公式 V=s__h 圆柱体 V=pi__r2h高考数学必考公式知识点1.适用条件:[直线过焦点],必有ecosA=(x-1)/(x+1),其中A为直线与焦点所在轴夹角,是锐角。
高中数学自查清单

数学自查清单一.集合与逻辑1.集合的运算(数集、点集、代表元)、集合间关系;2.逻辑(四种命题、充要条件、复合命题、全称和特称命题及其否定)二.复数与算法3.复数(纯虚数、复数相等、实部虚部、运算、模、共轭复数、在复平面中的表示、i n的周期性);4.算法(输出结果、判断条件、三种结构、二次不等式解法的程序框图);框图(知识结构图、组织结构图、工序流程图看课本例题。
)三.函数与导数5.函数的概念(定义域、解析式的求法(配方法、待定系数法、换元法、方程组法、直接法、相关点法)、值域的求法(单调性、图像法、配方法、导数法等)、相同函数的含义、分段函数);6.函数的性质(单调性判断和应用、奇偶性判断和应用、周期性(结论、应用)、对称性);7.函数图像(画法、应用、伸缩变换、平移变换、翻折变换、图像辨析);8.函数的零点及零点存在性定理、二分法;9.基本初等函数(二次函数(含给定区间求最值、根的分布、三个二次间的关系)、反比例函数、指数函数、对数函数、幂函数)的定义、图像和性质;10.导数(平均变化率、常见函数的导数、加减乘除的导数;导数切线的求法(两种);)11.导数研究函数单调性、极值(列表)、最值及其应用(不等式证明、恒成立问题、零点个数问题等)、常见技巧(构造函数、放缩法、分离变量等);四.三角与向量12.三角函数图像和性质(最值、对称中心和对称轴、单调性、周期性、奇偶性,重点是推广到y()f x kωφ=++的性质研究和五(六)点法作图);13.同角三角函数基本关系式、诱导公式、辅助角公式、和差倍角公式应用(求角、求值等);三角换元;14.正余弦定理及应用(含实际应用求高度、角度、距离;含在立体几何、解析几何中的应用),注意公式变形、边角互化、分类讨论解的个数;15.平面向量(概念、几何和坐标运算、共线向量(证明平行、等式)、平面向量基本定理及应用、数量积(含几何意义)、求模、夹角、证明垂直问题(等式));五.概率与统计16.概率(古典概型、几何概型(课本典型例题)、互斥事件、对立事件以及计算公式);17.统计(抽样方法(简单随机抽样、分层抽样、系统抽样)、频率分布直方图(画法、据图进行相关数据的研究)、茎叶图、众数、中位数、平均数、方差、标准差);18.回归直线(a、b求法、样本点中心、回归直线意义);19.独立性检验(含2*2列联表);六.立体几何20.线线、线面、面面平行与垂直的证明和性质;几何体体积的计算;三视图;七.不等式21.不等式的性质及适用条件;22.不等式解法(二次不等式、分数不等式、含参不等式、指数和对数不等式(化同底结合单调性)、理科含两个绝对值号的不等式、三角不等式的几何意义、推广。
高考数学 集合与常用逻辑用语考点及知识点总结解析(理科)

②若B≠∅,则2mm+-11≥≥-m2+,1, 2m-1≤5.
解得2≤m≤3.由①②可得,符合题意的实数m的取值范围为 (-∞,3].
[答案] (-∞,3]
[易错提醒] 将两个集合之间的关系准确转化为参数所满足的条 件时,应注意子集与真子集的区别,此类问题多与不等 式(组)的解集相关.确定参数所满足的条件时,一定要把 端点值代入进行验证,否则易产生增解或漏解.
考点贯通 抓高考命题的“形”与“神” 集合子集个数的判定
含有n真子集的个数为2n-2(除空集 和集合本身,此时n≥1).
[例1] 已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x
<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为
()
A.1
B.2
C.3
D.4
[解析] 由x2-3x+2=0得x=1或x=2,所以A={1,2}.由
题意知B={1,2,3,4},所以满足条件的集合C为{1,2},{1,2,3},
{1,2,4},{1,2,3,4},共4个.
[答案] D
[易错提醒] (1)注意空集的特殊性:空集是任何集合的子集,是 任何非空集合的真子集. (2)任何集合的本身是该集合的子集,在列举时千万 不要忘记.
∵
2x
-
3>0
,
∴
x>
3 2
,
∴
B
=
3 xx>2
.
∴
A∩B
=
{x|1<x<3}∩xx>32 =32,3. [答案] D
2022年高考数学考点分布细目表
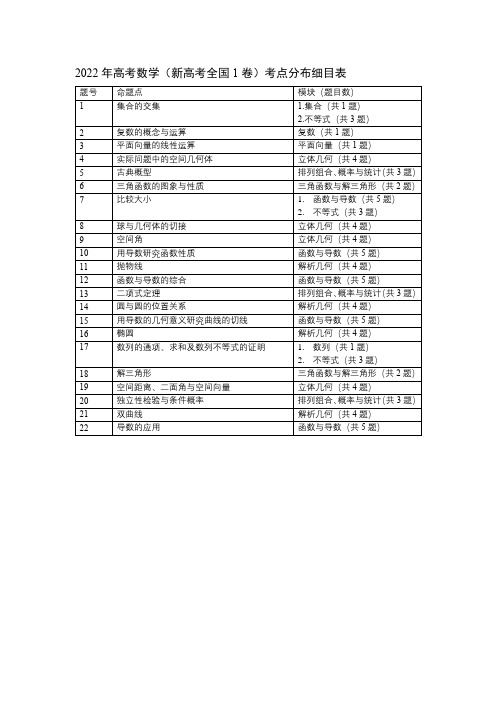
命题点
模块(题目数)
1
集合的补集运算
集合(共1题)
2
复数相等及复数的运算
复数(共1题)
3
平面向量的数量积
平面向量(共1题)
4
数列项的大小比较
1.数列(共2题)
2.不等式(共1题)
5
抛物线的几何性质
解析几何(共4题)
6
程序框图
算法初步(共1题)
7
空间中的线面位置关系
立体几何(共3题)
8
等比数列
数列(共2题)
18
等差数列
数列(共1题)
19
线面平行与几何体的体积
立体几何(共4题)
20
导数的几何意义
函数与导数(共4题)
21
抛物线
1.解析几何(共4题)
2.三角函数与解三角形(共3题)
3.不等式(共2题)
22
极坐标与参数方程
选修4-4(共1题)
23
不等式证明
选修4-5(共1题)
2022高考数学(全国乙卷理)考点分布细目表
18
面面垂直的证明与线面角
立体几何(共3题)
19
用样本估计总体、回归分析
概率统计(共3题)
20
椭圆方程及定点问题
解析几何(共4题)
21
导数的几何意义及函数零点
函数与导数(共3题)
22
极坐标与参数方程
选修4-4(共1题)
23
不等式证明
选修4-5(共1题)
2022高考数学真题(全国乙卷文)考点分布细目表
3
集合的运算
集合(共1题)
4
三视图
立体几何(共4题)
5
2020高考数学考前知识自查

最后的叮咛,高考数学考前知识自查亲爱的高三同学,当您即将迈进考场时,对于以下问题,您是否有清醒的认识?您的老师提醒您:1.函数有三要素:定义域、对应法则和值域。
定义域是函数的一个部分,求函数一定要指出其定义域,另外研究函数的性质时一定要先明确定义域(就如你早上起床要刷牙幺:)),定义域一定要写成集合的形式。
如:()f x 定义域为[]0,1,(2)f x 定义域为?10,2⎡⎤⎢⎥⎣⎦2.函数值域的一般求法你还记得吗?利用单调性、利用导数、利用函数的图像、利用基本不等式、利用常见函数的性质等。
求函数的最值,一般要指出取得最值时相应的自变量的值。
3.四种命题是指原命题、逆命题、否命题和逆否命题,它们之间有哪三种关系?只有互为逆否的命题同真假!复合命题的真值表你记住了吗?命题的否定和否命题不一样,差别在哪呢?“任意”的否定是“存在”,而“存在”的否定是“任意”;充分条件、必要条件和充要条件的概念记住了吗?如何判断?4.绝对值的几何意义是什么?与复数模的几何意义一样吗?都是距离哎!含绝对值的不等式的解法你都了解吗?不等式c b ax <+||,c b ax >+||)0(>c ,|()|()f x g x >,|()|()f x g x <,|()||()|f x g x <的解法都掌握了吗?去绝对值的三个绝招:讨论绝对值符号内式子的符号;平方;绝对值的性质。
5.如何利用二次函数求最值?注意对2x 项的系数进行讨论了吗?晓得2x 项前的系数是确定抛物线形状的,而其它参数仅是用来确定抛物线位置的;若2(2)2(2)10a x a x −+−−<对任意实数x 恒成立,你对2a −=0的情况进行讨论了吗?6.二次函数的三种形式:一般式、交点式、和顶点式,你了解各自的特点吗?特别提醒:二次方程02=++c bx ax 的两根即为不等式02>++c bx ax )0(<解集的端点值,也是二次函数c bx ax y ++=2的图象与x 轴的交点的横坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学(理)必考考点自查清单
高考数学(理)必考考点自查清单
核心考点(必考+高频):根据2014年山东省普通高校招生考试说明的精神及近3—5年山东省高考考试题、2013年高考新课标全国卷1
收集于网络,如有侵权请联系管理员删除
收集于网络,如有侵权请联系管理员删除
收集于网络,如有侵权请联系管理员删除
备注:掌握程度I 、II ——对知识内容要求掌握的程度分为I 和II 两个层次。
Ⅰ.对所列知识要知道其内容及含义,并能在有关问题中识别和直接使用,与课程标准中的“了解”和“认识” 相当。
Ⅱ.对所列知识要理解其确切含义及与其他知识的联系,能够进行叙述和解释,并能在实际问题的分析、综合、推理和判断等过程中运用。
与课程标准中的“理解”和“应用”相当。
义,标准方程与性质
36、直线与圆锥曲线的位置关系
III 2) 直线与圆锥曲线的综合问题(弦长、参数
范围、最值、定点定值、向量等)
概率 统计
计数原理 37、两个原理、排列组合 38、二项式定理
II I 1)两个原理与排列组合解决简单的实际问题 2)二项式定理解决二项展开式
概率
39、概型及事件
40、离散型随机变量分布列 41、期望与方差性质 42、正态分布
II III
1) 区别古典概型、几何概型、条件概型、独立、
重复试验等概型 2)区别互斥、对立、独立事件
3)求离散型随机变量的分布列,计算均值、方差 4)正态分布的概率密度曲线及性质
统计 43、三种抽样
44、用样本估计总体
45、变量的相关性与独立性检验 I 1)分层抽样和系统抽样的过程 2)频率分布直方图及数字特征 3)回归分析和独立性检验
算法 归纳推理
46、程序框图,数学归纳法, 归纳推理
I
1)程序框图的逻辑结构
2)用归纳类比进行简单的推理。
