管理统计学9一元线性回归
第9章-方差分析与线性回归
Xij X E
s nj
ST s
n
E
j
j 1
i 1
X ij X
j1 i1
s nj
X ij2 nX
j1 i1
X ij 2
2
2
s nj
X
EE(X
)j
s11ninj1jEs1Xinj1ijjE21(Xiinj1)X
1 n
s
nj ( j )
j 1
s nj
E( Xij2 ) nE( X 2 )
X12 X 22
As : N s , 2
X1s X 2s
X n11
X n2 2
X nss
每个总体相互独立. 因此, 可写成如 下的 数学模型:
ij
~
X ij j ij N (0, 2 ), 各ij独立
i 1, 2, , nj，j 1, 2, , s
方差分析的目的就是要比较因素A 的r 个水平下试验指标理论均值的 差异, 问题可归结为比较这r个总体 的均值差异.
i
ij (0, 2 ),各ij独立
1, 2, , nj，j 1, 2, , s
n11 n22 ... nss 0
假设等价于 H0 :1 2 s 0
H1 :1,2,
,
不全为零。
s
为给出上面的检验，主要采用的方法是平方和 分解。即
假设数据总的差异用总离差平方和 ST 分解为
第九章 回归分析和方差分析
关键词： 单因素试验 一元线性回归
方差分析(Analysis of variance, 简 称:ANOVA),是由英国统计学家费歇尔 (Fisher)在20世纪20年代提出的,可用于推 断两个或两个以上总体均值是否有差异 的显著性检验.
统计学一元线性回归模型
• 回归分析仅对存在因果关系而言。
正相关 线性相关 统计依赖关系 不相关 相关系数： 有因果关系 无因果关系 回归分析 相关分析 负相关 1 XY 1 正相关 非线性相关 不相关 负相关
1、关于模型关系的假设
• 模型设定正确假设。The regression model is correctly specified. • 线性回归假设。The regression model is linear in the parameters。
Yi 0 1 X i i
• 称为观察值围绕它的期望值的离差 （deviation），是一个不可观测的随机变量， 又称为随机干扰项（stochastic disturbance）或 随机误差项（stochastic error）。
i Yi E (Y | X i )
• 例2.1.1中，给定收入水平Xi ,个别家庭的支出 可表示为两部分之和：
• 回归分析构成计量经济学的方法论基础，其主 要内容包括：
– 根据样本观察值对经济计量模型参数进行估计，求得 回归方程；
– 对回归方程、参数估计值进行显著性检验；
– 利用回归方程进行分析、评价及预测。
二、总体回归函数 Population Regression Function, PRF
1、条件均值（conditional mean）
E (Y | X i ) f ( X i )
• 含义：回归函数（PRF）说明被解释变量Y的 平均状态（总体条件期望）随解释变量X变化 的规律。 • 函数形式：可以是线性或非线性的。 • 例2.1.1中，将居民消费支出看成是其可支配收 入的线性函数时:
一元线性回归方程的显著性检验
回归方程的显著性检验回归方程的显著性检验的目的是对回归方程拟合优度的检验。
F检验法是英国统计学家Fisher提出的，主要通过比较两组数据的方差S2，以确定他们的精密度是否有显著性差异。
回归方程显著性检验具体方法为：由于y的偏差是由两个因素造成的，一是x变化所引起反应在S回中，二是各种偶然因素干扰所致S残中。
将回归方程离差平方和S回同剩余离差平方和S残加以比较，应用F检验来分析两者之间的差别是否显著。
如果是显著的，两个变量之间存在线性关系；如果不显著，两个变量不存在线性相关关系。
n个观测值之间存在着差异，我们用观测值yi与其平均值的偏差平方和来表示这种差异程度，称其为总离差平方和，记为由于所以式中称为回归平方和，记为S回。
称为残差平方和，记为。
不难证明，最后一项。
因此S总＝S回＋S残上式表明，y的偏差是由两个因素造成的，一是x变化所引起，二是各种偶然因素干扰所致。
事实上，S回和S残可用下面更简单的关系式来计算。
具体检验可在方差分析表上进行。
这里要注意S回的自由度为1，S残的自由度为n－2，S总的自由度为n－1。
如果x与y有线性关系，则其中，F（1，n-2）表示第一自由度为1，第二自由度为n-2的分布。
在F表中显著性水平用表示，一般取0.10，0.05，0.01，1-表示检验的可靠程度。
在进行检验时，F值应大于F表中的临界值Fα。
若F<0.05(1,n-2)，则称x与y 没有明显的线性关系，若F0.05(1,n-2)<F<F0.01(1,n-2)，则称x与y有显著的线性关系；若F>F0.01(1,n-2)，则称x与y有十分显著的线性关系。
当x与y有显著的线性关系时，在表2-1-2的显著性栏中标以〝*〞；当x与y有十分显著的线性关系时，标以〝**〞。
统计学-第11章一元线性回归学习指导
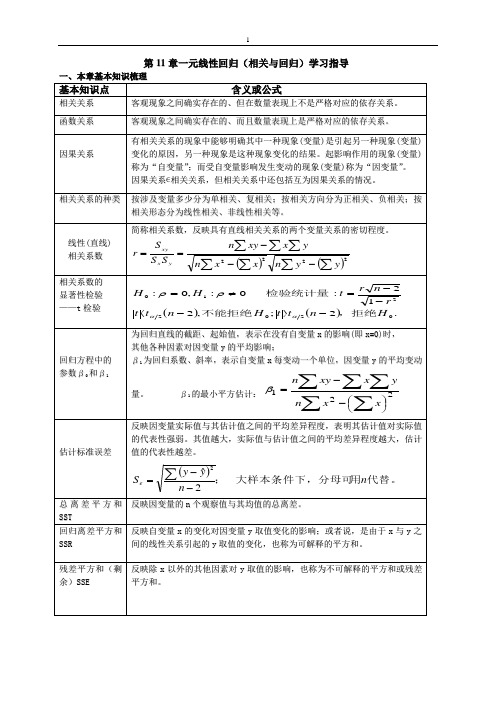
第11章一元线性回归（相关与回归）学习指导一、本章基本知识梳理基本知识点含义或公式相关关系 客观现象之间确实存在的、但在数量表现上不是严格对应的依存关系。
函数关系 客观现象之间确实存在的、而且数量表现上是严格对应的依存关系。
因果关系有相关关系的现象中能够明确其中一种现象(变量)是引起另一种现象(变量)变化的原因，另一种现象是这种现象变化的结果。
起影响作用的现象(变量)称为“自变量”；而受自变量影响发生变动的现象(变量)称为“因变量”。
因果关系∊相关关系，但相关关系中还包括互为因果关系的情况。
相关关系的种类 按涉及变量多少分为单相关、复相关；按相关方向分为正相关、负相关；按相关形态分为线性相关、非线性相关等。
线性(直线) 相关系数 简称相关系数，反映具有直线相关关系的两个变量关系的密切程度。
()()∑∑∑∑∑∑∑---==2222y yn x xn yx xy n SS S r yx xy相关系数的 显著性检验 ——t 检验 ()().2;,212:0:,0:020221Hn t t Hn t t rn r t HH，拒绝不能拒绝检验统计量-〉-〈--=≠=ααρρ回归方程中的 参数β0和β1为回归直线的截距、起始值，表示在没有自变量x 的影响(即x =0)时，其他各种因素对因变量y 的平均影响；β1为回归系数、斜率，表示自变量x 每变动一个单位，因变量y 的平均变动量。
β1的最小平方估计：∑∑∑∑∑⎪⎭⎫ ⎝⎛--=221x x n yx xy nβ估计标准误差反映因变量实际值与其估计值之间的平均差异程度，表明其估计值对实际值的代表性强弱。
其值越大，实际值与估计值之间的平均差异程度越大，估计值的代表性越差。
()代替。
用大样本条件下，分母可；n n yyS e 2ˆ2--=∑总离差平方和S S T反映因变量的n 个观察值与其均值的总离差。
回归离差平方和S S R 反映自变量x 的变化对因变量y 取值变化的影响；或者说，是由于x 与y 之间的线性关系引起的y 取值的变化，也称为可解释的平方和。
统计学一元线性回归分析练习题
统计学一元线性回归分析练习题一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。
总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。
本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法的学习与掌握。
同时，也介绍了极大似然估计法以及矩估计法。
本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。
统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。
本章还有三方面的内容不容忽视。
其一，若干基本假设。
样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。
Goss-markov定理表明OLS估计量是最佳线性无偏估计量。
其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。
二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为kids??0??1educ??随机扰动项?包含什么样的因素？它们可能与教育水平相关吗？上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。
统计学一元线性回归课后习题答案分析
(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形 态 (2)计算线性相关系数，说明两个变量之间的关系强度。 (3)利用最小二乘法求出估计的回归方程，并解释回归系数的实 际意义。
运送时间（天）
(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形态
(4)计算判定系数，并解释其意义。
= 81444968.68 =0.9963 81750763.71
人均GDP对人均消费的影响达到99.6%。
(5)检验回归方程线性关系的显著性(a=0.05)。
提出假设
H0：1=0 人均消费水平与人均GDP之间的
线性关系不显著 计算检验统计量F
F SSR 1 81444968.68 1 1331.6921 SSE (n 2) 305795.03 (7 2)
率
次数
1
81.1
21
2
76.6
58
3
76.6
85
4
75.7
68
5
73.8
74
6
72.2
93
7
71.2
72
8
70.8
122
9
91.4
18
10
68.5
125
1）绘制散点图，说明二者之间的股息形态
顾客投诉次数
140 120 100
80 60 40 20
0 0
20
40
60
航班正点率
二者之间为负的线性相关关系
1580.46315 E( y0 ) 2975.74999
人均GDP为5 000元时，人均消费水平95％的预 测区间为[1580.46315，2975.74999]。
(09)第9章 一元线性回归(2011年)
变量之间是否存在关系？ 如果存在，它们之间是什么样的关系？ 变量之间的关系强度如何？ 样本所反映的变量之间的关系能否代表总体 变量之间的关系？
9-9 *
9.1 变量间的关系 9.1.1 变量间是什么样的关系？
统计学 STATIS TICS
函数关系
(第四版) 1. 是一一对应的确定关系 2. 设有两个变量 x 和 y ，变量 y y 随变量 x 一起变化，并完 全依赖于 x ，当变量 x 取某 个数值时， y 依确定的关系 取相应的值，则称 y 是 x 的 函数，记为 y = f (x)，其中 x 称为自变量，y 称为因变量 x 3. 各观测点落在一条线上
y 是 x 的线性函数(部分)加上误差项 线性部分反映了由于 x 的变化而引起的 y 的变化 误差项 是随机变量 反映了除 x 和 y 之间的线性关系之外的随机因素 对 y 的影响 是不能由 x 和 y 之间的线性关系所解释的变异性 0 和 1 称为模型的参数
9 - 30 *
统 计 学 数据分析 (方法与案例)
作者 贾俊平
统计学 STATIS TICS
(第四版)
统计名言
不要过于教条地对待研究的结果， 尤其当数据的质量受到怀疑时。
——Damodar N.Gujarati
9-2 *
第 9 章 一元线性回归
9.1 9.2 9.3 9.4 变量间关系的度量 一元线性回归的估计和检验 利用回归方程进行预测 用残差检验模型的假定
9-7
*
第 9 章 一元线性回归
9.1 变量间的关系
9.1.1 变量间是什么样的关系？ 9.1.2 用散点图描述相关关系 9.1.3 用相关系数度量关系强度
统计学 一元线性回归
第11章 一元线性回归
第一节 变量间关系的度量 第二节 一元线性回归 第三节 利用回归方程进行估计和预测 第四节 残差分析
学习内容
1. 相关关系的分析方法 2. 一元线性回归的基本原理和参数的最小二乘估计 3. 回归直线的拟合优度 4. 回归方程的显著性检验 5. 利用回归方程进行估计和预测 6. 残差分析
r (x x)(y y) (x x)2 (y y)2
或化简为 r
n xy x y
n x2 x2 n y2 y2
相关系数的性质
性质1：r 的取值范围是 [-1,1]
|r|=1，为完全相关 r =1，为完全正相关 r =-1，为完全负相关
r = 0，讨论：r=0意为着什么？
3. 利用所求的关系式，根据一个或几个变量的 取值来预测或控制另一个特定变量的取值， 并给出这种预测或控制的精确程度。
回归分析的特点:
（1）相关分析所研究的两个变量是对等关系。 回归分析所研究的两个变量不是对等关系， 必须根据研究目的，先确定其中一个是自变 量，另一个是因变量。
（2）对两个变量x和y 来说，相关分析只能计算出一 个相关系数，计算中改变x和y 的地位不影响相关系 数的数值； 回归分析则不同，有时可以根据研究目的不同 分别建立两个不同的回归方程。即以x为自变量，y 为因变量，则可以得出y倚x 的回归方程；若以y 为 自变量，x为因变量，则可以得出x倚y 的回归方程。
影响
是不能由 x 和 y 之间的线性关系所解释的变异性 b0 和 b1 称为模型的参数
一元线性回归模型
(基本假定)
1. 因变量x与自变量y之间具有线性关系 2. 在重复抽样中，自变量x的取值是固定的，即假定x是非
统计学一元线性回归课后习题答案
要求： (1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并 说明二者之间的关系形态。
置信区间为
ˆ y0 t 2 ( n 2) se 1 n
x0 x 2 n xi x 2
i 1
1 2278.1078 2.5706*61159.007 7 13625127.29 1990.74915<E(y)2565.46399 人均GDP为5 000元时，人均消费水平95％的 置信区间为[1990.74915，2565.46399]
根据图表显示，二者可能存在正线性相关关系
(2)计算线性相关系数，说明两个变量之间的关系强度
运送距离x 运送距离x 1
运送时间y
运送时间y
0.94894
1
x与y的简单相关系数是0.9489，两 变量之间呈现高度正相关关系
(3)利用最小二乘法求出估计的回归方程，并解释回归系数的实际意义 ^ ^ ^= + x 最小二乘估计：y 0 1
（1）绘制产量与生产费用的散点图，判断二者之间的关系形态。
产量与生产费用 200 180 160 140 120 100 80 60 40 20 0 0 20 40 60 80 产量 100 120 140 160 系列1
费用
产量和费用存在正的线性相关系数
2）计算产量与生产费用之间的线性相关系数。
(1)绘制运送距离和运送时间的散点图，判断二者之间的关系形 态 (2)计算线性相关系数，说明两个变量之间的关系强度。 (3)利用最小二乘法求出估计的回归方程，并解释回归系数的实 际意义。
计量经济学 第二章 一元线性回归模型
计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述（1）确定性关系或函数关系：变量之间有唯一确定性的函数关系。
其一般表现形式为：一、回归模型的一般形式变量间的关系经济变量之间的关系，大体可分为两类：（2.1)（2）统计关系或相关关系：变量之间为非确定性依赖关系。
其一般表现形式为：(2.2)例如：函数关系：圆面积S =统计依赖关系/统计相关关系：若x和y之间确有因果关系，则称(2.2)为总体回归模型，x(一个或几个）为自变量（或解释变量或外生变量），y为因变量（或被解释变量或内生变量），u为随机项，是没有包含在模型中的自变量和其他一些随机因素对y的总影响。
一般说来，随机项来自以下几个方面：1、变量的省略。
由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。
2、统计误差。
数据搜集中由于计量、计算、记录等导致的登记误差；或由样本信息推断总体信息时产生的代表性误差。
3、模型的设定误差。
如在模型构造时，非线性关系用线性模型描述了；复杂关系用简单模型描述了；此非线性关系用彼非线性模型描述了等等。
4、随机误差。
被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。
若相互依赖的变量间没有因果关系，则称其有相关关系。
对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。
他们各有特点、职责和分析范围。
相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析，但在大多数情况下，则是和回归分析结合在一起，进行综合分析，作为回归分析方法的补充。
回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。
一元线性回归教案
一元线性回归教案引言一元线性回归是统计学中非常重要的一种回归分析方法。
它能够通过建立一个线性模型，根据自变量的值来预测因变量的值。
本教案将介绍一元线性回归的基本概念、原理和应用场景，并通过示例演示如何进行一元线性回归分析。
目录1.什么是一元线性回归？2.一元线性回归的原理3.数据的处理与准备4.拟合一元线性回归模型5.模型评估与预测6.应用案例分析7.总结1. 什么是一元线性回归？一元线性回归是指只有一个自变量和一个因变量的线性回归模型。
它的数学表达式为：Y = β0 + β1X + ε，其中Y是因变量，X是自变量，β0和β1是模型的参数，ε是误差项。
一元线性回归的目标是找到最合适的β0和β1，使得模型对观测数据点的拟合程度最优。
2. 一元线性回归的原理一元线性回归的原理基于最小二乘法，即通过最小化观测值与模型预测值之间的差异来确定模型的参数。
最小二乘法可以通过求解正规方程来获得最优的参数估计值。
3. 数据的处理与准备在进行一元线性回归分析之前，需要对数据进行处理和准备。
这包括数据清洗、变量选择和数据可视化等步骤。
本节将介绍常用的数据处理方法，以及如何选择适当的自变量和因变量。
4. 拟合一元线性回归模型拟合一元线性回归模型是通过最小二乘法来确定模型的参数估计值。
本节将介绍如何使用Python中的scikit-learn库来拟合一元线性回归模型，并分析模型的拟合结果。
5. 模型评估与预测在拟合一元线性回归模型之后，需要对模型进行评估和预测。
本节将介绍常用的评估指标，如均方误差（MSE）和决定系数（R-squared），以及如何使用模型进行预测。
6. 应用案例分析本节将通过一个实际的数据集来展示一元线性回归的应用场景。
通过分析数据集中的自变量和因变量之间的关系，我们可以建立一元线性回归模型，并对模型进行评估和预测。
7. 总结本教案从一元线性回归的基本概念和原理开始，通过示例和实践对一元线性回归进行了详细讲解。
一元线性回归模型检验
§2.4 一元线性回归的模型检验一、经济意义检验。
二、在一元回归模型的统计检验主要包括如下几种检验1、拟合优度检验(R2检验;2、自变量显著性检验(t检验;3、残差标准差检验(SE检验。
•主要检验模型参数的符号、大小和变量之间的相关关系是否与经济理论和实际经验相符合。
一、经济意义检验i•二、统计检验•回归分析是要通过样本所估计的参数来代替总体的真实参数,或者说是用样本回归线代替总体回归线。
•尽管从统计性质上已知,如果有足够多的重复抽样,参数的估计值的期望(均值就等于其总体的参数真值,但在一次抽样中,估计值不一定就等于该真值。
那么,在一次抽样中,参数的估计值与真值的差异有多大,是否显著,这就需要进一步进行统计检验。
1、拟合优度检验拟合优度检验:对样本回归直线与样本观测值之间拟合程度的检验。
度量拟合优度的指标:判定系数(可决系数R2(1、总离差平方和的分解已知由一组样本观测值(X i ,Y i ,通过估计得到如下样本回归直线ii X Y 10ˆˆˆββ+=i i i i i i i y e Y Y Y Y Y Y y ˆˆ(ˆ(+=-+-=-=总离差平方和的分解ii X Y 10ˆˆˆββ+=ˆ(ˆY Y y i i -=i i i i i i i ye Y Y Y Y Y Y y ˆˆ(ˆ(+=-+-=-=Y 的i 个观测值与样本均值的离差由回归直线解释的部分回归直线不能解释的部分离差分解为两部分之和总离差平方和的分解公式:TSS=RSS+ESS,TSS 总离差平方和,ESS 为回归平方和,RSS 为残差平方和.((((((((0ˆˆˆ,0.0ˆˆ(ˆ(ˆˆ(2ˆˆ: 1022222222ˆˆˆˆˆˆ=+===-=-=--+=+=-+-=-+--+-=-+-=-=∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑ii i i i i ii i i i i i i i i i i i i i i i i i i i i i X e e Y e e e Y Y e Y Y e Y Y ESS RSS y e Y Y Y Y TSS Y Y Y YY Y Y YY Y Y Y Y Y Y Y ββ而因为证明TSS=ESS+RSSY的观测值围绕其均值的总离差(total variation可分解为两部分:一部分来自回归线(ESS,另一部分则来自随机部分(RSS。
从统计学看线性回归（1）——一元线性回归
从统计学看线性回归（1）——⼀元线性回归⽬录1. ⼀元线性回归模型的数学形式2. 回归参数β0 , β1的估计3. 最⼩⼆乘估计的性质 线性性 ⽆偏性 最⼩⽅差性⼀、⼀元线性回归模型的数学形式 ⼀元线性回归是描述两个变量之间相关关系的最简单的回归模型。
⾃变量与因变量间的线性关系的数学结构通常⽤式（1）的形式：y = β0 + β1x + ε (1)其中两个变量y与x之间的关系⽤两部分描述。
⼀部分是由于x的变化引起y线性变化的部分，即β0+ β1x，另⼀部分是由其他⼀切随机因素引起的，记为ε。
该式确切的表达了变量x与y之间密切关系，但密切的程度⼜没有到x唯⼀确定y的这种特殊关系。
式（1）称为变量y对x的⼀元线性回归理论模型。
⼀般称y为被解释变量（因变量），x为解释变量（⾃变量），β0和β1是未知参数，成β0为回归常数，β1为回归系数。
ε表⽰其他随机因素的影响。
⼀般假定ε是不可观测的随机误差，它是⼀个随机变量，通常假定ε满⾜：（2）对式（1）两边求期望，得E(y) = β0 + β1x, （3）称式（3）为回归⽅程。
E(ε) = 0 可以理解为ε对 y 的总体影响期望为 0，也就是说在给定 x 下，由x确定的线性部分β0 + β1x 已经确定，现在只有ε对 y 产⽣影响，在 x = x0，ε = 0即除x以外其他⼀切因素对 y 的影响为0时，设 y = y0，经过多次采样，y 的值在 y0 上下波动（因为采样中ε不恒等于0），若 E(ε) = 0 则说明综合多次采样的结果，ε对 y 的综合影响为0，则可以很好的分析 x 对 y 的影响（因为其他⼀切因素的综合影响为0，但要保证样本量不能太少）；若 E(ε) = c ≠ 0，即ε对 y 的综合影响是⼀个不为0的常数，则E(y) = β0 + β1x + E(ε)，那么 E(ε) 这个常数可以直接被β0 捕获，从⽽变为公式（3）；若 E(ε) = 变量，则说明ε在不同的 x 下对 y 的影响不同，那么说明存在其他变量也对 y 有显著作⽤。
从统计学看线性回归（2）——一元线性回归方程的显著性检验
从统计学看线性回归（2）——⼀元线性回归⽅程的显著性检验⽬录1. σ2 的估计2. 回归⽅程的显著性检验 t 检验（回归系数的检验） F 检验（回归⽅程的检验） 相关系数的显著性检验 样本决定系数 三种检验的关系⼀、σ2 的估计 因为假设检验以及构造与回归模型有关的区间估计都需要σ2的估计量，所以先对σ2作估计。
通过残差平⽅和（误差平⽅和）（1）（⽤到和，其中）⼜∵（2）∴（3）其中为响应变量观测值的校正平⽅和。
残差平⽅和有n-2 个⾃由度，因为两个⾃由度与得到的估计值与相关。
（4）（公式（4）在《线性回归分析导论》附录C.3有证明）∴σ2的⽆偏估计量：（5）为残差均⽅，的平⽅根称为回归标准误差，与响应变量y 具有相同的单位。
因为σ2取决于残差平⽅和，所以任何对模型误差假设的违背或对模型形式的误设都可能严重破坏σ2的估计值的实⽤性。
因为由回归模型残差算得，称σ2的估计值是模型依赖的。
⼆、回归⽅程的显著性检验 ⽬的：检验是否真正描述了变量 y 与 x 之间的统计规律性。
假设：正态性假设（⽅便检验计算）1. t 检验 ⽤t 检验来检验回归系数的显著性。
采⽤的假设如下：原假设 H0：β1 = 0 （x 与 y 不存在线性关系）对⽴假设 H1：β1 ≠ 0 回归系数的显著性检验就是要检验⾃变量 x 对因变量 y 的影响程度是否显著。
下⾯我们分析接受和拒绝原假设的意义。
（1）接受 H0：β1 = 0 （x 与 y 不存在线性关系） 此时有两种情况，⼀种是⽆论 x 取值如何， y 都在⼀条⽔平线上下波动，即，如下图1，另⼀种情况为， x 与 y 之间存在关系，但不是线性关系，如图2。
图 1图 2 （2）拒绝 H0：β1 = 0 （x 对解释 y 的⽅差是有⽤的） 拒绝原假设也有两种情况，⼀种是直线模型就是合适的，如图 3，另⼀种情况为存在 x 对 y 的线性影响，也可通过 x 的⾼阶多项式得到更好的结果，如图 4。
一元线性回归公式
一元线性回归公式一元线性回归公式是一种基本的统计学模型，它在统计学和机器学习领域中都有广泛应用，可以用来预测和分析两个变量之间的关系。
一元线性回归的公式可以通俗地表达为：Y = +X，其中Y为因变量，X为自变量，α为截距项，β为斜率。
一元线性回归的本质就是对两个变量之间的线性关系进行拟合，同时计算出两个变量之间的斜率β和截距项α。
两个变量之间的线性关系能够概括为Y = +X，其中X是自变量，Y是因变量，α是压力，β是应力。
由于一元线性回归模型只分析两个变量之间的关系，因此该模型也称为双变量回归模型。
一元线性回归的原理是什么呢？一元线性回归的原理是使用最小二乘法（Least Squares）来找到最佳拟合参数，以使所有样本点和拟合曲线之间的总误差最小。
通过最小二乘法，系统可以根据输入数据自动计算出α和β参数，从而实现回归拟合。
一元线性回归公式是一种重要的统计模型，用于分析两个变量之间的关系。
它能够解决各种数量和定性难题，比如预测消费者行为、分析市场趋势等，以及帮助企业做出数据驱动的决策。
统计学家除了使用一元线性回归公式外，还可以使用多元线性回归来分析多个变量之间的关系，多元线性回归旨在更加准确地预测多元变量之间的关系，从而获得更准确的预测结果。
一元线性回归模型可以很容易地使用统计分析软件或者编程语言实现，它是实现数据驱动的管理层面的有力武器。
此外，一元线性回归模型在机器学习领域中也有着重要的作用，因为它可以用来训练算法，从而帮助计算机更准确地预测结果。
总的来说，一元线性回归公式是一种广泛应用的基础统计学模型，它可以帮助企业进行数据驱动的决策，也可以用于机器学习算法的训练，从而提高算法预测的准确性。
一元线性回归模型-Spss实现过程
【Anova】 （方差分析） 此表是所用模型的检验结果，一个标准的方差分析表。 Sig.（significant ）值是回归关系的显著性系数，sig.是F值的实际显著性概率即P值。当sig. <= 0.05的时候， 说明回归关系具有统计学意义。如果sig. > 0.05，说明二者之间用当前模型进行回归没有统计学意义，应该 换一个模型来进行回归。 由表可见所用的回归模型F统计量值=440.700 ，P值为0.000，因此我们用的这个回归模型是有统计学意义的， 可以继续看下面系数分别检验的结果。
2020/4/1
9、其它选项
在主对话框里单击“选项”按钮，将打开如图1-6所示的对话框
,注意：选项按钮只需要在选择方法为逐步回归后，才需要打开。
•“步进方法标准”单选钮组：设置纳入和排除标准，可 按P值或F值来设置。 •“在等式中包含常量”复选框：用于决定是否在模型中 包括常数项，默认选中。 •“缺失值”单选钮组：用于选择对缺失值的处理方式， 可以是不分析任一选入的变量有缺失值的记录（按列表 排除个案）而无论该缺失变量最终是否进入模型；不分 析具体进入某变量时有缺失值的记录（按对排除个案）； 2020/4/1 将缺失值用该变量的均数代替（使用均值替代）。
从上各图可以看出固体冲泡饮料对果汁的销量不构成影 响，而其它三种都构成了一定的影响。
2020/4/1
Wangshuanghu.
谢谢大家！
我校女大学生文胸选择倾向的调查
服装与艺术设计学院 王双虎
名词及其定义
文胸：文胸是支托、覆盖并保护女性胸部的衣物。又称为胸围、围胸、胸罩、胸衣等。 服装敏感色：服装色彩学中把白色，肉色，浅色系等颜色都称为敏感色。 模杯型文胸：通过模压工艺一次成型，也称作模杯文胸。 夹碗型文胸：通过车缝工艺完成各种杯型。适合自然胸形较好的女士穿着。
一元线性回归方程回归系数的假设检验方法
一元线性回归方程回归系数的假设检验方法
一元线性回归方程是一种统计学方法，用于研究两个变量之间的关系。
它可以
用来预测一个变量（被解释变量）的值，另一个变量（解释变量）的值已知。
回归系数是一元线性回归方程的重要参数，它可以用来衡量解释变量对被解释变量的影响程度。
回归系数的假设检验是一种统计学方法，用于检验回归系数是否具有统计学意义。
它的基本思想是，如果回归系数的值不是0，则表明解释变量对被解释变量有
显著的影响，反之则表明解释变量对被解释变量没有显著的影响。
回归系数的假设检验一般采用t检验或F检验。
t检验是检验单个回归系数是
否具有统计学意义的方法，而F检验是检验多个回归系数是否具有统计学意义的方法。
在进行回归系数的假设检验时，首先要确定检验的显著性水平，一般为0.05
或0.01。
然后，根据检验的类型，计算t值或F值，并与检验的显著性水平比较，如果t值或F值大于显著性水平，则拒绝原假设，即认为回归系数具有统计学意义；反之，则接受原假设，即认为回归系数没有统计学意义。
回归系数的假设检验是一种重要的统计学方法，它可以用来检验回归系数是否
具有统计学意义，从而更好地理解解释变量对被解释变量的影响程度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9.1 回归分析的基本概念
• 9.1.1 因变量(Y)与自变量(X)之间的关系 根据因变量与自变量之间的关系不同，可以分为两种类型：
函数关系
统计关系
9.1.1 因变量(Y)与自变量(X)之间的关系
1.函数关系
即对两个变量X，Y来说，当X值 确定后，Y值按照一定的规律唯一确定， 即形成一种精确的关系。
b1 CiYi i1
i1
表明b1是Yi 的线性组合
9.2.5 最小二乘估计量b0,b1的特性
同理，可得
n
b0 kiYi i 1
ki
1 n
Ci
X
b0是Yi线 性组合
9.2.5 最小二乘估计量b0,b1的特性
(2) 无偏性
可以证明b0和b1分别是β0 和β1的无偏估计
引例分析
n
b1
n
线性 (预测 Y)
70
60
50
40
30
20
观测点散布在统计关系直线周围，此 种情况说明Y的变化除了受自变量X 影响以外，还受其他因素的影响。
因此试图建立这样一个回归模型，通过对此模型 所作的一些假设，可以体现出上述统计关系所刻划的特征。
9.2.2 一元线性回归模型假设
根据统计关系特征，可以进行下述假设：
(1)对于自变量的每一水平X，存在着Y的一个概率分布；
引例分析
真实值与预测值的差就是回 归直线在每个给定点上的误 差，我们称之为残差（resid ual）。
从几何上讲，残差是回归直 线到样本数据点之间的垂直 距离，确定斜率和截距的方 程使回归直线位于样本点之 间。这样，从回归直线到样 本点之间的垂直距离相互抵 消，使总和为0。
y值与预测值
Y
预测 Y
80
图9-4 回归方程原理图
9.2.4 一元线性回归方程
n
2
令Q [Yi (b0b1Xi)]
i1
Q达到最小值 b0和b1称为最小二乘估计量
微积分中极值 的必要条件
bQ0 2i n1[Yi (b0b1Xi)]
bQ 12in1[Yi (b0b1Xi)X ]i
令偏导数为0
n
n
nb0 b1 Xi Yi
9.1.2 回归分析
回归分析(Regression Analysis)
就是应用统计方法，对大量的观测数据进行整 理、分析和研究，从而得出反映事物内部规律 性的一些结论。
9.2 一元线性回归模型
• 9.2.1 统计关系的特征
统计关系 特征
因变量Y随自变量X有规律的变化， 而统计关系直线描述了这一变化的 趋势。
➢回归分析适合研究哪类问题? ➢回归方程的显著性检验适合什么情况? ➢回归系数的显著性检验适合什么情况?
• 例 设有10个厂家的投入和产出如下，根据这些 数据，我们可以认为投入和产出之间存在相关性 吗？
厂家 1
2
3
4
56
7
8
9
10
投入 20 40 20 30 10 10 20 20 20 30
产出 30 60 40 60 30 40 40 50 30 70
i1
i1
n
n
n
b0 Xi b1 Xi2 XiYi
i1
i1
i1
解方程
9.2.4 一元线性回归方程
n
( X i X )( Y i Y )
b1 i1 n
(X i X )2
i1
n
(
X iY i
i1
X i )( n
Yi)
n
X
2 i
(
i1
X i)2 n
(9-5)
b0 Yb1X
假设
(2)这些Y的概率分布的均值，有规律的随X变化而变化
9.2.3 一元线性回归模型
Y与X具有统计 关系而且是线性
建立 回归模型
Yi=β0+β1Xi+εi (i=1,2,···,n)
பைடு நூலகம்
其中，(X i,Yj)表示(X,Y)的第i个观测值，β0 , β1为参
数，β0+β1Xi为反映统计关系直线的分量，ε i为 反映在统计关系直线周围散布的随机分量ε i～N
9.2.4 一元线性回归方程
Yi=β0+β1Xi+εi β0和β1均未知
根据样本数据
对β0和β1
进行估计
β0和β1的估计
值为b0和b1
建立一元线性回归方程
Yˆ b0 b1X
9.2.4 一元线性回归方程
一般而言，所求的b0和b1应能使每个样本观测点(X i,Y i) 与回归直线之间的偏差尽可能小，即使观察值与拟 合值的误差平方和Q达到最小。
预测值 42.6316 66.3156 42.6316 54.4736 30.7896 30.7896 42.6316 42.6316 42.6316 54.4736
残差 -12.6316 -6.3156 -2.6316 5.5264 -0.7896 9.2104 -2.6316 7.3684 -12.6316 15.5264 0 .0 0 0 0
xiyi xi2
xi
yi
2
1.1842
xi
b 0y b 1 xn y i b 1
x i 1 8 .9 4 7 6 n
故回归方程为：
$ y18.94761.1842x
引例分析
厂家 1 2 3 4 5 6 7 8 9 10
投入(x) 20 40 20 30 10 10 20 20 20 30
产出(y) 30 60 40 60 30 40 40 50 30 70
(9-6)
9.2.5 最小二乘估计量b0,b1的特性
b0,b1的特性
线性 无偏性
9.2.5 最小二乘估计量b0,b1的特性
(1) 线性特性 由（9-5）得
n
n
(Xi X)(Yi Y) (Xi X)Yi
b1i1 n
(Xi
X)2
i1
n
(Xi
X)2
i1
i1
令
Ci n Xi X
(Xi X )2
则
n
例：某商品的销售额y与销售量x之间的关 系可表示为y=px(p是单价)，圆的面积可 表示为s=piR^2
9.1.1 因变量(Y)与自变量(X)之间的关系
2.统计关系
即当X值确定后，Y值不是唯一确定的， 但大量统计资料表明，这些变量之间还 是存在着某种客观的联系。
9.1.2 回归分析
在直角坐标平面上，标出了10个观测点的 坐标位置，他们表示以家庭为单位，某种 商品年需求量与该商品价格之间的10对 调查数据
(0,σ2)。
9.2.3 一元线性回归模型
对于任意Xi值有： ⑴ Yi服从正态分布
⑵E(Yi)=β0+β1Xi；
⑶2(Yi)2
⑷各Yi间相互独立 Yi～N(β0+β1Xi,σ2) 。
9.2.3 一元线性回归模型
图9-2
9.2.4 一元线性回归方程
Y与X之间 为线性关系
最小二乘法
选出一条最能反 映Y与X之间关系 规律的直线