第6章状态反馈控制与观测器设计
现代控制理论习题之状态观测设计

对应于原系统的观测器矩阵: ⎡0 ⎤ ⎡0 ⎤ P1 = V0 −1 ⎢ ⎥ = ⎢ ⎥, Po = [ p1 ⎣1 ⎦ ⎣1 ⎦
u
∑ ( A, B, C )
y
6.5
2
1 x
x1
15.3 x
x3
题 6-2 图 1
(2) 确定降维观测器的维数:m=1,n=3,则 n-m= 2。 分解输出系数矩阵 c,获得线性变换矩阵 T,对原状态空间表达式进行线性变换,使 各输出变量 y 变成各状态变量的单值函数:
f *(s) = (s + 3)(s + 4) = s2 + 7s +12 ⎡s 0⎤ ⎡−1 −1⎤ ⎡l1⎤ f (s) = sI − (A22 − LA 12) = ⎢ ⎥ −⎢ ⎥ + ⎢ ⎥[− 2 − 4] ⎣0 s⎦ ⎣−1 −1⎦ ⎢ ⎣l2⎥ ⎦ = s2 + (−4l2 − 2l1 + 2)s + (2l1 − 2l2) ⎡l ⎤ ⎡ 3.1667⎤ f *(s) = f (s) ⇒ L = ⎢ 1⎥ = ⎢ ⎥ ⎢l2⎦ ⎥ ⎣− 2.8333 ⎦ ⎣
系统能观,可设计观测器。 求希望特征多项式:
f * ( s ) = ( s + 3)( s + 4)( s + 5) = s 3 + 12 s 2 + 47 s + 60
求观测器特征多项式:
f ( s ) = sI − A + LC
一阶倒立摆系统模型分析状态反馈与观测器设计

一阶倒立摆系统模型分析状态反馈与观测器设计一阶倒立摆系统是控制工程中常见的一个具有非线性特点的系统,它由一个摆杆和一个质点组成,质点在摆杆上下移动,而摆杆会受到重力的作用而产生摆动,需要通过控制来实现倒立的功能。
以下是一阶倒立摆系统的模型分析、状态反馈与观测器设计的详细介绍。
一、系统模型分析:一阶倒立摆系统是一个非线性动力学系统,可以通过线性化的方式来进行模型分析。
在进行线性化之前,首先需要确定系统的状态变量和输入变量。
对于一阶倒立摆系统,可以将摆杆角度和质点位置作为状态变量,将水平推力作为输入变量。
在对系统进行线性化之后,可以得到系统的状态空间表达式:x_dot = A*x + B*uy=C*x+D*u其中,x是状态向量,u是输入向量,y是输出向量。
A、B、C和D是系统的矩阵参数。
二、状态反馈设计:状态反馈是一种常用的控制方法,通过测量系统状态的反馈信号,计算出控制输入信号。
在设计状态反馈控制器之前,首先需要确定系统的可控性。
对于一阶倒立摆系统,可以通过可控性矩阵的秩来判断系统是否是可控的。
如果可控性矩阵的秩等于系统的状态数量,则系统是可控的。
在确定系统可控性之后,可以通过状态反馈控制器来实现控制。
状态反馈控制器的设计可以通过选择适当的反馈增益矩阵K来实现。
具体的设计方法是,根据系统的状态空间表达式,将状态反馈控制器加入到系统模型中。
状态反馈控制器的输入是状态变量,输出是控制输入变量。
然后,通过调节反馈增益矩阵K的值,可以实现对系统的控制。
三、观测器设计:观测器是一种常用的状态估计方法,通过测量系统的输出信号,估计系统的状态。
在设计观测器之前,首先需要确定系统的可观性。
对于一阶倒立摆系统,可以通过可观性矩阵的秩来判断系统是否是可观的。
如果可观性矩阵的秩等于系统的状态数量,则系统是可观的。
在确定系统可观性之后,可以通过观测器来实现状态估计。
观测器的设计可以通过选择适当的观测增益矩阵L来实现。
具体的设计方法是,根据系统的状态空间表达式,将观测器加入到系统模型中。
现代控制实验状态反馈器和状态观测器的设计

现代控制实验状态反馈器和状态观测器的设计现代控制实验中,状态反馈器和状态观测器是设计系统的重要组成部分。
状态反馈器通过测量系统的状态变量,并利用反馈回路将状态变量与控制输入进行耦合,以优化系统的性能指标。
状态观测器则根据系统的输出信息,估计系统的状态变量,以便实时监测系统状态。
本文将分别介绍状态反馈器和状态观测器的设计原理和方法。
一、状态反馈器的设计:状态反馈器的设计目标是通过调整反馈增益矩阵,使得系统的状态变量在给定的性能要求下,达到所需的一组期望值。
其设计步骤如下:1.系统建模:通过对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
通常表示为:ẋ=Ax+Buy=Cx+Du其中,x为系统状态向量,u为控制输入向量,y为系统输出向量,A、B、C、D为系统的状态矩阵。
2.控制器设计:根据系统的动态性能要求,选择一个适当的闭环极点位置,并计算出一个合适的增益矩阵。
常用的设计方法有极点配置法、最优控制法等。
3.状态反馈器设计:根据控制器设计得到的增益矩阵,利用反馈回路将状态变量与控制输入进行耦合。
状态反馈器的输出为:u=-Kx其中,K为状态反馈增益矩阵。
4.性能评估与调整:通过仿真或实验,评估系统的性能表现,并根据需要对状态反馈器的增益矩阵进行调整。
二、状态观测器的设计:状态观测器的设计目标是根据系统的输出信息,通过一个状态估计器,实时估计系统的状态变量。
其设计步骤如下:1.系统建模:同样地,对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
2.观测器设计:根据系统的动态性能要求,选择一个合适的观测器极点位置,以及一个合适的观测器增益矩阵。
常用的设计方法有极点配置法、最优观测器法等。
3.状态估计:根据观测器设计得到的增益矩阵,通过观测器估计系统的状态变量。
状态观测器的输出为:x^=L(y-Cx^)其中,L为观测器增益矩阵,x^为状态估计向量。
4.性能评估与调整:通过仿真或实验,评估系统的状态估计精度,并根据需要对观测器的增益矩阵进行调整。
现代控制实验--状态反馈器和状态观测器的设计

现代控制实验--状态反馈器和状态观测器的设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN状态反馈器和状态观测器的设计一、实验设备PC 计算机,MATLAB 软件,控制理论实验台,示波器二、实验目的(1)学习闭环系统极点配置定理及算法,学习全维状态观测器设计法;(2)掌握用极点配置的方法(3)掌握状态观测器设计方法(4)学会使用MATLAB工具进行初步的控制系统设计三、实验原理及相关知识(1)设系统的模型如式所示若系统可控,则必可用状态反馈的方法进行极点配置来改变系统性能。
引入状态反馈后系统模型如下式所示:(2)所给系统可观,则系统存在状态观测器四、实验内容(1)某系统状态方程如下10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =理想闭环系统的极点为[]123---.(1)采用 Ackermann 公式计算法进行闭环系统极点配置;代码:A=[0 1 0;0 0 1;-4 -3 -2];B=[1; 3; -6];P=[-1 -2 -3];K=acker(A,B,P)Ac=A-B*Keig(Ac)(2)采用调用 place 函数法进行闭环系统极点配置;代码:A=[0 1 0;0 0 1;-4 -3 -2];B=[1;3;-6];eig(A)'P=[-1 -2 -3];K=place(A,B,P)eig(A-B*K)'(3)设计全维状态观测器,要求状态观测器的极点为[]---123代码:a=[0 1 0;0 0 1;-4 -3 -2];b=[1;3;-6];c=[1 0 0];p=[-1 -2 -3];a1=a';b1=c';c1=b';K=acker(a1,b1,p);h=(K)'ahc=a-h*c(2)已知系统状态方程为:10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =(1)求状态反馈增益阵K ,使反馈后闭环特征值为[-1 -2 -3];代码:A=[0 1 0;0 0 1;4 -3 -2];b=[1;3;-6];p=[-1 -2 -3];k=acker(A,b,p)A-b*keig(A-b*k)(2)检验引入状态反馈后的特征值与希望极点是否一致。
状态观测器设计

Chapter6 状态观测器设计在工程实际中能量测的信号只是系统的输出y ,而不是系统的内部状态。
有的状态变量是物理量,有的则不是物理量,因而状态变量未必都可以测量得到。
当状态不能全部量测时,我们就无法获得系统的状态信息,因而状态反馈在工程上就不能实现。
1964年,Luenberg er G D ⋅⋅(龙伯格)提出的“状态观测器”理论成功的解决了系统状态信息的获取问题。
Luenberg er G D ⋅⋅认为,当已知系统输入为u ,系统的输出为y ,他们必然与其内部状态x 有联系,也就是说我们应该能通过测量),(y u 对未知的状态量x 进行推论和估计。
“状态观测器”本质上是一个“状态估计器”(或称动态补偿器),其基本思路是利用容易量测的被控对象的输入u 和输出y 对状态进行估计(和推测)。
6.1 观测器设计考虑线性时不变系统Cx y Bu Ax x=+=,& (6-1) 基于(6-1)人为地构造一个观测器,观测器的输出为x ~,如果能满足 0)~(lim =-∞→x x t (6-2)则观测器的输出x ~可以作为内部状态)(t x 的估值,从而实现“状态重构-即重新构造“状态x ~”来作为“原状态x ”的估值。
观测器的输出x ~应该能由系统输入u 和系统输出y 综合而成(系统输入u 和系统输出y 在工程实际中容易检测到)。
∞→t 只是数学上的表述,实际工程中是很快的过程(<s 1)。
为了得到估计值x ~,一个很自然的想法是构造一个模拟系统 Bu x A x +=~~&,x C y ~~= (6-3) 用该模拟部件(6-3)去再现系统(6-1)。
因为模拟系统(6-3)是构造的,故x ~是可量测的信息,若以x ~作为x 的估值。
其估计误差为x x e -≡~,(6-3)减(6-1),满足方程 Ae e =& (6-4) 讨论:①若A 存在不具有负实部的特征值,Ae e=&将不会稳定,则当初始误差0)0(≠e ,即)0()0(~x x ≠时,有0)]()(~[lim ≠-∞→t x t x t ,这样x ~就不能作为x 的估计值,即Ae e =&不能作为一个观测器。
现代控制理论-6-状态反馈和状态观测器-第111讲
第6章 状态反馈和状态观测器
经典控制:只能用系统输出作为反馈控制器的输入; 现代控制:由于状态空间模型刻画了系统内部特征, 故而还可用系统内部状态作为反馈控制器的输入。 根据用于控制的系统信息:状态反馈、输出反馈
• 控制系统的动态性能,主要由其状态矩阵的特征 值(即闭环极点)决定。
• 基于状态空间表达式,可以通过形成适当的反馈 控制,进而配置系统的极点,使得闭环系统具有 期望的动态特性。
(2)确定将原系统化为能控标准型 (A, B,C ) 的变换阵 Pc2
若给定状态方程已是能控标准型,那么 Pc2 I ,无需转换
只需要求系统不变量 i
,
然后确定Pc
即可
2
系统不变量: f () I A n n1n1 1 0
1 0 0
n1 1
Pc2 [ An1b, An2b,, b]
2
0
1 2 n1 1
2019/7/21
20
(3)根据给定或求得的期望闭环极点,写出期望的特征多项式:
f *( ) ( 1() 2 )
(
n )
0
B
P 1 c2
B
0
1
能控标准型下,加入状态反馈后,系统矩阵为:
0
1
0
0
0
0
1
A BK
0
0
0
0
1
(0 k1 ) (1 k2 ) ( 2 k3 ) ( n1 kn )
现代控制理论状态反馈和状态观测器的设计实验报告

本科实验报告课程名称:现代控制理论实验项目:状态反馈和状态观测器的设计实验地点:中区机房专业班级:自动化学号:学生:指导教师:年月日现代控制理论基础一、实验目的(1)熟悉和掌握极点配置的原理。
(2)熟悉和掌握观测器设计的原理。
(3)通过实验验证理论的正确性。
(4)分析仿真结果和理论计算的结果。
二、实验要求(1)根据所给被控系统和性能指标要求设计状态反馈阵K。
(2)根据所给被控系统和性能指标要求设计状态观测器阵L。
(3)在计算机上进行分布仿真。
(4)如果结果不能满足要求,分析原因并重复上述步骤。
三、实验容(一)、状态反馈状态反馈是将系统的状态变量乘以相应的反馈系数,然后反馈到输入端与参考输入叠加形成控制作为受控系统的控制输入,采用状态反馈不但可以实现闭环系统的极点任意配置,而且也是实现解耦和构成线性最优调节器的主要手段。
1.全部极点配置给定控制系统的状态空间模型,则经常希望引入某种控制器,使得该系统的闭环极点移动到某个指定位置,因为在很多情况下系统的极点位置会决定系统的动态性能。
假设系统的状态空间表达式为(1)其中 n m C r n B n n A ⨯⨯⨯::;:;: 引入状态反馈,使进入该系统的信号为Kx r u -=(2)式中r 为系统的外部参考输入,K 为n n ⨯矩阵. 可得状态反馈闭环系统的状态空间表达式为(3)可以证明,若给定系统是完全能控的,则可以通过状态反馈实现系统的闭环极点进行任意配置。
假定单变量系统的n 个希望极点为λ1,λ2, …λn, 则可以求出期望的闭环特征方程为=)(*s f (s-λ1)(s-λ2)…(s-λn)=n n n a s a s +++- 11这是状态反馈阵K 可根据下式求得K=[])(100*1A f U c -(4)式中[]b A Ab b U n c 1-= ,)(*A f 是将系统期望的闭环特征方程式中的s 换成系统矩阵A 后的矩阵多项式。
例1已知系统的状态方程为u x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=•111101101112 采用状态反馈,将系统的极点配置到-1,-2,-3,求状态反馈阵K..其实,在MATLAB的控制系统工具箱中就提供了单变量系统极点配置函数acker(),该函数的调用格式为K=acker(A,b,p)式中,p为给定的极点,K为状态反馈阵。
第六章状态反馈和状态观测器1
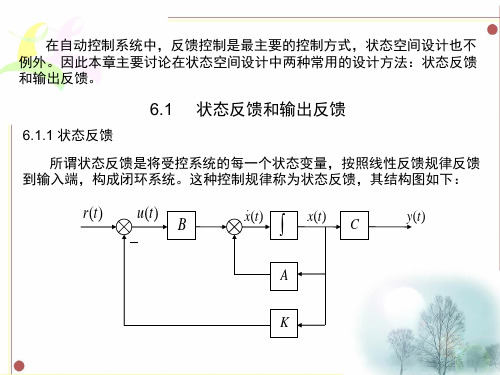
G(s)
s(s
1 6)(s
12)
s3
1 18s 2
72s
综合指标为: % 5%;tS 0.5s,ep 0,试用状态反馈实现上述指标。
解:将极点配置为一对主导极点和一个非主导极点;根据二阶
系统的性能指标,求出 0.707,n 10。取 0.707,n 10
则,主导极点为:
s1,2 0.707 j7.07
变量,也没有增加系统的维数,但可以通过K阵的选择自由地改变闭环系统 的特征值,从而使系统达到所要求的性能。
6.1.2 输出反馈
输出反馈是将受控系统的输出变量,按照线性反馈规律反馈到输入端, 构成闭环系统。这种控制规律称为输出反馈。经典控制理论中所讨论的反馈 就是这种反馈,其结构图如下 :
r(t) u(t) B
r(t) u(t) B
x(t) x(t) C
y(t)
A
K
图中受控系统的状态空间表达式为 (A, B,C)的状态空间表达式为 0 x Ax Bu
y Cx
式中,A为n×n矩阵;B为n×r矩阵;C为m×n矩阵。
状态反馈控制律为
u r Kx
式中,r为r×1参考输入;K为r×n状态反馈阵。对单输入系统,K为1×n的 行向量。
sn rn1sn1 r0 0
实际系统与希望系统的特征方程的系数应当相一致。
3、状态反馈阵K的计算步骤 1)判断A,b能控性 2)写出实际的闭环特征方程(传递阵的分母为0的方程)
SI [A bK] 0
3)根据要配置的特征根,写出希望的特征方程
f (s) (s 1)(s n ) 0
4)对应实际的与希望的特征方程,求出K。
被控系统 模拟系统
x Ax Bu y Cx xˆ (A GC)xˆ Bu Gy yˆ Cxˆ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统的传递函数为
G(s)
c n 1 s n 1 c1 s c 0 s n a n 1 s n 1 a1 s a 0
8
6.1.4
状态反馈对传递函数的影响
u r Kx
x ( A b K )x b r y cx
引入状态反馈
则闭环系统的动态方程为
Modern Control Engineering
第6章 状态反馈控制与状态 观测器设计
教材:
王万良,现代控制工程,高等教育出版社,2011
第6章 状态反馈控制与状态观测器设计
问题:1、反馈控制的作用? 2、古典控制理论中的反馈控制方式? 3、现代控制理论中的反馈控制方式? 由于采用了状态方程描述系统,所以可以采用状态变量进行 反馈。 由于状态空间描述了系统内部信息的传递关系,比微分方程、 传递函数等外部描述更深入地揭示了系统的动态特性,所以, 采用状态反馈比采用输出反馈具有更好的控制特性。 采用状态反馈不但可以实现闭环系统的特征值任意配置,而 且也是实现系统解耦和构成线性最优调节器等的主要手段。
16
6.3
状态观测器设计方法
要实现状态反馈,需要测量到每个状态量,并可以作为反馈信 号。但有些状态很难测量,或者受到经济上和使用上的限制, 不能设置太多的传感器,有些状态变量没有物理意义而无法测 量。因此,需要设计状态观测器估计实际状态,实现状态反馈。 状态观测器是指一个在物理上可以实现的动态系统,它在被 观测系统的输入和输出的驱动下,产生一组逼近于被观测系统 的状态变量。状态观测器所输出的一组状态变量可以作为被观 测系统的状态估计值,因此状态观测器又称为状态估计器,或 状态重构器。
0 b 0 1
c 1 0 0
13
6.2.2 单输入系统的极点配置方法
因为
1 0 0 rankSC rank0 1 18 3 1 6 36
所以,系统能控, 可以任意配置极点。
(2)计算系统的非奇异变换阵T
72 6 1 18 1 0 1 0 0
12
0
( 12)( 6) 3 182 72
a2 18
a1 72
a0 0
15
6.2.2 单输入系统的极点配置方法
(4)确定系统期望的特征多项式:
f ( ) ( 7.07 j 7.07)( 7.07 j 7.07)( 100) 3 114.142 1514 9997
Sc
1
T1 [0 0 1]S C
1
[1 0 0]
0 0 T1 1 T T1 A 0 1 0 2 T1 A 0 12 1
14
6.2.2 单输入系统的极点配置方法
(3)确定系统的特征多项式
f ( ) det (I A) det 0 0 1 0 1 6
18
6.3.1 全维状态观测器设计
2.渐近状态观测器问题
具有实际应用价值的是下图所示状态观测器。它和开环状态 观测器的差别在于增加了反馈校正通道。被控系统的输出与观 测器的输出进行比较,其差值作为校正信号。
ˆ ˆ ˆ x Ax bu K e ( y y ) ˆ ˆ Ax bu K e y K e cx ˆ ( A K e c ) x bu K e y
下面只讨论无噪声干扰下的状态观测器设计问题,并详细介绍 单输入单输出系统的状态观测器的设计原理和设计步骤。
17
6.3.1 全维状态观测器设计
1. 开环状态观测器 设单输入单输出线性定常系统的状态空间表达式为:
x Ax bu y cx
若要估计系统的状态, 一个直观的想法是采用 仿真技术构造一个和被 控系统具有同样动态方 程的物理装置,如右图 所示。
定理
线性连续或离散系统能镇定的充分必要条件: 系统的不能控极点都是稳定极点。
10
6.2.2 单输入系统的极点配置方法
按指定极点配置设计状态反馈增益阵的一般方法: 对于线性(连续或离散)单输入系统 A, b, c ,按指定极点配 置设计状态反馈增益矩阵的基本方法,是选择状态反馈增益 矩阵使系统的特征多项式 det[λ I ( A bK)] 等于期望的特征多 项式 f * ( ) ,即 det[λ I ( A bK )] f * ( ) 按指定极点配置设计状态反馈增益阵的一般步骤为: (1)判断系统能控性 (2)求能控标准型的变换矩阵T
9
6.2
状态反馈设计方法
6.2.1 极点配置问题
极点配置定理 线性(连续或离散)多变量系统能任意配 置极点的充分必要条件是,该系统状态完全能控。 能镇定的或能稳定的系统 如果不能控的极点全部是稳定极点,则可以采用状态反 馈使能控部分的极点配置到期望值,从而使整个闭环系统稳 定,因此,称这样的系统为能镇定的或能稳定的系统。
T1 0 0 1S C
SC b
Ab An 1b
1
T1 TA T 1 n 1 T1 A
11
6.2.2 单输入系统的极点配置方法
3)求出被控对象的特征多项式
f ( ) det[I A] n an1n1 a1 a0
* a2 114.14
* a1 1514
* a0 9997
(5)计算能控标准型下的状态反馈增益阵为
K 9997 72 1514 18 114.14 9997 1442 96.14
(6)求给定状态的反馈增益阵
K KT 9997 288.32 96.14
20
6.3.1 全维状态观测器设计
定理:线性(连续或者离散)定常系统存在状态观测器,并且 能够任意配置极点的充分必要条件是系统完全能观测。 此定理也适用于MIMO系统。 设计状态观测器的一般步骤为: ①判别系统能观性; ②求 f ( ) detI ( A K c) e ③根据状态观测器的期望极点,求 ④由
设状态反馈阵为
K k1 k 2 k n
则状态反馈系统的传递函数为
G( s) c n 1 s n 1 c1 s c 0 s n (a n 1 k n ) s n 1 (a1 k 2 ) s (a 0 k1 )
结论: 引入状态反馈改变了系统的极点,但没有改变系统的零点。
f * ( )
f ( ) f * ( ) 确定 K e
21
ቤተ መጻሕፍቲ ባይዱ
6.3.1 全维状态观测器设计
例: 设计状态观测器,使其特征值为 1 2 10
1 0 0 A , b 1 , 2 3 c [2 0]
解: 判断系统的能观性
c 2 rank rank cA 0
如果系统没有直接传输,则状态空间模型和闭环传递函数阵:
x ( A BK ) x Br y Cx
GK (s) C (sI A BK ) B
5
1
6.1.2 输出反馈
输出反馈是将系统的输出量乘以相应的系数反馈到输入端,与 参考输入相加,其和作为被控系统的控制信号,如下图所示。
4)根据指定的闭环极点求出期望的闭环特征多项式
* * f ( ) n an 1n 1 a1 a0
5)
写出对于能控标准型下的状态反馈增益阵
K a0 a 0
a1 a1 an1 an1
6)求定状态的反馈增益阵 7)状态反馈下的控制律为
在任何形如 u(t ) r (t ) K (t ) x(t ) 的状态反馈下,状态反馈闭环系 统 K A BK , B, C 完全能控的充要条件是被控对象完全能控。 2.状态反馈系统的能观性 虽然状态反馈保持了动态方程的能控性,但往往会破坏动态 方程的能观性。 定理:输出反馈闭环系统能控的充要条件是被控系统能控; 输出反馈闭环系统能观的充要条件是被控系统能观。 参见P146 例6.1、例6.2
u r Hy
如果没有直接传输D,则 x ( A BHC) x Br y Cx
且输出反馈的闭环传递函数阵为
G H (s) C (sI A BHC) 1 B
6
6.1.3 状态反馈系统的能控性与能观性
1.状态反馈系统的能控性 定理:多变量线性系统(定常的或时变的) 0 A, B, C ,
K KT
u Kx r
12
6.2.2 单输入系统的极点配置方法
例: 试设计如图所示系统中的状态反馈增益阵K,使闭环系统 的特征值为 1,2 7.07 j 7.07, 3 100
解: (1)判断系统是否可控。 系统的状态空间表达式为
0 A 0 0 1 12 0 0 1 6
19
6.3.1 全维状态观测器设计
ˆ ˆ x x Ax bu ( A K e c) x bu K e cx ˆ ( A K e c)( x x)
~ ˆ 令 x xx
则x ( A K e c) x
其解为 ~ (t ) e ( A K ec )t ~ (t 0 ) x x 可知,当选取 K e ,使得 A K e c 所有特征值具有负实部则有: 若观测器和系统的初始状态相同,观测器的状态与系统实 际状态完全相同; 若观测器初始状态与系统初始状态不相等,观测器状态以 x 指数收敛到系统的实际状态, 即 lim ~(t ) 0 。因此,这 t 种观测器称为渐近状态观测器。
7
6.1.4 状态反馈对传递函数的影响
若某能控系统
