数学模型--- 1双层玻璃的功效
初等方法建模1双层玻璃窗的功效--数学建模案例分析
第一章 初等方法建模如果研究对象的机理比较简单，一般用静态、线性、确定性模型描述就能达到建模目的时，我们基本上可以用初等数学的方法来构造和求解模型。
通过下面介绍的若干例子能够看到，用很简单的数学方法已经可以解决一些饶有兴味的实际问题。
需要强调的是，如果对于某个实际问题可以用初等的方法解决，就不要用更高等的方法。
§1 双层玻璃窗的功效背景 将双层玻璃窗与用同样多材料做成的单层窗的热传导进行对比，对双层窗能减少多少热量损失给出定量分析结果。
模型假设1、热量的传播只有传导，没有对流，即假定窗户的密封性能很好，两层玻璃间的空气是不流动的。
2、室内温度1T 和室外温度2T 保持不变，热传导过程已处于稳定状态，即沿热传导方向，单位时间通过单位面积的热量是常数。
3、玻璃材料均匀，热传导系数是常数。
模型构成与求解记 a T —内层玻璃的外侧温度b T —外层玻璃的内侧温度1K —玻璃的热传导系数2K —空气的热传导系数空气Q —单位时间通过双层窗单位面积的热量'Q —单位时间通过单层窗单位面积的热量 由热传导过程的物理定律：dT K Q ∆=，得到 dT T K l T T K d T T K Q b b a a 21211-=-=-= （1） d T T K Q 2211'-= （2） 从（1）中消去b a T T ,，可得dl h K K h S S d T T K Q ==+-=,,)2()(21211 （3） 22+='S Q Q （4） 显然Q Q '<，且S 越大，比例越悬殊，331108~104--⨯⨯=K （焦耳/CM ·秒·度），42105.2-⨯=K （焦耳/CM ·秒·度），于是31~1621=K K ,做最保守的估计，即取1621=K K ，由(3)、(4)即有 dl h h Q Q =+=',181 （5） 模型分析 比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，h 不宜选择过大，通常建筑要求是4≈h ，按此模型，%3≈'Q Q ，即使用同样材料制成的双层窗较单层窗节约热量97%左右。
双层玻璃功效问题
双层玻璃功效问题（模型建立）
【模型建立】
根据热传导定律，对于双层玻璃的情况，单位时间内通过单 位面积的热量：
Tb − T2 Ta − Tb T1 − Ta = k2 = k1 Q = k1 d L d
双层玻璃功效问题（模型求解）
由上面等式，消去Ta、Tb, 可得
k1 (T1 − T2 ) Q= , d ( s + 2)
Q 2 2 1 k L = = = (因为，s = 1 h = 16h ，h = ） Q' s + 2 16h + 2 8h + 1 k2 d
双层玻璃功效问题（模型求解）
如果假设玻璃的厚度d=1, 则h=L/d=L.
Q 1 1 = = Q ' 8h + 1 8 L + 1
故热量损失比为：
当0<L<6时，热量损失比
双层玻璃功效问题
【问题提出】使房子加热是日常预算中较为昂贵的部分。
如煤、煤气、电等用来加热的燃料成本近些年明显的增加。将 尽可能多的热量保持在居室内是非常重要的。据分析，热量的 损失主要是通过墙、窗、屋顶和地面发出去，将窗户安装成双 层玻璃是控制热量损失的有效方法之一（如图）。试建立一个 模型来描述热量通过窗户的流失过程，并将双层玻璃与用同样 多材料做成的单层玻璃的热量流失进行对比，对双层玻璃窗能 够减少多少热量损失给出定量分析结果。
k 2 = 2.5 × 10 −4 ~ 8 × 10 −4 (焦尔 / 厘米 ⋅ 秒 ⋅ 度）
而这空气是干燥的、不流通的. 作为模型假设的这个条件在实际 环境下是不可能完全满足的. 所以, 实际上双层窗户的功效要比 上述结果要差一些. 双层玻璃窗户出奇的保热功效是房屋设计和房屋装修的重要 参考依据.
数学建模实例-双层玻璃的功效教学提纲
数学建模实例-双层玻璃的功效双层玻璃的功效北方城镇的有些建筑物的窗户是双层的，即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气，如下左图所示，据说这样做是为了保暖，即减少室内向室外的热量流失。
我们要建立一个模型来描述热量通过窗户的热传导（即流失）过程，并将双层玻璃窗与用同样多材料做成的单层玻璃窗（如下右图，玻璃厚度为d2）的热量传导进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果。
一、模型假设1、热量的传播过程只有传导，没有对流。
即假定窗户的密封性能很好，两层玻璃之间的空气是不流动的；2、室内温度T和室外温度2T保持不变，热传导过程已处于稳定1状态，即沿热传导方向，单位时间通过单位面积的热量是常数；3、 玻璃材料均匀，热传导系数是常数。
二、 符号说明1T ——室内温度2T ——室外温度d ——单层玻璃厚度l ——两层玻璃之间的空气厚度a T ——内层玻璃的外侧温度b T ——外层玻璃的内侧温度k ——热传导系数Q ——热量损失三、 模型建立与求解由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：厚度为d 的均匀介质，两侧温度差为T ∆，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量Q ，与T ∆成正比，与d 成反比，即dT k Q ∆= （1） 其中k 为热传导系数。
1、双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为： dT T k d T T k d T T k Q b b a a 21211-=-=-= （2）由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2就将（2）中a T 、b T 消去，变形可得： ()dl h k k h s s d T T k Q ==+-= , , 2)(21211 （3）2、单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户，容易写出热量流失为： dT T k Q 2211-=' （4）3、 单层玻璃窗和双层玻璃窗热量流失比较比较（3）（4）有：22+='s Q Q （5） 显然，Q Q '<。
数学建模案例分析报告报告材料2.双层玻璃地功效
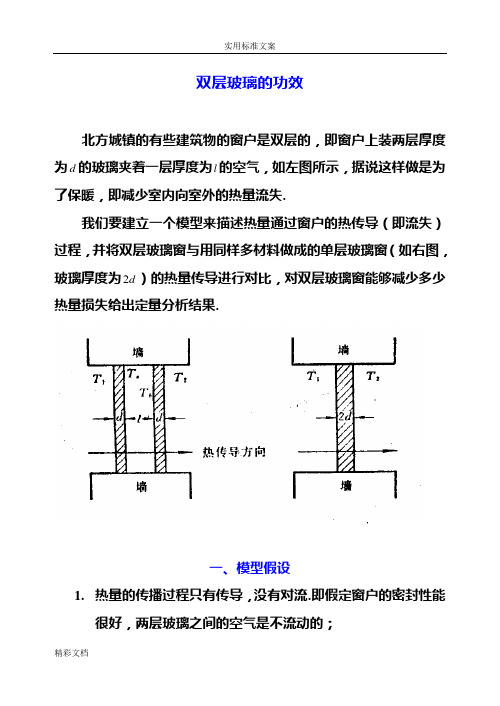
双层玻璃的功效北方城镇的有些建筑物的窗户是双层的，即窗户上装两层厚度为d的玻璃夹着一层厚度为l的空气，如左图所示，据说这样做是为了保暖，即减少室内向室外的热量流失.我们要建立一个模型来描述热量通过窗户的热传导（即流失）过程，并将双层玻璃窗与用同样多材料做成的单层玻璃窗（如右图，玻璃厚度为d2）的热量传导进行对比，对双层玻璃窗能够减少多少热量损失给出定量分析结果.一、模型假设1.热量的传播过程只有传导，没有对流.即假定窗户的密封性能很好，两层玻璃之间的空气是不流动的；2.室内温度T和室外温度2T保持不变，热传导过程已处于稳定1状态，即沿热传导方向，单位时间通过单位面积的热量是常数；3.玻璃材料均匀，热传导系数是常数.二、符号说明T——室内温度1T——室外温度2d——单层玻璃厚度l——两层玻璃之间的空气厚度T——内层玻璃的外侧温度aT——外层玻璃的内侧温度bk——热传导系数Q——热量损失三、模型建立与求解由物理学知道，在上述假设下，热传导过程遵从下面的物理规律：厚度为d的均匀介质，两侧温度差为T∆，则单位时间由温度高的一侧向温度低的一侧通过单位面积的热量为Q，与T∆成正比，与d成反比，即dT k Q ∆= （1） 其中k 为热传导系数.1. 双层玻璃的热量流失记双层窗内窗玻璃的外侧温度为a T ，外层玻璃的内侧温度为b T ，玻璃的热传导系数为1k ，空气的热传导系数为2k ，由（1）式单位时间单位面积的热量传导（热量流失）为：d T T k d T T k d T T k Q b b a a 21211-=-=-= （2） 由d T T k Q a -=11及dT T k Q b 21-=可得1212)(k Qd T T T T b a --=- 再代入d T T k Q b a -=2就将（2）中a T 、b T 消去，变形可得： ()dl h k k h s s d T T k Q ==+-=, , 2)(21211 （3） 2. 单层玻璃的热量流失对于厚度为d 2的单层玻璃窗户，容易写出热量流失为： d T T k Q 2211-=' （4）3. 单层玻璃窗和双层玻璃窗热量流失比较比较（3）（4）有：22+='s Q Q （5） 显然，Q Q '<.为了获得更具体的结果，我们需要21,k k 的数据，从有关资料可知，不流通、干燥空气的热传导系数42105.2-⨯=k （J/cm.s.ºC ），常用玻璃的热传导系数331108~104--⨯⨯=k （J/cm.s.ºC ），于是32~1621=k k 在分析双层玻璃窗比单层玻璃窗可减少多少热量损失时，我们作最保守的估计，即取1621=k k ，由（3）（5）可得：d l h h Q Q =+=' 181 （6） 4. 模型讨论 比值Q Q '反映了双层玻璃窗在减少热量损失上的功效，它只与d l h =有关，下图给出了h Q Q ~'的曲线，当h 由0增加时，Q Q '迅速下降，而当h 超过一定值（比如4>h ）后Q Q '下降缓慢，可见h 不宜选得过大.四、模型的应用这个模型具有一定的应用价值.制作双层玻璃窗虽然工艺复杂会增加一些费用，但它减少的热量损失却是相当可观的.通常，建筑规范要求4≈h.按照这个模型，%3≈'QQ，即双层玻璃窗比用同=d l样多的玻璃材料制成的单层窗节约热量97%左右.不难发现，之所以有如此高的功效主要是由于层间空气的极低的热传导系数k，而2这要求空气是干燥、不流通的.作为模型假设的这个条件在实际环境下当然不可能完全满足，所以实际上双层玻璃窗的功效会比上述结果差一些.。
双层玻璃窗的功效
数学模型 之 初等模型
双层玻璃窗的功效
2012-9-18
初等模型： 如果研究对象的机理比较简 单，一般用静态、线性、确定性 模型描述就能达到建模目的时， 我们基本上使用初等数学的方法 来构造和求解模型。 另外需要指出，衡量一个模 型的优劣全在于它的应用，而不 是采用了多么高深的数学方法。
问题归纳：两层厚度为d的玻璃夹着一层厚 度为l的空气。试描述热量通过窗户的传导过 程，并与厚度为2d的单层玻璃窗相比较。
模 型 构 成
热传导定律：设厚度为d的均匀介质， 两侧温度差为，则单位时间内从温 度高的一侧向温度低的一侧通过单位面 积的热量Q与 成正比，与d成反比， 即 T Q k , (1) d 其中k为热传导系数。
设 双 层 窗 内 层 玻 璃 外 侧 温 度 为 Ta ， 外 层玻璃内侧温度为Tb，玻璃的热传导 系数为k1，空气的热传导系数为k2。由 (1)，单位时间内通过单位面积的热量为
1 2
得：
Q Q
1 8h 1 ,
h
l d
.
(6)
Q
由图知，当h增加时， Q/ Q' 迅速下降， 而当h>4后，下降变 缓。所以h不宜过大。
Q
0.06 0.03 0应用：
通 常 建 筑 要 求 h = l / d 4 , 于 是 ， Q/ Q ' 3%。因此，双层玻璃窗比用同样多的 玻璃材料制成的单层玻璃窗节约热量97% 左右。当然，由于其他因素的存在，实际情况 没这么好。
1 1 2
(4)
Q
Q s 2
2
.
(5)
显然， Q Q .
由数据资料知道，常用玻璃的热传导系数 k1=410-3~ 810-3(焦耳/厘米· 度) ，干燥 秒· 不流通的空气的热传导系数k2=2.510-4(焦 耳/厘米· 度)。 秒· 所以，
数学建模双层玻璃的功效模型评价
数学建模双层玻璃的功效模型评价
双层玻璃是一种常见的建筑材料，具有一些独特的功效。
本文将基于数学建模方法，对双层玻璃的功效进行评价。
首先，我们可以通过数学模型评估双层玻璃的保温性能。
双层玻璃的两层之间通常会填充一种叫做气体的绝热材料，如氩气或氪气。
这些气体具有较低的热传导性，可以减少室内与室外的热量传递。
我们可以利用传热学中的热传导理论，建立数学模型来计算双层玻璃的热传导系数。
通过对比单层玻璃和双层玻璃的热传导系数，我们可以评估双层玻璃在保温方面的功效。
其次，我们可以利用数学模型来研究双层玻璃的隔音效果。
双层玻璃通过夹层的气体和两层之间的距离，可以有效吸收声波的能量，减少声音的传播。
我们可以运用声学原理，建立声波传播的数学模型，计算双层玻璃的声学性能指标，如声传递系数和噪音减少量。
通过与单层玻璃进行对比，我们可以评估双层玻璃在隔音方面的功效。
此外，数学建模还可以应用于评估双层玻璃的安全性能。
双层玻璃的两层之间可以夹入一层薄膜，以增强玻璃的抗冲击能力和防护性能。
我们可以运用力学原理建立数学模型，评估双层玻璃在受力情况下的强度和稳定性。
通过计算双层玻璃的抗压强度和抗张强度，我们可以对其安全性能进行评价。
总之，数学建模是评价双层玻璃功效的有效工具。
通过建立合适的数学模型，我们可以准确评估双层玻璃在保温、隔音和安全性能方面的优势，为建筑设计和使用提供科学依据。
数学建模基础 12.10双层玻璃的功效
Q
k1
T1 T2
,
而
Q 2 , Q Q Q s 2
说明双层玻璃比单层玻璃保温,为得定量结果, 考虑的s的值,查资料有
常用玻璃:k1=410-3 ~ 810-3 (焦耳/厘米.秒.度) 静止的干燥空气:k2=2.510 - 4 (焦耳/厘米.秒.度)
若取最保守的估计,有
问题:北方城镇的窗户玻璃是双层的,这样做主要是为室内
保温目的,试用数学建模的方法给出双层玻璃能减少热量损 失的定量分析结果
模型准备:热量的传播形式,温度,与热量传播的有关结果:
厚度为d的均匀介质,两侧温度差为T,则单位时间由温度高 的一侧向温度低的一侧通过单位面积的热量Q,与T成正 比,与d成反比,即:Q=k T/d
Ta
T1
T2
L
Tb
模型构成:
由热量守恒定律: 过内层玻璃的热量=过中间空气层的热量=过外层玻璃的热量
Q
k1
T1
d
Ta
k2
Ta
Tb L
k1
Tb
d
T2
消去不方便测量的T1 ,T2,有
Q
k1
T1 T2 d(s 2)
,
s h k1 , h L k2 d
对中间无缝隙的双层玻璃,可以视为厚为2d的单层 玻璃,有热传导:
k为热传导系数.物理定律
模型假设:(根据上定律做假设)
1.室内的热量传播只有传导(不考虑对流,辐射)
2.室内温度与室外温度保持不变(即单位时间通过窗户 单位面积的热量是常数)
3.玻璃厚度一定,玻璃材料均匀(热传导系数是常数)
符号说明: d:玻璃厚度 T1:室内温度, T2:室外温度 Ta:靠近内层玻璃温度, T2:靠近外层玻璃的温度 L:玻璃之间的距离 k1:玻璃热传导系数 k2:空气热传导系数
双层玻璃的功效
2d k2 L1 L2 Ln k1
验
由此可以发现，当 d 一定时，决定保温性能的其实是 L1 至 Ln 之和。也就是说，与
内 玻璃层数无关。玻璃厚一点（ d 大一些），间隙大一些（ L 大一些）即可。
容
由以上分析可知，当T1 20C ，T2 10C ， d 1cm ， L 2d 时，
容
二、模型假设
○1 室内的热量传播只有传导形式（不考虑对流、辐射）；
及
○2 室内温度与室外温度保持不变（即单位时间通过窗户单位面积的热量是常数）；
○3 玻璃厚度均匀，玻璃材料均匀（即热传导系数是常数）。
数
三、符号说明
据
T1
处
T2
理
Ta
Tb
d
室内温度 室外温度 内层玻璃的外侧温度 外层玻璃的内侧温度 单层玻璃厚度
k2
Ta
Tb d
,
可得：
内
外
Q2
k1k2 (T1 T2 ) 2dk2 Lk1
.墙图 2 双层玻 Nhomakorabea示意图2
实验编号： 01
组别：10
设 s h k1 , h 1 ,
k2
d
则：
Q2
k1 (T1 d(S
T2 ) . 2)
所以 Q1 2 1, 显然双层玻璃减少了热量散失。 Q2 S 2
1
实验编号： 01
L k Q
两层玻璃之间的空气厚度 热传导系数
热量损失
组别：10
根据热传导物理定律，即厚度为 d 的均匀介质，两侧的温度差为 T T1 T2 ，则
单位时间内温度高的一侧向温度低的一侧通过单位面积的热量与 T 成正比，与成 d 反比，即：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数学与计算科学学院实验报告
实验项目名称双层玻璃的功效
所属课程名称数学实验
实验类型综合
实验日期
班级
学号
姓名
成绩
附录1：源程序
附录2：实验报告填写说明
1．实验项目名称：要求与实验教学大纲一致。
2．实验目的：目的要明确，要抓住重点，符合实验教学大纲要求。
3．实验原理：简要说明本实验项目所涉及的理论知识。
4．实验环境：实验用的软、硬件环境。
5．实验方案（思路、步骤和方法等）：这是实验报告极其重要的内容。
概括整个实验过程。
对于验证性实验，要写明依据何种原理、操作方法进行实验，要写明需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验，在上述内容基础上还应该画出流程图、设计思路和设计方法，再配以相应的文字说明。
对于创新性实验，还应注明其创新点、特色。
6．实验过程（实验中涉及的记录、数据、分析）：写明具体实验方案的具体实施步骤，包括实验过程中的记录、数据和相应的分析。
7．实验结论（结果）：根据实验过程中得到的结果，做出结论。
8．实验小结：本次实验心得体会、思考和建议。
9．指导教师评语及成绩：指导教师依据学生的实际报告内容，给出本次实验报告的评价。