展开与折叠导学案
展开与折叠(2)活动单导学案
展开与折叠(2)活动单导学案
展开与折叠(2)活动单导学案
以下是查字典数学网为您推荐的展开与折叠(2)活动单导学案，希望本篇文章对您学习有所帮助。
展开与折叠(2)活动单导学案
【学习目标】
1.通过展开、折叠，感受立体图形与平面图形的关系.有些平面图形可以折叠成立体图形.
2.能根据表面展开图判断、制作简单几何体.
【学习重、难点】
通过操作，观察，思考图形在展开与折叠过程中的变化，发展空间想象能力.
【导学提纲】
做一做
1.将一个包装盒沿棱剪开展成平面图形，观察表面展开图的形状.再将展开的平面图形复原为包装纸盒，体会立体图形与平面图形的关系.
2.阅读课本P129-130问题2 3 4 完成课本提问.
3.如图有五个完全一样的正方形用胶水将邻边粘在一起，折叠后能得到一个无盖的正方体纸盒吗?
(1) 能否移动上图中一个正方形的位置，使得折叠后可以得到一个无盖的正方体纸盒。
画出移动后的图形，并用纸复制下来，然后折叠，验证你的想法.。
北师大版五年级数学下册《展开与折叠》导学案-精选文档
北师大版五年级数学下册《展开与折叠》导学案（一）学生自学活动单问题导读部分，完成导学问题。
1、剪一剪
把自己手中的正方体盒子沿着棱剪开。
2、说一说
正方体展开图是什么样子的？
3、将长方体盒子沿棱剪开，试试看。
4、比一比
相同点和不同点分别是什么？
(二)学生自主思考后在小组内交流。
做一做
观察正方体和长方体的展开图。
1、围成正方体所需的条件有哪些？
2、用手中的材料尝试折叠。
3、独立想一想那些图形符合要求？
1.第1部分的内容先由学生独立完成,小组全部完成后获得汇报机会,并给予个人加分。
教师适时点拨。
2.第2部分的学习内容由学生独立思考完成后在组内交流,并请最先完成的两个小组竞赛（第一名先展示），无错者给予小组加分，否则机会自动转入第二名。
展示中教师适时点拨并后做小结。
三,当堂检测
按照要求完成活动单问题检测部分
15分1、指出下列各长方体的前后、左右和上下六个面。
2、相交于一个顶点的三条棱分别叫长方体的（）、（）、（）。
3、长方体的表面最多有（）个正方形。
4、至少需要（）个大小相同的小正方体才可以拼成一个大正方体。
个人独立完成,组内订对结果.小组长依据检测结果给予个人加分。
展开与折叠 1 导学案
5.3展开与折叠(1)班级学号姓名学习目标：1．通过展开、折叠，感受立体图形与平面图形的关系；2．能够把常见的立体图形展开成平面图形；3．能够把一些平面图形折叠成立体图形。
学习重难点：重点：展开图回到立体图形难点：展开与折叠的实际应用学习过程：【情境创设】一只虫子从圆柱上A点处绕圆柱爬到B点处，你能画出它爬行的最短路线吗？【合作探究】活动一：⑴沿虚线剪开圆柱形纸筒的侧面，得到什么平面图形？小虫从A点绕圆柱爬到B点的最短路线是什么？请画出圆柱的侧面展开示意图和小虫爬行的最短路线。
⑵延虚线剪开圆锥形冰淇淋纸筒得到什么平面图形？请画出它的示意图。
（3）沿着图中的粗线将无盖的正方体纸盒剪开展平，得到什么图形？活动二：数学实验室1、将一个正方体纸盒沿棱剪开展成一个平面图形。
2、你能得到哪些不同形状的平面图形？请画出来并与同学交流。
活动三：下列图形是某些几何体的平面展开图，先尝试猜想．．．．这些几何体的名称，然后用纸将这些图形复制下来，折叠验证．．．．你的想法。
活动四：【课堂练习】1、课本P 129练一练1、2题。
2、左图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的情况（图中阴影部分），其中正确的是（ ）【拓展提高】1．下面两图形分别是哪种多面体的展开图？若不能确定，做一做再回答。
⑴ ⑵2．如图所示是一多面体的展开图形，每个面都标有字母，请根据要求回答提问：（1）如果面A 在多面体的底部，那么面 在上面。
（2）如果面F 在前面，从左面看是面B ，则面 在上面。
（3）从右面看是面C ，面D 在后面，面 在上面。
【课堂小结】请同学们说一说有哪些收获？【作业布置】课本习题5.3第1、2、3题。
【学后反馈】A B E C DF。
展开与折叠导学案1
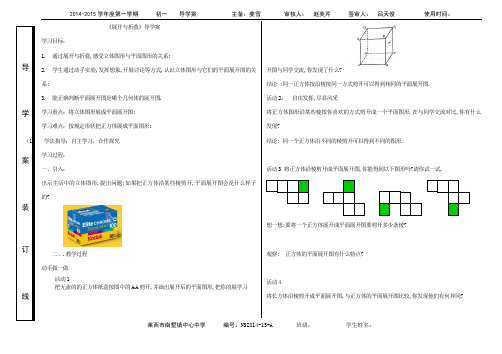
三.练一练
将下面四个图形折叠，你能说出这些多面体的名称吗?
四.小结:畅所欲言
1.你学会了什么?
2.你最喜欢的一个环节是什么?
3.你收获了什么?
五当堂检测
2.如图是一个正方体纸盒的展开图，请在图中的6个正方形中分别填入1、2、3、4、5、6时展开图沿虚线折叠成正方体后相对面上的两个数和为7.
活动2：自由发挥,尽显风采
将正方体图形沿某些棱按你喜欢的方式剪开成一个平面图形.在与同学交流对比,你有什么发现?
结论:同一个正方体沿不同的棱剪开可以得到不同的图形.
活动3将正方体沿棱剪开成平面展开图,你能得到以下图形吗?请你试一试.
想一想:要将一个正方体展开成平面展开图要剪开多少条棱?
观察:正方体的平面展开图有什么特点?
《展开与折叠》导学案
学习目标：
1.通过展开与折叠,感受立体图形与平面图形的关系;
2.学生通过动手实验,发挥想象,开展讨论等方式,认识立体图形与它们的平面展开图的关系;
3.能正确判断平面展开图是哪个几何体的展开图.
学习重点：将立体图形展成平面展开图;
学习难点：按规定形状把正方体展成平面图形;
（1）学法指导：自主学习，合作探究
学习过程：
一、引入：
出示生活中的立体图形,提出问题:如果把正方体沿某些棱剪开,平面展开图会是什么样子的?
二、.教学过程
动手做一做
活动1
把无盖的的正方体纸盒按图中的A1A剪开,并画出展开后的平面图形,把你的展学习
开图与同学交流,你发现了什么?
结论:同一正方体按沿棱按同一方式剪开可以得到相同的平面展开图.
五:布置作业
小组合作探讨:将正方体沿棱展开成平面图形,到底回出现多少种不同的图形,剪一剪,试一试,把所得的图形在纸上画出
《展开与折叠》导学案
2.在你得到的平面图形中,有三个面连成一排的吗?有 几种情况?请你画出来.
有四种,作图如下:
3.在你得到的平面图形中,有两个面连成一排的吗?有 哪几种情况?
有一种,作图如下:
有一种,作图如下:
【归纳总结】正方体沿不同的棱剪开 7 条棱可以得到不 同的平面图形,这样的平面图形有 11 种. 【讨论】见教材P 8中的“议一议”.
1 展开与折叠
1.能将正方体的表面沿某些棱剪开,展开成一个平面图形. 2.知道圆柱、圆锥的侧面展开图,能根据展开图判断和制作简单 的立体图形. 3.经历展开与折叠、模型制作等活动过程,发展空间观念,积累 活动经验. 4.重点:认识立体图形与平面图形的关系,能根据展开图判断和 制作简单的立体模型.
旧知回顾
【归纳总结】圆柱的表面展开图是 两 个圆和一个 圆 的周长 ,其中 的周长 等于长方形的长;圆锥的表面展开图是一个
圆 和一个 扇形 ,其中 圆的周长__等于扇形的弧长;棱柱的表 面展开图是 两 个形状相同的多边形和几个 平行四边形___, 棱柱的底面 边 数与侧面数相同,棱柱的两个底面分别在侧
面展开图的两侧. 【预习自测】下列各平面图形中,圆锥的表面展开图是 ( C )
互动探究 1 下面每个图片都是由6个大小相同的正方形组 成,其中不能折成正方体的是 ( B )
互动探究 2 下列图形中(每个小正方形皆为全等的正 方形),可以是一个正方体表面展开图的是 ( C )
互一动个探正究方3体的每个面上都写有一个汉字,其平面展开 图如图所示,那么在该正方体中,和“超”相对的字 是___自___.
1.八棱柱有 24 条棱, 8 条侧棱,它的侧面展开 图是 长方形 ,它的上下底面是相同的 八 边形.
2.正方体是 四 棱柱,它的侧面展开图是__长__方__形. 问题探究一 阅读教材P 8的“做一做”,并动手操作,完 成下列问题.
《展开与折叠》导学案
《展开与折叠》导学案
班级
姓名
日期
月日
学习目标
1、通过展开与折叠等操作活动，知道长方体、正方体的展开图，加深对长方体、正方体的认识，渗透对应思想。
2、在想象、操作活动中，发展空间观念。
学习过程
一、合作探究：
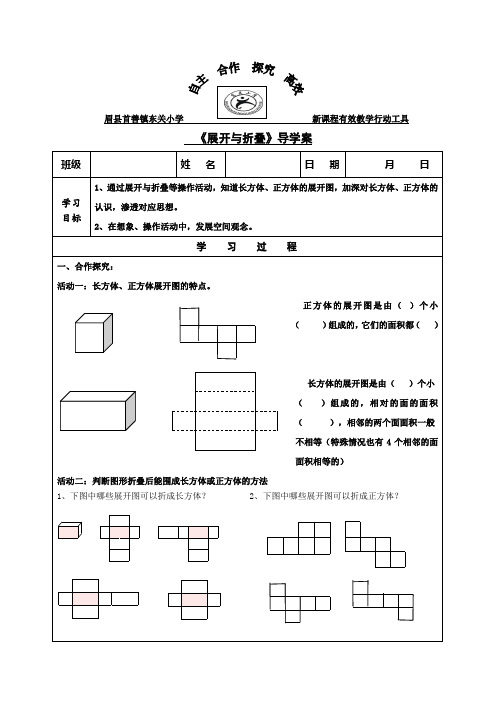
活动一：长方体、正方体展开图的特点。
正方体的展开图是由（）个小（）组成的，它们的面积都（）
3、如图所示的立方体，如果把它展开，可以是下列图形中的（）
4.笑笑制作了一个正方体礼品盒，其对面图案都相同，方体的展开图，找出相对的两个面，并分别标出对应的是长方体中的哪个面？
6.下图是一个正方体展开图，正方体的六个面分别写上“祝你学习进步”六个字，请你说出每个字相对的面上的字是哪个字？ 自我评价：（）小组评价：（）老师评价：（）
长方体的展开图是由（）个小
（）组成的，相对的面的面积（（），相邻的两个面面积一般
不相等（特殊情况也有4个相邻的面面积相等的）
活动二：判断图形折叠后能围成长方体或正方体的方法
1、下图中哪些展开图可以折成长方体？2、下图中哪些展开图可以折成正方体？
二、课堂检测
1、下图中能围成正方体的是（）号图形。
2、下面的图形经过折叠不能围成一个长方体的是（）
初中数学最新版《展开与折叠》精品导学案(2022年版)
1.2 展开与折叠1.经历图形的展开与折叠的活动，开展空间观念，积累数学活动经验。
2.了解圆柱、圆锥、棱柱的侧面展开图，能根据展开图判断和制作简单的立体模型。
3.通过观察发现、大胆猜测、动手操作、自主探究、合作交流，在学习中体验到：数学活动充满着探究和创造，以提高学习兴趣。
1、前置准备：〔1〕在棱柱中，任何相邻两个面的交线都叫做▁▁▁▁▁。
棱柱的所有▁▁▁▁▁都相等。
棱柱的▁▁▁▁▁相同。
▁▁▁▁▁的形状都是长方形。
〔2〕一底面是正方形的棱柱高为4cm ，正方形的边长都为2cm ，那么此棱柱共有▁▁▁▁▁条棱，所有棱长之和为▁▁▁▁▁cm 。
2、 自主学习p14“做一做〞，并把结论写下来 〔1〕▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁。
〔2〕▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁。
〔3〕▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁。
3、合作交流完成p14“想一想〞，你有什么新收获：▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁。
4、归纳总结：▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁。
5、当堂训练：〔1〕如以以下图所示，图形能围成一个正方体的是〔 〕①② ③ 〔2〕如图某些多面体的平面展开图，把多面体的名称写在横线上▁▁▁▁▁▁ ▁▁▁▁▁▁▁ 1、 如图，三棱柱底面边长为3cm ，侧棱长5cm ，那么此三棱柱共▁▁个面， 侧面展开图的面积为▁▁▁ cm ²。
2、 要把一个长方体剪成平面图形，需要剪▁▁▁条棱。
A B C D4、 以下几何体能展成如以下图图形的是▁▁▁。
A 、三棱柱B 、四棱柱C 、五棱柱D 、六棱柱5、如图，把一个圆锥的侧面沿图中的线剪开，那么会得到图形▁▁▁。
A 、 A 、三角形B 、圆C 、圆弧D 、扇形6、一个多面体的顶点数为v ，棱数为e ，面数为f ，以下四种情况中肯定不会出现的是▁▁▁。
A 、v 、e 、f 都是奇数B 、v 、e 、f 都是奇数C 、v 、e 、f 两奇一偶D 、v 、e 、f 一奇两偶 中考真题如图，一个3×5的方格纸，现将其剪为三局部，使每一局部都可以折成一个无盖的小方盒，问如何剪？第1课时 代入法1．会用代入法解二元一次方程组．(重点) 一、情境导入 《一千零一夜》中有这样一段文字：有一群鸽子，其中一局部在树上，另一局部在地上．树上的一只鸽子对地上的鸽子说：“假设从你们中飞上来一只，那么地上的鸽子为整个鸽群的三分之一；假设从树上飞下去一只，那么树上、地上的鸽子一样多．〞你知道树上、地上各有多少只鸽子吗？我们可以设树上有x 只鸽子，地上有y 只鸽子，得到方程组⎩⎪⎨⎪⎧x ＋y ＝3〔y －1〕，x －1＝y ＋1.可是这个方程组怎么解呢？有几种解法？二、合作探究探究点：用代入法解二元一次方程组 【类型一】 用代入法解二元一次方程组用代入法解以下方程组：(1)⎩⎪⎨⎪⎧2x ＋3y ＝－19，①x ＋5y ＝1；② (2)⎩⎪⎨⎪⎧2x －3y ＝1，①y ＋14＝x ＋23.②解析：对于方程组(1)，比拟两个方程系数的特点可知应将方程②变形为x ＝1－5y ，然后代入①求解；对于方程组(2)，应将方程组变形为⎩⎪⎨⎪⎧2x －3y ＝1，③4x －3y ＝－5，④观察③和④中未知数的系数，绝对值最小的是2，一般应选取方程③变形，得x ＝3y ＋12.解：(1)由②，得x ＝1－5y.③把③代入①，得2(1－5y)＋3y ＝－19， 2－10y ＋3y ＝－19，－7y ＝－21，y ＝3.把y ＝3代入③，⎩⎪⎨⎪⎧x ＝－14，y ＝3.(2)将原方程组整理，得⎩⎪⎨⎪⎧2x －3y ＝1，③4x －3y ＝－5.④由③，得x ＝3y ＋12.⑤把⑤代入④，得2(3y ＋1)－3y ＝－5， 3y ＝－7，y ＝－73.把y ＝－73代入⑤，得x ＝－3.所以原方程组的解是⎩⎪⎨⎪⎧x ＝－3，y ＝－73.方法总结：用代入法解二元一次方程组，关键是观察方程组中未知数的系数的特点，尽可能选择变形后比拟简单的或代入后容易消元的方程进行变形．【类型二】 整体代入法解二元一次方程组解方程组：⎩⎪⎨⎪⎧x ＋13＝2y ，①2〔x ＋1〕－y ＝11.②解析：把(x ＋1)看作一个整体代入求解．解：由①，得x ＋1＝6y.把x ＋1＝6y 代入②，得2×6y－y ＝11.解得y ＝1.把y ＝1代入①，得x ＋13＝2×1，x ⎩⎪⎨⎪⎧x ＝5，y ＝1.方法总结：当所给的方程组比拟复杂时，应先化简，但假设两方程中含有未知数的局部相等时，可把这一局部看作一个整体求解．【类型三】 方程组的解，用代入法求待定系数的值⎩⎪⎨⎪⎧x ＝2，y ＝1是二元一次方程组⎩⎪⎨⎪⎧ax ＋by ＝7，ax －by ＝1的解，那么a －b 的值为( ) A ．1 B ．－1 C ．2 D ．3解析：把解代入原方程组得⎩⎪⎨⎪⎧2a ＋b ＝7，2a －b ＝1，解得⎩⎪⎨⎪⎧a ＝2，b ＝3，.方法总结：解这类题就是根据方程组解的定义求，即将解代入方程组，得到关于字母系数的方程组，解方程组即可．三、板书设计解二元一,次方程组)⎩⎪⎨⎪⎧根本思路是“消元〞代入法解二元一次方程组的一般步骤回忆一元一次方程的解法，借此探索二元一次方程组的解法，使得学生的探究有很好的认知根底，探究显得十分自然流畅．充分表达了转化与化归思想．引导学生充分思考和体验转化与化归思想，增强学生的观察归纳能力，提高学生的学习能力．。
展开与折叠导学案
年级：七年级班级：学生姓名：制作人：李兴林
教师个性化设计、学法指导或学生笔记
一、明确学习目标：（1分钟）
1、明白将一个正方体的表面沿某些棱剪开得到的11种平面展开图；并能总结归纳它们的特点及规律，培养观察、动手操作、归纳、合作探究能力；
2、会用多种方法对正方体展开与折叠的实践操作，在经历和体验图形的转换过程中，初步建立空间概念，培养发散思维；
五、总结反思：（4分钟）
回顾、总结正方体的11种平面展开图的特点：
六、课后练习：
1、如图，把左边的图形折叠起来，它会变为（）
2、如图，把左边的图形折叠起来，它会变成（）
3、完成教材习题1.3。
4、完成同步导学相关练习。
课后反思：
3、在充分经历实践、探索、交流的过程中，获得成功的体验，逐步养成正确的学习态度和价值观。
二、自主预习：（5分钟）
预习教材：第8页
三、合作探究：（15分钟）
1.（先把正方体的每一个面打上记号），然后把一个正方体的表面沿某些棱剪开，展成一个平面图形，能得到哪些平面图形？把它们画出来与同伴进行交流。
2、正方体的平面展开图有什么特点，能否将他们分类？请归纳。（包括排列、相对面和邻面）
四、当堂检测：（15分钟）
1、下面的图形经过折叠可以得到正方体吗？若不能，你能通过移动使之能吗？
2、下面哪些平面展开图能折叠成一个正方体？你能通过移动来使之能吗？
（1）（2）（3）
（4）（5）6）
3、如图是一个正方体纸盒的展开图，请在图中的6个正方形中分别填入1、2、3、-1、-2、-3时，展开图折叠成正方体后相对面上的两个数互为相反数。
北师大版七年级数学《展开与折叠》第一课时导学案
1 / 2北师大版七年级数学《展开与折叠》第一课时导学案【学习目标】1、经历图形的展开与折叠的活动，发展空间观念，积累数学活动经验。
2、熟练掌握正方体的几种侧面展开图，正确找出对面。
3、通过观察发现、大胆猜想、动手操作、自主探究、合作交流，在学习中体验到：数学活动充满着探究和创造，以提高学习兴趣。
【学习重点】 体会数学伴随着人类的进步与发展，人类离不开数学。
【学习难点】 结合具体例子，体会数学与我们的成长密切相关。
【学习过程】 一、温故知新：（1）在棱柱中，任何相邻两个面的交线都叫做 。
棱柱的所 有 都相等。
棱柱的 相同。
的形状都是长方形。
（2）一底面是正方形的棱柱高为4cm ，正方形的边长都为2cm ，则此棱柱共 有 条棱，所有棱长之和为 cm 。
二、自主学习P8“做一做”，动手试一试，并把结论写下来 把一个正方体沿某些棱剪开，展成一个平面图形。
你能得到哪些形状的平面图形？并把它们画出来。
三、合作交流（1）想一想：下面图形经过折叠能否围成一个正方体？（2）议一议：下图可以折成一个正方形的盒子，折好后，与1 相邻的数是什么？相对的数是什么？先想一想，再折一折，看看怎么样。
2 / 2四、达标训练：如下图所示，图形能围成一个正方体的是（ ）（1） （2） （3） 五、谈收获1、我的收获： 。
2、我的不足： 。
六、能力提升1、如图，三棱柱底面边长为3cm ，侧棱长5cm ，则此三棱柱共 个面，侧面展开图的面积为 cm²。
2、要把一个正方体剪成平面图形，需要剪 条棱。
3、下面展开图能组成正方体的是。
A B C D4、在图中增加1个小正方形使所得图形经过折叠能够围成一个正方体，先想一想，再试一试。
七、布置作业：P9问题解决3、4题。
《展开与折叠》导学案 2022年北师大版数学七上2
《1.2 展开与折叠》学案（2） 北师大版学习目标：经历图形的展开与折叠活动，了解棱柱展开图的形状，能正确地判断和制作简单的立体模型．学习重点：在操作活动中，发展空间观念，积累数学活动经验．认识棱柱的某些特征，形成规范的语言。
学习难点：根据棱柱的展开图判断和操作简单的立体图形一、知识链接1.棱柱有什么与众不同的特征呢？(1)棱柱的上、下底面是_____________．(2)棱柱的侧面都是______________．(3)棱柱的所有侧棱长都_____________．(4)棱柱侧面的个数与底面多图形的边数 _____________ 。
棱柱各元素间的数量关系如下二、自主预习 1．左边的图形经过折叠，能围成右边如图2的棱柱吗？2.下面图形经过折叠能否围成棱柱？不能围成的再作适当的修改使所得的图形能围成一个棱柱。
三、自主探究1.圆柱的表面展开图是_________作底面和______________作侧面．2.圆锥的表面展开图是___________作底面和_______________作侧面．四、展示提升 名称 底面形状 顶点数 棱数 侧棱数 侧面数 侧面形状 总面数 n 棱柱A ．B ．C ．D ．E D CB A1、骰子是一种特的数字立方体（见图），它符合规则：相对两面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是（ ）A ．B ．C ．D ．2、下列四个图中，是三棱锥的表面展开图的是（ ）3、已知为圆锥的顶点，M 为圆锥底面上一点，点在OM 上．一只蜗牛从点出发，绕圆锥侧面爬行，回到点时所爬过的最短路线的痕迹如右图所示．若沿OM 将圆锥侧面剪开并展开，所得侧面展开图是 （ ）4.5多边形和圆的初步认识班别 组别 姓名学习目标：1、经历从现实世界中抽象出平面图形的过程，感受图形世界的丰富多彩。
2、了解多边形的有关概念，认识多边形的边、内角、顶点、对角线。
认识正多边形。
3、了解圆的有关概念，认识圆的半径、圆弧、圆心角，扇形，会计算圆心角的度数。
【2021年】【教材】5.3 展开与折叠 导学案 - 陈煜
课题：5.3展开与折叠（1）
【学习目标】
1.通过展开、折叠，感受立体图形与平面图形之间的关系：有些立体图形可以
按不同的方式展开成平面图形。
2.能想象并画出简单几何体的表面展开图。
3.经历体验图形的变化过程，发展空间观念，养成研究性学习的良好习惯
4.通过克服困难的经历和获得成功的体验，培养对数学的兴趣．
【导学提纲】
一.课前准备：
1.自制一个圆柱形纸筒、一个圆锥形纸筒、一个无盖的正方体纸盒
2.自制两个正方体纸盒沿棱剪开展成一个平面图形
二、探究学习
探究活动一：
1.自制一个圆柱形纸筒、一个圆锥形纸筒、一个无盖的正方体纸盒.（课前准备）
2.阅读课本P129做一做1 2 完成操作.
3.阅读课本P129做一做3，将无盖的正方体纸盒展开，得到什么图形？
问题一：
（1）图中纸筒纸盒沿红线或侧棱剪开，能展开成平面图形吗？会是什么形状呢？
（2）下列各图是几何体的展开图，请写出它们各是什么几何体的展开图.
探究活动二：【数学实验室】
1.将正方体纸盒沿棱剪开展成一个平面图形.你能得到下面的几何图形吗？你
还能得到哪些不同形状的平面图形？请与同学讨论交流并展示.
2.剪开正方体纸盒的哪些棱你能得到下图中的平面图形
备用图1 备用图2 备用图3 备用图4
三、脑力大冲浪
1.如图：一只无盖的圆桶下方有一只壁虎，上方有一只蚊子，壁虎要想尽快吃到蚊子，从侧面应该走哪条路径？
壁虎
2.一只壁虎在正方体的顶点A，要爬到距它最远的另一个顶点B去，哪条路径最短？
四、收获
五.作业
请将长方体纸盒沿部分冷剪开展成一个平面图形，并把你得到的平面图形与同学交流。
《展开与折叠》导学案
中学生自主学习导学案班级________组号________姓名________一：新知探索：活动准备：请每一位同学用硬纸片自己制作三个以上的正方体，带上剪刀。
1.活动一：请同学们将准备好的小正方体纸盒沿某条棱任意剪开，看看能得到哪些平面图形?注意：剪开正方体棱的过程中，正方体的6个面中每个面至少有一条棱与其它面相连。
请同学们将剪好的平面图形画出来：2.能否将得到的平面图形分类？你是按什么规律来分类的？3.一个正方体要将其展开成一个平面图形，必须沿几条棱剪开？活动二：把一个正方体剪成如图所示的平面图形，你能剪成吗?活动三：1.面A 、面B 、面C 的对面各是哪个面？科 目 数学 课 题§1.2.1展开与折叠（1） 授课时间 设 计 人学案序号学习目标1、经历展开与折叠、模型制作等活动过程，发展空间观念，积累数学学习的经验。
重 点 利用实物模型，发现并认识正方体的一些特征。
难 点 对正方体展开图的认识和应用。
教师寄语 相信自己，超越自己。
A B C D E F2. 1、下列图形可以折成一个正方体形的子．折好以后，与 1 相邻的数是什么？相对的数是么？先想一想，再具体折一折，看看你的想法是否正确。
二．谈谈本节课你的收获与疑虑：三：课堂检测：1.如图所示是一多面体的展开图形，每个面都标有字母，请根据要求回答提问：（1）如果面A 在多面体的底部，那么面 在上面。
（2）如果面F 在前面，从左面看是面B ，则面 在上面。
（3）从右面看是面C ，面D 在后面，面 在上面。
2、将下图中左边的图形折叠起来围成一个正方体，应该得到右图中的（ ）。
3、想想看：下面的图形中 是正方体的展开图(只要填序号)。
3 2 1 64 5 A B EC DF学（教）后记：。
4[展开与折叠]导学案导学案
![4[展开与折叠]导学案导学案](https://img.taocdn.com/s3/m/71eedccf866fb84ae55c8d76.png)
4[展开与折叠]导学案导学案张老师黄墩中心学校六年级数学课教学设计年级六年级课题展开与折叠（2）备课教师马长举执教马长举1、结合具体的长方体和长方体的展开与折叠的情镜，经历探究长方体和正方体 6 学习目标重点难点个面相对位置的投资过程，准确获取长方体和正方体 6 个面的展开与折叠情况； 2、认识长方体和正方体，具有初步的立体存储空间想象能力； 3、经历对梯形正方体的认识过程，体验观察、比较、分类的思想和方法。
掌握长方体和正方体的 6 个面的展开与折叠的情况，展开与折叠的技巧。
教学环节一、激趣导入时间分配活动内容观察长方体、正方体说一说它们的特征社尾庄是什么？有什么相同点和不同点？（一）学生自学活动单问题导读部分，完成导学问题。
1、剪一剪把自己手中的正四面体盒子沿着棱剪开。
2、说一说正方体展开图是什么看着的？3、将长方体盒子沿棱剪开，试试看。
4、比一比相同点和不同点分别是什么？ (二)学生自主思考后在小组内交流。
做一做观察柱体和长方体的展开图。
1、四边正方体所需的条件有哪些？ 2、用手中的材料尝试折叠。
3、独立想一想那些图形相符要求？导学策略与方法备注出示课件复习导入3分主要导学过程二、探究新知： 18 分1.第 1 部分的内容先由学生独立完成,小组全部完成后获得汇报机会, 并给予个人加分。
教师适时点拨。
2.第 2 部分的学习参考资料由学生独立思考完成后在组内交流,并请最先完成的两个小组竞赛（第一名先展示），无错者给于小组加分，否则机会自动转入第二名。
展示中教师适时求教并后做小结。
1、指出下列各长方体的前后、大约和上下六个面。
三,当堂检测按照要求完成活动单问题检测部分2、相交交叉点于一个顶点的三条棱分别叫长方体的（）、（）、（）。
3、长方体的光滑最多有（）个正方形。
4、至少需要（）个大小相同的小正方体才可以替换成一个大正方体。
15 分个人独立完成,组内订对结果.小组长的依据检测结果给予个人加分四. 小结与评价五. 布置作业板书设计3分 1分本节课你有什么收获? 完成资源与学案个人谈收获展开与折叠正方体是由全然相等的 6 个面组成的，长方体 6 个面的大小不相同。
1.2《展开与折叠》学案
1 《展开与折叠》导学案 姓名：________【学习目标】1、认识立体图形与平面图形的关系，知道立体图形可由平面图形围成，立体图形可展开为平面图形；2、通过展开与折叠的实践操作，经历和体验图形的转换过程中，建立空间概念，发展几何直觉。
3、体验数学与日常生活是密切相关的，体验数学研究的原型源于生活实际，反过来，众多的实际问题也可以借助数学方法来解决。
一、情景导入，提出问题 给出一个正方体模型，提问：这是一个什么，你知道它是怎样做的吗？它有几个面围成的，它有几条棱，你能有前剪刀沿着棱剪开，得到一个不会断开的一个平面图形吗？今天我们来学习正方体的展开与折叠。
（温故互查，同桌对改） 1、在棱柱中，任何相邻两个面的交线都叫做 。
棱柱的所有 都相等。
棱柱的 相同。
的形状都是长方形。
2、一底面是正方形的棱柱高为4cm ，正方形的边长都为2cm ，则此棱柱共有 条棱，所有棱长之和为 cm 。
3、圆柱与棱柱，底面是圆的是_______，侧面是曲面的是_______，侧面是平面的是_______。
4、三棱锥的每个面都是_______形，它有_______个面，_______条侧棱，共_______条棱。
三、设问导读，自主学习 自学课本P8，并讨论回答下列问题 1、沿正方体的12条棱剪开，得到了_______互不连接的正方形， 2、要将正方体纸合沿棱剪开，成为一个六个正方形相连的整体，应剪____剪刀， 3、将一个正方体的表面沿某些棱剪开，展开成一个平面图形，这个图形叫正方体的_______，每个展开图沿着一定的路径可重新_______成一个几何体。
动手操作，合作探究1、请同学们将准备好的小正方体纸盒沿某条棱任意剪开，看看能得到哪些平面图形?有几种就剪几种，注意剪开正方体棱的过程中，正方体的6个面中每个面至少有一条棱与其它面相连。
你能得到哪些形状的平面图形？并把它们画出来。
4、引导观察这11个图形，这11个图形有什么共同的特征（引导学生回答：至多3层，每层至多4个），你能将得到的平面图形分类吗，你是怎样分的，说说你的理由，经过讨论得出分为4类： 第一类，中间四连方，两侧各一个，共六种。
展开与折叠导学案
展开与折叠导学案
学习目标：
1、我能听过展开与折叠等操作活动，知道长方体、正方体的展开图；
2、我能正确判断展开图能否折叠成长方体或正方体。
教学重点：知道长方体、正方体展开图的特点；
教学难点：能正确判断展开图能否折叠成长方体或正方体。
一、复习导入（全班统一回答）
说一说长方体有几个面？几条棱？几个顶点？哪些面的形状一定相同？哪些棱的长度一定相等？
二、自主学习，探究新知（自学，教师巡视指导）
自学教材14页，然后拿出各自准备好的正方体小纸盒，用剪刀沿其棱剪开（注：每两个面之间至少有一条棱相连）。
三、小组合作交流（小展示，教师巡视指导）
1、小组长把各自小组的作品收起来，粘到你们的小黑板上（请不要重复）。
2、仔细观察看一看别人剪的和自己的有什么不同。
四、合作探究（大展示，教师巡视指导）
1、仔细观察其他小组的作品，收集自己小组没有的展开图，然后整理画在自己的练习本上。
2、看一看大家总共可以得到多少种不同的展开图？你会将它们分类吗？
3、通过大家的努力探究，我们总共得到了（）种正方体不同的展开图，实际上正方体总共有（）种不同的展开图，接下来由老师给大家补充说明。
4、分类总结：
5、拿回自己的展开图，在每个面上分别标上1、2、3、4、5、6几个数字，然后将这些展开图还原成正方体，看一看1号面、2号面、3号面相对的分别是哪几个面？你发现了什么？
五、课堂检测
1、下列展开图折叠后哪几个能围成正方体
2、如图是一个正方体的平面展开图，则正方形4的对应面是正方形（）。
展开与折叠教学设计（五篇材料）
展开与折叠教学设计（五篇材料）第一篇：展开与折叠教学设计《展开与折叠》教学设计一、教材简介《义务教育教科书（五·四学制）·数学》六年级上册第一章《丰富的图形世界》的第二节《展开与折叠》第1课时.二、教学目标（一）最近目标让学生进一步认识几何体，发展空间想象能力，逐步树立起空间观念．具有很好的空间观念是新课标的一个重要目标，图形的展开与折叠在各实验教材中占有很重要的地位，中考所占的分值也逐年增大。
（二）教材分析《丰富的图形世界》一章是从学生身边丰富多彩的实物开始认识立体图形和平面图形，它通过“生活中的立体图形”、“展开与折叠”、“截一个几何体”、“从三个不同方向看物体的形状图”四小节内容，初步让学生从几何直观的角度建立起立体图形与平面图形之间的联系.图形直观是人们理解自然界和社会现象的绝妙工具，它在空间与图形的学习中将给学生带来无穷无尽的直觉源泉，这种直觉将有效地增进学生对空间的理解.“展开与折叠”以及后面即将学习的“截一个几何体”、“从不同方向看”都是采用了化归的方法，将几何体转化为学生比较熟悉的平面图形，从平面的角度去研究几何体.本节共分为两课时，第1课时主要是研究直棱柱与它的平面展开图之间的关系，第2课时主要是研究正方体和平面展开图之间的关系.本节课从直观图形入手，通过学生动手剪、展、折叠等操作积累经验，建立起正方体与平面展开图之间的联系.本节首先遵循从立体到平面的方向，将几何体展开，得到平面上的展开图形，然后又将平面图形折叠，还原得到几何体，进行平面到立体的转化.（三）学情分析在小学的学习过程中，学生已有的更多的是关于平面图形的认识，缺少的是对立体图形的认识.对刚刚升入初中的七年级的学生来说，动手能力还显得很弱，学生的认知条件也有差异，尤其是初次从立体图形到平面图形，再从平面图形到立体图形两个角度研究几何图形，会给学生带来一定的困难.因此确定本节课的教学难点是：能准确识别正方体的表面展开图.解决难点的关键是通过观察、操作、想象、推理、交流等大量的数学活动，逐步使学生形成对正方体与平面展开图之间关系的认识.（四）经验剖析新课程标准中的“基本理念”中指出：“教师应帮助学生在自主探究和合作交流的过程中真正理解和掌握基本的数学知识与技能，数学思想和方法，获得广泛的数学活动的经验.”为了使学生能生动活泼地学习，能充分地展示自己，能在思辨中探求新知，小组合作学习便成为教学中实现这一理念的主要方法之一.小组合作学习将班级授课制条件下学生个体间的学习竞争关系变为“组内合作，组间竞争”的关系；将传统教学师生之间的单向交流变为师生、生生之间的多向交流.这不仅提高了学生学习的主动性、教学效率，也促进了学生间良好的人际合作关系.（五）课时目标本节是从学生周围熟悉的物体入手，使学生进一步认识立体图形与平面图形的关系：不仅要让学生了解多面体可由平面图形围成，而且立体图形可按不同方式展开成平面图形，更重要的是让学生通过观察、思考和自己动手操作，经历和体验图形的变化过程，进一步发展学生的空间观念，为后续章节的学习打下基础。
1.2 展开与折叠第二课时导学案
七年级数学（上）第一章一一一一丰富的图形世界1.2 展开与折叠（2）班级：姓名：评价： ____ ＊＊学习目标＊＊1.在操作活动中，进一步丰富对棱柱、圆锥、圆柱的认识；2.了解棱柱、圆柱、圆锥的侧面展开图，能根据展开图判断和制作简单的立体模型.【复习新知】上节课探究了正方体的展开图，我们一起来看看下面平面图形：（1）如图，这个图形是正方体的展开图吗？（2）下面这些平面图形经过折叠可以围成一个正方体吗？（3）下面这两个平面图形经过折叠可以得到正方体吗？它们是相同的吗？【探究新知】议一议：将下图的棱柱沿着某些棱剪开，展成一个平面图形，你能得到哪些形状的平面图形？想一想：（1）下列哪些图形经过折叠可以围成棱柱？（2）将不能围成棱柱的图形进行适当的修改使得图形能围成一个棱柱.结论：（1）棱柱的底面边数与侧面边数__________________________.（2）棱柱的两个底面要分别在侧面展开图的_________________.小试牛刀：（1）如图所示，是那种几何体表面展开的图形 ( )A. 三棱柱B. 正方体C. 长方体D. 圆柱（2）下图中两个图形能围成哪种几何体？11 想一想：将圆柱、圆锥的侧面展开，会得到什么图形？结论：圆柱的侧面展开图是____________________，圆锥的侧面展开图是____________________.思考：是不是所有的立体图形都能展成平面图形呢？【落实基础】1.如图,圆柱的侧面展开后得到的平面图形是( )A. B. C. D.2.如图,圆柱的表面展开后得到的平面图形是( )A. B. C. D.3.如图是哪种几何体表面展开的图形 ( )A. 棱柱B. 球C. 圆柱D. 圆锥4.已知一个圆柱的侧面展开图如图所示,长为π6，宽为π4，求这个圆柱底面圆的半径.5.如图所示的四棱柱（1）它的侧面展开图是什么图形？（2）若底面周长是20cm ，侧棱长8cm ，则它的所有侧面面积之和是？。
展开与折叠(二)导学案
第一章丰富的图形世界
2．展开与折叠（二）
一、教学目标如下：
1、知识与技能目标：通过展开与折叠活动，了解三棱柱、四棱柱、五棱柱、圆柱、圆锥的侧面展开图；能根据展开图判断和制作简单的立体模型。
2、过程与方法目标：经历展开与折叠、模型制作等活动，发展空间观念，积累数学活动经验；在动手实践制作的过程中学会与人合作，学会交流自己的思维与方法。
二、教学过程：
第一环节：创设情景，导入课题
内容：将图中的棱柱沿某些棱剪开，展成一个平面图形，你能得到哪些形状的平面图形？
第二环节：探索什么样的图形能围成棱柱
内容：以下哪些图形经过折叠可以围成一个棱柱?
（1）（2）
（3）（4）
你能将图形（1）、（3）修改后使其能折叠成棱柱吗?
第三环节：探索圆柱、圆锥的侧面展开图
内容：把圆柱的侧面展开，会得到什么图形？把圆锥的侧面展开，会得到什么图形？
第四环节：巩固提升
内容：1、哪种几何体的表面能展开成下面的平面图形？
（1）（2）
2、图中的两个图形经过折叠能否围成棱柱？
（1）（2）
第五环节：布置作业
习题1.4第1、2题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
蓬莱市实验中学数学课堂教学导学案
课题：展开与折叠（1）
班级______ 姓名__________ 教师评价____________
学习目标：
1、经历展开与折叠、模型制作等活动过程，发展空间观念，积累数学学习的经验。
2、在操作活动中认识棱柱的某些特征；
3、知道棱柱、圆柱、圆锥的侧面展开图，认识到它们的多样性；能根据展开图判断和制作简单的立体模型。
学习重点：利用实物模型，发现并认识棱柱的一些特征。
学习难点：对棱柱性质的概括和空间想像的验证。
课型：新授课
使用说明：
1、请先认真自学课本，结合课本内容理解并掌握几何体的展开与折叠，形成自己的知识树。
2、和上课本，认真思考，独立完成导学案，不会的或是有疑问的做好标记，以备小组合作解决。
导学过程：
一、预习检测
如图：(1)长方体有_____个顶点，_____条棱，_____个面，这些面形状
都是_____.
(2)哪些面的形状和大小一定完全相同？
(3)哪些棱的长度一定相等？
二、自主学习，小组交流：
从做一做中认识棱柱的特性
回答问题（1）：这棱柱的上、下底面一样吗？它们各有几条边？
问题（2）：这个棱柱有几个侧面？侧面的形状是什么图形？
问题（3）：侧面的个数与底面图形的边数有什么关系？
三、自主学习，合作探究：
1、我们关于这个棱柱讨论了很多了.怎么用自己的语言来描述一下棱柱的性质呢？
设计人：郝兆霞审核人：审批人: 审批时间：编号：
四、巩固练习：
如下图，哪些图形经过折叠可以围成一
个棱柱？先想一想，再折一折.
五、拓展延伸：
1.想一想，再折一折，右面两图经过折叠能否围成棱柱？
分析：先想一想，是对学生空间想像能力的更高要求，但也不可忽
视折一折的作用，先想一想，再动手操作，是培养空间观念的重要
环节.
2.一个六棱柱模型如图，它的底面边长都是5厘米，侧棱长4厘
米.(课本第七页图1—3)
观察这个模型，回答下列问题：
(1)这个六棱柱一共有多少个面？它们分别是什么形状？哪些面的形状和大小完全相同？
(2)这个六棱柱一共有多少条棱？它们的长度分别是多少？
六、我的收获：（包括知识点、解题方法和技巧等方面）
七、达标检测
1．三棱锥的展开图是由个形组成的。
2．圆椎的展开图是由一个和一个形组成的图形。
3．看图，这些图经过折叠可以围成一个棱柱吗？想一想，亲自动手折一折。
4、请写出图中，各个几何体的展开图是什么几何体的展开图。
八、学（教）后反思：
蓬莱市实验中学数学课堂教学导学案
课题：展开与折叠（2）
班级______ 姓名__________ 教师评价____________
学习目标：
1、经历展开与折叠、模型制作等活动过程，发展空间观念，积累数学学习的经验。
2、知道正方体、圆柱、圆锥的侧面展开图，认识到它们的多样性；能根据展开图判断和制作简单的立体模型。
学习重点：利用实物模型，发现并认识正方体的一些特征。
学习难点：对正方体展开图的认识和应用。
课型：新授课
使用说明：
1、请先认真自学课本，结合课本内容理解并掌握几何体的展开与折叠，形成自己的知识树。
2、和上课本，认真思考，独立完成导学案，不会的或是有疑问的做好标记，以备小组合作解决。
导学过程：
一、预习检测
下列第二行的哪种几何体的表面能展开成第一行的平面图形？请对应连线。
(可以折一折)
2、表面展开图是扇形的是（）
A、圆柱
B、棱柱
C、圆锥
D、棱锥
二、自主学习，小组交流：
按照课本想一想中的方法把圆柱、圆锥的侧面展开，会得到什么图形？先想一想，再试一试。
三、自主学习，合作探究：
拿出准备的正方体纸盒，将它沿某些棱剪开，展成一个平面图形。
（要求独立做，以避免雷同）然后回答：
（1）你剪开了几条棱？你的同伴剪开了几条棱？至少需要剪开几条棱？
（2）用不同的方式去剪，你能得到哪些平面图形？把它们画出来，与同伴进行交流。
（3）你能设法得到课本图1—4中的平面图形吗？
设计人：郝兆霞 审核人： 审批人: 审批时间： 编号：
（4）课本图1—5中的图形经过折叠能否围成一个正方体？试一试 四、巩固练习：
1、下列平面图经过折叠后不能围成正方体的是 （ ）
2．一个同学画出了正方体的展开图的一个部分，还缺一个正方形（如下图所示），请在图中添上这个正方形。
五、拓展延伸：
1．一个正方体的平面展开图的如图所示，则正方形4的对面是正方形 。
2.如图所示的立方体，如果把它展开，可以是下列图形中的 （ ）
A B C D
六、我的收获：（包括知识点、解题方法和技巧等方面） 七、达标检测
1. 想想看：下面的图形中 是正方体的展开图(只要填序号)。
2.
（1）如果面A 在多面体的底部，那么面 在上面。
（2）如果面F 在前面，从左面看是面B （3）从右面看是面C ，面D 在后面，面 在上面。
八、学（教）后反思：
12
34
56
5. 想想看：下面的图形中是正方体的展开图(只要填序号)。