偏好与效用
尼科尔森《微观经济理论-基本原理与扩展》(第9版)课后习题详解(第3章--偏好与效用)
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第2篇选择与需求 第3章偏好与效用课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.画出下列效用函数的无差异曲线,并判断它们是否是凸状的(即边际替代率MRS 是否随着x 的增加而递减)。
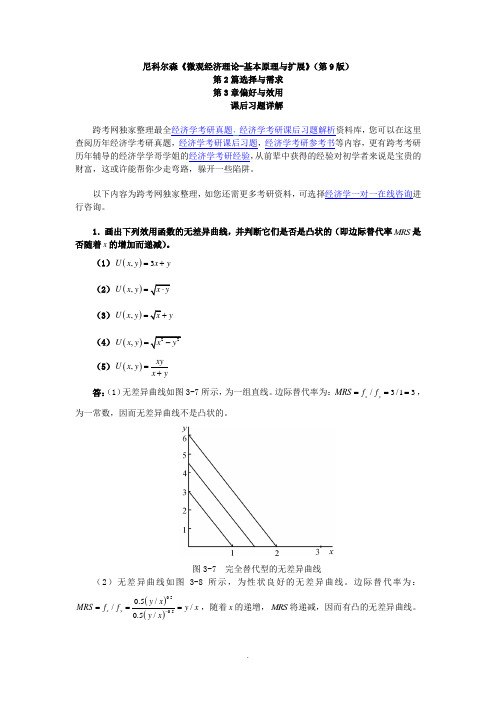
(1)(),3U x y x y =+ (2)(),U x y x y =⋅ (3)(),U x y x y =+ (4)()22,U x y x y =- (5)(),xyU x y x y=+ 答:(1)无差异曲线如图3-7所示,为一组直线。
边际替代率为:/3/13x y MRS f f ===,为一常数,因而无差异曲线不是凸状的。
图3-7 完全替代型的无差异曲线(2)无差异曲线如图3-8所示,为性状良好的无差异曲线。
边际替代率为:()()0.50.50.5///0.5/x y y x MRS f f y x y x -===,随着x 的递增,MRS 将递减,因而有凸的无差异曲线。
图3-8 凸状的无差异曲线(3)无差异曲线如图3-9所示。
边际替代率为:0.5/0.5x y MRS f f x -==,因而边际替代率递减,无差异曲线是凸状的,此为拟线性偏好的效用函数。
图3-9 拟线性型的无差异曲线(4)无差异曲线如图3-10所示。
边际替代率为:()0.522220.5/0.52/0.5()2/x y MRS f f x y x x y y x y --==-⋅-⋅=,因而边际替代率递增,无差异曲线不是凸状的。
图3-10 凹状的无差异曲线(5)无差异曲线如图3-11所示。
第一讲偏好与效用

13
14
定理 当X是有限集合时,一个理性的偏好关系一定能够 用效用函数表示
令X1 是X中最差选项的集合 如果X- X1 非空;令X2是X- X1中最差选项的集合, …. 如果X-(X1∪X2…∪Xn-1)非空;令Xn是X-(X1∪X2…∪Xn-1)中最差选 项的集合 • 直到 X =X1∪ X2 …,∪Xk • 因为X是有限的,所以k最大是|X|,而且根据引理Xn不是空集 ,n=1,2,…,k • 定义: u(x)=k, if x∈ Xk – 如果a b,那么 a∉X1∪X2…∪Xu(b)-1,所以u(a) u(b) • • • •
3
4
偏好关系
• 一个有效的回答一般排除以下情形 – 反应缺乏判断比较能力
• x和y不可比较 • 我不知道x是什么 • 我没有想法
偏好关系
• 理性的偏好关系
– 是定义在选择集 X 上满足以下条件的二元关系 • 完备性 (Completeness) 任意两个消费束 x, , y,都有 都有x y 或 y x。 • 传递性 (Transitivity) 任意消费束x, y, z,如果x y和y z, 那么就有x z
19
(2 ) li n→∞ x n = x 和 lim lim li n→∞ y n = y 那么,就有 x (x) x y y {yn} y x
– 所以有 yn ≻ xn – 与条件矛盾,所以假设不成立。
20
证明:D1与D2等价
• D2ÆD1
– 给定偏好满足D2,令x≻y,B(x,r) 和B(y,r) – 假设对任意领域B(x,r) 和B(y,r) ,都存在 z∈ B(y), w∈ B(x) 使得 z w. – 由假设得到存在 xn ∈ B(x,1/n), yn ∈ B(y,1/n), 使得yn xn – 而且有 lim nÆ∞ xn=x, lim nÆ∞ yn=y。 – 所以,由D2得到 y x。 – 与条件矛盾,所以假设不成立
中级微观经济学讲义-2

第二讲 消费者理论
四、显示偏好简介
(一)显示偏好弱公理
与古典的从偏好关系到效用函数再到需 求函数的逻辑思路不同, 求函数的逻辑思路不同,萨缪尔森从行为结 果本身推导人的行为准则,抛却了效用理论 果本身推导人的行为准则, 中的许多主管假定,而仅需要一些隐含的、 中的许多主管假定,而仅需要一些隐含的、 弱的要求,比如一致性。 弱的要求,比如一致性。
第二讲 消费者理论
二、效用最大化与支出最小化
(二)效用最大化-续(2) 效用最大化-
罗伊恒等式】 【罗伊恒等式】 构造拉格朗日函数 L( x , λ ) = u( x ) + λ ( y − px ), ∂v ( p, y ) ∂L( x * , λ* ) 根据包络定理, 根据包络定理, = = λ*以及 ∂y ∂y ∂v ( p, y ) ∂L( x * , λ* ) = = − λ* x i*,可以得到 ∂ pi ∂p i ∂v ( p , y ) − ∂ pi x i* = x i ( p, y ) = ∂v ( p , y ) ∂y
x 2 f x1 , ∀t ∈ [0,1] ⇒ x t = tx 2 + (1 − t )x1 ~ x1 f ~ 公理 7 : 严格凸性 x 2 ≠ x1 , x 2 f x1 ⇒ x t f x1 ~ (排除了无差异集凹向原 点 < 多元化消费 > )
第二讲 消费者理论
一、偏好、效用与预算 偏好、
第二讲 消费者理论
一、偏好、效用与预算 偏好、
(一)偏好关系-续(1) 偏好关系-
偏好公理: 偏好公理: 公理 4 : 局部非饱和性 公理 5 : 严格单调性 公理 6 : 凸性 ∀x 0 ∈ R n , ∃ε > 0 , ∃x ∈ B ε ( x 0 ) I R n ⇒ x f x 0 + + (排除了无差异区域的存 在 ) ∀x 0, x1 ∈ R n , x1 ≥ x 0 ⇒ x1 f x 0 + ~ (排除了无差异集向上弯 曲)
金融经济学第二章-偏好、效用与风险厌恶

(1)风险补偿
(2)绝对风险厌恶与相对风险厌恶
• 绝对风险厌恶
• Arrow(1970)和Pratt(1964)首先提出将
A(w)定义为风险厌恶程度的度量,所以也称
为Arrow-Pratt风险厌恶测度。
(2)绝对风险厌恶与相对风险厌恶
• 绝对风险厌恶
• 我们可以根据绝对风险厌恶函数关于w的增减性
Marshall
边际效用价值论
奥地利学派
效用价值论稍占上风
引言
效用的表达:
基数效用论
边际效用学派
序数效用论
新古典综合派
(一般均衡论)
序数效用论占上风
2.1
偏好关系
问题的提出:
微观经济学中如何用数学的语言来描述
个人的选择问题:
偏好的假定?
偏好与效用函数之间在什么条件下可以
存在对应关系?
比投资者2的效用函数更厉害。定理2.4的4条
判别准则其实说的都是这同一个道理。
第二章小结
偏好、选择的理性基础
以效用表示偏好
不确定性条件下的偏好关系与期望效用函数
第二章小结
理性ቤተ መጻሕፍቲ ባይዱ非理性:独立性公理
第二章小结
风险厌恶
风险补偿
风险厌恶的比较
第二章小结
期望效用函数的存在性
定理 2.2:对于建立在有限概率分布空间 P 上
的偏好关系 p ,满足 2.3 节所述的三条行为公
理(理性选择、独立性、阿基米德性),则期
望效用函数存在,且在严格正的仿射变换意义
下是唯一的。
小结
小结
小结
小结
2.5 阿里亚斯悖论
尼科尔森《微观经济理论—基本原理与扩展》(第11版)笔记和课后习题详解-偏好与效用【圣才出品】

图 3-1 无差异曲线 ②无差异曲线的特点 第一,由于假定效用函数的连续性,所以,在同一坐标平面上的任何两条无差异曲线之 间,存在着无数条无差异曲线。离原点越近的无差异曲线所代表的效用水平越低,离原点越
3 / 38
圣才电子书 十万种考研考证电子书、题库视频学习平台
远的无差异曲线所代表的效用水平越高。 第二,在同一坐标平面上的任意两条无差异曲线不会相交。
源于个人将其用于购买效用最大的消费品。
当讨论个人的劳动—闲暇选择时有:效用=U(c,h),其中 c 表示消费,h 表示在一段
给定时间内的非工作时间(即闲暇)。
当讨论在不同时段内个人的消费决策问题时有:效用=U(c1,c2),其中 c1 表示在现时
段的消费,c2 表示在下一时段的消费。
2 / 38
圣才电子书
并不唯一,因此不能在不同人之间比较效用。
(3)其他条件不变的假定
影响效用度量的因素有很多:①所消费的实物商品的影响;②内心的态度;③来自同阶
层的心理压力;④个人经历;⑤所处的一般文化环境等等。
所以,对效用最大化选择的经济分析中,为了使选择分析形式简单、易于处理,一般都
假定其他条件不变。
(4)效用函数
2.效用及其表示方法 (1)效用的含义 效用是指消费者消费或拥有一定数量的某种商品时所获得的满足程度。一种商品给消费 者所带来的效用不同于该商品的使用价值,它是消费者对所消费商品给予的主观评价,不同 的消费者在相同的时间、地点消费相同数量的商品组合可以分别获得不同的效用,即使同一 消费者在不同的时期、不同的地点消费同样数量的商品组合也可获得不同的满足程度。效用
图 3-2 相交的无差异曲线意味着偏好不一致
第三,在正常情况下,无差异曲线总是凸向原点的。这一特点是由商品的边际替代率递
偏好与效用函数

1
2
公理1:完备性(Completeness)。对于任意属 1 2 2 1 x x x 于X的两个消费束x 和 ,要么 ~ ,要 么 x2 x 1 ,要么二者同时成立。 ~ 公理2:传递性(Transitivity)。对于任意属于 2 3 1 x x x x2 , X的三个消费束 、 和 ,如果有 x 1 ~ 2 3 1 3 x x 。 且x ,则有 x ~ ~
对于 X= R2 ,图 2.2 展示了满足公理 1、公理 2 和公理 3 的偏好。如图 2.2 所示,位于曲线上的点的集合以及位于曲 线内的点的集合所代表的消费束与点 x 0 所代表的消费束无差 异,位于曲线上方的点的集合所代表的消费束严格地偏好于
x 0 ,而 x 0 又严格地偏好于位于曲线下方点的集合所代表的消
公 理 3 连 续 性 ( Continuity ) 。 对 于 所 有 0 0 0 n n { x : x x } { x : x x } x R R 的 和集合 在 均 ,集合 ~ ~ 0 0 { x : x x } { x : x x } 是闭的。由此,还可推断出 和 都是开集。 连续性公理保证突然的偏好逆转不会出现。根 0 0 x }集 x }和 { X : x 据公理3,由于集合{ X : x ~ ~ n 合在 R 均是闭的,所以集合{x : x ~ x 0 }也是闭的。 这样就排除了图2.1中无差异集的开区域。
公理1和公理2意味着消费者能够完整地对消费 集X中任何有限数目的消费束排序,从最好到 最坏,当然也有可能消费者对有些消费束之间 的偏好无差异。总之,偏好关系使消费者能够 对消费集中的消费束建立一种排序。
对于X= R2 ,图2.1展示了满足公理1和公理2假 设的偏好。如图2.1所示,位于曲线上(不包 括虚线)点的集合以及虚线内的点的集合所代 表的消费束与点 x 0 所代表的消费束无差异;位 于曲线上方的点的集合包括两条虚线中位于右 上方那一条虚线上的点的集合所代表的消费束 严格地偏好于x 0,而 x 0 又严格地偏好于位于曲 线下方的点的集合包括两条虚线中位于左下方 那一条虚线上的点的集合所代表的消费束集。
高级微观经济学- 偏好与效用

(一) 偏好的无满足性
(x X )(y X )(x y)
欲望无止境:在人的一个欲望 得到了满足之后,接着会产生 另一个更大的欲望。没有理由 限制人的欲望的不断产生。 偏好的无满足性正是对消费者 欲望无止境的准确表述:任何 一种消费方案都无法满足消费 者无止境的欲望。
X 境 止 无 望 欲 y
桃 梨
苹果
李四的不传递的偏好
(四) 无差异曲线
根据偏好关系的自反性、完全性和传递性,无差异关系 是消 费集合 X 上的等价关系,即满足如下三个公理: Axiom 1 (自反性):(xX ) ( x x ) Axiom 2 (对称性):(x, yX )(( x y )( y x )) Axiom 3 (传递性):(x, y, zX )((( x y)( y z ))( x z)) 对于 xX,集合 [x]={yX : y x} 称作 x 的等价类或者无差异 类或者无差异曲线,它由两两无差异(一样好)的消费方案构成。
第3讲 偏好与效用
新古典理性对消费者的基本假定是:消费者具有良好的偏好或 效用函数,追求效用最大化。满足这一假定的消费者,叫做理性消 费者。因此,行为理性存在于消费者的偏好或效用函数之中。 我们将在商品空间 R 中讨论,即假定市场上共有 种可供选择 的商品。可供选择是说,这些商品既可供消费者选择一定的数量进 行消费,也可供消费者选择一定的数量向社会提供。我们将在对消 费集合分析的基础上,来揭示这种选择的逻辑。
●
一、效用的自我比较
效用可以自我比较, 就是说消费者能够对消费集合 X 中的任 何两种消费方案 x 和 y 都可作出 x y 或 x y 或 x y 的评价,并且 评价不会自相矛盾,即评价 x y、x y、x y 中只能出现一个,而 不能同时出现两个或三个。
第一章 偏好与效用

性组合至少应当与原来的消费束中的差者一样 好。
3.4偏好的实例—一些特殊的无差异曲线
• 1、完全替代品
–消费者愿意按照固定的比率用一种商品来替代另一种 商品。
–例如,面额为10元的人民币和面额为1元的人民币总可 以1比10的比例互相替代(假定不考虑携带不便)这对 持币人(消费者)来讲是完全替代品。
数
• x2 f (x1) 代表这条无差异曲线,当 0 1
时,一定存在:f x10 (1 )x11 f (x10) (1 ) f (x11)
• 可以做出如下图形
x2
f x20 (x10 )
无差异曲线凸性图
f x2 (x1)
~
x0
f x2 (x1)
f (x10 ) (1 ) f (x11)
x2
餍足点或 最佳点
x1
Better
3.4偏好的实例——离散商品
• 5、离散商品:只能以整数(离散)数量获得的商
品。
• 假设商品2是一连续变量商品——汽油,商品1是 一离散变量商品——飞机,无差异曲线如何呢?
汽油
无差异“曲线” 是一 些离散点的集合。
0 1 2 3 4 飞机
4、无差异曲线—偏好的图形描述
4 3 2 1
x1
用无差异曲线推出效用函数
数学方法:已知无差异曲线,运用数学 方法找出一个函数,沿每条无差异曲 线它都是一个常数,并且对较高的无 差异曲线指派较大的数字。
定性分析后确定:假定已知偏好的图形, 我们尽量考虑消费者试图使之实现最 大化的是什么——哪一种商品组合能 描述消费者的选择行为,能有效描述 消费者的选择行为的函数就是效用函 数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从无差异曲线构造一个效用函数
画出一条对角线,测量对角线与每条无差异曲线交点到 原点的距离,将这些距离标记在相应的无差异曲线上。
4、效用函数的实例
• 完全替代品
–用人民币总数测定效用。 –选U(x1,x2)=x1+10x2作为效用函数。 –该效用函数的任何单调变换都是描述完全替代 品合适的效用函数。
(3)无差异曲线—偏好的图形描述
• 无差异曲线是一个上水平集或上等高集 • 表示在二维平面上,消费者有商品x和y组成的 任意数量组合上所得到的效用水平不存在差异 • 无差异曲线的边界可以被看成为一个常数 • 无差异曲线一般具有良好性状的偏好性质 • 无差异曲线具有以下性质:是凸向原点的凸函 数;距离原点越远代表的效用水平越高;不同 的无差异曲线两两不能相交
餍足点或 最佳点
Better
x1
偏好的实例——离散商品
• 6、离散商品:只能以整数(离散)数量获得的商
品。 • 假设商品2是一连续变量商品——汽油,商品1是 一离散变量商品——飞机,无差异曲线如何呢? 汽油
无差异“曲线” 是一 些离散点的集合。
0
1
2
3
4 飞机
x0
u ( x) a3
u ( x) a2 u( x) a1
o
x
不同水平的无差异曲线
1
(5)良好性状的无差异曲线 第一假设:多多益善(单调性)
单调类偏好。(x1 ,x2 ) 右上方的消费束比(x1 ,x2 ); (x1 ,x2 )左下方的消费束比(x1 ,x2 )差。
良性形状无差异曲线 第二假设:平均束好于端点束
图A 为凸偏好;图B 和图C 为非凸偏好,其中图C 为凹偏好
• 指消费者可以不消费
{0,0,…,0}⊆R
0 ⊆X
3、偏好
• (1)偏好的定义 • 消费者的偏好实际上是指消费者根据自 身的愿望对不同消费束之间的一个排序, 即在一个消费中,两个消费束哪个更受 到消费者的偏好,使得消费者在心理上 对那个消费方案更加趋向。 • 偏好关系有以下几个:没有差别(~);严 格的偏好关系(>,<)和弱偏好关系(≤,≥) 。
–因此消费束 (4,1) , (2,2) 是在同一条无差异曲线上,效用水 平 U 4 –消费束(2,3) 是在另一条无差异曲线上,效用水平 U 6.
p
(4,1) ~ (2,2).
(2,3)
p
x2
(2,2) ~ (4,1)
U6 U4
x1
效用函数和无差异曲线
• 效用函数和无差异曲线的关系
1 1 1 1 2
0 x0 ( x10 , x2 )
0
• 可以做出如下图形
无差异曲线凸性图
x2
x
0 2
x2
f (x )
1
f (x
0 1
)
x
0
x2
f (x )
1
~
1 f ( x10 ) (1 ) f ( x1 )
x0 (1 ) x1
1 f x10 (1 ) x1
严格凸偏好的无差异曲线必须是弧形的
•
u 的无差 和 x ( x , x ) 是效用为 0 1 x , x R 的定义函 异曲线上的两个点, 数 • x2 f ( x1 ) 代表这条无差异曲线,当 0 1 1 1 时,一定存在: f ( x10 ) (1 ) f ( x1 f x10 (1 ) x1 )
效用函数的导数
• 若效用函数为:
u u( x1, x2 ,
, xn )
u xn
u u mu(x) , , x1 x2
边际效用
边际效用的意义
6、效用函数的凹性和拟凹性
• 凹性是指对于任意给定的两个消费束,一定存 在一个任意的线性组合,使得加权平均消费的 效用水平至少和单独消费每一种商品所得到的 消费效用水平及其加权平均效用水平相一致。 • 对某一种商品而言,其边际效用是非递增的。 • 拟凹性又称为准凹性,即对于任意给定的两个 消费束,则它们的任意加权消费束的效用水平 至少与原消费束的差者一样好 • 这个性质的存在排除了无差异曲线凹向原点和 平直的部分
2、效用函数的存在性
• 效用函数的存在性由德布鲁于1954年首次提出, 随后有许多经济学家进行了补充。在证明中, 只要能够存在一个消费束x和另一个消费束y, 使得u(x)≥u(y)成立,满足x≧y的性质, 那么函数u(x)就是代表偏好的效用函数。 • 效用函数就是按照一定的偏好特征给消费束赋 值,使之保持一定的次序。在次序不变的情况 下,可以有多种赋值方法
4
x2
效用函数的实例
– 每条无差异曲线都是一条单一无差异曲线 垂直移动得到的。 – x2 =k-v (x1) – U(x1,x2) =k=x2+v (x1)
• 拟线性偏好:
x1
4 效用函数的实例
• 柯布-道格拉斯效用函数
U(x1,x2) = x1a x2b a > 0 and b > 0
x2
– 柯布-道格拉斯效用函数一 般用来描述良好性状偏好
x2 2 I2 I1
10
描述完全替代品偏好的无差异曲 线具有固定的斜率。 I2 上的消费束严格偏好于I1上的 消费束。
1
20
x1
偏好的实例——完全互补品
• 2、完全互补品——是指必须以固定比例搭配起来才 能满足消费者某种需求的两种或多种商品。
x2 (左鞋)
45o
I2 上的消费束严格 偏好于I1上的消费束。
9
5 5 9 I1
I2
x1 (右鞋)
偏好的实例——厌恶品
• 3、厌恶品 • 希望东西越少越好
– 比如:
•垃圾 污染: 噪音、灰尘、污染空气
弱偏好集
休闲
偏好的实例-中性商品
4.中性商品(neutral good)是指某种商品,消费
者有它也行无它也可。
偏好的实例-饱和点
5.饱和点:某个消费束严格偏好于其他消 费束,这个消费束就是一个餍足点或最 佳点。 x2
• (1)保持k值不变,可画出与之相对应的无差异曲线。 • (2)改变k值,可以画出k = 1,2,… n时的多条无差异曲线。
x2
4 3 1
2
x1
用无差异曲线推出效用函数
数学方法:已知无差异曲线,运用数学 方法找出一个函数,沿每条无差异曲 线它都是一个常数,并且对较高的无 差异曲线指派较大的数字。 定性分析后确定:假定已知偏好的图形, 我们尽量考虑消费者试图使之实现最 大化的是什么——哪一种商品组合能 描述消费者的选择行为,能有效描述 消费者的选择行为的函数就是效用函 数。
x1
u x0 (1 ) x1
u1
x1 2
f (x )
1 1
u( x0 ) u( x1 ) u 0
x
0 1
x (1 ) x
0 1
1 1
x
1 1
x1
食品和衣服的无差异曲线(Eastwood and Craven,1981)
(6)偏好关系的性质
• 1、偏好的连续性:即偏好不应具有“跳跃” • 2、偏好的强单调性:即消费者总是偏好更多 的商品,或者在心理上反映为多多益善。 • 3、偏好的局部非饱和性,或称局部非餍足性: 即对于任意的消费都不存在充分的满足。 • 4、偏好的严格凸性:即任意两个消费束的线 性组合至少应当与原来的消费束中的差者一样 好。
hR
u ( x) [u ( x)]q u ( x) ln[u ( x)]
m0
q
为奇数
一个正单调变换
A 图为单调函数,它是递增的函数。B 图的函数不是单 调的,因为它有时增有时减。
• 效用函数的单调变换是一个新的效用函 数,它代表的偏好与原效用函数相同。
3、 效用函数和无差异曲线
• 效用函数和无差异曲线的关系
–考虑以下消费束 (4,1), (2,3) and (2,2).
假设(2,3)
–分配给上述消费束保持偏好顺序的任何效用
e.g. U(2,3) = 6 > U(4,1) = U(2,2) = 4
• 这些被分配的效用称为效用水平。
–无差异曲线表示相同偏好的消费束集合。 –相同偏好同样的效用水平
• 无差异曲线上所有消费束有同样的效用水平
– 比较更多的消费束,会得到更大的无差异 集合和消费者更好地描述。 – 无差异曲线与效用函数是等价的。 x2
x1
U6 U4 U2
用效用函数推出无差异曲线
–知道效用函数U(x1, x2)要绘制无差异曲线只要标出所有 使得U(x1, x2)=常数的点即可。 –假设效用函数U(x1,x2)=x1x2=k
第一章 消费者理论
一、偏好与优先理论 二、效用函数 三、效用最大化的选择 四、显示偏好理论
一、偏好与优先理论
1、消费空间
消费空间是指消费者在进行消费时所能选择的 商品组合,也称为消费集。 它可以用一个n元商品组合的向量描述,记为x, 在几何上x为n维欧式空间上的一点。 整个消费组合可以用 X R n 来表示。
习题
习题
二、效用函数
效用函数(Utility Function)是对每个可能 的消费束都赋予数值的一种方法,这种方法 要做到对于更受偏好的消费束,赋值更大。
1、效用函数—偏好的数学表示
• 效用是指消费者从消费某种物品中得到 的满意程度,或者说商品满足人的欲望 和需要的能力和程度。 • 效用函数刻画了满足水平与所消费的商 品之间的关系。 • 基数效用论和序数效用论 • 函数可以表示为 u f ( x1 , x2 , xn )
