第十章时间序列分析
统计学-第十章 时间序列分析

1
38(a1)
2
42(a2)
3
39(a3)
4
37(a4)
5
41(a5)
解: a 38 42 39 37 41 39.(4 台/天) 11111
三、平均发展水平
3.由绝对数时间序列计算的序时平均数
(2)由时点序列计算序时平均数
②间隔不相等的连续的时点数列
a af
季度在某地区销售量的走势 250 200
图。
150
100
那么,如何预测该品牌 50
空调2018年各个季度在该地 0
区的销售量呢?
单位:销售量(百台)
3
第一节 时间序列概述
一、时间序列概述
1.定义:将表明社会经济现象在不同时间发展 变化的某同一指标数值,按时间先后顺序排列所形 成的序列。(规模和水平)
③序列中每个指标的数值,通 常通过连续不断的登记取得。
由反映某种现象在一定 时点(瞬间)上发展状况的总量 指标所构成的绝对数动态序列所 处的数量水平。其中时点序列无 时点长度;两个相邻时点间的时 间距离称为时点间隔。也可为 日、周、旬、季、年等。
①序列中各个指标的 数值不可以直接相加;
②序列中指标数值的大小与其 时间间隔长短没有直接联系;
表9.3 我国普通高校毕业生数(时期序列)
年份 1912-1948 1978 1995 2000 2004 2014 2016
毕业生数(万人) 21.08 16.5 80.5 95 239.1 669.4 756
10
第二节 时间序列分析的基本原 理 一、时间序列分析的意义
:以时间序列为依据,对影响动态序列变 动过程的主要因素及其相互关系进行分解与综合, 以认识社会经济现象发展变量的规律性,借以鉴别 过去、预测未来的分析研究工作。
第10章时间序列3季节指数法

21.6 21.2 107.1% 21.4%
21.5 21.9 108.6 21.7%
25.5
100
25.04
100
127.8
25.6%
21
二、实际预测 1、情形一:已知年度预测值,预测其它各季度值。
计算公式:某季度预测值=年度预测值×该季的季节比重 例题:已知2006年度预测值为7385吨,要求利用季节变差预测各值。
一、数据模式的分析法
1、叠加法
y
H
k
t 水平型: Y=H+S 或
y
k t
Y=H+S+C+I T
S +0
S
s>0 t
s<0
t1
t
+
t1
t
t1
趋势型: Y=T+S
Y=T+S+C+I
t
2
第一节 季节变动数据模式分析法及预测步骤
2、乘积法
y
H
S
k
k
t
t
水平季节型: Y=H×S 或 Y=H×S×C×I
y
T
S
85.8 87.3 86.3 84.7 428.3 85.7%
86.3 87.8 86.0 87.6 434.5 86.9%
102.6 103.0 102.0 100.2 511.0 102.2%
表中第一个数据来源:2150/1710.75=1.257=125.7% 其它数据同上。
12
第二节 季节指数预测法
年份
第一季度
2001
2150
2002
2192
2003
2089
第10章-时间序列分析

67885
•1991~1996年平均国内生产总值:
•时期数列
•2023/5/3
•【例】
年份
•19941998年中 国能源生产 总量
1994 1995 1996 1997 1998
能源生产总量(万吨标 准煤) 118729 129034 132616 132410 124000
•2023/5/3
❖2.绝对指标时点数列的序时平均数
如:1991—1996年间,我国逐年的GDP,构
成一个时间序列。
记:a1 , a2 , … , an ( n项 ) 或:a0 , a1 , a2 , … , an ( n+1项 )
•2023/5/3
•
时间数列的构成要素:
1. 现象所属的时间;
2. 不同时间的具体指标数值。
•2023/5/3
例如
年底人数
(万 人)
8350 9949 11828 14071 16851 18375
间隔年数 3 2 3 2 2
•间断时点数列(间隔不等)
•2023/5/3
•我国第三产业平均从业人数:
•2023/5/3
•【例】 •某地区1999年社会劳动者人数资料如下
:
•单位:万人
时间 1月1日 5月31日 8月31日 12月31日
•2023/5/3
•定基和环比发展速度相互关系
•2023/5/3
【例】
❖ 某产品外贸进出口量各年环比发展速度资料如下: ❖ 1996年为103.9%,1997年为100.9%, ❖ 1998年为95.5%,1999年为101.6%,2000年为
108%,试计算2000年以1995年为基期的定基发 展速度。 ❖ (109.57%)
第十章时间序列预测法-季节指数法

时间序列 预测法
四、 季节指数预测法
❖ 本法适用于有季节变动特征的经济现象数量预测
销量
200
150
销售量(万元)
100
销量
季度
50
1998年 1999年 2000年 2001年
0
0
4
8
12
16
20
第一季度 148 138 150 145 第二季度 62 64 58 66
第三季度 76 80 72 78
年份 一季度 二季度 三季度 四季度
1995 120 1996 124 1997 138 1998 142
165 182 197 218
282 312 354 370
114 123 140 148
年份
一季度
1995
120
1996
124
1997
138
1998
142
各年同季平 均数
131
季节指数度 四季度
165
282
114
182
312
123
197
354
140
218
370
148
190.5 329.5 131.25
97.41% 168.49% 67.11% 213.82 369.83 147.32
同年各季 平均数 170.25 185.25 207.25 219.50
2 、季节指数预测法的步骤
第1步 第2步
n
计算各年同季(或同月)的平均值
yi
yi
i 1
n
n
计算所有年所有季(或月)的总平均值
y
yi
i 1
n
第3步 计算各季(或月)的季节比率(即季节指数)
统计学课后答案(第3版)第10章时间序列分析习题答案
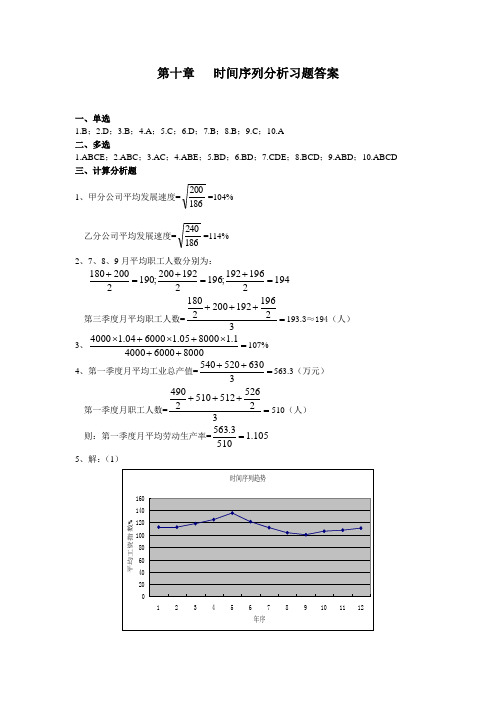
第十章 时间序列分析习题答案一、单选1.B ;2.D ;3.B ;4.A ;5.C ;6.D ;7.B ;8.B ;9.C ;10.A 二、多选1.ABCE ;2.ABC ;3.AC ;4.ABE ;5.BD ;6.BD ;7.CDE ;8.BCD ;9.ABD ;10.ABCD 三、计算分析题1、甲分公司平均发展速度=186200=104% 乙分公司平均发展速度=186240=114% 2、7、8、9月平均职工人数分别为:1942196192;1962192200;1902200180=+=+=+ 第三季度月平均职工人数==+++321961922002180193.3≈194(人) 3、=++⨯+⨯+⨯8000600040001.1800005.1600004.14000107%4、第一季度月平均工业总产值==++3630520540563.3(万元)第一季度月职工人数==+++325265125102490510(人) 则:第一季度月平均劳动生产率=105.15103.563=5、解:(1)(2)年序t 平均工资指数(环比)5期移动平均趋势1 112.70% —2 112.60% —3 118.50% 120.80%4 124.80% 122.60%5 135.40% 122.50%6 121.70% 119.52%7 112.10% 114.60%8 103.60% 108.76%9 100.20% 106.00%10 106.20% 105.78%11 107.90% —12 111.00% —各年份移动平均趋势值和原序列如下:移动平均可以消除原序列中的一些随机扰动和短期波动,期数越长,平滑作用越强;移动平均的作用就是消除序列随机和短期影响,从而能够发现序列的趋势。
(3)年份平均工资指数(环比)指数平滑值α=0.3误差平方指数平滑值α=0.5误差平方1 112.70% ————2 112.60% 112.70% 1E-06 112.70% 1E-063 118.50% 112.67% 0.003399 112.65% 0.0034224 124.80% 114.42% 0.010777 115.58% 0.008515 135.40% 117.53% 0.031922 120.19% 0.0231426 121.70% 122.89% 0.000142 127.79% 0.0037137 112.10% 122.54% 0.01089 124.75% 0.0159948 103.60% 119.40% 0.024979 118.42% 0.0219739 100.20% 114.66% 0.020919 111.01% 0.01168910 106.20% 110.32% 0.001701 105.61% 3.53E-0511 107.90% 109.09% 0.000141 105.90% 0.00039912 111.00% 108.73% 0.000515 106.90% 0.00168—109.41% —108.95% —合计 — — 0.105385 — 0.09056从上表数据看,采用平滑系数α=0.5拟合效果好。
统计学的时间数列习地的题目及答案详解

第十章时间数列分析和预测一、填空题1.同一现象在不同时间的相继____________排列而成的序列称为_______________。
2.时间序列在__________重复出现的____________称为季节波动。
3.时间序列在___________呈现出来的某种持续_______________称长期趋势。
4.增长率是时间序列中_________观察值与基期观察值______减1 后的结果。
5.由于比较的基期不同,增长率可分为_____________和______________。
6.复合型序列是指含有___________季节性和___________的序列。
7.某企业2005年的利润额比2000年增长45%,2004年2000年增长30%,则2005年比2004年增长_______;2004年至2000年平均增长率__________。
8.指数平滑法是对过去的观察值__________进行预测的一种方法。
9.如果时间序列中各期的逐期增减量大致相等,则趋势近似于_____________;各期环比值大体相等,则趋势近似于___________。
10.测定季节波动的方法主要有____________和_____________。
二、单项选择题1.用图形描述时间序列,其时间一般绘制在()A. 纵轴上B. 横轴上C. 左端D. 右端2.求解()趋势参数方法是先做对数变换,将其化为直线模型,然后用最小二乘法求出模型参数A. 三次曲线B. 指数曲线C. 一次直线D. 二次曲线3.对运用几个模型分别对时间序列进行拟合后,()最小的模型即位最好的拟合曲线模型A. 判定系数B. 相关系数C. 标准误差D.D—W值4.当数据的随机波动较大时,选用的移动间隔长度K应该()A. 较大B. 较小C. 随机D. 等于n5.在进行预测时,最新观察值包含更多信息,可考虑权重应()A. 更大B. 更小C. 无所谓D. 任意6. 按季度资料计算的季节指数S的取值范围是()A. 0≤ S ≤4B. 0 ≤S≤ 1C. 1 ≤S ≤4D. 1≤ S≤ 2三、多项选择题1. 时间序列可以分解为下列因素的影响 ( )A. 长期趋势B. 季节变动C. 周期波动D. 不规则变动E. 随机误差因素2. 某地区国民收入2000年为140亿元,2005年比2000年增长45%,则()A. 国民收入2005年比2000年增加了63亿元B. 2000年每增长1%的绝对值为1.4亿元C. 五年间平均增长率是9%D. 国民收入2005年达到210亿元E. 国民收入2005年达到203亿元3.测定季节变动A. 可以依据年度资料B. 可以依据月度资料C. 可以依据季度资料D. 需要三年以上资料E. 可以依据任何资料4. 时间序列分解较常用的模型有()A. 加法模型B. 乘法模型C. 直线模型D. 指数模型E. 多项式模型5.一次指数平滑法的初值的确定可以()A. 取第一期的实际值B. 取最初三期的加权平均值C. 取最初几期的平均值D. 取初值=1E. 取任意值四、简答题1. 简述时间序列的构成要素2. 利用增长率分析时间序列时应注意哪些问题3. 简述用平均趋势剔除法求季节指数的步骤4. 简述用剩余法求循环波动的基本步骤5. 试比较移动平均法与一次指数平滑法五、计算题1.某企业利润额资料如下:要求:(1) 求出直线趋势方程(2)预测2006年的利润额2.已知某煤矿(1)求五期移动平均;(2)取α= 0.9,求一次指数平滑3.某地财政收入资料如下试用指数曲线拟合变动趋势4.某商场销售资料如下:(单位:百万元)试就其进行季节变动分析5.某企业职工人数逐年增加,有1992—2004年的资料,求得∑t = 0,∑ty=9100,∑y = 15600;试求出直线趋势方程,并估计2006年职工人数。
时间序列分析
时间序列分析时间序列数据的特点是观测值之间存在时间上的依赖关系,即一个观测值的取值可能与之前的多个观测值存在相关性。
时间序列分析主要考虑以下几个方面:1. 趋势分析:时间序列数据中存在的长期增长或下降趋势可以通过趋势分析来判断。
趋势分析可以采用移动平均法、指数平滑法等方法来拟合趋势线,从而预测未来的趋势。
2. 季节性分析:时间序列数据中的季节性波动是一种按照固定的季节循环出现的规律变动。
季节性分析可以通过季节性指数、分解法等方法来对季节性波动进行分析和预测。
3. 周期性分析:周期性是指时间序列数据中存在的较长周期的波动。
周期性分析可以通过傅里叶分析、自相关函数等方法来分析和预测周期性波动。
4. 随机性分析:时间序列数据中的随机变动是指除趋势、季节性、周期性之外的不可预测的波动。
随机性分析可以通过残差项的分析来判断数据中是否存在随机波动。
时间序列分析的方法包括统计方法和经典时间序列分析方法。
统计方法主要包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)等。
经典时间序列分析方法主要包括指数平滑法、趋势法、季节性指数法等。
时间序列分析的应用领域广泛。
在经济学中,时间序列分析可以用来预测经济指标的变动趋势,为政府决策提供依据。
在金融学中,时间序列分析可以用来预测股市的走势,帮助投资者制定投资策略。
在气象学中,时间序列分析可以用来预测天气变化,为农民和旅行者提供参考。
在医学中,时间序列分析可以用来预测疾病的传播趋势,为疾病防控提供支持。
然而,时间序列分析也存在一些挑战和限制。
首先,时间序列数据的质量和可靠性对分析结果的影响很大,因此数据的采集、清洗和处理是很重要的。
其次,时间序列数据的非线性和非平稳性使得分析方法的选择和应用更为复杂。
此外,时间序列数据同时受到多种因素的影响,如外部环境、政策变化等,这些因素需要合理地加以考虑。
总的来说,时间序列分析是一种重要的统计分析方法,可以用来揭示时间序列数据内部的潜在规律和特征,并通过对过去数据的观察和分析来预测未来的趋势。
第10章时间序列分析指标
第10章时间序列分析指标时间序列分析指标是一种对时间序列数据进行分析和预测的方法。
它可以揭示出时间序列数据中的规律和趋势,并用以预测未来的变化。
时间序列是按时间顺序排列的一系列数据点。
时间序列分析指标可以帮助我们了解时间序列数据的特征和规律。
在金融领域,时间序列分析指标可以应用于股市分析、经济预测等多个方面。
常用的时间序列分析指标包括趋势指标、周期指标、季节性指标和波动指标。
趋势指标是用来分析时间序列数据中的长期趋势的指标。
常见的趋势指标包括移动平均线和线性趋势线。
移动平均线是用来平滑时间序列数据的一种方法,它可以过滤掉噪音和周期性波动,反映出数据的长期趋势。
线性趋势线则是用来表示时间序列数据中的线性关系,可以帮助我们判断数据的上涨或下跌趋势。
周期指标是用来分析时间序列数据中的周期性变化的指标。
周期指标可以帮助我们预测未来的周期性变化。
常见的周期指标包括季节性调整指标和周期性调整指标。
季节性调整指标可以消除时间序列数据中的季节性影响,展示出数据的长期趋势。
周期性调整指标则可以帮助我们找到时间序列数据中的周期性变化,以便更好地进行预测。
季节性指标是用来分析时间序列数据中的季节性变化的指标。
季节性指标可以帮助我们了解时间序列数据中的季节性规律,并进行相应的调整和预测。
常见的季节性指标包括季节性分解法和指数平滑法。
季节性分解法可以将时间序列数据拆分成长期趋势、季节性趋势和误差项三个部分,以便更好地进行分析和预测。
指数平滑法则是用来对时间序列数据进行平滑处理和季节性调整的方法。
波动指标是用来分析时间序列数据中的波动性变化的指标。
波动指标可以帮助我们了解时间序列数据的波动情况,以便更好地进行风险控制和预测。
常见的波动指标包括波动率和变异系数。
波动率是用来衡量时间序列数据的波动性的指标,可以帮助我们了解数据的风险程度。
变异系数则是用来衡量时间序列数据的波动性相对于平均水平的变化程度,可以帮助我们比较不同时间序列数据的波动性。
计量经济学第十章 时间序列计量经济模型
H0
第三步:对一阶差分序列作单位根检验得到序列的单整阶数 为了得到人均可支配收入(SR)序列的单整阶数,在单位根检 验(Unit Root Test)对话框(图10.3)中,指定对一阶差分序 列作单位根检验,选择带截距项(intercept),滞后差分项 (Lagged differences)选2阶,点击OK,得到估计结果,见表 10.5。
t(t T )
举例:
1、连续性随机过程:心电图,用 Y t 表示。
2、离散型随机过程:GDP,DPI等,用 Y1 , Y2 ,...,Yt 表示。记住,这 些Y中的每一个都是一个随机变量,而这些随机变量按时间编排形 成的集合就是一个随机过程。
讨论:如何理解GNP是一个随机过程呢?
理论上讲,某一年的GNP数字可能是任何一个数字,取决 于当时的政治与经济环境。某个数字只是所有这些可能性 中的一个特定的实现,也可以看成是某年GNP所有可能值 得均值。因此,我们可以说,GNP是一个随机过程,而我 们在某个时期期间所观测到的实际值只是这个过程的一个 特定实现(即样本)。与我们利用截面数据中的样本数据 对总体进行推断一样,在时间序列中,我们利用这些实现 对其背后的随机过程加以推断。
-0.7791体现了对偏离的修正,上一期偏离越远,本 期修正的量就越大,即系统存在误差修正机制。
第十章 时间序列计量经济模型
本章主要讨论:
时间序列的基本概念
时间序列平稳性的单位根检验 协整
第一节 时间序列基本概念
本节基本内容:
●伪回归问题 ●随机过程的概念 ●时间序列的平稳性
一、伪回归问题
传统计量经济学模型的假定条件:序列的平稳性、正态性。
所谓“伪回归”,是指变量间本来不存在相依关系,但回归 结果却得出存在相依关系的错误结论。即表现在:两个本来没 有任何因果关系的变量,却有很高的相关性(有较高的R2)。 例如:用美国人口数和中国GDP回归,也可能会得到很高的 可决系数。 20世纪70年代,Grange、Newbold 研究发现,造成“伪回归” 的根本原因在于时序序列变量的.,Ytn
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第10章 时间序列数据的基本回归分析【圣才出
第10章时间序列数据的基本回归分析10.1复习笔记一、时间序列数据的性质时间序列数据与横截面数据的区别:(1)时间序列数据集是按照时间顺序排列。
(2)时间序列数据与横截面数据被视为随机结果的原因不同。
①横截面数据应该被视为随机结果,因为从总体中抽取不同的样本,通常会得到自变量和因变量的不同取值。
因此,通过不同的随机样本计算出来的OLS估计值通常也有所不同,这就是OLS统计量是随机变量的原因。
②经济时间序列满足作为随机变量是因为其结果无法事先预知,因此可以被视为随机变量。
一个标有时间脚标的随机变量序列被称为一个随机过程或时间序列过程。
搜集到一个时间序列数据集时,便得到该随机过程的一个可能结果或实现。
因为不能让时间倒转重新开始这个过程,所以只能看到一个实现。
如果特定历史条件有所不同,通常会得到这个随机过程的另一种不同的实现,这正是时间序列数据被看成随机变量之结果的原因。
(3)一个时间序列过程的所有可能的实现集,便相当于横截面分析中的总体。
时间序列数据集的样本容量就是所观察变量的时期数。
二、时间序列回归模型的例子1.静态模型假使有两个变量的时间序列数据,并对y t和z t标注相同的时期。
把y和z联系起来的一个静态模型(staticmodel)为:10 1 2 t t t y z u t nββ=++=⋯,,,,“静态模型”的名称来源于正在模型化y 和z 同期关系的事实。
若认为z 在时间t 的一个变化对y 有影响,即1t t y z β∆=∆,那么可以将y 和z 设定为一个静态模型。
一个静态模型的例子是静态菲利普斯曲线。
在一个静态回归模型中也可以有几个解释变量。
2.有限分布滞后模型(1)有限分布滞后模型有限分布滞后模型(finitedistributedlagmodel,FDL)是指一个或多个变量对y 的影响有一定时滞的模型。
考察如下模型:001122t t t t ty z z z u αδδδ--=++++它是一个二阶FDL。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 时间序列分析Ⅰ.学习目的本章阐述常规的时间序列分析方法,通过学习,要求:1.理解时间序列的概念和种类,掌握时间序列的编制方法;2.掌握时间序列分析中水平指标和速度指标的计算及应用;3.掌握时间序列中长期趋势、季节变动、循环变动及不规则变动等因素的基本测定方法;4.掌握基本的时间序列预测方法。
Ⅱ.课程内容要点 第一节 时间序列分析概述一、时间序列的概念将统计指标的数值按时间先后顺序排列起来就形成了时间序列。
二、时间序列的种类反映现象发展变化过程的时间序列按其统计指标的形式不同,可分为总量指标时间序列、相对指标时间序列和平均指标时间序列三种类型。
其中总量指标时间序列是基础序列,相对指标和平均指标时间序列是派生序列。
根据总量指标反映现象的时间状况不同,总量指标时间序列又可分为时期指标时间序列和时点指标时间序列。
三、时间序列的编制方法:(一)时间长短应一致;(二)经济内容应一致;(三)总体范围应一致;(四)计算方法与计量单位要一致。
第二节 时间序列的分析指标一、时间序列分析的水平指标(一)发展水平。
发展水平是时间序列中与其所属时间相对应的反映某种现象发展变化所达到的规模、程度和水平的指标数值。
(二)平均发展水平。
将一个时间序列各期发展水平加以平均而得的平均数,叫平均发展水平,又称为动态平均数或序时平均数。
1.总量指标时间序列序时平均数的计算(1)时期序列:ny n y y y y in ∑=+++=Λ21 (2)时点序列①连续时点情况下,又分为两种情形:a .若掌握的资料是间隔相等的连续时点 (如每日的时点) 序列,则ny n y y y y in ∑=+++=Λ21 b .若掌握的资料是间隔不等的连续时点序列,则∑∑=++++++=ii i n n n f f y f f f f y f y f y y ΛΛ212211②间断时点情况下。
间断时点也分两种情况:a .若掌握的资料是间隔相等的间断时点,则采用首末折半法:122122212113221-++++=-++++++=--n y y y y n y y y y y y y nn n n ΛΛ b .若掌握的资料是间隔不等的间断时点序列,计算公式为: ∑∑=ii i f f y y 12111232121)(21)(21)(21---+++++++++=n n n n f f f f y y f y y f y y ΛΛ 2.相对指标和平均指标时间序列序时平均数的计算。
若相对指标或平均指标表示为b ay =,则有ba y = 式中:y 为相对指标或平均指标时间序列的序时平均数;a 代表作为分子的时间序列序时平均数;b 代表作为分母的时间序列序时平均数。
(三)增长量指标增长量是表明某种现象在一段时期内增长的绝对量,它等于报告期水平减其基期水平。
1.逐期增长量逐期增长量是报告期水平与前一期水平之差:1--i i y y 。
2.累计增长量累计增长量是报告期水平与某一固定时期水平(通常是时间序列最初水平)之差:1y y i -。
3.年距增长量。
它等于本期发展水平比上年同期发展水平增加(减少)的数量。
(四)平均增长量指标平均增长量是时间序列中逐期增长量的序时平均数,其计算公式为:平均增长量 =1)(1-∑--n y y i i 或平均增长量 =11--n y y i 。
二、时间序列分析的速度指标 (一)基期水平报告期水平发展速度=1.固定基期水平报告期水平定基发展速度=1y y i =2.前一期水平报告期水平环比发展速度= 1-=i i y y3.上年同期水平报告期水平年距发展速度=(二)基期水平报告期增长量增长速度=基期水平基期水平报告期水平-=%100-=发展速度由于增长量有逐期增长量和累计增长量之分,增长速度因所采用基期不同,分为环比增长速度和定基增长速度。
100%1⨯=环比增长速度逐期增长量的绝对值增长100前一期水平=1001001111----=⨯--=i i i i i i y y y y y y(三)平均发展速度和平均增长速度平均发展速度是一定时期内各期环比发展速度的序时平均数,常用的计算方法有几何平均法和高次方程法。
1. 几何平均法:11-=n n y y x 或 112312--⨯⨯=n n n y y y y y yx Λ 2. 高次方程法:解高次方程1212y y x x x ni i n ∑=++=-Λ 所得到的正根就是平均发展速度x 。
平均增长速度=平均发展速度-1。
第三节 长期趋势的测定一、时间序列的构成与分解(一)时间序列的构成:1.趋势变动,指现象在发展变化过程中由于受到某种固定的、起根本性作用的因素的影响而在较长时间内展现出来的总态势;2.季节变动,指现象在一年内由于受社会、政治、经济、自然等因素的影响,形成的以一定时期为周期的有规律的重复变动;3.循环波动,指现象围绕长期趋势出现的,以若干年为周期的有涨有落的周期性运动;4.随机变动。
指现象由于各种偶然因素的影响而呈现的不规则运动。
(二)时间序列的分解:时间序列分解的主要任务就是将各种变动对时间序列指标值的影响状况分别测定出来,通常以长期趋势值(T )为绝对量基础,再根据各类变动对时间序列的影响是否独立,建立两种组合模型,即加法模型和乘法模型。
1.加法模型:I C S T Y +++=。
此模型假定四类变动是相互独立的,对时间序列的影响程度以绝对数表示; 2.乘法模型:I C S T Y ⨯⨯⨯=。
此模型假定四类变动之间存在着交互作用,则其它各类变动对时间序列各期指标值的影响程度是以相对数的形式表示出来。
二、长期趋势的测定方法(一)移动平均法。
其基本思想是:随机因素的影响是相互独立的,因此,短期数据由于随机因素而形成的差异,在加总平均的过程中会相互抵消,其平均数就显示了现象由于其本质因素所决定的趋势值。
1.奇数项移动平均法。
若所平均的项数是奇数,则其中间项的趋势测定值经过一次移动平均就可得到,用)1(t M 表示一次移动平均数,计算公式为:)(1211121)1(-++---++++++=N t t t t N t t y y y y y N M ΛΛ2.偶数项移动平均数法若所移动平均的项数为偶数,则计算出来的移动平均数对应的中间项是在两个时期之间,不能代表任一时期的趋势值,则需对一次移动平均数再做一次项数为2的移动平均, 即计算二次移动平均数来作为长期趋势值,用)2(t M 表示,如: )(21)2(5.3)1(5.2)2(3M M M +=,作为第3期的趋势值。
(二)趋势模型法趋势模型法也称曲线配合法,它根据时间序列长期趋势的表现形态,建立一个合适的趋势方程来描述现象各期指标值随时间变动的趋势规律性,并据此进行各期趋势值的测定。
常见的趋势模型有:线性模型bt a y t +=ˆ;二次曲线模型221ˆt b t b a yt ++=;指数曲线模型t t ab y =ˆ;修正的指数曲线模型tt ab k y +=ˆ;逻辑曲线模型tt abk y +=1ˆ 和龚珀资曲线模型tb t ka y=ˆ等。
将各期时间t 的取值代入已估计出参数的趋势模型,得出的因变量数值就是相应时期的趋势变动测定值。
第四节 季节变动和循环波动测定一、季节变动的测定方法季节变动测定的基本思路是:设各种变动因素是以乘法模型进行组合形成时间序列,则以时间序列中不含季节变动的长期趋势值为衡量基准,计算加入季节变动后各期的指标值与原趋势值的比率,以此衡量各期指标值受季节变动影响的程度。
具体步骤:第一步,取移动平均的项数为周期的长度,对时间序列进行移动平均,消除随机变动和季节变动的影响,所得的中心化移动平均数就是趋势变动和循环变动综合作用的结果即C T ⨯。
第二步,剔除趋势变动和循环变动对时间序列的影响,得出仅包含季节变动和随机变动的时间序列资料,即:I S C T Y⨯=⨯。
第三步,对各年内同期的季节比率求平均,可以在相当程度上消除随机变动的影响,所得的结果即各期的季节指数S。
二、循环变动的测定方法第一步,先求季节指数S ,以剔除季节变动的影响,得I C T SI C S T S Y ⨯⨯=⨯⨯⨯=。
第二步,对剔除季节变动后的时间序列求趋势值T ,以剔除趋势变动的影响,得I C TIC T ⨯=⨯⨯。
第三步,对第二步的结果进行移动平均,以消除随机变动的影响,就可得到各期相应的循环指数C 。
三、随机变动的测定方法随机变动是趋势变动、季节变动和循环变动不能解释的部分。
在乘法模型中,不规则变动同样可用“剩余法”来测定,即利用已经计算得到的仅包含循环变动C 和不规则变动I 的数据资料(I C ⨯),除以循环变动指数C ,即可得到随机变动指数I 。
第五节 时间序列预测方法一、趋势外推法趋势外推法就是运用趋势模型对现象在未来的变动趋势进行测算。
只需把预测期相对应的时间自变量t 的取值代入趋势模型,即可得出未来趋势值的估计。
趋势外推法适用于具有明显上升或下降趋势的时间序列的预测。
二、自回归预测法当各期指标值之间呈线性相关关系时,相应的自回归模型的一般形式为: n t n t t t y b y b y b b y---++=Λ22110ˆ 三、移动平均和指数平均滑法(一)移动平均预测法。
相应的预测公式是:)(1ˆ11)1(1+--+++==N t t t t t y y y NM yΛ 式中,)1(t M 是第t 期的一次移动平均数,用它作为第t +1期的预测值。
一般来说,近期值比远期值更重要,因而在移动平均时应给予更大的权重,相应的移动平均法称加权移动平均法,其预测公式为:11011110)1(1ˆ-+---+++++==N N t N t t wt t w w w y w y w y w M y ΛΛ 。
(二)指数平滑法1.一次指数平均滑法。
指数平滑法的一般公式为:)1(1)1()1(1)1()1()1(---+=⇒=--t t t t t t S αy αS y αS αS式中,1)1(ˆ+=t t y S ,是t +1期的预测值;t t y S ˆ)1(1=-,是t 期的预测值,因此,上式等价于:)ˆ(ˆˆ1t t t t y y αy y -+=+。
一般情况下,可以取1)1(0y S =作为近似值进行计算。
在确定平滑系数α的取值时,若时间序列平稳度较高,则各期权数i αα)1(-的衰减速度就应小些,那么平滑系数α就要取较小值;若时间序列的波动幅度较大,则各期权数i αα)1(-的衰减速度应大些,远期值对预测值的影响就越小,相应的平滑系数α就要取较大值。
2.二次指数平均滑法。
主要用于变参数线性趋势时间序列的预测,它是对一次指数平滑值)1(t S 计算的平滑值,即)2(1)1()2()1(--+=t ttSαSαS。
