2质点运动定律习题思考题
练习册第2章《质点力学的运动定律守恒定律》答案(1)

练习册第2章《质点⼒学的运动定律守恒定律》答案(1)第2章质点⼒学的运动定律守恒定律⼀、选择题1(C),2(E),3(D),4(C),5(C),6(B),7(C),8(C),9(B),10(C),11(D),12(A),13(D)⼆、填空题(1). ω2=12rad/s ,A=0.027J (2). 290J (3). 3J (4). 18 N ·s(5). j t i t 2323+ (SI) (6). 16 N ·s , 176 J (7). 16 N ·s ,176 J (8). M k l /0,Mknm M Ml +0(9). j i5- (10).2m v ,指向正西南或南偏西45°三、计算题1. 已知⼀质量为m 的质点在x 轴上运动,质点只受到指向原点的引⼒的作⽤,引⼒⼤⼩与质点离原点的距离x 的平⽅成反⽐,即2/x k f -=,k 是⽐例常数.设质点在 x =A 时的速度为零,求质点在x =A /4处的速度的⼤⼩.解:根据⽜顿第⼆定律x m t x x m t m xk f d d d d d d d d 2vv v v =?==-= ∴ ??-=-=4/202d d ,d d A Ax mx kmx x k v v v v vk mAA A m k 3)14(212=-=v ∴ )/(6mA k =v2. 质量为m 的⼦弹以速度v 0⽔平射⼊沙⼟中,设⼦弹所受阻⼒与速度反向,⼤⼩与速度成正⽐,⽐例系数为K,忽略⼦弹的重⼒,求:(1) ⼦弹射⼊沙⼟后,速度随时间变化的函数式; (2) ⼦弹进⼊沙⼟的最⼤深度.解:(1) ⼦弹进⼊沙⼟后受⼒为-Kv ,由⽜顿定律tmK d d vv =- ∴ ??=-=-v v v v vv 0d d ,d d 0t t m K t m K∴ mKt /0e -=v v(2) 求最⼤深度解法⼀: t xd d =vt x mKt d ed /0-=vt x m Kt txd e d /000-?=v∴ )e 1()/(/0mKt K m x --=vK m x /0m ax v =解法⼆: x m t x x m t m K d d )d d )(d d (d d vvv v v ===- ∴ v d K mdx -=v v d d 000m a x ??-=K mx x∴ K m x /0m ax v =3. ⼀物体按规律x =ct 3在流体媒质中作直线运动,式中c 为常量,t 为时间.设媒质对物体的阻⼒正⽐于速度的平⽅,阻⼒系数为k ,试求物体由x =0运动到x =l 时,阻⼒所作的功.解:由x =ct 3可求物体的速度: 23d d ct tx==v 物体受到的阻⼒⼤⼩为: 343242299x kc t kc k f ===v ⼒对物体所作的功为:=W W d =-lx x kc 03432d 9 =7273732l kc -4. ⼀质量为2 kg 的质点,在xy 平⾯上运动,受到外⼒j t i F 2244-= (SI)的作⽤,t = 0时,它的初速度为j i430+=v (SI),求t = 1 s 时质点的速度及受到的法向⼒n F .解: j t i m F a 2122/-==t a d /d v = ∴ t j t i d )122(d 2-=v=?vv vd ?-t t j t i 02d )122(∴ j t i t 3042-=-v vj t i t j t i t )44()23(42330-++=-+=v v当t = 1 s 时, i51=v 沿x 轴故这时, j a a y n12-==j a m F n n24-== (SI)5.⼀辆⽔平运动的装煤车,以速率v 0从煤⽃下⾯通过,每单位时间内有质量为m 0的煤卸⼊煤车.如果煤车的速率保持不变,煤车与钢轨间摩擦忽略不计,试求:(1) 牵引煤车的⼒的⼤⼩;(2) 牵引煤车所需功率的⼤⼩;(3) 牵引煤车所提供的能量中有多少转化为煤的动能?其余部分⽤于何处?解:(1) 以煤车和?t 时间内卸⼊车内的煤为研究对象,⽔平⽅向煤车受牵引⼒F 的作⽤,由动量定理: 000)(v v M t m M t F -+=?? 求出: 00v m F = (2) 2000v v m F P ==(3) 单位时间内煤获得的动能: 2021v m E K =单位时间内牵引煤车提供的能量为 P E ===21/E E K 50%即有50%的能量转变为煤的动能,其余部分⽤于在拖动煤时不可避免的滑动摩擦损耗.6.⼀链条总长为l ,质量为m ,放在桌⾯上,并使其部分下垂,下垂⼀段的长度为a .设链条与桌⾯之间的滑动摩擦系数为µ.令链条由静⽌开始运动,则(1)到链条刚离开桌⾯的过程中,摩擦⼒对链条作了多少功?(2)链条刚离开桌⾯时的速率是多少?解:(1)建⽴如图坐标.某⼀时刻桌⾯上全链条长为y ,则摩擦⼒⼤⼩为 g lym f µ=摩擦⼒的功 ??--==0d d al al f y gy lmy f W µ=22al y lmg-µ =2)(2a l lmg--µ(2)以链条为对象,应⽤质点的动能定理 ∑W =222121v v m m - 其中 ∑W = W P +W f ,v 0 = 0 W P =?la x P d =la l mg x x l mg la 2)(d 22-=? 由上问知 la l mg W f 2)(2--=µal -a-a1)(22)(v m a l l mg l a l mg =---µ得 []21222)()(a l a l lg ---=µv7. 如图所⽰,在中间有⼀⼩孔O 的⽔平光滑桌⾯上放置⼀个⽤绳⼦连结的、质量m = 4 kg 的⼩块物体.绳的另⼀端穿过⼩孔下垂且⽤⼿拉住.开始时物体以半径R 0 = 0.5 m 在桌⾯上转动,其线速度是4 m/s .现将绳缓慢地匀速下拉以缩短物体的转动半径.⽽绳最多只能承受 600 N 的拉⼒.求绳刚被拉断时,物体的转动半径R 等于多少?解:物体因受合外⼒矩为零,故⾓动量守恒.设开始时和绳被拉断时物体的切向速度、转动惯量、⾓速度分别为v 0、J 0、ω0和v 、J 、ω.则ωωJ J =00 ①因绳是缓慢地下拉,物体运动可始终视为圆周运动.①式可写成R mR R mR //20020v v =整理后得: v v /00R R =②物体作圆周运动的向⼼⼒由绳的张⼒提供 R m F /2v = 1分再由②式可得: 3/12020)/(F mR R v =当F = 600 N 时,绳刚好被拉断,此时物体的转动半径为R = 0.3 m8.设两个粒⼦之间相互作⽤⼒是排斥⼒,其⼤⼩与粒⼦间距离r 的函数关系为3r k f =,k 为正值常量,试求这两个粒⼦相距为r 时的势能.(设相互作⽤⼒为零的地⽅势能为零.)解:两个粒⼦的相互作⽤⼒ 3r k f =已知f =0即r =∞处为势能零点, 则势能∞∞∞=?==r r P P r r kW E d d 3r f)2(2r k =1. 汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒能使汽车前进吗?使汽车前进的⼒是什么⼒?参考解答:汽车发动机内⽓体对活塞的推⼒以及各种传动部件之间的作⽤⼒都是汽车系统的内⼒,内⼒只会改变内部各质点的运动状态,不会改变系统的总动量,所以不能使汽车前进。
力学答案 第二章 质点运动学(思考题)

第二章 质点运动学思考题2.1质点位置矢量方向不变,质点是否作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?解答:质点位置矢量方向不变,质点沿直线运动。
质点沿直线运动,质点位置矢量方向不一定不变。
如图所示。
2.2若质点的速度矢量的方向不变仅大小改变,质点作何种运动?速度矢量的大小不变而方向改变作何种运动?解答:质点的速度矢量的方向不变仅大小改变,质点作变速率直线运动;速度矢量的大小不变而方向改变作匀速率曲线运动。
2.3“瞬时速度就是很短时间内的平均速度”这一说法是否正确?如何正确表述瞬时速度的定义?我们是否能按照瞬时速度的定义通过实验测量瞬时速度? 解答:“瞬时速度就是很短时间内的平均速度”这一说法不正确。
因为瞬时速度与一定的时刻相对应。
瞬时速度的定义是质点在t 时刻的瞬时速度等于t 至t+△t 时间内平均速度t /r ∆∆,当△t →0时的极限,即dt r d t r lim v 0t=∆∆=→∆。
很难直接测量,在技术上常常用很短时间内的平均速度近似地表示瞬时速度,随着技术的进步,测量可以达到很高的精确度。
2.4试就质点直线运动论证:加速度与速度同号时,质点作加速运动;加速度与速度反号时,作减速运动。
是否可能存在这样的直线运动,质点速度逐渐增加但加速度却在减小?解答:,dt dv t v lim a xx 0t x =∆∆=→∆加速度与速度同号时,就是说,0a ,0v 0a ,0v x x x x <<>>或以0a ,0v x x >>为例,速度为正表示速度的方向与x 轴正向相同,加速度为正表示速度的增量为正,t t ∆+时刻的速度大于t 时刻的速度,质点作加速运动。
同理可说明,0a ,0v x x <<质点作加速运动。
质点在作直线运动中速度逐渐增加但加速度却在减小是可能存在的。
例如初速度为x 0v ,加速度为t 6a x -=,速度为20t0x 0x t21t 6vdt )t 6(v v -+=-+=⎰,,0v ,0a 6t x x >><时,速度逐渐增加。
质点动力学习题解答2

作业04(质点动力学2)1. 质量为m 、速度大小为V 的质点受到某个力作用后,其速度的大小未变,但方向改变了θ,则这个力的冲量大小为[ ]。
A.)2/cos(2θmvB. )2/sin(2θmvC. )2/cos(θmvD. )2/sin(θmv 答:[B ]解:如图,由动量定理,冲量等于动量的变化 im v j m v i m v i m v j m v i m v v m v m v m I -+=-+=-=∆=θθθθsin cos sin cos /// 冲量的大小为 )2/s i n (2c o s 22s i n )c o s (222θθθθv m mv v v v m I I =-=+-==2. 一质量为kg m 60=的人静止站在一条质量为kg M 300=、且正以12-⋅=s m V 的速率向湖岸驶进的小木船上,湖水是静止的,其阻力不计。
现在人相对于船以一水平速度v 沿船的前进方向向河岸跳去,该人起跳后,船速减为原来的一半,v 应该是[ ]A. 12-⋅s mB. 13-⋅s mC. 15-⋅s mD. 16-⋅s m答:[C ]解:以地面为参考系。
人与船为系统。
人相对于地面的起跳速度为v V +,起跳后,船向岸边运动的速度为2/V ;原来人与船以水平速度V 一起向岸边运动。
水平方向不受外力 V M m MV v V m )(21)(+=++,)(5602230022-⋅=⨯⨯==s m m MV v 也可以原船为参考系(也是惯性系),人与船为系统。
人相对于原船的起跳速度为v ,起跳后,船相对于原船的运动速度为2/V -;在原船参考系中,起跳前,人与船静止。
水平方向不受外力,由动量守恒,得到VM mv 210-=,)(5602230022-⋅=⨯⨯==s m m MV v 3. 下列叙述中正确的是[ ]A. 质点的动量不变,则动能也不变。
B 质点的动能不变,则动量也不变C. 质点的动量变化,则动能也一定变化。
质点力学思考题解答

第一章 质点力学1.1平均速度与瞬时速度有何不同?在上面情况下,它们一致?答:平均速度是运动质点在某一时间间隔t t t ∆+→内位矢大小和方向改变的平均快慢速度,其方向沿位移的方向即沿t ∆对应的轨迹割线方向;瞬时速度是运动质点在某时刻或某未知位矢和方向变化的快慢程度其方向沿该时刻质点所在点轨迹的切线方向。
在0→∆t 的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r -=而非r ?为什么θθr r a 20+=而非θθ r r +?你能说出r a 中的2θ r -和θa 中另一个θ r 出现的原因和它们的物理意义吗?答:质点运动时,径向速度r V 和横向速度θV 的大小、方向都改变,而r a 中的r 只反映了rV 本身大小的改变,θa 中的θθr r +只是θV 本身大小的改变。
事实上,横向速度θV 方向的改变会引起径向速度r V 大小大改变,2θ r -就是反映这种改变的加速度分量;经向速度r V 的方向改变也引起θV 的大小改变,另一个θ r 即为反映这种改变的加速度分量,故2θ r r a r -=,.2θθθ r r a +=。
这表示质点的径向与横向运动在相互影响,它们一起才能完整地描述质点的运动变化情况1.3 在内禀方程中,n a 是怎样产生的?为什么在空间曲线中它总沿着主法线方向?当质点沿空间运动时,副法线方向的加速度b a 等于零,而作用力在副法线方向的分量b F 一般不等于零,这是不是违背了牛顿运动定律呢?答:内禀方程中,n a 是由于速度方向的改变产生的,在空间曲线中,由于a 恒位于密切面内,速度v 总是沿轨迹的切线方向,而n a 垂直于v 指向曲线凹陷一方,故n a 总是沿助法线方向。
质点沿空间曲线运动时,0,0≠=b b F a z 何与牛顿运动定律不矛盾。
因质点除受作用力F ,还受到被动的约反作用力R ,二者在副法线方向的分量成平衡力0=+b b R F ,故0=b a 符合牛顿运动率。
第2章《质点运动学》习题解答
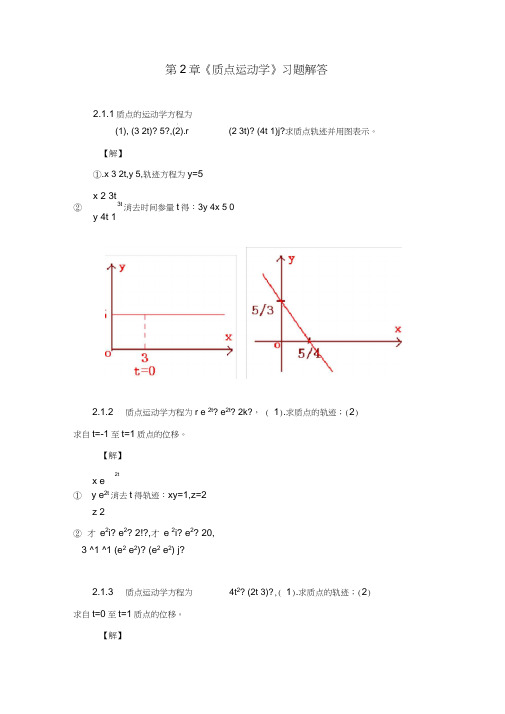
第2章《质点运动学》习题解答2.1.1质点的运动学方程为I(1), (3 2t)? 5?,(2).r(2 3t)? (4t 1)j?求质点轨迹并用图表示。
【解】①.x 3 2t,y 5,轨迹方程为y=5x 2 3t②3t消去时间参量t 得:3y 4x 5 0y 4t 12.1.2 质点运动学方程为r e 2t ? e 2t ? 2k?, ( 1).求质点的轨迹;(2)求自t=-1至t=1质点的位移。
【解】2tx e ① y e 2t 消去t 得轨迹:xy=1,z=2z 2② 才 e 2i? e 2? 2!?,才 e 2i? e 2? 20,3 ^1 ^1 (e 2 e 2)? (e 2 e 2) j?2.1.3 质点运动学方程为求自t=0至t=1质点的位移。
【解】4t 2? (2t 3)?,( 1).求质点的轨迹;(2)①.x 4t 2, y 2t 3,消去t 得轨迹方程x (y 3)2②r 0 3?』2.2.1雷达站于某瞬时测得飞机位置为R i 4100m, i 33.70,°.75s 后测得R 2 4240m, 2 29.3°, R,R 2均在铅直平面内。
求飞机瞬时速率的近似值和飞行方向(a 角)。
R i 2 R ; 2RR, cos( i 2)代入数值得: .41002 42402 -2 4100 4240cos 4.4°349.385(m)利用正弦定理可解出34.8902.2.2 一小圆柱体沿抛物线轨道运动,抛物线轨道为y x 2 / 200 (长度mm 。
第一次观察到圆柱体在349.3850.75 465.8(m/s)x=249mn 处,经过时间2ms 后圆柱体移到 x=234mn 处。
求圆柱体瞬时速度的近似4i? 5? r4? 2?t[解]19.6mm/ms152 36.22522112.502.2.3 一人在北京音乐厅内听音乐,离演奏者 17m 另一人在广州听同一 演奏的转播,广州离北京2320km 收听者离收音机2m 问谁先听到声音?声速 为340m/s,电磁波传播的速度为3.0 108m/s 。
质点力学习题与参考解答

【郑重说明】《理论力学》课程的习题及解答方面的参考书很多,学习者可以通过各种形式阅读与学习,按照学院对教学工作的要求,为了满足学习者使用不同媒体学习的实际需要,通过各种渠道收集、整理了部分习题及参考解答,仅供学习者学习时参考。
由于理论力学的题目解答比较灵活,技巧性也比较强,下面这些解答不一定是最好的方法,也可能会存在不够完善的地方,希望阅读时注意之。
学习理论力学课程更重要的是对物理概念的掌握与理解,学习处理问题的思想与方法,仅盲目的做题目或者阅读现成的答案,很难达到理想的结果。
质点动力学思考题与习题及参考解答思考题(1) 有一质量为m 的珠子, 沿一根置于水平面内的铁丝滑动, 采用自然坐标法描述. 珠子受重力g m W=, 铁丝施与的约束力b Nb n Nn t Nt Ne F e F e F F ++=.t Nt e F 即为滑动摩擦力f F, 设动摩擦因数为μ. 试判断下列各式正误: (1) mg F f μ=; (2) Nb f F F μ= (3)Nn f F F μ=;(4) 22Nb Nnf F F F +=μ(2) 用极坐标系描述单摆的运动. 某甲如思考题(2图(a)规定θ角正向, 得到动力学方程θθsin mg ml -= ; 某乙如思考题(2图(b)规定θ角正向, 则得到θθsin mg ml += . 你认为谁的做法正确?(a) (b)思考题(2图(3) 质量为m 的质点, 由静止开始自高处自由落下. 设空气阻力f F与速度成正比, 比例系数为k . 某甲建立竖直向上的坐标如思考题(3图(a), 得到方程为y k mg y m+-=. 某乙建立竖直向下的坐标如思考题(3图(b), 得到方程为y k mg y m-=.他们列出的方程对吗?(a) (b)思考题(3(4)有人认为: 用极坐标系讨论质点的平面运动时, 如果0≡r F , 则沿径向动量守恒,==rm p r 常量;若0≡θF , 则沿横向动量守恒. 这种看法对吗? (5) 试判断以下二论断是否正确:(1) 若质点对固定点O 的角动量守恒, 则对过O 点的任意固定轴的角动量守恒. (2) 若质点对固定轴的角动量守恒, 则对该轴上任一固定点的角动量守恒.(6) 一质点动量守恒, 它对空间任一固定点的角动量是否守恒? 如质点对空间某一固定点角动量守恒, 该质点动量是否守恒?(7) 当质点做匀速直线运动时, 其动量是否守恒? 角动量是否守恒?(8) 在固定的直角坐标系Oxyz 中, 质量为m 的质点的速度k v j v i v v z y x++=, 所受合力为k F j F i F F z y x ++=. 能否将质点的动能定理r F mv d )21(d 2⋅=向x 轴方向投影而得出分量方程x F mv x x d )21(d 2= 该方程是否正确?思考题解答(1) 仅(4)式正确.(2) 甲正确. 乙错在角度不可以定义为从动线指向定线.(3) 乙的方程正确. 甲错在空气阻力亦应为yk -,y 取负值,y k -取正值. (4) 仅对固定方向才有动量守恒的分量形式. 径向和横向均不是空间固定方向. (5) (1)对;(2)错. (6) 一质点动量守恒,则对空间任一固定点角动量守恒. 质点对空间某一固定点角动量守恒,其动量不一定守恒.(7) 质点作匀速直线运动时,其动量和角动量均守恒.(8) 动能定理是标量方程,不可能投影而得出分量方程. 但xF mv x d )21(d 2=是正确的. 仿照动能定理的导出,用x t v x d d =乘牛顿第二定律的x 分量方程x xF t v m=d d 即可证明.质点动力学习题及参考解答【1】研究自由电子在沿x 轴的振荡电场中的运动. 已知电场强度i t E E)cos(0ϕω+=,ϕω,,0E 为常量. 电子电量为e -, 质量为m . 初始时, 即当0=t 时i x r00=, i v v 00=. 忽略重力及阻力, 求电子的运动学方程.【解】力为时间的函数,积分两次可得)cos(200ϕωω+++=t m eE t V X x ,其中ϕωcos 2000m eE x X -=,ϕωsin 00m eE v V +=.【2】 以很大的初速度0v自地球表面竖直上抛一质点, 设地球无自转并忽略空气阻力, 求质点能达到的最大高度. 已知地球半径为R , 地球表面处重力加速度为g .【解】以地心O 为原点,建立x 轴经抛出点竖直向上. 质点受万有引力沿x 轴负方向. 所以2x GMm xm -= . 因为2R GMmmg =,故g R GM 2=. 故有22x g R x -= . 做变换)2(d d d d d d d d 2x x x x x t x x x x ===,则x x g R x d )2(d 222-= . 积分并用0=t 时R x =,0v x = 定积分常数,得到 )11()(212202R x g R v x -=- . 质点达最大高度时H R x +=,0=x,可求出 1220)21(2--=Rg v g v H .三点讨论:(1)令∞=H ,对应Rg v 20=为第二宇宙速度.(2)若Rg v 220<<,则回到重力场模型所得结果. (3)题中不考虑地球自转及空气阻力,均不大合理,试进一步讨论之.【3】 将质量为m 的质点竖直上抛, 设空气阻力与速度平方成正比, 其大小22gv mk F R =.如上抛初速度为0v , 试证该质点落回抛出点时的速率2201v k v v +=.【解】质点运动微分方程为(Oy 轴竖直向上);上升阶段22y g mk mg y m--=,下降阶段22y g mk mg ym +-=. 【4】向电场强度为E 、磁感应强度为B 的均匀稳定电磁场中入射一电子. 已知B E⊥, 电子初速0v 与E 和B 均垂直, 如题4图所示. 试求电子的运动规律. 设电子电量为e -.题4图【解】令m eB=ω,电子运动微分方程为y xω-=, (1) m eEx y-= ω, (2)0=z . (3)对(2)式求导,利用(1)式得02=+y yω,解出)sin(αω+=t A y . 0=t 时0=y 故0=α,由t A y ωωcos = ,且0=t 时m eBv Ee y0+-= ,故B Bv E A 0+-=,则t B Bv E y ωsin 0+-= . 积分得)cos 1()(20t m eB eB Bv E m y -+-=. 代入(1)式积分可得t m eB eB Bv E m t B E x sin )(20--=.【5】 旋轮线如题5图所示, 可理解为一半径为a 的圆轮在直线上做无滑滚动时轮缘上一点P 的轨迹, 其参数方程为)sin (ϕϕ+=a x , )cos 1(ϕ-=a y . 在重力场中, 设y 轴竖直向上, 一质点沿光滑旋轮线滑动, 试证质点运动具有等时性(绕O 点运动周期与振幅无关).题5图【解】(旋轮线是如图圆轮在直线AB 上作无滑滚动时P 点的轨迹,曲线上P 点切线方向即为轮上P 点速度方向. 因无滑,0P 为瞬心,故P 点切线与P P 0垂直,因此可知P 点切线与x 轴夹角为2ϕ. )以曲线最低点(0=ϕ)为自然坐标原点,弧长正方向与t e 一致. 质点运动微分方程为2sinϕmg s m -= .对曲线参数方程求微分,得ϕϕd )cos 1(d +=a x 和ϕϕd sin d a y =,所以ϕϕd 2cos 2d d d 22a y x s =+=,积分并用0=ϕ时0=s 定积分常数,得2sin 4ϕa s =. 代入质点运动微分方程消去ϕ,得到4=+s a gs ,s 作简谐振动而具有等时性. 其解为)cos(0αω+=t A s ,a g40=ω与振幅无关.【6】 一小球质量为m , 系在不可伸长的轻绳之一端, 可在光滑水平桌面上滑动. 绳的另一端穿过桌面上的小孔, 握在一个人的手中使它向下做匀速运动, 速率为a , 如题【6图所示. 设初始时绳是拉直的, 小球与小孔的距离为R , 其初速度在垂直绳方向上的投影为0v . 试求小球的运动规律及绳的张力.题6图【解】小球运动微分方程为T F r r m -=-)(2θ , (1) 0)2(=+θθr r m , (2)a r-= . (3) 由(3)式求出at R r -=,代入(2)式求出)/(0at R t v -=θ,再由(1)式求出3220)(at R R mv F T -=.【7】 一质量为m 的珠子串在一半径为R 的铁丝做成的圆环上, 圆环水平放置. 设珠子的初始速率为0v , 珠子与圆环间动摩擦因数为μ, 求珠子经过多少弧长后停止运动 (根据牛顿第二定律求解).【解】珠子的运动微分方程为2b 2n d d N N F F t v m+-=μ, (1)n 2/N F mv =ρ, (2)mg F N -=b 0, (3)R =ρ(约束方程). (4)把(2)、(3)、(4)式代入(1)式,作变换sv t v d /)21(d d d 2=,可求出]/)ln[()2/(224020Rg g R v v R s ++=μ.【8】 质量为m 的小球沿光滑的、半长轴为a 、半短轴为b 的椭圆弧滑下, 此椭圆弧在竖直平面内且短轴沿竖直方向. 设小球自长轴端点开始运动时其初速度为零. 求小球达到椭圆弧最低点时对椭圆弧的压力 (根据牛顿第二定律求解). 【解】以椭圆最低点为自然坐标原点O ,弧长正方向指向小球初始位置,θ为切向与水平方向的夹角,小球的运动微分方程为θsin mg vm -= , (1) θρcos /2mg F mv N -=. (2)Oy 竖直向上,将s y d /d sin =θ代入(1)式得s y g s v v d /d d /d -=,积分可求出小球达最低点时gb v 22=. 由轨道方程22x a a by --=求出当0=x 时0='y ,2/a b y ='',由公式可求出22/32)1(1a b y y ='+''=ρ. 再由(2)式求出0=θ时)/21(/cos 22a b mg mv mg F N +=+=ρθ.【9】 力1F 和2F分别作用在长方体的顶角A 和B 上, 长方体的尺寸和坐标系如题【9图所示. 试计算1F 和2F对原点O 及3个坐标轴的力矩.题9图【解】11bF M x =,11aF M y -=,01=z M ,2222/b a bcF M x +=,2222/b a acF M y +-=,02=z M .【10】 已知质量为0m 的质点做螺旋运动, 其运动学方程为t r x ωcos 0=, t r y ωsin 0=,kt z =,k r ,,0ω为常量. 试求: (1)t 时刻质点对坐标原点的角动量;(2) t 时刻质点对过),,(c b a P 点, 方向余弦为),,(n m l 的轴的角动量.【解】由运动学方程求出→v ,根据定义即可求出→→→→→→++--=⨯=k r m j t t t r km i t t t r km v r m L ωωωωωωω200000000)sin (cos )cos (sin ,)]cos ()sin )([(]cos )()sin ([000000),,(a t r k t r c kt m m t r c kt b t r k l m L n m l -+-----=ωωωωωω)sin cos (00200t br t ar r n m ωωωωω--+.【11】 如题【11图所示, 质量为m 的小球安装在长为l 的细轻杆的A 端, 杆的B 端与轴21O O 垂直地固连. 小球在液体中可绕21O O 轴做定轴转动, 轴承1O 和2O 是光滑的. 转动中小球所受液体阻力与角速度成正比, ωαm F R =,α为常量. 设初始角速度为0ω,试求经多少时间后, 角速度减小为初始值的一半,以及在这段时间内小球所转圈数.(忽略杆的质量及所受阻力.)题 11图【解】由对21O O 轴的角动量定理ωαωm l ml t -=)(d d2,积分可得lt /0e αωω-=,求出α/)2ln (l t =. 将角动量定理化为l /d d θαω-=,积分可以求得αωαωθπ4/)r a d (2/00l l ==(圈)【12】 质量为m 的质点沿椭圆轨道运动, 其运动学方程为kt a x cos =, kt b y sin = (k b a ,,为常量). 用两种方法计算质点所受合力在0=t 到k t 4π=时间内所做的功.【解】(1)由动能定理)(4121212222122b a mk mv mv W -=-=.(2)用曲线积分算⎰⎰+=⋅=→→2121)d d (y ym x x m r d F W ,把轨道参数方程kt b y kt a x sin ,cos ==代入,则曲线积分化为对t 的积分,可得同样结果.【13】 试用动能定理求解7题.【解】珠子的动能定理为sF F mv N N d )21(d 2b 2n 2--=μ,参见3.7提示【14】 有一小球质量为m , 沿如题【14图所示的光滑的水平的对数螺旋线轨道滑动. 螺旋线轨道方程为θa e r r -=0, a 为常数. 已知当极角0=θ时,小球初速为0v . 求轨道对小球的水平约束力N F 的大小. (用角动量及动能定理求解, 图中δ为θe 与v 方向间夹角,a =δtg.)题14图【解】因机械能守恒,小球动能不变,因此0v v =.过O 点作z 轴竖直向上(垂直纸面向外),质点对z 轴的角动量δcos rmv L z =. 质点所受对z 轴力矩δsin N z rF M -=. 由对z 轴的角动量定理得δδsin )cos (d d0N rF rmv t -=.由于θθθθθ ar ar t r r v a r -=-===-e d d d d 0,θθ r v =. 故a v v r =-=θδtan . 将它代入角动量定理方程,得到N N arF rF rmv -=-=δtan 0 . 而δδsin sin 0v v v r r -=-== ,所以θδδδa N a r mv a r mv ar mv ar mv F e 11tan 1tan sin 2020220222020+=+=+==.【15】 已知质点所受力F 的3个分量为z a y a x a F x 131211++=,z a y a x a F y232221++=, z a y a x a F z 333231++=,系数)3,2,1,(=j i a ij 都是常量. 这些ij a 满足什么条件时与力F相关的势能存在? 在这些条件被满足的条件下, 计算其势能.【解】当0=⨯∇→F 时势能存在,要求311332232112,,a a a a a a ===. 以原点为势能零点,则)222(21132312233222211xz a zy a xy a z a y a x a V +++++-=.【16】 一带有电荷q 的质点在电偶极子的场中所受的力为3c o s 2r pq F r θ=,3sin r pq F θθ=,p 为偶极距, r 为质点到偶极子中心的距离.试证此力场为有势场.【解】)/cos (d d d )d d (d 2r pq r F r F e r e r F r F r r θθθθθ-=+=+⋅=⋅→→→→→,故为有势场 【17】 如题17图所示, 自由质点在Oxy 平面内运动, 静止中心A 和B 均以与距离成正比的力吸引质点M , 比例系数为k . 试证明势能存在并求出质点的势能.v题【17图【解】y ky x kx y ky ky x b x k b x k r F d 2d 2d )(d )]()([d --=--+--+-=⋅→→)](d [22y x k +-=.故势能存在. 以O 为势能零点,则)(22y x k V +=.【18】 试用机械能守恒定律求解8题.【解】根据机械能守恒定律,以椭圆弧最低点为势能零点,mgbmv =221,可知gb v 2=,参见3.8提示.【20】 将质量为m 的质点竖直抛上于有阻力的媒质中。
大学物理教材习题答案

⼤学物理教材习题答案第⼀章质点运动习题解答⼀、分析题1.⼀辆车沿直线⾏驶,习题图1-1给出了汽车车程随时间的变化,请问在图中标出的哪个阶段汽车具有的加速度最⼤。
答: E 。
位移-速度曲线斜率为速率,E 阶段斜率最⼤,速度最⼤。
2.有⼒P 与Q 同时作⽤于⼀个物体,由于摩擦⼒F 的存在⽽使物体处于平衡状态,请分析习题图1-2中哪个可以正确表⽰这三个⼒之间的关系。
答: C 。
三个⼒合⼒为零时,物体才可能处于平衡状态,只有(C )满⾜条件。
3.习题图1-3(a )为⼀个物体运动的速度与时间的关系,请问习题图1-3(b )中哪个图可以正确反映物体的位移与时间的关系。
答:C 。
由v-t 图可知,速度先增加,然后保持不变,再减少,但速度始终为正,位移⼀直在增加,且三段变化中位移增加快慢不同,根据v-t 图推知s-t 图为C 。
三、综合题:1.质量为的kg 50.0的物体在⽔平桌⾯上做直线运动,其速率随时间的变化如习题图1-4所⽰。
问:(1)设s 0=t 时,物体在cm 0.2=x 处,那么s 9=t 时物体在x ⽅向的位移是多少?(2)在某⼀时刻,物体刚好运动到桌⼦边缘,试分析物体之后的运动情况。
解:(1)由v-t 可知,0~9秒内物体作匀减速直线运动,且加速度为:220.8cm/s 0.2cm/s 4a == 由图可得:0 2.0cm s =,00.8cm/s v =, 1.0cm/s t v =-,则由匀减速直线运动的位移与速度关系可得:22002() t a s s v v -=- 2200()/2t s v v a s =-+ 22[0.8( 1.0)]/20.2 2.0cm =--?+1.1c m =(2)当物体运动到桌⼦边缘后,物体将以⼀定的初速度作平抛运动。
2.设计师正在设计⼀种新型的过⼭车,习题图1- 5为过⼭车的模型,车的质量为0.50kg ,它将沿着图⽰轨迹运动,忽略过⼭车与轨道之间的摩擦⼒。
质点运动学习题思考题

质点运动学习题思考题⼤学物理第⼀章习题11-1.已知质点位⽮随时间变化的函数形式为(cos sin )r =R ωt i ωt j +其中ω为常量.求:(1)质点的轨道;(2)速度和速率。
解:(1) 由(cos sin )r =R ωt i ωt j +,知:cos x R t ω= ,sin y R t ω=消去t 可得轨道⽅程:222x y R +=∴质点的轨道为圆⼼在(0,0)处,半径为R 的圆;(2)由d rv dt= ,有速度:sin Rcos v R t i t j ωωωω=-+⽽v v = ,有速率:1222[(sin )(cos )]v R t R t R ωωωωω=-+=。
1-2.已知质点位⽮随时间变化的函数形式为24(32)r t i t j =++ ,式中r 的单位为m ,t 的单位为s 。
求:(1)质点的轨道;(2)从0=t 到1=t 秒的位移;(3)0=t 和1=t 秒两时刻的速度。
解:(1)由24(32)r t i t j =++,可知24x t = ,32y t =+ 消去t 得轨道⽅程为:x =2(3)y -,∴质点的轨道为抛物线。
(2)由d r v dt= ,有速度:82v t i j =+从0=t 到1=t 秒的位移为:1100(82)42r v d t t i j d t i j ?==+=+??(3)0=t 和1=t 秒两时刻的速度为:(0)2v j =,(1)82v i j =+ 。
1-3.已知质点位⽮随时间变化的函数形式为22r t i t j =+,式中r 的单位为m ,t 的单位为s .求:(1)任⼀时刻的速度和加速度;(2)任⼀时刻的切向加速度和法向加速度。
解:(1)由d r v dt = ,有:22v t i j =+ ,d v a dt= ,有:2a i = ;(2)⽽v v = ,有速率:12222[(2)2]21v t t =+=+∴t d v a dt=221t t =+,利⽤222t n a a a =+有: 22221n t a a a t =-=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题2-1. 质量为m 的子弹以速度0v 水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1) 子弹射入沙土后,速度随时间变化的函数式;(2) 子弹进入沙土的最大深度。
解:(1)由题意和牛顿第二定律可得:dtdvmkv f =-=, 分离变量,可得:vdtdvm k =- 两边同时积分,所以:t m ke v v -=0 (2)子弹进入沙土的最大深度也就是v=0的时候子弹的位移,则:由vdt dv m k =- 可推出:dv km vdt -=,而这个式子两边积分就可以得到位移:00max 0v m mx vdt dv v k k==-=⎰⎰ 。
2-2. 一条质量分布均匀的绳子,质量为M 、长度为L ,一端拴在竖直转轴OO ′上,并以恒定角速度ω在水平面上旋转.设转动过程中绳子始终伸直不打弯,且忽略重力,求距转轴为r 处绳中的张力T ( r ).解:在绳子中距离转轴为r 处取一小段绳子,假设其质量为dm ,可知:LMddm =,分析这dm 的绳子的受力情况,因为它做的是圆周运动,所以我们可列出: LMdrr rdm r dT 22ωω==)(。
距转轴为r 处绳中的张力T ( r )将提供的是r 以外的绳子转动的向心力,所以两边积分:)()()(2222r L LM r dT r T Lr-==⎰ω2-3. 已知一质量为m 的质点在x 轴上运动,质点只受到指向原点的引力作用,引力大小与质点离原点的距离x 的平方成反比,即2/x k f -=,k 是比例常数.设质点在A x =时的速度为零,求质点在4/A x =处的速度的大小。
解:由题意和牛顿第二定律可得:dx dv mv dt dx dx dv m dt dv m xk f ===-=2再采取分离变量法可得:mvdv dx x k=-2 , 两边同时取积分,则:mvdv dx xkv A A ⎰⎰=-024/ 所以:mAkv 6=2-4. 一质量为kg 2的质点,在xy 平面上运动,受到外力j i F 2244t -=(SI)的作用,0=t 时,它的初速度为j i v 430+=(SI),求s t 1=时质点的速度及受到的法向力n F .解:由题意和牛顿第二定律可得:dtd m m va f ==,代入f 与v ,并两边积分,v j i md dt t vv ⎰⎰=-0)244(21, )]43([284j i v j i +-⨯=-i v 5=速度是i 方向,也就是切向的,所以法向的力是j 方向的,则24=-F j2-5. 如图,用质量为1m 的板车运载一质量为2m 的木箱,车板与箱底间的摩擦系数为μ,车与路面间的滚动摩擦可不计,计算拉车的力F 为多少才能保证木箱不致滑动?解:根据题意,要使木箱不致于滑动,必须使板车与木箱具有相同的加速度,所以列式:21222msx F m gf a m m m m μ'===+可得:g m m F )(21+μ2-6. 如图所示一倾角为θ的斜面放在水平面上,斜面上放一木块,两者间摩擦系数为)(θμtg <。
为使木块相对斜面静止,求斜面加速度a 的范围。
解:在斜面具有不同的加速度的时候,木块将分别具有向上和向下滑动的趋势,这就是加速度的两个范围,由题意,可得: (1)当木块具有向下滑动的趋势时(见图a ),列式为:mg N N =+θθμcos sinma N N =-θμθcos sin 可计算得到:此时的θμμθtan 1tan 1+-=a g(2)当木快具有向上滑动的趋势时(见图b ),列式为:θθμcos sin N mg N =+ ma N N =+θμθcos sin 可计算得到:此时的θμμθtan 1tan 2-+=a g所以tan tan 1tan 1tan g a g θμθμμθμθ-+≤≤+-2-7. 一质量为M 、顶角为α的三角形光滑物体上。
放有一质量为m 的物块,如图所示。
设各面间的摩擦力均可忽略不计。
试按下列三种方法:(1)用牛顿定理及约束方程;(2)用牛顿定律及运动叠加原理;(3)用非惯性系中力学定律;求解三角形物块的加速度M a .解:隔离物块和斜面体,画图分析力,列出方程,发现方程完备性不够,即未知数比方程数多,关键在于,M 与m 的运动有联系的,M 沿地面运动,m 沿斜面运动,这就是约束条件。
取地面作为参考系,则m 的运动为:s i n x N m a α-= (1)cos y N mg ma α-= (2)M 的运动方程为:sin M N Ma α= (3)下面列出约束条件的方程:取M 作为参考系,设m 在其中的相对加速度为a ',在x,y 方向的分量分别为'x a 与'y a ,那么:tan yxa a α'=' 利用相对运动的公式,a a a M m '+= 所以:M x x a a a -='y y a a ='于是:tan y y x x Ma a a a a α'=='- 即:sin cos sin x y M a a a ααα-= (4) 由(1)(2)(3)(4)联立,计算可得:2sin cos sin M m a g M m ααα=+2-8. 圆柱形容器内装有一定量的液体,若它们一起绕圆柱轴以角速度ω匀速转动,试问稳定旋转时液面的形状如何? 解:受力分析如图y m s i n N 2ωΔα= (1) mg cos N Δα= (2)两式相比 dydz g y tan 2==ωα dy g y dz 2⎰⎰=ω C y gωz +=222当 0=y 时 0z z = 所以 0z C =0222z y gωz += 稳定旋转时液面是一个抛物面由于旋转后成为立体,故方程变为【2220()2z x y z gω=++】2-9. 质量为2m 的物体可以在劈形物体的斜面上无摩擦滑动,劈形物质量为1m ,放置在光滑的水平面上,斜面倾角为θ,求释放后两物体的加速度及它们的相互作用力。
解:隔离物块和斜面体,分析力,列出方程,发现方程完备性不够,即未知数比方程数多,关键在于,m 1与m 2的运动有联系的,m 1沿地面运动,m 2沿斜面运动,这就是约束条件。
取地面作为参考系,则m 2的运动为:x a m N 2s i n =-θ (1)y a m g m N 22cos =-θ (2)m 1的运动方程为:11sin N m a θ= (3)下面列出约束条件的方程:取m 1作为参考系,设m 2在其中的相对加速度为a ',在x,y 方向的分量分别为'x a 与'y a ,那么:xy a a ''=θtan利用相对运动的公式,21a a a '=+ 所以:1x x a a a '=- y y a a ='于是:1tan yy x x a a θ'==' 即:1sin cos sin x y a a a θθθ-= (4) 由(1)(2)(3)(4)联立,计算可得:21212sin cos sin m a g m m θθθ=+;12212sin cos sin m a g m m θθθ=-+;12212()sin sin m m a g m m θθ+'=+ 相互作用力N=g m m m m θθ22121sin cos + 2-10. 一小环套在光滑细杆上,细杆以倾角θ绕竖直轴作匀角速度转动,角速度为ω,求:小环平衡时距杆端点O 的距离r . 解:根据题意,当小环能平衡时,其运动为绕Z 轴的圆周运动,所以可列式:mg N =θsinθωθsin cos 2r m N =所以,可得:θθωsin tan 2gr =2-11. 设质量为m 的带电微粒受到沿x 方向的电力i F )(cx b +=,计算粒子在任一时刻t 的速度和位置,假定0=t 时,0,000==x v .其中c b 、为与时间无关的常数,m 、F 、x 、t 的单位分别为kg 、N 、m 、s .解:根据题意和牛顿第二定律,可列式:22)(dt d m cx b x=+=i F ,整理可得二阶微分方程:022=--b cx dtd m x。
令mc=2ω 下面分c 为正负再做进一步讨论。
当00222=-+m b x dtd c ωx 时,,可得:c b t c b x -=ωcos一次求导,得到:t cb v ωωsin -=当00222=--m b x dtd c ωx 时, ,可得:c be e c b x t t -+=-)(2ωω 一次求导,得到:)(2t te e cb v ωωω--=2-12. 在光滑的水平面上设置一竖直的圆筒,半径为R ,一小球紧靠圆筒内壁运动,摩擦系数为μ,在0=t 时,球的速率为0v ,求任一时刻球的速率和运动路程。
解:在法向上有 Rv m N 2= 而 N μf =在切向上有 dtdv mf =- 由上面三个式子可得 Rv μdt dv 2-= dt R μdv v t vv ⎰⎰=-0201 t μv R R v v 00+= )1ln(00000R t μv μRt μv R dt R v vdt S tt+=+==⎰⎰思考题2-1. 质量为m 的小球,放在光滑的木板和光滑的墙壁之间,并保持平衡,如图所示.设木板和墙壁之间的夹角为α,当α逐渐增大时,小球对木板的压力将怎样变化?解:假设墙壁对小球的压力为N 1,木板对小球的压力为N 2。
由受力分析图可知:mg N =αsin 2所以当所以α增大,小球对木板的压力为N 2将减小; 同时:12cos N N =ααm g c t g N =1 所以α增大,小球对墙壁的压力1N 也减小。
2-2. 质量分别为m 1和m 2的两滑块A 和B 通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的摩擦系数均为μ,系统在水平拉力F 作用下匀速运动,如图所示.如突然撤消拉力,则刚撤消后瞬间,二者的加速度a A 和a B 分别为多少 ?解:分别对A ,B 进行受力分析,由受力分析图可知:g m m F )(21+=μg m kx F 1μ+= g m kx 2μ=所以.0,121=+=B A a g m m m a μ2-3. 如图所示,用一斜向上的力F (与水平成30°角),将一重为G 的木块压靠在竖直壁面上,如果不论用怎样大的力F ,都不能使木块向上滑动,则说明木块与壁面间的静摩擦系数μ的大小为多少?解:假设墙壁对木块的压力为N ,由受力分析图可知:N G F μα+=sinαcos F N =整理上式,并且根据题意,如果不论用怎样大的力F ,都不能使木块向上滑动,则说明:F G F 2321μ+≤ 即当F F 2321μ此式中F 无论为多大,总成立,则可得:33μ2-4. 质量分别为m 和M 的滑块A 和B ,叠放在光滑水平桌面上,如图所示.A 、B 间静摩擦系数为s μ,滑动摩擦系数为k μ,系统原处于静止.今有一水平力作用于A 上,要使A 、B 不发生相对滑动,则F 应取什么范围?解:根据题意,分别对A ,B 进行受力分析,要使A ,B 不发生相对滑动,必须使两者具有相同的加速度,所以列式:Mm gM m F a s msx μ=+=可得:g MM m m F s)(+μ2-5. 如图,物体A 、B 质量相同,B 在光滑水平桌面上.滑轮与绳的质量以及空气阻力均不计,滑轮与其轴之间的摩擦也不计.系统无初速地释放,则物体A 下落的加速度是多少?解:分别对A ,B 进行受力分析,由受力分析图可知:111a m T g m =-222a m T =1221a a =则可计算得到:g a 541=2-6. 如图所示,假设物体沿着竖直面上圆弧形轨道下滑,轨道是光滑的,在从A 至C 的下滑过程中,下面哪个说法是正确的?(A) 它的加速度大小不变,方向永远指向圆心。
