理论力学非惯性参考系
大学物理非惯性系惯性力

惯性力只存在于非惯性系中,在惯性参考系中不存在惯性力 。通过引入惯性力的概念,我们可以将非惯性系中的物理问 题转化为惯性系中的问题,从而应用牛顿运动定律进行求解 。
03
非惯性系中的惯性力表现
科里奥利力
总结词
由于地球自转导ห้องสมุดไป่ตู้的旋转参考系中的力。
详细描述
科里奥利力是在旋转参考系中,当物体有相对于旋转轴的相对速度时,由于地球自转而受到的力。这个力垂直于 物体速度的方向,并改变物体运动的方向。在北半球,科里奥利力使物体偏向右方;在南半球,则偏向左方。
总结词
相对论效应是指由于时空相对性导致的物理 现象,表现为时间膨胀和长度收缩。
详细描述
根据爱因斯坦的相对论,当物体以接近光速 运动时,会观察到时间膨胀和长度收缩的现 象。时间膨胀是指相对于静止观察者,运动 物体的时间变慢;长度收缩是指相对于静止 观察者,运动物体的长度缩短。相对论效应
在高速运动和强引力场中具有重要应用。
在现实生活中,许多问题都是在 非惯性参考系中考虑的,例如车 辆动力学、航天器运动等。研究 非惯性系惯性力有助于解决这些 实际问题。
促进物理学科发展
非惯性系惯性力是经典力学中的 一个重要概念,研究它有助于推 动物理学科的发展,促进人们对 自然界运动规律的认识。
02
非惯性系与惯性力定义
非惯性系定义
非惯性系是指相对于惯性参考系加速 运动的参考系。在非惯性系中,牛顿 运动定律不再适用。
非惯性系通常指相对于惯性参考 系加速或减速运动的参考系。
惯性力是由于非惯性系相对于惯 性参考系的加速或减速运动,而
使物体受到的一种虚拟力。
为什么研究非惯性系惯性力
深入理解牛顿运动
定律
惯性参考系和非惯性参考系

r m
2 Fi mr en
(方向沿半径向外)
7
如果质点相对匀速转动参考系(非惯性系)运动, 则所受的惯性力较为复杂。除了受到惯性(离心)力的 作用外,还受到一种叫科里奥利力的惯性力。
Fc 2m 式中为转台的角速度,为质
点相对转台的速度。
可以证明,科里奥利力的计算公式为
五. 惯性参考系和非惯性参考系
1.惯性参考系 从运动的描述来说 ,参考系的选择是任意的,这 主要由研究问题的方便而定。但是,如果问题涉及 运动和力的关系,即要应用牛顿定律时,参考系是否 也能任意选择呢? 如图2-7所示,车厢A在地面上以加速度a向右运 动。 乙 车厢内的光滑桌面上 m k 有一与弹簧相连的质量m 甲 a 的小球, 弹簧的另一端系 A 在车厢壁上。现在来分析 这个 弹簧、小球 力学系 图2-7 统的运动情况。
求楔块的加速度 a0和物体对斜面的下滑加速度 a 。 '
N2
a0
m1
m2 m2g 图2-1
a'
m2 a 0
y
a0
x
N1
m1
N2 '
m1g
10
对m1: x方向
N' 2 sin m1a0
N2
a0
N1
m1
m2
a'
m2 a 0
y x
N2 '
m 1g
北半球的河床右岸为什么 受到较厉害的冲刷?赤道的信 风是怎样形成的?这些都是科 里奥利力作用的结果。
m
图2-10
可以在图书馆找周衍柏《理论力学》p141
8
北半球的河流由西向东流动,由于科里奥利力向南, 使河流的右岸受到冲刷。南半球反向,使河流的左岸受 到冲刷(试分析之)
理论力学 非惯性参考系

§5.2 非惯性系中的动力学方程 惯性力 惯性系中: 惯性系中: m d2rI /dt2 = F 非惯性系: 非惯性系: mδ2r/δt2 =F -m[d2R /dt2+β×r +ω×(ω×r) +2ω×v'] β ω ω ω v' δ δ F = Feff 1,平移力 , - md2R /dt2 ← 动系平动加速 2,方位力 , - mβ × r β ← 动系转动加速 3,惯性离心力 , - m[ω × (ω × r ) ← 动系相对固定系转动 ω ω 4,科里奥利力 , - 2mω × v' ω ← 质点相对动系运动
= ω t t = 1 ln 2 + 3 ω
(
)
可证明,引入非惯性力 ,质点动量定理,角动 质点动量定理, 可证明, 量定理和动能定理的形式都保持不变. 量定理和动能定理的形式都保持不变. 例:角动量定理 : r' v') δ L' / δt = δ(r' × mv' / δt = δ(r' δt × mv' + r' × mδv'/ δt r')/δ v' δv' = r' × ( F + F惯性) 动能定理: v' 动能定理 ∵ m δv'/ δ t = F + F惯性 → m δv' δr / δt = (F + F惯性 ) δr F → m v' δv' = (F + F惯性 ) δr F F → δ(mv'2/2) = (F + F惯性 ) δr F 即: δT = (F + F惯性 ) δr
d L 2 L 2 d L 1 L 1 d df df = + & & & dt q dt q q q dt q dt q dt df f f df 2 f 2f & & Q q+ q+ = ∴ = 2 dt q t q dt q qt d df d f 2 f 2f & = q = q 2 q + qt & dt q dt dt d L 1 L 1 d L 2 L 2 因此, 因此,当 = 0时, =0 & & dt q dt q q q
大学物理 2.5非惯性系
4
2 即: f s m r 0
S:
2 f s man m (r )
m r
2
─ 惯性离心力 (inertial centrifugal force)
大学 物理
2-5 非惯性系
惯性离心力与向心力的比较: 作用在同一物体上 向心力是真实力作用的表现
大学 物理
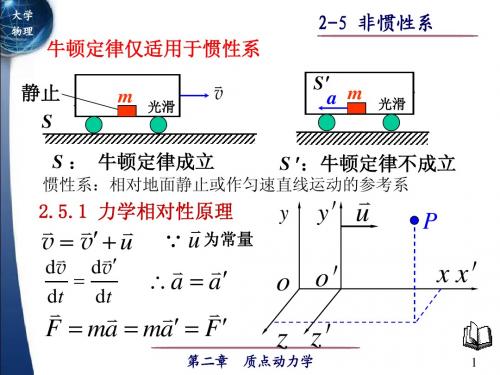
2-5 非惯性系 牛顿定律仅适用于惯性系
S
静止 静止 S
m
光滑
v
a m
光滑
a
S : 牛顿定律成立 2.5.1 力学相对性原理
S :牛顿定律不成立
惯性系:相对地面静止或作匀速直线运动的参考系
v v u
为常量 u d v d v o' a a o dt dt F ma ma F z z'
第二章
T
m2 a
f惯1
m1 g
f惯2
m2 g
88质点动力学大学 物理2-5 非惯性系
m1 m2 讨论 a ( a0 g ) m1 m2 m1 m2 a ( g | a0 |) m1 m2 2m1m2 T ( g | a0 |) m1 m2
当电梯加速下降时,a0 < 0,得
惯性离心力是虚拟力,是运动物体的惯性在
转动参考系中的表现
本质上是物体惯性的体现。它不是物体间的相互作用, 没有反作用力,但有真实的效果
f f惯 ma物对非
地球近似看作惯性系(自转,公转),相对地面静止 或做匀速直线运动的物体均可作为惯性系
自转:an 3.4 102 (m / s2 )
m2 g
o
7
理论力学 第一章 非惯性系中的质点动力学

aC 0
ae 0
FIe FIC 0 mar F
所有相对于惯性参考系作匀速直线平移的参考系 都是惯性参考系 发生在惯性参考系中的任何力学现象都无助于发 觉该参考系本身的运动情况----相对性原理
(3)质点相对于动参考系静止
ar 0 ,r 0
P FIe
将上式投影到轨迹的切向轴t上 得
d2s m 2 ( P FIe ) sin m( g a0 ) sin dt
当摆作微振动时 角很小 有 sin 且 s l 上式成为 d 2 m l 2 m( g a0 ) dt 令
mgsin FIe cos mae cos ae g tan
(2)当加速度 ae 2g tan 时
FN F Ie
FIe 2mg tan
应用相对运动动能定理,有
m 2 vr 0 ( FIe cos )l (mg sin )l 2 m 2 r (mg sin )l 2
t
2h g
2h g
2h cos x 3
此时
x 为正值, 偏移向东。
这就是地球上的落体偏东现象。
§ 1-2 非惯性系中质点的动能定理
质点的相对运动动力学基本方程为
dvr m F FIe FIC dt
式中 FIe mae ,FIC maC 2m vr
a
解: (1)在平板上固结一动参考系 Oxy
FIe mae
FN F Ie
FIC 0
小球相对静止, 方程为
F F
从中解出 得
x y
0 ,FN mg cos FIe sin 0 0 , mg sin FIe cos 0
理论力学简明教程第三章非惯性参考系课后答案

第三章 非惯性参考系不识庐山真面目,只缘身在此山中。
地球的多姿多彩,宇宙的繁荣,也许在这里可以略见一斑。
春光无限,请君且放千里目,别忘了矢量语言在此将大放益彩。
【要点分析与总结】1 相对运动t r r r '=+t t dr dr dr dr dr r dt dt dt dt dtυω'''==+=++⨯ t r υυω''=++⨯()t dv dv d v r a dt dt dtω''+⨯==+222**22()t d r d r d dr r v r dt dt dt dtωωωω'''''=++⨯+⨯+⨯+⨯()2t a a r r v ωωωω''''=++⨯+⨯⨯+⨯t c a a a '=++〈析〉仅此三式便可以使“第心说”与“日心说”归于一家。
(1) 平动非惯性系 (0ω=)t a a a '=+ 即:()t ma F ma '=+-(2) 旋转非惯性系 (0t t a υ==)()2a a r r ωωωωυ''''=+⨯+⨯⨯+⨯2 地球自转的效应(以地心为参考点)2mr F mg m r ω=--⨯写成分量形式为:2sin 2(sin cos )2cos x y z mx F m y my F m x z mz F mg m y ωλωλλωλ⎧=+⎪=-+⎨⎪=-+⎩ 〈析〉坐标系选取物质在地面上一定点O 为坐标原点,x 轴指向南方,y 轴指向东方,铅直方向为 z 轴方向。
2mr F mg m r ω=--⨯ 为旋转非惯性系 ()2F mg mr m r m r m r ωωωω-=+⨯+⨯⨯+⨯在 ,rR ωω条件下忽略 m r ω⨯与 ()m r ωω⨯⨯所得。
正因如此,地球上的物体运动均受着地球自转而带来的科氏力 2m r ω-⨯的作用,也正是它导致了气旋,反气旋,热带风暴,信风,河岸右侧冲刷严重,自由落体,傅科摆等多姿多彩的自然现象。
非惯性参考系

第15、16课时非惯性参考系一、知识概要:凡牛顿第一定律成立的参照系叫惯性参照系,简称惯性系。
凡相对惯性系静止或匀速运动的参照系,都是惯性系。
例如,在不考虑地球自转,在研究较短时间内物体的运动情况时,地球可看成是近似程度相当好的惯性系。
凡牛顿第一定律不成立的参照系统称为非惯性系。
同样牛顿第二定律也不再适用。
但在引入惯性力的概念后,就可以利用牛顿定律的形式来解决动力学问题了。
直线系统中的惯性力:F惯=-ma注:惯性力只是一种假想的力,实际不存在,即不能找到施力物体,因而也找不到它的反作用力。
惯性力起源于物体惯性,是在非惯性系中物体惯性的体现。
二、典型例题分析:复习:物体间相对运动知识;整体牛顿定律求解思想;约束方程(根据物体间形状关系,如何确定物体间位移、速度、加速度的关系);1、倾角为θ,质量为M的光滑斜面放在光滑水平面上,一质量为m的物体放在斜面上后,沿斜面向下滑动,同时斜面也发生运动,求:物体在斜面上相对斜面向下滑动的过程中,斜面沿水平面运动的加速度多大?2、汽车以匀加速度a0行驶,在车中用悬线挂一小球,当小球稳定时,悬线与竖直方向偏离多大的角度?3、如图,质量为10 Kg的物体A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为5 N 时,物体处于静止状态,若小车以加速度a = 1 m·S-2向右开始运动后,则:()A、物体A相对于小车仍然静止;B、物体A受到的摩擦力减小;C、物体A受到的摩擦力大小不变;D、物体A受到的弹簧的拉力增大。
4、如图,质量为m A 、m B 的两个物体A 、B ,用细绳相连跨过光滑的滑轮,将A 置于倾角为θ的斜面上,B 悬空,斜面的质量为M 。
如果A 在斜面上沿斜面加速向下滑动的过程中,问:1)水平地面对斜面在竖直方向上的作用力多大? 2)斜面作用在高出地面壁上的水平方向的力多大?5、如图一个装有水的烧杯,总质量为M ,放在与水平面成α角的斜面上,与斜面之间的动摩擦因素为μ,当烧杯沿斜面向下平动时,若液面正好与斜面平行,试证明:沿斜面方向作用在烧杯上的推力大小等于斜面 对烧杯的摩擦力,即F =μMgcos α。
高一物理惯性系和非惯性系知识精讲
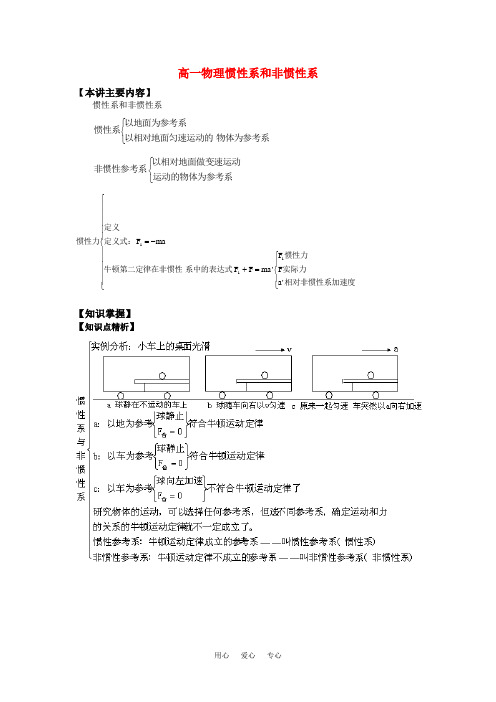
高一物理惯性系和非惯性系【本讲主要内容】惯性系和非惯性系⎩⎨⎧物体为参考系以相对地面匀速运动的以地面为参考系惯性系 ⎩⎨⎧运动的物体为参考系以相对地面做变速运动非惯性参考系 ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧=+-=相对非惯性系加速度实际力惯性力系中的表达式牛顿第二定律在非惯性定义式:定义惯性力'a F F 'ma F F maF i i i【知识掌握】【知识点精析】⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧=+⎪⎩⎪⎨⎧-=⎪⎪⎩⎪⎪⎨⎧-=-=相对非惯性系加速度实际受力惯性力系中数学表达式牛顿第二定律在非惯性达式牛顿第二定律的数学表是惯性力定义式、不是、、惯性力无反作用力力,无施力物体加速效应力,不是真实、惯性力是假想的力,注意定义式:度方向相反方向:与非惯性系加速积与非惯性系加速度的乘大小:等于物体的质量惯性力速效应,假想的力,叫由于非惯性系本身的加定义:在非惯性系中,惯性力度方向相反。
负号表示与车的加速惯性力,力我们认为受到一向左的成立,。
为了使牛顿运动定律为球应受向左的力,大小向左。
按牛顿运动定律,速,加速度为惯性系)。
小球向左加中,以车为参考系(非在上述实例分析'a F F 'ma F F ma F 321maF ma F ——ma a C i i i i i 【解题方法指导】例1. 质量为60kg 人,站在电梯的磅秤上,当电梯以0.5m/2s 加速度匀加速上升时,求磅秤读数?解:方法一:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+⨯=+=∴=--∴N 618N 618N 618)5.08.9(60)a g (m N 0ma mg N 读数为压力为据牛顿第三定律人对秤人相对电梯静止性系)以电梯为参考系(非惯方法二:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+⨯=+=∴=-∴N 618N 618N 618)5.08.9(60)a g (m N mamg N 读数为压力为据牛顿第三定律人对秤人相对地向上加速系)以地面为参考系(惯性分析:两个参考系得结果一样,只不过一个应用平衡条件,一个应用牛顿第三定律、原因选不同参考系,观察效果不同。
