广东省佛山市高中数学 第三章 直线与方程 3.33.4 点到直线的距离和平行线间的距离学案(无答案)
高中数学《第三章直线与方程3.3直线的交点坐标与距离公式3.3.4两条平行线间的距离》851PPT课件

[解] 设直线的斜率为 k,由斜截式得 l1 的方程 y=kx+ 1,即 kx-y+1=0,由点斜式可得 l2 的方程 y=k(x-5),即 kx-y-5k=0.在直线 l1 上取点 A(0,1),则点 A 到直线 l2 的距 离 d=|11++5kk2|=5,∴25k2+10k+1=25k2+25,∴k=152.
第三章 直线与方程
1.直接利用两平行直线间的距离公式. 2.在一条直线上任意选取一点,利用点到直线的 距离公式求解(一般要选特殊的点,如直线与坐标轴的交 点、坐标为整数的点).
第三章 直线与方程
例2 直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2, 且l1与l2的距离为5,求l1,l2的方程.
|2×4+232+×302-10|=
2 =2 13
13 13 .
[解法二] 因为 l1∥l2 且 C1=-8,C2=-10,所以由两
条平行直线间的距离公式得
d=|-8-22+-3120|=2
13 13 .
第三章 直线与方程
第三章 直线与方程
例3 已知直线l经过点A(2,4),且被平行直线l1:x -y+1=0与l2:x-y-1=0所截得的线段的中点M在直 线x+y-3=0上.求直线l的方程.
则点 M 到 l1,l2 的距离相等,
则|t-3-t+1|=|t-3-t-1|,解得
2
2
t=32,
∴M(32,32).
又 l 过点 A(2,4),
第三章 直线与方程
由两点式得4y--3232=2x--3232, 即 5x-y-6=0, 故直线 l 的方程为 5x-y-6=0.
高中数学《第三章直线与方程3.3直线的交点坐标与距离公式3.3.4两条平行线间的距离》854PPT课件

Y
Q P
B
A X
解:直线BA的斜率 kBA
30 2 (4)
1 2
直线PQ的斜率 kPQ
2 1 1 (3)
1 2
因为 kBA kPQ ,所以直线 BA// PQ
例12,求证:顺次连结(A 2,
3)、B(5,-
7 2
)、C(2,3)
D( 4,4)四点所得的四边形是梯形。 y
D●
4C
3
●
分析:1.什么是梯形?
PQ得
1m 1 m1 3
1,解得
m
2
所以当m 2 时,直线 AB 与直 线 PQ 垂直
学完一节课或一个内容,
应当及时小结,梳理知识
一、知识内容上
l1 // l2 k1 k2(前提:两条直存线在不)重合,斜率都
l1
l2
k1k2
1
(前提:两条直线都有斜率, 并且都不等于零)
二、思想方法上
(1)运用代数方法研究几何性质及其相互位置关系 (2)数形结合的思想
y l2
l2
l1
y l1
O
α1
α2
xO
x
结论2:
L1 ⊥ L2
k1k2=-1
或直线L1 与 L2中有 一条斜率为零,另一条 斜率不存在
两条直线垂直,一定是它们的斜率 乘积为-1这种情况吗?
例1.已知A(2,3),B(-4,0),P(-3,1), Q(-1,2),试判断直线BA与PQ的位置关系, 并证明你的结论。
x o -4
2
5
2.怎么样处理直线平行?
-3
●
A
●B
解:Q
k AB
7 (3) 2 52
高中数学 第三章 直线与方程 3.3.3 点到直线的距离 3.3.4 两条平行直线间的距离教案 新人教A版必修2
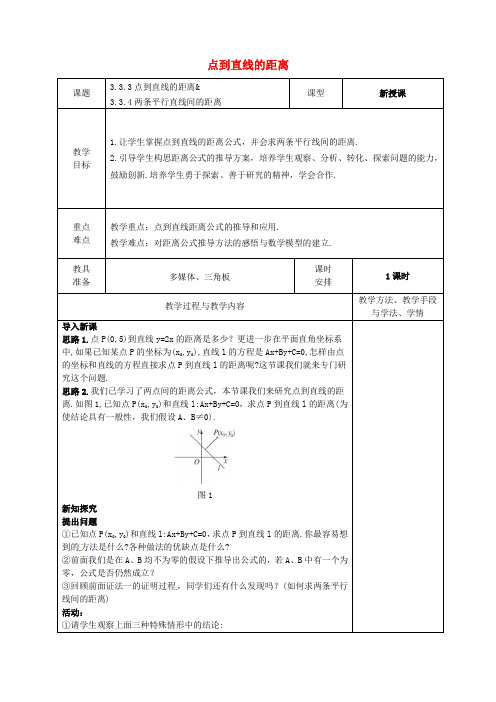
∴Ax0+By0+C1=0.∴C1=-Ax0-By0.
代入(*)得|P′N|= 即d= ,.
②可以验证,当A=0或B=0时,上述公式也成立.
③引导学生得到两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离d= .
证明:设P0(x0,y0)是直线A x+By+C2=0上任一点,则点P0到直线Ax+By+C1=0的距离为d= .
例3求平行线2x-7y+8=0和2x-7y-6=0的距离.
解:在直线2x-7y-6=0上任取一点,例如取P(3,0),则点P(3,0)到直线2x-7y+8=0的距离就是两平行线间的距离.因此,
d= .
点评:把求两平行线间的距离转化为点到直线的距离.
变式训 练
求两平行线l1:2x+3y-8=0,l 2:2x+3y-10=0的距离.答案: .
作业
P110 9.10.
板
书
3.3.3点到直线的距离&
3.3.4两条平行直线间的距离
两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离d= .
点P(x0,y0)到直线l:Ax+By+C=0的距离d=
教学
反思
相应的||PO|-|PM||的最大值为|MO′|= .
课堂小结
通过本节学习,要求大家:
1.掌握点到直线的距离公式,并会求两条平行线间的距离.
2.构思距离公式的推导方案,培养学生观察、分析、转化、探索问题的能力,鼓励创新.培养学生勇于探索、善于研究的精神,学会合作.
高中数学第三章直线与方程3.3点到直线的距离3.4两条平行直线间的距离课件新人教A版必修

已知实数x,y满足关系式x+y+1=0,求S= x2 y2 2x 2y 2 的最小值. 思路点拨 S= x2 y2 2x 2 y 2 = (x 1)2 ( y 1)2 ,它表示点(x,y)与点(1,1)间的距离,可用点 到直线的距离公式求最小值,也可以用x表示y,将求S的最小值转化为求二次函数 的最小值. 解析 解法一:因为S= x2 y2 2x 2 y 2 = (x 1)2 ( y 1)2 , 所以它可以看作一个动点M(x,y)与一个定点N(1,1)间的距离,即点N(1,1)与直线l:x +y+1=0上任意一点M(x,y)的距离. 所以|MN|的最小值为点N到直线l的距离,
3.3.3 点到直线的距离 3.3.4 两条平行直线间的距离
定义 公式
距离公式
点到直线的距离
两条平行直线间的距离
点到直线的垂线段的长度
夹在两条平行直线间公垂线段 的长
点P0(x0,y0)到直线l:Ax+By+C=0
| Ax0 By0 C |
的距离d=①
A2 B2
(A2+B2≠0)
两条平行直线l1:Ax+By+C1=0与l 2:Ax+By+C2=0(A2+B2≠0,C1≠C2)
间的距离d=②
| C1 C2 | A2 B2
判断正误,正确的画“√”,错误的画“✕”.
1.在利用点到直线的距离公式求距离时,直线方程必须是一般式方程. ( √ ) 2.在求两条平行直线间的距离时,可以在其中一条直线上任取一点,转化为求点到 直线的距离. ( √ ) 3.使用两条平行直线间的距离公式求距离时,两直线方程中x、y的系数必须对应 相等. ( √ )
高中数学《第三章直线与方程3.3直线的交点坐标与距离公式3.3.4两条平行直线间的距离》283PPT课件

A
l
A’
4、直线关于直线的对称直线问题
直线关于直线对称的情形:
相交对称
l1
平行对称
l1
l
l
l2
l2
例:直线2x y 0关于y轴对称的直线方程为______ 直线3x 4 y 5 0关于x轴对称的直线方程为______
例 : 求直线l1 : x y 2 0关于直线 l : 3x y 3 0对称的直线l2的方程.
注: 在使用该公式前,须将 直线方程化为一般式.
❖ A=0或B=0,此公式也成立, 但当A=0或B=0时一般不用此 公式计算距离.
(如:点A(-1,3)到直线x=6的 距离是____7____.)
y
P(x0,y0)
x d Ax0 By0 C
O
A2 B2
l:Ax+By+C=0
1.此公式的作用是求点到直线的距离;
直线方程为:x y 1 0
3、点关于直线的对称点问题
明确点A关于直线l对称的点A’之间的关
系。
① kl • kAA' 1
②A和A’的中点在直 线l上.
A
l
A’
求点A(2,2)关于直线2x 4 y 9 0的 对称点A'的坐标.
解法:设所求的点是A’ (a,b),利用A与A’两点连 线与原直线垂直关系,得 出两点所在直线的斜率关 系(1),又利用中点坐标 公式求出中点,代入原方 程得关系(2),解方程组 求出a和b即可.
3.3.3 点到直线的距离 3.3.4 两条平行直线间的距离
求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。
P(x0,y0)y P
高中数学《第三章直线与方程3.3直线的交点坐标与距离公式3.3.4两条平行线间的距离》975PPT课件

即:x y 4 0 .
y
点C1,0 到x y 4 0的距离
1 0 4
h
5
.
12 12
2
AB 3 12 1 32 2 2 .
1
5
因此, SABC
2 2
2
5. 2
4A
3
2h
1
C
-1 O 1 2
B
3x
过程设计
例▪3
⑴已知点 A2,3 到直线 y ax 1
的距离为1,求 a 的值;
▪
▪ ⑵ 已知点 A2,3 到直线 y x a
《点到直线的距离》
复习引入
两点间的距离公式是什么?
已知点 P1x1, y1,P2 x2, y2 ,则
P1P2 x2 x1 2 y2 y12 .
y
P2
N2
M2
O
Q
M1 x N1 P1
点到直线距离公式
1 特殊情况
y
|x0|
y0
P0 (x0,y0)
|y0|
O
x0
x
点到直线距离公式
y
|y1-y0|
课堂练习:3.求与直线 l:5x-12y+6=0 平行且与直线 l 距离 为 3 的直线方程.
解 ∵与l平行的直线方程为5x-12y+b=0,
根据两平行直线间距离公式得 | b 6 | =3, 52 (12)2
解之得c=45或c=-33, 所以所求直线方程为:5x-12y+45=0或5x-12y -33=0.
Q·R·
O P·2,0 x
过程设计
问题1 如何求点P(2,0) 到直线 x y 0 的距离?
方法③ 利用三角函数
PQ OP sin 45o
广东省佛山市高中数学 第三章 直线与方程 3.33.4 点到直线的距离和平行线间的距离学案(无答案)

3.3-3.4 点到直线的距离和平行线间的距离【学习目标】1.掌握点到直线的距离公式及其结构特征;2.理解两平行线间的距离的概念,掌握两平行线间距离的计算方法;3.进一步体会“数形结合”与“化归”的数学思想方法. 【重点难点】重点:两到直线的距离公式和平行线间的距离公式. 难点:点到直线距离公式的应用. 【学法指导】阅读教材,认真理解两点间距离公式 【学习过程】 一.课前预习阅读教材106~107P P 的内容,通过自学你能明白以下问题吗? 1.点11(,)A x y 到x 轴的距离是d = . 2.点11(,)A x y 到y 轴的距离是d = . 3.点(2,0)A 到直线y x =的距离是d = . 4.点(,)06A -到直线y x =-的距离是d = .5.对于直线l :0Ax By C ++=,如何求点00(,)P x y 到l 的距离? 二.课堂学习与研讨1.师生探究·合作交流新知1:点00(,)P x y 到直线0Ax By C ++=的距离:d = . 仔细体会下面的证明思路:(1)如图,0RP 平行于x 轴,0SP 平行于y 轴,由00(,)P x y 的坐标如何得出R ,S 的坐标? (2)在0Rt RP S ∆中,求出斜边RS 的长;(3)由面积相等,得等式000||||||||RP SP RS P Q ⋅=⋅, 从而得出点到直线的距离公式.注意:运用点到直线的距离公式,必须把直线方程化为 . 特殊情况:00(,)P x y 到直线x a =的距离d = ;00(,)P x y 到直线y b =的距离d = .新知2:两平行直线10Ax by C ++=与20Ax by C ++=的距离d = . 注意:求两平行直线距离,必须将直线方程化为 , 且x 、y 的系数 .2.例题选讲例1.求过点(1,2)P -练习1.求过点(1,2)M ,且与点(2,3)A ,(4,5)B -的距离相等的直线l 的方程.例2.若直线1l 与直线2l 34200x y --=平行且距离为3,求直线1l 的方程.练习2.已知平行线2330x y +-=与2390x y +-=,求与它们等距离的平行线的方程.例3.在直线30x y +=上找一点,使它到原点和直线320x y +-=的距离相等.练习3.求直线211160x y ++=关于点(0,1)P 对称的直线方程.3.归纳与小结(1)点00(,)P x y 到直线l :0Ax By C ++=(A , B 不同时为0)的距离:d =.使用该公式时应该注意:①公式中的直线方程必须化为一般式;②若点00(,)P x y 在直线l 上,则P 到直线l 的距离为0,此时公式仍适用; ③特别地,点00(,)P x y 到x 轴的距离为0||y ,到y 轴的距离为0||x .2.两条平行直线1l :10Ax By C ++=,2l :20Ax By C ++=(12C C ≠)之间的距离:d =两条平行直线1l 与2l 的形式必须是一般式,同时x 和y 前面的系数必须分别化为一致. 三.达标检测A 基础巩固1.教材138P :练习1,2,32.点P 在x 轴上,若它到直线4330x y --=的距离等于1,则P 的坐标是 ( ) A.(2,0)-或1(,0)2- B.(2,0)或1(,0)2C.(2,0)-或1(,0)2D.(2,0)或1(,0)2-3.动点P 在直线240x y +-=上,O 为原点,则OP 的最小值为 ( )A.5B.5C.5D.5B 提升练习4.直线l 过点(5,10)P ,且与原点的距离等于5,则直线l 的方程为 .5.1l :2340x y ++=,2l :4650x y +-=之间的距离为 . 四.拓展延伸与巩固1.已知点(3,4),(6,3)A B --到直线:10l ax y ++=的距离相等,求a 的值。
高中数学 第三章 直线与方程 3.3.33.3.4 点到直线的距

探究二
探究三
思维辨析 当堂检测
(2)解法一:把直线方程化为一般式为 x-2=0. 由点到直线的距离公式,得 d=|-1+0×2-2|=3.
12+02
解法二:∵直线 x=2 与 y 轴平行, ∴由图知 d=|-1-2|=3.
探究一
探究二
探究三
思维辨析 当堂检测
ቤተ መጻሕፍቲ ባይዱ
(3)解法一:由点到直线的距离公式,得 d=|-1×0+2-1|=1.
答案:-1+ 2
探究一
探究二
探究三
思维辨析 当堂检测
两平行线间的距离 【例2】求与直线l:5x-12y+6=0平行,且与直线l距离为3的直线方 程. 思路分析:设出所求直线的方程,用待定系数法求解.
解:设所求直线方程为 5x-12y+c=0, 则由题意,得 |������-6| =3,解得 c=-33 或 c=45.
2的直线方程
2
为
.
解析:显然直线x=-1到原点的距离为1,所以所求直线的斜率是存
在的.
设所求直线的方程为y-2=k(x+1),化成一般式为kx-y+2+k=0.
由题意,得
|2+������| =
������2+1
22,解得 k=-1 或-7.
故适合题意的直线方程为y-2=-(x+1)或y-2=-7(x+1),即x+y-1=0
即 d=|0+2×0-1| =
12+22
55,
所以 x2+y2 的最小值是
5 5
2
= 15.
答案:15
探究一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3-3.4 点到直线的距离和平行线间的距离
【学习目标】
1.掌握点到直线的距离公式及其结构特征;
2.理解两平行线间的距离的概念,掌握两平行线间距离的计算方法;
3.进一步体会“数形结合”与“化归”的数学思想方法. 【重点难点】
重点:两到直线的距离公式和平行线间的距离公式. 难点:点到直线距离公式的应用. 【学法指导】
阅读教材,认真理解两点间距离公式 【学习过程】 一.课前预习
阅读教材106~107P P 的内容,通过自学你能明白以下问题吗? 1.点11(,)A x y 到x 轴的距离是d = . 2.点11(,)A x y 到y 轴的距离是d = . 3.点(2,0)A 到直线y x =的距离是d = . 4.点(,)06A -到直线y x =-的距离是d = .
5.对于直线l :0Ax By C ++=,如何求点00(,)P x y 到l 的距离? 二.课堂学习与研讨
1.师生探究·合作交流
新知1:点00(,)P x y 到直线0Ax By C ++=的距离:d = . 仔细体会下面的证明思路:
(1)如图,0RP 平行于x 轴,0SP 平行于y 轴,由00(,)P x y 的坐标如何得出R ,S 的坐标? (2)在0Rt RP S ∆中,求出斜边RS 的长;
(3)由面积相等,得等式000||||||||RP SP RS P Q ⋅=⋅, 从而得出点到直线的距离公式.
注意:运用点到直线的距离公式,必须把直线方程化为 . 特殊情况:00(,)P x y 到直线x a =的距离d = ;
00(,)P x y 到直线y b =的距离d = .
新知2:两平行直线10Ax by C ++=与20Ax by C ++=的距离d = . 注意:求两平行直线距离,必须将直线方程化为 , 且x 、y 的系数 .
2.例题选讲
例1.求过点(1,2)P -
练习1.求过点(1,2)M ,且与点(2,3)A ,(4,5)B -的距离相等的直线l 的方程.
例2.若直线1l 与直线2l 34200x y --=平行且距离为3,求直线1l 的方程.
练习2.已知平行线2330x y +-=与2390x y +-=,求与它们等距离的平行线的方程.
例3.在直线30x y +=上找一点,使它到原点和直线320x y +-=的距离相等.
练习3.求直线211160x y ++=关于点(0,1)P 对称的直线方程.
3.归纳与小结
(1)点00(,)P x y 到直线l :0Ax By C ++=(A , B 不同时为0)的距离:
d =
.
使用该公式时应该注意:
①公式中的直线方程必须化为一般式;
②若点00(,)P x y 在直线l 上,则P 到直线l 的距离为0,此时公式仍适用; ③特别地,点00(,)P x y 到x 轴的距离为0||y ,到y 轴的距离为0||x .
2.两条平行直线1l :10Ax By C ++=,2l :20Ax By C ++=(12C C ≠)之间的距离:
d =
两条平行直线1l 与2l 的形式必须是一般式,同时x 和y 前面的系数必须分别化为一致. 三.达标检测
A 基础巩固
1.教材138P :练习1,2,3
2.点P 在x 轴上,若它到直线4330x y --=的距离等于1,则P 的坐标是 ( ) A.(2,0)-或1(,0)2- B.(2,0)或1(,0)2
C.(2,0)-或1(,0)2
D.(2,0)或1(,0)2
-
3.动点P 在直线240x y +-=上,O 为原点,则OP 的最小值为 ( )
A.
5
B.5
C.5
D.5
B 提升练习
4.直线l 过点(5,10)P ,且与原点的距离等于5,则直线l 的方程为 .
5.1l :2340x y ++=,2l :4650x y +-=之间的距离为 . 四.拓展延伸与巩固
1.已知点(3,4),(6,3)A B --到直线:10l ax y ++=的距离相等,求a 的值。
2.两平行直线1l ,2l 分别过(1,0)A ,(0,5)B .(1)1l ,2l 之间的距离为5,求两直线方程; (2)若1l ,2l 之间的距离为d ,求d 的取值范围.
【学习后记】请同学们把对本课内容的学习心得体会写下来。
