八年级下册数学平面直角坐标系
精品试题冀教版八年级数学下册第十九章平面直角坐标系专题训练练习题(精选含解析)

八年级数学下册第十九章平面直角坐标系专题训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、将含有30角的直角三角板OAB 按如图所示的方式放置在平面直角坐标系中,OB 在x 轴上,若4OA =,将三角板绕原点O 逆时针旋转,每秒旋转60︒,则第2022秒时,点A 的对应点'A 的坐标为( )A .(0,4)B .(2)-C .2)D .(0,4)-2、如图,在AOB 中,4OA =,6OB =,AB =AOB 绕原点O 逆时针旋转90°,则旋转后点A 的对应点A '的坐标是( )A .()4,2-B .()-C .()-D .(- 3、在平面直角坐标系xOy 中,若ABC 在第三象限,则ABC 关于x 轴对称的图形所在的位置是( )A .第一象限B .第二象限C .第三象限D .第四象限4、在平面直角坐标系中,若点()2,3A -与点B 关于x 轴对称,则点B 的坐标是( )A .()2,3-B .()2,3C .()2,3--D .()2,3-5、如图是北京地铁部分线路图.若崇文门站的坐标为(4,)1-,北海北站的坐标为(2,4)-,则复兴门站的坐标为( )A .(1,7)--B .()7,1-C .(7,1)--D .(1,7)6、如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将三角形ABC 绕点P 旋转90°,得到△A ′B ′C ′,则点P 的坐标为( )A .(0,4)B .(1,1)C .(1,2)D .(2,1) 7、下列命题中为真命题的是( )A .三角形的一个外角等于两内角的和BC 2π,227都是无理数D .已知点E (1,a )与点F (b ,2)关于x 轴对称,则a +b =﹣18、在平面直角坐标系中,点P (-2,3)在( )A .第一象限B .第二象限C .第三象限D .第四象限9、如图,树叶盖住的点的坐标可能是( )A .()2,3B .()2,3-C .()3,4--D .()2,4-10、在平面直角坐标系中,将点A (﹣3,﹣2)向右平移5个单位长度得到的点坐标为( )A .(2,2)B .(﹣2,2)C .(﹣2,﹣2)D .(2,﹣2)第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图所示,是由北京国际数学家大会的会徽演化而成的图案,其主体部分是由一连串的等腰直角三角形依次连接而成,其中∠MA 1A 2=∠MA 2A 3…=∠MAnAn +1=90°,(n 为正整数),若M 点的坐标是(-1,2),A 1的坐标是(0,2),则A 22的坐标为___.2、在平面直角坐标系中,点M 的坐标是(12,)5-,则点M 到x 轴的距离是_______.3、点()3,4P -关于y 轴的对称点的坐标是______.4、一般地,在平面直角坐标系中,将点(x ,y )向右平移a 个单位长度,可以得到对应点_________;将点(x ,y )向左平移a 个单位长度,可以得到对应点_________;将点(x ,y )向上平移b 个单位长度,可以得到对应点_________;将点(x ,y )向下平移b 个单位长度,可以得到对应点_________.5、请将命题“坐标轴上的点至少有一个坐标为0”改写成“如果⋯那么⋯”的形式__.三、解答题(5小题,每小题10分,共计50分)1、在平面直角坐标系中,已知点A (﹣3,1),B (﹣2,0),C (0,1),请在图中画出△ABC ,并画出与△ABC 关于y 轴对称的图形.2、如图,在平面直角坐标系中,点(2,3)A --,点A 关于x 轴的对称点记作点B ,将点B 向右平移2个单位得点C .(1)分别写出点B C 、的坐标:B (____)、C (____);(2)点D 在x 轴的正半轴上,点E 在直线1y =上,如果CDE △是以CD 为腰的等腰直角三角形,那么点E 的坐标是_____.3、在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在正方形网格的格点(网格线的交点)上.(1)请在如图所示的网格平面内作出平面直角坐标系,使点A 坐标为(1,3),点B 坐标为(2,1);(2)请作出△ABC 关于y 轴对称的△A 'B 'C ',并写出点C '的坐标;(3)△ABC 是 三角形,理论依据 .4、如图,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(﹣2,4),B(﹣4,2),C(﹣3,1),按下列要求作图.(1)画出△ABC关于x轴对称的图形△A1B1C1(点A、B、C分别对应A1、B1、C1);(2)△A1B1C1的面积=;(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A1B1C1内部的对应点M1的坐标;(4)请在y轴上找出一点P,满足线段AP+B1P的值最小,并写出P点坐标.5、如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).(1)在图中画出△ABC关于y轴对称的图形△A′B′C′;并写出点B′的坐标.(2)在图中x轴上作出一点P,使PA+PB的值最小.-参考答案-一、单选题1、C【解析】【分析】求出第1秒时,点A的对应点'A的坐标为(0,4),由三角板每秒旋转60︒,得到此后点'A的位置6秒一循环,根据2022除以6的结果得到答案.【详解】解:过点A作AC⊥OB于C,∵4OA=,∠AOB=30,∴122AC OA==,∴OC∴A2).∵4OA=,∠AOB=30,将三角板绕原点O逆时针旋转,每秒旋转60︒,∴第1秒时,点A的对应点'A的坐标为2),∵三角板每秒旋转60︒,∴此后点'A的位置6秒一循环,∵20223376=⨯,∴则第2022秒时,点A 的对应点'A 的坐标为2),故选:C【点睛】此题考查了坐标与图形的变化中的旋转以及规律型中点的坐标,根据每秒旋转的角度,找到点'A 的位置6秒一循环是解题的关键.2、C【解析】【分析】过点A 作AC ⊥x 轴于点C ,设OC a = ,则6BC a =- ,根据勾股定理,可得2222AB BC OA OC -=-,从而得到2OC = ,进而得到∴AC =,可得到点(2,A ,再根据旋转的性质,即可求解.【详解】解:如图,过点A 作AC ⊥x 轴于点C ,设OC a = ,则6BC a =- ,∵222AC OA OC =- ,222AC AB BC =-,∴2222AB BC OA OC -=-,∵4OA =, AB =∴(()222264a a --=- , 解得:2a = ,∴2OC = ,∴AC ,∴点(2,A ,∴将AOB 绕原点O 顺时针旋转90°,则旋转后点A 的对应点A ''的坐标是()2-,∴将AOB 绕原点O 逆时针旋转90°,则旋转后点A 的对应点A '的坐标是()-.故选:C【点睛】本题考查坐标与图形变化一旋转,解直角三角形等知识,解题的关键是求出点A 的坐标,属于中考常考题型.3、B【解析】【分析】设ABC 内任一点A (a ,b )在第三象限内,可得a <0,b <0,关于x 轴对称后的点B (-a ,b ),则﹣a >0,b <0,然后判定象限即可.【详解】解:∵设ABC 内任一点A (a ,b )在第三象限内,∴a <0,b <0,∵点A 关于x 轴对称后的点B (a ,-b ),∴﹣b >0,∴点B (a ,-b )所在的象限是第二象限,即ABC 在第二象限.故选:B .【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.4、B【解析】【分析】根据若两点关于x 轴对称,则横坐标不变,纵坐标互为相反数,即可求解.【详解】解:∵点()2,3A -与点B 关于x 轴对称,∴点B 的坐标是()2,3.故选:B【点睛】本题主要考查了平面直角坐标系内点关于坐标轴对称的特征,熟练掌握若两点关于x 轴对称,则横坐标不变,纵坐标互为相反数;若两点关于y 轴对称,则横坐标互为相反数,纵坐标不变是解题的关键.5、B【解析】【分析】根据已知点坐标确定直角坐标系,即可得到答案.【详解】由题意可建立如图所示平面直角坐标系,则复兴门站的坐标为()7,1 .故选:B .【点睛】此题考查了平面直角坐标系中点坐标特点,由点坐标确定直角坐标系,由坐标系得到点坐标,属于基础题型.6、C【解析】【分析】选两组对应点,连接后作其中垂线,两中垂线的交点即为点P .【详解】解:选两组对应点,连接后作其中垂线,两中垂线的交点即为点P ,由图知,旋转中心P 的坐标为(1,2)故选:C.【点睛】本题主要考查坐标与图形的变化﹣旋转,解题的关键是掌握旋转变换的性质.7、D【解析】【分析】利用三角形的外角的性质、最简二次根式的定义、无理数的定义及关于坐标轴对称的点的特点分别判断后即可确定正确的选项.【详解】解:A、三角形的外角等于不相邻的两个内角的和,故原命题错误,是假命题,不符合题意;BC、227是有理数,故原命题错误,是假命题,不符合题意;D、已知点E(1,a)与点F(b,2)关于x轴对称,a=1,b=-2,则a+b=﹣1,正确,为真命题,符合题意.故选:D.【点睛】考查了命题与定理的知识,解题的关键是了解三角形的外角的性质、最简二次根式的定义、无理数的定义及关于坐标轴对称的点的特点,难度不大.8、B【解析】【分析】根据点横纵坐标的正负分析得到答案.【详解】解:点P (-2,3)在第二象限,故选:B .【点睛】此题考查了平面直角坐标系中各象限内点的坐标特点,熟记各象限内横纵坐标的正负是解题的关键.9、B【解析】【分析】根据平面直角坐标系的象限内点的特点判断即可.【详解】∵树叶盖住的点在第二象限,∴()2,3-符合条件.故选:B .【点睛】本题主要考查了平面直角坐标系象限内点的特征,准确分析判断是解题的关键.10、D【解析】【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减解答即可得答案.【详解】∵将点A(﹣3,﹣2)向右平移5个单位长度,∴平移后的点的横坐标为-3+5=2,∴平移后的点的坐标为(2,-2),故选:D.【点睛】此题主要考查了坐标与图形的变化,熟练掌握横坐标,右移加,左移减;纵坐标,上移加,下移减的变化规律是解题关键.二、填空题1、(10-+)--,102221【解析】【分析】探究规律,利用规律解决问题即可.【详解】解:观察图象可知,点的位置是8个点一个循环,∵22÷8=26,∴A22与A6的位置在第三象限,且在经过点A2、M的直线上,∵第一个等腰直角三角形的直角边长为1,∴点A2(0,3),设直线A2M的解析式为y=kx+3,把M点的坐标(-1,2)代入得:-k+3=2,解得:k=1,∴直线A 2M 的解析式为y =x +3,即A 22点在直线y =x +3上,…,第n )n -1,∴第22)21,可得A 22M =21,∴A21 A 1212010112=+=+1,∴A 22 的横坐标为:1021--,A 22 的纵坐标为:101021322y =--+=-+,∴A 22(1021--,1022-+),故答案为:(1021--,1022-+).【点睛】本题考查了勾股定理,坐标与图形的性质,等腰直角三角形的性质等知识,解题的关键是学会探究规律,利用规律解决问题,属于中考常考题型.2、5【解析】【分析】根据到x 轴的距离等于纵坐标的绝对值解答即可.【详解】解:∵点M 的坐标是(12,)5-,∴点M 到x 轴的距离是55-=,故答案为:5.【点睛】此题考查了点的坐标,关键是掌握点到x 轴的距离等于纵坐标的绝对值,到y 轴的距离等于横坐标的绝对值.3、(3,4)【解析】【分析】根据关于y 轴对称的点的坐标特征:横坐标互为相反数,纵坐标不变,即可求得.【详解】点()3,4P -关于y 轴的对称点的坐标是()3,4故答案为:()3,4【点睛】本题考查了平面直角坐标系中关于y 轴对称的点的坐标特征,掌握此特征是关键.4、 (x +a ,y ) (x -a ,y ) (x ,y +b ) (x ,y -b )【解析】略5、如果一个点在坐标轴上,那么这个点至少有一个坐标为0【解析】【分析】命题是由题设与结论两部分组成,如果后面的是题设,那么后面的是结论,根据定义直接改写即可.【详解】解:将命题“坐标轴上的点至少有一个坐标为0”改写成“如果⋯那么⋯”的形式:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.故答案为:如果一个点在坐标轴上,那么这个点至少有一个坐标为0.【点睛】本题考查的命题的组成,把一个命题改写成“如果⋯那么⋯”的形式,平面直角坐标系坐标轴上点的坐标特点,掌握“命题是由题设与结论两部分组成”是解本题的关键.三、解答题1、见解析【解析】【分析】先在平面直角坐标系中,分别描出点A (﹣3,1),B (﹣2,0),C (0,1),再顺次连接,可得△ABC ,然后求出点A (﹣3,1),B (﹣2,0),C (0,1)关于y 轴对称的点分别为(3,1),(2,0),(0,1),再顺次连接,可得与△ABC 关于y 轴对称的图形,即可求解.【详解】解:画出图形如下图所示:根据题意得:点A (﹣3,1),B (﹣2,0),C (0,1)关于y 轴对称的点分别为(3,1),(2,0),(0,1) .【点睛】本题主要考查了在平面直角坐标系中描点,画轴对称图形,熟练掌握若两点关于y 轴对称,则横坐标互为相反数,纵坐标不变是解题的关键.2、 (1)()2,3-;()0,3(2)(4,1)【解析】【分析】(1)根据点的平移、对称规律求解即可;(2)作EF x ⊥轴于F ,得到COD DFE ≌,求出3,1====DF OC EF OD 进而得到(4,1)E .(1)解:将点(2,3)A --关于x 轴的对称点B 的坐标为(2,3)-,将点B 向右平移2个单位得点C ,(0,3)C ∴,故答案为:(2,3)B -,(0,3)C ;(2)作EF x ⊥轴于F ,如下图所示:由题意可知,COD DFE ≌,3,1DF OC EF OD ∴====,E ∴点的坐标为(4,1),故答案为(4,1).【点睛】此题主要考查了关于x轴对称点的性质以及平移的性质,正确掌握点的坐标特点是解题关键.3、(1)见解析;(2)图见解析,C'的坐标为(﹣5,5);(3)直角;如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角.【解析】【分析】(1)根据点A及点C的坐标,易得y轴在A的左边一个单位,x轴在A的下方3个单位,建立直角坐标系即可;(2)根据关于y轴对称的点的坐标,可得各点的对称点,顺次连接即可;(3)根据勾股定理的逆定理判断即可;【详解】解:(1)如图所示:(2)如图所示:△A'B'C'即为所求:C'的坐标为(﹣5,5);(3)直角三角形,∵AB2=1+4=5,AC2=4+16=20,BC2=9+16=25,∴AB2+AC2=BC2,∴△ABC是直角三角形.依据:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角.【点睛】本题考查了轴对称作图的知识及直角坐标系的建立,解答本题的关键是掌握轴对称的性质,准确作图.4、 (1)见解析(2)2(3)(x,-y)(4)点P见解析,(0,2)【解析】【分析】(1)直接利用关于x轴对称点的性质得出对应点位置,进而得出答案;(2)利用割补法进行计算,即可得到△A1B1C1的面积;(3)根据点M和M1关于x轴对称可得结果;(4)直接利用轴对称求最短路线的方法得出答案.【小题1】解:如图所示:△A1B1C1点即为所求;【小题2】△A1B1C1的面积=111⨯-⨯⨯-⨯⨯-⨯⨯=2;23112213222【小题3】由题意可得:M1的坐标为(x,-y);【小题4】如图所示:点P即为所求,点P的坐标为(0,2).【点睛】此题主要考查了轴对称变换,正确得出对应点位置是解题关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.5、(1)作图见解析,点B′的坐标为(-4,1);(2)见解析【解析】【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;(2)作出点A关于x轴的对称点A″,再连接A″B,与x轴的交点即为所求.【详解】解:(1)如图所示,△A′B′C′即为所求.点B′的坐标为(-4,1);(2)如图所示,点P即为所求.【点睛】本题主要考查了作图-轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.注意:关于y轴对称的点,纵坐标相同,横坐标互为相反数.。
冀教版八年级下册数学教学课件 第19章 平面直角坐标系19.2 平面直角坐标系(第2课时)

4.如图所示,点A(-2,1)到y轴的距离为
(C)
A.-2 B.1 C.2 D. 5
解析:根据点到x轴的距离等于纵坐标的绝对值,到y
轴的距离等于横坐标的绝对值即可得出答案.由点A
的坐标为(-2,1),可得点A到y轴的距离为2.故选C.
5.如图所示,下列各点在阴影区域内的是 ( A )
A.(3,2)
(3)关于x轴的对称点分别是点A和点D,点 B和点C,点E和点L,点F和点K,点G和点J, 点H和点I.关于y轴的对称点分别是点A 和点J,点B和点I,点C和点H,点D和点G,点 E和点F,点L和点K.关于原点的对称点分 别是点A和点G,点B和点H,点C和点I,点D 和点J,点E和点K,点F和点L.
谢 谢 大 家 听课时有问题,应先举手,经教师同意后,起立提问。
上课期间离开教室须经老师允许后方可离开。 上课必须按座位表就坐。 要爱护公共财物,不得在课桌、门窗、墙壁上涂写、刻划。 要注意保持教室环境卫生。 离开教室要整理好桌椅,并协助老师关好门窗、关闭电源。
解析:∵点P(m+3,m-1)在x轴上,∴m-1=0,解得m=1,∴m+3=1+3=4,∴ 点P的坐标为(4,0).故选C.
8.(1)在坐标平面内画出点P(2,3). (2)分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标. 解析:(1)根据平面直角坐标系的定义作出图形即可;(2)根
探究2 关于x轴,y轴和原点对称的点的特征
在上图中分别找出A,B两点关于x轴,y轴和原点对称的点,写 出它们的坐标,填写下表.
请同学们建立平面直角坐标系并描出点P(-3,4),再按照下列要求 画出它的对称点,然后回答提出的问题. (1)画出点P关于x轴的对称点P1; (2)画出点P关于y轴的对称点P2; (3)画出点P关于坐标原点的对称点P3. 观察上述各对对称点的坐标特点,你有什么发现?
初中数学八年级下册第3章图形与坐标3.1平面直角坐标系教学

我思 我进步
通过本节课,你有什么收获? 你还存在哪些疑问,和同伴交流.
练习
3.如图是某动物园的部分平面示意图,试建立适当的 平面直角坐标系, 用坐标表示大门、百鸟园、大象馆、 狮子馆和猴山的位置.
解:如图,以大门所在点为原点O,在网格中以过点O
的水平直线和垂直直线分别作为x 轴,y 轴建立平面直
角坐标系.
y
由图可知大门、百鸟园、大象
馆、狮子馆和猴山的位置为:
大门(0,0),百鸟园(5,
2 O1 学校
-5-4-3-2-1 1 2 3 4 5 x -1
B电影院-2 -3
有时还可借助方向和距离(或称方 位) 来刻画两物体的相对位置.
-4 -5 C汽车站
思考
(1)如图,李亮家距学校1000 m,如何用方向和距离来
描述李亮家相对于学校的位置?(2)反过来,学校相对
于李亮家的位置怎样描述呢?
如图,以学校所在位置为原点,分别以正东、正北方向为x
轴, y 轴的正方向,建立平面直角坐标系, 规定1 个单位长
度代表100 m长. 根据题目条件,点A(5,4.5) 是书
北
y 5
A书店
4
店的位置,点B(-2.5,-3)是电影
3
院的位置, 点C(4,-6) 是汽车站 的位置. 在日常生活中, 除了用平面直角 坐标系刻画物体之间的位置关系外,
分析:如图,设H 岛所在的位置 为C,△ABC 是直角三角形, ∠CAB = 90°,利用勾股定理可 以求出BC间的距离.
解:在Rt△ABC 中, ∵ AC = 30海里, AB = 40海里,∠CAB = 90°,
BC AC2 AB2 302 402 50海里.
由于在点B处测得H岛在北偏西 53°6′的方向上, 则∠BCA = 53°6′. 故此时,渔政船在H岛南偏东53°6′ 的方向, 距H岛50海里的位置.
(完整版)八年级数学《平面直角坐标系》经典例题

考点1:考点的坐标与象限的关系知识解析:各个象限的点的坐标符号特征如下:(特别值得注意的是,坐标轴上的点不属于任何象限.)1、在面直角坐标中,点M (-2,3)在( )A .第一象限B .第二象限C .第三象限D .第四象限 2、在平面直角坐标系中,点P (-2,2x +1)所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 3、若点P (a ,a -2)在第四象限,则a 的取值范围是( ).A .-2<a <0B .0<a <2C .a >2D .a <0 4、点P (m ,1)在第二象限内,则点Q (-m ,0)在( )A .x 轴正半轴上B .x 轴负半轴上C .y 轴正半轴上D .y 轴负半轴上 5、若点P (a ,b )在第四象限,则点M (b -a ,a -b )在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限 6、在平面直角坐标系中,点(12)A x x --,在第四象限,则实数x 的取值范围是 . 7、对任意实数x ,点2(2)P x x x -,一定不在..( ) A .第一象限B .第二象限C .第三象限D .第四象限8、如果a -b <0,且ab <0,那么点(a ,b)在( )A 、第一象限B 、第二象限C 、第三象限,D 、第四象限.考点2:点在坐标轴上的特点x 轴上的点纵坐标为0, y 轴上的点横坐标为0.坐标原点(0,0)1、点P (m+3,m+1)在x 轴上,则P 点坐标为( )A .(0,-2)B .(2,0)C .(4,0)D .(0,-4) 2、已知点P (m ,2m -1)在y 轴上,则P 点的坐标是 。
考点3:考对称点的坐标知识解析:1、关于x 轴对称: A (a ,b )关于x 轴对称的点的坐标为(a ,-b )。
2、关于y 轴对称: A (a ,b )关于y 轴对称的点的坐标为(-a , b )。
3、关于原点对称: A(a,b)关于原点对称的点的坐标为(-a,-b)。
〖人教版〗八年级数学下册期末复习试卷第十九章平面直角坐标系

〖人教版〗八年级数学下册期末复习试卷第十九章平面直角坐标系创作人:百里灵明创作日期:2021.04.01审核人:北堂正中创作单位:北京市智语学校一、选择题(本大题有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:(1)(2,1),(2,0),(3,0),(3,4);(2)(3,6),(0,4),(6,4),(3,6).你发现所得的图形是( C )A.两个三角形B.房子C.雨伞D.电灯2.在平面直角坐标系中,点P(-2,-3)所在的象限是( C )A.第一象限B.第二象限C.第三象限D.第四象限3.如图,在平面直角坐标系中,点A的坐标是( D )A.(-2,-3)B.(3,-2)C.(2,3)D.(-2,3)4.平面直角坐标系内的点A(-1,2)与点B(-1,-2)的位置关系是( B )A.关于y轴对称B.关于x轴对称C.关于原点对称D.无法确定5.在平面直角坐标系中,点P的坐标为(-2,a2+1),则点P所在的象限是( B )A.第一象限B.第二象限C.第三象限D.第四象限6.在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则△ABO的面积为( D )A.15 B.7.5 C.6 D.37.如图,在边长为1的正方形网格中,将△ABC向右平移2个单位长度得到△A′B′C′,则与点B′关于x轴对称的点的坐标是( D )A.(0,-1)B.(1,1)C.(2,-1)D.(1,-2)8.在坐标平面内,将点A(0,0)、B(2,4)、C(3,0)、D(5,4)、E(6,0)顺次连接起来,此图形是英文字母( D )A .VB .EC .WD .M9.若点P(a ,a-2)在第四象限,则a 的取值范围是( B )A.-2<a <0B.0<a <2C.a >2D.a <010.小明住在学校正东方向200米处,从小明家出发向北走150米就到了李华家.若选取李华家为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,则学校的坐标为( B )A .(-150,-200)B .(-200,-150)C .(0,-50)D .(-150,200)11.(·邢台县期中)如图,在5×4的方格纸中,每个小正方形的边长为1,点O ,A ,B 在方格纸的交点(格点)上,在第四象限内的格点上找点C ,使△ABC 的面积为3,则这样的点C 共有( B )A .2个B .3个C .4个D .5个第11题图第13题图12.若点A(a +2,b -1)在第二象限,则点B(-a ,b -1)在( A )A .第一象限B .第二象限C .第三象限D .第四象限13.如图,一艘轮船位于灯塔P 的北偏东60°方向,与灯塔P 的距离为30海里的A 处,轮船沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则此时轮船所在位置B 处与灯塔P 之间的距离为( D )A .60海里B .45海里C .203海里D .303海里14.在平面直角坐标系中,把△ABC 的各顶点的横坐标都除以14,纵坐标都乘13,得到△DEF ,把△DEF 与△ABC 相比,下列说法中正确的是( A )A .横向扩大为原来的4倍,纵向缩小为原来的13B .横向缩小为原来的14,纵向扩大为原来的3倍 C .△DEF 的面积为△ABC 面积的12倍D .△DEF 的面积为△ABC 面积的11215.在平面直角坐标系内的机器人接受指令“[α,A]”(α≥0,0°<A <180°)后的行动结果为:在原地顺时针旋转A 后,再向正前方沿直线行走α.若机器人的位置在原点,正前方为y 轴的负半轴,则它完成一次指令[4,30°]后位置的坐标为( B )A .(-2,23)B .(-2,-23)C .(-2,-2)D .(-2,2)16.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P 1,再将点P 1绕原点旋转90°得到点P 2,则点P 2的坐标是( D )A .(3,-3)B .(-3,3)C .(3,3)或(-3,-3)D .(3,-3)或(-3,3)二、填空题(本大题有3个小题,共10分.17~18小题各3分;19小题有2个空,每空2分.把答案写在题中横线上)17.(·定州市期中)若点P(m+3,m+1)在x轴上,则点P的坐标为________.18.同学们玩过五子棋吗?它的比赛规则是只要同色五子先成一条直线就算胜.如图是两人玩的一盘棋,若的位置是(1,-5),的位置是(2,-4),现轮到黑棋走,你认为黑棋放在________位置就获得胜利了.第18题图第19题图19.如图,将边长为2的等边三角形沿x轴正方向连续翻折次,依次得到点P1,P2,P3,…,P,则点P1的坐标是________,点P的坐标是________.三、解答题(本大题有7个小题,共68分.解答应写出文字说明、证明过程或演算步骤)20.(8分)在平面直角坐标系中,已知点P的坐标为(2a+6,a-3).(1)当点P的坐标为(4,-4)时,求a的值;(2)若点P在第四象限,求a的取值范围.21.(9分)如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.(1)图中“象”的位置可表示为____________;(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.22.(9分)如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:(1)图中距小明家距离相同的是哪些地方?(2)学校、商场和停车场分别在小明家的什么方位?(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?23.(9分)如图,四边形ABCD是边长为4的正方形,在正方形的一个角上剪去长方形C EFG,其中E,G分别是边CD,BC上的点,且CE=3,CG=2,剩余部分是六边形ABGFE D,请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标.24.(10分)△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.(1)分别写出下列各点的坐标:A′________;B′________;C′________;(2)说明△A′B′C′由△ABC经过怎样的平移得到;(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为________;(4)求△ABC的面积.25.(11分)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足a-4+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B →A →O 的线路移动.(1)a =________,b =________,点B 的坐标为________;(2)当点P 移动4秒时,请指出点P 的位置,并求出点P 的坐标;(3)在移动过程中,当点P 到x 轴的距离为5个单位长度时,求点P 移动的时间.26.(12分)已知△ABC 是等腰直角三角形,AB =2,把△ABC 沿直线BC 向右平移得到△DEF.如果E 是BC 的中点,AC 与DE 交于P 点,以直线BC 为x 轴,点E 为原点建立直角坐标系.(1)求△ABC 与△DEF 的顶点坐标;(2)判断△PEC 的形状;(3)求△PEC 的面积.答案17.(2,0) 18.(2,0)或(7,-5)19.(1,3) (4031,3) 解析:∵等边三角形的边长为2,∴P 1(1,3),而P 1P 2=P 2P 3=2,∴P 2(3,3),P 3(5,3),依此类推,P n (1+2n -2,3),即P n (2n -1,3).当n =时,P 的坐标是(4031,3).20.解:(1)∵点P 的坐标为(4,-4),∴⎩⎨⎧2a +6=4,a -3=-4,解得a =-1.(3分) (2)∵点P (2a +6,a -3)在第四象限,∴⎩⎨⎧2a +6>0,a -3<0,(5分)解得-3<a <3.(8分) 21.解:(1)(5,3)(3分)(2)“马”下一步可到达的位置有(1,1),(3,1),(4,2),(1,5),(3,5),(4,4);(6分)“象”下一步可到达的位置有(3,1),(7,1),(3,5),(7,5).(9分)22.解:(1)∵点C 为OP 的中点,∴OC =12OP =12×4=2(cm).(2分)∴OC =OA ,即距小明家距离相同的是学校和公园.(3分)(2)学校在小明家北偏东45°方向,商场在小明家北偏西30°方向,停车场在小明家南偏东60°方向.(6分)(3)图上1cm 表示400÷2=200(m),商场距离小明家2.5×200=500(m),停车场距离小明家4×200=800(m).(9分)23.解:分别以边AB ,AD 所在的直线为坐标轴,建立直角坐标系,如图所示.(3分) ∵点A 是原点,∴A (0,0).∵点B ,D 分别在x 轴、y 轴上,且AB =AD =4,∴B (4,0),D (0,4).(5分)∵点D ,E 的纵坐标相等,且DE =CD -CE =1,∴E (1,4).(6分)∵点B ,G 的横坐标相等,且BG =BC -CG =2,∴G (4,2).(7分)∵点F 与点E 的横坐标相等,与点G 的纵坐标相等,∴F (1,2).(8分)综上所述,六边形ABGFED 各顶点的坐标分别为A (0,0),B (4,0),G (4,2),F (1,2),E (1,4),D (0,4).(答案不唯一)(9分)24.解:(1)(-3,1) (-2,-2) (-1,-1)(3分)(2)△ABC 先向左平移4个单位,再向下平移2个单位得到△A ′B ′C ′.(5分)(3)(a -4,b -2)(7分)(4)S △ABC =2×3-12×2×2-12×1×3-12×1×1=2.(10分) 25.解:(1)4 6 (4,6)(3分)(2)∵点P 从原点出发,以每秒2个单位长度的速度沿着O →C →B →A →O 的线路移动,∴2×4=8.∵OA =4,OC =6,∴当点P 移动4秒时,在线段CB 上,离点C 的距离是8-6=2,(6分)∴点P 的坐标是(2,6).(7分)(3)由题意可得,在移动过程中,当点P 到x 轴的距离为5个单位长度时,存在两种情况:第一种情况,当点P 在OC 上时,点P 移动的时间是5÷2=2.5(秒);(9分)第二种情况,当点P 在BA 上时,点P 移动的时间是(6+4+1)÷2=5.5(秒).故在移动过程中,当点P 到x 轴的距离为5个单位长度时,点P 移动的时间是2.5秒或5.5秒.(11分)26.解:(1)连接AE ,CD .∵△ABC 是等腰直角三角形,E 是BC 的中点,∴AE ⊥BC ,∴AE 2+CE 2=2CE 2=AC 2,∴CE =22AC .(2分)又∵△DEF 是由△ABC 平移得到的,∴CE =AE =BE =CF =CD =22AC =22×2=1,EF =2CE =2.(4分)∴A (0,1),B (-1,0),C (1,0),D (1,1),E (0,0),F (2,0).(5分)(2)根据平移的性质,可知DE ∥AB ,∴∠PEC =∠B =45°,∠EPC =∠A =90°,∴△PEC 是等腰直角三角形.(9分)(3)S △PEC =12PC ·PE =12PC 2=12×12CE 2=14.(12分。
八年级数学平面直角坐标系知识点归纳
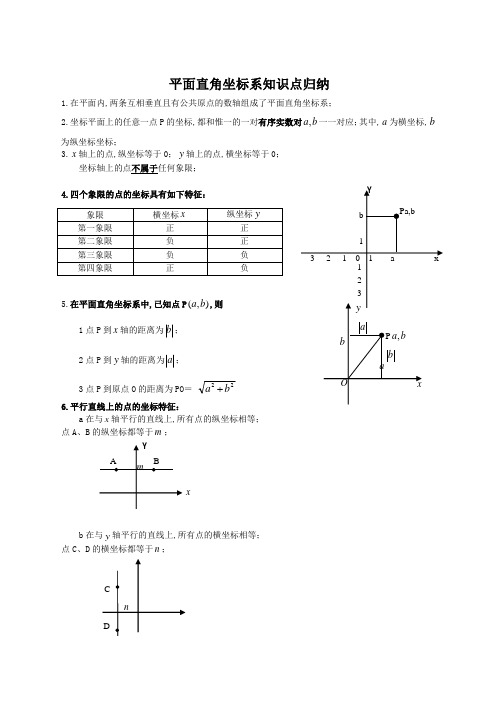
x
平面直角坐标系知识点归纳
1.在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系;
2.坐标平面上的任意一点P 的坐标,都和惟一的一对有序实数对b a ,一一对应;其中,a 为横坐标,b 为纵坐标坐标;
3.x 轴上的点,纵坐标等于0;y 轴上的点,横坐标等于0;
坐标轴上的点不属于任何象限;
4.四个象限的点的坐标具有如下特征:
5.在平面直角坐标系中,已知点P ),(b a ,则
1点P 到x 轴的距离为b ;
2点P 到y 轴的距离为a ;
3点P 到原点O 的距离为PO = 22b a 6.平行直线上的点的坐标特征:
a 在与x 轴平行的直线上,所有点的纵坐标相等; 点A 、B 的纵坐标都等于m ;
b 在与y 轴平行的直线上,所有点的横坐标相等; 点C 、D 的横坐标都等于n ;
7.对称点的坐标特征:
A 点P ),(n m 关于x 轴的对称点为),(1n m P -, 即横坐标不变,纵坐标互为相反数;
B 点P ),(n m 关于y 轴的对称点为),(2n m P -, 即纵坐标不变,横坐标互为相反数;
C 点P ),(n m 关于原点的对称点为),(3n m P --,即横、纵坐标都互为相反数;
8.两条坐标轴夹角平分线上的点的坐标的特征:
A 若点P n m ,在第一、三象限的角平分线上,则n
m =,即横、纵坐标相等;
B 若点P n m ,在第二、四象限的角平分线上,则n
m -=,即横、纵坐标互为相反数;
在第一、三象限的角平分线上 在第二、四象限的角平分线上
X X P X -X。
冀教版八年级数学_19.2.2 平面直角坐标系点的坐标特征

知1-练
感悟新知
2. 下列说法错误的是( C ) A.象限内的点的坐标可用一个有序数对来表示 B.坐标轴上的点的坐标可用一个有序数对来表 示 C.过点P向x轴作垂线,点P与垂足之间的线段 长是点P的纵坐标 D.过点P向y轴作垂线,点P与垂足之间的线段 长不一定是点P的横坐标
知1-练
感悟新知
3. 【中考·荆门】在平面直角坐标系中,若点A(a, 知1-练
标为(0,0)
-2 第三象限 -3 第四象限
(-,-)
-4 -5
(+,-)
知1-讲
感悟新知
1、点P(x,y)在第一象限 2、点P(x,y)在第二象限 3、点P(x,y)在第三象限 4、点P(x,y)在第四象限
x>0,y>0. 知1-讲 x<0,y>0. x<0,y<0. x>0,y<0.
感悟新知
例 1 [中考·湛江]在平面直角坐标系中,点A(2,-3)
在第( D )象限.
A.一
B.二
C.三
D.四
知1-讲
导引:根据平面直角坐标系中四个象限内的点的坐标 特征,即可确定点的位置. 答案:D
感悟新知
归纳
知1-讲
由点的坐标(a,b)确定点的位置的方法:
方法一:由点的坐标的符号确定点的位置,即(+,+)的
知2-讲
坐标轴上的点的坐标:
点M(x,y)所处的位置
坐标特征
点M在x轴上
在x轴正半轴上:M(正,0) 在x轴负半轴上:M(负,0)
点M在y轴上
在y轴正半轴上:M(0,正) 在y轴负半轴上:M(0,负)
感悟新知
拓展: 平行于x轴的直线上的点的纵坐标相等; 平行于y轴的直线上的点的横坐标相等.
华师版数学八年级下册同步练习课件-第17章-17.2 1平面直角坐标系

思维训练
▪ 18.如图,在平面直角坐标系中,每个最小 方格的边长均为1个单位长度,P1、P2、 P3、…(50均5,50在5) 格点上,其顺序按图中“→”方
第一向P象解4限排(析1的:,角列由平-,规分律线1如,上)、.得:∵20P点1P95P÷1(3((4-10=,1,)5、1004P,)…7、(2…,-23P),、12P∴(1)10点(、3,,P312)0P,1)9、在∴6(-P31(1,2,)1、)、… 点P根2019(据505,5这05)个. 规律,点P2019的坐+.1,(0,m+-32))在x轴上,则点P的A坐标为(
)
▪ C.(0,-4)
D.(4,0)
▪ 6.如果电影院中“5排6号”记作(5,6),那么(3,5)表示的意义是
__________.
3排5号
▪ 7.【浙江杭州中考】P(3,-4)到x轴的距4 离是_____.
第17章 函数及其图象
17.2 函数的图象
1 平面直角坐标系(第一课时)
名师点睛
▪ 知识点1 平面直角坐标系及点的坐标
▪ (1)平面直角坐标系:在平面上画两条原点重 合、互相垂直且具有相同单位长度的数轴, 这就建立了平面直角坐标系.通常把其中水 平的数轴叫做x轴或横轴,取向右为正方向; 铅直的数轴叫做y轴或纵轴,取向上为正方向; 两条数轴的交点O叫做坐标原点.
3
基础过关
▪ 1.根据下列表述,能确定位置的D是( ) ▪ A.红星电影院2排 B.北京市四环路
▪ C.北偏东30° D.东经118°,北纬40°
▪ 2.【2019·湖南株洲中考】在平面直角坐标系中,点A(2,-3)
位于 ( )
D
▪ A.第一象限
B.第二象限
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,正方形ABCD的边长为6.
(1)如果以点A为原点,AB所在的直线为x轴,建立平面坐标系,那么y轴是哪条线?
(2)写出正方形的顶点A、B、C、D的坐标.
(3)请另建立一个平面直角坐标系,此时正方形的顶点A、B、C、D的坐标又分别是多少?与同学交流一下.
老师问学生【目标3,10分钟】
杨林中学“两段四问”教学案八年级数学
课题:7平面直角坐标系
八年级数学组
1课时
学
习
目
标
A类:
1、能建立适当的直角坐标系,确定点的坐标。
B类:
2、在给定的直角坐标系中,会根据坐标描出点的位置.
C类:
3、能根据点的位置关系探索坐标之间的关系,以及根据坐标之间的关系探索点的位置关系.
4、.经历画坐标系、描点、连线,等过程,发展学生的数形结合的意识,合作交流的意识.
2、点的平移
课前检测:
教师导学
学生活动
学生问教材【目标1,10分钟】
象限的概念:
写出图中点A、B、C、D,E的坐标
学生问学生【目标2,10分钟】
先在x轴上找出表示4的点,再在y轴上找出表示5的点,过这两个点分别作x轴和y轴的垂线,垂线的交点就是A.
在平面直角坐标系中描出下列各点:A(4,5), B(-2,3), C(-4,-1),
口答:分别说出下列各个点在哪个象限内或在哪条坐标轴上?
A(6,-2),B(0,3),C(3,7),
D(-6,-3)方形ABCD的长和宽分别是6和4.以C为坐标原点,分别以CD、CB所在的直线为x轴、y轴建立直角坐标,则长方形各顶点坐标分别是多少?
预习指导:
1、阅读课本p23-P25
