第6章弯曲变形
第6章 弯曲变形(土木)

w x 0 0, w x l 0 A, B
M Fs
x 0 x 0 x 0
0,
xபைடு நூலகம்l
0 B, D 0 B, D 0 A, B, C , D
0, M 0, Fs
x l x l
例题 画挠曲线大致形状
依据 1. 约束条件; 2. 荷载情况; 3. 凹凸情况——由w″即M的正负号决定; 4. 光滑连续特性。
~
A
~
A
~
~~
~
A
~
~
~
A
AA
wA = 0
wA 0
A 0
wA
弹簧变形 -
挠曲线必受边界约 束限制。
AA
~ ~
AA
~ ~
光滑连续条件
在挠曲线的任意点处要 保持光滑和连续。
w AL = w AR
w AL = w AR
AL AR
~
A A
A A A
边界条件 A A
A
A
A A
~
~
例1 求梁的转角方程和挠度方程,并求最大转角和最大挠度, 梁的EI已知。
解
1)由梁的整体平衡分析可得:
L
F
FAx 0, FAy F (), M A Fl (
2)写出x 截面的弯矩方程
)
y
M ( x ) F (l x ) F ( x l )
3)列挠曲线近似微分方程并积分 d 2w EI 2 M ( x) F ( x l ) dx dw 1 积分一次 EI EI F ( x l )2 C dx 2 1 再积分一次 EIw F ( x l )3 Cx D 6
材料力学(理工科课件)第六章 弯曲变形)

§6-1 基本概念及工程实例 (Basic concepts and example problems)
一、工程实例(Example problem)
(Deflection of Beams)
但在另外一些情况下,有时却要求构件具有较大的弹性变 形,以满足特定的工作需要.
例如,车辆上的板弹簧,要求有足够大的变形,以缓解车辆受
M 0 w 0
x
O
M 0 w 0
M
(Deflection of Beams)
w (1 w )
2 3 2
M ( x) EI
2 w 与 1 相比十分微小而可以忽略不计,故上式可近似为
w"
M ( x) EI
(6.5)
此式称为 梁的挠曲线近似微分方程(differential equation of the deflection curve) 近似原因 : (1) 略去了剪力的影响; (2) 略去了 w2项; (3) tan w w( x )
x Cx D
4
(Deflection of Beams)
边界条件x=0 和 x=l时, w 0
梁的转角方程和挠曲线方程 A 分别为 q 2 3 3 (6lx 4 x l ) 24 EI qx 2 3 3 w (2lx x l ) 24 EI 最大转角和最大挠度分别为 在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
A a l D B
b
(Deflection of Beams)
解: 梁的两个支反力为
FRA F FRB F b l a l
x
l x
F FRA
A 1 a D b 2
材料力学第六章 弯曲变形

4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 (rad)
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w (3)校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知:EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
材料力学习题册答案-第6章 弯曲变形

第六章弯曲变形一、是非判断题1.梁的挠曲线近似微分方程为EIy’’=M(x)。
(√)2.梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角为零。
(×)3.两根几何尺寸、支撑条件完全相同的静定梁,只要所受载荷相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
(×)4.等截面直梁在弯曲变形时,挠曲线的曲率最大值发生在转角等于零的截面处。
(×)5.若梁上中间铰链处无集中力偶作用,则中间铰链左右两侧截面的挠度相等,转角不等。
(√)6.简支梁的抗弯刚度EI相同,在梁中间受载荷F相同,当梁的跨度增大一倍后,其最大挠度增加四倍。
(×)7.当一个梁同时受几个力作用时,某截面的挠度和转角就等于每一个单独作用下该截面的挠度和转角的代数和。
(√)8.弯矩突变的截面转角也有突变。
(×)二、选择题1. 梁的挠度是(D)A 横截面上任一点沿梁轴线方向的位移B 横截面形心沿梁轴方向的位移C横截面形心沿梁轴方向的线位移D 横截面形心的位移2. 在下列关于挠度、转角正负号的概念中,(B)是正确的。
A 转角的正负号与坐标系有关,挠度的正负号与坐标系无关B 转角的正负号与坐标系无关,挠度的正负号与坐标系有关C 转角和挠度的正负号均与坐标系有关D 转角和挠度的正负号均与坐标系无关3. 挠曲线近似微分方程在(D)条件下成立。
A 梁的变形属于小变形B 材料服从胡克定律C 挠曲线在xoy平面内D 同时满足A、B、C4. 等截面直梁在弯曲变形时,挠曲线的最大曲率发生在(D)处。
A 挠度最大B 转角最大C 剪力最大D 弯矩最大5. 两简支梁,一根为刚,一根为铜,已知它们的抗弯刚度相同。
跨中作用有相同的力F,二者的(B)不同。
A支反力 B 最大正应力 C 最大挠度D最大转角6. 某悬臂梁其刚度为EI,跨度为l,自由端作用有力F。
为减小最大挠度,则下列方案中最佳方案是(B)A 梁长改为l /2,惯性矩改为I/8B 梁长改为3 l /4,惯性矩改为I/2C 梁长改为5 l /4,惯性矩改为3I/2D 梁长改为3 l /2,惯性矩改为I/47. 已知等截面直梁在某一段上的挠曲线方程为:y(x)=Ax²(4lx - 6l²-x²),则该段梁上(B)A 无分布载荷作用B 有均布载荷作用C 分布载荷是x 的一次函数D 分布载荷是x 的二次函数 8. 图1所示结构的变形谐条件为:(D ) A f A=f BB f A+△l=fBCfA +fB =△l DfA-fB=△l三、填空题1. 用积分法求简支梁的挠曲线方程时, 若积分需分成两段,则会出现 4 个积分常数,这些积分常数需要用梁的 边界 条件和 光滑连续 条件来确定。
材料力学第6章弯曲变形

M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下,弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时,梁截面上有弯矩也有剪力,对于跨 度远大于截面高度的梁,剪力对弯曲变形的影响可以 省略,(a)式便可以作为横力弯曲变形的基本方程。其 中,M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合, 造成磨损不匀,产生噪音, 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大,会 使梁上小车行走困难, 出现爬坡现象,还会引 起较严重的振动。
变形超过允许数值,即 使在弹性范围内,也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为: 3 1 Fb 2 2 wmax l b 9 3 EIl
刘鸿文版材料力学第六章

F6bl
(l2
b2 ) x1
CB 段: a x2 l
y
F
A A
DC
FAy x1
x2
a
ym ax b
B B x
FBy
EI
Fb 2 2l
2
x2
F 2
(
x2
a)2
Fb (l2 6l
b2 )
EIy2
Fb 6l
x32
F 6
(
x2
a)3
F6lb (l2 b2 ) x2
目录
§6-3 用积分法求弯曲变形
目录
§6-5 简单超静定梁
例7 梁AB 和BC 在B 处铰接,A、C 两端固定,梁的抗弯刚度均为EI,F = 40kN, q = 20kN/m。画梁的剪力图和弯矩图。
解 从B 处拆开,使超静定结构变成两个悬臂 梁。
MA
FA FB
FB FB
yB2
yB1
FB
变形协调方程为: 物理关系
yB1 yB 2
4
EI
ql 4 48EI
ql 4 16 EI
11ql 4 ( ) 384 EI
3
ql 3
B i 1 Bi 24EI
ql 3 16EI
ql 3 3EI
11ql 3 ( ) 48EI
目录
§6-4 用叠加法求弯曲变形
例4 已知:悬臂梁受力如图示,q、l、
yC
EI均为已知。求C截面的挠度yC和转角C
§6-4 用叠加法求弯曲变形
讨论 叠加法求变形有什么优缺点?
目录
§6-5 简单超静定梁
1.基本概念: 超静定梁:支反力数目大于有效平衡方程数目的梁 多余约束:从维持平衡角度而言,多余的约束 超静定次数:多余约束或多余支反力的数目。 相当系统:用多余约束力代替多余约束的静定系统
材料力学_陈振中_习题第六章弯曲变形
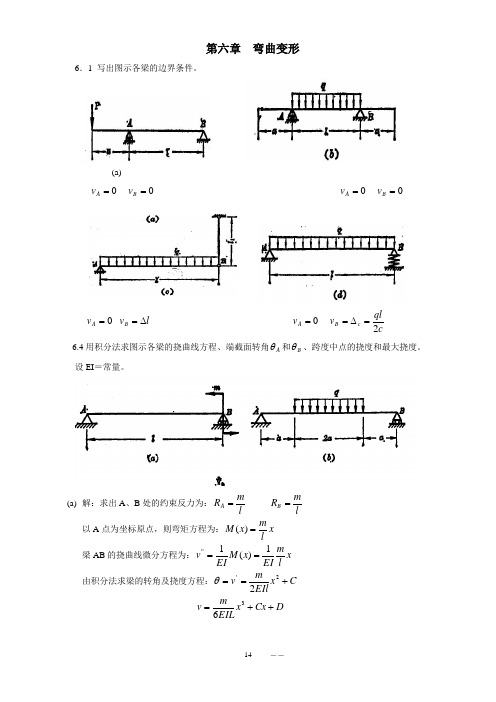
第六章 弯曲变形6.1 写出图示各梁的边界条件。
(a)0=A v 0=B v 0=A v 0=B v0=A v l v B ∆= 0=A v cql v c B 2=∆= 6.4用积分法求图示各梁的挠曲线方程、端截面转角A θ和B θ、跨度中点的挠度和最大挠度。
设EI =常量。
(a) 解:求出A 、B 处的约束反力为:l m R A =lm R B = 以A 点为坐标原点,则弯矩方程为:x lm x M =)( 梁AB 的挠曲线微分方程为:x lm EI x M EI v 1)(1''== 由积分法求梁的转角及挠度方程:C x EIlm v +==2'2θ D Cx x EILm v ++=36梁的边界条件:0=A v 、 0=B v ,由此求出积分常数:l EImC 6-= D =0 则梁AB 的挠曲线方程为:)(623x l x EIl m v -=;转角方程为:)3(622l x EIlm -=θ x=0:EI ml A 6-=θ; x=l: EI ml B 3=θ ; x=l/2:EIm l f l x 1622/-==由0'==v θ求出:3l x =处为挠度的极值点:EIml f 392max -=b)解:求出A 、B 处的约束反力为:qa R R B A ==以A 点为坐标原点,则弯矩方程分别为AC 段:)0()(a x qax x M ≤≤= CD 段:)3()(21)(2a x a a x q qax x M ≤≤--= DB 段:)43)(4()(a x a x a qa x M ≤≤-= 梁的挠曲线微分方程分别AC 段为:qax EIv 1''= CD 段:⎥⎦⎤⎢⎣⎡--=2'')(211a x q qax EI v DB 段: )4(1''x a qa EI v -= 由积分法求梁的转角及挠度方程: AC 段:12'21C qax EI v +==θ 11361D x C qax EIv ++= CD 段: 232')(61211C a x q qax EI v +⎥⎦⎤⎢⎣⎡--==θ ()2243241611D x C a x q qax EI v ++⎥⎦⎤⎢⎣⎡--=DB 段: ()32'421C x a qa EI v +-==θ ()333461D x C x a qa EIv ++-= 梁的边界条件:x=0: 0=A v ;x = a:右左右左==v v ,θθ;x = 3a:右左右左==v v ,θθ; x = 4a: 0=B v由此求出积分常数:4333232131322,611,0,6110611qa EID qa EI C D qa EI C D aq EI C -===-=-,=,= 则梁AC 段的转角方程为:⎪⎭⎫ ⎝⎛-=32611211qa qax EI θ 挠曲线方程为:⎪⎭⎫ ⎝⎛-=x qa qax EI v 33611611梁CD 段的转角方程为:()⎥⎦⎤⎢⎣⎡---=32261161211qa a x q qax EI θ 挠曲线方程为: ()⎥⎦⎤⎢⎣⎡---=x qa a x q qax EI v 343611241611梁DB 段的转角方程为:⎥⎦⎤⎢⎣⎡+--=32611)4(211qa x a qa EI θ 挠曲线方程为: ⎥⎦⎤⎢⎣⎡-+-=433322611)4(611qa x qa x a qa EI v x=0:3611qa EI A -=θ; x=4a: 3611qa EIB =θ ; 由0'==v θ求出:x=2a 处为挠度的极值点: 4max 2819qa EIf f a x -=== 6.5求图示悬臂梁的挠曲线方程及自由端的挠度和转角。
弯曲变形——精选推荐

第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比,因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件,就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同,则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段,只要梁不具有中间铰,梁的挠曲线仍然是一条光滑、连续的曲线。
”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。
”9、“只要材料服从虎克定律,则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁,只要所受的载荷相同,则两梁所对应的截面的挠度和转角相同,而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用,当梁的直径减少一半而其他条件不变时,最大正应力是原来的倍;最大挠度是原来的倍。
若梁的长度增大一倍,其他条件不变,最大弯曲正应力是原来的倍,最大挠度是原来的倍。
A:2; B:16 C:8 D:4;2、y’’=M(x)/EI在条件下成立。
A:小变形; B:材料服从虎克定律;C:挠曲线在xoy面内; D:同时满足A、B、C;3、等直梁在弯曲变形时,挠曲线最大曲率发生在处。
A:挠度最大; B:转角最大 C:剪力最大; D:弯矩最大;4、在简支梁中,对于减少弯曲变形效果最明显。
A:减小集中力P; B:减小梁的跨度;C:采用优质钢; D:提高截面的惯性矩5、板条弯成1/4圆,设梁始终处于线弹性范围内:①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果?A:①正确、②正确;B:①正确、②错误; C:①错误、②正确; D:①错误、②错误;6、应用叠加原理求横截面的挠度、转角时,需要满足的条件是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC段 CB段
1
Fb 6EIl
(l 2
b2
3x12 )
y1
Fbx1 6EIl
(l
2
b2
x12
)
2
Fb 6EIl
(l 2
b2
3x22 )
3l b
( x2
a)2
y2
Fb 6EIl
(l 2
b2
x22 )x2
l b
( x2
a)3
(5)求指定截面的位移
截面A的转角 截面C的挠度
(5) 最大挠度和最大转角
梁的最大挠度和最大转角都发生在自由端处
max
ql 3 6EI
ymax
ql 4 8EI
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
(1)弯矩连续函数,积分常数可由其边界条件来确定。 (2)弯矩方程为分段函数时,除了使梁满足边界条件
以外,还要满足连续性条件。 连续性条件
y 1 EI
M (x)dx dx Cx D
边界条件确定积分常数 C、D
3 、常见边界条件 1) 简支梁和外伸梁,两个铰支座处的挠度等于零;
2)悬臂梁,固定端处的挠度和转角都等于零。
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
例6−1 图6-3所示等截面悬臂梁AB,承受均布载荷q作
F
A
x1 FAy
C
x2 l
AC段 CB段
Fb M (x1) l x1
(0 x1 a)
Fb M (x2 ) l x2 F(x2 a) (a x2 l)
B
x
FBy
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
(2)分段建立挠曲线近似微分方程,并积分
AC段 CB段
y1
1 EI
相邻梁段在交界处具有相同的挠度和转角
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
例6−2 图6-4所示简支梁受集中载荷F作用,梁的抗弯刚
度为EI,试求梁的挠曲线方程和转角方程,并求截面C
的挠度和截面A的转角。
解 (1)求支座约束力,分段 y
a
F b
建立弯矩方程
FAy
b l
F
FBy
a l
材料力学电子教案 C 机械工业出版社
§6.3 叠加法求变形
例6−3 图6−5所示简支梁的抗弯刚度为EI,受均布载荷
q和集中力偶Me作用。试用叠加法求梁跨中点C的挠度
和截面A、B的转角。
y
Me
q
解 均布载荷单独作用下
A
yCq
5ql 4 384 EI
Aq
ql 3 24EI
Bq
ql 3 24EI
q 24
(l
x)4
Cx
D
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
(3) 确定积分常数
y
q
在固定端 y(0) 0 (0) 0
Ax
EI
Bx
C ql 3
D ql 4
l
6
24
(4) 转角方程和挠曲线方程
qx (x2 3lx 3l 2 )
6EI
y qx 2 (x2 4lx 6l 2 ) 24EI
Fb l x1
1
1 EI
Fb 2l
x12
C1
y1
1 EI
Fb 6l
x13
C1x1
D1
y2
1 EI
Fb l
x2
F (x2
a)
2
1 EI
Fb 2l
x22
F 2
( x2
a)2
C2
y2
1 EI
Fb 6l
x23
F 6
( x2
a)3
C2 x2
D2
材料力学电子教案 C 机械工业出版社
用。梁的弯曲刚度为EI,试求梁的挠曲线方程和转角方
程,并确定最大挠度ymax和最大转角θmax。
解 (1) 列出梁的弯矩方程 y
q
M (x) 1 q(l x)2 2
(2) 建立挠曲线近似微分
Ax
EI l
方程并积分
y
M (x) EI
1 EI
q 2
(l
x)
2
Bx
1 EI
q 6
(l
x)3
C
y
1 EI
A
Fb(l 2 6EIl
b2)
yC
Fab (l 2 6EIl
b2
a2)
材料力学电子教案 C 机械工业出版社
§6.3 叠加法求变形
一、叠加法的应用前提 小变形和材料遵从胡克定律。
二、叠加法 当梁上同时作用多个载荷时,可分别算出每一 载荷单独作用所引起的位移,这些位移的总和 (代数和或矢量和)即为各载荷同时作用所引起 的位移,这就是计算弯曲变形的叠加法。
§6.1 梁的挠曲线近似微分方程
二、挠曲线近似微分方程
纯弯曲时梁轴线的曲率
1M
EI
横力弯曲时
1 M (x)
(x) EI
平面曲线任一点的曲率
1
y
(x) 1 ( y)2 3/ 2
y
M (x)
1 ( y)2 3/ 2
EI
小变形情况下
y M (x) EI
材料力学电子教案 C 机械工业出版社
A
C
l/2
B
l/2
B
x
集中力偶单独作用下
yCM
Mel2 16EI
AM
Mel 3EI
将以上两个结果叠加
yC
yCq
yCM
5ql 4 384EI
Mel2 16EI
A
ql3 24EI
M el 3EI
B
ql 3 料力学电子教案 C 机械工业出版社
第6章 弯曲变形
§6.1 梁的挠曲线近似微分方程 §6.2 积分法求变形 §6.3 叠加法求变形 §6.4 梁的刚度条件 §6.5 变形比较法解超静定梁 §6.6 提高梁抗弯刚度的措施
材料力学电子教案 C 机械工业出版社
§6.1 梁的挠曲线近似微分方程
一、挠度和转角 1、挠度
y
F
A
Cy
x C
q
B
x
1) 挠曲线 梁的轴线变为图中虚线所示的平面曲线。
2) 挠度 y 轴线上各点在y轴方向的线位移
3) 挠曲线方程
y y(x)
2、转角
1) 转角θ 横截面绕中性轴转过的角度
2) 转角方程
tan dy y(x)
dx
图示坐标系中,规定: 向上的挠度和逆钟向的转角为正。
材料力学电子教案 C 机械工业出版社
§6.1 梁的挠曲线近似微分方程
正负号选取
y
M 0
M y 0 M
O
x
当弯矩M(x)>0时,梁的挠曲线向下凸,曲率 y 0 。
取正号
y M (x) EI
上式称为挠曲线近似微分方程。
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
1、转角
y
1 EI
M (x)dx C
2、挠度
§6.2 积分法求变形
(3)利用边界条件及连续条件确定积分常数
边界条件
y1(0) 0 y2(l) 0
连续条件
y a
F b
A
x1 FAy
C
x2 l
y1(a) y2(a) 1(a) 2(a)
B
x
FBy
C1
C2
Fb 6l
(l 2
b2)
D1 D2 0
材料力学电子教案 C 机械工业出版社
§6.2 积分法求变形
§6.3 叠加法求变形
