中国离散型人口模型分析_刘赛瑜
改进的Leslie离散型人口模型在我国人口预测中的应用_张曙光

s ( t )=1 -μ ( t ) ; 第t 年婴儿的成活率记为 s t ) . i i 00 ( ( 5)b ( t ) 表示第 t 年 i 岁女性的生育率 ( 平 i 均生育率 ) ; [i 1, i 2 ] 表示育龄区间 . ( 6)k ( t ) 表示第 t 年 i 岁人口的女性比 , 则 i 第 t 年 i 岁的女性人数为 k ( t ) x ( t ). i i 以上 t = 0, 1, 2…; i =0 , 1, 2, …, m . 1. 2 模型的建立 由假设 , 第 t 年 i 周岁的人活到第 t +1 年成 为 i +1 周岁的人数为 x t +1) =( 1 -u ( t ) ) x ( t ) ; i + 1( i i i = 0, 1, 2, …, m -1; t =0 , 1, 2… 第 t 年出生的人数为 x t )= ∑ b ( t ) K ( t ) x ( t ) . 00 ( i i i
30
第 t +1年为 1 岁的人数为 x t +1) =s t ) s t ) x t ) . 1( 0( 00 ( 00 ( ( 2) 令生育率 b ( t ) =β( t ) h ( t ) ,h ( t ) 为生育模式 i i i ( 用于控制生 育率的加 权因子 ) , 则有 β( t )= t ) , 即表示第 t 年所有育龄妇女总和生育 ∑ b(
[ 参考文献 ]
[ 1] 宿娟 , 李树勇 , 韩天勇 . 一类含扩散与时滞的竞争 L o t k a -V o l t e r r a 型 系统 的周 期解 [ J ]. 四 川师 范大 学 学 报( 自然科学版 ) , 2007, 30( 4) : 458 -462. [ 2] WA N GC h a n g-y o u .P e r i o d i cs o l u t i o no f p r e yp r e d a t o r mo d e l w i t hd i f f u s i o na n dd i s t r i b u t e dd e l a y e f f e c t s [J ]. 重
基于logistic模型对中国未来人口的预测分析

基于logistic模型对中国未来人口的预测分析【摘要】中国人口问题一直备受关注,本文基于logistic模型对中国未来人口进行预测分析。
在介绍中国人口的背景和研究意义。
在深入分析了logistic模型的原理,介绍了数据来源和处理方法,讨论了模型构建及参数估计的过程,并展示了未来人口预测结果的分析。
提出了针对未来人口发展趋势的政策建议。
在总结了中国未来人口的发展趋势预测,探讨了logistic模型的优劣势,以及本研究的意义和未来展望。
通过本文的研究,可以为中国人口政策制定提供科学依据,引领中国人口发展走向更加健康稳定的方向。
【关键词】logistic模型、中国人口、预测分析、数据来源、模型构建、参数估计、人口政策、人口发展趋势、优劣势、研究意义、未来展望1. 引言1.1 背景介绍中国作为世界上人口最多的国家,人口问题一直备受关注。
随着经济社会的发展,人口结构和数量的变化对中国的发展产生着重要影响。
近年来,随着经济发展水平的提高,中国的人口增长速度逐渐放缓,人口老龄化问题日益突出。
城乡人口结构的差异也在逐步扩大。
人口是经济社会发展的基础,预测未来人口变化对政府决策具有重要意义。
基于logistic模型的人口预测方法被广泛应用于人口学领域,其准确性和可靠性受到学术界和政府部门的认可。
通过对中国未来人口进行logistic模型的预测分析,可以更好地了解未来人口的变化趋势,为制定相关人口政策提供科学依据。
本文将基于logistic模型对中国未来人口的预测进行分析,探讨人口变化对中国经济社会发展的影响,提出相应的人口政策建议,旨在为解决中国人口问题提供参考和支持。
1.2 研究意义中国人口众多,人口问题一直是中国社会发展的重要议题。
人口变化对国家经济、社会政治等方面都有深远影响,因此对中国未来人口的预测分析具有重要的研究意义。
基于logistic模型对中国未来人口进行预测,可以帮助政府制定更科学合理的人口政策,有效应对人口老龄化、性别比例失衡等问题。
中国人口预测模型(精)

中国人口预测模型天津师范大学数学科学学院1003班刘瑶(10505135)周丽(10505110)2013年6月17日星期一中 国 人 口 预 测 模 型摘 要为了加快中国的经济建设进程,全面落实科学的发展观,按照构建社会主义和谐社会的要求,实现人口与经济社会资源环境的协调和可持续发展。
我们确定人口发展战略,必须既着眼于人口本身的问题,又处理好人口与经济社会资源环境之间的相互关系,构建社会主义和谐社会,统筹解决人口数量、素质、结构、分布等问题。
本文是以《中国人口统计年鉴》公布的部分人口数据为基准(其他部分数据通过网站查询得到),通过合理的假设和数学模型得到了对于中国人口增长预测的统计模型。
对Leslie 人口模型改进,构建了反映生育率和死亡率变化率负指数函数。
基于leslie 的改进模型:(t)X B B B +(t)X A A A =t)▽n +X(t 22)-(n 32112)-(n 321此模型考虑到了生育率的变化,并是针对总人口分布处理的,克服了leslie 模型的不足,很适合做长期预测。
得到结论:人口数量先增大后减小,峰值出现在2040年,届时人口数量将达到最大,为15.869亿。
关键词: 人口预测, Leslie 人口模型改进 , 长期预测一 问题的背景中国是世界上人口最多的发展中国家,人口多,底子薄,耕地少,人均占有资源相对不足,是我国的基本国情,人口问题一直是制约中国经济发展的首要因素。
新中国成立50多年来,我国人口发展经历了前30年高速增长和后20年低速增长两大阶段:从建国初期到上世纪70年代初,中国人口再生产由旧中国的高出生、高死亡率进入高出生、低死亡率的人口高增长时期,1950-1975年人口出生率始终保持在30‰以上, 最高达到37‰(附录1)。
70年代以后,人口过快增长的势头得到迅速扭转,人口出生率、自然增长率、妇女总和生育率有了明显下降,人口出生率由70年代初的33‰大幅度下降到80年代的21‰, 妇女总和生育率也由6下降到2.3左右。
中国离散型人口模型分析_刘赛瑜

中国离散型人口模型分析
刘赛瑜 黄国祥
( 上海交通大学安泰经济与管理学院 , 上海 200052)
摘 要 应用 L e s l i e 矩阵建立了离散预测模型 , 得到中短期人口 预测值 及其变 化规律 。 在 对 L e s l i e矩阵改 进的基 础上 , 得到 中长期的人口预测模 型 , 并将利用微积分法建立的人口连续偏微分模型与 离散预测模型 进行对照 , 为实现 人口发展战 略目标 提出了有效性的建议 。 关键词 阶梯效应 L e s l i e 矩阵 R o m b e r g 求积公式 中图法分类号 O29; 文献标志码 A
图 1 我国长期人口发展趋势图
5228
科 学 技 术 与 工 程
10 卷
短期预测中 , 假设人口出生率和人口死亡率是 恒定的 , 当用来预测中国人口在一个长期的时间内 的发展变化 , 显然有失精密 性 , 即对于 不同的年份 阶段 , 应该有不同的人口出 生率和人口死 亡率 , 所 以把未来一个长时期内比如 50年 , 划分成若干个阶 段 , 每个阶段包括若干个连 续的年份 , 而对于同一 个阶段的不同年份 , 仍假设它们具有相同的人口出 生率和人口死亡 率 , 这样处 理之后 , 不 仅在一定程 度上简化了计算的复杂性和烦琐性 , 也提高了一定 的精确性 , 得到如下图所示结果
2 离散模型前提
对于中国未来人口数量这个问题 , 前人做了许 多研究工作 。 人口的预测模型有一元线性回归法 、 自回归法 、指 数函 数法 、幂 函数法 、多 元回 归模 型 法、 灰色系统法 、系统动力学法等 。 但在采用 一元 线性回归法 、 自回归法 、指数函数法 、 幂函数法多元
5226
[ 1]
龄的分布就可以求出后一年 的人口数和人口 关于 年龄的分布 , 且无后 效性 , 即后 一年的结果只 与其 前一年结果和前一年该年龄 人口的死亡率和 出生 率有关 。 对于年龄为 r 的人口 , 用 i 地区且性别为 s 的人口所占全国总人口的比 例乘以该人口的 死亡 率( 题中已给出 ) , 然后对不同地区 、性别 的人口种 ( 1) 数进行加和处理 , 就得到了以往各年各个年龄总的 死亡率与各年龄妇女的生育率 ;
基于Leslie模型中国未来人口策略模拟研究

基于Leslie模型中国将来人口策略模拟探究一、引言中国是世界上人口最多的国家之一,人口问题一直是中国政府关注的重点。
为了猜测将来的人口变化趋势以及制定相应的人口政策,探究人口模型成为必要的手段之一。
Leslie模型是一种经典的人口模型,通过构建各年龄组的人口转移率矩阵,可以猜测将来人口的变化。
本文旨在基于Leslie模型模拟探究中国将来人口的变化,并提出相应的人口策略。
二、Leslie模型简介Leslie模型是由英国统计学家Patrick G. Leslie于1945年提出的,它是一种离散的人口模型。
该模型将人口划分为不同的年龄组,以年龄为单位进行猜测。
Leslie模型的核心是矩阵运算,在矩阵中,每一行代表不同年龄组的人口数量,每一列代表不同年龄组之间的迁移率。
通过计算不同年龄组之间的人口迁移矩阵与初始人口矩阵的乘积,可以得到下一年度的人口分布。
通过迭代运算,可以猜测将来的人口变化。
三、中国将来人口策略模拟探究1. 数据收集和构建为了进行中国将来人口策略模拟探究,起首需要收集相关的人口数据。
我们可以利用中国统计年鉴的数据来得到中国各年龄组的人口数量和迁移率。
依据收集到的数据,构建初始的人口矩阵。
2. 模型参数设置在进行Leslie模型的模拟探究时,需要设置一些参数。
参数的设定需要思量到中国的实际状况和政策因素。
例如,思量到规划生育政策的实施,可以设置适当的生育率和死亡率等。
3. 模拟试验和结果分析在获得初始人口矩阵和模型参数后,可以进行模拟试验。
通过对人口矩阵进行一系列迭代运算,可以得到将来人口的猜测结果。
同时,还可以通过改变不同参数的设定,模拟不同的人口政策对将来人口的影响。
依据模拟结果,可以进行相关的结果分析。
例如,可以分析将来人口的年龄结构变化、人口增长速度以及人口总量等指标的趋势。
分析结果可以为政府制定人口政策提供参考依据。
四、结论与展望本探究基于Leslie模型,对中国将来人口进行模拟,通过构建人口转移率矩阵,猜测了将来人口的变化。
基于Logistic模型的中国城市群人口分布预测

Abstract
This paper selected population data of China’s megaregions from 2006 to 2018, and utilized the
综上所述,本文将考虑城市群的交通配套设施对人口的吸引力,以公路密度、城市道路密度、轨道 交通密度构建城市群交通吸引因子,拟合该因子与人口的关系。在城市群内外部交通设施逐年增长完善 的情况下,进行城 2019 年,国务院共批复了 11 个国家城市群的发展规划,并明确各个城市群的定位以及发展 目标。由于哈长城市群对常住人口的统计工作缺失,无法通过插值弥补,因此本文将省去该城市群。另 一方面,山东半岛城市群和海西城市群较早进行规划,形成一定的城市群形态,本文将这两个城市群纳 入研究范围之内。综上,本文研究的城市群为:京津冀、长三角、珠三角、成渝、长江中游、关中平原、 中原、呼包鄂榆、兰西、北部湾、山东半岛以及海西(具体空间范围见表 1 和图 1),共研究 12 个城市群。
河南省:郑州、开封、洛阳、平顶山、新乡、焦作、许昌、漯河、济源、鹤壁、商丘、周口、安阳、 濮阳、三门峡、南阳、信阳、驻马店;
安徽省:毫州、宿州、阜阳、淮北、蚌埠; 山东省:聊城、菏泽 山西省:长治、晋城
内蒙古自治区:呼和浩特、包头、鄂尔多斯;陕西省:榆林
甘肃省:兰州市、白银市、定西市、临夏回族自治州; 青海省:西宁市、海东市、海北藏族自治州、海南藏族自治州、黄南藏族自治州
Open Access
1. 引言
人口是区域发展的重要要素。人口分布是指在一定时间节点上人口在各地区的分布情况,是人口数 据在空间上的表现形式[1]。研究人口分布,不仅可以了解一定区域人的人口空间特征,还可以分析人口 的空间变化趋势,进而为区域制定相关政策、资源合理分配等问题提供科学的参考依据。
Leslie人口模型及例题详解

L e s l i e人口模型及例题详解The saying "the more diligent, the more luckier you are" really should be my charm in2006.Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化;如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型;20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型;模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化;假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;2 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记第i 年龄组女性生育率为i b 注:所谓女性生育率指生女率,女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;3 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;4 生育率仅与年龄段有关,存活率也仅与年龄段有关;建立模型与求解根据以上假设,可得到方程 )1(1+t n =∑=mi i i t n b 1)()()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b 1 记)]0(,),0(),0([)0(21m n n n n = 2假设n 0和矩阵L 已经由统计资料给出,则为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:i s i > 0,i =1,2,…,m -1;ii b i 0≥,i =1,2,…,m ,且b i 不全为零;易见,对于人口模型,这两个条件是很容易满足的;在条件i 、ii 下,下面的结果是成立的: 定理1t1+tL 矩阵有唯一的单重的正的特征根0λλ=,且对应的一个特征向量为*n =1,s 1/0λ,s 1s 2/20λ,…,s 1s 2 …s m -1/10-m λT3 定理2若1λ是矩阵L 的任意一个特征根,则必有01λλ≤;定理3若L 第一行中至少有两个顺次的0,1>+i i b b ,则i 若1λ是矩阵L 的任意一个特征根,则必有01λλ<;ii t t t n 0/)(lim λ+∞>-=*cn , 4 其中c 是与n 0有关的常数;定理1至定理3的证明这里省去;由定理3的结论知道,当t 充分大时,有*)(0n c t n t λ≈ 5 定理4记121i i i b s s s β-=,q λ=1β/λ+2β/λ2+…+m β/m λ,则λ是L 的非零特征根的充分必要条件为q λ=1 6所以当时间充分大时,女性人口的年龄结构向量趋于稳定状态,即年龄结构趋于稳定形态,而各个年龄组的人口数近似地按λ-1的比例增长;由5式可得到如下结论:i 当λ>1时,人口数最终是递增的;ii 当λ<1时,人口数最终是递减的;iii 当λ=1时,人口数是稳定的;根据6式,如果λ=1,则有b 1 + b 2s 1 + b 3s 1s 2 + … + b m s 1 s 2…s m-1=1记R = b 1 + b 2s 1 + b 3s 1s 2 + … + b m s 1 s 2…s m-1 7R 称为净增长率,它的实际含义是每个妇女一生中所生女孩的平均数;当R >1时,人口递增;当R <1时,人口递减;Leslie 模型有着广泛应用,这里我们给出一个应用的例子,供大家参考;公园大象管理南非的一家大型自然公园放养了大约11000头大象,管理部门希望为大象创造一个健康的生存环境,将大象的总数控制在11000头左右;每年,公园的管理人员都要统计当年大象的总数;过去20年里,公园每年都要处理一些大象,以便保持大象总数维持在11000头左右,通常都是采用捕杀或者迁移的方法来实现;统计表明,每年约处理600-800头大象;近年来,公众强烈反对捕杀大象行为,而且即使是迁移少量的大象也是不允许的;但是一种新的给大象打避孕针的方法也被研制成功;一只成年母象打了避孕针后,两年内不再怀孕;公园有一些关于大象的资料,供建模参考:1几乎不再迁入或迁出大象;2目前性别比接近1:1,采取控制后,也希望维持这个比例;3初生象的性别比也是大约1:1,生双胎的比例为%4母象初次怀孕大约在10-12岁,一直到60岁大约每年怀胎一次,60岁后不再受孕,怀孕期为22个月;5避孕针可能引起大象每个月都发情,但不受孕,因为大象通常每年生育1次,所以按月循坏的方案是不足取的;6避孕针对母象没有副作用,打了避孕针的母象2年内不再受孕;7初生象存活到1岁的比例为70%-80%,此后,直至60岁前,存活率都比较均匀,大约在95%以上,大象一般只活到70岁;8公园里不存在捕杀行为,偷猎可以不考虑;公园管理部门有一份过去两年移出公园大象的粗略统计,不幸的是没有捕杀或公园大象的具体数据;你的任务是,构造一个模型,利用模型研究如何采用避孕措施控制公园大象的总数.同时需要完成以下任务:1 建立并利用模型推算2-60岁大象可能的存活率,以及目前的大象年龄结构;2估计每年需要避孕多少大象,才能保证大象总数控制在11000头左右,说明数据不确定性对你的结论的影响,评价一下年龄结构的变化以及对旅游的影响,你可能被要求观察30-60年;3假设每年可以移出50-300头大象,避孕大象数可以减少多少,评价如何根据经济效益平衡两种方案;4有一些反对观点认为,假如出现疾病或者失控的偷猎,使大象总数突然大幅度下降,即使停止避孕,也会对大象群的恢复存在不良影响,研究并回答这个问题;5公园公管理部门正在构造模型,特别希望批驳那些以缺乏完整数据为由而嘲笑利用模型指导决策的观点.希望你的模型包括一份技术报告能给公园管理部门提一些建议,提高公园管理部门的信心,除此之外,你的报告,还应该包括一个详细的技术流程最多3页回答公共关心的问题;6假如非洲其它公园对你的模型感兴趣,有意利用你的模型,请为公园大象数在300-25000头规模的公园提供一份避孕计划,顺便考虑一下存活率稍有不同或者可以有迁移的情况.附过去两年的迁出数据年龄 0 1 2 3 4 5 6 7 8 9总量1 103 77 71 70 68 61 58 51 52 51母象1 50 36 41 29 31 30 28 24 22 29总量2 98 74 69 61 60 54 52 59 58 57母象2 57 34 33 29 34 28 27 31 25 25年龄 10 11 12 13 14 15 16 17 18 19总量1 51 50 51 48 47 49 48 47 43 42母象1 27 27 26 27 26 25 28 27 19 25总量2 60 63 64 60 63 59 52 55 49 50母象2 26 36 38 30 33 34 24 30 21 30年龄 20 21 22 23 24 25 26 27 28 29总量1 42 37 39 41 42 43 45 48 49 47母象1 18 16 19 24 17 25 21 26 29 27总量2 53 57 65 53 56 50 53 49 43 40母象2 29 27 40 23 29 24 21 26 24 16年龄 30 31 32 33 3 4 35 36 37 38 39总量1 46 42 44 44 46 49 47 48 46 41母象1 24 22 20 22 24 24 23 25 21 24总量2 38 35 37 33 20 33 30 29 29 26母象2 17 16 18 18 15 18 12 17 16 13年龄 40 41 42 43 4 4 45 46 47 48 49总量1 41 42 43 38 34 34 33 30 35 26母象1 24 19 26 20 20 15 16 13 20 11总量2 10 24 25 22 21 22 11 21 21 19母象2 6 11 14 10 10 12 8 11 12 9年龄 50 51 52 53 54 55 56 57 58 59总量1 21 18 14 5 9 7 6 0 4 4母象1 10 9 8 4 4 4 3 0 3 2总量2 15 5 10 9 7 6 5 4 7 0母象2 6 4 5 4 4 2 3 2 4 0年龄 60 61 62 63 64 65 66 67 68 69 70总量1 4 3 2 2 1 3 0 2 1 0 2母象1 2 1 1 1 0 3 0 0 1 0 2总量2 2 3 0 2 0 2 0 1 0 0 0母象2 2 1 0 0 0 1 0 1 0 0 0假设与分析1大象性别比接近1:1,初生象的性别比也是大约1:1,采取控制后,也希望维持这个比例;2过去两年迁出的大象是随机抽样,其结构反映了象群总体的年龄结构;3 避孕是随机的,母象是否避孕是不可识别的,假设各个年龄的母象是等比例避孕的,比例系数为k,仅通过调节k 来控制公园大象数量;4母象初次怀孕大约在10-12岁,简化假设大象初孕时间为11岁,当前状态下,成年象的成活率为s,生育母象率为r ,老年象的成活率是线性逐渐递减的,因此其成活率可表示为设初生象活到1岁的存活率为0s ;5避孕针对母象没有副作用,打了避孕针的母象2年内不再受孕;且无论打避孕针前母象是否怀孕,一旦打了避孕针,母象就被避孕或中止怀孕,平均每年有γ比例的母象处于避孕状态;每年母象的避孕率为η,每年的避孕方案时瞬时完成的;6 假设大象的年龄结构是稳定的;数据处理与分析12-60岁大象的存活率与年龄结构母象生育率为r =1/+1+/2=头/年12岁的母象生育母象的生育率为r /6;由题设知道存活率)99.0,95.0(∈s ;以下是第一年迁移出0至70岁大象数据x1=103,77,71,70,68,61,58,51,52,51,51,50,51,48,47,49,48,47,43,42,42,37,39,41,42,43,45,48,49,47,46,42,44,44,46,49,47,48,46,41,41,42,43,38,34,34,33,30,35,26,21,18,14,5,9,7,6,0,4, 4, 4 ,3,2,2,1,3,0,2,1,0,2 ;以下是第二年迁移的0-70岁大象数据x2=98,74 69 61 60 54 52 59 58 57 60 63 64 60 63 59 52 55 49 50 53 57 65 53 56 50 53 49 43 40 38 35 37 33 20 33 30 29 29 26 10 24 25 22 21 22 11 21 21 19 15 5 10 9 7 6 5 4 7 0 2 3 0 2 0 2 0 1 0 0 0;x=x1+x2;x0=x/normx,1;以下是第一年迁移的0-59岁母象数据y1=50 36 41 29 31 30 28 24 22 29 27 27 26 27 26 25 28 27 19 25 18 16 19 24 17 25 21 26 29 27 24 22 20 22 24 24 23 25 21 24 24 19 26 20 20 15 16 13 20 11 10 9 8 4 4 4 3 0 3 2;以下是第二年迁移的0-59岁母象数据y2=57 34 33 29 34 28 27 31 25 25 26 36 38 30 33 34 24 30 21 30 29 27 40 23 29 24 21 26 24 16 17 16 18 18 15 18 12 17 16 13 6 11 14 10 10 12 8 11 12 9 6 4 5 4 4 2 3 2 4 0;考虑到有些数据较小及抽样的随机性,我们取两次抽样的平均值作为分析的基本数据;t1=x12:11;t2=x22:11;tt=t1+t2;tt1=tt1:9;tt2=tt2:10;tn=tt2./tt1;meantnans =t1=x112:21;t2=x212:21; tt=t1+t2; tt1=tt1:9;tt2=tt2:10;tn=tt2./tt1; meantnans =t1=x112:31;t2=x212:31; tt=t1+t2; tt1=tt1:19;tt2=tt2:20;tn=tt2./tt1; meantnans =t1=x112:41;t2=x212:41; tt=t1+t2; tt1=tt1:29;tt2=tt2:30;tn=tt2./tt1; meantnans =t1=x112:51;t2=x212:51; tt=t1+t2; tt1=tt1:39;tt2=tt2:40;tn=tt2./tt1; meantnans =t1=x112:60;t2=x212:60; tt=t1+t2;tt1=tt1:48;tt2=tt2:49;tn=tt2./tt1; meantnans =n1=zeros1,71;n11=1;n12=;for i=3:61n1i=n1i-1;endn1;for i=62:71n1i=n1611-i-61/10;endn1;N1=n112:50;xx=x12:50;xx=100xx/normxx,1;N1=100N1/normN1,1;t=1:39;plott,N1,t,xx;axis10,40,0,5;title'图1'通过以上分析大致可以得到,1-60岁大象的存活率约为;0-70岁年龄结构向量见图2; y0=100x0/normx0,1;a=0:70;bara,y0,'stacked';title'图2'下面我们取0120.75,0.98s s s ===;m1=zeros1,71;m11=1;m12=;for i=3:61m1i=m1i-1;endm1;for i=62:71m1i=m1611-i-61/10;endm1;m1=100m1/normm1,1;bara,m1,'stacked';title'图3 稳定的年龄结构'plota,m1,'r-',a,y0,'b-.';title'图4 年龄结构当前状态与稳定状态比较'polyfity0,m1,1ans =从所给的数据来看,象群的年龄结构还没有达到相对稳定的状态;根据以上数据,大体可以得到l=zeros71,71; l1,13=6;l2,1=;for i=14:61l1,i=;endl;for j=3:61lj,j-1=;end; l;for k=62:71lk,k-1=eigl;矩阵的唯一正特征值为;对于不同的存活率,得到的唯一正特征值为:下面我们估计每年处于避孕状态母象的比率γ;此时,女性生育率为0.1448(1)γ-;记由6式得解得1-1/^111/6+ans =即每年应该有%的母象处于避孕状态;为了保证有%的母象处于避孕状态,下面分析每年应该打避孕针母象的比例η;在假设3和假设5的前提下,如果每年打避孕针母象比例为η;母象可以分成3类:即当年被打避孕针而上一年没有被打避孕针或上一年被打避孕针而本年没有被打避孕针,比例为2(1)ηη-;连续两年被打避孕针2η;连续两年没有被打避孕针;只有最后一类母象具有生育能力;因此,只需要η满足方程1-sqrtans =ans =5500ans =+003解得 0.387η=,即每年大约需要给2127头母象打避孕针;在方案实施过程中,实际上根本不需要打这么多针,因为许多小象还是可以识别的;可以采取随机抽样的打针方式,对于抽到的小象只计数不打针,直至计满2127头母象,就算完成当年任务;采取打避孕针的方案对象群的年龄结构是由一些影响的,下面给出了打与不打避孕针情况下稳定的象群年龄结构与各你阿爸年龄段象群数的比较;m1=zeros1,71;m11=1;m12=;for i=3:61m1i=m1i-1;end; m1;for i=62:71m1i=m1611-i-61/10;end; m1;n1=zeros1,71;n11=1;n12=;for i=3:61n1i=n1i-1;end; n1;for i=62:71n1i=n1611-i-61/10;end;n1;subplot1,2,1a=0:70;plota,m1,'r-',a,n1,'b--';title'图5年龄结构比较';axis0,70,0,1;M1=5500m1/normm1,1;N1=5500n1/normn1,1;a=0:70;subplot1,2,2plota,M1,'r-',a,N1,'b--'title'图5各年龄段大象数比较图'axis-0,70,0,300通过以上两个图的比较,可以发现采取避孕措施,将使幼象、小象数减少,中老年象数增加;由于采取避孕措施,使得初生小象数减少,因此会不可避免地引起象群年龄结构的改变,下面分析,15年、30年、60年后的象群年龄结构;L=zeros71,71;L1,13=6;L2,1=;for i=14:61L1,i=;end; L;for j=3:61Lj,j-1=; end; L;for k=62:71Lk,k-1= end; L;eigL;n15=L^15x0';n30=L^15n15;n60=L^30n30;n15=100n15/normn15,1;n30=100n30/normn30,1;n60=100n60/normn60,1;M15=5500n15/normn15,1;M30=5500n30/normn30,1;M60=5500n60/normn60,1;bara,55y0title'图6a 避孕前种群量分布';axis0,70,0,250bara,M15title'图6b 避孕15年后种群量分布';axis0,70,0,250bara,M30title'图6c避孕30年后种群量分布';axis0,70,0,250M60=5500n60/normn60,1;bara,M60title'图6d 避孕前种群量分布';axis0,70,0,250n70=L^70x0';n70=100n70/norm n70,1;k1=100m1/normm1,1;图7给出了避孕前后年龄结构稳定状态的比较plot a,k 1,'r-',a,n70,'b-.';title'图7 避孕前后稳定的年龄结构';axis0,70,0,5数据不确定性对结果的影响分别取0120.7,0.8,0.95,0.99s s s ===1-1/^111/6+ans =1-sqrtans =1-1/^111/6+ans =1-sqrtans =每年需避孕的母象比例为%—% ;对于每年可以迁移50-300头大象及0120.75,0.98s s s ===,下面分析避孕方案的变化及最经济的方案;设增长率为p ,对于 0120.75,0.98s s s ===令当 1.01p =,每年的避孕率为%,每年迁出110头; 当 1.02p =,每年的避孕率为%,每年迁出220头; 当 1.025p =,每年的避孕率为%,迁出275头;1-1/^111/6+ans =1-sqrtans =p=;1-p ^12./^111/6+./p-./p.^49/./pans =1-sqrtans =p=;1-p.^12./^111/6+./p-./p^49/pans =1-sqrtans =p=;1-p.^12./^111/6+./p-./p^49/pans =1-sqrtans =进一步分析可以知道,对于 0120.75,0.98s s s ===,如果增长率为(1 1.0322,11000(p-1))p p ≤≤即每年移,令每年需要避孕的母象为5500'γ,每年需要迁移的大象数为11000(1)p -;从相关的文献中我们大致可以得到,设平均每迁移一头大象的成本约避孕一头大象费用的λ倍,由此得到增长率为p 时的总费用函数为记易见,1,0.3868, 1.01,0.346, 1.02,0.396p y p y p y ======clear ;p=1::;q =1-p.^12./^111/6+./p-./p.^49././pq =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17a =1-sqrt1-qa =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17y=a+15p-1y =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17。
2007年全国大学生数学建模竞赛A题优秀论文—人口预测模型
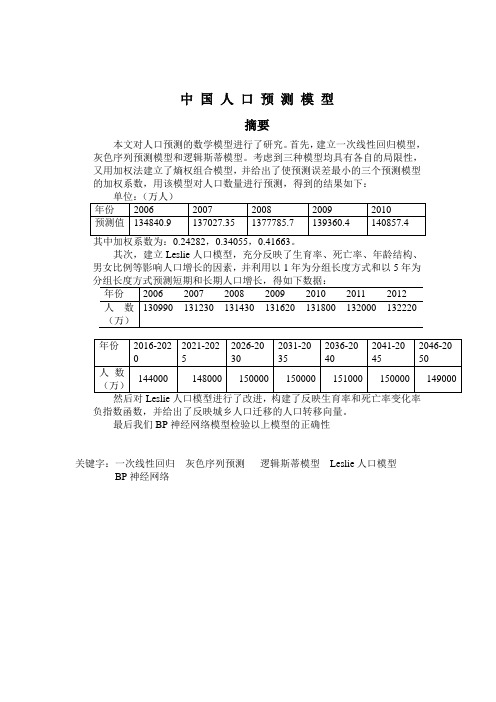
中国人口预测模型摘要本文对人口预测的数学模型进行了研究。
首先,建立一次线性回归模型,灰色序列预测模型和逻辑斯蒂模型。
考虑到三种模型均具有各自的局限性,又用加权法建立了熵权组合模型,并给出了使预测误差最小的三个预测模型的加权系数,用该模型对人口数量进行预测,得到的结果如下:其次,建立Leslie人口模型,充分反映了生育率、死亡率、年龄结构、男女比例等影响人口增长的因素,并利用以1年为分组长度方式和以5年为负指数函数,并给出了反映城乡人口迁移的人口转移向量。
最后我们BP神经网络模型检验以上模型的正确性关键字:一次线性回归灰色序列预测逻辑斯蒂模型Leslie人口模型BP神经网络一、问题重述1. 背景人口增长预测是随着社会经济发展而提出来的。
在过去的几千年里,由于人类社会生产力水平低,生产发展缓慢,人口变动和增长也不明显,生产自给自足或进行简单的以货易货,因而对未来人口发展变化的研究并不重要,根本不用进行人口增长预测。
而当今社会,经济发展迅速,生产力达到空前水平,这时的生产不仅为了满足个人需求,还要面向社会的需求,所以必须了解供求关系的未来趋势。
而人口增长预测是对未来进行预测的各环节中的一个重要方面。
准确地预测未来人口的发展趋势,制定合理的人口规划和人口布局方案具有重大的理论意义和实用意义。
2. 问题人口增长预测有短期、中期、长期预测之分,而各个国家和地区要根据实际情况进行短期、中期、长期的人口预测。
例如,中国人口预期寿命约为70岁左右,因此,长期人口预测最好预测到70年以后,中期40—50年,短期可以是5年、10年或20年。
根据2007年初发布的《国家人口发展战略研究报告》(附录一)及《中国人口年鉴》收集的数据(附录二),再结合中国的国情特点,如老龄化进程加速,人口性别比升高,乡村人口城镇化等因素,建立合理的关于中国人口增长的数学模型,并利用此模型对中国人口增长的中短期和长期趋势做出预测,同时指出此模型的合理性和局限性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
科 学 技 术 与 工 程
10 卷
回归模型法时有一定的限制条件 , 当其 F检验值大 于其临界值时方可使用 此类方法进行 预测 。 其中 较为著名的是 19 世纪中叶荷兰生 物学家 V e r h u l s t 提出的阻滞增长模型 , 又称为 L o g i s t i c 模型 。 但这些 模型只是考虑了人口总数与总的增长率 , 并没有涉 及到年龄结构 、性别比例等 因素的影响 。 事实上 , 在人口预测中 , 人口按年龄分布以及按性别分布状 况是非常重要的 , 因为不同年龄人的生育率和死亡 率有着很大的差别 。 两个国家或地区 目前人口总 数一样 , 如果一个国家或地区年轻人的比例高于另 一国家或地区 , 那么二者人口的发展状况将大不一 样; 同样 , 如果二者的性别比例不同 , 那么二者人口 的发展状况也将不同 。 因而可以得出结论 : 人口的发展状况与老龄化 程度 、性别比例 、不同地区的人口分布状况 、妇女生 育率等因素有着密切的联系 。 基于以上的考虑 , 可 知使人口数量和结构发生变化的不外 乎各个年龄 的出生率 、 死亡率以及迁移 , 结合具体的背景资料 , 不考虑人口迁移所带来的影响 。 对于出生率 , 可以 认为其与 国家政 策以及 人口 素质 有关 ; 对于 死亡 率 , 其与人们的生活水平有关 , 由于在短时间内 , 人 们的生活水平不会有太大的变化 , 所以认为在短时 间内 , 中国人口的死亡率不会变化 , 而在长时间内 , 则要考虑人口死亡率的变化 。 现建立的主要人口模型假设如下 : ( 1) 在对中国人口数量进行预测时 , 不考虑人 口迁入国境和迁出国境的情况 , 即认为无人口的迁 入与迁出 ; ( 2) 短时期的各个年份内不考虑因为天灾人祸 或生活水平对出生率与死亡率的影响 ; ( 3) 假设 90 岁以及 90 岁以上年龄的人口都看 成是 90 岁 ; ( 4) 在短期的人口预测中 , 其各个年龄的人口 死亡率以及各年龄妇女的生育率均保持不变 。
中国离散型人口模型分析
刘赛瑜 黄国祥
( 上海交通大学安泰经济与管理学院 , 上海 200052)
摘 要 应用 L e s l i e 矩阵建立了离散预测模型 , 得到中短期人口 预测值 及其变 化规律 。 在 对 L e s l i e矩阵改 进的基 础上 , 得到 中长期的人口预测模 型 , 并将利用微积分法建立的人口连续偏微分模型与 离散预测模型 进行对照 , 为实现 人口发展战 略目标 提出了有效性的建议 。 关键词 阶梯效应 L e s l i e 矩阵 R o m b e r g 求积公式 中图法分类号 O29; 文献标志码 A
到 7. 58‰, 妇女总和生育率也下降到 2 以下 。 进入
1 中国人口发展状况
中国是 世界 上人口 最多 的发 展 中国 家 , 人口 多、 底子薄 、耕地少 、人均占有资源相对不足是我国 的基本国情 , 人口问题一直是制约中国经济发展的 首要因素 。 新中国成立 60 多年来 , 我国人口发展经 历了前 30年 高速增长和后 30 年低速 增长两大阶 段: 从建国初期到 20世纪 70 年代初 , 中国人口再生 产由旧中国的高 出生 、高死 亡率进入高出 生 、低死 亡率的人口高增长时期 , 1950年 — 1975 年人口出生 率始终保持在 30‰以上 , 最 高达到 37‰。 70 年代 以后 , 人口过快增长的势头 得到迅速扭转 , 人口出 生率 、自然增长率 、妇女总和生育率有了明显下降 , 人口出 生率由 70 年代初的 33 ‰大幅度下降 到 80 年代的 21‰, 妇女总 和生育率 也由 6‰下降到 2 . 3‰左右 。 90年代以来 , 随着我国经济高速发展 , 人 民文化和健康水平逐步提高 , 计划生育工作的不断 深入 , 在 20 岁 — 29 岁生育旺盛人数年均超过 1 亿 的情况下 , 人口出生率依 然呈现大幅下 降的趋势 , 到 2000 年底人口出生率从 1990 年的 21. 06 ‰ 下降 到 14. 03 ‰, 自然增长率由 1990 年的 14. 未来人口数量这个问题 , 前人做了许 多研究工作 。 人口的预测模型有一元线性回归法 、 自回归法 、指 数函 数法 、幂 函数法 、多 元回 归模 型 法、 灰色系统法 、系统动力学法等 。 但在采用 一元 线性回归法 、 自回归法 、指数函数法 、 幂函数法多元
5226
率的影响 , 即人口数目的增长应为新出生人口数量 和死亡数量之差 , 所以由此可建立人口数量与出生 率和死亡率的函数关系式 , 但在此之 前 , 中国 人口 数量较大 , 可以将总的人口数目看成是时间 t 的连 续函数 , 则人口数量变化可用微分方程建立中国特 色的人口增长模型 。 但由于对于不同年龄的人口 , 其死亡率是不相同的 , 所以死亡率不仅是时间的函 数 , 也是年龄的函数 ; 而对于出生率 , 刚出生的人口 是 0 岁 , 而对于其他年龄 , 是不存在出生率的 , 所以 说总人口数目也是时间和年龄的函数 , 这样处理会 更准确些 。 模型中变量符号定义如下 : r : 表示各个年龄 ; x t ): 该函数表示在第 t 年 , 年龄为 r 的人口数 r( 量; [ 万人 ] x t ): 该函数表示在第 t 年 , 性别为 s 年龄为 r r( 的人口数量 ; [ 万人 ] x t ): 该函数表示在第 t 年, 在 i 区域 、 年龄为 r( r 、 性别为 s 人口数量 ; [ 万人 ] b t ): 该函数表示在第 t 年 , 年龄为 r 的中国生 r( 育妇女人数占该年龄中国妇女总人数的率比例 ; b ′ t ) : 该函数表示在第 t 年 , 年龄为 r 的中国 r( 生育妇女人数占该年龄中国总人数的率比例 ; b t ): 该函数表示在第 t 年 , 年龄为 r 的在第 i r( 个区域的生育妇女人数占该 区域该年龄妇女 总人 口的比例 ; 即区域妇女生育率 ; d t ) : 该函数表示在第 t 年 , 年龄为 r 的中国人 r( 口的死亡率 ; 即在第 t 年 , 年龄为 r 的中国死亡人口 占该年龄总人口数量的比例 ; d t ): 该函数表示在第 t 年 , 年龄为 r 的在第 i r( 个区域性别为 s 的人口的死亡人数占该区域总人口 的比例 ; 即区域年龄性别死亡率 ; e t ): 该函数表示在第 t 年 , 年龄为 r 的在第 i r( 个区域性别为 s 的人口数占该区域性别为 s 的总人 口的比例 ; 即区域年龄性别比率 ; n 表示第 t 年 , 老年人人口总数 ; [ 万人 ] 1t : n 表示第 t 年的人口老龄化程度 , 即第 t 年老 2t : 年人人口总数占总人口的比例 ; r 妇女开始生育年龄 ; 0 :
第 10 卷 第 21 期 2010 年 7月 1671-1815( 2010) 21-5225-05
科 学 技 术 与 工 程
S c i e n c eT e c h n o l o g ya n dE n g i n e e r i n g
o l . 10 N o . 21 J u l y2010 V 2010 S c i . T e c h . E n g n g .
图 1 我国长期人口发展趋势图
5228
科 学 技 术 与 工 程
10 卷
短期预测中 , 假设人口出生率和人口死亡率是 恒定的 , 当用来预测中国人口在一个长期的时间内 的发展变化 , 显然有失精密 性 , 即对于 不同的年份 阶段 , 应该有不同的人口出 生率和人口死 亡率 , 所 以把未来一个长时期内比如 50年 , 划分成若干个阶 段 , 每个阶段包括若干个连 续的年份 , 而对于同一 个阶段的不同年份 , 仍假设它们具有相同的人口出 生率和人口死亡 率 , 这样处 理之后 , 不 仅在一定程 度上简化了计算的复杂性和烦琐性 , 也提高了一定 的精确性 , 得到如下图所示结果
2010 年 4月 13日收到 第一作者简介 : 刘赛瑜 , 男 , 湖南 人 , 硕士 研究生 。 E m a i l : s a i y u . l i u @s j t u . e d u . c n 。
90 年代末期 , 我国人口再生产实现了低出生 、低死 亡、 低增长的历史性转变 。 中国政府自 1980 年在全国城乡实行计划生育 基本国策以来成果卓著 。 若从 70年代算起 , 至今至 少少生 3 亿人口 , 这有效地控制了人口的快速增长 , 为中国现代化 建设 、全面 实现 小康打 下坚 实的 基 础 , 这同时也是对世界人口的增长和控制做出了杰 出贡献 。 但是由于中国人口基数大 , 人口增长问题 依然十分严峻 , 每年平均净增人口约 1300 万 , 这仍 然对我国社会和 经济产生巨大的 压力 。 在我 国现 代化进程中 , 必须 实现人口与经 济 、社会 、资源 、环 境协调发展和可持续发 展 , 进一 步控制人口数量 , 提高人口质量 , 改善人 口结构 。 因此 , 运用准 确的 模型建立方式 , 对中国未来人口的发展做出分析和 预测 , 为中国经济 和社会发展决 策提供科学依据 , 对于加速推进我国现代化建 设的宏伟大业有 着极 为重要的现实意义 。
3 2
:
d x t ) r( = b ′ t ) x t )d t ) x t )= r( r( r( r( d t [b ′ t ) d t ) ]x t ) r( r( r( x 0= x r( r 0
在求解时 , 把 结果进行离散 化 , 即时 间取一些 整数 , 而且对于出生率和死 亡率是分段函 数 , 在一 年之内是不会改变的 , 这样就完成了从连续到离散 的过度 。 利用 L e s l i e 矩阵进 行求解 会更切 合实际 情况 x t+1)x ( t )=Δx t+1) = t [ b ′ t )r + 1( r r( r( d t ) ]x t ) d t= r( r( [b ′ t )d t ) ]x t ) ( 2) r( r( r( 只要知道了前一 年的人口数以及 人口关于年 b 0 t 1d 0 t 0 L= 0 0 0 b 1 t 0 1d 1 t 0 … … b 2 t 0 0 1d 2 t 0 …
