初等数学基本概念与公式总结
初数数学中的三角恒等式公式详解

初数数学中的三角恒等式公式详解三角函数是数学中重要的一部分,它们在解决几何问题和物理问题中有着广泛的应用。
而在初等数学中,我们经常会遇到三角恒等式公式,它们是解决三角函数之间关系的基础。
本文将详细解析一些常见的三角恒等式公式,帮助读者更好地理解和应用它们。
一、正弦恒等式正弦恒等式是三角函数中最基本的一组恒等式。
根据定义,正弦函数的定义域为整个实数集,值域为[-1, 1]。
1. 互余恒等式正弦函数的互余恒等式表达了两个角的正弦函数值之间的关系。
给定一个角θ,它的补角为90°-θ,它们的正弦函数值满足以下关系:sinθ = cos(90°-θ)2. 倍角恒等式正弦函数的倍角恒等式表达了角的两倍角的正弦函数值与原角正弦函数值之间的关系。
对于任意角θ,其正弦函数的倍角正弦函数值满足以下关系:sin(2θ) = 2sinθcosθ二、余弦恒等式余弦恒等式是三角函数中另一个基本的一组恒等式。
根据定义,余弦函数的定义域为整个实数集,值域也为[-1, 1]。
1. 互余恒等式余弦函数的互余恒等式表达了两个角的余弦函数值之间的关系。
给定一个角θ,它的补角为90°-θ,它们的余弦函数值满足以下关系:cosθ = sin(90°-θ)2. 倍角恒等式余弦函数的倍角恒等式表达了角的两倍角的余弦函数值与原角余弦函数值之间的关系。
对于任意角θ,其余弦函数的倍角余弦函数值满足以下关系:cos(2θ) = cos²θ - sin²θ三、正切恒等式正切恒等式是三角函数中最复杂的一组恒等式。
根据定义,正切函数的定义域为实数集中除去所有使得余弦函数为零的实数值,值域为整个实数集。
1. 倍角恒等式正切函数的倍角恒等式表达了角的两倍角的正切函数值与原角正切函数值之间的关系。
对于任意角θ,其正切函数的倍角正切函数值满足以下关系:tan(2θ) = (2tanθ) / (1 - tan²θ)四、其他常见恒等式除了上述基本的三角恒等式公式外,还有一些其他常见的恒等式公式。
初等数学常用公式

附录:初等数学常用公式一、初等代数 1.乘法公式1) (a ±b )2 = a 2±2ab + b 2 2) (a ±b )3 = a 3±3a 2b + 3a b 2±b 3 3) ( a+ b+c ) 2 = a 2+ b 2+ c 2+2ab +2bc +2ca 4) (a -b ) (a+b ) = a 2- b 2 5) (a ±b ) ( a 2 ab + b 2) = a 3±b 3 2.绝对值1) | a |=2a2) -| a | ≤ a ≤ | a | 3) | a | ≤ k⇔-k≤ a ≤ k , | a | < k ⇔-k < a < k4) | a |-| b | ≤ | a ± b | ≤ | a | + | b | 3.一元二次方程 a x 2 + b x + c = 01) 判别式 Δ= b 2 -4 a c2) 根:a b 2Δ±-;两根和为ab 2-;两根积为ac ;Δ> 0时,为两不等实根;Δ = 0 时,为两等实根;Δ < 0时,为一对共轭虚根。
4. 级数1) 设等差级数首项为 a 1,公差为 d ,则:通项公式 a n= a 1+(n -1)d ;前n 项和公式 S n =d n n na a a n n )1(21)(211-+=+2) 设等比级数首项为 a 1,公比为 q ,则:通项公式 a n = a 1 q n -1;前n 项和公式 S n = q q a q q a a n n --=--1)1(1115.指数律 (a > 0, b > 0)1) a m • a n = a m+n 2) a m ÷ a n = a m -n 3) (a m ) n = a m n 4) (a b ) m = a m b m 5) (ab ) m =mma b6)m n nma a )(=6.对数律 (a > 0, a ≠1)1)若 a x = M ,则 log a M = x ; l g x = x 10log2)x ax a=log 3) 01log a =4)1log =aa 5)y x xy a a a log log )(log +=6)y x yxa a alog log log -= 7))0(log log >=x x a x a a a8) ax x b b a log log log =9)1log log =⋅a b b a7.排列、组合与二项式公式1)设n m A 为m 个元素中取n 个的排列数,则nm A = m (m -1) (m-2)…(m -n +1)2)设n m C 为m 个元素中取n 个的组合数,则!n m !n !m C n m)(-=3)k n k n k n C C C 11+-=+4)(a + b ) n = a n +1n C a n -1 b +… +k n C a n -k b k +…+ b n二、平面三角 1 弧度=π180≈57°17′45″,1°=180π弧度≈0.0174533弧度1.基本关系 1) sin x ²csc x=1 2) cos x ²sec x=1 3) tan x ²cot x=1 4) sin 2 x+cos 2 x=1 5) 1+tan 2 x=sec 2 x6) 1+cot 2 x=csc 2 x7) tan x =cosx sinx8) cot x=sinxcosx2.两角和的三角函数1) sin (α±β) = sin αcos β± cos αsin β 2) cos (α±β) = cos αcos βsinαsin β3) tan (α±β) = βαβ±α tan tan 1tan tan3.倍角公式1)sin 2 x= 2sin xcos x2)cos 2 x= cos 2 x -sin 2 x=1-2sin 2 x=2 cos 2 x -13)tan 2 x=xx2tan 12tan -4)sin 3 x= 3sin x -4sin 3 x 5) cos 3 x= 4 cos 3 x -3 cos x4.半角公式1)s i n 2cosx 12-±=x 或 sin 2 2cosx 12-=x 2)c o s 2x cos 12+±=x 或 cos 22cosx 12+=x3)t a n cosx1sinxsinx cosx 12+=-=x5.和差化积公式1)sin α+ sin β= 2sin 2βα+cos 2βα-2)sin α-sin β= 2 cos 2βα+ sin 2βα-3)cos α+ cos β= 2cos 2βα+cos 2βα-4)cos α-cos β= -2sin 2βα+sin 2βα-6.积化和差公式 1)sin αcos β= 21[sin(α+β)+sin(α-β)] 2)cos αcos β=21[cos (α+β)+ cos (α-β)]3)s i n αs i n β= -21[cos (α+β)- cos (α-β)]7.设三角形三边a, b, c 所对的三个角分别为A ,B ,C ,外接圆半径为R ,则有1)正弦定理R 2sinC c sinB b sinA a === 2)余弦定理 c 2 = a 2+ b 2-2 a b cosC 8.反三角函数恒等式1)arc s i n x + a r c cos x = 2π 2)arc t a n x + a r c co t x =2π3)arc t a n x = a r c s i n 21xx +4)arc s i n x = a r c t a n 21xx -三、平面解析几何下述公式中出现的点P ,Q ,M 的坐标分别为(x 1 , y 1),(x 2 , y 2),(x 0 , y 0)1.P ,Q 两点的距离:|PQ| =212212)()(y y x x -+-2.定比分点公式:λλλλ++=++=1 1210210y y y ,x x x ,这里M 点是线段PQ 的分点,且λ=MB AM。
高一数学必修一第二章基本初等函数知识点总结
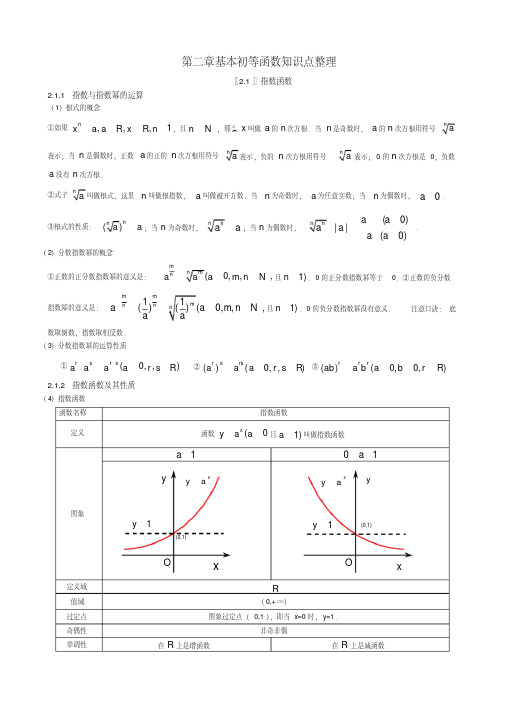
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
初等数学公式及其函数图像

f (a) b f 1 (b) a .
27. 若 函 数 y f ( kx b) 存 在 反 函 数 , 则 其 反 函 数 为 y
1 [f k
1
( x ) b] , 并 不 是
y [ f 1 (kx b) ,而函数 y [ f 1 (kx b) 是 y
者的一个必要而不是充分条件.特别地, 方程 ax bx c 0(a 0) 有且只有一个实根在
2
(k1 , k 2 ) 内,等价于 f (k1 ) f (k 2 ) 0 ,或 f (k1 ) 0 且 k1
k1 k 2 b k2 . 2 2a
9.闭区间上的二次函数的最值
A CU B CU A B R
4.容斥原理
card ( A B) cardA cardB card ( A B ) card ( A B C ) cardA cardB cardC card ( A B ) card ( A B) card ( B C ) card (C A) card ( A B C ) .
1
ab 对称. 2m
( x) 的图象关于直线 y=x 对称. 25.若将函数 y f ( x) 的图象右移 a 、上移 b 个单位,得到函数 y f ( x a ) b 的图 象;若将曲线 f ( x, y ) 0 的图象右移 a 、上移 b 个单位,得到曲线 f ( x a, y b) 0 的图
11.定区间上含参数的二次不等式恒成立的条件依据 (1)在给定区间 (,) 的子区间 L (形如 , , , , , 不同)上含参数 的二次不等式 f ( x, t ) 0 ( t 为参数)恒成立的充要条件是 f ( x, t )min 0( x L) . (2)在给定区间 (,) 的子区间上含参数的二次不等式 f ( x, t ) 0 ( t 为参数)恒成立 的充要条件是 f ( x, t )man 0( x L) .
常用初等数学公式

常用初等数学公式1.乘法公式:-(a+b)×c=a×c+b×c-(a-b)×c=a×c-b×c-(a+b)×(c+d)=a×c+a×d+b×c+b×d-(a-b)×(c-d)=a×c-a×d-b×c+b×d2.平方公式:- (a + b)² = a² + 2ab + b²- (a - b)² = a² - 2ab + b²3.立方公式:- (a + b)³ = a³ + 3a²b + 3ab² + b³- (a - b)³ = a³ - 3a²b + 3ab² - b³4.四则运算:-a+b=b+a-a-b=-(b-a)-a×b=b×a-a÷b=a/b5.分式运算:- 分式相加:a/b + c/d = (ad + bc) / bd- 分式相减:a/b - c/d = (ad - bc) / bd- 分式相乘:(a/b) × (c/d) = ac / bd- 分式相除:(a/b) ÷ (c/d) = (ad) / (bc)6.指数公式:-a⁰=1-a¹=a-a²=a×a-aᵐ×aⁿ=a^(m+n)(同底数的指数相乘,等于底数不变,指数相加)-(aⁿ)ᵐ=a^(n×m)(指数的幂,等于底数不变,指数相乘)-a⁻ⁿ=1/aⁿ(负指数的运算)7.开方公式:-平方根:√a×√a=a- a × √b × √b = ab- √(ab) = √a × √b-aⁿ/ⁿ√a=√a8.百分数运算:-百分数变小数:移动两位小数点向左-小数变百分数:移动两位小数点向右-分数变百分数:分子变化,分母变100-百分数变分数:分子不变,分母变1009.比例运算:-比例:a:b=c:d,即a/b=c/d-相等比例:a:b=c:b-倒数比例:a:b=1/b:1/a-反比例:a×b=k(k为常数)10.连续整数运算:-连续整数的和:n个连续整数之和=(第一个整数+最后一个整数)×n/2-连续整数的平均数:n个连续整数的平均数=(第一个整数+最后一个整数)/2-连续偶数的和:n个连续偶数之和=(第一个偶数+最后一个偶数)×n/2-连续奇数的和:n个连续奇数之和=n²或n²+n11.平行线运算:-共线角性质:对内(内错角):互补角之和为180°;对内(内析角):互余角之和为180°;对外角与内错角互补;对外角与内析角互余-切线性质:切线与半径垂直;相交弧(两条)所对圈角相等;切线之间平行12.角度运算:-直角的两个补角相等-锐角的两个角平分线的和等于180°-相邻补角:两个角的和等于180°-对顶角:两个补角叫做一个对顶角13.园及圆周运算:-圆的面积:A=πr²-圆的周长:C=2πr-弧长公式:L=2πr(α/360°)(α为圆心角)-扇形面积公式:A=1/2r²α/360°(α为圆心角)- 弓形面积公式:A = 1/2r²(α - sinα)14.角正弦、余弦、正切公式:- 正弦公式:sinA = 对边/斜边- 余弦公式:cosA = 邻边/斜边- 正切公式:tanA = 对边/邻边15.直角三角形中的特殊比值:- 正弦:sin45° = cos45° = √2/2- 余弦:cos45° = sin45° = √2/2- 正切:tan45° = 1, tan30° = 1/√3- 三角函数的反函数:sin(-A) = -sinA,cos(-A) = cosA,tan(-A) = -tanA16.四边形运算:-平行四边形的性质:对角线互相平分;对角线互相垂直-矩形的性质:所有内角为90°;对角线相等-正方形的性质:所有边相等;所有内角为90°;对角线相等且互相垂直-菱形的性质:所有边相等;对角线互相垂直;对角线互相平分-梯形的性质:上底+下底×高/2=面积以上为常用的初等数学公式,涵盖了乘法公式、平方公式、四则运算、分式运算、指数公式、开方公式、百分数运算、比例运算等多个方面。
初等数学函数公式

·余弦定理: c = a + b − 2ab cos C 余弦定理:
2 2 2
α
2
·正弦定理: 正弦定理:
·反三角函数性质: arcsin x = 反三角函数性质:
π
2
− arccos x arctgx =
π
2
− arc诱导公式: ·诱导公式: 函数 角A -α 90°-α 90°+α 180°-α 180°+α 270°-α 270°+α 360°-α 360°+α ·和差角公式: 和差角公式: sin -sinα cosα cosα sinα -sinα -cosα -cosα -sinα sinα cos cosα sinα
sin α + sin β = 2 sin
α +β
2 2 α+β α−β sin α − sin β = 2 cos sin 2 2 α+β α −β cos α + cos β = 2 cos cos 2 2 α+β α −β cos α − cos β = 2 sin sin 2 2
cos
α −β
初等数学函数公式 初等数学函数公式 函数
一些初等函数: 一些初等函数: 两个重要极限: 两个重要极限:
ex − e−x 2 x e + e −x 双曲余弦 : chx = 2 shx e x − e − x = 双曲正切 : thx = chx e x + e − x 双曲正弦 : shx = arshx = ln( x + x 2 + 1) archx = ± ln( x + x 2 − 1) 1 1+ x arthx = ln 2 1− x
初数数学中的根式公式详解

初数数学中的根式公式详解根式是初等数学中的重要概念之一,它在数学表达中广泛应用。
本文将详细介绍根式的定义、性质和常见的根式公式,帮助读者更好地理解和应用根式。
一、根式的定义在初数数学中,根式是指形如√a的数学表达式,其中a为被开方数,√为开方号。
其中,√a表示a的平方根。
二、根式的性质1. 非负性质:对于任意实数a,当a≥0时,根式√a定义有意义且非负;当a<0时,根式√a无意义。
2. 加减性质:对于非负实数a和b,有以下运算规则:(1)√a ± √b = √(a ± b)(2)√a ∓ √b ≠ √(a ∓ b)3. 乘法性质:对于非负实数a和b,有以下运算规则:(1)√a × √b = √(ab)4. 除法性质:对于非负实数a和b,有以下运算规则:(1)√(a/b) = √a / √b,其中b不等于0。
5. 乘方性质:对于非负实数a和整数n,有以下运算规则:(1)(√a)^n = a^(n/2),其中n为偶数时,右边的等式成立。
三、根式的化简对于给定的根式,可以通过化简的方法使其更加简洁。
下面举例说明:例1:化简根式√48解:首先,我们观察48的因数,可以发现48=16×3=4×4×3。
因此,√48=√(16×3)=√(4×4×3)=4√3例2:化简根式√75解:同样地,我们观察75的因数,可以发现75=25×3=5×5×3。
因此,√75=√(25×3)=√(5×5×3)=5√3通过以上例子,我们可以看出,在化简根式时,我们需要找出被开方数的完全平方数因子,从而将根号内的数化为多个因子相乘的形式。
四、常见的根式公式1. 平方差公式:(a + b) × (a - b) = a^2 - b^22. 奇数幂的根式:a^(2n+1) = (a^n) × √a3. 偶数幂的根式:a^(2n) = (a^n)^2五、根式的应用根式在实际应用中有着广泛的运用,例如在几何学中,根式可以描述图形的边长和面积关系;在物理学中,根式可以用于计算速度和加速度等物理量。
初数数学中的平均数公式详解

初数数学中的平均数公式详解平均数是初等数学中一个基础的概念,用于描述一组数据的集中趋势。
在统计学和概率论等领域中,平均数常常作为数据分析的重要工具。
本文将详细介绍初数数学中常见的三种平均数公式:算术平均数、几何平均数和调和平均数,并探讨它们的性质和应用。
算术平均数算术平均数是最常见的平均数公式,一般用于描述一组数据的集中位置。
它的计算方法是将所有数据相加,然后除以数据的个数。
设有n 个数a1, a2, ..., an,则它们的算术平均数记作x,公式表示如下:x = (a1 + a2 + ... + an) / n算术平均数是一组数据的中心位置,它具有以下性质:1. 平均数在数据中具有唯一性,即只有一个数是平均数。
2. 当数据分布比较均匀时,平均数能够较好地代表整组数据。
3. 对于任意一个数据,若增加或减少一个相同的常数,平均数也会相应地增加或减少这个常数。
几何平均数几何平均数常用于计算一组数据的比例关系或增长率。
它的计算方法是将所有数据相乘,然后开n次方根,其中n为数据的个数。
设有n个正数a1, a2, ..., an,则它们的几何平均数记作g,公式表示如下:g = (a1 * a2 * ... * an)^(1/n)几何平均数具有以下性质:1. 几何平均数一般小于等于算术平均数,当且仅当数据全部相等时,二者相等。
2. 几何平均数可以用于计算复利的平均增长率,以及一组数据的百分比变化。
调和平均数调和平均数常用于计算一组数据的平均速度或平均耗时。
它的计算方法是将数据个数除以每个数据的倒数之和。
设有n个正数a1, a2, ..., an,则它们的调和平均数记作h,公式表示如下:h = n / (1/a1 + 1/a2 + ... + 1/an)调和平均数具有以下性质:1. 调和平均数一般小于等于几何平均数,当且仅当数据全部相等时,二者相等。
2. 调和平均数能够有效地表示一组速度或耗时的整体平均水平,它对个别较小数值的数据较为敏感。
