二次函数综合性质应用
中考重点二次函数的性质与应用

中考重点二次函数的性质与应用中考重点:二次函数的性质与应用二次函数是初中数学中的重要内容之一,它在中考中的考查频率较高。
掌握二次函数的性质与应用,能够帮助我们解决与二次函数相关的问题,提高解题能力。
本文将重点讨论二次函数的性质和应用,探索其在数学中的作用。
一、二次函数的定义及一般式表示二次函数是形如y = ax² + bx + c的函数,其中a、b、c为常数且a≠0。
其中,a决定了二次函数的开口方向,b决定了函数的对称轴位置,c表示函数与y轴的交点。
二次函数的一般式表示形式为y = ax² + bx + c,其中a、b、c为实数且a≠0。
一般式可以转化为顶点式表示或者因式分解式表示,从而更方便地研究二次函数的性质。
二、二次函数的性质1. 对称性:二次函数的图像关于对称轴对称。
对称轴的表示为x = -b / (2a),在二次函数图像上即为顶点的横坐标。
2. 开口方向:当a>0时,二次函数开口向上;当a<0时,二次函数开口向下。
3. 极值点与最值:二次函数的极值点即顶点,其横坐标为-x / (2a),纵坐标为f(-x /(2a))。
当a>0时,二次函数的最小值为f(-x / (2a));当a<0时,二次函数的最大值为f(-x / (2a))。
4. 零点:二次函数与x轴的交点称为零点,可以通过求解二次方程ax² + bx + c = 0来确定。
二次函数有两个零点时称为有两个实根,有一个零点时称为有一个实根,没有实根时称为无实根。
三、二次函数的应用1. 求解问题:二次函数常常用于求解与平面图形有关的问题。
例如,已知抛物线y = ax² + bx + c与x轴交于A、B两点,求抛物线经过的最高点的坐标。
通过求解顶点坐标可以得到问题的解。
2. 最值问题:二次函数能够用于解决最值问题。
例如,已知二次函数y = ax² + bx + c,在一定范围内求函数的最值。
中考数学全效复习:专题提升(7) 二次函数的图象和性质的综合运用

专题提升(七) 二次函数的图象和性质的综合运用(人教版九上P47习题第5题)画出函数y =x 2-2x -3的图象,利用图象回答: (1)方程x 2-2x -3=0的解是什么; (2)x 取什么值时,函数值大于0; (3)x 取什么值时,函数值小于0.【思想方法】 二次函数y =ax 2+bx +c(a≠0)的图象与x 轴的交点的横坐标x 1,x 2就是一元二次方程ax 2+bx +c =0(a≠0)的两个根,因此,我们可以通过解方程ax 2+bx +c =0来求抛物线y =ax 2+bx +c 与x 轴交点的横坐标;反过来,也可以由y =ax 2+bx +c 的图象来求一元二次方程ax 2+bx +c =0的解.1.[2019·广安]二次函数y =ax 2+bx +c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x =1,下列结论:①abc<0;②b<c ;③3a +c =0;④当y>0时,-1<x<3.其中正确的结论有( )A .1个B .2个C .3个D .4个2.[2019·南充]已知抛物线y =ax 2+bx +c(a,b,c 是常数),a>0,顶点坐标为⎝ ⎛⎭⎪⎫12,m ,有下列结论:①若点(n,y 1)与⎝ ⎛⎭⎪⎫32-2n ,y 2在该抛物线上,当n<12时,则y 1<y 2;②关于x 的一元二次方程ax 2-bx +c -m +1=0无实数解.那么( )A .①正确,②正确B .①正确,②错误C .①错误,②正确D .①错误,②错误3.[2019·遂宁]二次函数y =x 2-ax +b 的图象如图所示,对称轴为直线x =2,下列结论不正确的是 ( )A .a =4B.当b=-4时,顶点的坐标为(2,-8)C.当x=-1时,b>-5D.当x>3时,y随x的增大而增大4.[2019·湖州]已知抛物线y=2x2-4x+c与x轴有两个不同的交点.(1)求c的取值范围;(2)若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m和n的大小,并说明理由.5.[2018·泰州]在平面直角坐标系xOy中,二次函数y=x2-2mx+m2+2m+2的图象与x轴有两个交点.(1)当m=-2时,求二次函数的图象与x轴的交点坐标;(2)过点P(0,m-1)作直线l⊥y轴,二次函数图象的顶点A在直线l与x轴之间(点A不在直线l上),求m的范围;(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.6.[2019·原创]已知二次函数y=x2-2mx+m2-1.(1)当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;(3)在(2)的条件下,x轴上是否存在一点P,使得PC+PD最短?若点P存在,求出点P的坐标;若点P 不存在,请说明理由.7.[2019·东营节选]已知抛物线y=ax2+bx-4经过点A(2,0),B(-4,0),与y轴交于点C.(1)求这条抛物线的解析式;(2)如图,点P是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点P的坐标.8.[2018·宜宾改编]在平面直角坐标系xOy 中,已知抛物线的顶点坐标为(2,0),且经过点(4,1).如图,直线y =14x 与抛物线交于A,B 两点,直线l 为y =-1.(1)求抛物线的解析式;(2)在l 上是否存在一点P,使PA +PB 取得最小值?若存在,求出点P 的坐标;若不存在,请说明理由.如图,已知抛物线y =ax 2+bx +c 经过A(-1,0),B(3,0),C(0,3)三点,直线l 是抛物线的对称轴. (1)求抛物线的解析式;(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标.参考答案【教材母题】图象略 (1)x 1=-1,x 2=3 (2)x<-1或x>3 (3)-1<x<3 【中考变形】1.D 2.A 3.C4.(1)c<2 (2)m<n,理由略 5.(1)(-2+2,0)和(-2-2,0) (2)-3<m<-1 (3)m =-326.(1)y =x 2-2x 或y =x 2+2x (2)C(0,3),D(2,-1) (3)存在,P(1.5,0)7.(1)y =12x 2+x -4 (2)P(-2,-4)8.(1)y =14x 2-x +1 (2)存在,P ⎝ ⎛⎭⎪⎫2813,-1 【中考预测】(1)y =-x 2+2x +3 (2)P(1,2)关闭Word 文档返回原板块。
二次函数的性质与应用

二次函数的性质与应用二次函数是指形如f(x) = ax^2 + bx + c的函数,其中a、b和c是实数且a ≠ 0。
二次函数是一种重要的函数类型,在数学和实际问题中具有广泛的应用。
本文将介绍二次函数的性质与应用。
一、二次函数的基本性质1. 解析式:二次函数的一般形式为f(x) = ax^2 + bx + c,其中a、b和c分别代表函数的系数。
a控制开口方向和开口程度,正值使函数开口向上,负值使函数开口向下;b决定了函数的对称轴位置,对称轴的横坐标为-x/b;c是函数的常数项,表示函数与y轴的交点y=c。
2. 零点:二次函数的零点是使f(x) = 0的横坐标值。
一般情况下,二次函数有两个零点,可以用求根公式x = (-b±√(b^2-4ac))/(2a)求得。
3. 顶点:二次函数的顶点是函数图像的最高点或最低点。
顶点的横坐标为-x/b,纵坐标为f(-b/2a)。
对于a > 0,函数的图像开口向上,顶点是最低点;对于a < 0,函数的图像开口向下,顶点是最高点。
二、二次函数的图像特征1. 开口方向:二次函数的开口方向由a的正负决定。
当a > 0时,函数图像开口向上;当a < 0时,函数图像开口向下。
2. 开口程度:a的绝对值越大,函数图像开口越窄;a的绝对值越小,函数图像开口越宽。
当|a| < 1时,函数图像会比较平缓;当|a| > 1时,函数图像则会比较陡峭。
三、二次函数的应用1. 最值问题:通过观察二次函数的开口方向和顶点,我们可以判断函数的最值。
对于开口向上的函数,最小值为顶点的纵坐标;对于开口向下的函数,最大值为顶点的纵坐标。
这在实际问题中有很多应用,例如优化问题、成本最小化等。
2. 运动问题:二次函数可以用来描述某些运动的轨迹。
例如,一个物体从某个高度落下,忽略空气阻力的影响,可以用二次函数表示物体的高度随时间的变化。
通过求解函数的零点和顶点,可以确定物体的落地时间和最高高度。
二次函数的性质和应用

二次函数的性质和应用二次函数是一种常见的函数形式,在数学中具有重要的地位。
本文将讨论二次函数的性质和应用,希望能帮助读者更好地理解这种函数形式。
一、二次函数的定义和基本性质二次函数的标准形式为f(x)=ax²+bx+c,其中a、b、c都是实数,且a ≠ 0。
它的图象是一个开口向上或向下的抛物线。
1. 对称轴:二次函数的对称轴是垂直于x轴的直线,它的方程式为x=-b/2a。
对称轴把图象分成两个对称的部分。
2. 零点:一个二次函数可以有两个、一个或零个零点。
其中,零点是函数的根,即f(x)=0的解。
3. 最值和顶点:当a>0时,f(x)的最小值为y=c-b²/4a,它位于对称轴上,称为抛物线的最小值。
当a<0时,f(x)的最大值为y=c-b²/4a,它位于对称轴上,称为抛物线的最大值。
最小值或最大值统称为顶点。
4. 函数的增减性:当a>0时,如果x₁<x₂,则f(x₁)<f(x₂)。
当a<0时,如果x₁<x₂,则f(x₁)>f(x₂)。
二、二次函数的应用1. 抛物线的运动学应用:抛物线可以描述物体的抛体运动轨迹,因此它在物理学中经常被使用。
例如,在高尔夫球运动中,运动员需要考虑到地面的摩擦力和空气的阻力等因素,以确定击球的位置和力度。
抛物线方程可以帮助运动员做出更精确的计算,从而提高得分率。
2. 光学应用:抛物线的形状与光的传播有关。
例如,抛物面反射镜常用于望远镜、卫星通信等光学领域中,因为它可以使光线以特定的角度集中在一个点上,从而使视野更宽广。
3. 非线性回归分析:在生物统计学、社会科学、经济学和金融学等领域中,二次函数经常被用于分析非线性回归方程。
非线性回归是指,回归方程中包含二次函数或更高次的函数。
例如,经济学家常用二次函数分析消费者的支出模式,这会帮助他们预测市场的需求变化。
4. 工程应用:二次函数也可以用于工程领域中的计算。
二次函数总结

二次函数总结二次函数是数学中一种常见且重要的函数形式。
它的一般形式可以表示为f(x) = ax^2 + bx + c,其中a、b和c为常数,且a不等于零。
二次函数是一个拱形曲线,它在数学、物理和经济等领域都有广泛的应用。
在本文中,将对二次函数的性质、图像、方程以及实际问题中的应用进行总结和探讨。
一、二次函数的性质二次函数有一些重要的性质,其中最基本的是二次项的系数a 决定了函数的开口方向。
当a大于零时,二次函数的图像开口向上,形成一个U型;当a小于零时,二次函数的图像开口向下,形成一个倒U型。
另一个重要性质是二次函数的对称轴与顶点。
对称轴是函数图像上对称的线,它通过顶点,并且与x轴垂直。
顶点是二次函数图像的最低点或最高点,它的横坐标可以通过-b/2a来确定。
二、二次函数的图像二次函数的图像是一个拱形曲线,其形状由a的正负决定。
当a大于零时,图像开口向上,当a小于零时,图像开口向下。
图像的形状还与常数b和c的取值相关。
常数b决定了图像在x方向上的平移,即左右移动;常数c决定了图像在y方向上的平移,即上下移动。
通过改变这些常数的取值,可以使图像的位置和形状发生变化,从而满足不同的条件。
三、二次函数的方程解二次函数的方程是一个重要的应用技巧,因为它可以帮助我们找到函数图像与坐标轴的交点。
二次函数的方程可以通过将f(x)设置为零来表示,即ax^2 + bx + c = 0。
解这个方程可以使用公式x = (-b ± √(b^2 - 4ac)) / 2a,也称为二次方程的根式解。
这个解式给出了二次函数与x轴的交点的横坐标。
方程的解有三种情况:当Δ = b^2 - 4ac大于零时,方程有两个不同的实数解;当Δ等于零时,方程有一个实数解;当Δ小于零时,方程没有实数解。
四、二次函数在实际问题中的应用二次函数在实际问题中有广泛的应用。
其中一个常见的应用是抛物线的运动模型。
当我们抛出一个物体时,它的运动轨迹可以用二次函数来描述。
二次函数的性质与应用

二次函数的性质与应用二次函数是数学中常见的一类函数,它的特点是含有二次项的多项式函数,通常表示为y=ax^2+bx+c(其中a、b、c为实数且不全为零),在本文中我们将探讨二次函数的性质与应用。
一、二次函数的基本性质二次函数的图像为抛物线,其性质如下:1. 开口方向:由二次项的系数a的正负决定,若a>0,则抛物线开口向上;若a<0,则抛物线开口向下。
2. 顶点坐标:抛物线的顶点坐标为(-b/2a,f(-b/2a)),其中f(x)为二次函数,即抛物线的对称轴为x=-b/2a。
3. 对称性:抛物线关于对称轴对称,即f(x)=f(-b/2a+x)。
4. 零点:二次函数的零点为使得f(x)=0的x值,可以通过解二次方程ax^2+bx+c=0来求得。
二、二次函数的应用由于二次函数具有较为简洁的数学表达式和良好的图像特点,因此在实际问题中有广泛的应用,以下是几个典型的应用场景:1. 物体运动的模拟二次函数可以用来模拟抛体运动的轨迹。
假设一个物体从地面上沿着水平方向射出,经过一段时间后,它的轨迹可以用二次函数表示。
其中,抛物线的开口方向取决于物体的发射角度和初速度大小,而顶点坐标则可以表示物体的最高和最远点。
2. 经济学中的成本和收益问题在经济学中,成本和收益通常与产量或销售额等变量相关。
二次函数可以用来描述成本和收益之间的关系,从而帮助企业或个人做出决策。
例如,一个生产商可以通过分析其成本函数来确定最佳产量,从而实现成本最小化。
3. 工程学中的曲线拟合在工程学中,需要对一些实验数据进行拟合,以找出合适的曲线来描述数据之间的关系。
二次函数可以较好地拟合一些非线性数据,因为它具有一定的弹性和灵活性。
通过拟合二次函数,可以预测未知数据点的取值,并帮助工程师做出正确的决策。
4. 地理学中的地形分析地理学研究中,经常需要对地形进行分析和描述。
二次函数可以用来模拟山脉和河流的起伏曲线,帮助研究人员理解地理变量之间的关系,比如高度和距离之间的关系。
二次函数的性质及应用

二次函数的性质及应用二次函数是一类形式为y = ax² + bx + c(a ≠ 0)的函数,它在数学中具有重要的性质和广泛的应用。
本文将介绍二次函数的性质以及它在实际问题中的应用。
一、二次函数的性质1. 函数图像二次函数的图像通常为抛物线,具体的形状取决于a的正负和大小:- 当a > 0时,图像开口向上,形状类似于“U”字型;- 当a < 0时,图像开口向下,形状类似于倒置的“U”字型。
2. 对称性二次函数关于其顶点具有对称性。
设二次函数的顶点坐标为(h, k),则函数图像关于直线x = h对称。
3. 零点与判别式二次函数的零点即为方程ax² + bx + c = 0的解。
一元二次方程的判别式Δ = b² - 4ac可以判断二次函数的零点情况:- 当Δ > 0时,方程有两个不相等的实根,函数图像与x轴有两个交点;- 当Δ = 0时,方程有两个相等的实根,函数图像与x轴有一个切点;- 当Δ < 0时,方程无实根,函数图像与x轴无交点。
4. 极值点二次函数在最高点(开口向下)或最低点(开口向上)取得极值。
当二次函数开口向上时,极小值等于函数的最低点y = k;当二次函数开口向下时,极大值等于函数的最高点y = k。
二、二次函数的应用1. 物理学应用二次函数在物理学中有广泛的应用,例如抛物线运动。
抛物线运动可以用二次函数的形式进行建模,通过分析和解决相关的二次函数问题,可以求得抛物线物体的最高点、运动轨迹等信息。
2. 经济学应用经济学中的一些问题也可以通过二次函数来描述和解决。
比如,成本函数和利润函数常常使用二次函数来表示,通过求解这些二次函数的极值点,可以确定最低成本、最大利润等关键数据。
3. 工程学应用工程学中的一些问题也可以用二次函数进行建模。
比如,在建筑设计中,可以用二次函数来描述一个拱形或穹顶的形状;在电子工程中可以通过二次函数来描述某些电子元件的特性和响应等等。
中考数学 考点系统复习 第三章 函数 第八节 二次函数性质的综合运用
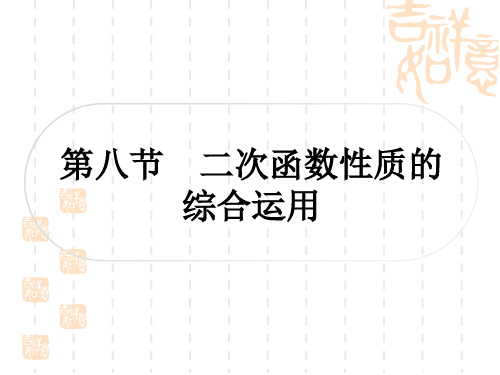
∴PQ=-x-3-(x2+2x-3)=-x2-3x=-x+322+94,
3
9
∴当 x=-2时,PQ 取得最大值,最大值为4.
(2)若点 D 是抛物线 L1上 A,C 两点之间的一动点,横坐标为 x(-3<x<0),
求四边形 ABCD 的面积 S 关于点 D 的横坐标 x 的函数解析式,并求 S 的最
(1)将抛物线向左平移 1 个单位长度,再向上平移 2 个单位长度,则平移 后的抛物线的解析式为yy==--xx22++2x2+x+2 2;
(2)将抛物线向左平移,平移后的抛物线过点(0,1),则平移后的抛物线 的解析式为 y=-x22++1 1;
(3)若抛物线平移后顶点一直在直线 y=x+1 上,则可设平移后抛物线的 顶点坐标为((mm,,mm++11)),平移后抛物线的解析式为 yy==--((xx--mm))22++m+m+1 1;
B.-4<a≤-32
(C )
C.-32≤a<0
D.-32<a<0
6.★如图,在“探索函数 y=ax2+bx+c 的系数 a,b,c 与图象的关系”
的活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,
1),D(2,3),同学们探索了经过其中三个点的二次函数的图象,发现这
些图象对应的函数解析式各不相同,其中 a 的最大值为
(1)若点 P 是线段 AC 上一点,过点 P 作 PQ⊥x 轴交抛物线 L1于点 Q.求 PQ
长的最大值; 解:抛物线 L1 的解析式为 y=x2+2x-3,
将点 A(-3,0)代入 y=kx-3,得-3k-3=0,解得 k=-1,
∴直线 AC 的解析式为 y=-x-3,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的图像和性质
二次函数的性质
例1. 关于抛物线2
21y x x =--,下列说法错误的是( )
A . 顶点坐标为()1,2-
B . 与y 轴的交点坐标为()0,1-
C . 抛物线上两点()()121,4,A y B y -和,则有12y y <
D . 当x >1时,y 随x 的增大而减小
1. 已知函数y =-x 2
-2x ,当________时,函数值y 随x 的增大而增大.
2. 抛物线2
21219y x x =-+的顶点坐标是( )
A. (3,1)
B. (3,-1)
C. (-3,1)
D. (-3,-1)
3. 2+bx +c (a ≠0)图象上部分点的坐标(x ,y )对应值列表如下:
则该函数图象的对称轴是( ) A. 直线x =-3 B. 直线x =-2 C. 直线x =-1 D. 直线x =0
函数平移
例2. 已知抛物线y =x 2
-4x +3与x 轴相交于点A ,B (点A 在点B 左侧),顶点为M ,平移该抛物线,使点M 平移后的对应点M ′落在x 轴上,点B 平移后的对应点B ′落在y 轴上,则平移后的抛物线解析式为( )
A. y =x 2+2x +1
B. y =x 2
+2x -1
C. y =x 2-2x +1
D. y =x 2
-2x -1
1. 要将抛物线y =x 2+2x +3平移后得到抛物线y =x 2
,下列平移方法正确的是( ) A. 向左平移1个单位,再向上平移2个单位 B. 向左平移1个单位,再向下平移2个单位 C. 向右平移1个单位,再向上平移2个单位 D. 向右平移1个单位,再向下平移2个单位
2. 在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°
得到抛物线y =x 2
+5x +6,则原抛物线的解析式是( )
A. y =-(x -52)2-114
B. y =-(x +52)2-11
4
C. y =-(x -52)2-14
D. y =-(x +52)2+1
4
3. 已知正方形ABCD 中A (1,1)、B (1,2)、C (2,2)、D (2,1),有一抛物线y =(x +1)2
向下平移m 个单位(m >0)与正方形ABCD 的边(包括四个顶点)有交点,则m 的取值范围是________.
函数图像与系数,,a b c 的关系
例3、二次函数y =ax 2
+bx +c ()0a ≠的图象如图所示,有下列9个结论①0abc >;②a
+c >b ;③2a +b=0;④0a b c ++>;⑤23c b <;⑥()a b m am b +≥+;
⑦2
40b ac ->;⑧()2
2
a c
b +>;
⑨
3c
a
>-正确的是__________
1、二次函数y =ax 2+bx +c 的图象如图所示,下列结论:①4ac <b 2
;②a +c >b ;③2a +b >0.其中正确的有 ( )
A .①②
B .①③
C .②③
D .①②③
2、如图是抛物线y 1=ax 2
+bx +c (a ≠0)的一部分图象,抛物线的顶点坐标是A (1,3),与x 轴的一个交点是B (4,0),直线y 2=mx +n (m ≠0)与抛物线交于A ,B 两点,下列结论:①abc
>0;②方程ax 2
+bx +c =3有两个相等的实数根;③抛物线与x 轴的另一个交点是(-1,0);④当1<x <4时,有y 2>y 1;⑤x (ax +b )≤a +b ,其中正确的结论是__________.(只填写序号)
3. (2013长沙10题3分)二次函数y =ax 2
+bx +c 的图象如图所示,则下列关系式错误..的是( )
A . a >0
B . c >0
C . b 2-4ac >0
D . a +b +c >0
4、已知二次函数2
y ax bx c =++(a ≠0)的图象如图所示,现有下列结论:①b 2
-4ac >0;②abc >0;③c a
>-8;④ 9a +3b +c <0.其中,正确结论的个数是( )
A. 1
B. 2
C. 3
D. 4
5、已知二次函数2
y ax bx c =++(a>0)经过点M (-1,2)和点N (1,-2),交x 轴于点A ,
B ,交y 轴于点
C . 现有以下四个结论:①2b =-;②该二次函数图象与y 轴交于负半轴;
③存在实数a ,使得M ,A ,C 三点在同一条直线上;④若1a =,则OA ·OB =OC 2
.其中,正
确的结论有( )
A. ①②③④
B. ②③④
C. ①②④
D. ①②③
函数图像的判断
例4、已知直线y =bx -c 与抛物线y =ax 2
+bx +c 在同一直角坐标系中的图象可能是( )
1、在同一平面直角坐标系中,函数y=ax+b 与y=ax 2
-bx 的图象可能是
( )
2. (2014长沙10题3分)函数y =a x
与y =ax 2
(a ≠0)在同一平面直角坐标系中的图象可能是( )
函数与不等式的关系
例5. 如图,直线y =mx +n 与抛物线y =ax 2
+bx +c 交于A (-1,p ),
B (4,q )两点,则关于x 的不等式mx +n >ax 2+bx +c 的解集是____.
1、如图,直线y =x +m 和抛物线y =x 2
+bx +c 都经过点A (1,0)
和B (3,2),不等式x 2
+bx +c >x +m 的解集为____________.
二次函数的最值
例6 已知二次函数y =x 2
-2mx (m 为常数),当-1≤x ≤2时,函数值y 的最小值为-2,则m 的值是( )
A. 32
B. 2
C. 32或 2
D. -3
2或 2
1、已知二次函数2
21y x x =-+
(1)若x 为任意实数,求函数的的最小值
(2)若12x ≤≤,求函数的的最大值和最小值
(3)若01x ≤≤,求函数的的最大值和最小值
(4)若20x -≤≤,求函数的的最大值和最小值
(5)若x 为整数,求函数的最小值
函数与方程的关系
例7、在平面直角坐标系xoy 中,抛物线2
43y x x =-+与x 轴交于点A ,B (点A 在点
B 的左侧),与y 轴交于点
C .
(1)求直线BC 的表达式;
(2)垂直于y 轴的直线l 与抛物线交于点P (x 1,y 1),Q (x 2,y 2),与直线BC 交于点N(x 3,y 3).若x 1<x 2<x 3,结合函数的图象,求x 1+x 2+x 3的取值范围.
1、已知关于x 的一元二次方程()2
510x k x k +-+-=,其中k 为常数.
(1)求证:无论k 为何值,方程总有两个不相等实数根;
(2)已知函数()2
51y x k x k =+-+-的图象不经过第三象限,求k 的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k 的最大整数值.
2、已知:二次函数2
2y ax bx =+-的图象经过点(1,0),一次函数图象经过原点和点(1,-b ),其中a >b >0且a 、b 为实数.
(1)求一次函数的表达式(用含b 的式子表示); (2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x 1、x 2,求|x 1-x 2|的取值范围.。
