第3章 排队系统与性能分析(1)-
单队 队长无限 先到先服务
2.队长
假定N(t)表示在时刻t系统中的顾客数，包括正在被服 务的顾客数，即N(t)表示时刻t系统的队长，t0，且令 pij(t)＝P{N(t+t)＝j|N(t)＝i}，i,j＝0,1,2,… 则 1)pi,i+1(t)＝P{在t内到达一个而服务未完成} ＋ P {在t内到达j个而服务完j-1个} ＝P{1t，1>t} ＋
描述排队系统的主要数量指标
c ——系统中并联服务台的数目； λ ——顾客的平均到达率； 1／λ ——顾客的平均到达间隔； μ ——服务台的平均服务率； 1/μ ——平均服务时间； N —— 稳态系统任一时刻的状态（即系统中所 有顾客数）；
描述排队系统的主要数量指标
ρ——服务强度，即每个服务台单位时间内的平 均服务时间，—般有ρ=λ／(cμ)，这是衡量排队 系统繁忙程度的重要尺度。
排队论起源于20世纪初丹麦电信工程师A.K. Erlang对电信系统的研究，现已发展成为一门 应用广泛的学科，在电信、交通运输、生产与 库存管理、计算机系统设计、计算机通信网络、 军事作战、柔性制造系统和系统可靠性等众多 领域，有着非常重要的应用。
排队的概念
排队是日常生活和工作中常见的现 象，由两个方面构成： 1. 要求得到服务——顾客 2. 提供服务——服务员或服务台 3. 顾客与服务台(二者缺一不可)就构 成一个排队系统，或称为随机服务 系统。
j1 j1
1+…+j+1t<1+…+j+2} i＝1,2,3,…
＝(1-e-t)e-t＋o(t) ＝t＋o(t)
3) 类似分析可得
pij(t)＝o(t)， |i-j|2
队长(续2)
综合上述1)2)3)得
t o( t ) j i 1, i 0 p ij ( t ) t o( t ) j i 1, i 1 o( t ) | i j | 2
问题的叙述
顾客到达为参数(>0)的泊松过程，即相继到 达的间隔时间序列{n ，n1}独立、服从参数为 (>0)的负指数分布F(t)＝1-e-t，t0； 顾客所需的服务时间序列{n,n1}独立、服从参
数为(>0)的负指数分布G(t)＝1-e-t，t0；
系统中只有一个服务台；
几个经典排队系统的符号表示
Mr/M/1/：顾客以每批为固定的r个成批到达， 批与批的到达间隔时间独立、服从负指数分布， 服务时间独立、服从负指数分布，有1个服务 台，容量为无穷的等待制系统 MX/Mr/1/：顾客成批到达，每批到达的数量 X是具有某个离散型概率分布律的随机变量， 批与批的到达间隔时间独立、服从负指数分布； 顾客成批服务、每批为r个顾客，且服务时间 独立、服从负指数分布；有1个服务台；容量 为无穷的等待制系统
及正则性
p 0 ( t ) p1 ( t ) 1
由初始条件p0(0)=1，或p1(0)=0（表示开始时服务窗 空闲着）可以解出 -( ) t p0 (t ) e 因系统仅有两个互通的状态，故存在平稳分布，也 即 lim p 0 ( t ) 存在，事实上由上式可知 t
①系统中顾客数(队长)的期望值E(N)；
②排队等待的顾客数(排队长)的期望值E(Nq)； ③顾客在系统中全部时间(逗留时间)的期望值
W；
④顾客排队等待时间的期望值Wq。
第2节 单服务窗口简单排队系统 损失制M/M/1/1
等待制M/M/1/∞ 混合制M/M/1/m
§2.1 损失制M/M/1/1
描述排队系统的主要数量指标
队长：系统中的顾客数(包括正在接受服务的顾客) 等待队长：系统中的排队等待的顾客数 等待时间：顾客进入系统的时刻起到开始接受服务止这 它们都是随机变量，是顾客和服务 忙期反映了系统中服务员的工作强 段时间 机构双方都十分关心的数量指标， 度。在排队系统中，统计平衡下忙 应确定它们的分布及有关矩。 逗留时间：顾客在系统中的等待时间与服务时间之和 期与闲期是交替出现的。 系统的忙期：从顾客到达空闲的系统，服务立即开始， 在假定到达与服务是彼此独立的条 刻画输出过程的主要指标是相继离 直到系统再次变为空闲的这段系统连续繁忙的时间 件下，等待时间与服务时间是相互 去的间隔时间和在一段已知时间内 独立的。它们是顾客最关心的数量 系统的闲期：系统连续保持空闲的时间 离去顾客的数目，这些指标从一个 指标，应用中关心的是统计平衡下 忙期循环：相邻两次忙期开始的时间间隔 侧面反映了系统的工作效率。 它们的分布及期望值。 输出过程：也称离去过程，指接受服务完毕的顾客相继 离开系统的过程。 。
网络分析与测试
顾 军 jgu@
第3章 排队系统与性能分析
1. 排队论简介
2. 单服务窗口简单排队系统
3. 具有可变输入率的M/M/1/ 4. 具有可变服务率的M/M/1/ 5. 具有不耐烦顾客的M/M/1/ 6. 单服务窗闭合式排队模型M/M/1/m/m
7. M/M/排队系统
数为(>0)的负指数分布G(t)＝1-e-t，t0；
系统中只有一个服务台； 容量为无穷大，而且来自达过程与服务过程彼此独立。
输入过程服从 顾客源 参数为 的 Poisson过程
生灭过程
排队系统
服务时间服从 参数为 的 负指数分布
无 限
排队结构
排队规则
服务 机构
服务规则
接受服务 后离去
1 p1 1
2
e (1 p1 ) p 0
1
§2.2 等待制排队系统M/M/1/ 顾客来源是无限的
输入过程是简单流 服务时间服从负指数分布
1. 问题的叙述
顾客到达为参数(>0)的泊松过程，即相继到 达的间隔时间序列{n ，n1}独立、服从参数为 (>0)的负指数分布F(t)＝1-e-t，t0； 顾客所需的服务时间序列{n,n1}独立、服从参
几个经典排队系统的符号表示
M/M/c/：输入过程是泊松流，服务时间服从 负指数分布，有c个服务台平行服务(0<c)， 容量为无穷的等待制系统 M/G/1/：输入过程是泊松流，服务时间独立、 服从一般概率分布，只有1个服务台，容量为 无穷的等待制系统 Ek/G/1/K：相继到达的间隔时间独立、服从k 阶爱尔朗分布，服务时间独立、服从一般概率 分布，只有1个服务台，容量为k(0k<)的混 合制系统 D/M/c/K：相继到达的间隔时间独立、服从定 长分布，服务时间独立、服从负指数分布，有 c个服务台平行服务，容量为k(ck<)的混合 制系统
j 2
P {1+…+jt<1+…+j+1，
j 2
1+…+j-1t<1+…+j}
＝(1-e-t)e-t＋o(t)
＝t＋o(t)
i＝0,1,2,…
队长(续1)
2) pi,i-1(t)＝P{在t内未到达而服务完成一个} ＋ P {在t内到达j个而服务完j+1个} ＝P{1>t，1t} ＋ P{1+…+jt<1+…+j+1，
1 p 0 lim p 0 ( t ) t 1
其中ρ表示系统的负荷水平或强度。
当系统中已有一个顾客时，新来的顾客只好离去， 故p1就是系统的损失概率P损，它等于
P损 p1 1 p 0
1
单位时间内平均损失的顾客数和平均进入系统的顾 客数各为
系统容量为1，即仅有一个排队位置而无排队等
待位置。
M/M/1/1排队模型的状 态流图
0
1
由K氏微分方程，可知t时刻系统处于空闲或 忙着的概率p0(t)或p1(t)分别满足下列方程
p '0 ( t ) p 0 ( t ) p1 ( t ) ' p1 ( t ) p1 ( t ) p 0 ( t )
服务机构
1) 服务台的数目
在多个服务台的情况下，是串联或是并联
2) 顾客所需的服务时间服从什么概率分布，
每个顾客所需的服务时间是否相互独立，
是成批服务或是单个服务
排队论所要研究解决的问题
面对拥挤现象，人们通常的做法是增加服 务设施，但是增加的数量越多，人力、物力的 支出就越大，甚至会出现空闲浪费，如果服务 设施太少，顾客排队等待的时间就会很长，这 样对顾客会带来不良影响。如何做到既保证一 定的服务质量指标，又使服务设施费用经济合 理，恰当地解决顾客排队时间与服务设施费用 大小这对矛盾，就是随机服务系统理论——排队 论所要研究解决的问题。
服务 机构
服务规则
接受服务 后离去
输入过程
描述顾客来源及顾客按怎样的规律抵达。
1) 顾客总体数
顾客的来源可能是有限的，也可能是无限的
2) 到达类型
顾客是单个到达，还是成批到达
3) 顾客相继到达的间隔时间服从什么概率分布， 分布函数是什么，到达的间隔时间之间是否独 立 在排队论中，一般假定顾客到达的间隔时间序列 {n|n1}相互独立、同分布。
经典排队系统的符号表示方法
一个排队系统是由许多条件决定的， 为简明起见，在经典的排队系统中，常 采用3～5个英文字母表示一个排队系统， 字母之间用斜线隔开： 第一个字母表示输入的分布类型 第二个字母表示服务时间的分布类型 第三个字母表示服务台的数目 第四个字母表示系统的容量 第五个字母表示顾客源中的顾客数目。
8. M/M/c/排队系统 9. M/M/c/K混合制排队系统 10. 多服务窗闭合式排队模型M/M/n/m/m
排队论问题实验报告(3篇)
第1篇一、实验背景排队论是运筹学的一个重要分支，主要研究在服务系统中顾客的等待时间和服务效率等问题。
在现实生活中，排队现象无处不在，如银行、医院、超市、餐厅等。
通过对排队问题的研究，可以帮助我们优化服务系统，提高顾客满意度，降低运营成本。
本实验旨在通过模拟排队系统，探究排队论在实际问题中的应用。
二、实验目的1. 理解排队论的基本概念和原理。
2. 掌握排队模型的建立方法。
3. 熟悉排队系统参数的估计和调整。
4. 分析排队系统的性能指标，如平均等待时间、服务效率等。
5. 培养运用排队论解决实际问题的能力。
三、实验内容1. 建立排队模型本实验以银行排队系统为例，建立M/M/1排队模型。
该模型假设顾客到达服从泊松分布，服务时间服从负指数分布，服务台数量为1。
2. 参数估计根据实际数据，估计排队系统参数。
假设顾客到达率为λ=2（人/分钟），服务时间为μ=5（分钟/人）。
3. 模拟排队系统使用计算机模拟排队系统，记录顾客到达、等待、服务、离开等过程。
4. 性能分析分析排队系统的性能指标，如平均等待时间、服务效率、顾客满意度等。
四、实验步骤1. 初始化参数设置顾客到达率λ、服务时间μ、服务台数量n。
2. 生成顾客到达序列根据泊松分布生成顾客到达序列。
3. 模拟排队过程（1）当服务台空闲时，允许顾客进入队列。
（2）当顾客进入队列后，开始计时，等待服务。
（3）当服务台服务完毕，顾客离开，开始下一个顾客的服务。
4. 统计性能指标记录顾客等待时间、服务时间、顾客满意度等数据。
5. 分析结果根据实验数据，分析排队系统的性能，并提出优化建议。
五、实验结果与分析1. 平均等待时间根据模拟结果，平均等待时间为2.5分钟。
2. 服务效率服务效率为80%，即每分钟处理0.8个顾客。
3. 顾客满意度根据模拟结果，顾客满意度为85%。
4. 优化建议（1）增加服务台数量，提高服务效率。
（2）优化顾客到达率，降低顾客等待时间。
（3）调整服务时间，缩短顾客等待时间。
《运筹学排队论》课件
合理分配服务器资源，以提高系统的吞吐量 和响应时间。
最优服务策略问题
总结词
研究如何制定最优的服务策略，以最大化系 统的性能指标。
服务顺序策略
确定服务器的服务顺序，以最小化顾客的等 待时间和平均逗留时间。
服务中断策略
在服务器出现故障时，选择最优的服务中断 策略，以最小化对顾客的影响。
服务时间分布策略
等待队长
指在某一时刻，正在等待服务的顾客总数。
逗留时间与等待时间
逗留时间
指顾客从到达系统到离开系统所经过的时间 。包括接受服务和等待的时间。
等待时间
指顾客到达系统后到开始接受服务所经过的 时间。
忙期与空闲期
要点一
忙期
指系统连续有顾客到达并接受服务的时间段。在这个时间 段内，系统内的顾客数可能会超过系统的容量。
03
02
交通运输
分析铁路、公路、航空等交通系统 的调度和运输效率。
计算机科学
研究计算机网络、云计算、分布式 系统的性能和优化。
04
排队论的基本概念
服务器
提供服务的设施或 人员。
等待时间
顾客到达后到开始 接受服务所需的时 间。
顾客
需要接受服务的对 象。
队列
顾客按到达顺序等 待服务的排列。
服务时间
顾客接受服务所需 的时间。
《运筹学排队论》ppt课件
目录
• 排队论简介 • 排队系统的组成 • 排队模型的分类 • 排队模型的性能指标 • 排队论的优化问题 • 排队论的发展趋势与展望
01
排队论简介
排队论的定义与背景
1
排队论（Queueing Theory）是运筹学的一个重 要分支，主要研究排队系统（Queueing Systems）的行为特性。
银行排队系统实验报告
一、实验目的1. 熟悉银行排队系统的基本原理和设计方法；2. 掌握使用C语言实现银行排队系统的基本操作；3. 培养团队合作精神和实践能力。
二、实验环境1. 操作系统：Windows 102. 编程语言：C语言3. 开发工具：Visual Studio三、实验内容1. 银行排队系统简介银行排队系统是一种模拟真实银行排队场景的程序，主要功能包括：客户到达、排队、服务、离开等。
通过模拟银行排队过程，我们可以了解银行排队系统的基本原理，并为实际应用提供参考。
2. 系统设计（1）数据结构本系统采用队列数据结构来存储排队客户。
队列是一种先进先出（FIFO）的数据结构，适用于模拟银行排队场景。
（2）功能模块本系统主要包括以下功能模块：1）客户到达模块：模拟客户到达银行，并随机生成客户信息，如客户ID、到达时间、服务时间等；2）排队模块：根据客户到达顺序，将客户信息依次加入队列；3）服务模块：按照客户排队顺序，为每位客户提供服务，并更新客户状态；4）离开模块：客户服务完成后，从队列中移除该客户信息；5）统计模块：记录客户服务次数、平均等待时间、最长等待时间等数据。
（3）实现方法1）客户到达模块：使用随机数生成器生成客户信息，并将客户信息存入队列；2）排队模块：当客户到达时，将客户信息加入队列尾部；3）服务模块：从队列头部取出客户信息，为该客户提供服务，并更新客户状态；4）离开模块：当客户服务完成后，从队列中移除该客户信息；5）统计模块：记录客户服务次数、平均等待时间、最长等待时间等数据。
3. 实验步骤（1）初始化系统，设置窗口数量和客户到达时间间隔；（2）模拟客户到达，生成客户信息并加入队列；（3）按照客户到达顺序，为每位客户提供服务；（4）记录客户服务次数、平均等待时间、最长等待时间等数据；（5）统计实验结果，分析银行排队系统性能。
四、实验结果与分析1. 实验结果通过实验，我们得到了以下数据：（1）客户服务次数：100次；（2）平均等待时间：5分钟；（3）最长等待时间：15分钟。
07：排队网络模型的性能分析
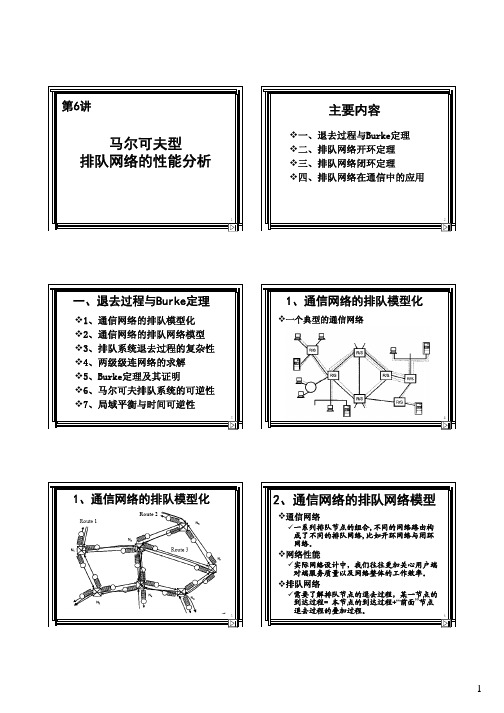
一个典型的通信网络8泊松分布过程的一个例子。
10111522 237、局部平衡与时间可逆性30312、Jackson网络－独立性假设几点独立性假设9相互独立的外部到达、泊松过程9相互独立的服务时间、负指数分布•同一个顾客在不同的排队节点遵循相互独立、且有可能不同参数的负指数分布。
9相互独立的路由策略•在某一节点接受完服务后独立地决定下一节点的路由、或者退出该排队网络。
322、Jackson网络－稳态概率()()()111212,,,,mi i j jij m m i r P I Q r r r λλλγλλλγ−=+Λ−Λ∑L L ＝对于节点，顾客到达率如下：用矩阵形式可以表示为：＝其中：＝＝33111212122212m m m mm m P P P P P P QPP P ⎛⎞⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎝⎠L L M M M M L Q矩阵的性质9对于开环网络来说，至少存在一个节点i有ri>0或者mij 1P 0>∑j=0－343、Jackson定理Jackson 定理9对于一个平稳状态的Jackson网络，在任一节点内的顾客数与其它节点的存在的顾客数无关。
9队长的概率分布Pn=P(n1,n2,…n m )等于每个单个节点队列长度概率分布的积。
353、Jackson定理()()()()()()()121122001100,,,!!!!iii i i i i i mm mn ii i i i i sn s i i i i n s s i i in i i i i ii i iP n n n p n p n p n ap n s n p n a p n s s a a s p n s s a s i a ρλµ−−−==⋅⎧≤⎪⎪=⎨⎪>⎪⎩⎛⎞=+⋅⎜⎟−⎝⎠=∑L L ，，为第个排队节点的服务者数,363、杰克逊网络通信量方程解）非奇异性，存在唯一（）＝－（则＝令稳态总体流量：通信量方程：Q -I Q I }{},{11γλλλλγλγλij i Mi i j Mi jij i i q Q q q ==+=∑∑==iiλiγiq 11λMiM q λ38399虽然外部顾客以泊松过程到达节点i，但实际到达于第i个节点的顾客为非泊松分布过程。
排队理论实验报告
一、实验目的1. 了解排队理论的基本概念和原理。
2. 掌握排队模型的应用，分析排队系统中的服务质量和效率。
3. 通过实验，提高对排队理论在实际生活中的应用能力。
二、实验背景排队理论是研究在有限资源条件下，顾客（或实体）排队等待服务的规律和特点的学科。
排队理论广泛应用于服务行业、交通、物流等领域。
通过研究排队理论，可以优化资源配置，提高服务质量，降低顾客等待时间。
三、实验内容1. 实验设备：计算机、排队理论软件（如Minitab、R等）。
2. 实验数据：模拟排队系统的顾客到达时间、服务时间等数据。
3. 实验步骤：（1）建立排队模型：根据实验需求，选择合适的排队模型，如M/M/1、M/M/c等。
（2）输入实验数据：将模拟排队系统的顾客到达时间、服务时间等数据输入到排队理论软件中。
（3）运行实验：启动排队理论软件，进行实验模拟。
（4）分析结果：观察并分析排队系统的性能指标，如平均等待时间、平均排队长度、服务台利用率等。
（5）优化排队系统：根据实验结果，调整排队系统参数，如服务台数量、顾客到达率等，以提高系统性能。
四、实验结果与分析1. 实验结果（1）平均等待时间：5.2分钟（2）平均排队长度：3.5人（3）服务台利用率：0.82. 分析（1）平均等待时间较长，说明排队系统在高峰时段可能存在拥堵现象，需要进一步优化。
（2）平均排队长度较高，可能导致顾客满意度下降，需要提高服务台数量或调整顾客到达率。
（3）服务台利用率较低，说明服务台资源未得到充分利用，可以考虑增加服务台数量。
五、实验结论通过本次实验，我们了解了排队理论的基本概念和原理，掌握了排队模型的应用，分析了排队系统中的服务质量和效率。
实验结果表明，排队系统在实际应用中存在一定的问题，需要通过调整系统参数来提高系统性能。
六、实验建议1. 优化排队模型：根据实际情况，选择合适的排队模型，以提高实验结果的准确性。
2. 调整实验数据：根据实际情况，调整顾客到达时间、服务时间等数据，以更真实地反映排队系统性能。
第三章_3 MG1型排队系统
Xidian Univ.
P-K公式
下面我们将证明，M/G/1排队系统的平均等待时间 为
X 2 W 21
其中，
X
该式称为P-K（Pollaczek-Khinchin）公式。
Broadband Wireless Communications Laboratory, Xidian University
Broadband Wireless Communications Laboratory, Xidian University
Xidian Univ.
P-K公式
例 返回n－ARQ系统的时延性能分析
设返回n－ARQ系统中的分组到达过程是速率为
的Poisson过程，
分组（帧）长度相同，为一个单位， 等待应答的最长时间（重传间隔）为
2 1
m 21
Broadband Wireless Communications Laboratory, Xidian University
Xidian Univ.
假设m个信道变成以时隙为基础，时隙的宽度为m个单位，所
有m个信道，每个信道的分组到达率为
m ，
每个分组的传输时间为m个单位时间，即服务时
间
1 m
。
在该系统中，只要分组到达时信道空闲，该分组就会
立即得到服务。显然每个信道是标准的M/D/1排队系统，
其等待时间为
＝ m
W FDM
( m) 1 m
M t
1 r d 0 t
t
i 1
1 2 Xi 2
第三章_系统需求分析及可行性分析
第三章 系统需求分析及可行性分析
黄 海 bupthuanghai@
基于计算机系统的系统分析
可行性分析 系统体系结构建模 系统流程图 系统分析的总结
2
§3.1 基于计算机系统的 系统分析
计算机系统是元素的集合或排列
➢ 软件：是指计算机程序、数据结构、逻辑方法、过程 或控制的相关文档。
➢ ACD“建立了待实现系统与系统运行环境之 间的信息边界”，即ACD定义了系统使用信 息的所有外部生产者、系统创建消息的所有 外部消费者、以及所有通过界面通信或完成 维护和自测试的实体。
26
§3.3 系统体系结构建模
条码阅读器
条码
传送带
速度指示器
分类点 操作员
请求 查询及报告
传送带分类系统
分类命令
13
§3.2 可行性分析
(1) 成本估算技术
➢ 代码行技术 ➢ 功能点技术 ➢ 任务分解技术 ➢ 经验估算模型 ➢ COCOMO模型 ➢ 软件方程式 ➢ 其他成本估算内容(设备、人力、材料、管理等)
普通存在的问题是：成本估算往往偏低，其结果 是一次次地追加费用，造成骑虎难下的局面。
14
§3.2 可行性分析
1
9.6
2
9.6
3
9.6
4
9.6
5
9.6
1.0500 9.1429
9.1429
1.1025 8.7075
17.8503
1.1576 8.2928
26.1432
1.2155 7.8979
34.0411
1.2763 7.5219
41.5630
16
§3.2 可行性分析
办事大厅排队叫号系统(排队机,呼叫器,LED显示屏等)解决计划1.doc
办事大厅排队叫号系统(排队机,呼叫器,LED显示屏等)解决方案1聚宝SMARTQ大厅版排队系统一、SMARTQ排队系统简介(2)二.系统综述(3)2.1系统概述(3)2.2系统组成(3)2.2.1系统组成平面结构示意图(4)2.2.2系统组成拓展结构示意图(4)三、服务大厅场地布局(6)四、系统产品介绍及布线安排(8)4.1 产品介绍(8)4.1.1 自动取号机(8)4.1.2 物理呼叫终端(10)4.1.3 窗口显示终端（屏）(10)4.1.4语音系统(12)4.1.5星级评价系统(13)4.1.6系统分配器(15)4.2系统连接方式(15)4.3系统的布线安排(16)4.4 系统的故障检测(16)4.5 各硬件设备接口类型(16)五、系统的使用方法(17)5.1办事流程(17)5.2案例说明(17)5.3系统功能介绍(19)六、售后服务承诺及技术保障(19)前言非常感谢您选用ＳＭＡＲＴＱ排队系统！聚宝科技（杭州）有限公司是新加坡SMARTQ SYSTEMS 公司与海外上市公司：聚宝科技在中国杭州设立的一家专业从事排队叫号管理系统销售与服务于一体的高科技代理企业，直接负责中国市场的开拓与服务.母公司新加坡SMARTQ SYSTEMS公司成立于1980年，从事于排队管理系统至今已有20余年历史，完成项目数以千计，业务遍及全世界，成绩斐然。
SMARTQ排队管理系统是近年来为改善服务机构及医院传统排队管理所存在的一些混乱、无序等弊端而开发的，系统能很好地解决顾客在排队中所遇到的各种拥挤和混乱等现象，为顾客办事及单位管理带来莫大的方便和愉悦，做到人人公正，合理有序.同时，系统也对顾客情况及服务员工的工作状况作出各种统计，为管理层进一步正确决策提供了有力的依据.。
公司依拓新加坡总部研发中心，现已开发了电脑型PCQS、程控型CTQS、立队型SAQS、简易型SCQS四类排队管理系统，它们广泛适用于银行、医院、移动、电信、邮政、工商、公安、税务、交通等各等候区域和办事大厅.产品自投放市场以来，赢得了用户的信赖和好评，取得了良好的经济效益和社会效益。
《2024年带(N,n)抢占优先权的排队系统研究》范文
《带(N,n)抢占优先权的排队系统研究》篇一一、引言排队系统作为运筹学中的一个重要研究领域，广泛应用于电信、计算机、交通等多个领域。
其中，具有抢占优先权的排队系统更是在现实应用中具有重要的价值。
本文将对带(N,n)抢占优先权的排队系统进行研究，通过对系统的特性进行建模和模拟，以探究其运行机制及性能特点。
二、系统概述带(N,n)抢占优先权的排队系统是一种具有特殊性质的排队系统。
在这种系统中，顾客的到达遵循一定的概率分布，每个顾客都有其优先级，当有更高优先级的顾客到达时，当前服务的顾客会被打断并由新到的顾客取而代之。
这里，“N”代表系统的服务台数量，“n”表示同时能服务的最大顾客数。
这种系统的设计能够提高服务质量并保证关键任务及时得到处理。
三、模型建立为了研究带(N,n)抢占优先权的排队系统，我们首先需要建立数学模型。
该模型包括以下几个部分：1. 顾客到达模型：我们假设顾客的到达遵循某种概率分布，如泊松分布或负指数分布等。
2. 服务时间模型：服务时间同样遵循一定的概率分布，如正态分布等。
3. 优先级模型：我们设定每个顾客有一个优先级，并依据此决定服务的先后顺序。
高优先级的顾客会抢占正在接受服务的低优先级顾客。
4. 系统状态模型：我们需要描述系统在不同条件下的状态变化，如等待的顾客数、服务的顾客数等。
四、性能分析通过数学建模和仿真模拟，我们可以对带(N,n)抢占优先权的排队系统的性能进行分析。
主要包括以下几个方面：1. 等待时间：分析顾客在系统中的平均等待时间，包括从进入系统到开始接受服务的时间以及从等待到完成服务的时间。
2. 吞吐量：研究系统的服务能力，即单位时间内能处理的顾客数量。
3. 效率：评估系统的效率，包括服务效率和服务台的利用率等。
4. 稳定性：分析系统的稳定性，即在不同条件下系统的运行状态是否稳定。
五、实验与结果分析为了验证模型的准确性，我们进行了大量的实验和仿真模拟。
通过改变不同的参数（如服务台数量、顾客到达率、服务时间等），我们观察了系统性能的变化。
运筹学中的排队网络模型-教案
运筹学中的排队网络模型-教案一、引言1.1排队现象的普遍性1.1.1生活中的排队：超市结账、银行柜台1.1.2工业中的排队：机器维修、订单处理1.1.3交通中的排队：车辆排队、信号灯控制1.1.4计算机网络中的排队：数据包传输、服务器响应1.2排队网络模型的重要性1.2.1提高服务效率：通过模型优化减少等待时间1.2.2资源合理分配：平衡服务点的工作负载1.2.3预测系统性能：评估不同场景下的系统表现1.2.4支持决策制定：为服务设施设计和管理提供依据1.3教学目标和结构安排1.3.1理论与实践结合：理解排队理论及其应用1.3.2分析与建模能力：学会构建和解决排队网络模型1.3.3综合案例分析：通过实例深化理解1.3.4教学方法：讲授、讨论、练习和项目作业相结合二、知识点讲解2.1排队论基础2.1.1排队系统的基本组成：顾客源、队列和服务设施2.1.2排队系统的性能指标：队长、等待时间、服务利用率2.1.3排队论的典型模型：M/M/1、M/M/c、M/G/12.1.4排队论的数学工具：概率论、随机过程2.2排队网络模型2.2.1单节点排队网络：单个服务设施2.2.2多节点排队网络：多个服务设施串联或并联2.2.3开放排队网络：顾客可以加入或离开系统2.2.4封闭排队网络：顾客总数固定2.3排队网络的分析方法2.3.1平衡方程法：求解稳态概率分布2.3.2矩阵几何法：适用于多节点网络2.3.3计算机仿真法：模拟排队过程2.3.4最优化方法：优化网络设计和服务策略三、教学内容3.1排队网络模型的构建3.1.1确定模型类型：根据实际情况选择单节点或多节点模型3.1.2参数估计：利用历史数据估计到达率、服务率等参数3.1.3模型验证：通过与实际数据对比验证模型的准确性3.1.4模型简化：在保持精度的前提下简化模型以提高计算效率3.2排队网络模型的求解3.2.1稳态分析：求解稳态概率分布和性能指标3.2.2瞬态分析：研究系统随时间的动态变化3.2.3灵敏度分析：评估参数变化对系统性能的影响3.2.4启发式算法：在复杂模型中寻找近似解3.3排队网络模型的应用3.3.1服务业中的应用：银行、医院、呼叫中心3.3.2制造业中的应用：生产线的优化、设备维护3.3.3交通运输中的应用：机场登机、交通信号控制3.3.4计算机网络中的应用：数据中心的设计、网络协议的优化四、教学目标4.1知识与技能目标4.1.1理解排队论的基本概念和组成4.1.2掌握单节点和多节点排队网络的特点4.1.3学会构建和求解排队网络模型4.1.4能够运用排队网络模型解决实际问题4.2过程与方法目标4.2.1培养学生的逻辑思维和抽象思维能力4.2.2提高学生的数据分析能力和数学建模能力4.2.3增强学生的计算机操作能力和软件应用能力4.2.4锻炼学生的团队合作能力和沟通协调能力4.3情感态度与价值观目标4.3.1培养学生对运筹学的兴趣和热情4.3.2增强学生对科学方法的认识和理解4.3.3提高学生的创新意识和解决问题的能力4.3.4培养学生的社会责任感和职业道德五、教学难点与重点5.1教学难点5.1.1排队网络模型的构建：确定模型类型和参数估计5.1.2排队网络模型的求解：稳态分析和瞬态分析5.1.3排队网络模型的应用：实际问题的解决和优化5.2教学重点5.2.1排队论的基本概念和性能指标5.2.2单节点和多节点排队网络的特点和区别5.2.3排队网络模型的求解方法和应用领域5.3教学难点与重点的关系5.3.1教学难点是学生在学习过程中可能遇到的困难和挑战5.3.2教学重点是学生需要掌握的核心知识和技能5.3.3教学难点和重点相互关联，解决难点有助于掌握重点5.3.4教学难点和重点的突破需要教师的有效引导和学生的积极参与六、教具与学具准备6.1教具准备6.1.1投影仪和电脑：用于展示教学课件和实例分析6.1.2白板和马克笔：用于讲解和演示排队网络模型6.1.3教学软件：用于模拟和求解排队网络模型6.1.4实际案例资料：用于分析和讨论排队网络模型的应用6.2学具准备6.2.1笔记本和教材：用于记录和复习排队网络模型的知识点6.2.2计算器：用于计算和求解排队网络模型的性能指标6.2.3计算机软件：用于构建和求解排队网络模型6.2.4实际案例数据：用于分析和解决实际问题6.3教具与学具的使用6.3.1教具的使用：教师应根据教学内容和目标选择合适的教具6.3.2学具的使用：学生应根据学习任务和目标选择合适的学具6.3.3教具与学具的结合使用：教师和学生应共同参与教学活动，促进互动和合作6.3.4教具与学具的评价：教师和学生应定期评估教具和学具的效果和适用性七、教学过程7.1导入新课7.1.1引入排队现象和排队网络模型的概念7.1.2提出问题：如何优化排队网络和提高服务效率7.1.3引发学生的兴趣和思考7.1.4导入新课的教学目标和内容7.2课堂讲解7.2.1讲解排队论的基本概念和组成7.2.2介绍单节点和多节点排队网络的特点和区别7.2.3讲解排队网络模型的构建和求解方法7.2.4通过实例分析和讨论排队网络模型的应用7.3课堂练习与讨论7.3.1布置课堂练习：构建和求解排队网络模型7.3.2分组讨论：分析和解决实际问题7.3.3教师指导和解惑：解答学生的疑问和困惑7.3.4学生展示和分享：展示练习成果和讨论结果7.4课堂小结与作业布置7.4.2强调学生的掌握程度和存在的问题7.4.3布置课后作业：巩固和拓展排队网络模型的知识7.4.4提醒学生下节课的教学内容和预习要求八、板书设计8.1排队网络模型的基本概念8.1.1排队系统的基本组成8.1.2排队系统的性能指标8.1.3排队论的典型模型8.1.4排队论的数学工具8.2排队网络模型的构建与求解8.2.1单节点排队网络8.2.2多节点排队网络8.2.3开放排队网络8.2.4封闭排队网络8.3排队网络模型的应用8.3.1服务业中的应用8.3.2制造业中的应用8.3.3交通运输中的应用8.3.4计算机网络中的应用九、作业设计9.1基础练习题9.1.1排队网络模型的基本概念和性能指标9.1.2单节点和多节点排队网络的特点和区别9.1.3排队网络模型的构建和求解方法9.2实际案例分析题9.2.1分析和解决实际问题9.2.2建构和求解实际排队网络模型9.2.3评估排队网络模型的性能和优化效果9.3探究性课题9.3.1研究排队网络模型的扩展和应用9.3.2探讨排队网络模型在其他领域的应用9.3.3创新排队网络模型的理论和方法十、课后反思及拓展延伸10.1教学反思10.1.1教学内容的深度和广度10.1.2教学方法和手段的有效性10.1.3学生的参与度和理解程度10.1.4教学目标达成情况的评估10.2拓展延伸10.2.1排队网络模型在其他领域的应用10.2.2排队网络模型的最新研究和发展10.2.3排队网络模型与其他运筹学方法的结合10.2.4排队网络模型在实际问题中的应用案例重点关注环节的补充和说明：1.教学内容的深度和广度：在讲解排队网络模型时，应注重理论与实践相结合，通过实际案例分析加深学生对理论的理解和应用能力。