三角形、四边形测试题
新北师大版数学四年级下册第2单元《认识三角形和四边形》测试卷含答案

北师大版数学四年级下册第2单元《认识三角形和四边形》测试卷含答案姓名: 班级: 得分:一、选择题(10分)1.下面四根小棒中,哪三根不能围成一个三角形()。
① 10cm ② 8cm ③ 3cm ④ 7cmA.①②③B.②③④C.①②④D.①③④2.在三角形的三个内角中,至少有()。
A.一个直角和一个钝角B.一个钝角和一个锐角C.两个锐角3.只有一组对边平行的四边形是()。
A.长方形B.正方形C.梯形D.平行四边形4.一个等腰三角形的两条边长分别是6厘米和14厘米,这个三角形的周长是()厘米。
A.34 B.26 C.18 D.425.当一个三角形的两条边分别长2厘米、5厘米时,第三条边的长度可能是()厘米。
A.6 B.8 C.76.做房屋的屋架是运用了三角形的()。
A.有三条边的特性B.易变形的特性C.稳定不变形的特性7.—个等腰三角形的周长是48厘米,腰长是18厘米,底边长是()厘米。
A.15 B.12 C.108.—个等腰三角形,其中一个底角是68°,顶角是()。
A.68°B.44°C.36°9.一个三角形有两个角分别是52°、38°,这个三角形是()。
A.直角三角形B.钝角三角形C.锐角三角形10.下图是一个( )三角形。
A.锐角B.钝角C.直角二、填空题(28分)11.把一个大三角形剪成两个小三角形,小三角形的内角和是(_______)度。
12.在直角三角形中,两个锐角相等,这个三角形的内角分别是(______)、(______)、(_____)。
13.三个角都是60°的三角形既是(_______)三角形,又是(________)三角形。
14.三角形的其中两个内角分别是54°和37°,按角分它是(__________)三角形。
15.两根小棒分别长4厘米和8厘米,再有一根至少长(__________)厘米的小棒就能围成一个三角形了。
三角形四边形看图形周长面积专项练习30题(有答案)ok
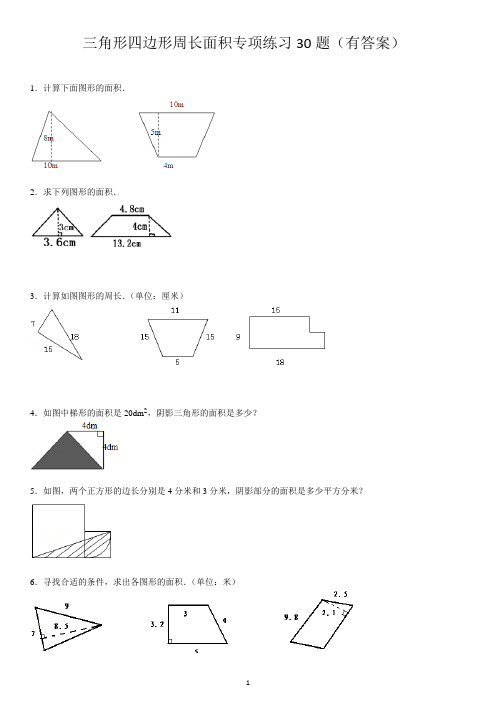
三角形四边形周长面积专项练习30题(有答案)1.计算下面图形的面积.2.求下列图形的面积.3.计算如图图形的周长.(单位:厘米)4.如图中梯形的面积是20dm2,阴影三角形的面积是多少?5.如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?6.寻找合适的条件,求出各图形的面积.(单位:米)7.算出下面图形的面积.8.求阴影部分面积.单位:厘米.9.图形王国展风采.(求下面图形的周长,单位:厘米.)10.找准所需条件,计算下列图形的面积.(单位:米)11.求下面图形的面积.12.如图:三角形ABC的面积是6cm2,AB长4cm,求AB边上的高CD的长.13.如图所示,BC长为5,求画阴影线的两个三角形的面积之和.14.找准所需条件,计算下列图形的面积.(单位:米)15.如图,直角三角形的三条边分别长3cm、4cm、5cm,求最长边上的高为多少厘米.16.17.选择合适的数据计算下面图形的面积.18.求下面图形的面积.(单位:厘米)请同学们先写出每个图形的面积计算字母公式,然后再进行计算.19.计算下面图形或阴影部分的面积.(单位:cm)20.找出如图所需数据再求出面积.(单位:cm)21.一个三角形的底长是5m,如果底边延长1m,那么面积就增加1.5m2,请你求出原来三角形的面积是多少平方米?22.三角形ABC是一个正三角形,求这个图形的周长.23.求下面图形中阴影部分的面积.24.求下面各图形中涂色部分的面积25.如图,长方形的长是12cm,宽是5cm,三角形①的面积是24cm2,阴影部分面积是多少?26.求下面图形的面积.(单位:厘米)27.28.下面平行四边形中,涂色部分的面积是10平方分米求空白部分的面积.(单位:分米)29.30.如图数字分别表示两个长方形和一个直角三角形的面积,另一个三角形面积是_________.参考答案:1.三角形的面积:10×8÷2=80÷2,=40(m2);梯形的面积:(4+10)×5÷2=14×5÷2,=35(m2);答:三角形的面积为40(m2);梯形的面积为35(m2).2.(1)3.6×3÷2=5.4(平方厘米);(2)(4.8+13.2)×4÷2,=18×4÷2,=36(平方厘米);答:三角形的面积是5.4平方厘米,梯形的面积是36平方厘米3.①7+15+18=40(厘米);②5+11+15×2,=16+30,=46(厘米);③(18+9)×2=27×2,=54(厘米).答:三角形的周长是40厘米,等腰梯形的周长是46厘米,六边形的周长是54厘米.4.20﹣4×4÷2,=20﹣8,=12(平方分米),答:阴影三角形的面积是12平方分米.5.(4+3)×3÷2﹣(3×3﹣×3.14×32),=7×3÷2(9﹣7.065),=10.5﹣1.935,=8.565(平方分米);答:阴影部分的面积是8.565平方分米6.(1)三角形的面积:7×8.5÷2,=59.5÷2,=29.75(平方米);(2)梯形的面积:(3+5)×3.2÷2,=8×3.2÷2,=25.6÷2,=12.8(平方米);(3)平行四边形的面积:9.8×2.1=20.58(平方米);答:三角形的面积是29.75平方米,梯形的面积是12.8平方米,平行四边形的面积是20.58平方米7.(1)3.6×2.5÷2=4.5(平方厘米);(2)(1.4+4.6)×3.2÷2=6×3.2÷2=9.6(平方分米);(3)6.2×3.5=21.7(平方米);答:三角形的面积是4.5平方厘米;梯形的面积是9.6平方分米;平行四边形的面积是21.7平方米.8.12×12×=36(平方厘米);答:阴影部分的面积为36平方厘米.9.①6+7+9=22(厘米);②(13+24)×2=37×2,=74(厘米);③7+8+6+5+3+4=33(厘米);④32×4=128(厘米);答:三角形的周长是22厘米,长方形的周长是74厘米,六边形的周长是33厘米,正方形的周长是128厘米.10.(1)6×8÷2=24(平方米);(2)(14+24)×10÷2,=38×10÷2,=190(平方米);答:三角形的面积是24平方米;梯形的面积是190平方米11.(1)2.4×0.9÷2=1.08(平方厘米);(2)2.2×1.2+2.2×0.8÷2,=2.64+0.88,=3.52(平方分米);答:甲图形的面积是1.08平方厘米,乙图形的面积是3.52平方分米.12.6×2÷4,=12÷4,=3(cm);答:AB边上的高CD的长为3厘米.13.(5×5÷2﹣5×2÷2)×2,=(12.5﹣5)×2,=7.5×2,=15,答:阴影线的两个三角形的面积之和是15.14.三角形的面积:3×4÷2,=12÷2,=6(平方米);梯形的面积:(8+12)×10÷2,=20×10÷2,=200÷2,=100(平方米);组合图形的面积:6.3×4×2,=25.2×2,=50.4(平方米);答:三角形的面积是6平方米,梯形的面积是100平方米,组合图形的面积是50.4平方米15.3×4÷2×2÷5,=12÷5,=2.4(厘米),答:这个三角形最长边上的高2.4厘米,16.(27×2÷9)×5÷2,=(54÷9)×5÷2,=6×5÷2,=30÷2,=15(平方米);答:阴影部分的面积是15平方米.17.(1)30×40÷2,=1200÷2,=600(平方厘米),答:三角形的面积是600平方厘米;(2)15×8=120(平方分米),答:平行四边形的面积是120平方分米;(3)(8+15)×10÷2,=23×10÷2,=230÷2,=115(平方厘米),答:梯形的面积是115平方厘米.18.S△=ah÷2,=8×6÷2,=48÷2,=24(平方厘米);S▱=ah,=12×15,=180(平方厘米);S梯形=(a+b)h÷2,=(10+18)×12÷2,=28×12÷2,=336÷2,=168(平方厘米);答:三角形、平行四边形和梯形的面积分别是24平方厘米、180平方厘米和168平方厘米19.(1)12×4.5÷2,=4.5×6,=27(平方厘米),(2)8×8=64(平方厘米),(3)42×2÷15=5.6(厘米),(4.5+15)×5.6÷2,=19.5×5.6÷2,=54.6(平方厘米).20.(1)20×22÷2=220(平方厘米);答:三角形的面积是220平方厘米.(2)(18+12)×10÷2,=30×10÷2,=150(平方厘米);答:图形的面积是150平方厘米.(3)10×8=80(平方厘米);答:平行四边形的面积是80平方厘米21.原三角形的高:1.5×2÷1=3(米),原三角形的面积:5×3÷2=7.5(平方米);答:原来三角形的面积是7.5平方米.22.6×2+3.14×6×,=12+9.42,=21.42(厘米),答:这个图形的周长是21.42厘米.23.14×12÷2=84(平方厘米);答:阴影部分的面积是84平方厘米.24.(60+80)×30÷2﹣60×20÷2,=2100﹣600,=1500(平方厘米);答:图形中涂色部分的面积1500平方厘米25.阴影部分的面积:12×5﹣24=36(平方厘米);答:阴影部分的面积是36平方厘米.26.(1)8×6÷2,=48÷2,=24(平方厘米);(2)12×15=180(平方厘米);(3)(10+18)×12÷2,=28×12×,=28×6,=168(平方厘米),答:三角形的面积是24平方厘米,平行四边形的面积是180平方厘米,梯形的面积是168平方厘米.27.8×5÷2,=40÷2,=20,答:阴影部分是面积是20.28.因为空白部分的高=阴影部分的高,所以空白部分梯形的高为:10×2÷5=4(分米);空白部分的面积:(3+3+5)×4÷2,=11×4÷2,=44÷2,=22(平方分米);答:空白部分的面积是22平方分米.29.7×4﹣7×4÷2,=28﹣14,=14(平方厘米).答:阴影部分的面积是14平方厘米.30.因为AO×OD=15,OC×OE=12,所以AO×OD×OC×OE=15×12,而OD×OE=5×2=10,所以OA×OC=15×12÷10=18,所以另一个三角形面积是:18÷2=9,答:另一个三角形面积是9,故答案为:9。
三角形四边形中考经典综合题
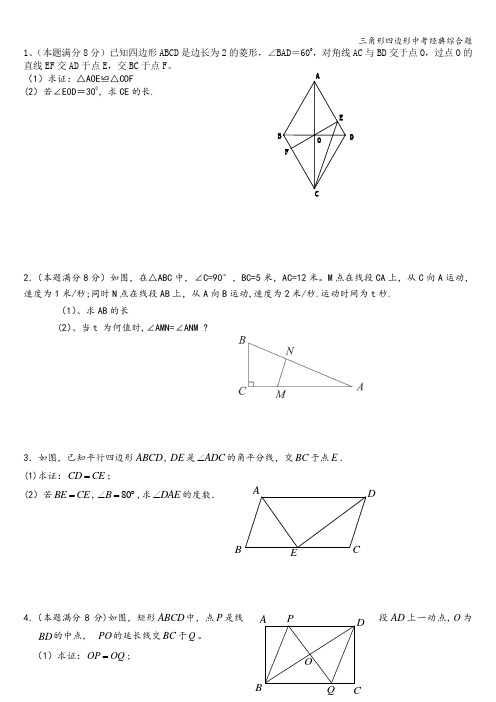
1、(本题满分8分)已知四边形ABCD 是边长为2的菱形,∠BAD =600,对角线AC 与BD 交于点O ,过点O 的直线EF 交AD 于点E ,交BC 于点F 。
(1)求证:△AOE ≌△COF(2)若∠E0D =300,求CE 的长.2.(本题满分8分)如图,在△ABC 中,∠C=90°,BC=5米,AC=12米。
M 点在线段CA 上,从C 向A 运动,速度为1米/秒;同时N 点在线段AB 上,从A 向B 运动,速度为2米/秒.运动时间为t 秒.(1)、求AB 的长(2)、当t 为何值时,∠AMN=∠ANM ?3.如图,已知平行四边形ABCD ,DE 是ADC ∠的角平分线,交BC 于点E . (1)求证:CD CE =;(2)若BE CE =,80B ∠=︒,求DAE ∠的度数.4.(本题满分8分)如图,矩形ABCD 中,点P 是线段AD 上一动点,O 为BD 的中点, PO 的延长线交BC 于Q 。
(1)求证:OP OQ =;OFEDQ P ODCBAEDCBA(2)若8AD =厘米,6AB =厘米,P 从点A 出发,以1厘米/秒的速度向D 运动(不与D 重合)。
设点P 运动时间为t 秒,请用t 表示PD 的长; 并求t 为何值时,四边形PBQD 是菱形.5.(本题满分6分)如图,在ABC ∆中,90C ∠=︒,点D 、E 分别在AC 、AB 上,BD 平分ABC ∠,DE AB ⊥,AE=3,CD=4. 求(1)求AD 的长;(2)求BC 的长.6.(本题满分10分)如图,在Rt OAB ∆中,90OAB ∠=︒,6OA AB ==,将OAB ∆绕点O 沿逆时针方向旋转90︒得到11OA B ∆.(1)线段1OA 的长是 ,1AOB ∠的度数是 ;(2)连结1AA ,求证:四边形11OAA B 是平行四边形;(3)求四边形11OAA B 的面积.7.(本题满分6分)如图,B C E ,,是同一直线上的三个点,四边形ABCD 与四边形CEFG 都是正方形,连结BG DE ,. (1)观察图形,猜想BG 与DE 之间的大小关系,并证明你的结论; (2)若延长BG 交DE 于点H ,求证:BH DE ⊥.8.Rt △ABC 与Rt △FED 是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB 与DE 重合.(1)求证:四边形ABFC 为平行四边形;(2)取BC 中点O ,将△ABC 绕点O 顺时钟方向旋转到如图(二)中△C B A '''位置,直线C B ''与AB 、CF 分别相交于P 、Q 两点,猜想OQ 、OP 长度的大小关系,并证明你的猜想.(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB 为菱形,并说明理由。
四边形单元测试题及答案

四边形单元测试题及答案一、选择题1. 下列哪个图形不是四边形?A. 正方形B. 长方形C. 平行四边形D. 三角形答案:D2. 一个四边形的对角线数量是多少?A. 1B. 2C. 3D. 4答案:B3. 菱形具有以下哪些特性?A. 对角线相等B. 对角线互相垂直C. 四边相等D. 所有选项都正确答案:D二、填空题1. 一个平行四边形的对边_________。
答案:平行且相等2. 正方形是特殊的_________。
答案:平行四边形3. 菱形的对角线_________。
答案:互相垂直且平分三、简答题1. 请简述四边形的基本性质。
答案:四边形是一个平面图形,由四条直线段依次首尾相连组成。
其基本性质包括:对边平行且相等,对角线互相平分。
2. 什么是梯形?请简述其特点。
答案:梯形是一个四边形,其中一组对边平行,另一组对边不平行。
其特点是:非平行的两边称为腰,平行的两边称为底,两底之间的距离称为高。
四、计算题1. 已知一个平行四边形的两邻边长分别为3厘米和5厘米,求其对角线的长度。
答案:由于题目没有给出足够的信息,无法直接计算对角线的长度。
需要知道平行四边形的其他信息,如角度或对角线与边的关系。
2. 如果一个正方形的边长为4厘米,计算其面积。
答案:正方形的面积 = 边长× 边长 = 4厘米× 4厘米 = 16平方厘米。
五、解答题1. 如何证明一个四边形是平行四边形?答案:要证明一个四边形是平行四边形,可以采用以下方法之一:- 两组对边分别平行。
- 两组对边分别相等。
- 对角线互相平分。
2. 已知一个菱形的边长为6厘米,求其面积。
答案:菱形的面积可以通过以下公式计算:面积 = (对角线1 ×对角线2) / 2。
由于题目没有给出对角线的长度,我们可以使用菱形的边长和其特性来求解。
设对角线分别为d1和d2,根据菱形的性质,d1² + d2² = 4 × 边长² = 4 × 6² = 144。
北师大版数学四年级下册-《认识三角形和四边形》达标测试卷

认识三角形和四边形一、填一填。
(每空1分,共18分)1.两条边相等的三角形是( )三角形,有一个角是90°的三角形是( )三角形。
2.红领巾,按角分属于( )三角形,按边分属于( )三角形。
3.用四个完全一样的等边三角形拼成一个大三角形,这个大三角形的内角和是( )。
4.( )和( )都是特殊的平行四边形。
5.将房屋的屋架做成三角形,是因为三角形具有( )。
6.在一个等腰三角形中,顶角的度数是90°,底角的度数是( )。
7.一个三角形三条边的长度分别为3厘米、3厘米、4厘米,按照边来分这是一个( )三角形,围成这个三角形需要( )厘米长的绳子。
8.一个三角形的两条边长分别是8厘米和5厘米,第三条边长必须比( )厘米大,比( )厘米小。
9.在直角三角形中,较大锐角的度数是较小锐角的2倍,两锐角分别是( )和( )。
10.一个等腰三角形的两条边的长度分别是3厘米和8厘米,这个等腰三角形的周长是( )厘米。
11.在一个三角形中,最多有( )个钝角,最少有( )个锐角。
二、选一选。
(每题2分,共12分)1.三个小朋友分别测量一个等腰三角形的边长,你能发现谁量错了吗?( )A.媛媛:腰长为2.5 cm,底边为5.5 cm。
B.君君:腰长为3.2 cm,底边为6 cm。
C.璐璐:腰长为4.7 cm,底边为6.2 cm。
2.在锐角三角形中,任意两个锐角的和一定( )90°。
A.小于B.等于C.大于3.一个三角形,如果它的两个内角的度数之和小于第三个内角的度数,那么它是( )三角形。
A.锐角B.直角C.钝角4.两个完全相同的梯形一定能拼成一个( )。
A.梯形B.平行四边形C.长方形5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形中的两个锐角分别是( )。
A.45°和45° B.60°和60° C.30°和60°6.一个三角形的下部被一张纸遮住了(如图),只露出了一个角,这个三角形是( )三角形。
三角形、平行四边形练习题

一、判断正误,对的打√,错的打×1、两个等底等高的三角形能拼成一个平行四边形。
()2.两个面积相等的三角形,它们的底和高也一定相等。
()3.三角形的面积等于平行四边形的面积的一半。
()4.一个平行四边形可以分成两个完全一样的三角形。
()5.两个面积相等的三角形可以拼成一个平行四边形。
()6. 直角三角形的面积等于它的两条直角边的乘积的一半。
()7.三角形的底和高都扩大2倍,面积也扩大2倍。
()8.如果三角形与平行四形的底相等,高也相等,那么它们的面积也相等。
()9、三角形的面积是和它等底等高的平行四边形面积的一半。
()10、等底等高的三角形形状不一定相同,面积一定相等。
()11、三角形面积的大小与它的底和高有关,与它的形状和位置无关。
()12. 两个面积相等的三角形,一定能拼成一个平行四边形。
()13. 3平方米>3米。
()14. 三角形的底扩大2倍,高扩大3倍,面积就扩大6倍。
()15. 任何三角形都有三条高。
()16. 平行四边形的底越长,它的面积就越大。
()一、填空1.利用割补法,可以把一个平行四边形转化成一个(),它的面积与平行四边形的面积(),它的()与平行四边形的底相等,它的()与平行四边形的高相等。
因为它的面积等于(),所以平行四边形边的面积等于()。
2.平行四边形的面积公式用字母表示可以写作(),也可以写作()。
还可以写作()。
;三角形的面积的计算公式用字母表示是()。
3. 平行四边形的底是2分米5厘米,高是底的 1.2倍,它的面积是()平方厘米。
4.一个三角形的底是4分米,高是30厘米,面积是()平方分米。
5.一个三角形的高是7分米,底是8分米,和它等底等高的平行四边形的面积是()平方分米。
6.一个三角形的面积是4.8平方米,与它等底等高的平行四边形的面积是()7.一个平行四边形的面积是280平方厘米,与它的等底等高的三角形的面积是()平方厘米。
8.一个三角形的面积是280平方厘米,与它等底等高的平行四边形的面积是()平方厘米。
真题精选:三角形和四边形(二)

《三角形与四边形》真题精选1.(2012·上海市文来中学分班卷)∠l、∠2、∠3是三角形的三个内角。
∠2的度数是∠1的2倍,∠3的度数是∠1的3倍。
这个三角形是()三角形。
2.(2012·南京市南师附中仙林学校初中部招生卷)一根长60 cm的铁丝围成一cm。
个长方形,如果长和宽都是质数,它的面积最大是()23.(2012·杭州市采荷实验学校分班卷)如图,梯形上底与下底的比是2:3,阴影三角形的面积为18平方厘米,空白三角形的面积是()平方厘米。
4.(2012·苏州市迎春中学招生卷)如下图,∠1=()。
5.(2011·青岛市青开四中分班卷)下图的长方形中,三角形的面积比梯形的面积小35平方厘米,则梯形的上底长为()厘米。
6.(2011·广州市六中珠江中学招生卷)如下图,每相邻三个点所形成的三角形都是面积为12cm 的正三角形,则△ABC 的面积为( )2cm 。
7.(2012·长沙市沙坪中学分班卷)三条边长分别是6㎝、8㎝、10㎝的直角三角形,将它的最短边对折使它与斜边相重合(如图),重叠后的三角形即阴影部分的面积是( )2cm 。
8.(2012·北京市三帆中学分班卷)一个等腰三角形底和高的比是8:3,把它沿底边上的高剪开,拼成一个长方形,这个长方形面积是192平方厘米。
那么这个长方形的周长是( )厘米。
9.(2011·天津市培杰中学分班卷)如下图,在长方形ABCD 中,三角形ABP 的面积为45平方厘米,三角形CPQ 的面积为60平方厘米,则四边形EPFQ 的面积为( )平方厘米。
10.(2011·太原市山大附中招生卷)如图,在三角形ABC中,EF和AB互相平行,DE和BC互相平行。
四边形BDEF的面积是120平方厘米。
三角形AEF(阴影部分)的面积是()平方厘米。
11.(2012·上海市文绮中学招生卷)如下图,将四条边长为16 cm、宽为 2 cm 的方形纸条垂直相交平放在桌面上,则桌面被盖住的面积是()。
数的三角形与四边形练习题

数的三角形与四边形练习题
一、选择题(每题4分,共20分)
1. 下面哪个图形是三角形?
A. 正方形
B. 长方形
C. 圆形
D. 梯形
2. 下面哪个图形是四边形?
A. 圆形
B. 三角形
C. 梯形
D. 半圆形
3. 一个三角形有几个顶点?
A. 2
B. 3
C. 4
D. 5
4. 一个正方形有几个边?
A. 2
B. 3
C. 4
D. 5
5. 一个长方形有几个直角?
A. 0
B. 1
C. 2
D. 3
二、填空题(每题6分,共30分)
1. 一个三角形有___ 条边。
2. 一个长方形有___ 个直角。
3. 一个正方形的所有边长都相等,它有___ 条对等边。
4. 一个梯形有___ 对平行边。
5. 一个圆形的边界称为___ 。
三、解答题(共50分)
1. 画出一个直角三角形,并标明它的各个边和角。
2. 画出一个平行四边形,并标明它的对等边。
3. 画出一个梯形,并标明它的平行边和非平行边。
4. 画出一个正方形,并标明它的对等边和直角。
5. 画出一个五边形,并标明它的顶点和边。
参考答案:
一、1. B 2. C 3. B 4. C 5. C
二、1. 3 2. 2 3. 4 4. 2 5. 圆周
三、略
请根据上述题目进行订正。
注意:请根据孩子们的年级和水平适量调整题目的难易程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三、第四单元测试题
一、选择题(每题3分,共30分)
1.不能判定四边形ABCD为平行四边形的题设是()
(A)AB平行且等于CD。
(B)∠A=∠C,∠B=∠D。
(C)AB=AD,BC=CD。
(D)AB=CD,AD=BC。
2.下面性质中菱形有而矩形没有的是()
(A)邻角互补(B)内角和为360°(C)对角线相等(D)对角线互相垂直
3、顺次连结任意四边形四边中点所得的四边形一定是()
A、平行四边形
B、矩形
C、菱形
D、正方形
4.如图
中,∠C=108°,BE平分∠ABC,
则∠ABE等于( )
A.18°
B.36°
C.72°
D.108°
5.下列命题中,真命题是(
)
A、有两边相等的平行四边形是菱形
B、对角线垂直的四边形是菱形
C
、四个角相等的菱形是正方形 D、两条对角线相等的四边形是矩形
6、平行四边形各内角平分线若围成一个四边形,则这个四边形一定是()
A、矩形
B、平行四边形
C、菱形
D、正方形
7、下列几组图形中,既是轴对称图形,又是中心对称图形,完全正确的一组是()
A.正方形、菱形、矩形、平行四边形
B.正三角形、正方形、菱形、矩形
C.正方形、菱形、矩形、
D.平行四边形、正方形、等腰三角形
8.一个多边形的内角和是900°,这个多边形的边数是()
A. 4
B. 5
C. 6 D.7
9.直角三角形的两边长分别是6,8,则第三边的长为()
A.10 B.2C.10或2D.无法确定
10.在Rt△ABC中,∠C=90°,下列式子不一定成立的是()
A.sinA=sinB B.cosA=sinB C.sinA=cosB D.∠A+∠B=90°
二、填空题(每题3分,共24分)
11.计算
12.在中,,,则.
13.如图,在菱形ABCD中,DE⊥AB,垂足为E,DE=6cm,,则
菱形ABCD的面积是__________.
14.等腰三角形一腰上的高与另一腰的夹角为30°,它的顶角为__________________
15中,∠A=50°,则∠B=__________。
16、菱形ABCD的周长为36,其相邻两内角的度数比为1:5,则此菱形的面积为_________。
17、对角线长为22的正方形的面积为__________。
18.如图,在矩形ABCD中,点E、F分别在AB、DC上,BF∥DE,若AD=12cm,
AB=7cm,•且AE:EB=5:2,则阴影部分的面积为_______cm
三、解答题(共48分)
19.(6分)计算:|3
-|
30
tan
3
-
5
1
-
)
6(1-
0︒+
+
-)
(
π
20.(6分)如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB,求证:∠A=∠E
21.(6分)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为
30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点
在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:
≈1.414,≈1.732)
E D
C
B
A
B C
A D
O
22. (6分)海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
23.(7分)如图:已知在△ABC 中,AB=AC ,D 为BC 上任意一点,DE ∥AC 交AB 于E , DF ∥AB 交AC 于F ,求证:DE+DF=AC
24. (7分)如图,在菱形ABCD 中,∠ABC 与∠BAD 的度数比为1:2,周长是48cm .求: (1)两条对角线的长度;
(2)菱形的面积.
25.(10分)如图,△ABC 中,点O 为AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的外角平分线CF 于点F ,交∠ACB 内角平分线CE 于E . (1)求证:EO=FO ;
(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论;
(3)若AC 边上存在点O ,使四边形AECF 是正方形,猜想△ABC 的形状并证明你的结论。
