大连理工大学2006高等代数
大连理工大学数值分析历年真题与答案(研究生期末卷)
课 程 名 称: 授课院 (系) :
考试日期: 2006 年 12 月 11 日
一 标准分 得 装 订 线 分
二
三
四
五
六
七
八
总分
一、填空(共 30 分,每空 2 分) (1)误差的来源主要有
.
(2)按四舍五入的原则,取 22 4.69041575 具有四位有效数字的近似值
a=
,则绝对误差界为
,相对误差界为
A-5
1 3 四、 (4 分)求 Householder 变换矩阵将向量 x 2 化为向量 y 0 . 2 0
五、 (12 分)写出解线性方程组的 Jacobi 法,G-S 法和超松弛(SOR)法的矩阵表示形式, 并根据迭代法 x ( k 1) Bx ( k ) f 对任意 x ( 0) 和 f 均收敛的充要条件为 ( B) 1 , 证明若线性方 程组 Ax b 中的 A 为严格对角占优矩阵, 则超松弛(SOR)法当松弛因子 (0,1] 时收敛.
师:张宏伟
一、填空(每一空 2 分,共 42 分) 1.为了减少运算次数,应将表达式.
装
16 x 5 17 x 4 18 x 3 14 x 2 13 x 1 x 4 16 x 2 8 x 1
1
2
改写为_______; 2.给定 3 个求积节点: x0 0 , x1 0.5 和 x2 1 ,则用复化梯形公式计算积分 e x dx
x1 3 x2 3 x1 x2 2 x x 2 1 4 4 4 x3 7
A 1, L , U
m1
(1)列主元消元法求出上述方程组的解,并计算
大连理工 考研 科目 参考 用书
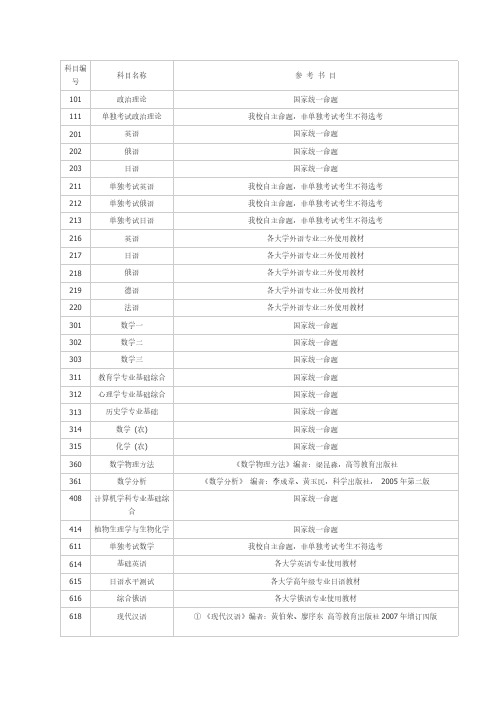
科目编科目名称参考书目号101 政治理论国家统一命题111 单独考试政治理论我校自主命题,非单独考试考生不得选考201 英语国家统一命题202 俄语国家统一命题203 日语国家统一命题211 单独考试英语我校自主命题,非单独考试考生不得选考212 单独考试俄语我校自主命题,非单独考试考生不得选考213 单独考试日语我校自主命题,非单独考试考生不得选考216 英语各大学外语专业二外使用教材217 日语各大学外语专业二外使用教材218 俄语各大学外语专业二外使用教材219 德语各大学外语专业二外使用教材220 法语各大学外语专业二外使用教材301 数学一国家统一命题302 数学二国家统一命题303 数学三国家统一命题311 教育学专业基础综合国家统一命题312 心理学专业基础综合国家统一命题313 历史学专业基础国家统一命题314 数学(农) 国家统一命题315 化学(农) 国家统一命题360 数学物理方法《数学物理方法》编者:梁昆淼,高等教育出版社361 数学分析《数学分析》编者:李成章、黄玉民,科学出版社,2005年第二版408 计算机学科专业基础综国家统一命题合414 植物生理学与生物化学国家统一命题611 单独考试数学我校自主命题,非单独考试考生不得选考614 基础英语各大学英语专业使用教材615 日语水平测试各大学高年级专业日语教材616 综合俄语各大学俄语专业使用教材618 现代汉语①《现代汉语》编者:黄伯荣、廖序东高等教育出版社2007年增订四版②《现代汉语语法研究教程》编者:陆俭明,北京大学出版社,2005年版619 传播学《传播学原理》,编者:张国良复旦大学出版社1995年12月《传播学教程》,编者:郭庆光中国人民大学出版社1999年11月620 民商法原理《民法》编者:魏振瀛,北京大学出版社、高等教育出版社,第三版《商法》编者:范健,北京大学出版社、高等教育出版社,第三版621 马克思主义哲学原理《马克思主义哲学原理》编者:陈先达,中国人民大学出版社,第二版《马克思主义哲学教程》编者赵家祥,聂锦芳,张立波,北京大学出版社,2003年622 管理学基础(1)《管理学》编者:汪克夷等,大连理工大学出版社,2006年第4版(2)《行政管理学》编者:夏书章,高等教育出版社、中山大学出版社,2008年版(3)《教育管理学》编者:陈孝彬,北京师范大学出版社,1999年修订本注:(2)、(3)任选其一623 城市规划历史与理论《中国城市建设史》中国建筑工业出版社《外国城市建设史》中国建筑工业出版社《城市规划原理》中国建筑工业出版社(第3版)624 建筑设计理论综合《中国建筑史》中国建筑工业出版社《外国建筑史(19世纪末叶以前)》中国建筑工业出版社《外国近现代建筑史》中国建筑工业出版社625 中外美术史《中国美术史》洪再新编著,中国美术学院出版社《外国美术简史》中央美术学院美术史系外国美术史教研室编著,高等教育出版社或中国青年出版社626 分析化学及分析化学实《分析化学》编者宫为民等,大连理工大学出版社,2006年第三版验《仪器分析》编者刘志广等,大连理工大学出版社,2007年第二版627 药物化学《药物化学》郑虎主编,第五版,人民卫生出版社《药物化学》,仉文生,李安良主编,高等教育出版社630 无机化学《无机化学》无机化学教研室主编,高等教育出版社,2006 第五版631 分子生物学《现代分子生物学》编者:朱玉贤、李毅,北京高等教育出版社636 体育学专业基础综合《学校体育学》人民体育出版社出版,周登嵩主编,2004《运动训练学》人民体育出版社,体育院校通用教材《运动生理学》人民体育出版社,体育院校通用教材678 社会保障学《社会保障学》编者:陈树文、郭文臣,大连理工大学出版社,第一版501 建筑设计(6小时)《中国建筑史》建工出版社《外国建筑史(19世纪末以前)》建工出版社《建筑空间组合论》编者:彭一刚502 规划设计(6小时)《城市规划资料集》中国建筑工业出版社,第5、6分册,城市设计503 命题创作(手绘)(6小时)801 英语专业综合语言学部分(50分):参考书目:《语言学教程》(修订版),胡壮麟,北京大学出版社。
高等代数 矩阵.

a. A有n个线性无关的特征向量 A相似于对角形
b. A有n个不同的特征根,则A相似于对角形。
c.设n阶矩阵A有s个不同的特征根 1, 2 , , s ,A
s
的属于 i 的线性无关特征向量的个数为ni, ni n i 1
A相似于对角形。
d.A的初等因子都是一次因式 A相似于对角形.
(8)若
1
1
A
若AB=BA, 则B是A的多项式.
1
4.方阵的行列式
(1) 若A是 n 阶矩阵,AT 是 A的转置矩阵,则| AT || A |;
(2) 若A是n阶矩阵,则 | kA | k n | A |; (3) 若A, B都是n阶矩阵,则 | AB || A || B |;
(4) 若A是n阶矩阵,则 | A || A |n1; (5) 若A是n阶可逆矩阵,则 | A1 || A |1;
的特征向量是方程组 (I A)X 0 的所有非零解.
(1) n阶方阵A的特征多项式
f () | I A | n a1n1 an1 an ,
其中
ak (1) k 1i1i2 ik n Aii11
i2 i2
ik
ik
n
特别地, a1 aii , an (1)n | A | . i 1
e.若r(A)=r,则
A
P
Ir
0
00Q,其中| P | 0,| Q | 0.
f. A=TBT-1,其中B是上三角形矩阵且对角线上的元 素是A的特征根。
g. 若r(A)=r,则A=PR,R是上三角形的矩阵,其主 对角线上前r个元素为1,后n-r个元素为0而|P|≠0.
h. A=B·C,其中BT=B,CT=-C. i. 对任意n阶矩阵A有A=BU,其中B是半正定矩阵, U为酉矩阵。
高等代数考研真题 第一章 多项式

第一章 多项式1、(清华2000—20分)试求7次多项式()f x ,使()1f x +能被4(1)X -整除,而()1f x -能被4(1)X +整除。
2、(南航2001—20分)(1)设x 2-2px+2∣x 4+3x 2+px+q ,求p,q 之值。
(2)设f(x),g(x),h(x)∈R[x],而满足以下等式 (x 2+1)h(x)+(x -1) f(x)+ (x -2) g(x)=0 (x 2+1)h(x)+(x+1) f(x)+ (x+2) g(x)=0 证明:x 2+1∣f(x),x 2+1∣g(x) 3、(北邮2002—12分)证明:x d -1∣x n -1的充分必要条件是d ∣n (这里里记号d ∣n 表示正整数d 整除正整数n )。
4、、(北邮2003—15分)设在数域P 上的多项式g 1(x),g 2(x ),g 3(x ),f(x),已知g 1(x)∣f(x),g 2(x)∣f(x), g 3(x)∣f(x),试问下列命题是否成立,并说明理由:(1)如果g 1(x),g 2(x), g 3(x)两两互素,则一定有g 1(x),g 2(x),g 3(x)∣f(x) (2)如果g 1(x),g 2(x), g 3(x)互素,则一定有g 1(x)g 2(x)g 3(x)∣f(x) 5、(北师大2003—25分)一个大于1的整数若和其因子只有1和本身,则称之为素数。
证明P 是素数当且仅当任取正整数a ,b 若p ∣ab 则p ∣a 或p ∣b 。
6、(大连理工2003—12分)证明:次数>0且首项系数为1的多项式f(x)是某一不可约多项式的方幂主充分必要条件是,对任意的多项式g(x),h(x) ,由f(x)∣g(x) h(x)可以推出f(x)∣g(x),或者对某一正整数m ,f(x)∣h m (x)。
7、(厦门2004—16分)设f(x),g(x)是有理数域上的多项式,且f(x)在有理数域上不可约。
高等代数

第八章 λ-矩阵一 内容概述 1 基本概念 1)λ-矩阵 设p 是一个数域,λ是一个文字,则称以数域P 上λ的多项式作为元素的矩阵为λ—矩阵,记为 A (λ),B(λ)等。
2)λ—矩阵的运算:加法,减法,乘法,数乘和转置等,伴随矩阵,行列式,λ—矩阵的秩。
可逆λ—矩阵,λ—矩阵的初等变换,λ—矩阵的等价。
3)行列式因子:设m*n 的 —矩阵A(λ)的秩为r ,对于正整数k,1≤k ≤r 在A(λ)中所有k 级子式的首项系数为1的最大公因式称为 A(λ) 的K 级行列式因子。
记为D K (λ). 4)—矩阵的标准形,不变因子()()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0...0...21x r x x d d d r ≥1,d i (λ)(i=1,2….r )是首项系数为1的多项式且d i (λ)|d 1+i (λ)(i=1,2,…r -1)称为A(λ) 的标准形。
d 1(λ),d 2(λ),…d r (λ)称为A(λ) 的不变因子。
5)行列式因子与不变因子的关系:D K (λ)=d 1(λ)…d k (λ)k=1,2,…r. d 1(λ)=D 1(λ)d k (λ)=()()λλ1-K K D D K=6)初等因子,设 A 与 n*n 矩阵,把A 的每个次数大于0不变因子分解成互不相同的一次因式之方幂的乘积,所有这些一次因式的方幂(相同的按出现的次数计算)称为A 的初等因子。
A 的初等因子和不变因子相互唯一决定。
7)若当标准形⎪⎪⎪⎪⎪⎭⎫⎝⎛S J J J ...21 J i 为若当块 2. 矩阵等价的充分必要条件:设A ()λ与B ()λ都是s ⨯n 的λ--矩阵 则A ()λ≅B ()λ 〈=〉P ()λA ()λQ ()λ=B ()λ其中P ()λ和Q ()λ都是可逆矩阵A ()λ与B ()λ有相同的标准形 〈=〉A ()λ 与B ()λ有相同的行列式因子 〈=〉A ()λ与B ()λ有相同的不变因子3.矩阵相似的充分必要条件: 设A,B 都是n 阶方阵则 〈=〉λE-A ≅λE-B〈=〉A 与B 有相同的初等因子 〈=〉A 与B 有相同的不变因子〈=〉λE-A 与λE-B 有相同的标准形4矩阵A 与对角矩阵相似的充分必要条件: (1) 有个线性无关的特征向量 (2) 初等因子全是一次的 (3) 最小多项式无重根5如何求矩阵A 的若当标准形。
大连理工大学10,11,12,13上学期工科数学分析基础试题答案

-03cos 2lnlim 0=+=®xx (10分)四、解:(1)0)cos )((lim 00sin )(lim 00=-¢=÷øöçèæ-=®®x x g x x x g a x x (4分)(2)200sin )(lim )0()(lim )0(x xx g x f x f f x x-=-=¢®® =12)0(2sin )(lim 2cos )(lim 00=¢¢=+¢¢=-¢®®g x x g x x x g x x∴ ïîïíì=¹---¢=¢时时010,)sin )(()cos )(()(2x x x x x g x x g x x f (8分) (3)200)sin )(()cos )((lim )(lim x x x g x x g x x f x x ---¢=¢®® =xx x g x x g x x x g x 2)cos )(()sin )((cos )(lim 0-¢-+¢¢+-¢® =)0(12)0(f g ¢==¢¢,因此)(x f ¢在(-∞,+∞+∞))连续。
连续。
(10分)五、解五、解:: 设x x x f ln)(=,由2ln 1)('xxx f -=,可知,当e x >时)(x f 单调减少单调减少 (5分)若e a b >>,则有b b a a ln ln >,推出a b b a ln ln >,即有a b b a > 2011201220122011> (10分)分)所以六、解:2)()()(x x f x f x x x f -¢=¢÷øöçèæ(4分)分) 令)()()(x f x f x x g -¢=,)()(x f x x g ¢¢=¢,令0)(=¢x g ,得0=x (唯一驻点),当0<x 时,0)(<¢x g ,当0>x 时,0)(>¢x g ,故)0(g 为最小值,故0)0()0()(>-=³f g x g ,∴0)(>¢÷øöçèæx x f ,即x x f )(单调增加。
2015大连理工考研参考书及考试科目

科目代码
科目名称
参考书目
818
交通工程学
《交通工程学》(第二版),编者:任福田 刘小明 荣建等,人民交通出版社,2008
科目代码
科目名称
参考书目
431
金融学综合
《金融学》(第二版),黄达编著,中国人民大学出版社,2009《财务管理》,李延喜主编,科学出版社,2010
804
高等代数
《高等代数》,编者:王萼芳等高等教育出版社,2003年第三版
806
量子力学
《量子力学》,编者:宋鹤山,大连理工大学出版社,第二版;《量子力学导论》,编者:曾谨言,北京大学出版社,第二版
《现代分子生物学(第三版)》编者:朱玉贤,高等教育出版社;《微生物学》编者:沈萍,高等教育出版社
880
生物化学及生物化学实验
《生物化学》,编者:王镜岩等,高等教育出版社,第三版 ;《生物化学实验原理和方法》,编者:陈雅蕙等,北京大学出版社,第二版
882
环境科学与工程概论
《环境化学》(2009年版),陈景文、全燮编著,大连理工大学出版社;《水污染控制工程》(第三版)下册,高廷耀、顾国维、周琪主编,高等教育出版社。
852
信号系统与通信原理
《信号与线性系统》,编者:管致中,高教出版社,第三版或第四版 《通信原理》,编著:樊昌信等,国防工业出版社,第5版
853
电路理论
《电路》,主编:邱关源(第五版),修订:罗先觉,高等教育出版社《电路理论基础》,主编:陈希有(第三版),高等教育出版社
初试考试科目参考书目

产业经济学
《产业经济学教程》,杨公朴等,上海财经大学出版社,2002年修订版
F0704
国际贸易理论与实务综合
《国际贸易》,陈同仇,对外经济贸易大学出版社2000年版
《国际贸易实务》,黎孝先,对外经济贸易大学出版社2000年版
F0705
管理科学与工程综合
《管理学原理》,杨文士,中国人民大学出版社,2004年版
《全国大学英语四级考纲》
301
数学一
全国统考科目
302
数学二
全国统考科目
303
数学三
全国统考科目
313
历史学基础
全国统考科目
337
工业设计工程
《工业设计概论》(第二版),程能林主编,机械工业出版社
357
英语翻译基础
《中国译学理论史稿》,陈福康著,上海外语教育出版社,2002
《高级英汉翻译理论与实践》,叶子南,清华大学出版社,2001
专业综合(二)
《纺织材料实验技术》,余序芬等编,中国纺织出版社2004年版
《纤维和纺织品测试技术》,李汝勤主编,东华大学出版社2005年版
F0103
专业综合(三)
《纺织材料学》于伟东,中国纺织出版社2006年版
F0301
专业综合知识
《物理化学》(第四版),南京大学,高等教育出版社
《材料科学与工程基础》,顾宜,化学工业出版社2002年
初试考试科目参考书目
复试考试科目参考书目
同等学力加试科目参考书目
说明:为帮助广大考生复习备考,也应广大考生的要求,提供2011年初试专业课考研复习大纲,请单击考试科目编号。大纲将陆续上载,请注意网站更新。
考生请注意:考生在复习备考时,应全面复习,复习大纲仅供参考。如果对大纲的内容及形式等问题存在疑问的,请考生致电各学院的联系人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大连理工大学2006年高等代数试题
一.(15分)计算行列式
51000110001100
01100011a
a a a D a a a a a -⎛⎫ ⎪--
⎪ ⎪=--
⎪-- ⎪ ⎪--⎝⎭
二.(10分) 设三元非奇次线性方程组的系数矩阵的秩为1,已知123,,ηηη是它的三个解向量,且12(1,2,3)'ηη+=,23(0,1,1)'ηη+=- ,31(1,0,1)'ηη+=-.求该方程组的通解,其中对任
意向量b ,'b 表示b 的转置<下同>.
三.(10分) 设1110n n n a a a λλλ--++++ 是n 级可逆方阵A 的特征多项式,请用A 的特征多
项式表示A 的逆矩阵1A -于伴随矩阵*A .
四.(15分) 已知3级实对称阵A 的特征值为1,-1,0,其中11λ=与30λ=的特征向量分别为1(0,1,0)'P =及3(1,0,0)'P =,求矩阵A .
五.(10分) 若方阵A 的所有特征值为1,证明:存在0k ≥使得()0k E A -=.
六.(15分) 令A 是具有互不相同特征值的n 级实对称矩阵,λ是其任一特征值,x 是相应的特征向量,证明:矩阵'0E A x x λ-⎛⎫ ⎪⎝⎭
(其中E 是单位矩阵)非奇异,并将结论推广到A 为非对称情形.
七.(15分) 令A,B 均为具有互不相同特征值的n 级实对称矩阵,满足AB BA =,证明:存在正交矩阵Q ,使得'Q AQ ,'Q BQ 均为实对角矩阵.
八.(15
分) 令S 为n 维欧式空间n R 的(0)r r n <<维子空间,{|'0,}n S
y R x y x S ⊥=∈=∀∈,详细证明:n R S S ⊥=⊕.
九.(15分) 证明:m n ⨯级实对称矩阵A 的秩数为1的充要条件是存在非零向量m n R ∈和
n v R ∈使得'A uv =.
十.(15分) 若A 是实对称正交矩阵,则存在实对称正定矩阵B,使得2A B =.
十一.(15分) 证明:设()f x 是整系数多项式,且(1)(2)(3)f f f p ===<p 为素数>,则不存在整数m,使()2f m p =.。
