多跨静定梁的定义(精)
合集下载
3-3 多跨静定梁
§3-3
多跨静定梁
4）多跨静定梁的形式
多跨静定梁有以下两种形式：
第 一 种 形 式
C E D F
A
B
计算简图
E D F
C
A
B
支撑关系图
§3-3
多跨静定梁
第 二 种 形 式
A
C B
D
E F
计算简图
C A
B
D E F
支撑关系图
§3-3
5）多跨静定梁的计算
多跨静定梁
由于作用在附属部分上的荷载不仅使附属部 分产生内力，而且还会使基本部分也产生内力。 而作用在基本部分上的荷载只会使基本部分产 生内力。因此计算应该从附属部分开始。 例：求图示多跨静定梁的弯矩和剪力图。
2
相应简支梁的弯矩图
C A B
E
D
F
支撑关系图
§3-3
基 本 部 分
A
B
多跨静定梁
附 属 部 分E
D
附 属 部 分
F
C
支撑关系图
我们把ABC称为：基本部分，把CDE、EF称为： 附属部分。显然作用在附属部分上的荷载不仅使附 属部分产生内力，而且还会使基本部分也产生内力。 作用在基本部分上的荷载只会使基本部分产生内力。
M 0 Y 0
F
FYG
FYF
224
3 5.33 4 1.33 kN
5.33 kN
§3-3
CEF部分：
C
3kN -1.33kN F D E
多跨静定梁
C
M
0 FY E
3 2 1.33 4 3
0.23
FYC
FYE
Y
《静定多跨梁》课件
建筑结构
多跨梁在大型建筑结构中使用，如长跨度的体育馆和机场终端建筑。
输电线路
多跨梁用于支撑输电线路，能够跨越大片区域，减少杆塔数量。
静定多跨梁的基本概念
1 节点约束
静定多跨梁的节点具有约束，使节点处的位 移为零。
2 荷载传递
静定多跨梁通过节点传递荷载，实现梁体的 平衡。
静定多跨梁的分析方法
静力学平衡原理
2
案例二：三跨连续梁
通过位移法分析三跨连续梁的受力情况，确定各节点的位移和反力。
力方法的应用
1
案例一：两跨连续梁
通过力方法分析两跨连续梁的受力情况，确定各节点的受力和反力。
2
案例二：三跨连续梁
通过力方法分析三跨连续梁的受力情况，确定各节点的受力和反力。
结论
静定多跨梁的基本分析方法
静定多跨梁的分析方法包括静力学平衡原理、 平衡方程式的建立以及求解方法。
学习静定多跨梁对于工程师的意义
掌握静定多跨梁的分析方法，可以更好地设计 和建造多跨梁结构，保证结构的安全和稳定。
《静定多跨梁》PPT课件
对于静定多跨梁的介绍，包括其基本概念、应用领域以及分析方法。
什么是静定多跨梁
静定多跨梁是指在静力学条件下，由两个或多个跨度组成的梁结构。多跨梁可以承受更大的荷载，并且在工程 中具有广泛的应用。
多跨梁的应用领域
桥梁工程
多跨梁在桥根据静力学平衡原理，对整个 多跨梁进行受力分析，确定各 节点处的受力情况。
平衡方程式的建立
建立平衡方程式，根据节点约 束条件和荷载情况求解未知节 点力和反力。
求解方法：位移，力方法
静定多跨梁的分析方法包括位 移法和力方法，根据具体情况 选择合适的方法求解。
多跨梁在大型建筑结构中使用，如长跨度的体育馆和机场终端建筑。
输电线路
多跨梁用于支撑输电线路，能够跨越大片区域，减少杆塔数量。
静定多跨梁的基本概念
1 节点约束
静定多跨梁的节点具有约束，使节点处的位 移为零。
2 荷载传递
静定多跨梁通过节点传递荷载，实现梁体的 平衡。
静定多跨梁的分析方法
静力学平衡原理
2
案例二：三跨连续梁
通过位移法分析三跨连续梁的受力情况，确定各节点的位移和反力。
力方法的应用
1
案例一：两跨连续梁
通过力方法分析两跨连续梁的受力情况，确定各节点的受力和反力。
2
案例二：三跨连续梁
通过力方法分析三跨连续梁的受力情况，确定各节点的受力和反力。
结论
静定多跨梁的基本分析方法
静定多跨梁的分析方法包括静力学平衡原理、 平衡方程式的建立以及求解方法。
学习静定多跨梁对于工程师的意义
掌握静定多跨梁的分析方法，可以更好地设计 和建造多跨梁结构，保证结构的安全和稳定。
《静定多跨梁》PPT课件
对于静定多跨梁的介绍，包括其基本概念、应用领域以及分析方法。
什么是静定多跨梁
静定多跨梁是指在静力学条件下，由两个或多个跨度组成的梁结构。多跨梁可以承受更大的荷载，并且在工程 中具有广泛的应用。
多跨梁的应用领域
桥梁工程
多跨梁在桥根据静力学平衡原理，对整个 多跨梁进行受力分析，确定各 节点处的受力情况。
平衡方程式的建立
建立平衡方程式，根据节点约 束条件和荷载情况求解未知节 点力和反力。
求解方法：位移，力方法
静定多跨梁的分析方法包括位 移法和力方法，根据具体情况 选择合适的方法求解。
结构力学——静定多跨梁讲解
静定平面刚架(frame)
悬臂刚架
静
定
A
D
刚
简支刚架
架
B
C
三铰刚架
D
E
刚架--具有刚结点的由 直杆组成的结构。
有基、附关系的刚架
超静定刚架
一个多余约束
三个多余约束
刚结点处的 变形特点
保持角度不变
平面刚架受力分析
结构特点：
PB
C
PB
C
A
D
B、C—铰结点
（受力简单，空间小 ）
A
D
B、C —刚结点
组 成 例 子
F2 F1
F2
F1
分析顺序：先附属部分，后基本部分。 荷载仅在基本部分上，只基本部分受力，附属 部分不受力； 荷载在附属部分上，除附属部分受力外，基本 部分也受力。
例
18
叠层关系图
先附属，后基本，区段叠加
10
10 5
12
例
例：图示多跨静定梁全长受均布荷载 q，各跨长度均为 l。欲使梁上最大正、负弯矩的绝对值相等，试确 定铰 B、E 的位置。
FAy ql / 2 M / l FAy
FBy
MB ql2 / 2 M FAyl 0 FBy ql / 2 M / l M A ql2 / 2 M FByl 0
理力、材力相关内容复习
悬臂梁AB受图示荷载作用，试求A的支
座反力。
MA
q
M
Fx FAx 0 FAx A
刚体上一个力系的等效平移
理力、材力相关内容复习
y 坐标单位 m
FP1
FP1 10 2 kN (FP1, i ) 450
04-讲义：3.3 多跨静定梁
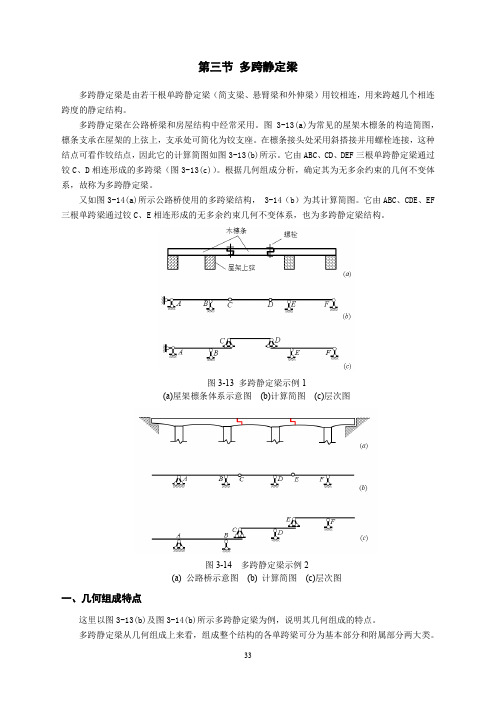
第三节多跨静定梁多跨静定梁是由若干根单跨静定梁（简支梁、悬臂梁和外伸梁）用铰相连，用来跨越几个相连跨度的静定结构。
多跨静定梁在公路桥梁和房屋结构中经常采用。
图3-13(a)为常见的屋架木檩条的构造简图，檩条支承在屋架的上弦上，支承处可简化为铰支座。
在檩条接头处采用斜搭接并用螺栓连接，这种结点可看作铰结点，因此它的计算简图如图3-13(b)所示。
它由ABC、CD、DEF三根单跨静定梁通过铰C、D相连形成的多跨梁（图3-13(c)）。
根据几何组成分析，确定其为无多余约束的几何不变体系，故称为多跨静定梁。
又如图3-14(a)所示公路桥使用的多跨梁结构， 3-14（b）为其计算简图。
它由ABC、CDE、EF 三根单跨梁通过铰C、E相连形成的无多余约束几何不变体系，也为多跨静定梁结构。
图3-13 多跨静定梁示例1(a)屋架檩条体系示意图(b)计算简图(c)层次图图3-14 多跨静定梁示例2(a) 公路桥示意图(b) 计算简图(c)层次图一、几何组成特点这里以图3-13(b)及图3-14(b)所示多跨静定梁为例，说明其几何组成的特点。
多跨静定梁从几何组成上来看，组成整个结构的各单跨梁可分为基本部分和附属部分两大类。
基本部分是指本身能独立维持平衡的部分，而需要依靠其他部分的支承才能保持平衡的部分称为附属部分。
因此，多跨静定梁从几何组成上来看见，是先固定基本部分，再固定附属部分。
如图3-13(b)中多跨静定梁，梁段ABC 由三根不平行也不交于一点的三根链杆固定于基础，它不依赖于其他部分就能独立维持自身的几何不变性；梁段DEF 虽然只有两根链杆与基础相连，但在竖向荷载作用下自身也能维持平衡。
因此，梁段ABC 、梁段DEF 均为基本部分。
而梁段CD 支承于前述两个基本部分上，它必须依赖于梁段ABC 、梁段DEF 才能保持几何不变，所以是附属部分。
为了更清楚地表明多跨静定梁中各梁段之间的支承关系，常把基本部分画在附属部分的下方，附属部分画在基本部分的上方，如图3-13(c)所示，称为层次图。
多跨静定梁的类型(共3张PPT)
其基前本边 梁的段基是本一梁个段简以支及梁后、边外的伸双梁支或座悬梁臂段梁都。是用中间铰链相连，搭 基根本据梁 多段跨与静基定础梁组的成几一何个组无成多规余律约，束将的多几跨何静不定变梁体分。为三种类型。 型后，边如 的上双图支（座梁c）段所与示地。基则用两个链杆支座约 型后，边如 的上双图支（座梁c）段所与示地。基则用两个链杆支座约
型用，这如 种上方图式（组成c）的所多示跨。静定梁称连续简支型，如下图（a）所示。
用（这2）种间方束隔式搭相组接成连型的。。多若跨静搭定接梁称梁连段续简是支间型隔，如出下现图（的a），所将示这。 种多跨静定梁称间隔搭接
用 （这1）种连方续式简组支成型的。多跨静定梁称连续简支型，如下图（a）所示。
）所示。 型，如上图（c 基后本边梁 的段双与支基座础梁组段成与一地个基无则多用余两约个束链的杆几支何座不约变体。
多跨静定梁
多跨静定梁的类型
根据多跨静定梁的几何组成规律，将多跨静定梁分为三种类型。
（1）连续简支型。基本梁段是一个简支梁，也可以是外伸梁或悬臂 梁。基ቤተ መጻሕፍቲ ባይዱ梁段与基础组成一个无多余约束的几何不变体。单支座梁段与 基本梁段总是用一个中间铰链相连，而与地基则用一个可动铰支座相连。 用这种方式组成的多跨静定梁称连续简支型，如下图（a）所示。
后型边，的 如双上支图座（梁c（）段所3与示）地。基混则合用型两个。链由杆支简座支约与搭接混合形成的多跨静定梁称混合型多跨静定梁，如上图
（e）所示。
多跨静定梁
图1
多跨静定梁
（2）间隔搭接型。基本梁段是一个简支梁、外伸梁或悬臂梁。
型基，本如 梁上段基图是本（一个c）梁简所支段示梁。与、外基伸梁础或组悬臂成梁。一个无多余约束的几何不变体。搭接梁段与
型用，这如 种上方图式（组成c）的所多示跨。静定梁称连续简支型，如下图（a）所示。
用（这2）种间方束隔式搭相组接成连型的。。多若跨静搭定接梁称梁连段续简是支间型隔，如出下现图（的a），所将示这。 种多跨静定梁称间隔搭接
用 （这1）种连方续式简组支成型的。多跨静定梁称连续简支型，如下图（a）所示。
）所示。 型，如上图（c 基后本边梁 的段双与支基座础梁组段成与一地个基无则多用余两约个束链的杆几支何座不约变体。
多跨静定梁
多跨静定梁的类型
根据多跨静定梁的几何组成规律，将多跨静定梁分为三种类型。
（1）连续简支型。基本梁段是一个简支梁，也可以是外伸梁或悬臂 梁。基ቤተ መጻሕፍቲ ባይዱ梁段与基础组成一个无多余约束的几何不变体。单支座梁段与 基本梁段总是用一个中间铰链相连，而与地基则用一个可动铰支座相连。 用这种方式组成的多跨静定梁称连续简支型，如下图（a）所示。
后型边，的 如双上支图座（梁c（）段所3与示）地。基混则合用型两个。链由杆支简座支约与搭接混合形成的多跨静定梁称混合型多跨静定梁，如上图
（e）所示。
多跨静定梁
图1
多跨静定梁
（2）间隔搭接型。基本梁段是一个简支梁、外伸梁或悬臂梁。
型基，本如 梁上段基图是本（一个c）梁简所支段示梁。与、外基伸梁础或组悬臂成梁。一个无多余约束的几何不变体。搭接梁段与
第三章2 多跨静定梁
l
↓↓↓↓↓↓↓↓↓↓↓↓↓↓ MG
q(l 2 x) 2
1 2 q(l 2 x) M B = × x + qx 2 2
ql MB = 解得： 12 3 3 6 l
2
ql 2 M B M = MB MG可按叠加法求得： G = 8 2
q(l 2 x) x qx ql + = 代入上式： 2 2 12
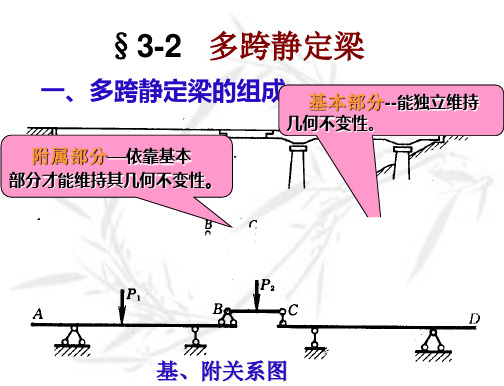
§3-2 多跨静定梁
一、多跨静定梁的组成
附属部分— 附属部分—依靠基本
部分才能维持其几何不变性。
基本部分-基本部分--能独立维持
几何不变性。 几何不变性。
基、附关系图
常见多跨静定梁的形式：
第一种，由伸臂梁与简支梁交叉排列
附属部分 基本部分
竖向荷载： 竖向荷载： 基本部分 水平荷载： 水平荷载： 附属部分
2 2
解得： x =
MB=ql2/12 q ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
A G B C D E F
l/2 MG=ql2/12
ql2/24 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
MG=ql2/8
由于多跨静定梁设置了带伸臂的基本部分，这不仅使中 间支座处产生了负弯矩，它将降低跨中正弯矩;另外减少了附 属部分的跨度。因此多跨静定梁较相应的多个简支梁弯矩分 布均匀，节省材料，但其构造要复杂一些！！
第二种，每个部分都是伸臂梁
第三种，由前两种形式混合组成
练习:区分基本部分和附属部分并画出关系图 练习 区分基本部分和附属部分并画出关系图
1 2 3 4
1
2
3
二、多跨静定梁的内力计算
受力特点：力作用在基本部分时附属部分不受力， 受力特点：力作用在基本部分时附属部分不受力，
多跨连续梁
多跨连续梁
连续梁是指含有多余约束的结构， 常用的多跨连续梁的支座都是固定 支座。至于多跨，就是两跨以上 。
多跨连续梁为超静定结构，其优点是内力小、 刚度大、抗震性能好、安全储备高，其缺点是 对支座变形敏感，当支座产生不均匀沉降时， 会引起附加内力。
多跨静定梁是指每跨都是静定的，就是所 说的板凳梁。 连续梁是指含有多余约束的 结构，常用的多跨连续梁的支座都是固定 支座。
为了避免这一缺点，根据多跨连续梁的 弯矩图，可在连续梁的弯矩为零处断梁 设铰,使之成为多跨静定梁。它既具有多 跨连续梁相同的受荷能力，又不会因支 座不均匀沉降产生附加内力。但问题是， 在可变荷载作用下，弯矩为零的点是不 确定的，因此多跨静定梁的受力显然不 如多跨连续梁好。
ห้องสมุดไป่ตู้
我国东海大桥 我国东海大桥于2005年5月建成，起始于上海南 汇区芦潮港，北与沪芦高速公路相连，南跨杭州湾北部海域， 直达浙江嵊泗县小洋山岛，全长32.5公里，是世界上最长的跨 海大桥之一。
圣地亚哥-科罗娜多大桥 圣地亚哥-科罗娜多大桥是由电视秀建 造的最著名的几座大桥之一。此3.2公里长的大桥连接美国南 加州的圣地亚哥和科罗娜多二个城市，于1969年开始运营。
Khaju大桥 这座桥建在伊朗的伊斯法罕，由伊朗王二世建成于17世纪。它 既是一座桥，也是一座坝。当桥洞封闭时，桥两侧的水位便会产生变化。 桥有两层拱隆，采用不同颜色的地砖区分开。在桥中央，还有两个很大的 亭子，叫做国王会客厅。这座宏伟壮观的靓桥横跨在Zayandeh河上，是伊 朗最有名的大桥之一。
东海大桥工程2002年6月26日正式开工建设，历经35个月的艰苦施工，于 2005年5月25日实现结构贯通。大桥宽31.5米，分上、下行双幅桥面，双向6 车道，设计时速每小时80公里。大桥全线按高速公路标准设计，设计基准期 为100年。大桥的最大主航通孔，离海面净高达40米，相当于10层楼高，可 满足万吨级货轮的通航要求。东海大桥在2005年建成通车。它是目前世界上 最长的外海跨海大桥；159米高的两座大跨度海上斜拉桥主塔在国内最高； 位于颗珠山岛和大乌龟岛之间的深海大堤绵延1.22公里，也是国内的突破和 创新；而最大的奇迹在于建设速度——在风高浪急的外海，运用高效、科学 的施工技术，实现大桥贯通仅用3年！
连续梁是指含有多余约束的结构， 常用的多跨连续梁的支座都是固定 支座。至于多跨，就是两跨以上 。
多跨连续梁为超静定结构，其优点是内力小、 刚度大、抗震性能好、安全储备高，其缺点是 对支座变形敏感，当支座产生不均匀沉降时， 会引起附加内力。
多跨静定梁是指每跨都是静定的，就是所 说的板凳梁。 连续梁是指含有多余约束的 结构，常用的多跨连续梁的支座都是固定 支座。
为了避免这一缺点，根据多跨连续梁的 弯矩图，可在连续梁的弯矩为零处断梁 设铰,使之成为多跨静定梁。它既具有多 跨连续梁相同的受荷能力，又不会因支 座不均匀沉降产生附加内力。但问题是， 在可变荷载作用下，弯矩为零的点是不 确定的，因此多跨静定梁的受力显然不 如多跨连续梁好。
ห้องสมุดไป่ตู้
我国东海大桥 我国东海大桥于2005年5月建成，起始于上海南 汇区芦潮港，北与沪芦高速公路相连，南跨杭州湾北部海域， 直达浙江嵊泗县小洋山岛，全长32.5公里，是世界上最长的跨 海大桥之一。
圣地亚哥-科罗娜多大桥 圣地亚哥-科罗娜多大桥是由电视秀建 造的最著名的几座大桥之一。此3.2公里长的大桥连接美国南 加州的圣地亚哥和科罗娜多二个城市，于1969年开始运营。
Khaju大桥 这座桥建在伊朗的伊斯法罕，由伊朗王二世建成于17世纪。它 既是一座桥，也是一座坝。当桥洞封闭时，桥两侧的水位便会产生变化。 桥有两层拱隆，采用不同颜色的地砖区分开。在桥中央，还有两个很大的 亭子，叫做国王会客厅。这座宏伟壮观的靓桥横跨在Zayandeh河上，是伊 朗最有名的大桥之一。
东海大桥工程2002年6月26日正式开工建设，历经35个月的艰苦施工，于 2005年5月25日实现结构贯通。大桥宽31.5米，分上、下行双幅桥面，双向6 车道，设计时速每小时80公里。大桥全线按高速公路标准设计，设计基准期 为100年。大桥的最大主航通孔，离海面净高达40米，相当于10层楼高，可 满足万吨级货轮的通航要求。东海大桥在2005年建成通车。它是目前世界上 最长的外海跨海大桥；159米高的两座大跨度海上斜拉桥主塔在国内最高； 位于颗珠山岛和大乌龟岛之间的深海大堤绵延1.22公里，也是国内的突破和 创新；而最大的奇迹在于建设速度——在风高浪急的外海，运用高效、科学 的施工技术，实现大桥贯通仅用3年！
静定梁的内力—多跨静定梁的内力图(建筑力学)
(3) 计算顺序
先计算附属部分后计算基本部分，即先附属后基础。
§ 8.6 多跨静定梁的内力
多跨静定梁的概念和特点 多跨静定梁的内力图
知识回顾
(1) 多跨静定梁的受力特点 当荷载只作用在基本部分上时，附属部分不受力，即
只有基本部分有内力，而附属部分没有内力；
F
A
BC
当荷载只作用在附属部分上时，基本部分上也会受力， A 附属部分和基本部分都有内力。
(2) 计算顺序 先计算附属部分后计算基本部分，即先附属后基础。
BC
D
例
[例1] 绘制如图所示多跨静定梁的剪力图和弯矩图。
(a) 30kN
20kN.m
20kN/m
解： （1）绘制层次图
AB和CE梁均为基本部分，BC梁为附属部分（图b所示）。
(c)
（2）画受力图，求约束力
FBx
先附属后基础
8kN/m
12kN
A
FAy 5kN 3m
B
C
D
E
FG
FCy 30.75kN FDy 32.25kN FFy 16kN
1m
4m
1m 3m 1m
(c) 15kN.m
10kN
12kN
A
B
E
FG
FAy
FFBBy 15kN 8kN/m
FEy F4Eky N
FFy
(b) 15kN.m
B 10kN
A
B
(c)
附属部分： 在去掉与其他部分的联系之后（与基础的联系不去掉），本身不能独立维持平衡的部分
称为附属部分，如CE和EF部分。
基本部分：AC、 DF
(b) A
附属部分： CD