测边网.测角网.导线网典型计算
条件平差中必要观测数的确定
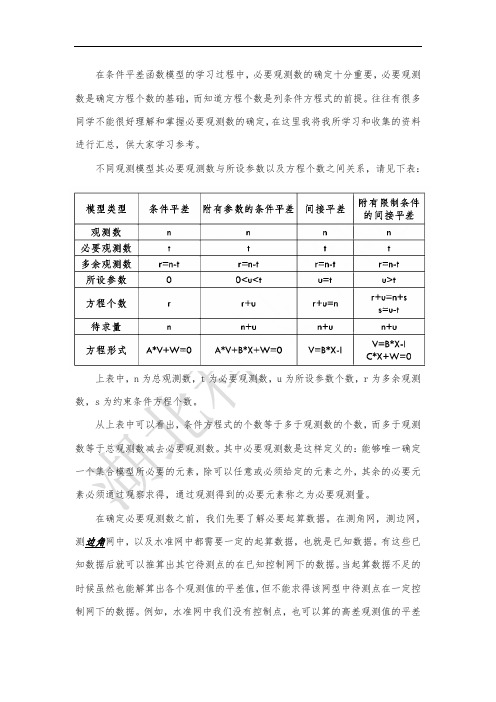
在知道必要起算数据后,我们根据图形中提供的起算数据就可以分类讨论必 要起算数了。具体见下表:
必要观测数的确定就看上表。让我们先来看一个例题:
图1 上图中,是一个测角网,其中没有起算数据。总共观测了 16 个角度值,其 中这个几何图形中,一共有 6 个点,那么它的必要观测数 t=2p-4=12-4=8,多于 观测数 r=n-t=16-8=8 个。也就是说这个图形一共应该列出 8 个条件方程式。那 么这些条件方程式中,有几个图形条件,有几个极条件呢? 回答上面的问题,也就是我们接下来要讲的,如何确定独立测角网和独立测 边网,以及独立测边角网中,条件方程式的不同种类。请注意,我用了三个独立, 什么是独立呢?独立就是该网的起算数据小于或等于该网的必要起算数据。例如 测角网的给定的起算数据小于或等于 4。测边网和测边角网给定起算数据小于或 等于 3。
在确定必要观测数之前,我们先要了解必要起算数据。在测角网,测边网, 测边角网中,以及水准网中都需要一定的起算数据,也就是已知数据。有这些已 知数据后就可以推算出其它待测点的在已知控制网下的数据。当起算数据不足的 时候虽然也能解算出各个观测值的平差值,但不能求得该网型中待测点在一定控 制网下的数据。例如,水准网中我们没有控制点,一个已知控制点了,我们就可 以推算出所有待求点的高程。
不同网型必要起算数据不同,见下表:
其中,水准网必要起算数据是 1 个,有一个点高程就可以推算出所有点的高 程。测角网,必要起算数据为 4,起算数据为 2 点坐标,即 2 对点的 x、y 就有 4 个起算数据了。或者一个点的坐标 x、y,以及一条边的边长 s,还有一个方位角 α。测边网和边角网相同,需要 3 个必要起算数据,就是 1 个点坐标 x、y,以及 一个方位角。
测量规程考试习题答案

测量规程考试习题1、一个矿区应采用统一的坐标和高程系统。
为了便于成果、成图的相互利用。
,应尽可能采用国家30带高斯平面坐标系统,矿区高程尽可能采用1985年国家高程基准。
2、本规程以中误差与允许误差作为评定测量精度的标准,允许误差一般采用中误差的两倍。
3、矿区地面平面控制网可采用三角网、边角网、测边网和导线网等布网方法建立。
4、在进行矿区地面各级平面控制测量、矿井联系测量和重要工程测量前应调整好经纬仪三轴关系,然后进行下列项目的检验与校正:1、照准部旋转是否正确的检验;2、光学测微器行差的测定与校正;2、垂直微动螺旋使用正确性的检验;4、照准部旋转时,仪器底座位移而产生的系统误差的检验;5、光学对点器的检验和校正。
5、测回的含义是照准目标一次,读数四次。
6、±(A+B·D)为测距仪的标称精度,其中:A为固定误差,单位mm,B为比例误差,单位m m/Km,D为测距长度;单位Km。
7、矿区地面高程控制网可采用水准测量和三角高程测量方法建立。
三角高程测量又分为光电测距三角高程测量和经纬仪三角高程测量两种。
8、矿区地面高程首级控制网一般采用水准测量方法建立。
9、三角高程测量主要用于山区和丘陵地带的高程控制和平面控制网点的高程测定。
10、矿区地面高程首级控制网应布设成环形网,加密时宜布设成符合路线或结点网,只有在山区或丘陵地带,才允许布设水准支线。
各等水准网中最弱点的高程中误差(相对于起算点)不得大于±2CM。
11、矿区地面各级平面控制点的高程可采用三角高程测量方法测定,并按四等水准测量的要求连测,控制点高程和起算点高程都必须布设成三角高程网或高程导线。
12、三角高程一般应进行对向观测。
13、仪器高和觇标高应用钢尺丈量两次,当互差不大于5mm时,取其平均值作为最终结果。
14、为了井上、下采用统一的平面坐标系统和高程系统,应进行联系测量。
联系测量应至少独立进行两次,在互差不超过限差时,采用加权平均值或算术平均值作为测量成果。
《煤矿测量规程》

煤矿测量规程第一篇总则第一条煤矿测量工作是矿山生产建设的重要要环节,也是矿山建设、生产、改造和编制长远发展规划等各项工作的基础。
为了实现煤矿测量工作标准化,进一步提高工作质量,使煤矿测量更好地为煤矿安全生产和合理开采煤炭资源服务,不断提高煤矿企业的经济效益和社会效益,特制定本规程。
第二条煤矿测量工作的只要任务是:1、建立矿区地面和井下(露天坑)测量控制系统,为煤矿各项测量工作提供起算数据:2、依据设计文件,进行采掘(剥)、土建、管线和机电安装等工程测量工作,并在煤矿基本建设和生产各个阶段,对采掘(剥)工程是否按设计施工进行检查和监督;3、利用测绘资料,解决煤矿生产、建设和改造中提出的各种测绘问题,并为煤矿灾害的预防、救护提供有关的测绘资料;4、测绘各种煤矿测量图,满足煤矿生产、建设和规划各阶段的需要;5、定期进行矿井“三量”(开拓煤量、准备煤量和回采煤量)、露天矿“二量”(开拓煤量、回采煤量)和露天矿采剥量的统计分析;正确反映煤矿采掘(剥)关系现状。
按《产矿井储量管理规定》的要求;对煤矿各级储量动态及损失量进行统计个管理工作,对煤炭资源的合理开采进行业务监督。
6、建立地表、岩层和建(构)筑物变形观测站,开展矿区地表与岩层移动规律、采矿或非采矿沉陷综合治理以及环境保护工作的研究;7、根据矿区地表和岩层移动变形参数,设计和修改各类煤柱。
参与“三下”(铁路下、水柱下和建筑物下)采煤和塌陷区综合治理以及土地征用和村庄搬迁的方案设计和实施。
8、进行矿区范围内的地籍测量;9、参与本矿区(矿)月度、季度、年度生产计划和长远发展规划的编制工作。
第3条测量工作开始前,应根据任务要求,收集和分析有关测量资料,进行必要的现场勘踏,制定经济合理的技术方案,编写技术设计书,在施册过程中,外业观测工作本身须有校核。
对起算数据、外业记录和计算成果均需经过严格的检查或对算。
对磁性介质存储的软件和数据,在使用前必须进行考机。
重要测量工作必须独立地进行两次或两次以上的观测和计算,工程结束后要编写技术总结(或说明)并做好资料整理归档工作。
(整理)测边网.测角网.导线网典型计算

目录摘要0第1章测边网坐标平差 (1)1.1近似坐标计算 (2)1.2计算误差方程的系数及常数项 (3)1.3误差方程 (3)1.4计算观测值的权 (4)1.5组成法方程 (4)1.6平差值计算 (4)1.6.1 坐标平差值 (4)1.6.2 边长平差值计算 (5)1.7精度计算 (5)1.7.1 单位权中误差 (5)1.7.2 待定点坐标中误差 (5)第2章三角网坐标平差 (6)2.1测角网函数模型 (7)2.2坐标方位角计算 (8)2.2.1 近似坐标方位角计算 (8)2.2.2 坐标方位角计算 (8)2.3近似坐标增量、近似边长与误差方程系数 (8)2.4误差方程的组成 (9)2.5确定权和组成法方程 (10)2.6法方程系数阵的逆阵与参数改正数 (10)2.7平差值计算及精度评定 (10)2.7.1 待定点的最或然值 (10)2.7.2 观测值的改正数 (11)2.7.3 点位中误差 (11)2.7.4 观测值平差值 (11)第3 章导线网间接平差 (12)3.1计算各边坐标方位角改正数方程的系数 (14)3.2确定角和边的权 (15)3.3计算角度和边长误差方程系数和常数项 (17)3.4误差方程的组成和解 (17)3.5平差值计算 (23)3.6精度计算 (23)3.6.1 单位权中误差 (23)3.6.2 待定点点位中误差计算 (23)参考文献 (24)指导老师评语 (25)摘要本课程设计介绍了综合运用测量平差基础知识来解决测边网、三角网、导线网坐标平差及精度评定问题,先设定未知参数,根据空间几何关系找出相应的平差模型,按照间接平差的原理,列出观测值误差方程,求出法方程的各系数矩阵,解算未知参数、观测值的改正数,最后进行精度评定,完成课题要求。
通过这一课题,拓宽我们测量数据处理的知识面,启发我们处理实际生产问题的新思路,针对某一实际问题,用经典的误差理论和比较前沿的数据处理方法进行合理的求解,以巩固和加强我们对误差理论和现代测量数据处理方法的理解,增强我们用所学的理论方法解决实际问题的能力。
第五章 大地测量的基本技术与方法(1)

② 技术设计的内容和方法 [1] 搜集和分析资料 (1)测区内各种比例尺的地形图。 (2)已有的控制测量成果(包括全部有关技术文件、图表、手簿 等等)。 (3)有关测区的气象、地质等情况,以供建标、埋石、安排作业 时间等方面的参考。 (4)现场踏勘了解已有控制标志的保存完好情况。 (5)调查测区的行政区划、交通便利情况和物资供应情况。若在 少数民族地区,则应了解民族风俗、习惯。 对搜集到的上述资料进行分析,以确定网的布设形式,起始 数据如何获得,网的未来扩展等。 其次还应考虑网的坐标系投影带和投影面的选择。 此外还应考虑网的图形结构,旧有标志可否利用等问题。
上海港GPS扩展网网图
2 甚长基线干涉测量(VLBI) 甚长基线干涉测量系统是在甚长基线的两端(相距几千公里), 用射电望远镜,接收银河系或银河系以外的类星体发出的无线电辐 射信号,通过信号对比,根据干涉原理,直接确定基线长度和方向 的一种空间技术。长度的相对精度可优于10-6,对测定射电源的空 间位置,可达0.001”,由于其定位的精度高,可在研究地球的极移 、地球自转速率的短周期变化、地球固体潮、大地板块运动的相对 速率和方向中得到广泛的应用。
(3)从安全生产方面考虑 点位离公路、铁路和其他建筑物以及高压电线等应有一定的 距离。 图上设计的方法及主要步骤 图上设计宜在中比例尺地形图(根据测区大小,选用1:25 000~1 :100 000地形图)上进行,其方法和步骤如下: a 展绘已知点; b 按上述对点位的基本要求,从已知点开始扩展; c 判断和检查点间的通视; d 估算控制网中各推算元素的精度; e 据测区的情况调查和图上设计结果,写出文字说明,并拟定作业 计划。
2. 大地控制网应有足够的精度。 国家三角网的精度,应能满足大比例尺测图的要求。在测图中 ,要求首级图根点相对于起算三角点的点位误差,在图上应不 超过±0.1mm,相对于地面点的点位误差则不超过 ±0.1Nmm(N 为测图比例尺分母)。 为使国家三角点的误差对图点的影响可以忽略不计,应使相邻国 家三角点的点位误差小于(1/3) ×0.1Nmm。
三角网条件平差计算

§3-4 三角网条件平差计算2学时三角网测量的目的,是通过观测三角形的各角度或边长,计算三角网中各未知点的坐标、边的长度及方位角等。
三角网按条件平差计算时,首要的问题是列出条件方程。
因此了解三角网的构成,总结其条件方程的种类及各种条件方程的组成规律是十分重要的。
三角网的种类比较多,网的布设形式也比较复杂。
根据观测内容的不同,有测角网、测边网、边角同测网等;根据网中起始数据的多少,有自由三角网和非自由三角网。
自由三角网是指仅具有必要起算数据的三角网,网中没有多余的已知数据。
如果测角三角网中,只有两个已知点(或者已知一个已知点的坐标、一条已知边的长度和一个已知的方位角),根据数学理论,以这两个已知点为起算数据,再结合必要的角度测量值,就能够解算出网中所有未知点的坐标。
如果三角网中除了必要的起算数据外还有其它的已知数据,或者说已知数据有冗余,就会增加对网形的约束,从而增强其可靠性,这种三角网称之为非自由三角网。
无论多么复杂的三角网,都是由单三角形、大地四边形和中点多边形组合而成的。
在本节,我们先讨论三角网条件平差中条件方程个数的确定问题,然后主要讨论测角三角网的条件方程的形式问题。
一、网中条件方程的个数三角网平差的目的,是要确定三角点在平面坐标系中的坐标最或然值。
如图3-9所示,根据前面学到的测量基础知识,我们知道,必须事先知道三角网中的四个数据,如两个三角点的4个坐标值,或者一个三角点的2个坐标值、一条边的长度和一个方位角,这4个已知数据我们称之为三角网的必要起算数据。
有了必要起算数据,就可以确定三角网在平面坐标系中的位置、网的大小及其方位,就可以计算三角网中未知点的坐标。
要对三角网进行平差计算,还必须先知道网中的总观测数n、判定必要观测数t,从而确定了多余观测数:r = n - t由条件平差原理知,多余观测数与条件方程数是相等的,有了多余观测数,也就确定出了条件方程的个数。
因此,问题的关键是判定必要观测数t。
第五章条件平差

二、法方程及改正数方程
将V T PV min的原则作用于条件方程 。
组成新函数:
V T PV-2k T AV W
式中
r 1
k k a , kb , k r 条件方程联系数
T
对新函数求导: T T 2V P 2A k ---改正数方程
dSCD ˆ f T dL SCD ˆ SCD T 2 T ˆ f D f f QL ˆL ˆ ˆL ˆ f 0 L S CD
得测边相对中误差为: 3、大地四边形测角网
2
ˆS
CD
SCD
=
ˆ 0 f T QL ˆL ˆ f
设
F ( f1 , f 2 , f m )
T T
G ( g1 , g 2 , g m ) 有
均为m维向量函数,且 f i、g i 均为x的函数, d F G dG F T dG T dF F G dx dx dx dx
注意:当N为满秩方阵时,才有 N 1唯一存在,法方程才有唯
测方向网
测角网
测角网
三角网
测边网
测边长
测边+测方向
边角网
(导线网) 测边+测角
三、三角网的布设--从高级到低级逐级布设 四、三角网平差的方法 1。严密平差 ----遵守VTPV=min原则 ; 2。近似平差
5.3 测角网条件平差
独立网(经典自由网)---只有必要起算数据d。
非独立网(附合网)---已知条件超过必要起算数据。
3 图形条件: n=12 t=2×2+4=8 r =4 1 极条件:
v2 v1 v6 v5 v11 v10 W1 0
测绘数据处理-自由网平差

4
d就是网中必要的起算数据个数。且有:
二、秩亏自由网平差思路 为了求得未知参数的唯一确定解,除了遵循最小二乘准则外 ,还必须增加新的约束条件,从而达到求得唯一解的目的 。由于约束条件不同,秩亏自由网平差可分为如下几种情 况: (1)、经典自由网平差。它是在假设网中有d个必要起算数据 的条件下,求定未知参数的最佳估计。这种方法早就已为 人们所熟知。不难理解,该法的平差结果(未知参数X的 解及其协因数阵 )将随着假设的d个必要起算数据的不同 而不同,即随着已知点位置的改变而改变。
第七行划去,剩下的6三行u列的阵即为三维测边网平差时的附
加阵。 很明显,上述的附加阵G均未标准化,即只是满足了BG=0, 但尚未满足的条件。
2019/2/15
17
阵标准化
1、用原始阵 2、设 和 阵,求出相应的阵 ; 相应 中第i行主对角元素为gii,把原始阵
的第i行数据均乘以
即可得到标准化阵的相应数据;
2019/2/15
2
在最小二乘准则下,得其法方程为 (1-7-3) 其中N= PB,W= 。此时,系数阵N为满秩方阵,即 (1-7-4) 当平差网没有起算数据时,网中所有的点均为待定点。设未知 参数的个数为u,误差方程为 (1-7-5) 组成的法方程为
2019/2/15
det(N)
,N为非奇异阵,有唯一解,其解为
2019/2/15
26
点号
P1 P2 P3 P4
/m
2019/2/15
27
(1)计算网的重心点坐标
(2)计算以加权重心点坐标为坐标原点的各待定点的坐标值
点号
P1 P2 P3
/km
P4
2019/2/15
