2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数章末总结
2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数 第10讲 Word版含解析

一、选择题1.在某种新型材料的研制中,实验人员获得了下列一组实验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )A.y =2x -2 B .y =12(x 2-1)C .y =log 2xD .y =log 12x解析:选B.由题中表可知函数在(0,+∞)上是增函数,且y 的变化随x 的增大而增大得越来越快,分析选项可知B 符合,故选B.2.某工厂6年来生产某种产品的情况是:前3年年产量的增长速度越来越快,后3年年产量保持不变,则该厂6年来这种产品的总产量C 与时间t (年)的函数关系图象正确的是( )解析:选A.前3年年产量的增长速度越来越快,说明呈高速增长,只有A 、C 图象符合要求,而后3年年产量保持不变,故选A.3.一种放射性元素的质量按每年10%衰减,这种放射性元素的半衰期(剩余质量为最初质量的一半所需的时间叫作半衰期)是(精确到0.1,已知lg 2=0.301 0,lg 3=0.477 1)( )A .5.2B .6.6C .7.1D .8.3解析:选B.设这种放射性元素的半衰期是x 年,则(1-10%)x =12,化简得0.9x =12,即x=log 0.912=lg12lg 0.9=-lg 22lg 3-1=-0.301 02×0.477 1-1≈6.6(年).故选B.4.某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10 m 3的,按每立方米m 元收费;用水超过10 m 3的,超过部分加倍收费.某职工某月缴水费16m 元,则该职工这个月实际用水为( )A .13 m 3B .14 m 3C .18 m 3D .26 m 3解析:选 A.设该职工用水x m 3时,缴纳的水费为y 元,由题意得y =⎩⎪⎨⎪⎧mx (0<x ≤10),10m +(x -10)·2m (x >10), 则10m +(x -10)·2m =16m ,解得x =13.5.某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x ,y 应为( )A .x =15,y =12B .x =12,y =15C .x =14,y =10D .x =10,y =14解析:选A.由三角形相似得24-y24-8=x 20.得x =54(24-y ),所以S =xy =-54(y -12)2+180,所以当y =12时,S 有最大值,此时x =15.检验符合题意.6.某类产品按工艺共分10个档次,最低档次产品每件利润为8元.每提高一个档次,每件利润增加2元.用同样工时,可以生产最低档次产品60件,每提高一个档次将少生产3件产品,则每天获得利润最大时生产产品的档次是( )A .7B .8C .9D .10解析:选C.由题意,当生产第k 档次的产品时,每天可获利润为y =[8+2(k -1)][60-3(k -1)]=-6k 2+108k +378(1≤k ≤10,k ∈N *),配方可得y =-6(k -9)2+864,所以当k =9时,获得利润最大.选C.二、填空题注:“累计里程”指汽车从出厂开始累计行驶的路程. 在这段时间内,该车每100千米平均耗油量为________升.解析:因为每次都把油箱加满,第二次加了48升油,说明这段时间总耗油量为48升,而行驶的路程为35 600-35 000=600(千米),故每100千米平均耗油量为48÷6=8(升).答案:88.某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km 按起步价付费);超过3 km 但不超过8 km 时,超过部分按每千米2.15元收费;超过8 km 时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________km.解析:设出租车行驶x km 时,付费y 元, 则y =⎩⎪⎨⎪⎧9,0<x ≤3,8+2.15(x -3)+1,3<x ≤8,8+2.15×5+2.85(x -8)+1,x >8,由y =22.6,解得x =9.答案:99.里氏震级M 的计算公式为:M =lg A -lg A 0,其中A 是测震仪记录的地震曲线的最大振幅,A 0是相应的标准地震的振幅.则8级地震的最大振幅是5级地震最大振幅的________倍.解析:设8级地震的最大振幅和5级地震的最大振幅分别为A 1,A 2,则8=lg A 1-lg A 0=lgA 1A 0,则A 1A 0=108, 5=lg A 2-lg A 0=lgA 2A 0,则A 2A 0=105,所以A 1A 2=103. 即8级地震的最大振幅是5级地震最大振幅的1 000 倍.答案:1 00010.某汽车销售公司在A 、B 两地销售同一种品牌的汽车,在A 地的销售利润(单位:万元)为y 1=4.1x -0.1x 2,在B 地的销售利润(单位:万元)为y 2=2x ,其中x 为销售量(单位:辆),若该公司在两地共销售16辆该种品牌的汽车,则能获得的最大利润是________万元.解析:设公司在A 地销售该品牌的汽车x 辆,则在B 地销售该品牌的汽车(16-x )辆,所以可得利润y =4.1x -0.1x 2+2(16-x )=-0.1x 2+2.1x +32=-0.1⎝⎛⎭⎫x -2122+0.1×2124+32.因为x ∈[0,16]且x ∈N ,所以当x =10或11时,总利润取得最大值43万元.答案:43三、解答题11.某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y (微克)与时间t (小时)之间近似满足如图所示的曲线.(1)写出第一次服药后y 与t 之间的函数关系式;(2)据进一步测定,每毫升血液中含药量不少于0.25微克时治疗疾病有效,求服药一次后治疗疾病有效的时间.解:(1)由题图,设y =⎩⎪⎨⎪⎧kt ,0≤t ≤1,⎝⎛⎭⎫12t -a ,t >1,当t =1时,由y =4得k =4,由⎝⎛⎭⎫121-a=4得a =3.所以y =⎩⎪⎨⎪⎧4t ,0≤t ≤1,⎝⎛⎭⎫12t -3,t >1.(2)由y ≥0.25得⎩⎪⎨⎪⎧0≤t ≤1,4t ≥0.25或⎩⎪⎨⎪⎧t >1,⎝⎛⎭⎫12t -3≥0.25,解得116≤t ≤5.因此服药一次后治疗疾病有效的时间是5-116=7916(小时).12.某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,t 小时内供水总量为1206t 吨(0≤t ≤24),(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少存水量是多少吨?(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象.解:(1)设t 小时后蓄水池中的存水量为y 吨, 则y =400+60t -1206t ;令6t =x ,则x 2=6t ,即y =400+10x 2-120x =10(x -6)2+40,所以当x =6,即t =6时,y min =40,即从供水开始到第6小时时,蓄水池存水量最少,只有40吨. (2)令400+10x 2-120x <80,即x 2-12x +32<0, 解得4<x <8,即4<6t <8,83<t <323.因为323-83=8,所以每天约有8小时出现供水紧张现象.。
2019高考数学文一轮:第2章函数的概念与基本初等函数 第1讲

则 f(-a)=( )
A.-2
B.0
C.1
D.-1
解析:选 B.因为 f(x)=3x3+2x+1,
所以 f(a)+f(-a)=3a3+2a+1+3(-a)3+2×(-a)+1=2,所
以 f(-a)=2-f(a)=0,故选 B.
(必修 1 P18 例 2 改编)下列哪个函数与 y=x 相等( )
A.y=xx2
A.3
B.6
C.9
D.12
解析:选 C.因为-2<1,
所 以 f( - 2) = 1 + log2(2 + 2) = 1 + log24 = 1 + 2 = 3. 因 为 log212>1,所以 f(log212)=2log212-1=122=6.
所以 f(-2)+f(log212)=3+6=9.故选 C.
2.已知 f(x)是二次函数且 f(0)=2,f(x+1)-f(x)=x-1,则 f(x) =________. 解析:设 f(x)=ax2+bx+c(a≠0), 因为 f(0)=2,所以 c=2. 又 f(x+1)-f(x)=x-1, 所以ff( (12) )- -ff( (01) )= =- 0. 1,
(必修 1 P24 A 组 T3(4)改编)已知函数 y=ax2-6x+7a(a≠0) 的值域为[-2,+∞),则 a 的值为( )
A.-1
B.-97
C.1
D.2
解析:选 C.由 y=ax2-6x+7a(a≠0)的值域为[-2,+∞)知 a
>0,且4a×7a-4a(-6)2=-2.
即 7a2+2a-9=0,
求分段函数的函数值时,应首先确定所给自变量的取值属于哪 一个范围,然后选取相应的对应关系.若自变量值为较大的正 整数,一般可考虑先求函数的周期.若给出函数值求自变量值, 应根据每一段函数的解析式分别求解,但要注意检验所求自变 量的值是否属于相应段自变量的范围.
2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数第5讲

一、选择题1.函数f (x )=1-e |x |的图象大致是( )解析:选A.将函数解析式与图象对比分析,因为函数f (x )=1-e |x |是偶函数,且值域是(-∞,0],只有A 满足上述两个性质.2.化简4a 23·b -13÷⎝ ⎛⎭⎪⎫-23a -13b 23的结果为( ) A .-2a 3b B .-8a bC .-6a bD .-6ab 解析:选C.原式=⎣⎢⎡⎦⎥⎤4÷⎝ ⎛⎭⎪⎫-23a 23-⎝ ⎛⎭⎪⎪⎫-13b -13-23 =-6ab -1=-6a b,故选C. 3.已知实数a ,b 满足等式⎝ ⎛⎭⎪⎫12a =⎝ ⎛⎭⎪⎫13b,下列五个关系式: ①0<b <a ;②a <b <0;③0<a <b ;④b <a <0;⑤a =b .其中不可能成立的关系式有( )A .1个B .2个C .3个D .4个解析:选B.函数y 1=⎝ ⎛⎭⎪⎫12x 与y 2=⎝ ⎛⎭⎪⎫13x 的图象如图所示.由⎝ ⎛⎭⎪⎫12a =⎝ ⎛⎭⎪⎫13b 得,a <b <0或0<b <a 或a =b =0. 故①②⑤可能成立,③④不可能成立.4.若函数f (x )=a |2x -4|(a >0,a ≠1),满足f (1)=19,则f (x )的单调递减区间是( ) A .(-∞,2] B .[2,+∞)C .[-2,+∞)D .(-∞,-2]解析:选B.由f (1)=19得a 2=19, 所以a =13或a =-13(舍去),即f (x )=⎝ ⎛⎭⎪⎫13|2x -4|. 由于y =|2x -4|在(-∞,2]上递减,在[2,+∞)上递增,所以f (x )在(-∞,2]上递增,在[2,+∞)上递减,故选B.5.设a =1.90.9,b =0.91.9,c =0.99.1,则a ,b ,c 的大小关系为( )A .a >b >cB .b >a >cC .a >c >bD .c >a >b解析:选A.因为函数y =0.9x 在R 上是减函数,所以0.91.9>0.99.1,且0.91.9<0.90=1.即c <b <1.又函数y =1.9x 在R 上是增函数.所以1.90.9>1.90=1即a >1.所以a >b >c .故选A.6.若函数f (x )=2x +12x -a是奇函数,则使f (x )>3成立的x 的取值范围为( ) A .(-∞,-1) B .(-1,0)C .(0,1)D .(1,+∞)解析:选C.因为f (x )为奇函数,所以f (-x )=-f (x ),即2-x +12-x -a =-2x +12x -a, 整理得(a -1)(2x +1)=0,所以a =1,所以f (x )>3即为2x +12x -1>3,当x >0时,2x -1>0, 所以2x +1>3·2x -3,解得0<x <1;当x <0时,2x -1<0,所以2x +1<3·2x -3,无解.所以x 的取值范围为(0,1).二、填空题7.函数y =16-4x 的值域是________.解析:因为4x >0,所以16-4x <16,所以0≤16-4x <16,即0≤y <4.答案:[0,4)8.若函数f (x )=a x -1(a >0,a ≠1)的定义域和值域都是[0,2],则实数a =________.解析:当a >1时,f (x )=a x -1在[0,2]上为增函数,则a 2-1=2,所以a =±3,又因为a >1,所以a = 3.当0<a <1时,f (x )=a x -1在[0,2]上为减函数,又因为f (0)=0≠2,所以0<a <1不成立.综上可知,a = 3. 答案: 39.若函数f (x )=2|x -a |(a ∈R )满足f (1+x )=f (1-x ),且f (x )在[m ,+∞)上单调递增,则实数m 的最小值等于________.解析:因为f (x )=2|x -a |,所以f (x )的图象关于x =a 对称.又由f (1+x )=f (1-x ),知f (x )的图象关于直线x =1对称,故a =1,且f (x )的增区间是[1,+∞),由函数f (x )在[m ,+∞)上单调递增,知[m ,+∞)⊆[1,+∞),所以m ≥1,故m 的最小值为1.答案:110.已知函数y =a x +b (a >0,且a ≠1,b >0)的图象经过点P (1,3),如图所示,则4a -1+1b的最小值为________,此时a ,b 的值分别为________.解析:由函数y =a x+b (a >0且a ≠1,b >0)的图象经过点P (1,3),得a +b =3,所以a -12+b 2=1,又a >1,则4a -1+1b =⎝ ⎛⎭⎪⎫4a -1+1b (a -12+b 2)=2+12+2b a -1+a -12b ≥52+22b a -1·a -12b =92,当且仅当2b a -1=a -12b ,即a =73,b =23时取等号,所以4a -1+1b的最小值为92. 答案:92 73,23三、解答题11.已知函数f (x )=b ·a x (其中a ,b 为常量,且a >0,a ≠1)的图象经过点A (1,6),B (3,24).若不等式⎝ ⎛⎭⎪⎫1a x +⎝ ⎛⎭⎪⎫1b x -m ≥0在x ∈(-∞,1]上恒成立,求实数m 的取值范围. 解:把A (1,6),B (3,24)代入f (x )=b ·a x,得⎩⎪⎨⎪⎧6=ab ,24=b ·a 3, 结合a >0,且a ≠1,解得⎩⎪⎨⎪⎧a =2,b =3. 所以f (x )=3·2x .要使⎝ ⎛⎭⎪⎫12x +⎝ ⎛⎭⎪⎫13x ≥m 在x ∈(-∞,1]上恒成立,只需保证函数y =⎝ ⎛⎭⎪⎫12x +⎝ ⎛⎭⎪⎫13x 在(-∞,1]上的最小值不小于m 即可.因为函数y =⎝ ⎛⎭⎪⎫12x +⎝ ⎛⎭⎪⎫13x 在(-∞,1]上为减函数, 所以当x =1时,y =⎝ ⎛⎭⎪⎫12x +⎝ ⎛⎭⎪⎫13x 有最小值56. 所以只需m ≤56即可. 即m 的取值范围为⎝⎛⎦⎥⎤-∞,56. 12.已知函数f (x )=⎝ ⎛⎭⎪⎫13ax 2-4x +3. (1)若a =-1,求f (x )的单调区间;(2)若f (x )有最大值3,求a 的值.解:(1)当a =-1时,f (x )=⎝ ⎛⎭⎪⎫13-x 2-4x +3, 令g (x )=-x 2-4x +3,由于g (x )在(-∞,-2)上单调递增,在(-2,+∞)上单调递减,而y =⎝ ⎛⎭⎪⎫13t 在R 上单调递减,所以f (x )在(-∞,-2)上单调递减,在(-2,+∞)上单调递增,即函数f (x )的单调递增区间是(-2,+∞),单调递减区间是(-∞,-2).(2)令g (x )=ax 2-4x +3,f (x )=⎝ ⎛⎭⎪⎫13g (x ), 由于f (x )有最大值3,所以g (x )应有最小值-1,因此必有⎩⎪⎨⎪⎧a >0,3a -4a=-1,解得a =1, 即当f (x )有最大值3时,a 的值为1.。
2019年高考数学(文科)一轮分层演练:第2章函数的概念与基本初等函数第8讲(含答案解析)

一、选择题1.函数y =x sin x 在[-π,π]上的图象是( )解析:选A.容易判断函数y =x sin x 为偶函数,排除D.当0<x <π2时,y =x sin x >0,当x =π时,y =0,排除B 、C ,故选A.2.定义一种运算:g ⊗h =⎩⎪⎨⎪⎧g (g ≥h ),h (g <h ),已知函数f (x )=2x ⊗1,那么函数f (x -1)的大致图象是( )解析:选B.由定义知,当x ≥0时,2x ≥1,所以f (x )=2x ,当x <0时,2x<1,所以f (x )=1,所以f (x )=⎩⎪⎨⎪⎧2x,x ≥0,1,x <0,其图象易作,f (x -1)的图象可由f (x )的图象向右平移1个单位长度得到,故选B.3.已知函数y =f (x )的图象如图所示,则函数y =log 12f (x )的图象大致是( )解析:选C.法一:由函数y =f (x )的图象知,当x ∈(0,2)时,f (x )≥1,所以log 12f (x )≤0,结合选项知,选C.法二:由函数f (x )的图象知,函数f (x )在(0,1)上是减函数,在(1,2)上是增函数,所以y =log 12f (x )在(0,1)上是增函数,在(1,2)上是减函数.结合各选项知,选C.4.图中阴影部分的面积S 是关于h 的函数(0≤h ≤H ),则该函数的大致图象是( )解析:选B.由题图知,随着h 的增大,阴影部分的面积S 逐渐减小,且减小得越来越慢,结合选项可知选B.5.(2018·河南焦作模拟)函数f (x )=|x |+ax2(其中a ∈R )的图象不可能是( )解析:选C.当a =0时,函数f (x )=|x |+a x 2=|x |,函数的图象可以是B ;当a =1时,函数f (x )=|x |+a x 2=|x |+1x 2,函数的图象可以类似A ;当a =-1时,函数f (x )=|x |+a x 2 =|x |-1x 2,x >0时,|x |-1x 2=0只有一个实数根x =1,函数的图象可以是D ;所以函数的图象不可能是C.故选C.6.(2017·高考全国卷Ⅰ)已知函数f (x )=ln x +ln(2-x ),则( ) A .f (x )在(0,2)单调递增 B .f (x )在(0,2)单调递减C .y =f (x )的图象关于直线x =1对称D .y =f (x )的图象关于点(1,0)对称解析:选C.法一:由题意知,f (x )=ln x +ln(2-x )的定义域为(0,2),f (x )=ln[x (2-x )]=ln[-(x -1)2+1],由复合函数的单调性知,函数f (x )=ln x +ln(2-x )在(0,1)单调递增,在(1,2)单调递减,所以排除A ,B ;又f (12)=ln 12+ln(2-12)=ln 34,f (32)=ln 32+ln(2-32)=ln 34,所以f (12)=f (32)=ln 34,所以排除D ,故选C.法二:由题意知,f (x )=ln x +ln(2-x )的定义域为(0,2),f ′(x )=1x +1x -2=2(x -1)x (x -2),由⎩⎪⎨⎪⎧f ′(x )>00<x <2,得0<x <1;由⎩⎪⎨⎪⎧f ′(x )<00<x <2,得1<x <2,所以函数f (x )=ln x +ln(2-x )在(0,1)单调递增,在(1,2)单调递减,所以排除A ,B ;又f (12)=ln 12+ln(2-12)=ln 34,f (32)=ln 32+ln(2-32)=ln 34,所以f (12)=f (32)=ln 34,所以排除D ,故选C.二、填空题7.如图,定义在[-1,+∞)上的函数f (x )的图象由一条线段及抛物线的一部分组成,则f (x )的解析式为________.解析:当x ∈[-1,0]时,设y =kx +b ,由图象得⎩⎪⎨⎪⎧-k +b =0,k ×0+b =1,解得⎩⎪⎨⎪⎧k =1,b =1,所以y =x +1; 当x ∈(0,+∞)时,设y =a (x -2)2-1, 由图象得0=a ·(4-2)2-1, 解得a =14,所以y =14(x -2)2-1.综上可知,f (x )=⎩⎪⎨⎪⎧x +1,x ∈[-1,0],14(x -2)2-1,x ∈(0,+∞). 答案:f (x )=⎩⎪⎨⎪⎧x +1,x ∈[-1,0],14(x -2)2-1,x ∈(0,+∞)8.使log 2(-x )<x +1成立的x 的取值范围是________.解析:在同一坐标系内作出y =log 2(-x ),y =x +1的图象,知满足条件的x ∈(-1,0).答案:(-1,0)9.已知函数f (x )的定义域为R ,且f (x )=⎩⎪⎨⎪⎧2-x -1,x ≤0,f (x -1),x >0,若方程f (x )=x +a 有两个不同实根,则实数a 的取值范围为________.解析:当x ≤0时,f (x )=2-x -1,0<x ≤1时,-1<x -1≤0,f (x -1)=2-(x -1)-1. 故x >0时,f (x )是周期函数,如图所示.若方程f (x )=x +a 有两个不同的实数根,则函数f (x )的图象与直线y =x +a 有两个不同交点, 故a <1,即a 的取值范围是(-∞,1). 答案:(-∞,1)10.函数f (x )=⎩⎨⎧ln x (x >0),--x (x ≤0)与g (x )=|x +a |+1的图象上存在关于y 轴对称的点,则实数a 的最小值为________.解析:设y =h (x )与y =f (x )的图象关于y 轴对称,则h (x )=f (-x )=⎩⎨⎧ln (-x ),x <0,-x ,x ≥0,作出y =h (x )与y =g (x )的函数图象如图所示.因为f (x )与g (x )图象上存在关于y 轴对称的点,所以y =h (x )与y =g (x )的图象有交点,所以-a ≤-e ,即a ≥e.即a 的最小值为e 答案:e 三、解答题11.已知函数f (x )=⎩⎪⎨⎪⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5].(1)在如图所示给定的直角坐标系内画出f (x )的图象;(2)写出f (x )的单调递增区间;(3)由图象指出当x 取什么值时f (x )有最值. 解:(1)函数f (x )的图象如图所示.(2)由图象可知,函数f (x )的单调递增区间为[-1,0],[2,5]. (3)由图象知当x =2时,f (x )min =f (2)=-1, 当x =0时,f (x )max =f (0)=3.12.已知函数f (x )=x |m -x |(x ∈R ),且f (4)=0. (1)求实数m 的值;(2)作出函数f (x )的图象;(3)根据图象指出f (x )的单调递减区间;(4)若方程f (x )=a 只有一个实数根,求a 的取值范围. 解:(1)因为f (4)=0, 所以4|m -4|=0, 即m =4.(2)f (x )=x |x -4|=⎩⎪⎨⎪⎧x (x -4)=(x -2)2-4,x ≥4,-x (x -4)=-(x -2)2+4,x <4, f (x )的图象如图所示.(3)f (x )的单调递减区间是[2,4]. (4)从f (x )的图象可知,当a >4或a <0时,f (x )的图象与直线y =a 只有一个交点,方程f (x )=a 只有一个实数根,即a 的取值范围是(-∞,0)∪(4,+∞).。
2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数 第6讲 Word版含解析

一、选择题 1.函数f (x )=1(log 2x )2-1的定义域为( )A .⎝⎛⎭⎫0,12 B .(2,+∞) C .⎝⎛⎭⎫0,12∪(2,+∞) D .⎝⎛⎦⎤0,12∪[2,+∞) 解析:选C.要使函数有意义,(log 2x )2-1>0,即log 2x >1或log 2x <-1,所以x >2或0<x <12,即函数f (x )的定义域为(0,12)∪(2,+∞).2.设函数f (x )=log a |x |在(-∞,0)上单调递增,则f (a +1)与f (2)的大小关系是( ) A .f (a +1)>f (2) B .f (a +1)<f (2) C .f (a +1)=f (2) D .不能确定 解析:选A.由已知得0<a <1,所以1<a +1<2,又易知函数f (x )为偶函数,故可以判断f (x )在(0,+∞)上单调递减,所以f (a +1)>f (2).3.设a =log 510,b =log 612,c =log 714,则( ) A .c >b >a B .b >c >a C .a >c >bD .a >b >c解析:选 D.因为a =log 510=1+log 52,b =log 612=1+log 62,c =log 714=1+log 72,又0<log 25<log 26<log 27,所以log 52>log 62>log 72>0,所以a >b >c ,故选D.4.已知函数f (x )=log a (2x +b -1)(a >0,a ≠1)的图象如图所示,则a ,b 满足的关系是( )A .0<a -1<b <1B .0<b <a -1<1C .0<b -1<a <1D .0<a -1<b -1<1解析:选A.由函数图象可知,f (x )为单调递增函数,故a >1.函数图象与y 轴的交点坐标为(0,log a b ),由函数图象可知-1<log a b <0,解得1a <b <1.综上有0<1a<b <1.5.若函数f (x )=log a x (0<a <1)在区间[a ,2a ]上的最大值是最小值的3倍,则a 的值为( )A .24 B.22C .14 D.12解析:选A.因为0<a <1,所以函数f (x )是定义域上的减函数,所以f (x )max =log a a =1,f (x )min=log a 2a ,所以1=3log a 2a ⇒a =(2a )3⇒8a 2=1⇒a =24.故选A. 6.已知函数f (x )=-x +log 21-x 1+x+2,则f (1e )+f (-1e )的值为( )A .2B .4C .6D .10解析:选B.因为函数g (x )=-x +log 21-x 1+x是奇函数,所以g (1e )+g (-1e )=0,则f (1e )+f (-1e )=g (1e )+2+g (-1e )+2=4.故选B.二、填空题7.lg 2+lg 5+20+()5132×35=________.解析:lg 2+lg 5+20+()5132×35=lg10+1+523×513=32+5=132.答案:1328.设函数f (x )=⎩⎪⎨⎪⎧41-x,x ≤1,1-log 14x ,x >1,则满足不等式f (x )≤2的实数x 的取值集合为________.解析:原不等式等价于⎩⎨⎧x ≤1,41-x ≤2或⎩⎪⎨⎪⎧x >1,1-log 14x ≤2,解得12≤x ≤1或1<x ≤4,即实数x 的取值集合为⎩⎨⎧⎭⎬⎫x |12≤x ≤4.答案:⎩⎨⎧⎭⎬⎫x |12≤x ≤49.函数f (x )=log 2 x ·log 2(2x )的最小值为________.解析:依题意得f (x )=12log 2x ·(2+2log 2x )=(log 2x )2+log 2x =⎝⎛⎭⎫log 2x +122-14≥-14,当且仅当log 2x =-12,即x =22时等号成立,所以函数f (x )的最小值为-14.答案:-1410.设函数f (x )=|log a x |(0<a <1)的定义域为[m ,n ](m <n ),值域为[0,1],若n -m 的最小值为13,则实数a 的值为________.解析:作出y =|log a x |(0<a <1)的大致图象如图,令|log a x |=1.得x =a 或x =1a ,又1-a -⎝⎛⎭⎫1a -1=1-a -1-a a =(1-a )(a -1)a<0, 故1-a <1a -1,所以n -m 的最小值为1-a =13,a =23.答案:23三、解答题11.设f (x )=log a (1+x )+log a (3-x )(a >0,a ≠1),且f (1)=2. (1)求a 的值及f (x )的定义域;(2)求f (x )在区间⎣⎡⎦⎤0,32上的最大值.解:(1)因为f (1)=2,所以log a 4=2(a >0,a ≠1), 所以a =2.由⎩⎪⎨⎪⎧1+x >0,3-x >0,得x ∈(-1,3), 所以函数f (x )的定义域为(-1,3).(2)f (x )=log 2(1+x )+log 2(3-x )=log 2[(1+x )(3-x )]=log 2[-(x -1)2+4], 所以当x ∈(-1,1]时,f (x )是增函数;当x ∈(1,3)时,f (x )是减函数,故函数f (x )在⎣⎡⎦⎤0,32上的最大值是f (1)=log 24=2. 12.已知函数f (x )=log a (x +1)-log a (1-x ),a >0且a ≠1. (1)求f (x )的定义域;(2)判断f (x )的奇偶性并予以证明;(3)当a >1时,求使f (x )>0成立的解集.解:(1)要使函数f (x )有意义,则⎩⎪⎨⎪⎧x +1>0,1-x >0,解得-1<x <1.故所求函数f (x )的定义域为(-1,1). (2)f (x )为奇函数.证明如下: 由(1)知f (x )的定义域为(-1,1), 且f (-x )=log a (-x +1)-log a (1+x ) =-[log a (x +1)-log a (1-x )]=-f (x ), 故f (x )为奇函数.(3)因为当a >1时,f (x )在定义域(-1,1)内是增函数, 所以f (x )>0⇔x +11-x >1,解得0<x <1.所以使f (x )>0的x 的解集是(0,1).。
2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数 第2讲

一、选择题1.函数f(x)=x1-x在( ) A .(-∞,1)∪(1,+∞)上是增函数 B .(-∞,1)∪(1,+∞)上是减函数 C .(-∞,1)和(1,+∞)上是增函数 D .(-∞,1)和(1,+∞)上是减函数 解析:选C.函数f(x)的定义域为{x|x≠1}.f(x)=x 1-x =11-x -1,根据函数y =-1x的单调性及有关性质,可知f(x)在(-∞,1)和(1,+∞)上是增函数.2.已知函数f(x)为R 上的减函数,则满足f ⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪1x <f(1)的实数x 的取值范围是( ) A .(-1,1) B .(0,1) C .(-1,0)∪(0,1) D .(-∞,-1)∪(1,+∞)解析:选C.因为f(x)在R 上为减函数,且f ⎝ ⎛⎭⎪⎫1|x|<f(1),所以1|x|>1,即0<|x|<1, 所以0<x<1或-1<x<0.3.若函数f(x)=8x 2-2kx -7在[1,5]上为单调函数,则实数k 的取值范围是( ) A .(-∞,8] B .[40,+∞) C .(-∞,8]∪[40,+∞) D .[8,40]解析:选C.法一:由题意知函数f(x)=8x 2-2kx -7的图象的对称轴为x =k 8,因为函数f(x)=8x 2-2kx -7在[1,5]上为单调函数,所以k 8≤1或k8≥5,解得k≤8或k≥40,所以实数k 的取值范围是(-∞,8]∪[40,+∞).故选C.法二:取k =0,则函数f(x)=8x 2-7在[1,5]上为单调递增函数,所以排除B 、D ;取k =40,则函数f(x)=8x 2-80x -7在[1,5]上为单调递减函数,所以排除A.故选C.4.(2018·贵阳检测)定义新运算⊕:当a≥b 时,a ⊕b =a ;当a<b 时,a ⊕b =b 2,则函数f(x)=(1⊕x)x -(2⊕x),x ∈[-2,2]的最大值等于( )A .-1B .1C .6D .12 解析:选C.由已知得当-2≤x≤1时,f(x)=x -2,当1<x≤2时,f(x)=x 3-2,因为f(x)=x -2在[-2,1]上是增函数, 所以f(x)≤f(1)=-1,因为f(x)=x 3-2在(1,2]上是增函数, 所以f(x)≤f(2)=6, 所以f(x)max =f(2)=6.5.已知函数f(x)=log 2x +11-x,若x 1∈(1,2),x 2∈(2,+∞),则( )A .f(x 1)<0,f(x 2)<0B .f(x 1)<0,f(x 2)>0C .f(x 1)>0,f(x 2)<0D .f(x 1)>0,f(x 2)>0解析:选B.因为函数f(x)=log 2x +11-x在(1,+∞)上为增函数,且f(2)=0,所以当x 1∈(1,2)时,f(x 1)<f(2)=0;当x 2∈(2,+∞)时,f(x 2)>f(2)=0, 即f(x 1)<0,f(x 2)>0.6.(2018·湖北八校联考(一))设函数f(x)=2xx -2在区间[3,4]上的最大值和最小值分别为M ,m ,则m2M=( ) A .2 B .3C .83D .103解析:选C.易知f(x)=2x x -2=2+4x -2,所以f(x)在区间[3,4]上单调递减,所以M =f(3)=2+43-2=6,m =f(4)=2+44-2=4,所以m 2M =166=83.二、填空题7.函数f(x)=|x -1|+x 2的值域为________.解析:因为f(x)=|x -1|+x 2=⎩⎪⎨⎪⎧x 2+x -1,x ≥1x 2-x +1,x <1,所以f(x)=⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫x +122-54,x ≥1⎝ ⎛⎭⎪⎫x -122+34,x <1,作出函数图象如图,由图象知f(x)=|x -1|+x 2的值域为⎣⎢⎡⎭⎪⎫34,+∞.答案:⎣⎢⎡⎭⎪⎫34,+∞ 8.设函数f(x)=⎩⎪⎨⎪⎧1,x>0,0,x =0,-1,x<0,g(x)=x 2f(x -1),则函数g(x)的递减区间是________.解析:由题意知g(x)=⎩⎪⎨⎪⎧x 2,x>1,0,x =1,-x 2,x<1.函数图象如图所示,其递减区间是[0,1).答案:[0,1)9.已知函数f(x)=x|2x -a|(a>0)在区间[2,4]上单调递减,则实数a 的值是________.解析:f(x)=x|2x -a|=⎩⎪⎨⎪⎧x (2x -a ),x>a2,-x (2x -a ),x ≤a2(a>0),作出函数图象(图略)可得该函数的递减区间是⎣⎢⎡⎦⎥⎤a 4,a 2,所以⎩⎪⎨⎪⎧a4≤2,a2≥4,解得a =8.答案:810.已知函数f(x)=⎩⎪⎨⎪⎧3(a -3)x +2,x ≤1,-4a -ln x ,x>1,对于任意的x 1≠x 2,都有(x 1-x 2)[f(x 2)-f(x 1)]>0成立,则实数a 的取值范围是________.解析:由(x 1-x 2)[f(x 2)-f(x 1)]>0,得(x 1-x 2)·[f(x 1)-f(x 2)]<0,所以函数f(x)为R 上的单调递减函数,则⎩⎪⎨⎪⎧a -3<0,3(a -3)+2≥-4a ,解得1≤a<3.答案:[1,3) 三、解答题11.已知函数f(x)=1a -1x(a>0,x>0).(1)求证:f(x)在(0,+∞)上是增函数;(2)若f(x)在⎣⎢⎡⎦⎥⎤12,2上的值域是⎣⎢⎡⎦⎥⎤12,2,求a 的值. 解:(1)证明:任取x 1>x 2>0,则f(x 1)-f(x 2)=1a -1x 1-1a +1x 2=x 1-x 2x 1x 2,因为x 1>x 2>0, 所以x 1-x 2>0,x 1x 2>0,所以f(x 1)-f(x 2)>0,即f(x 1)>f(x 2), 所以f(x)在(0,+∞)上是增函数.(2)由(1)可知,f(x)在⎣⎢⎡⎦⎥⎤12,2上为增函数, 所以f ⎝ ⎛⎭⎪⎫12=1a-2=12,f(2)=1a -12=2,解得a =25.12.已知函数f(x)=2x -ax的定义域为(0,1](a 为实数).(1)当a =1时,求函数y =f(x)的值域;(2)求函数y =f(x)在区间(0,1]上的最大值及最小值,并求出当函数f(x)取得最值时x 的值.解:(1)当a =1时,f(x)=2x -1x ,任取1≥x 1>x 2>0,则f(x 1)-f(x 2)=2(x 1-x 2)-⎝ ⎛⎭⎪⎫1x 1-1x 2 =(x 1-x 2)⎝ ⎛⎭⎪⎫2+1x 1x 2. 因为1≥x 1>x 2>0,所以x 1-x 2>0,x 1x 2>0.所以f(x 1)>f(x 2),所以f(x)在(0,1]上单调递增,无最小值,当x =1时取得最大值1,所以f(x)的值域为(-∞,1].(2)当a≥0时,y =f(x)在(0,1]上单调递增,无最小值,当x =1时取得最大值2-a ;当a<0时,f(x)=2x +-ax ,当-a2≥1,即a∈(-∞,-2]时,y =f(x)在(0,1]上单调递减,无最大值,当x =1时取得最小值2-a ;当-a2<1,即a∈(-2,0)时,y=f(x)在⎝⎛⎦⎥⎤0,-a2上单调递减,在⎣⎢⎡⎦⎥⎤-a2,1上单调递增,无最大值,当x=-a2时取得最小值2-2a.。
2019高考数学文一轮分层演练:第2章函数的概念与基本初等函数第3讲

11 C.f 2 <f 3 <f(2)
11 D. f(2)< f 2 <f 3
解析: 选 C.由 f(2- x)= f (x)可知函数
f(x)的图象关于
x= 1 对称 ,所以
f
1 2
=f
3 2
,f
1 3
=
f
5 3
,又当
x≥ 1 时 , f(x)= ln x 单调递增
, 所以
f
3 2
<f
5 3
<f(2) , 即 f
f(x)= asin x+ b 3 x+ 4,若
f(lg 3) = 3,则
f
1 lg 3
=________.
解析: 由
f(lg 3) =asin(lg 3) + b 3
lg 3+ 4= 3 得
asin(lg
3)
+
3 b
lg 3=- 1,而
f
1 lg 3
= f(-
3
3
lg 3) =- asin(lg 3) - b lg 3 + 4=- [ asin(lg 3) + b lg 3] + 4= 1+ 4=5.
g(0) , g(-1) 之间的大小关系是 ________.
解析: 在 f(x)- g(x)=
1x 2 中, 用- x 替换
x, 得 f(- x)- g(- x)= 2x, 由于
f(x), g(x)分别
是定义在 R 上的奇函数和偶函数 ,
所以 f(- x)=- f(x) ,g(- x)= g(x),
C.f ( 2)< f(3)< f( π)
D. f( 2)< f( π )f<(3)
高考数学文一轮分层演练:第2章函数的概念与基本初等函数章末总结(1)
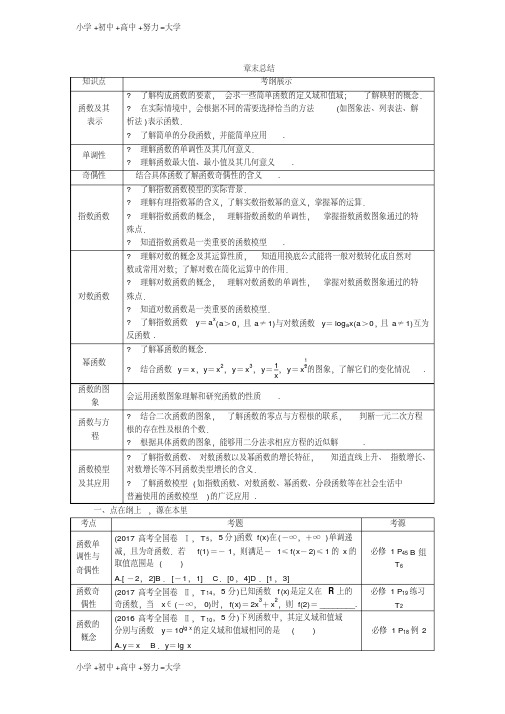
章末总结知识点考纲展示函数及其表示?了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.?在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.?了解简单的分段函数,并能简单应用.单调性?理解函数的单调性及其几何意义.?理解函数最大值、最小值及其几何意义.奇偶性结合具体函数了解函数奇偶性的含义.指数函数?了解指数函数模型的实际背景.?理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.?理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点.?知道指数函数是一类重要的函数模型.对数函数?理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.?理解对数函数的概念,理解对数函数的单调性,掌握对数函数图象通过的特殊点.?知道对数函数是一类重要的函数模型.?了解指数函数y=a x(a>0,且a≠1)与对数函数y=log a x(a>0,且a≠1)互为反函数.幂函数?了解幂函数的概念.?结合函数y=x,y=x2,y=x3,y=1x,y=x12的图象,了解它们的变化情况.函数的图象会运用函数图象理解和研究函数的性质.函数与方程?结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.?根据具体函数的图象,能够用二分法求相应方程的近似解.函数模型及其应用?了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.?了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.一、点在纲上,源在本里考点考题考源函数单调性与奇偶性(2017·高考全国卷Ⅰ,T5,5分)函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是()A.[-2,2]B.[-1,1] C.[0,4]D.[1,3]必修1 P45 B组T6函数奇偶性(2017·高考全国卷Ⅱ,T14,5分)已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=2x3+x2,则f(2)=________.必修1 P19练习T2函数的概念(2016·高考全国卷Ⅱ,T10,5分)下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是()A.y=x B.y=lg x必修1 P18例2C.y=2x D.y=1 x指数函数(2016·高考全国卷Ⅲ,T6,5分)已知a=243,b=425,c=2513,则()A.b<a<cB.a<b<cC.b<c<aD.c<a<b必修1 P57例7函数的奇偶性与函数图象(2016·高考全国卷Ⅰ,T7,5分)函数y=2x2-e|x|在[-2,2]的图象大致为()必修1 P36练习T1(1)、T2二、根置教材,考在变中一、选择题1.(必修 1 P58练习T2(1)改编)函数f(x)=32-x的定义域为A,值域为B,则A∩B=() A.(0,2] B.[1,2]C.[0,1] D.(1,2)解析:选B.因为A={x|x≤2},B={y|y≥1},所以A∩B=[1,2],故选B.2.(必修 1 P74A组T2(2)(3)(4)改编)设a=log87,b=log43,c=log73,则a,b,c的大小关系为()A.a>b>c B.a>c>bC.b>a>c D.b>c>a解析:选A.由a=log87得8a=7,即23a=7,2a=713,即a=log2713.由b=log43得4b=3,即22b=3,2b=312,即b=log2312.又()7136=49,()3126=27.所以713>312,则a>b.由于1<4<7,所以log43>log73,即b>c,所以a>b>c.3.(必修 1 P44A组T7改编)已知f(x)=a-x1+x,且f1b=-f(b)对于b≠-1时恒成立,则a的值为()A.0 B.1C.2 D.-1解析:选B.因为f(x)=a-x1+x,由f1b=-f(b),得a-1b1+1b=-a+b1+b,化简得(a-1)(b+1)=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3),[ - 3,0]上分别单调递增与单调递减 ,所以 xf(x)>0 的解集为 (- ∞, - 4)∪ (- 2,0)∪ (2,
4), 故选 D.
5. (必修 1 P36 练习 T1(2)改编 )函数 y= (x3- x)2|x|的图象大致是 (
必修 1 P57 例 7
函数的 奇偶性 与函数
图象
必修 1 P36 练习 T1(1) 、 T 2
二、根置教材 ,考在变中
一、选择题
1.(必修 1 P58 练习 T2(1)改编 ) 函数 f (x)= 3 2-x的定义域为 A,值域为 B,则 A∩B= (
)
A . (0, 2]
B .[1, 2]
C.[0, 1]
1
? 结合函数 y= x,y= x2, y= x3, y= 1, y= x2的图象,了解它们的变化情况 . x
函数的图 会运用函数图象理解和研究函数的性质 .
象
函数与方 程
? 结合二次函数的图象, 了解函数的零点与方程根的联系, 根的存在性及根的个数. ? 根据具体函数的图象,能够用二分法求相应方程的近似解
数或常用对数;了解对数在简化运算中的作用.
? 理解对数函数的概念, 理解对数函数的单调性, 掌握对数函数图象通过的特
对数函数 殊点.
? 知道对数函数是一类重要的函数模型. ? 了解指数函数 y= ax(a> 0,且 a≠ 1)与对数函数 反函数 .
y= logax(a>0,且 a≠ 1)互为
幂函数
? 了解幂函数的概念.
判断一元二次方程 .
函数模型
? 了解指数函数、 对数函数以及幂函数的增长特征, 知道直线上升、 指数增长、 对数增长等不同函数类型增长的含义.
及其应用 ? 了解函数模型 ( 如指数函数、对数函数、幂函数、分段函数等在社会生活中
普遍使用的函数模型 )的广泛应用 .
一、点在纲上 ,源在本里
考点
考题
考源
函数单 调性与 奇偶性
章末总结
知识点
考纲展示
? 了解构成函数的要素, 会求一些简单函数的定义域和值域; 了解映射的概念.
函数及其 表示
? 在实际情境中,会根据不同的需要选择恰当的方法 析法 )表示函数.
(如图象法、列表法、解
? 了解简单的分段函数,并能简单应用 .
单调性
? 理解函数的单调性及其几何意义. ? 理解函数最大值、最小值及其几何意义 .
B .a>c>b
C. b > a> c
D. b>c>a
1
1
解析: 选 A. 由 a= log87 得 8a =7,即 23a= 7,2a= 73,即 a= log 273.由 b= log 43 得 4b= 3,
( ) ( ) 1
1
即 22b= 3,2b=32, 即 b=log 232.又
1
73
6
= 49,
D. (1, 2)
解析: 选 B. 因为 A={ x|x≤ 2} , B={ y|y≥ 1} , 所以 A∩ B=[1 ,2], 故选 B.
2.(必修 1 P74A 组 T2(2)(3)(4) 改编 )设 a= log87,b=log 43,c=log 73,则 a,b,c 的大小关
系为 ( )
A . a>b>c
奇偶性
结合具体函数了解函数奇偶性的含义 .
? 了解指数函数模型的实际背景.
? 理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
指数函数 ? 理解指数函数的概念, 理解指数函数的单调性, 掌握指数函数图象通过的特
殊点.
? 知道指数函数是一类重要的函数模型 .
? 理解对数的概念及其运算性质, 知道用换底公式能将一般对数转化成自然对
(2017 ·高考全国卷 Ⅰ, T 5, 5 分 )函数 f(x)在 (-∞,+∞ )单调递 减,且为奇函数.若 f(1) =- 1,则满足- 1≤ f(x- 2)≤ 1 的 x 的 取值范围是 ( ) A.[ -2, 2]B . [-1, 1] C. [0, 4]D .[1, 3]
必修 1 P45 B 组 T6
16
11
32 = 27.所以 73>32, 则 a>b.由于 1<4<7 ,
所以 log43>log73, 即 b>c, 所以 a>b>c.
3.(修
1 P44A
组 T7 改编 )已知
f(x)= a- x,且 1+ x
f
1 b
=- f( b)对于
b≠- 1 时恒成立,
则a
的值为 ( )
A.0
B.1
C.2
)
必修 1 P19 练习 T2
必修 1 P18 例 2
指数函 数
A. y= x B .y= lg x C.y= 2x D. y= 1
x
4
2
1
(2016 ·高考全国卷 Ⅲ,T6,5 分) 已知 a=23,b= 45,c= 253,则 (
)
A. b<a<c B.a
<b<c C.b<c<a
D.c <a<b (2016 ·高考全国卷 Ⅰ, T 7, 5 分 )函数 y= 2x2- e|x|在 [- 2, 2] 的图 象大致为 ( )
D.- 1
1
解析: 选
B.因为
f (x)= a- x, 由 1+ x
f
1 b
a- b - a+ b
=- f(b), 得 1= 1+ b
1+ b
, 化简得 (a- 1)( b+ 1)=
0.要使上式对于 b≠- 1 恒成立 , 则 a-1= 0, 所以 a= 1. 4. (必修 1 P45B 组 T6 改编 )定义在 R 上的偶函数 f(x)满足: f (4)= f(- 2)= 0,在区间 (-
∞,- 3)与 [- 3,0]上分别单调递增和单调递减,则不等式 xf(x)>0 的解集为 ( )
A . (-∞,- 4)∪(4 ,+∞ )
B.( -4,- 2)∪ (2, 4)
C.( -∞,- 4)∪ (- 2, 0)
D. (-∞,- 4)∪(- 2, 0)∪ (2, 4) 解析: 选 D.因为 f (x)是偶函数 , 所以 f (4)= f(- 4)= f(2) =f(- 2)= 0,又 f( x)在 (-∞, -
函数奇 偶性
函数的 概念
(2017 ·高考全国卷 Ⅱ, T 14, 5 分 )已知函数 f (x)是定义在 R 上的 奇函数,当 x∈ (-∞, 0)时, f(x)= 2x3+ x2,则 f(2)= ________.
(2016 ·高考全国卷 Ⅱ, T 10, 5 分 )下列函数中,其定义域和值域
分别与函数 y= 10lg x 的定义域和值域相同的是 (
