数学分析第八章 不定积分
数学分析不定积分知识点总结

数学分析不定积分知识点总结不定积分是数学分析中的一个重要概念,它是微积分学的基础内容之一。
理解和掌握不定积分的相关知识对于进一步学习高等数学以及解决实际问题都具有重要意义。
下面我们将对不定积分的知识点进行详细总结。
一、不定积分的定义如果在区间\(I\)上,\(F'(x) = f(x)\),则称\(F(x)\)是\(f(x)\)在区间\(I\)上的一个原函数。
\(f(x)\)的原函数的全体称为\(f(x)\)在区间\(I\)上的不定积分,记为\(\int f(x)dx\)。
二、基本积分公式1、\(\int kdx = kx + C\)(\(k\)为常数)2、\(\int x^n dx =\frac{1}{n + 1}x^{n + 1} + C\)(\(n \neq -1\))3、\(\int \frac{1}{x}dx =\ln|x| + C\)4、\(\int e^x dx = e^x + C\)5、\(\int a^x dx =\frac{1}{\ln a}a^x + C\)(\(a >0\),\(a \neq 1\))6、\(\int \sin x dx =\cos x + C\)7、\(\int \cos x dx =\sin x + C\)8、\(\int \sec^2 x dx =\tan x + C\)9、\(\int \csc^2 x dx =\cot x + C\)10、\(\int \sec x \tan x dx =\sec x + C\)11、\(\int \csc x \cot x dx =\csc x + C\)这些基本积分公式是进行积分运算的基础,必须牢记。
三、不定积分的性质1、函数的和的不定积分等于各个函数不定积分的和,即\(\int f(x) + g(x)dx =\int f(x)dx +\int g(x)dx\)。
2、常数乘以函数的不定积分等于常数乘以该函数的不定积分,即\(\int kf(x)dx = k\int f(x)dx\)(\(k\)为常数)。
《数学分析》第八章_不定积分

则有换元公式
f(x)dx
f[(t)] (t)dt t(x)
其 中 (x)是 x(t)的 反 函 数 .
证 设 (t)为f[(t) ](t)的原函数,
1six n1si5n xC. 2 10
.
例13 求cscxdx.
解(一)
cscxdx
1 dx sinx
1 2sinxcosx
dx
22
1 tan2xcos2x2
d
2x
1 tanx
2
d
tanx 2
lntanxC lnx (c c x o )s C t c . 2
(使用了三角函数恒等变形)
.
说明 当被积函数是三角函数相乘时,拆开奇 次项去凑微分.
.
例12 求co3sxco2sxd.x
解 cA o cs B o 1 s [cA o B )s c (o A B s)(], 2
co 3xc so 2x s1(cxo cso 5x )s, 2
c3 o x cs2 o xs d 1 2 x (cx o cs 5 o x )d sx
§2 换元积分法和分部积分法
.
一、第一类换元法
问题 cos2xdxsi2n xC ,
解决方法 利用复合函数,设置中间变量.
过程 令 t2xdx 1dt, 2
cos2xdx
12costdt
1sint 2
C1sin2xC. 2
.
在一般情况下:
设 F (u)f(u),则 f(u )d u F (u )C .
.
例3
求
1 dx. x(12lnx)
解 x(112lnx)dx121lnxd(lnx)
1 212 1ln xd(12ln x)
《数学分析1》知识点总结:第八章-不定积分

第八章不定积分一、不定积分概念与基本积分公式1.原函数与不定积分①定义1:设函数f 与F 在区间I 上都有定义,若F’(x)=f(x),x ∈I ,则称F 为f 在区间I 上的一个原函数。
②定理8.1:若函数f 在区间I 上连续,则f 在I 上存在原函数F ,即F’(x)=f(x),x ∈I 。
·不连续的函数也可以有原函数③定理8.2:设F 是f 在区间I 上的一个原函数,则(i)F+C 也是f 在I 上的原函数,其中C 为任意常量函数;(ii)f 在I 上的任意两个原函数之间,只可能相差一个常数。
④定义2:函数f 在区间I 上的全体原函数称为f 在I 上的不定积分,记作∫f(x)dx 。
·[∫f(x)dx]’=[F(x)+C]’=f(x);·d ∫f(x)dx=d[F(x)+C];⑤不定积分的几何意义:积分曲线2.基本积分表①∫0dx=C ;②∫1dx=∫dx=x+C ;③)0,1(11>-≠++=⎰+x C x dx x αααα;④)0(||ln 1≠+=⎰x C x dx x ;⑤∫e x dx=e x +C ;⑥)0,1(ln >≠+=⎰a C aa dx a xx α;⑦)0(sin 1cos ≠+=⎰αC ax a axdx ;⑧)0(cos 1sin ≠+-=⎰αC ax a axdx ;⑨∫sec 2xdx=tanx+C ;⑩∫csc 2xd1=-cotx+C ;⑪∫secx ·tanxdx=secx+C ;⑫∫cscx ·cotxdx=-cscx+C ;⑬12arccos arcsin 1C x C x x dx+-=+=-⎰;⑭12cot arctan 1C x arc C x x dx +-=+=+⎰。
⑮定理8.3:若函数f 与g 在区间I 上都存在原函数,k 1,k 2为两个任意常数,则k 1f+k 2g 在I 上也存在原函数,且当k 1和k 2不同时为零时,有∫[k 1f(x)+k 2g(x)]dx=k 1∫f(x)dx +k 2∫g(x)dx二、换元积分法与分部积分法1.换元积分法①定理8.4(第一换元积分法/凑微分法):设函数f(x)在区间I 上有定义,φ(t)在区间J 上可导,且φ(J)⊆I 。
数学分析第八章 不定积分

或 df (x) f (x) C.
精品文档
3 不定积分的几何意义 函数f(x)的原函数的图形称 为f(x)的积分曲线。 函数f(x)的积分曲线有无限 多条。函数f(x)的不定积分 表示f(x)的一簇积分曲线, 而f(x)正是积分曲线的斜率。
结论: 若函数F为f 在区间I上的一个原函数,则 {F(x) c | c R}为f 在I上的原函数全体.
精品文档
(二) 不定积分
1. 定义2:函数f (x)在区间I上的全体原函数, 称 为f 在I上的不定积分,记作
f (x)dx
(3)
积分号 被积函数 积分变量
注1. 符号 f (x)dx 是一个整体记号.
1 (102x 102x ) 2x c 2 ln 10
精品文档
8) sec2 xdx tanx C
8 (tanx)' sec2 x
9) csc2 xdx cotx C 9 (cotx)' csc2 x
10) dx arcsin x C 10 (arcsin x)' 1
1 x2
1 x2
11)
dx 1 x2
arctanx C
11
(f g) = f g + f g ,
(f [ ]) = f [ ] 这些计算方法加上基本初等函数的导数公式, 我们可以解决初等函数的求导问题,即是,若 f 为 初等函数, f 的表达式能求出.
精品文档
我们现在来研究第五章求导问题的逆问题。
问题:在已知 f 的表达式时,f 的表 达式是什么形式呢?
1 (arctanx)' 1 x2
精品文档
数学分析第八章不定积分

数 , 则 k1 f + k2 g 在 I 上也存在原函数 , 且
∫ ∫ ∫ [ k1 f ( x ) + k2 g( x) ] d x = k1 f ( x) d x + k2 g( x ) d x .
( 5)
证 这是因为
∫ ∫ ∫ ∫ k1 f ( x )d x + k 2 g( x) d x ′= k1 f ( x )d x ′+ k 2 g( x) d x ′
知函数 .提出这个逆问题 , 首先是因为它出现在许多实际问题之中
.例如 : 已知速
度求路程 ; 已知加速度求速度 ; 已知曲线 上每一 点处 的切线 斜率 ( 或斜率 所满 足
的某一规律 ) , 求曲线方程等等 .本章与 其后两 章 ( 定 积分与 定积 分的 应用 ) 构 成
一元函数积分学 .一 原函数与不定积分源自(2 , 5) .3 . 验证
y=
x
2
sgn
x
是
| x| 在
∫ v( t) = ad t = at + C .
若已知 v( t0 ) = v0 , 代入上式后确定积分常数 C = v0 - at0 , 于是就有
v( t ) = a( t - t0 ) + v 0 . 又因 s′( t) = v( t ) , 所以又有
∫ s( t) = [ a( t - t 0 ) + v 0] d t
2 (-
1 cos 2x
都是 )′=
sin 2 x 在 ( - ∞ , + ∞ ) 上的原函数 ( - 1 cos 2 x + 1)′= sin 2 x .
, 因为
2
2
如果这些简单的例子都可从基本求导公式反推而得的话
高数不定积分

1 2
sin2x
+
C.
利用基本积分表与积分的性质,所能计算的不 定积分是非常有限的;我们可以把复合函数的微分 法反过来用于求不定积分,利用中间变量的代换, 得到复合函数的积分法,称为换元积分法。
x2 1 - x2 dx ? 令 x sint
x2 1 - x2dx (sint)2 1 - sin2 t costdt
2
2
例1140.
1
dx 4
sin2 x cos2 x
1 sin2
x
dx
-4ctg
x+C。
22
)
1 x
dx ln|x|+(C1,1)
1 dx arctgx+C。 1+ x2
例1151.
1 + x + x2 dx x(1 + x 2 )
x + (1 + x 2 ) dx x(1 + x 2 )
函数f(x)的原函数的图 形称为f(x)的积分曲线。
2xdx x 2 + C
y
函数f(x)的积分曲线也 有无限多条。函数f(x)的不 定积分表示f(x)的一簇积分 曲线,而f(x)正是积分曲线 的斜率。
C1 -1 O 1
y=x2+C1 y=x2
y=x2+C2 y=x2+xC3
C2
C3
例4.求过点(1, 3),且其切线斜率为2x的曲线方程。 解:设所求的曲线方程为 yf(x),则 y f (x) 2x, 即f(x)是2x 的一个原函数。
f
(x)dx
f
(x)
4) f ' (x)dx f (x) + C
《数学分析》第八章 不定积分
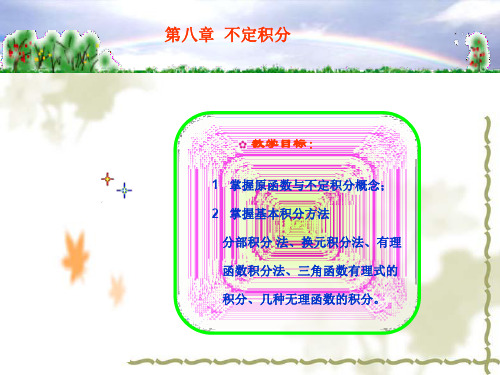
⑶ 0时, f (x)dx f (x)dx. ⑷ ( f (x) g(x))dx f (x)dx g(x)dx.
由⑶、⑷可见, 不定积分是线性运算, 即对 , R , 有
(f (x) g( x))dx f (x)dx g( x)dx.
( 当 0 时,上式右端应理解为任意常数. )
数的不定积分:
x dx ( 1) a x dx a x C
ln a
1 x
dx
ln
x
C
sin xdx cos x C
sec 2 xdx tgx C
csc2 dx ctgx C
sec x tgxdx sec x C
csc x ctgxdx csc x CBiblioteka dx arcsin x C
定义(原函数) 如果在区间 I 上 F ( x) f ( x) ,则称 F( x) 为
f (x) 在区间 I 上的原函数。
例如例 1 中的 A cos t C 是 A sin t 的原函数;
m
m
x 1 C 是 x ( 1) 的原函数,等等 1
因为常数导数为零,所以如果 f (x) 的原函数 F( x) 存在,则对任
上的不定积分。记作 f (x)dx 。 其中 为积分号, f (x) 为积分
函数, x 为积分变量。 不定积分的几何意义
F(x)+C F(x)
一个函数的原函数尽管有无限多个, 但它们的几何图形是一模 一样的, 最多是在坐标系中的高低位置不一样, 相差一个上下平移 关系,
二 基本积分公式
怎样求不定积分呢?我们先按照不定积分的定义给出一些常见函
⑵
22x e3x1dx.
例 11 例 12
《数学分析》第8章 不定积分ppt课件

证 (i) 由 (F( x) C) F ( x) f ( x), 知 F( x) C 也是 f ( x) 在 I 上的原函数.
(ii) 设 F(x) 和 G(x) 是 f (x) 在 I 上的任意两个原 函数, 则
(F ( x) G( x)) F ( x) G( x) f ( x) f ( x) 0.
又如, 已知曲线在每一点处的切线斜率 k( x), 求 f ( x), 使 y f ( x) 的图象正是该曲线, 即使得
f ( x) k( x).
定义1 设函数 f 与 F 在区间 I 上都有定义,若 F ( x) f ( x), x I ,
则称 f 为 F 在区间 I 上的一个原函数.
例1 (i) 路程函数 s(t) 是速度函数 v(t) 的一个原函
三、不定积分的几何意义
若F (x)是 f (x) 的一个原函数, 则称 y = F (x) 的图
像是 f (x) 的一条积分曲线.
所有的积分曲线都是
y
y F(x)C
由其中一条积分曲线 沿纵轴方向平移而得 到的.
y F(x) ( x0 , y0 )
O
x
满足条件 F ( x0 ) y0 的原函数正是在积分曲线中 通过点( x0 , y0 )的那一条积分曲线. 例如, 质点以匀速 v0 运动时, 其路程函数
§1 不定积分概念与 基本积分公式
不定积分是求导运算的逆运算.
一、原函数 二、不定积分 三、不定积分的几何意义 四、基本积分表
一、原函数
微分运算的逆运算是由已知函数 f (x), 求函数F(x), 使
F ( x) f ( x). 例如 已知速度函数 v(t ), 求路程函数 s(t ). 即求
s(t), 使 s(t) v(t).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x4 1
x
1
2
dx
x
4
1
1 x2
2
dx
(x2
1)( x2 1 x2
1)
2
dx
(
x2
1
1
2 x
2
)dx
1 x3 x 2arctanx C 3
例3. 求 (10x 10-x )2 dx
解: (10x 10-x )2 dx (102x 10-2x - 2)dx [(102 )x (10-2)x - 2]dx
2
2
sin 2x在(,)上一个原函数
问题: f在什么条件下存在原函数?存在时其个数? 若f存在原函数,如何求?
2 原函数存在定理
定理8.1若函数f 在区间I上连续,则f 在I上 存在原函数F,即 F '(x) f (x), x I.
•注1:初等函数在其定义域存在原函数. •注2:连续是原函数存在的充分而非必要条件
8) sec2 xdx tanx C
8 (tanx)' sec2 x
9) csc2 xdx cotx C 9 (cotx)' csc2 x
10)
dx arcsin x C 1 x2
10 (arcsin x)'
1 1 x2
11)
dx 1 x2
arctanx C
11
1 (arctanx)' 1 x2
f (x)dx F(x) C
其中C为任意常数
y y = F(x)+C1
y = F(x)+C2
y = F(x)+C3 y = F(x)+C4
0
x0
x
2. 不定积分的性质:
(1) ( f (x)dx)' f (x),先积后导正好还原 或d[ f (x)dx] f (x)dx,
(2) f '(x)dx f (x) C,先导后积需加上一个任常数
或 df (x) f (x) C.
3 不定积分的几何意义
函数f(x)的原函数的图 形称为f(x)的积分曲线。
函数f(x)的积分曲线有 无限多条。函数f(x)的不定 积分表示f(x)的一簇积分曲 线,而f(x)正是积分曲线的 斜率。
2xdx x2 C
y
y=x2+C1 y=x2
C1 -1 O 1
2 线性运算法则
定理8.3 若函数f与g在区间I上存在原函数, k1, k2为 两个任意常数,则k1 f k2g在I上也存在原函数,且
[k1 f (x) k2g(x)]dx k1 f (x)dx k2 g(x)dx (5)
注 线性运算法则的一般形式为
n
n
ki fi (x)dx ki fi (x)dx (6)
3 原函数之间的关系 定理8.2 如果F是 f 在I上的一个原函数 ,则 (1) FC 也是 f 在I上的原函数,其中 C 是任意常数。 (2) f 在I上的任意两个原函数之间,只可能相差一个常数
结论: 若函数F为f 在区间I上的一个原函数,则 {F(x) c | c R}为f 在I上的原函数全体.
y=x2+C2 y=x2+xC3
C2
C3
二. 基本积分公式
1 基本积分表 积分公式
导数公式
1) kdx kx C (k为常数)
1 (kx c)' k
2)
x
dx
1
1
x
1
C
( 1)
2 (x1)' ( 1)x
1
3) xdx ln | x | C
3 (ln x)' 1 x 0 x
(ln(x))' 1 x 0 x
dt
mm
这归结为已知dv 求v, dt
由求导运算
( A cost c)' Asist c m
c由初始时刻是静止的 (v(0) 0)确定
•一 原函数与不定积分 • (一)原函数概念
1 定义1 设函数 f与F在区间 I 上有定义,若
F (x)f(x), x I
1 (102x 102x ) 2x c 2 ln 10
例4. 求
c os2
1 x sin2
x
dx
解:
1 dx cos2 x sin2 x
则称函数 F为函数 f 在区间 I 上的一个原函数。
如: (1 x3)' x2, x (,) 3
F(x) 1 x3是x2在(,)上一个原函数 3
再如 : x (,)时
( 1 cos 2x)' ( 1 cos 2x 1)' (sin 2 x)' sin 2x,
2
2
F (x) 1 cos 2x, 1 cos 2x 1,sin2 x是
数学分析第八章 不定积分
第八章 不定积分
§1不定积分的概念与基本积分公式
在第五章我们研究了已知 f,如何求 f 的导数
f 的表达式,得到了一些计算法则,例如:
(f + g) = f + g ,
(f g) = f g + f g ,
(f []) = f []
这些计算方法加上基本初等函数的导数公式, 我们可以解决初等函数的求导问题,即是,若 f
为初等函数, f 的表达式能求出.
我们现在来研究第五章求导问题的逆问题。
问题:在已知 f 的表达式时,f 的表达式是
什么形式呢?
例1 一静止的物体,其质量为m,在力F Asin t
的作用下沿直线运动, 求物体的运动速度。
解:由牛顿第二定理a F Asin t , mm
即
dv a F Asin t
4) exdx ex C
5)
a
xdx
1 ln a
a
x
C
a 0, a 1
4 (ex )' ex
5 (ax )' ln a ax a 0, a 1
6) cos xdx sin x C
6 (sin x)' cos x
7) sin xdx cos x C 7 (cos x)' sin x
(二) 不定积分
1. 定义2:函数f (x)在区间I上的全体原函数, 称 为f 在I上的不定积分,记作
f (x)dx
(3)
积分号 被积函数 积分变量
注1. 符号 f (x)dx 是一个整体记号.
注2. 不定积分与原函数是总体与个体的关系。
设F(x)是f (x)在区间I上的一个原函数,习惯写成
i 1
i 1
例1. 设p(x) a0xn a1xn1 an1x an ,求 p(x)dx
解: p(x)dx
a0 xndx a1 xn1dx an1 xdx an dx
a0 n 1
x n 1
a1 n
xn
an1 2
x2
an x C
例2. 求
x4 1 1 x2 dx
解:
